Abstract
Data augmentation is needed to use Deep Learning methods for the typically small time series datasets. There is limited literature on the evaluation of the performance of the use of Generative Adversarial Networks for time series data augmentation. We describe and discuss the results of a pilot study that extends a recent evaluation study of two families of data augmentation methods for time series (i.e., transformation-based methods and pattern-mixing methods), and provide recommendations for future work in this important area of research.
1. Introduction
The benefits of Artificial Intelligence (AI) algorithms can be fully leveraged only when the required amount of data needed for the training of these models is available. This creates a practical problem as data may be costly to obtain, difficult to collect, scarce, they may raise privacy issues, or take too much time to be gathered while AI-based decisions are needed in a timely manner. This problem has been exacerbated in recent decades by the fact that Deep Learning has been powered by the increasing availability of graphic cards boarding a GPU and the democratization of GPU-powered platforms. This technology improvement has paved the way for the development of more complex models that require larger and larger datasets to overcome the risk of overfitting.
Data augmentation methods artificially create synthetic data to enrich the real ones obtained via observations or experiments. Already used for several years in the field of computer vision, its use is mainly based on the simple idea of generating multiple variations (based on rotation, scaling, contrast, etc.) of the images that are used to train Deep Learning algorithms, and thus improving their robustness and performance. Data augmentation is providing a practical solution to address the critical issues listed above by allowing the training of the models for those situations. As a result, the need for reliable data augmentation methods is particularly strong today, as they would enable the use of high-dimensional models while mitigating the risk of overfitting. The scope of applications for data augmentation ranges from clinical trials and scientific experiments to industrial testing and financial risk management. With today’s computational power, data augmentation is becoming an essential technique to train Machine Learning algorithms more efficiently.
As expected, it is not possible to identify a unique data augmentation method that is suitable and optimal under all practical circumstances. The choice of the data augmentation method to be used in a specific situation is expected to be a function of at least four main features:
- 1
- Type of data: Data may be tabular, images, time series, chemical structures, etc. The different types of data may require different data augmentation methods specifically designed to take into account the particular structure and intricacies of that type of data.
- 2
- Downstream task: The downstream processing of the augmented data affects the choice of the data augmentation method. For example, the type of neural network architecture will influence the choice of the data augmentation method, and also if the task is a classification task or not.
- 3
- Performance evaluation metrics: In order to select an optimal data augmentation method, it is necessary to be able to compare its performance against competing methods by using formally defined performance evaluation metrics. There is a need for more research studies to address in depth the related topic of comparison of data augmentation methods.
- 4
- Computation time, latency and determinism constraints: These constraints, regarding the nature and execution of the method, will affect the choice of the data augmentation method. Testing is required to identify the optimal data augmentation method for a given situation. As above, more research is needed regarding these important operational constraints.
As a side note, we need to mention that the term data augmentation has been previously introduced in the area of Bayesian Statistics in 1987 by Tanner and Wong [1], where it refers to the use of auxiliary variables to compute posterior distributions. Although the use of the same term may be confusing, its exact meaning should be clear from the context, either Deep Learning or Bayesian Statistics.
The literature on data augmentation for image datasets is very extensive, whereas the case of multivariate time series data remains much less covered to date. It is the application of data augmentation methods to time series data that is the focus of this brief report. We describe the results of a pilot study that has been performed as an extension of the evaluation study described in a recent comprehensive survey on the use of data augmentation methods for Deep Learning for time series [2]. For more information regarding image data augmentation for deep learning and time series data augmentation for deep learning the readers are referred to the recent surveys from [3,4], respectively.
In the field of time series recognition, the datasets are often very small. According to [2], data augmentation methods for time series and their application to time series classification with neural networks may be grouped into four different families:
- 1
- Transformation-based methods
- 2
- Pattern-mixing methods
- 3
- Generative models
- 4
- Decomposition methods
The comprehensive review [2] includes a thorough evaluation study of the most-used data augmentation methods for time series data, although the formal evaluation is focused on the first two families: transformation-based methods and pattern-mixing methods. To identify an optimal data augmentation method, the approach used by [2] is to train classification algorithms over both the original and the augmented dataset, and then evaluate their performance over a test dataset made out of non-augmented data. Although the evaluation study from [2] involves the comparison of 12 data augmentation methods for benchmarking purposes, one important recently developed approach is missing, even though the authors acknowledge its growing importance over the last few years: Generative Adversarial Networks (GANs).
Introduced in 2014 by [5], GANs are neural networks jointly trained in order to learn a non-linear mapping which transforms normally-distributed variables into samples which mimic the real training data and inherit their statistical properties. The goal of our pilot study was to expand the evaluation study from [2] by including GANs for time series data augmentation, along with testing their generative performance for a classification task relying on the synthetic dataset. It is important to note that the use of GANs to generate high-dimensional multivariate time series remains an active research area with many potential applications.
2. Materials and Methods
2.1. Datasets
The goal of the evaluation study from [2] was to assess the overall performance of each data augmentation method included in the study. The study considered a wide range of time series datasets, specifically those from the public database 2018 UCR Time Series Classification Archive, available at https://www.cs.ucr.edu/~eamonn/time_series_data_2018/, accessed on 9 June 2022. As stated above, in this pilot study we explored the use of GANs for data augmentation for time series. It is important to note that not all the datasets from the public repository are suited for GANs training because of the requirements on the minimum sample size needed to prevent overfitting. The need for external training is clearly stated in Section 6.3 of [2] as the reason for not including in the evaluation study data augmentation methods based on generative models, such as those based on GANs. On top of that, we did not consider time series obtained via image flattening, as this process naturally breaks the geometrical structure of the underlying image. It is important to note that GANs have been extensively studied and used for images, and high-performing models are available for this specific type of data [6,7,8,9]. Based on these considerations, we have chosen three datasets which belong to three different data types: Sensor, ECG and Spectro. These data types originate from domains which are most in need for either data augmentation or data anonymization [10,11,12,13], the latter being an important benefit of synthetic data generation. The main features of the chosen datasets are summarized in Table 1.

Table 1.
Selected datasets from the 2018 UCR Time Series Classification Archive.
2.2. Architecture
For the pilot study, we have decided to use the Recurrent Conditional GANs architecture [10]. The reasons for this selection are that it is one of the first GANs to generate continuous sequential data, and that its simple structure ensures fast training, while not being specifically tailored to a particular type of data and also allowing conditional generation. We refer the readers to [14] for a thorough review of available generative algorithms.
All trainings have been performed over 10,000 epochs. We define an epoch as being one generator’s weights update. As the discriminator may be updated more than once per generator update, this definition is important. Building upon the model proposed in [10], we implemented an architecture consisting of two discriminators, one which is MultiLayer Perceptron (MLP)-based and the other which is Long Short Time Memory (LSTM)-based. The importance of their respective feedback within the generator loss is calibrated via a dynamic parameter which evolves over the epochs. At the beginning of the training, the MLP-based discriminator triggers a much stronger gradient signal for the generator weights, whereas the LSTM-based discriminator plays a role mostly towards the end of the training.
The hybrid approach used in the pilot study is motivated by the results regarding the average classification performance of the models reported in Tables 1–3 from [2], where the models were trained on the non-augmented datasets. It is clear from those results that the MLP-based models outperform the LSTM-based models. On the other hand, LSTM-based models should catch the time series’ patterns missed by the non-recurrent models, such as the time-to-time conditional probabilities and long-short memory patterns. The best generative performance was indeed obtained when taking advantage of both types of discriminators in the order specified above. The trained generators for the three datasets listed in Table 1 are publicly available at https://storage.googleapis.com/ucrgen/generators.zip, accessed on 29 July 2022.
2.3. Experiments
The generative performance of the proposed architecture has been evaluated through downstream classification tasks [2]. Consistent with the specific datasets selected for the pilot study, we have used two classifiers: an MLP classifier and an LSTM classifier. We have selected these two models from those used in [2] as they are the most appropriate for the chosen datasets. For example, since we did not include image datasets, we did not use VGG and ResNet architectures for our experiments. Regarding the benchmarks, in Table 2 we report the performance of the data augmentation methods that have obtained the highest overall accuracy for the two retained classifiers according to Tables 1–3 from [2] (In [2], the authors explore the performance of 12 data augmentation algorithms via their average accuracy over the 128 datasets available in the 2018 UCR Time Series 97 Classification Archive https://www.cs.ucr.edu/~eamonn/time_series_data_2018/ (accessed on 9 June 2022) as reported by six classification networks.). The accuracy summary statistics (means and standard deviations) have been calculated over 10 differently-seeded trainings of the two classifiers.

Table 2.
Classification accuracy on the test sets derived from each selected dataset. Results are given in terms of means and standard deviations over 10 runs of the classification ( < 0.01). The best results are presented in bold.
3. Results
Table 2 summarizes the findings of our pilot study. It is important to clarify that our evaluation of the GANs performance for time series data augmentation is conservative: the benchmarks have been chosen as the best-performing data augmentation methods for each of the selected classification algorithms, regardless of the dataset type. It is clear that the performance of the GAN-based data augmentation methods varies considerably across the six combinations of a dataset (three options) and a classifier (two options), from the best performance for the (D3, LSTM) combination to the worst performance for the (D2, LSTM) combination.
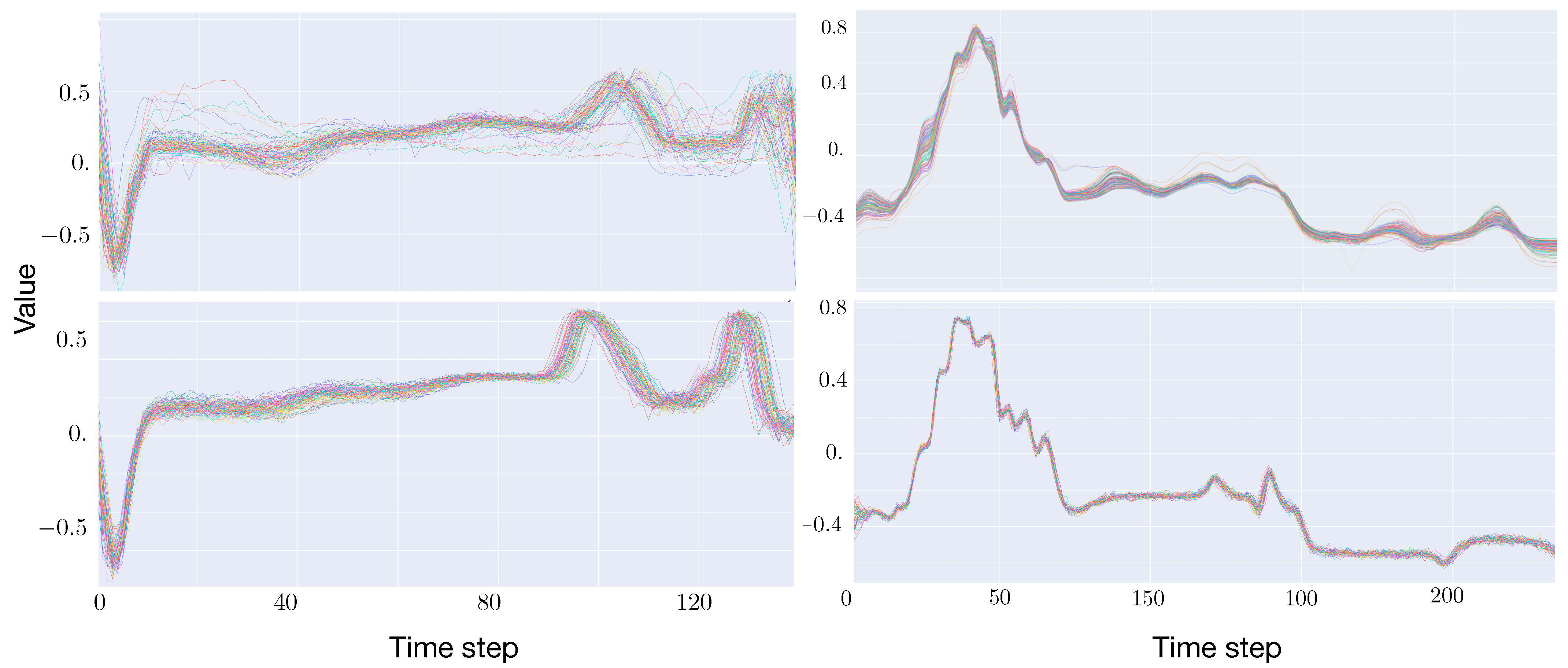
We conjecture that a possible reason for the observed fluctuating performance may be due to our architecture falling in the well-known mode-collapse, where the discriminator is being fooled via the repetitive generation of the same, still well-shaped sample [15]. This behavior is clearly evident in Figure 1 where we compare a batch of synthetic time series (top) against the same number of real samples (bottom) from the dataset D2 (left) and dataset D3 (right). It may be seen that, while the shape of the synthetic examples is qualitatively learned by the generator, the intra-variability of the batch of synthetic data is much smaller that that of the real data, possibly because the generator is basically reproducing one very similar example over and over again.
Figure 1.
Batch of time series from dataset D2 (left) and dataset D3 (right) using the GAN-based data augmentation method. (Top) Real data. (Bottom) Synthetic data.
4. Discussion
Based on the results of the pilot study, we conclude that the GAN architecture we have selected does not consistently improve the accuracy of the final classification task when compared against the chosen benchmarks.
We start the discussion with some general comments regarding the performance metrics used in our pilot study, metrics inherited from the evaluation study reported in [2]. Data augmentation methods are supposed to preserve the statistical properties of the original data by learning to draw samples from the joint distribution of the training dataset. Downstream classification tasks are not capable of thoroughly evaluating this capacity. For example, by simply reproducing the same time series per class, we can achieve high accuracy when performing a classification task, whereas the variability of the data will not be preserved. The use of more sophisticated statistical metrics is needed to quantify the degree to which the joint distribution of the original data is reproduced, even though currently there is no agreement regarding a unique way to fully characterize the statistical distribution of time series. For example, we could compare time series datasets in terms of conditional statistical distributions. Well-performing methods in Table 2, such as jittering, may report poor performance in reproducing these specific summary statistics. Adding noise to the original data may help a classifier to easily assign the correct class label, but the variability of the original data will clearly not be preserved.
By cross-comparing Table 1 and Table 2, we conclude that the generative performance may decrease when considering deeper and deeper time series in the training set, implying that Conditional Recurrent GANs [10] still miss long term memory effects, which may be captured by more advanced architectures (e.g., TimeGANs [16]). In addition, the modecollapse issue, conjectured to be a possible reason for the observed performance of the GAN-based data augmentation methods, may be addressed by implementing a Wasserstein loss function during optimization. Wasserstein GANs have indeed been shown to make training less prone to this problem [15]. Both these possible solutions to the problems identified during this pilot study will be the subject of future research.
5. Conclusions
In the pilot study, we have generated artificial data starting from a batch of real data. Upon data augmentation, a classifier was trained over a mixed synthetic-real dataset, and evaluated on a real test dataset. Following [10], a more rigorous approach would have required a two step evaluation: training on synthetic, testing on real, along with training on real, testing on synthetic. Low variability within the synthetic dataset (e.g., due to mode-collapse and/or other reasons) would lead to a poor performance when testing on real data. In the pilot study, such generative defect is hidden by the real highly variable data. Based on these considerations, it is also very important to formally evaluate the diversity of the synthetic time series generation [17].
For the datasets we have included in the pilot study, the neural networks deployed for the classification task show overall poor performance, in some cases the accuracy being close to the pure randomness level. It was proved in [18] that simpler approaches to such task may outperform neural networks-based approaches. Because a classifier reporting accuracy is not informative with regards to the underlying data augmentation efficiency, it will be useful to complement the above evaluation with more accurate algorithms, such as Dynamic Time Wrapping and its variations [19,20].
Our pilot study on the use of GAN-based data augmentation for time series had provided important preliminary information that could be used to design future evaluation studies. Based on these preliminary results, future studies on this topic should use more advanced GAN architectures, with Wasserstein loss function, involve a two-step evaluation process, and provide a formal assessment of the diversity of the synthetic time series generation.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ai3040047/s1.
Author Contributions
Conceptualization, N.M., M.R., D.G. and G.L.; methodology, N.M., M.R., D.G. and G.L.; software, N.M. and M.R.; validation, N.M. and M.R.; formal analysis, N.M., M.R., D.G. and G.L.; data curation, N.M. and M.R.; writing—original draft preparation, N.M., M.R. and D.G.; writing—review and editing, N.M., M.R., D.G. and G.L.; visualization, N.M. and M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research has received no external funding.
Data Availability Statement
The data presented in this study are available at https://www.cs.ucr.edu/~eamonn/time_series_data_2018/, accessed on 9 June 2022. The trained generators for the three datasets are publicly available at https://storage.googleapis.com/ucrgen/generators.zip, accessed on 29 July 2022. Related code is provided in the Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Intelligence |
| GAN | Generative Adversarial Network |
| MLP | MultiLayer Perceptron |
| LSTM | Long Short Time Memory |
References
- Tanner, M.A.; Wong, W.H. The Calculation of Posterior Distributions by Data Augmentation. J. Am. Stat. Assoc. 1987, 82, 528–540. [Google Scholar] [CrossRef]
- Iwana, B.K.; Uchida, S. An empirical survey of data augmentation for time series classification with neural networks. PLoS ONE 2021, 16, e0254841. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Xiao, W.; Zhang, M.; Guo, S.; Zhao, J.; Shen, F. Image Data Augmentation for Deep Learning: A Survey. arXiv 2022, arXiv:2204.08610v1. [Google Scholar]
- Wen, Q.; Sun, L.; Yang, F.; Song, X.; Gao, J.; Wang, X.; Xu, H. Time Series Data Augmentation for Deep Learning: A Survey. In Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence, IJCAI-21, Montreal, QC, Canada, 19–27 August 2021; Zhou, Z.H., Ed.; pp. 4653–4660. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. In Proceedings of the International Conference on Neural Information Processing Systems (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Zhu, J.Y.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks. arXiv 2017, arXiv:1703.10593. [Google Scholar]
- Choi, Y.; Choi, M.; Kim, M.; Ha, J.W.; Kim, S.; Choo, J. StarGAN: Unified Generative Adversarial Networks for Multi-Domain Image-to-Image Translation. arXiv 2017, arXiv:1711.09020. [Google Scholar]
- Karras, T.; Laine, S.; Aila, T. A Style-Based Generator Architecture for Generative Adversarial Networks. arXiv 2018, arXiv:1812.04948. [Google Scholar]
- Brock, A.; Donahue, J.; Simonyan, K. Large Scale GAN Training for High Fidelity Natural Image Synthesis. arXiv 2018, arXiv:1809.11096. [Google Scholar]
- Esteban, C.; Hyland, S.L.; Rätsch, G. Real-valued (Medical) Time Series Generation with Recurrent Conditional GANs. arXiv 2017, arXiv:1706.02633. [Google Scholar]
- Ghorbani, A.; Natarajan, V.; Coz, D.; Liu, Y. DermGAN: Synthetic Generation of Clinical Skin Images with Pathology. arXiv 2019, arXiv:1911.08716. [Google Scholar]
- Frid-Adar, M.; Diamant, I.; Klang, E.; Amitai, M.; Goldberger, J.; Greenspan, H. GAN-based Synthetic Medical Image Augmentation for increased CNN Performance in Liver Lesion Classification. arXiv 2018, arXiv:1803.01229. [Google Scholar] [CrossRef]
- Gupta, A.; Venkatesh, S.; Chopra, S.; Ledig, C. Generative Image Translation for Data Augmentation of Bone Lesion Pathology. arXiv 2019, arXiv:1902.02248. [Google Scholar]
- Brophy, E.; Wang, Z.; She, Q.; Ward, T. Generative adversarial networks in time series: A survey and taxonomy. arXiv 2021, arXiv:2107.11098. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Yoon, J.; Jarrett, D.; van der Schaar, M. Time-series Generative Adversarial Networks. In Advances in Neural Information Processing Systems; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2019; Volume 32. [Google Scholar]
- Bahrpeyma, F.; Roantree, M.; Cappellari, P.; Scriney, M.; McCarren, A. A Methodology for Validating Diversity in Synthetic Time Series Generation. MethodsX 2021, 8, 101459. [Google Scholar] [CrossRef] [PubMed]
- Xi, X.; Keogh, E.; Shelton, C.; Wei, L.; Ratanamahatana, C. Fast Time Series Classification Using Numerosity Reduction. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; Volume 2006, pp. 1033–1040. [Google Scholar] [CrossRef]
- Pkalska, E.; Duin, R.P.W.; Paclík, P. Prototype Selection for Dissimilarity-Based Classifiers. Pattern Recogn. 2006, 39, 189–208. [Google Scholar] [CrossRef]
- Wilson, D.; Martinez, T. Instance Pruning Techniques. In Proceedings of the Fourteenth International Conference (ICML’97), Nashville, TN, USA, 8–12 July 1997; pp. 403–411. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).