Contextual and Possibilistic Reasoning for Coalition Formation
Abstract
1. Introduction
- How to identify all possible coalitions that agents can form to fulfil their goals?
- How to evaluate the coalitions given a set of requirements?
- How to compute and evaluate coalitions taking also into account the uncertainty in the agents’ actions?
2. Background
2.1. Dependence Networks and Coalition Formation
2.2. Multi-Context Systems
2.2.1. Formalization
- KB is the set of well-formed knowledge bases of L. Each element of KB is a set of formulae.
- BS is the set of possible belief sets, where the elements of a belief set are a set of formulae.
- ACC: KB→ is a function describing the semantics of the logic by assigning to each knowledge base a set of acceptable belief sets.
2.2.2. Computational Complexity
2.3. Possibilistic Reasoning in MCS
2.3.1. Possibilistic Logic Programs
2.3.2. Possibilistic MCS
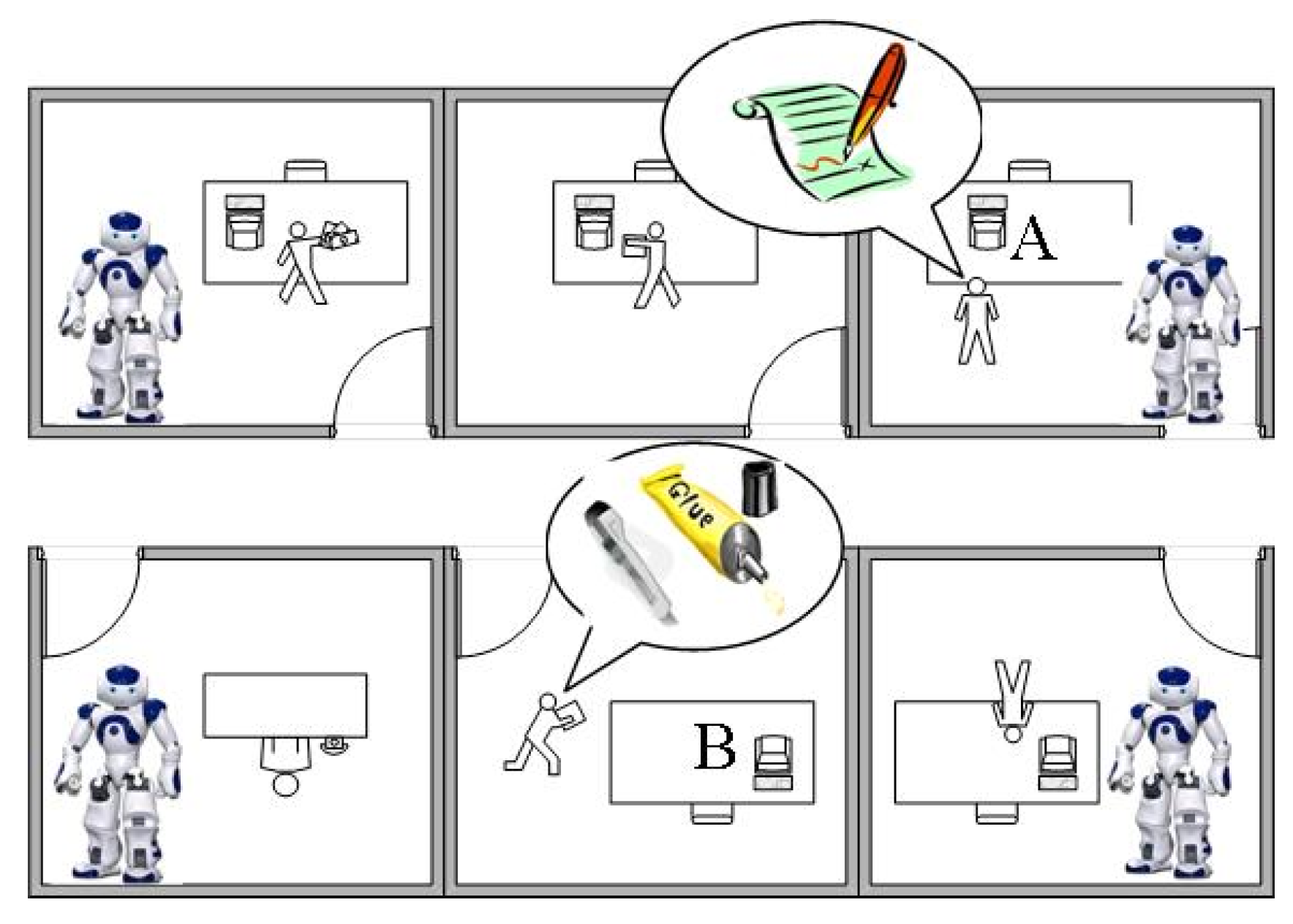
3. Main Example
4. Computing and Evaluating Coalitions in the Perfect World
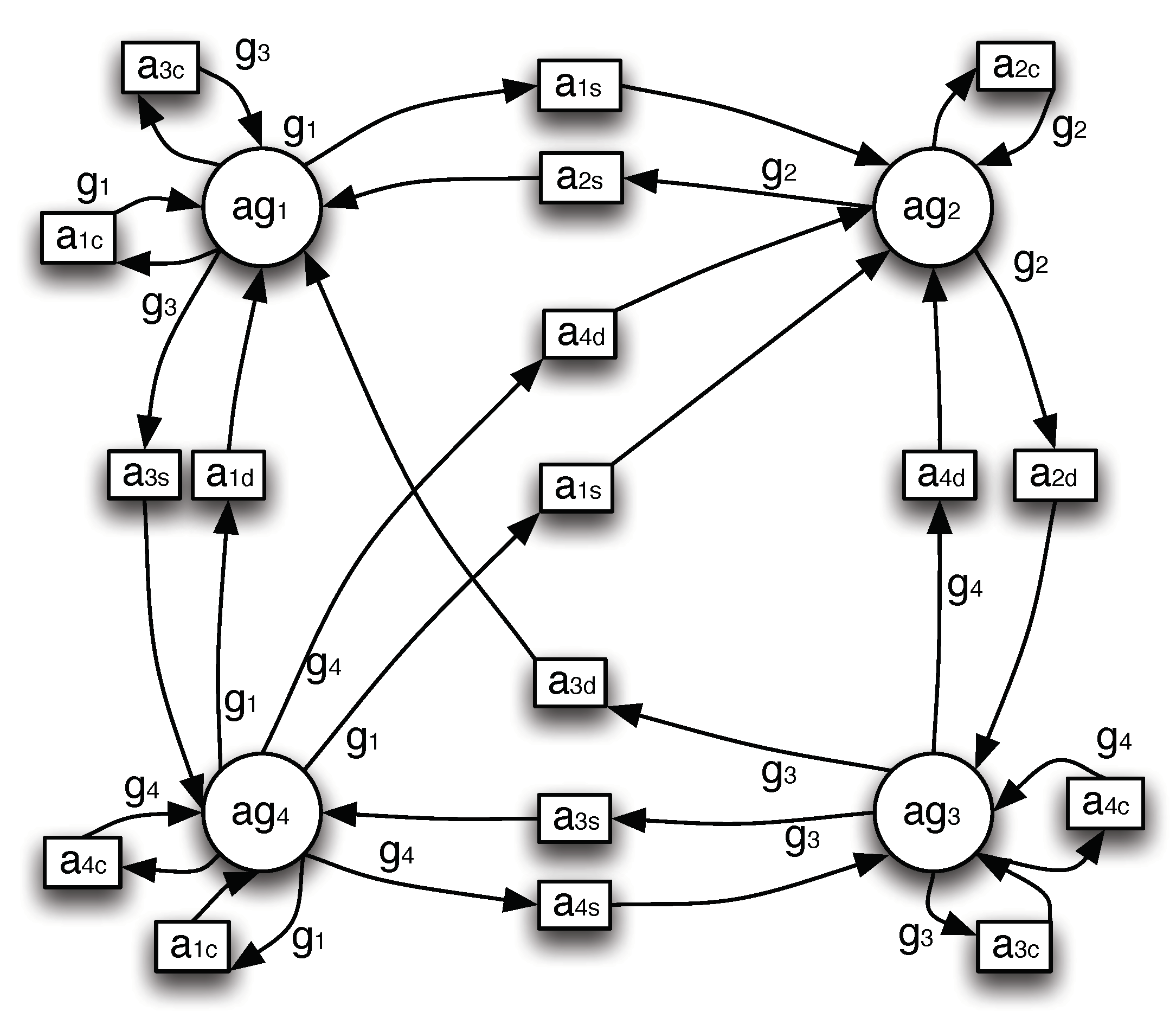
4.1. Modeling Dependencies
- provide the current location of the paper ()
- provide the location that the pen needs to be delivered to ()
- provide the location that the glue needs to be delivered to ()
- carry the pen or the glue ()
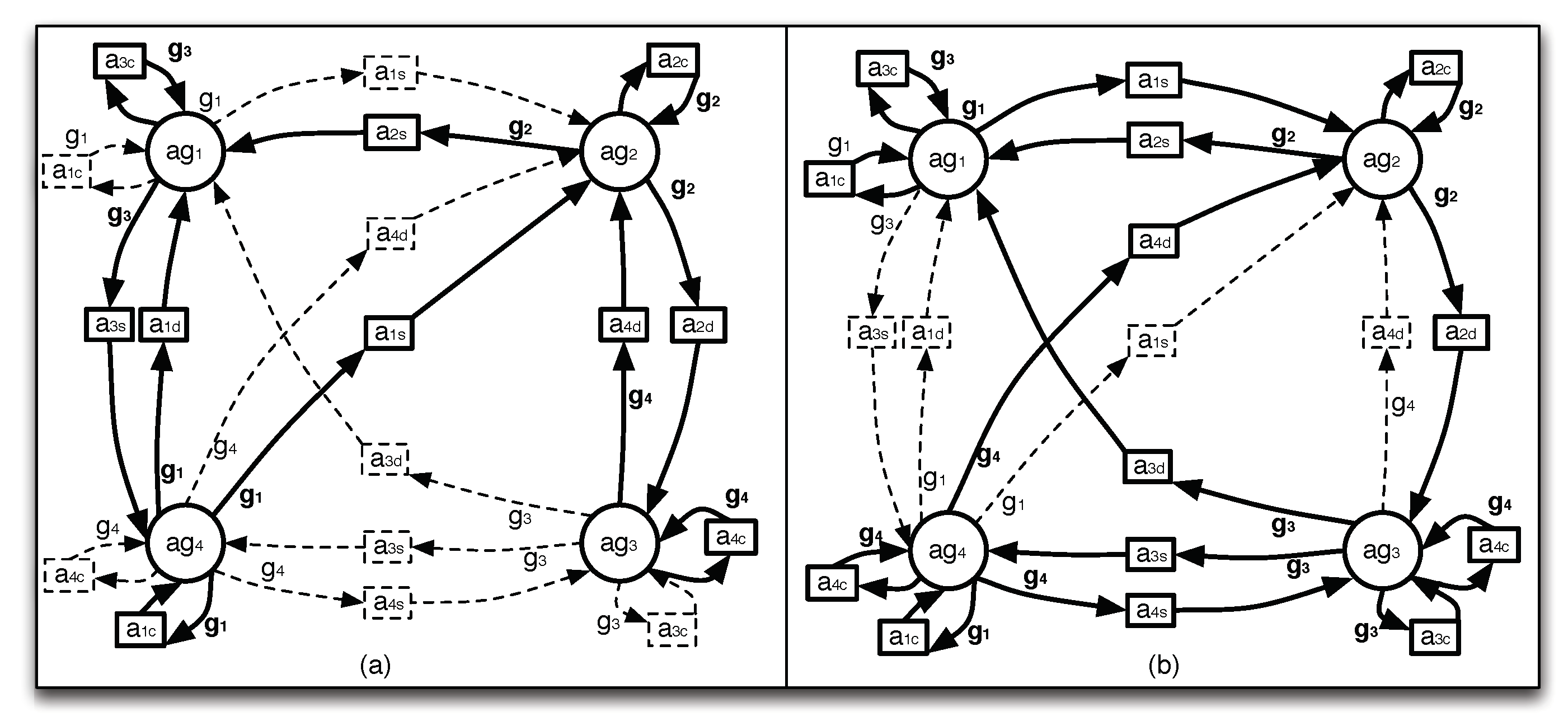
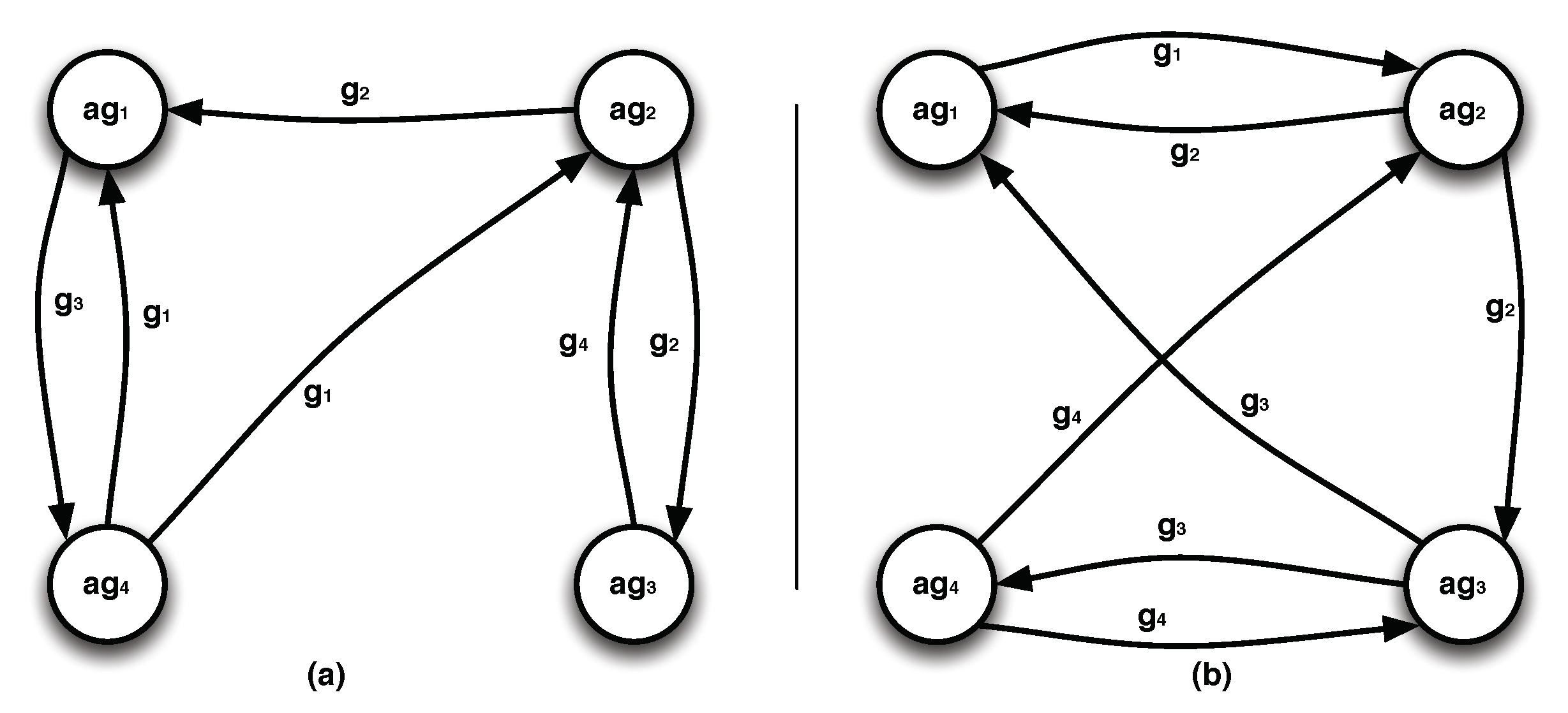
4.2. Computing Coalitions
- The MCS-IE system [43] implements a centralized reasoning approach that is based on the translation of MCS into HEX-programs [44] (an extension of answer set programs with external atoms), and on their execution in the dlv-hex system (http://www.kr.tuwien.ac.at/research/systems/dlvhex/).
- The algorithms proposed in [25] implement a distributed computation, which however assumes that all contexts are homogeneous with respect to the logic that they use (defeasible logic).
- The three algorithms proposed in [45] enable distributed computation of equilibria. DMCS assumes that each agent has minimal knowledge about the world, namely the agents that it is connected through the bridge rules, but does not have any further metadata, e.g., topological information, of the system. Its computational complexity is exponential to the number of literals used in the bridge rules. DMCS-OPT uses graph theory techniques to detect any cycle dependencies in the system and avoid them during the evaluation of the equilibria, improving the scalability of the evaluation. DMCS-STREAMING computes the equilibria gradually (k equilibria at a time), reducing the memory requirements for the agents. The three algorithms have been implemented in a system prototype (http://www.kr.tuwien.ac.at/research/systems/dmcs).
4.3. Evaluating the Coalitions
5. Computing Coalitions under Uncertainty
5.1. Modeling Uncertainty
5.2. Computing Coalitions under Uncertainty
5.3. Evaluating Coalitions under Uncertainty
- the Weighted Sum Method [66], according to which each criterion is given a weight , so that the sum of all weights is 1 (), and the overall score of each alternative is the weighted sum of , i.e., the scores of for each criterion :The optimal decision alternative is the one with the highest overall score (). This method can only be used in single-dimensional cases, in which all the score units are the same.
- the Weighted Product Method [67], which aggregates the individual scores using their product instead of their sum. Specifically, each decision alternative is compared with the others by multiplying several ratios, one for each criterion. Each ratio is raised to the power equivalent to the relative weight of the corresponding criterion. In general, to compare alternatives and , the following product must be calculated:where and are the scores of and respectively for criterion , and is the weight of criterion . If the ratio is greater than one, then is more desirable than . The best alternative is the one that is better, with respect to this ratio, than all other alternatives. This method is sometimes called dimensionless analysis because its structure eliminates any units of measure. It can, therefore, be used in both single- and multi-dimensional decision-making problems.
- TOPSIS (Technique for Order Preference by Similarity to Ideal Solution [68]), which is based on the concept that the chosen alternative should have the shortest geometric distance from the positive ideal solution and the longest geometric distance from the negative ideal solution. TOPSIS assumes that each alternative has a tendency of monotonically increasing or decreasing utility. Therefore, it is easy to locate the ideal and negative ideal solutions.
6. Related Work
7. Summary and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Anglano, C.; Canonico, M.; Castagno, P.; Guazzone, M.; Sereno, M. Profit-aware coalition formation in fog computing providers: A game-theoretic approach. Concurr. Comput. Pract. Exp. 2019. [Google Scholar] [CrossRef]
- Bullinger, M. Computing Desirable Partitions in Coalition Formation Games. In Proceedings of the 19th International Conference on Autonomous Agents and MultiAgent Systems; International Foundation for Autonomous Agents and Multiagent Systems, AAMAS ’20, Richland, SC, USA, 9–13 May 2020; pp. 2185–2187. [Google Scholar]
- Kashevnik, A.; Teslya, N. Blockchain-Oriented Coalition Formation by CPS Resources: Ontological Approach and Case Study. Electronics 2018, 7, 66. [Google Scholar] [CrossRef]
- Liu, C.; Zhu, E. A New Modeling of Cooperative Agents from Game-theoretic Perspective. In Proceedings of the 4th International Conference on Mathematics and Artificial Intelligence—ICMAI 2019, Chengdu, China, 12–15 April 2019; pp. 133–136. [Google Scholar]
- Rizk, T.; Awad, M. A quantum genetic algorithm for pickup and delivery problems with coalition formation. In Proceedings of the 23rd International Conference KES-2019, Budapest, Hungary, 4–6 September 2019; pp. 261–270. [Google Scholar]
- Guo, M.; Xin, B.; Chen, J.; Wang, Y. Multi-agent coalition formation by an efficient genetic algorithm with heuristic initialization and repair strategy. Swarm Evol. Comput. 2020, 55, 100686. [Google Scholar] [CrossRef]
- Bhateja, N.; Sethi, N.; Kumar, D. Study of Ant Colony Optimization Technique for Coalition Formation in Multi Agent Systems. In Proceedings of the 2018 International Conference on Circuits and Systems in Digital Enterprise Technology (ICCSDET), Kottayam, India, 21–22 December 2018; pp. 1–4. [Google Scholar]
- Zhang, K.; Hu, Y.; Tian, F.; Li, C. A coalition-structure’s generation method for solving cooperative computing problems in edge computing environments. Inf. Sci. 2020, 536, 372–390. [Google Scholar] [CrossRef]
- Su, X.; Wang, Y.; Jia, X.; Guo, L.; Ding, Z. Two Innovative Coalition Formation Models for Dynamic Task Allocation in Disaster Rescues. J. Syst. Sci. Syst. Eng. 2018, 27, 215–230. [Google Scholar] [CrossRef]
- Changder, N.; Aknine, S.; Dutta, A. An Effective Dynamic Programming Algorithm for Optimal Coalition Structure Generation. In Proceedings of the 2019 IEEE 31st International Conference on Tools with Artificial Intelligence (ICTAI), Portland, OR, USA, 4–6 November 2019; pp. 721–727. [Google Scholar]
- Pei, Z.; Piao, S.; Souidi, M. Coalition Formation for Multi-agent Pursuit Based on Neural Network. J. Intell. Robot. Syst. 2019, 95, 887–899. [Google Scholar] [CrossRef]
- Giunchiglia, F.; Serafini, L. Multilanguage hierarchical logics, or: How we can do without modal logics. Artif. Intell. 1994, 65, 29–70. [Google Scholar] [CrossRef]
- Ghidini, C.; Giunchiglia, F. Local Models Semantics, or contextual reasoning=locality+compatibility. Artif. Intell. 2001, 127, 221–259. [Google Scholar] [CrossRef]
- Brewka, G.; Eiter, T. Equilibria in Heterogeneous Nonmonotonic Multi-Context Systems. In Proceedings of the 22nd AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 22–26 July 2007; pp. 385–390. [Google Scholar]
- Lenat, D.B.; Guha, R.V. Building Large Knowledge-Based Systems; Representation and Inference in the Cyc Project; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Borgida, A.; Serafini, L. Distributed Description Logics: Assimilating Information from Peer Sources. J. Data Semant. 2003, 1, 153–184. [Google Scholar]
- Bouquet, P.; Giunchiglia, F.; van Harmelen, F.; Serafini, L.; Stuckenschmidt, H. C-OWL: Contextualizing Ontologies. In Proceedings of the International Semantic Web Conference, Sanibel, FL, USA, 20–23 October 2003; pp. 164–179. [Google Scholar]
- Parsons, S.; Sierra, C.; Jennings, N.R. Agents that reason and negotiate by arguing. J. Log. Comput. 1998, 8, 261–292. [Google Scholar] [CrossRef]
- Sabater, J.; Sierra, C.; Parsons, S.; Jennings, N.R. Engineering Executable Agents using Multi-context Systems. J. Log. Comput. 2002, 12, 413–442. [Google Scholar] [CrossRef]
- de Mello, R.R.P.; Gelaim, T.Â.; Silveira, R.A. Negotiating Agents: A Model Based on BDI Architecture and Multi-Context Systems Using Aspiration Adaptation Theory as a Negotiation Strategy. In Proceedings of the 12th International Conference on Complex, Intelligent, and Software Intensive Systems (CISIS-2018), Matsue, Japan, 4–6 July 2018; pp. 351–362. [Google Scholar]
- Lagos, N.; Mos, A.; Vion-Dury, J.Y. Multi-Context Systems for Consistency Validation and Querying of Business Process Models. In Proceedings of the 21st International Conference KES-2017, Marseille, France, 6–8 September 2017; pp. 225–234. [Google Scholar]
- Dao-Tran, M.; Eiter, T. Streaming Multi-Context Systems. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 1000–1007. [Google Scholar]
- Ellmauthaler, S. Multi-Context Reasoning in Continuous Data-Flow Environments. KI-Künstliche Intell. 2018, 33, 101–104. [Google Scholar] [CrossRef]
- Antoniou, G.; Papatheodorou, C.; Bikakis, A. Reasoning about Context in Ambient Intelligence Environments: A Report from the Field. In Principles of Knowledge Representation and Reasoning: Proceedings of the 12th Intl. Conference, KR 2010, Toronto, ON, Canada, 9–13 May 2010; AAAI Press: Palo Alto, CA, USA, 2010; pp. 557–559. [Google Scholar]
- Bikakis, A.; Antoniou, G.; Hassapis, P. Strategies for contextual reasoning with conflicts in Ambient Intelligence. Knowl. Inf. Syst. 2011, 27, 45–84. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, K.; Wen, L. Possibilistic Reasoning in Multi-Context Systems: Preliminary Report. In PRICAI 2012: Trends in Artificial Intelligence, Proceedings of the 12th Pacific Rim International Conference on Artificial Intelligence, Kuching, Malaysia, 3–7 September 2012; Springer: Berlin, Germany, 2012; pp. 180–193. [Google Scholar]
- Sichman, J.S.; Conte, R. Multi-agent dependence by dependence graphs. In Proceedings of the First International Joint Conference on Autonomous Agents and Multiagent Systems: Part 1, AAMAS 2002, Bologna, Italy, 15–19 July 2002; ACM: New York, NY, USA, 2002; pp. 483–490. [Google Scholar]
- Bikakis, A.; Caire, P. Computing Coalitions in Multiagent Systems: A Contextual Reasoning Approach. In Multi-Agent Systems, Proceedings of the 12th European Conference, EUMAS 2014, Prague, Czech Republic, 18–19 December 2014; Revised Selected Papers; Springer: Berlin, Germany, 2014; pp. 85–100. [Google Scholar]
- Sichman, J.S.; Demazeau, Y. On Social Reasoning in Multi-Agent Systems. Rev. Iberoam. Intel. Artif. 2001, 13, 68–84. [Google Scholar]
- Harman, H.; Simoens, P. Action graphs for proactive robot assistance in smart environments. J. Ambient Intell. Smart Environ. 2020, 12, 79–99. [Google Scholar] [CrossRef]
- Brings, J.; Daun, M.; Weyer, T.; Pohl, K. Goal-Based Configuration Analysis for Networks of Collaborative Cyber-Physical Systems. In Proceedings of the 35th Annual ACM Symposium on Applied Computing, SAC ’20, Brno, Czech Republic, 30 March–3 April 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1387–1396. [Google Scholar]
- Sauro, L. Formalizing Admissibility Criteria in Coalition Formation among Goal Directed Agents. Ph.D. Thesis, University of Turin, Turin, Italy, 2006. [Google Scholar]
- Eiter, T.; Fink, M.; Schüller, P.; Weinzierl, A. Finding Explanations of Inconsistency in Multi-Context Systems. In Principles of Knowledge Representation and Reasoning: Proceedings of the Twelfth International Conference, KR 2010, Toronto, ON, Canada, 9–13 May 2010; AAAI Press: Palo Alto, CA, USA, 2010. [Google Scholar]
- Eiter, T.; Fink, M.; Weinzierl, A. Preference-Based Inconsistency Assessment in Multi-Context Systems. In Logics in Artificial Intelligence, Proceedings of the 12th European Conference, JELIA 2010, Helsinki, Finland, 13–15 September 2010; Springer: Berlin, Germany, 2010; Volume 6341, pp. 143–155. [Google Scholar]
- Caire, P.; Bikakis, A.; Traon, Y.L. Information Dependencies in MCS: Conviviality-Based Model and Metrics. In Principles and Practice of Multi-Agent Systems, Proceedings of the 16th International Conference, Dunedin, New Zealand, 1–6 December 2013; Springer: Berlin, Germany, 2013; pp. 405–412. [Google Scholar]
- Dubois, D.; Lang, J.; Prade, H. Possibilistic Logic. In Handbook of Logic in Artificial Intelligence and Logic Programming-Nonmonotonic Reasoning and Uncertain Reasoning (Volume 3); Gabbay, D.M., Hogger, C.J., Robinson, J.A., Eds.; Clarendon Press: Oxford, UK, 1994; pp. 439–513. [Google Scholar]
- Nicolas, P.; Garcia, L.; Stéphan, I.; Lefèvre, C. Possibilistic uncertainty handling for answer set programming. Ann. Math. Artif. Intell. 2006, 47, 139–181. [Google Scholar] [CrossRef]
- Zadeh, L. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Somhom, S.; Modares, A.; Enkawa, T. Competition-based neural network for the multiple travelling salesmen problem with minmax objective. Comput. Oper. Res. 1999, 26, 395–407. [Google Scholar] [CrossRef]
- Cai, Z.; Peng, Z. Cooperative Co-evolutionary Adaptive Genetic Algorithm in Path Planning of Cooperative Multi-Mobile Robot Systems. J. Intell. Robot. Syst. 2002, 33, 61–71. [Google Scholar] [CrossRef]
- Koenig, S.; Likhachev, M. Fast replanning for navigation in unknown terrain. IEEE Trans. Robot. 2005, 21, 354–363. [Google Scholar] [CrossRef]
- Dao-Tran, M.; Eiter, T.; Fink, M.; Krennwallner, T. Dynamic Distributed Nonmonotonic Multi-Context Systems. In Nonmonotonic Reasoning, Essays Celebrating Its 30th Anniversary, Lexington, KY, USA, 22–25 October 2010; College Publications: London, UK, 2011; Volume 31, pp. 63–88. [Google Scholar]
- Bögl, M.; Eiter, T.; Fink, M.; Schüller, P. The mcs-ie System for Explaining Inconsistency in Multi-Context Systems. In Logics in Artificial Intelligence, Proceedings of the 12th European Conference, JELIA 2010, Helsinki, Finland, 13–15 September 2010; Springer: Berlin, Germany, 2010; pp. 356–359. [Google Scholar]
- Eiter, T.; Ianni, G.; Schindlauer, R.; Tompits, H. A Uniform Integration of Higher-Order Reasoning and External Evaluations in Answer-Set Programming. In Proceedings of the Nineteenth International Joint Conference on Artificial Intelligence, IJCAI-05, Edinburgh, UK, 30 July–5 August 2005; pp. 90–96. [Google Scholar]
- Dao-Tran, M.; Eiter, T.; Fink, M.; Krennwallner, T. Distributed Evaluation of Nonmonotonic Multi-context Systems. J. Artif. Intell. Res. (JAIR) 2015, 52, 543–600. [Google Scholar] [CrossRef][Green Version]
- O’Sullivan, A.; Sheffrin, S.M. Economics: Principles in Action; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Shapley, L.S. A Value for n-person Games. Ann. Math. Stud. 1953, 28, 307–317. [Google Scholar]
- Schmeidler, D. The nucleolus of a characteristic functional game. SIAM J. Appl. Math. 1969, 17, 1163–1170. [Google Scholar] [CrossRef]
- Kronbak, L.G.; Lindroos, M. Sharing Rules and Stability in Coalition Games with Externalities. Mar. Resour. Econ. 2007, 22, 137–154. [Google Scholar] [CrossRef][Green Version]
- Magaña, A.; Carreras, F. Coalition Formation and Stability. Group Decis. Negot. 2018, 27, 467–502. [Google Scholar] [CrossRef]
- Mesterton-Gibbons, M. An Introduction to Game-Theoretic Modelling; Addison-Wesley: Redwood, CA, USA, 1992. [Google Scholar]
- Caire, P.; Alcade, B.; van der Torre, L.; Sombattheera, C. Conviviality Measures. In Proceedings of the 10th International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS 2011), Taipei, Taiwan, 2–6 May 2011. [Google Scholar]
- Illich, I. Deschooling Society; Marion Boyars Publishers, Ltd.: London, UK, 1971. [Google Scholar]
- Caire, P. New Tools for Conviviality: Masks, Norms, Ontology, Requirements and Measures. Ph.D. Thesis, Luxembourg University, Luxembourg, 2010. [Google Scholar]
- Arenas, F.J.; Connelly, D.A. The Claim on Human Conviviality in Cyberspace. In Integrating an Awareness of Selfhood and Society into Virtual Learning; Andrew, S., Cynthia Calongne, B.T., Arenas, F., Eds.; IGI Global: Hershey, PA, USA, 2017; Chapter 3; pp. 29–39. [Google Scholar]
- Ellemers, N.; Fiske, S.T.; Abele, A.E.; Koch, A.; Yzerbyt, V. Adversarial alignment enables competing models to engage in cooperative theory building toward cumulative science. Proc. Natl. Acad. Sci. USA 2020, 117, 7561–7567. [Google Scholar] [CrossRef]
- Cabitza, F.; Simone, C.; Cornetta, D. Sensitizing concepts for the next community-oriented technologies: Shifting focus from social networking to convivial artifacts. J. Community Inform. 2015, 11, 11. [Google Scholar]
- Sandholm, T.; Larson, K.; Andersson, M.; Shehory, O.; Tohmé, F. Coalition Structure Generation with Worst Case Guarantees. Artif. Intell. 1999, 111, 209–238. [Google Scholar] [CrossRef]
- Dang, V.D.; Jennings, N.R. Generating Coalition Structures with Finite Bound from the Optimal Guarantees. In Proceedings of the 3rd International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS 2004), New York, NY, USA, 19–23 August 2004; pp. 564–571. [Google Scholar]
- Shehory, O.; Kraus, S. Methods for Task Allocation via Agent Coalition Formation. Artif. Intell. 1998, 101, 165–200. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Vasquez, D.; Large, F.; Fraichard, T.; Laugier, C. High-speed autonomous navigation with motion prediction for unknown moving obstacles. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems, Sendai, Japan, 28 September–2 October 2004; pp. 82–87. [Google Scholar]
- Hsiao, K.; Kaelbling, L.P.; Lozano-Pérez, T. Grasping POMDPs. In Proceedings of the 2007 IEEE International Conference on Robotics and Automation, ICRA 2007, Roma, Italy, 10–14 April 2007; pp. 4685–4692. [Google Scholar]
- Alterovitz, R.; Siméon, T.; Goldberg, K.Y. The Stochastic Motion Roadmap: A Sampling Framework for Planning with Markov Motion Uncertainty. In Proceedings of the Robotics: Science and Systems III, Atlanta, GA, USA, 27–30 June 2007. [Google Scholar]
- Zimmermann, H. Fuzzy Set Theory and Its Applications; Kluwer Academic: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Fishburn, P.C. Additive Utilities with Incomplete Product Sets: Applications to Priorities and Assignments. Oper. Res. 1967, 15, 537–542. [Google Scholar] [CrossRef]
- Miller, D.; Starr, M. Executive Decisions and Operations Research; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1969. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making Methods and Applications: A State-of-the-Art Survey; Springer: Berlin, Germany, 1981. [Google Scholar]
- Triantaphyllou, E. Multi-Criteria Decision Making Methods: A Comparative Study; Springer: Berlin, Germany, 2000. [Google Scholar]
- Gerkey, B.P.; Matarić, M.J. Sold!: Auction Methods for Multi-Robot Coordination. IEEE Trans. Robot. Autom. 2002, 18, 758–768. [Google Scholar] [CrossRef]
- Lemaire, T.; Alami, R.; Lacroix, S. A Distributed Tasks Allocation Scheme in Multi-UAV Context. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, ICRA 2004, New Orleans, LA, USA, 26 April–1 May 2004; pp. 3622–3627. [Google Scholar]
- Sichman, J.S. DEPINT: Dependence-based coalition formation in an open multi-agent scenario. J. Artif. Soc. Soc. Simul. 1998, 1, 1–3. [Google Scholar]
- Klusch, M.; Gerber, A. Dynamic Coalition Formation among Rational Agents. IEEE Intell. Syst. 2002, 17, 42–47. [Google Scholar] [CrossRef]
- Boella, G.; Sauro, L.; van der Torre, L. Algorithms for finding coalitions exploiting a new reciprocity condition. Log. J. IGPL 2009, 17, 273–297. [Google Scholar] [CrossRef]
- Grossi, D.; Turrini, P. Dependence theory via game theory. In Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2010), Toronto, ON, Canada, 10–14 May 2010; pp. 1147–1154. [Google Scholar]
- Caire, P.; Villata, S.; Boella, G.; van der Torre, L. Conviviality masks in multiagent systems. In Proceedings of the 7th International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS 2008), Estoril, Portugal, 12–16 May 2008; Volume 3, pp. 1265–1268. [Google Scholar]
- Tang, F.; Parker, L.E. ASyMTRe: Automated Synthesis of Multi-Robot Task Solutions through Software Reconfiguration. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, ICRA 2004, New Orleans, LA, USA, 26 April–1 May 2004; pp. 1501–1508. [Google Scholar]
- Zhang, Y.; Parker, L.E. IQ-ASyMTRe: Forming Executable Coalitions for Tightly Coupled Multirobot Tasks. IEEE Trans. Robot. 2013, 29, 400–416. [Google Scholar] [CrossRef]
- Liemhetcharat, S.; Veloso, M.M. Weighted synergy graphs for effective team formation with heterogeneous ad hoc agents. Artif. Intell. 2014, 208, 41–65. [Google Scholar] [CrossRef]
- Chella, A.; Sorbello, R.; Ribaudo, D.; Finazzo, I.V.; Papuzza, L.A.; Sorbello, R.; Ribaudo, D.; Finazzo, I.V.; Papuzza, L. A Mechanism of Coalition Formation in the Metaphor of Politics Multiagent Architecture. In AI*IA 2003: Advances in Artificial Intelligence, Proceedings of the 8th Congress of the Italian Association for Artificial Intelligence, Pisa, Italy, 23–26 September 2003; Cappelli, A., Turini, F., Eds.; Springer: Berlin, Germany, 2003; pp. 410–422. [Google Scholar] [CrossRef]
- Abdallah, S.; Lesser, V.R. Organization-Based Coalition Formation. In Proceedings of the 3rd International Joint Conference on Autonomous Agents and Multiagent Systems (AAMAS 2004), New York, NY, USA, 19–23 August 2004; pp. 1296–1297. [Google Scholar]
- Soh, L.; Li, X. Multiagent Coalition Formation for Distributed, Adaptive Resource Allocation. In Proceedings of the International Conference on Artificial Intelligence, IC-AI ’04, Las Vegas, NV, USA, 21–24 June 2004; CSREA Press: Sterling, VA, USA, 2004; Volume 1, pp. 372–378. [Google Scholar]
- Sen, S. An Intelligent and Unified Framework for Multiple Robot and Human Coalition Formation; AAAI Press: Palo Alto, CA, USA, 2015; pp. 4395–4396. [Google Scholar]
- Chalkiadakis, G.; Markakis, E.; Boutilier, C. Coalition Formation Under Uncertainty: Bargaining Equilibria and the Bayesian Core Stability Concept. In Proceedings of the 6th International Joint Conference on Autonomous Agents and Multiagent Systems, AAMAS ’07, Honolulu, HI, USA, 14–18 May 2007; ACM: New York, NY, USA, 2007; pp. 64:1–64:8. [Google Scholar] [CrossRef]
- Shehory, O.; Kraus, S. Feasible Formation of Coalitions Among Autonomous Agents in Non-Super-Additive Environments. Comput. Intell. 1999, 15, 218–251. [Google Scholar] [CrossRef]
- Kargin, V. Uncertainty of the Shapley Value. In Game Theory and Information; University Library of Munich: Munich, Germany, 2003; Number: 0309003. [Google Scholar]
- Mamakos, M.; Chalkiadakis, G. Probability Bounds for Overlapping Coalition Formation. In Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence, IJCAI 2017, Melbourne, Australia, 19–25 August 2017; pp. 331–337. [Google Scholar]
- Mittal, V.; Maghsudi, S.; Hossain, E. Distributed Cooperation Under Uncertainty in Drone-Based Wireless Networks: A Bayesian Coalitional Game. arXiv 2020, arXiv:2009.00685. [Google Scholar]
- Soh, L.; Tsatsoulis, C. Utility-based multiagent coalition formation with incomplete information and time constraints. In Proceedings of the IEEE International Conference on Systems, Man & Cybernetics, Washington, DC, USA, 5–8 October 2003; pp. 1481–1486. [Google Scholar]
- Vig, L.; Adams, J.A. Multi-robot coalition formation. IEEE Trans. Robot. 2006, 22, 637–649. [Google Scholar] [CrossRef]
- Gambetta, D. Can we trust? In Trust: Making and Breaking Cooperative Relations; Basil Blackwell: New York, NY, USA, 1988; pp. 213–237. [Google Scholar]
- Abdul-Rahman, A.; Hailes, S. Supporting Trust in Virtual Communities. In Proceedings of the 33rd Annual Hawaii International Conference on System Sciences, Maui, HI, USA, 7 January 2000; p. 6007. [Google Scholar]
- Granatyr, J.; Botelho, V.; Lessing, O.R.; Scalabrin, E.E.; Barthès, J.P.; Enembreck, F. Trust and Reputation Models for Multiagent Systems. ACM Comput. Surv. 2015, 48. [Google Scholar] [CrossRef]
- Griffiths, N.; Luck, M. Coalition Formation through Motivation and Trust. In Proceedings of the AAMAS03: Second International Conference on Autonomous Agents and Multiagent Systems, Melbourne Australia, 14–18 July 2003; Association for Computing Machinery: New York, NY, USA, 2003; pp. 17–24. [Google Scholar] [CrossRef]
- Rehák, M.; Foltýn, L.; Pechoucek, M.; Benda, P. Trust Model for Open Ubiquitous Agent Systems. In Proceedings of the 2005 IEEE/WIC/ACM International Conference on Intelligent Agent Technology, Compiegne, France, 19–22 September 2005; IEEE Computer Society: Washington, DC, USA, 2005; pp. 536–542. [Google Scholar]
- Ghanea-Hercock, R.; Ipswich, A.P. Dynamic Trust Formation in Multi-Agent Systems. In Proceedings of the Tenth International Workshop on Trust in Agent Societies at the Autonomous Agents and Multi-Agent Systems Conference, Honolulu, HI, USA, 15 May 2007. [Google Scholar]
- Tong, X.; Huang, H.; Zhang, W. Agent Long-Term Coalition Credit. Expert Syst. Appl. 2009, 36, 9457–9465. [Google Scholar] [CrossRef]
- Guo, L.; Wang, X.; Zeng, G. Trust-Based Optimal Workplace Coalition Generation. In Proceedings of the 2009 International Conference on Information Engineering and Computer Science, Wuhan, China, 19–20 December 2009; pp. 1–4. [Google Scholar]
- Zhou, Q.; Wang, C.; Xie, J. CORE: A Trust Model for Agent Coalition Formation. In Proceedings of the Fifth International Conference on Natural Computation, ICNC 2009, Tianjian, China, 14–16 August 2009; IEEE Computer Society: Washington, DC, USA, 2009; Volume 6, pp. 541–545. [Google Scholar]
- Erriquez, E.; van der Hoek, W.; Wooldridge, M. An Abstract Framework for Reasoning about Trust. In Proceedings of the The 10th International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2011), Taipei, Taiwan, 2–6 May 2011; International Foundation for Autonomous Agents and Multiagent Systems: Richland, SC, USA, 2011; Volume 3, pp. 1085–1086. [Google Scholar]
- Bairakdar, S.E.; Dao-Tran, M.; Eiter, T.; Fink, M.; Krennwallner, T. The DMCS Solver for Distributed Nonmonotonic Multi-Context Systems. In Logics in Artificial Intelligence, Proceedings of the 12th European Conference, JELIA 2010, Helsinki, Finland, 13–15 September 2010; Springer: Berlin, Germany, 2010; pp. 352–355. [Google Scholar]
| Robot | ||||||||
| Task | ||||||||
| Source | x | x | ||||||
| Destination | x | x | x | |||||
| Robot | ||||||||
| Task | ||||||||
| Source | x | x | ||||||
| Destination | x | |||||||
| Distances among Locations | ||||
|---|---|---|---|---|
| Robot | Pen | Paper | Glue | Cutter |
| 10 | 15 | 9 | 12 | |
| 14 | 8 | 11 | 13 | |
| 12 | 14 | 10 | 7 | |
| 9 | 12 | 15 | 11 | |
| Destination | Pen | Paper | Glue | Cutter |
| 11 | 16 | 9 | 8 | |
| 14 | 7 | 12 | 9 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bikakis, A.; Caire, P. Contextual and Possibilistic Reasoning for Coalition Formation. AI 2020, 1, 389-417. https://doi.org/10.3390/ai1030026
Bikakis A, Caire P. Contextual and Possibilistic Reasoning for Coalition Formation. AI. 2020; 1(3):389-417. https://doi.org/10.3390/ai1030026
Chicago/Turabian StyleBikakis, Antonis, and Patrice Caire. 2020. "Contextual and Possibilistic Reasoning for Coalition Formation" AI 1, no. 3: 389-417. https://doi.org/10.3390/ai1030026
APA StyleBikakis, A., & Caire, P. (2020). Contextual and Possibilistic Reasoning for Coalition Formation. AI, 1(3), 389-417. https://doi.org/10.3390/ai1030026






