Role of Lee Wave Turbulence in the Dispersion of Sediment Plumes

Abstract

Sediment plumes threatening benthic ecosystems are one of the environmental hazards associated with seafloor interventions such as bottom trawling, cabling, dredging, and marine mining operations. This study focuses on sediment plume release from hypothetical future deep-sea mining activities, emphasizing its interaction with turbulent ocean currents in regions characterized by complex seafloor topography. In such environments, turbulent lee waves may significantly enhance the scattering of released sediments, pointing to the clear need for appropriate impact assessment frameworks. Global-scale models are limited in their ability to resolve sufficiently high Reynolds numbers to accurately represent turbulence generated by seafloor topography. To overcome these limitations and effectively assess lee wave dynamics, models must incorporate the full physics of turbulence without simplifying the Navier–Stokes equations and must operate with significantly finer spatial discretization while maintaining a domain large enough to capture the full topographic signal. Considering a seamount in the Lofoten Basin of the Norwegian Sea as an example, we present a novel numerical analysis that explores the interplay between lee wave turbulence and sediment plume dispersion using a high-resolution Large Eddy Simulation (LES) framework. We show that the turbulence occurs within semi-horizontal channels that emerge beyond the topographic highs and extend into sheet-like tails close to the seafloor. In scenarios simulating sediment release from various sites on the seamount, our model predicts distinct behavior patterns for different particle sizes. Particles with larger settling velocities tend to deposit onto the seafloor within 50–200 m of release sites. Conversely, particles with lower settling velocities are more susceptible to turbulent transport, potentially traveling greater distances while experiencing faster dilution. Based on our scenarios, we estimate that the plume concentration may dilute below 1 ppm at about 2 km distance from the release site. Although our analysis shows that mixing with ambient seawater results in rapid dilution to low concentrations, it appears crucial to account for the effects of topographic lee wave turbulence in impact assessments related to man-made sediment plumes. Our high-resolution numerical simulations enable the identification of sediment particle size groups that are most likely affected by turbulence, providing valuable insights for developing targeted mitigation strategies.

1. Introduction

Humankind is increasing its presence at the seafloor thereby adding and amplifying stressors to deep-sea ecosystems. Examples include deep-sea installations of the offshore industries, bottom trawling, and most recently a renewed push to explore the seabed for mineral resources such as Fe/Mn nodules and crusts as well as massive sulfide deposits. One potential hazard associated with seafloor interventions is the formation of sediment plumes that can threaten benthic life. If the exploitation of deep sea minerals becomes a reality, seafloor mining operations will include machinery that reworks the seabed and, dependent on design, may form sediment plumes.

To assess the environmental impact of such mining activities, early in situ experiments on the seafloor have been conducted since the 1970s in the context of collecting nodules [1]. These experiments simulated mining activity by expelling benthic sediments a few meters above the seabed along presumed mining tracks with sediment traps at various distances recording the settling pattern. The experimental data from these studies have subsequently been used in numerical simulations [2] to characterize the sediment accumulation thickness as a function of distance from the mining tracks. However, the comparison between numerical results and the measurements was relatively poor, possibly highlighting the contribution from dynamic flow processes not captured in those numerical models.

Recent studies [3,4,5,6,7] emphasize the significance of density currents, driven by the density contrast between the fully saturated sediment fluid-waste and the surrounding ocean water, in the initial propagation of sediment plumes. The dynamics of density currents can create turbulent wakes on the seafloor, which can propagate under their momentum over 100’s of meters. In more detail, in situ experiments conducted in the Clarion Clipperton Zone (CCZ) abyssal plains [3] have demonstrated that 92–98% of the sediment plume created by a moving nodule collector vehicle are observed below two meters elevation from the seafloor with lateral spreading and settling over hundreds of meters. Despite the valuable insights from these experiments into the transport phenomena at the immediate vicinity of the discharge source, the environmental assessment of the suspended sediment fraction of the plume 2–8%, which does not settle in the direct vicinity, remains unexplored. In this context, it should be added that the nodule collection tests in the CCZ were performed in an area with relatively flat seabed topography and low seafloor ocean current disturbances. Episodic surface wind-induced mesoscale eddies in the Pacific have been shown to significantly influence deep ocean currents [8], which can persist for weeks and have substantial implications on the dispersion of sediment plumes from the CCZ mining areas.

Other seabed interventions, such as mining massive sulfides or Fe/Mn crusts, may occur in regions of significant bathymetric relief, complicating predictions on sediment plume evolution. Seabed topography, such as isolated volcanoes and clusters or chains of seamounts, modulates ocean currents. Seamounts can convert ocean tidal energy into smaller-length scale waves and act as sources and sinks of ocean eddies [9,10]. The interaction of a background flow with a seamount is complex and depends on the morphology, ocean stratification, and temporal variations in flow [9]. Early ideas on the interaction between a directional background flow and seamounts involved so-called Taylor caps, a stationary recirculating current with the potential to hydrodynamically isolate seamounts [11], with implications for trapping plankton and endemism [12]. The combined flow response at large seamounts to tides and steady inflow is complex and has been shown to affect the retention times of particles mobilized near the summit of a seamount [13].

Lee waves are internal waves that form on the downstream (lee) side of underwater features like seamounts or ridges when the ocean current flows over them. When these waves break, they generate turbulence and swirling motions (eddies) that greatly affect the local hydrodynamic conditions. Evidence for such waves is reported as flow turbulences behind sharp topographic ridges in the Samoan Passage [14], in the Drake Passage [15], and behind abyssal hills in the Pacific Ocean [16]. A series of numerical simulations to quantify lee waves caused by synthetic Gaussian-shaped obstacles in constant background flows has been documented [17]. The kinetic energy analysis of these experiments reveals specific signatures associated with the turbulence wake on the lee-side of the topography. Although such analyses provide crucial insights into the parameterization of vertical mixing processes for global ocean models [18], applying these turbulent flow solutions to natural examples is limited by the simplified bathymetry inputs.

Impact assessment of future mining operations in areas with substantial topographic features, therefore, need to account for the topography-induced potential turbulence of the ocean currents. Interactions between the released sediments and ocean current turbulences may increase the potential for longer-distance sediment dispersion, possibly enlarging the affected area. In this study, we address two primary research questions: (1) Can turbulent ocean currents surrounding seamount topography be predicted? (2) How do sediment plumes interact with these turbulent ocean currents? Addressing these questions requires a modeling framework that can bridge the gap between large-scale ocean dynamics and fine-scale, topography-induced turbulence. Previous studies have often been limited by simplified geometries or models that parameterize turbulence. Our study overcomes these limitations by applying a Large Eddy Simulation (LES) framework to a realistic, complex seamount bathymetry, allowing us to directly resolve the turbulent structures that are critical for sediment transport. With this, we quantify the sediment settling near hypothetical sites of seafloor interventions and the proportion of sediment that may be transported over larger distances with the background ocean currents. Furthermore, we determine the critical distance at which the suspended material concentrations drop to significantly low levels.

2. Methods

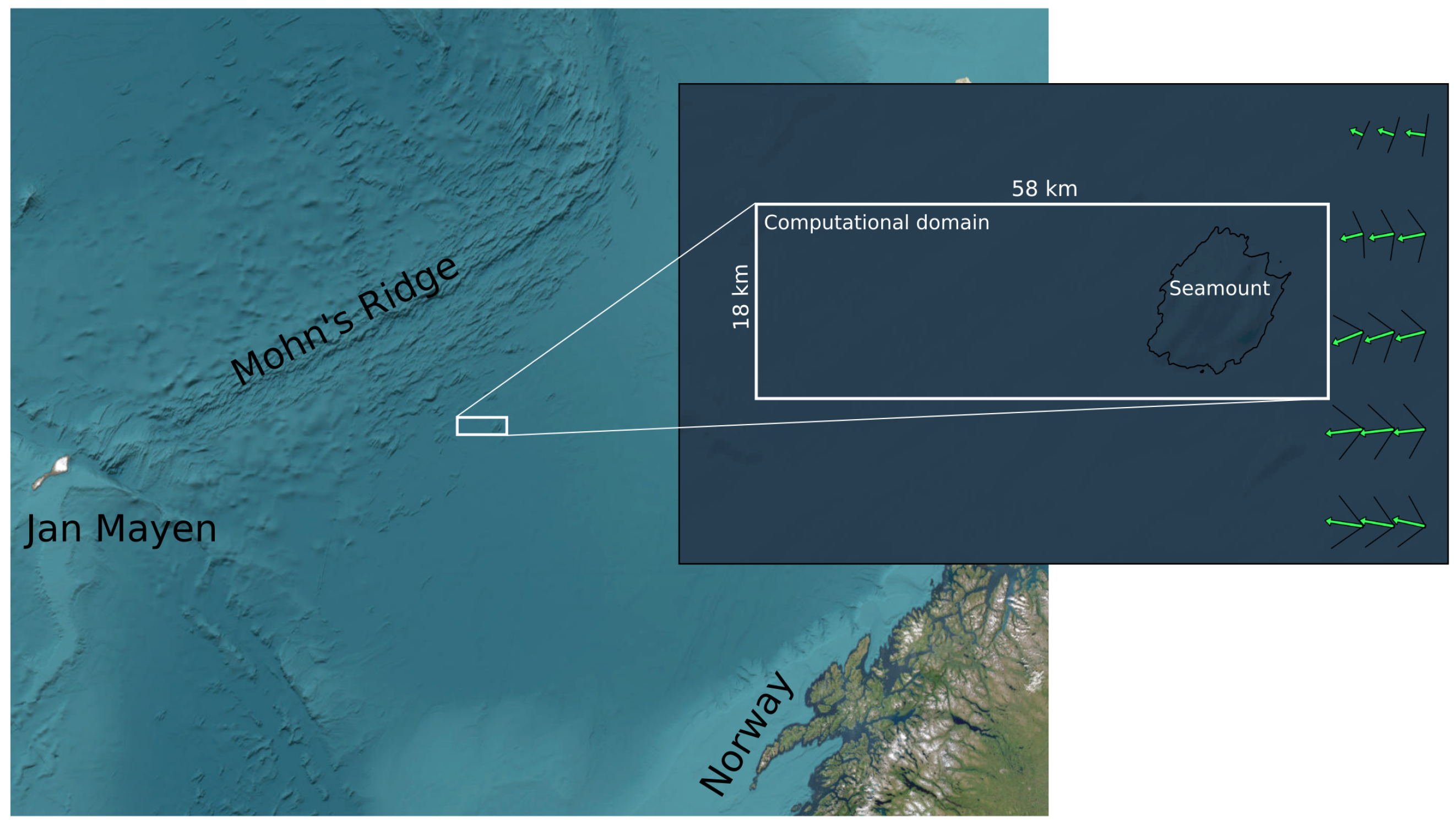
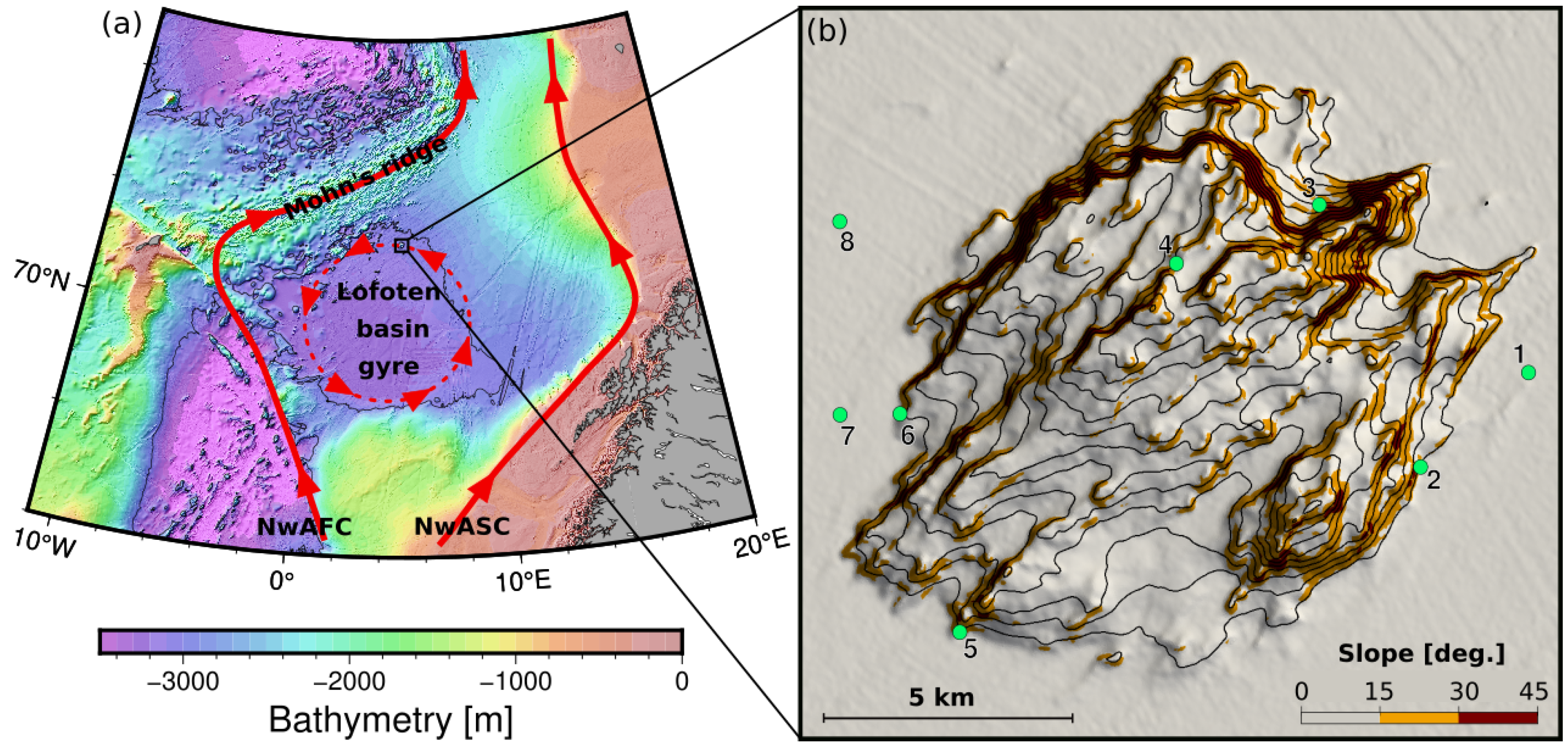
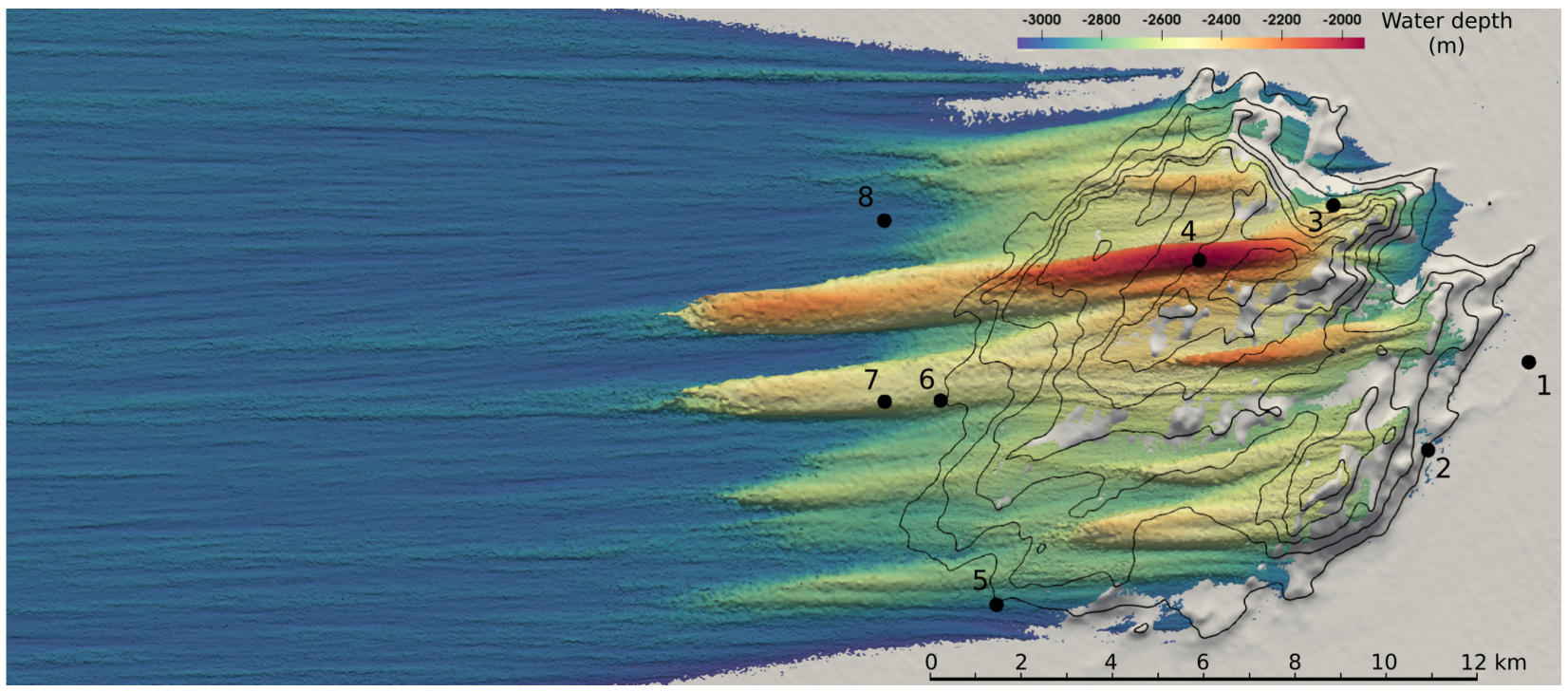
2.1. Region of Interest and Ocean Data

We base our study on a seamount located within the region recently designated by the Norwegian Parliament for future seabed mineral exploration. This particular seamount was chosen due to its distinct and isolated topographic features, which make it an ideal and representative site for our turbulence analysis. Rising from the abyssal plain at a depth of approximately 3000 m, the seamount is situated along the northwestern boundary of the Lofoten Basin in the Norwegian Sea (Figure 1). It exhibits an almost circular shape, with a diameter of roughly 12 km and a prominent elevation of about 700 m. The nearest significant topographic feature lies 25 km away, in the direction of Mohn’s Ridge, while the central axis of Mohn’s Ridge itself is located approximately 140 km to the northwest. The topography of the seamount is characterized by slopes below 30 degrees with some steeper escarpments (>50°) in the Northern sections. We use the digital elevation model from kartkatalog.geonorge.no with a resolution of 50 m as input to our models and applied a slight smoothing to remove sharp, probably erroneous, spikes.

The seamount is located at the margins of the large-scale cyclonic ocean gyre that covers the entire Lofoten Basin [19]. This ocean current is relatively well constrained at mid-water depths of 1000–1500 m [19,20] and shows seasonal fluctuations from 2 to 5 cm/s with a standard deviation of approximately 5 cm/s. A few measurements obtained from lowered acoustic Doppler current profilers (L-ADCP) within the Lofoten Basin show a uniform flow amplitude from mid-water to seafloor depths indicating a low flow stratification within the area [19,20]. In addition to these direct observations, we used the global ocean currents predictions from [21] to constrain the main background flow direction in the deep sea. While the general trend of westward flow is verified, the modeled predictions also show relatively large seasonal fluctuations as illustrated in Appendix A Figure A1.

2.2. Numerical Model

2.2.1. Large Eddy Simulation

We solve the full Navier–Stokes equations to model the flow around the seamount. However, resolving the temporal and spatial scales of the flow below our mesh resolution poses a challenge. To tackle this, we employ the Large Eddy Simulation (LES) method, enabling us to effectively account for energy dissipation in the sub-grid space and accurately capture the full dynamics and turbulence of the fluid flow within the scales we can simulate. The LES model is implemented with a Smagorinsky–Lilly sub-grid viscous term, defined based on the local grid size and the local magnitude of the strain tensor [22,23]. We use the open-source finite element Oasis solver [24] with the efficient Adam–Bashforth Crank–Nicholson IPCS scheme for solving the Navier–Stokes equations. Both the velocity and pressure fields are approximated using linear tetrahedral elements. A comprehensive set of numerical benchmarks for the Oasis solver is documented and published in the scientific literature [22,24] and is also available through the solver’s public GitHub repository (see Data Availability Statement). Appendix A 

Table A1. Numerical parameters used to set up the Oasis Navier–Stokes solver, using the LES Smagorinsky algorithm and the IPCS-ABCN fractional step scheme.

Parameters	Values
Water density	$999\mathrm{kg}/{\mathrm{m}}^3$
Water dynamic viscosity	$1.3\times {10}^{-3}\mathrm{kg}/(\mathrm{m}·\mathrm{s})$
Time steps	$2000\mathrm{s}$ for inlet velocity scenario of $2.5\mathrm{cm}/\mathrm{s}$
	$1000\mathrm{s}$ for inlet velocity scenario of $5\mathrm{cm}/\mathrm{s}$
	$500\mathrm{s}$ for inlet velocity scenario of $10\mathrm{cm}/\mathrm{s}$
Smagorinsky constant	$0.1677$

summarizes the numerical parameters used.

While our model resolves the Navier–Stokes equations and turbulence down to the minimal length scale of our grid (in the range of 10 m), it does not explicitly solve buoyancy-driven instabilities of two-phase flow between sediment-laden and ambient water immediately after release since this process occurs within the sub-grid scale. Any flow within the sub-grid space is stabilized effectively with the LES approach to the laminar regime.

2.2.2. Geometry and Mesh

The lateral extent of the model is 58 km in the East–West direction and 18 km in the North–South direction, with the top of the model at sea level, i.e., 3000 m above the seafloor. The seamount is positioned near the inflow boundary and the bottom boundary of the model follows the bathymetric data. To minimize boundary effects and to facilitate the flow analysis, we progressively smooth the seafloor towards the inlet and outlet borders. The stability and accuracy of fluid flow simulations rely heavily on mesh quality. Our model utilizes an unstructured tetrahedral element mesh specifically designed to capture the complex bathymetry of the study area. At the seafloor, the horizontal resolution is approximately 30 m, while the vertical resolution is controlled by a series of boundary layers at elevation of 9 m, 24 m, 44 m, and 74 m. Above these levels, we employ an adaptive mesh resolution that varies with depth, gradually increasing the element edge size to approximately 200 m at the ocean surface. This approach ensures high resolution in critical regions while maintaining computational efficiency in the upper water column. The final mesh consists of approximately 45 million elements. Figure A2 visually represents the mesh characteristics, illustrating Pope’s criterion [25] and confirming that our mesh size is sufficient for resolving topography-induced turbulence.

2.2.3. Initial and Boundary Conditions

It is a challenge to establish accurate flow boundary conditions for refined regional models, especially when influenced by a large-scale evolving structure like the Lofoten Basin gyre. While data from global-scale ocean models could be used, this approach faces two key difficulties: the resolution disparity between global and regional models, making direct interpolation of global-scale data impractical, and the hydrodynamic incompatibilities arising from the difference in effective Reynolds numbers between scales. Therefore we adopt a simplified representation of the background flow for the boundary conditions of our model where the eastern boundary (inlet) is set to a constant velocity and the western boundary (outlet) is set to constant hydrodynamic pressure. The top of the model, as well as the southern and northern walls, are also set to the constant inlet velocity condition. The latter are numerically more stable than free-surface and free-slip boundary conditions and do not alter the numerical solution in the region of interest. We apply a no-flow condition at the seafloor. The initial conditions are obtained by solving for the steady-state, inertia-free Stokes version of the problem, which provides a baseline for the flow behavior. From this starting point, we build up to fully developed Navier–Stokes flow and run three scenarios with the lateral inlet velocity uniformly set to 2.5, 5, and 10 cm/s. These scenarios approximate the seasonal variations in ocean current flow and the maximum measured values of the westward ocean flow.

2.2.4. Reynolds Number

The Reynolds number of the simulations, defined as $\mathrm{Re}={\displaystyle \frac{vL}{\nu }}$, where v is the inlet velocity, L is the seamount height ($L=700\mathrm{m}$), and $\nu$ is the effective kinetic viscosity of the model, must exceed 1000 to capture natural turbulent flow conditions [26,27]. Using an inlet velocity of 5 cm/s, our model exhibits effective viscosities ranging from 0.01 to 0.025 ${\mathrm{m}}^2/\mathrm{s}$ within the turbulent flow channels, resulting in Reynolds numbers between 3500 and 1400.

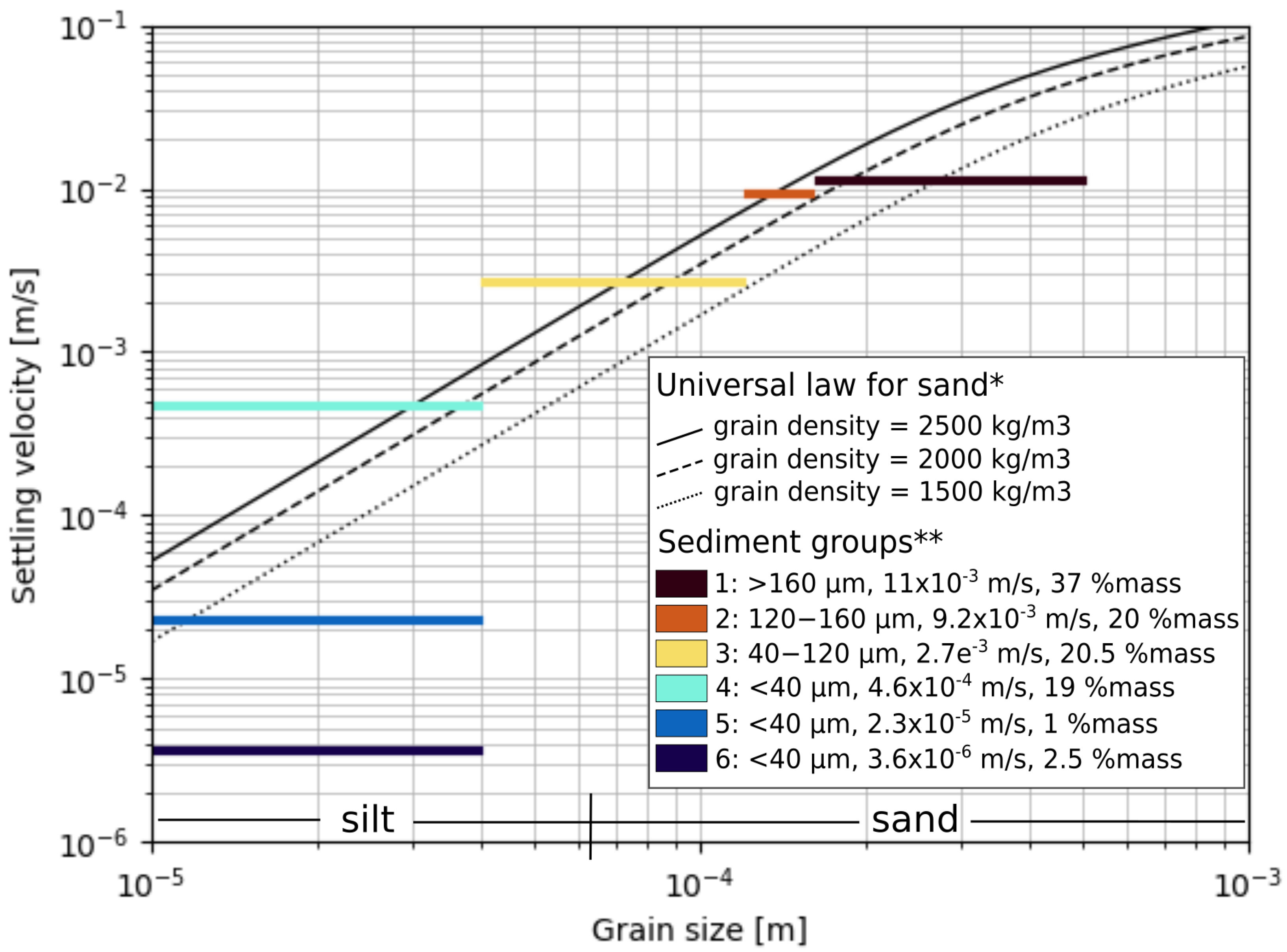
2.3. Particle Settling Model

One fundamental aspect in assessing the transport of particles entrained in the modeled flow is to accurately capture the grain size distribution and the settling velocity of the sediment composition. Different plumes can form at various stages of the mining operation. During rock excavation, the local benthic sediments and the excavation rock debris are potential sources of sediment plumes. However, the risk of sediment scatter at this stage can be minimized by using under-pressure suction risers that largely prevent plume formation. The main threat for plume formation arises from the disposal of waste material to the seafloor, for which the particles distribution will largely depend on the engineering methods used during ore processing. Due to the unavailability of site-specific ocean crust samples and processed material from the Norwegian Sea, we use data derived from similar crust pavements from the Tropical Seamount near the Canary Islands [28]. This dataset serves as a proxy for estimating the physical characteristics of processed crust debris.

While simplified universal laws [29] can provide a first-order estimate of the settling speed for coarse-grained sand, the behavior of finer silt particles, which can make up a significant portion of the total mass, is more complex. In Figure 2, we plot the settling velocities for crustal debris from [28], where the total sediment mass is split into several fractions (sediment groups 1 to 6, see caption). We superpose the universal law for sand from [29] that we extrapolate into the finer silt grain size region (10–62.5 µm). This law approximates the settling velocities of the larger particles of sediment groups 1 to 3 well, but deviations occur for sediment grains smaller than 40 µm. These finer sediments present a challenge, as their settling speed can vary by several orders of magnitude with the high settling speeds potentially controlled by flocculation processes [30]. Although sediments below 40 µm represent more than 20% of the total mass, only 3% of them (sediment groups 5 and 6) have a very low settling speed (<${10}^{-4}$ m/s), according to [28]. Nevertheless, this still constitutes a substantial fraction of the crustal debris sediments that can easily be mobilized by the background ocean current flow and travel considerable distances.

Due to the unavailability of site-specific ocean crust samples, we use the best available proxy data from [28], which is derived from similar crust pavements, as a reference to specify the sediment size composition and settling velocities for our particle tracking model. This forms the basis for our preliminary estimates. However, it is important to emphasize the need for the development of site-specific studies that account for the influence of local lithology and chosen engineering methodology on particle size and velocity distributions.

Particles are released in the modeled flow field as a post-processing step, assuming purely passive transport. Each particle is assigned a settling velocity based on the sediment group it represents, which is used to calculate its trajectory, and a representative sediment volume, which is used to compute concentrations. Particle positions are updated over time using a Lagrangian midpoint advection scheme. In this approach, the particle trajectory is advanced by evaluating the interpolated flow velocity twice per time step, following the equation ${\mathbf{x}}^{n+1}={\mathbf{x}}^n+{\displaystyle \frac{\Delta t}{2}}\left({\mathbf{v}}^n+{\mathbf{v}}^{n+{\displaystyle \frac{1}{2}}}\right)$, where $\mathbf{x}$ is the position, $\mathbf{v}$ the velocity, and $\Delta t$ the time step. Sediment concentrations are calculated by counting all neighboring particles located within a 1 m³ sphere centered on each particle’s position. The cumulative representative volume of the particles enclosed within this unit volume is then used to determine the local concentration. The minimum representative volume corresponds to 0.5 parts per million (ppm), representing the smallest concentration resolvable with our technique.

3. Results

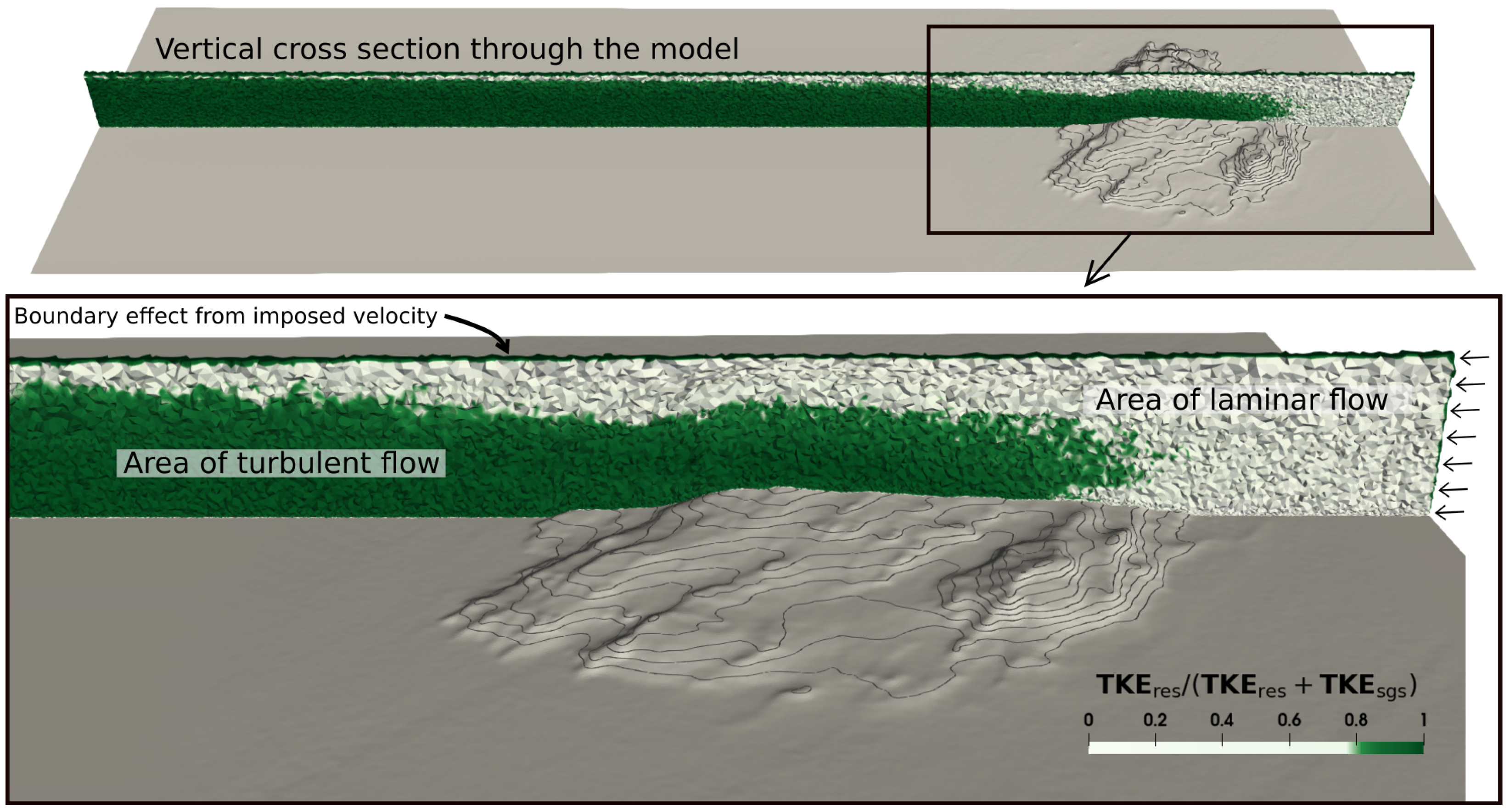
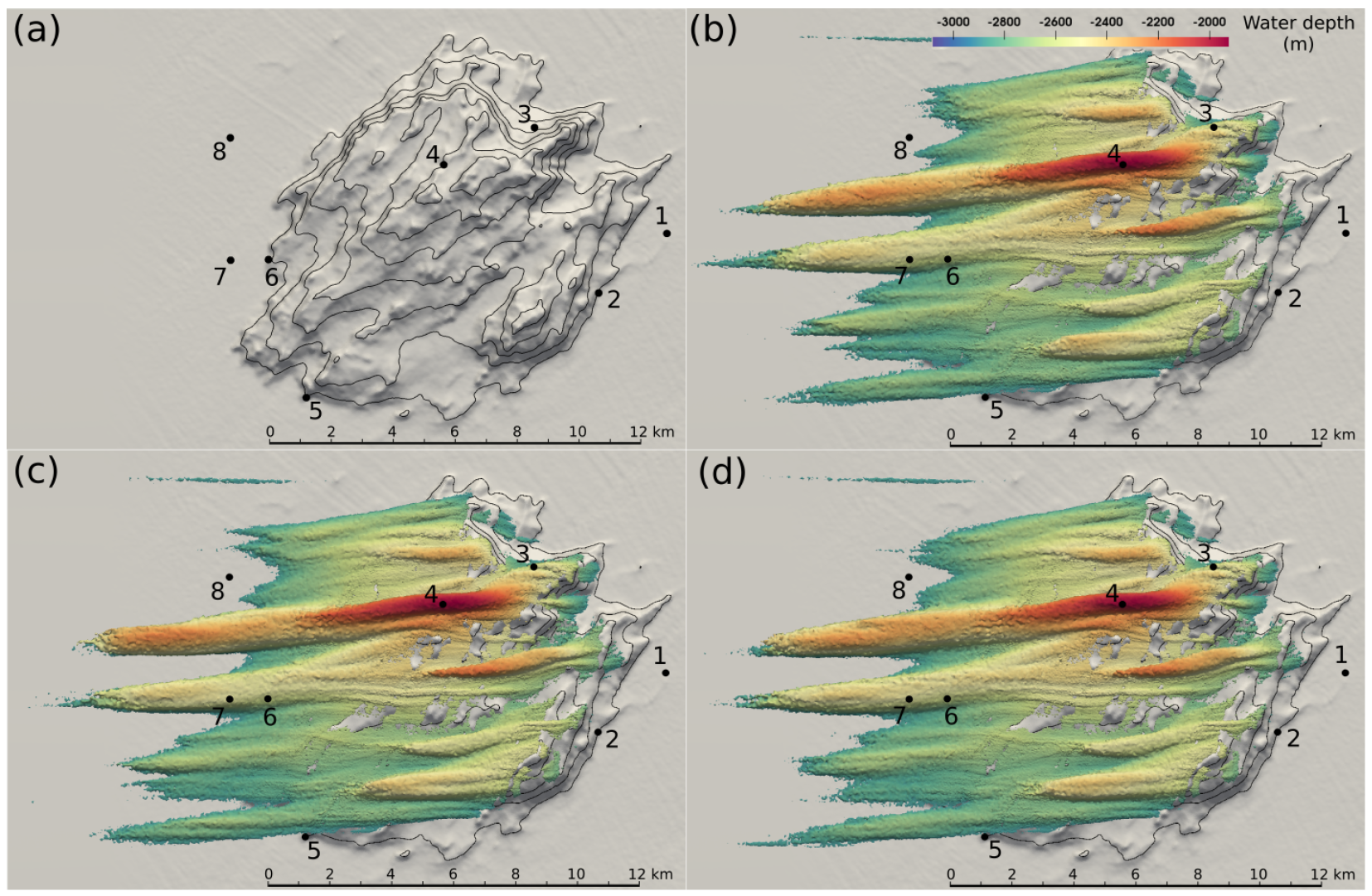
3.1. Turbulent Flow

All three scenarios of inlet velocity, representative of the natural variability in the ocean current, show a pervasive turbulent wake with eddies that propagate far into the lee side of the seamount (Figure 3, Supplementary Movie S1 for inlet velocity of 5 cm/s). The intensity of the turbulence that develops over and behind the seamount increases with the inlet velocity amplitude. However, despite the increase in turbulence intensity, the associated flow fluctuations remain small in comparison to the mean flow field. For the simulation with 5 cm/s inlet velocity, the simulated time was set to 20 days, including 10 days to initialize the turbulence from laminar conditions and 10 days of fully developed steady turbulence regime used to perform the statistical analysis and the sediment release studies. Notably, steady state turbulence was reached within 5 days for this scenario, providing an estimate of the time scale required for the turbulent patterns to stabilize. This stabilization time scale was observed to decrease by half for the 10 cm/s inlet velocity scenario and to double for the 2.5 cm/s inlet velocity scenario. To better quantify and illustrate where turbulence contributes significantly to the flow field, we calculate the ratio of the turbulent kinetic energy (TKE, based on the flow fluctuations) to the mean kinetic energy (MKE, based on the time-averaged velocities). Figure 4 shows the isosurface where the TKE contributes to at least 5% of the total energy balance. Choosing a different value for the isosurface has a minor impact on the observations discussed here. Regarding the distribution of turbulence, we observe prominent turbulent finger-like channels rooting from the highest topographic ridges and extending far into the lee side of the seamount (Figure 4). The main turbulent channel reaches heights of 1000 m (i.e., 2000 m water depth), which is about 250 m above the seamount summit and extends 10–15 km into the lee side. The morphology of the seamount appears to be the dominant parameter controlling the spatial distribution of the turbulent channels, whereas the background flow amplitude controls the intensity. The lateral extent of the 5% TKE/MKE isosurface, presented for the background velocity of 5 cm/s in Figure 4, is independent of the flow intensity and is nearly identical for the 2.5 and 10 cm/s background flow scenarios (Figure A3, Appendix A Section).

Another observation from Figure A3 is that the 5% TKE/MKE isosurface extends at low elevation far behind the seamount (blue tail), arguably showing that turbulence contributes significantly to the flow field within the first ca. 150 m above the abyssal plain. However, this is caused by the gradual reduction in the mean flow towards no-flow conditions at the seafloor rather than a vigorous turbulent regime near the seafloor. Any fluctuation from the above water column turbulence appears to have a significant impact on the total energy balance towards the seafloor, despite low turbulent flow in absolute amplitude. We should, therefore, distinguish this part of the isosurface from the finger-like turbulent channels directly connected to the seamount topography, where both mean and turbulent flow magnitudes are significant.

We further analyze the flow field in terms of its mean magnitude for the intermediate inlet flow scenario (5 cm/s) at four different heights above the seafloor (Figure 5). At the lowest 5 m elevation the velocities are reduced due to the no flow bottom boundary condition at the seafloor (see Section 2.2.3). At 10 m height we start to see increased velocities in front (with respect to the applied flow) of topographic highs and decreased velocities right behind them. The picture at 50 m height is rather complex and dominated by the effects of the various topographic highs and lows. We discern corridors of lower and higher average flow magnitudes over the seamount followed by clear extensions into the lee side. The separation of the flow into different corridors is even more pronounced at 100 m above the seafloor.

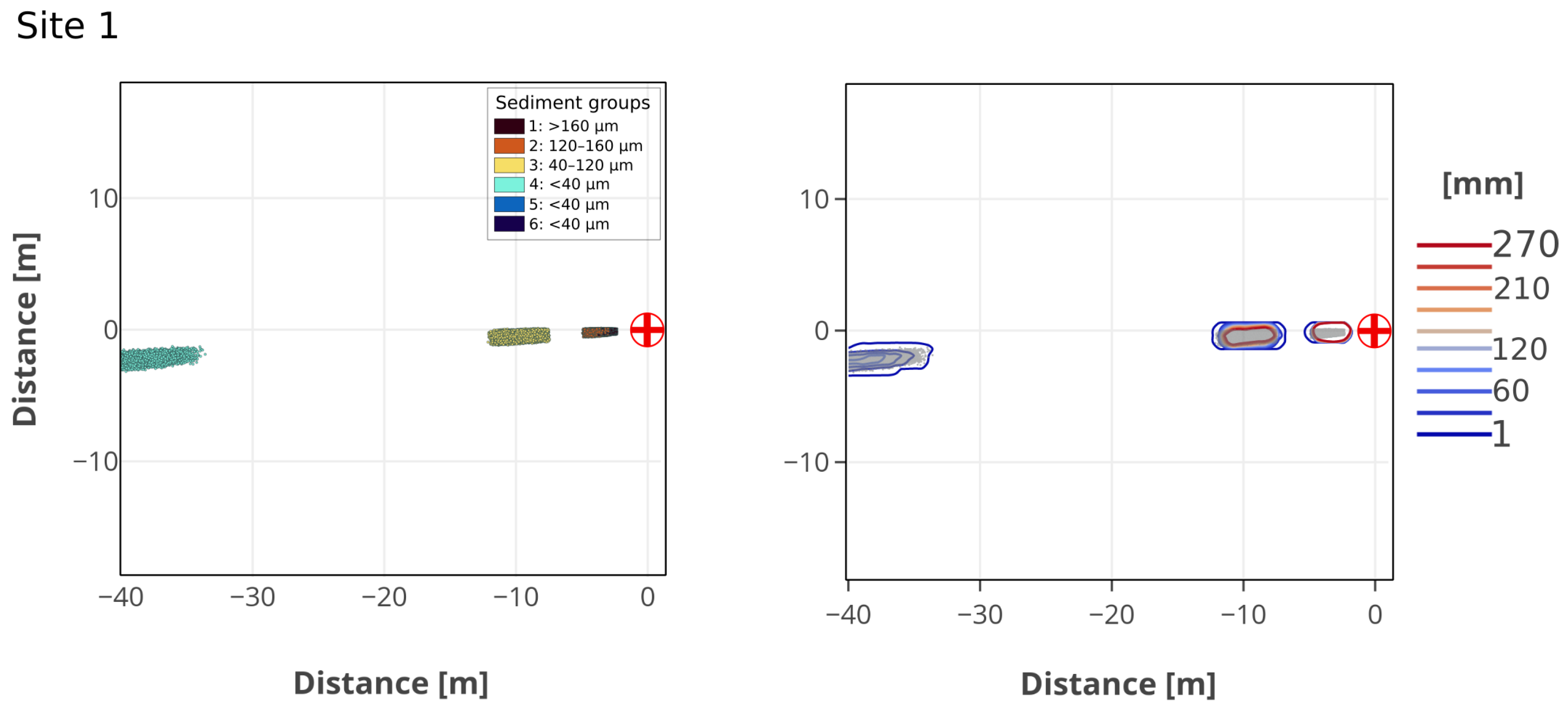
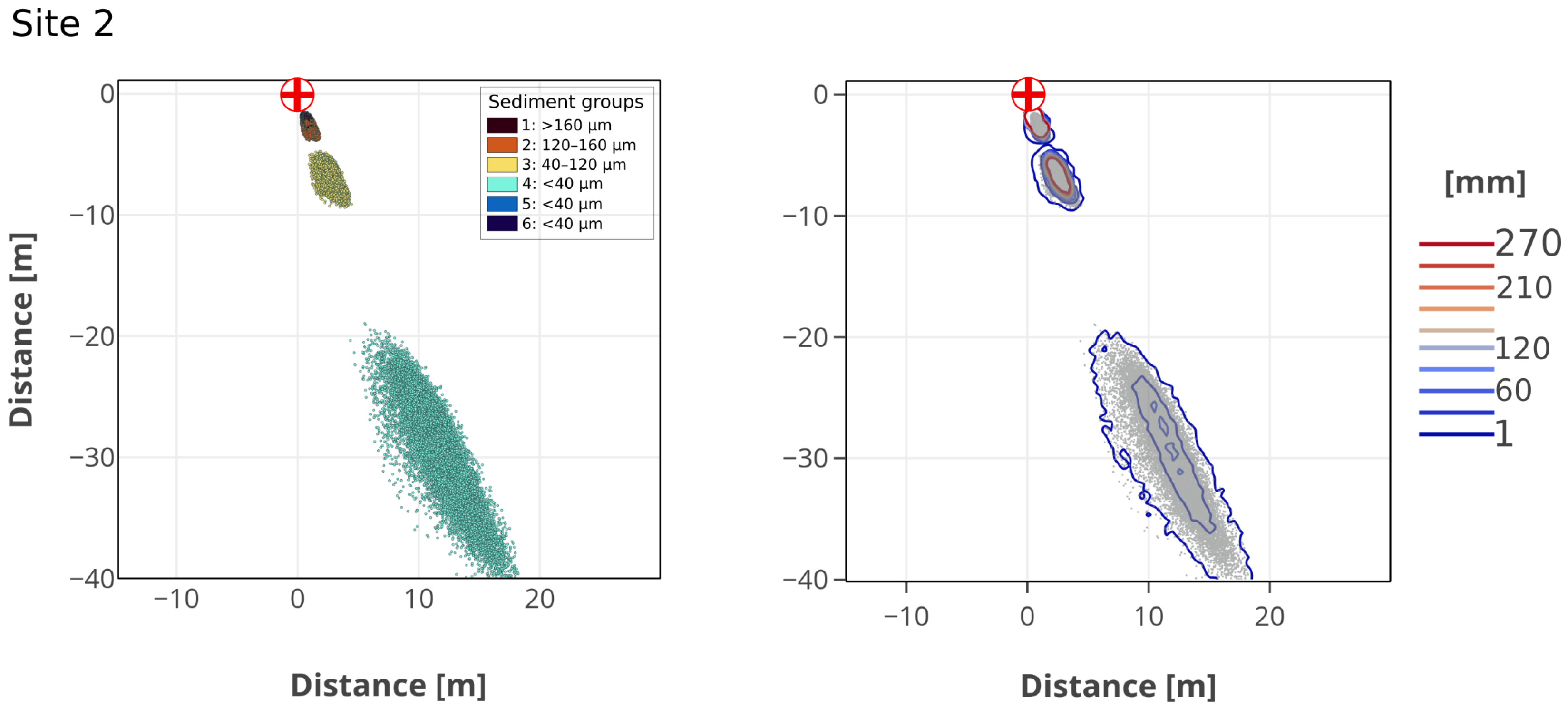
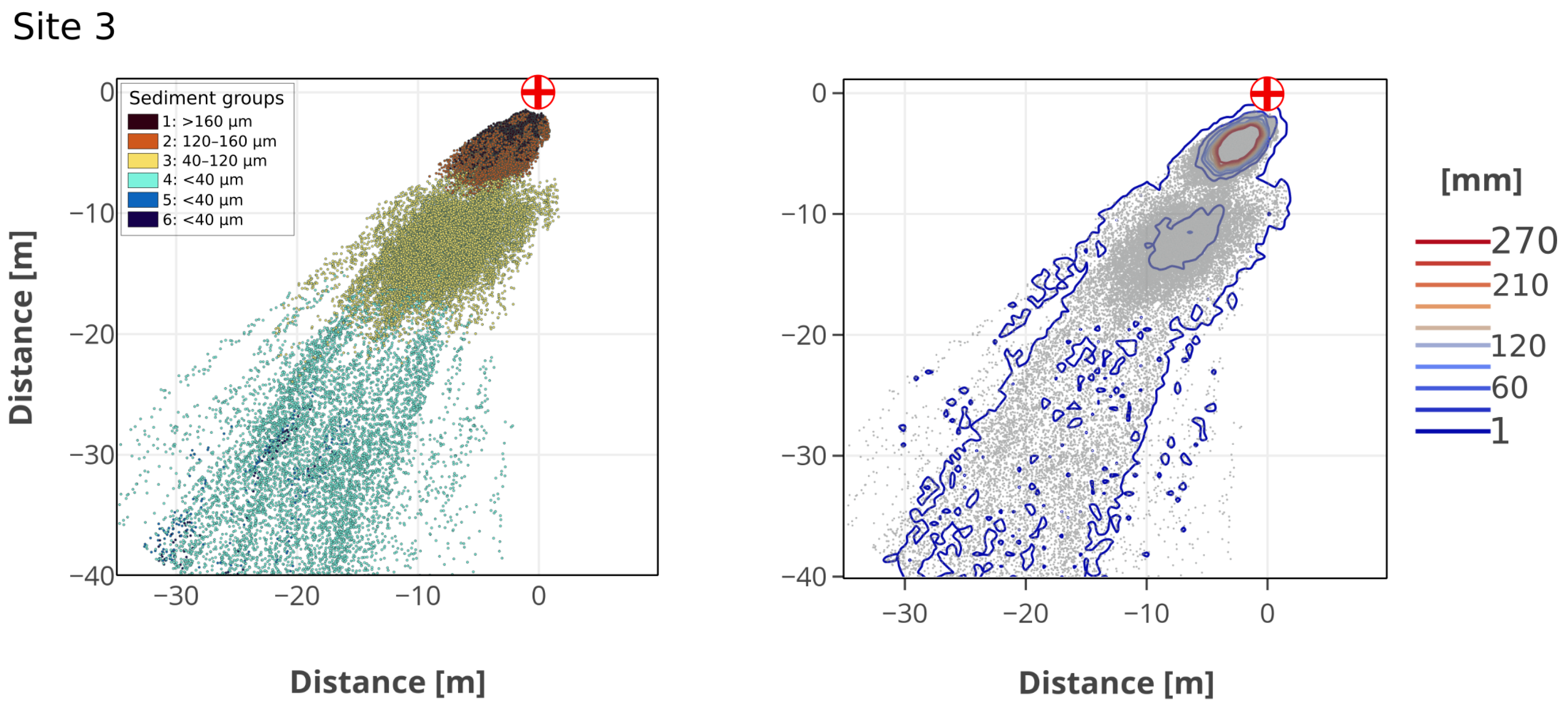
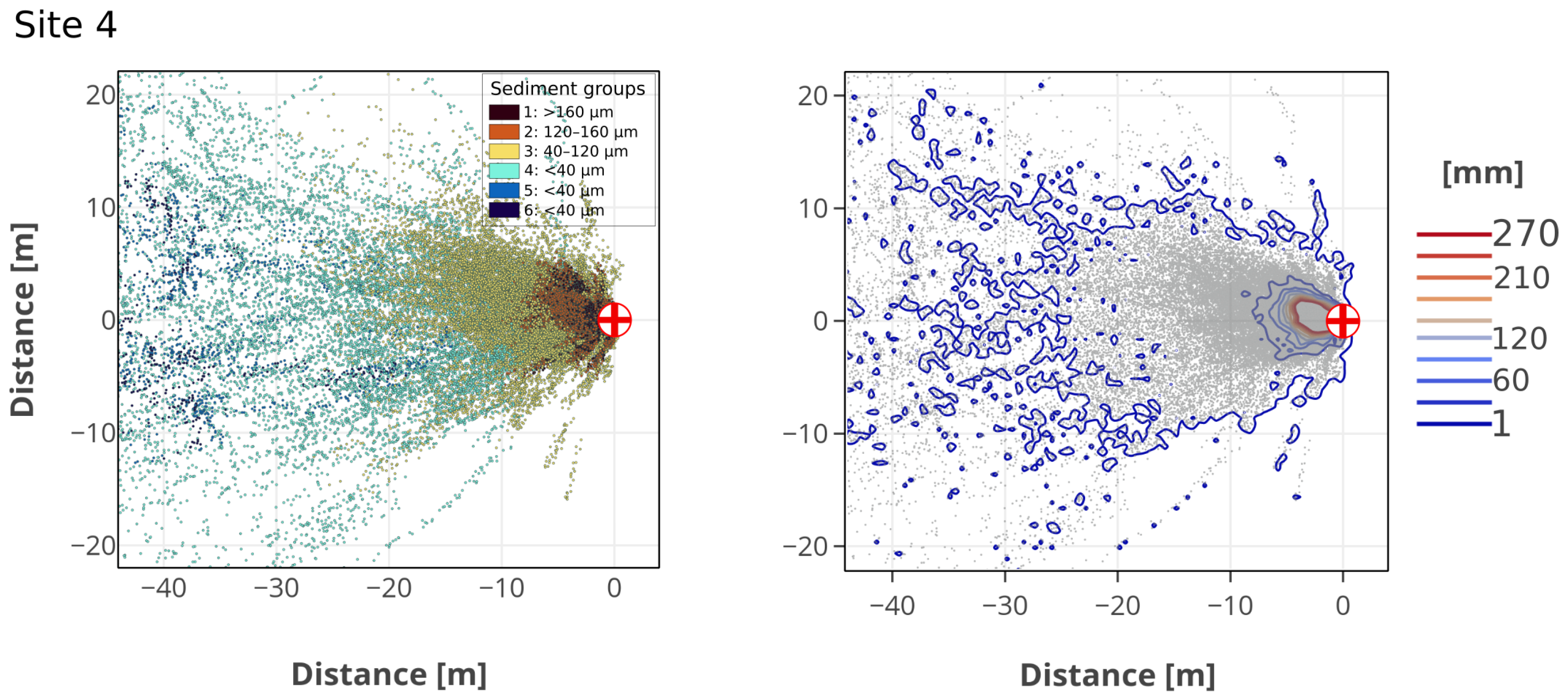
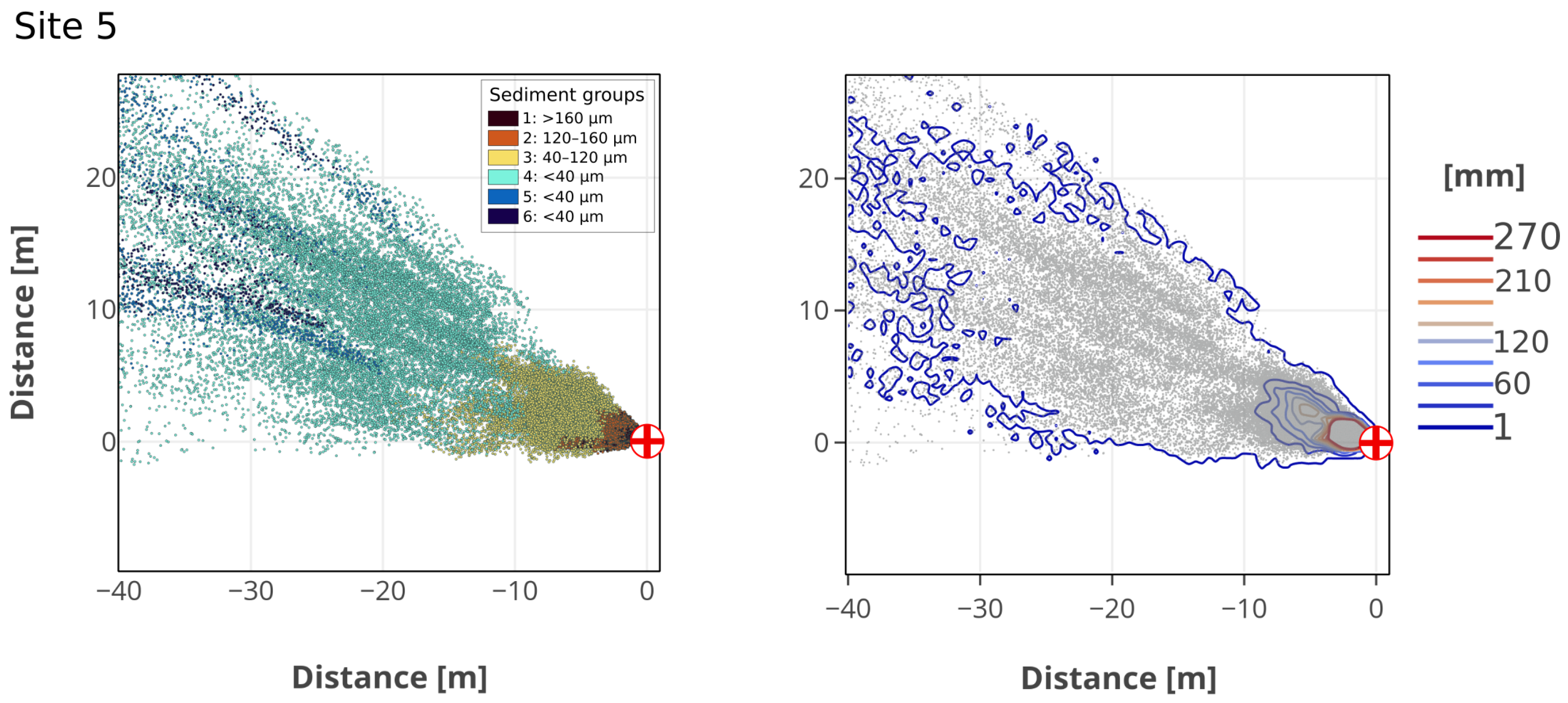
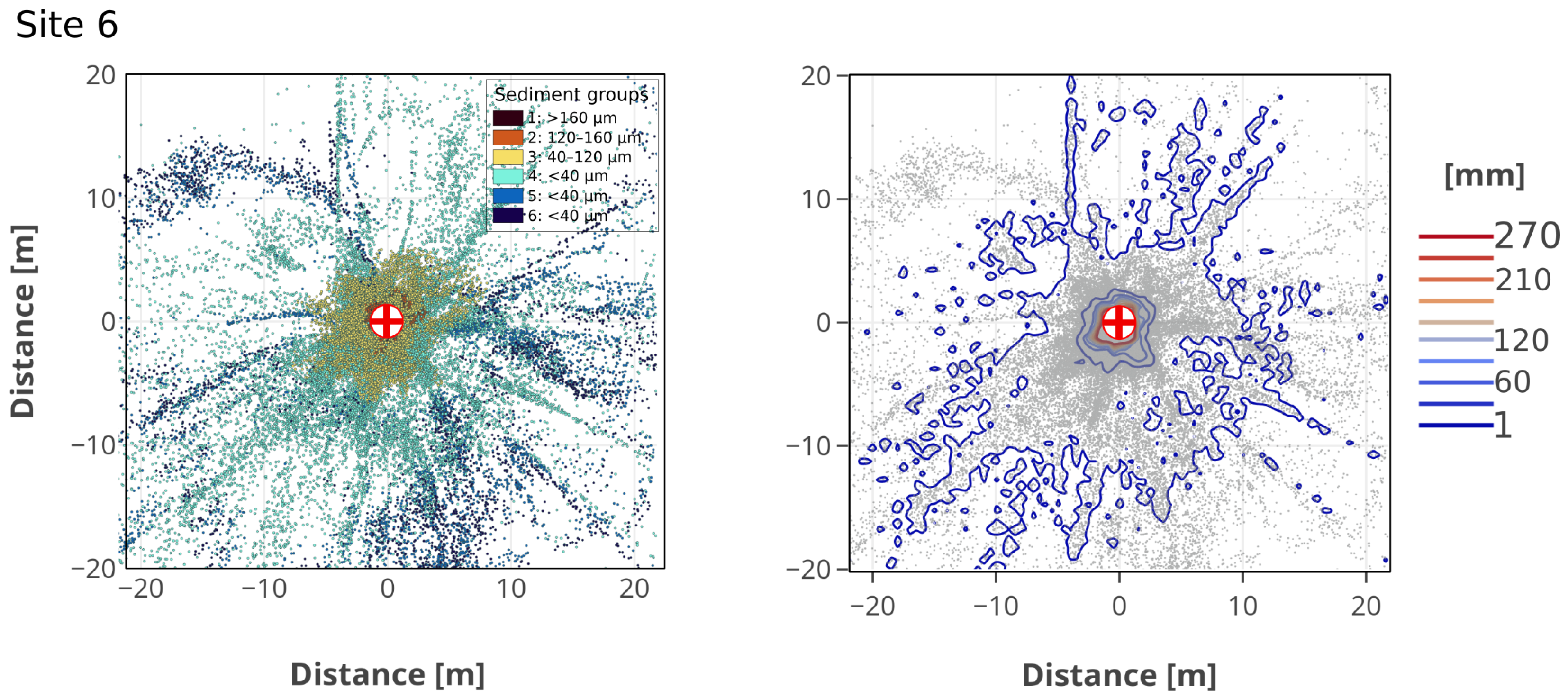
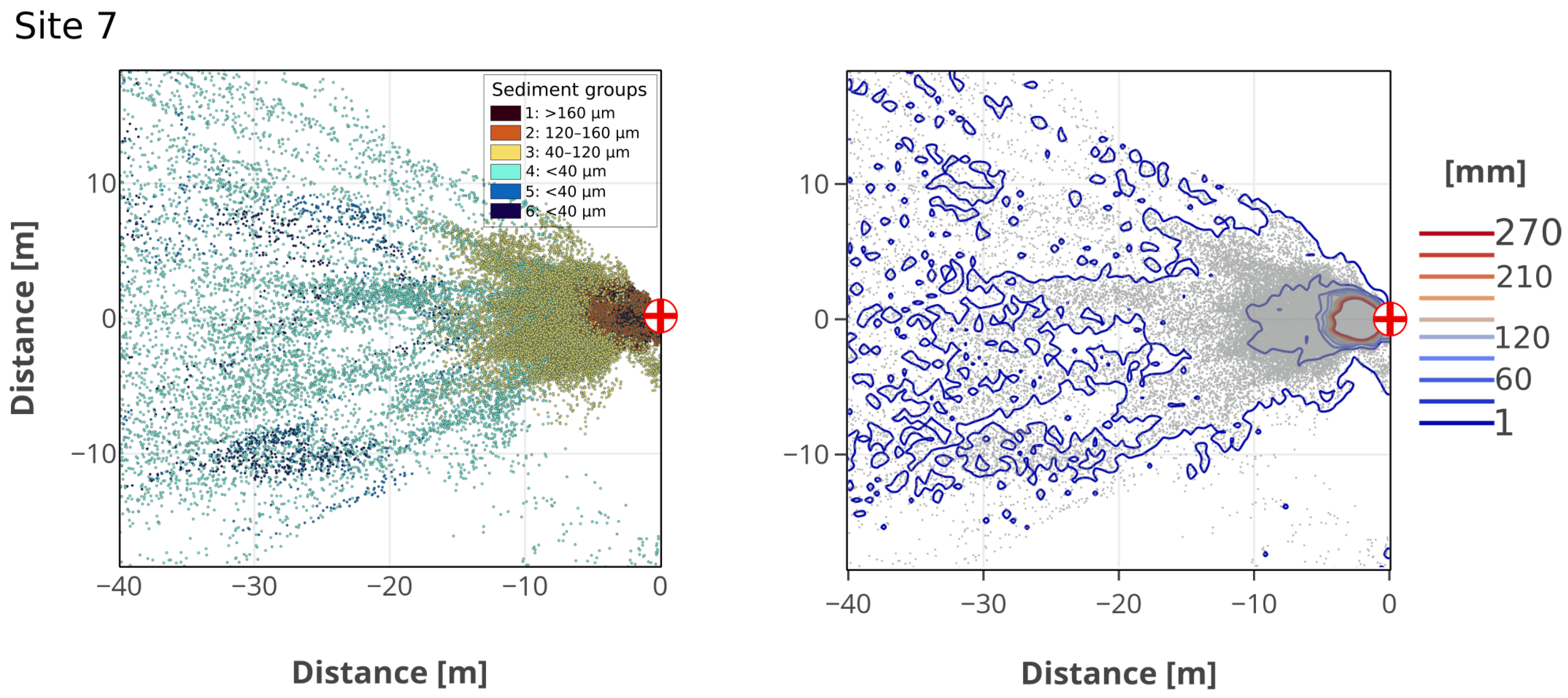
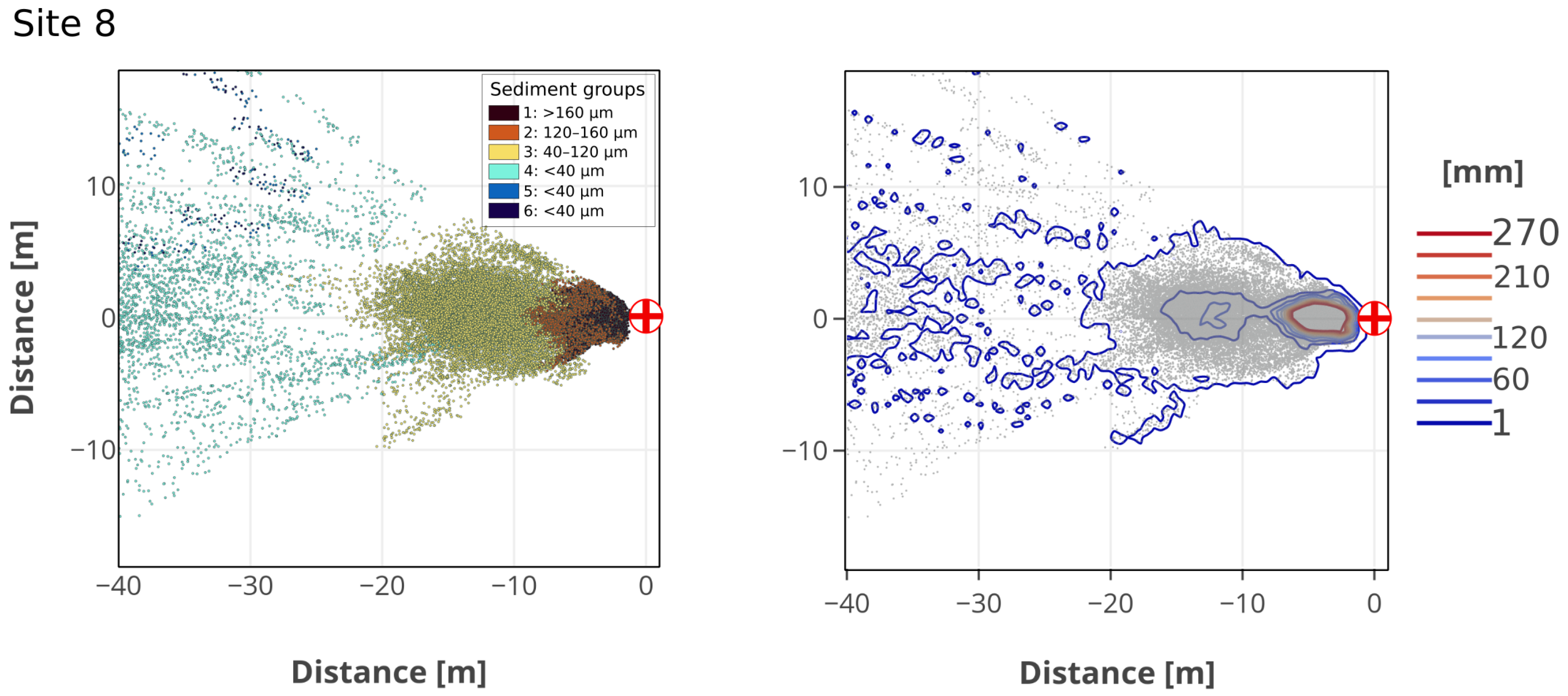
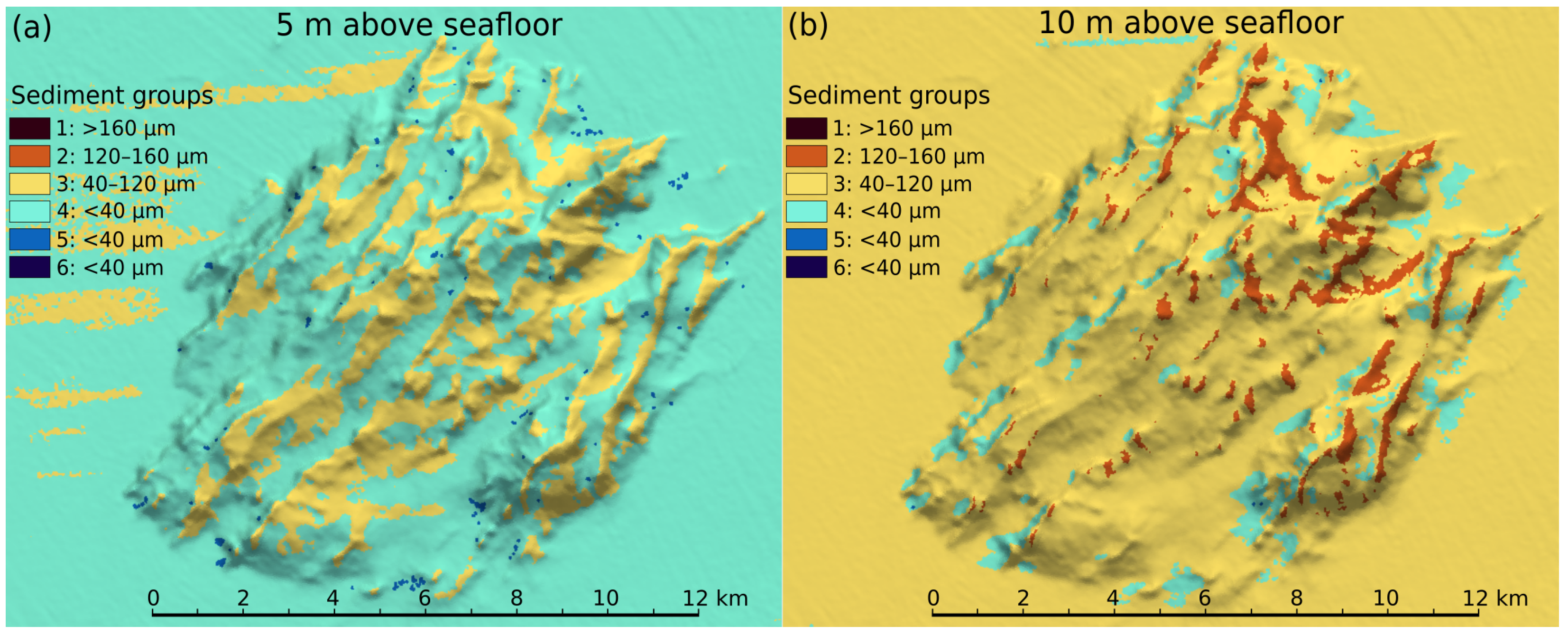
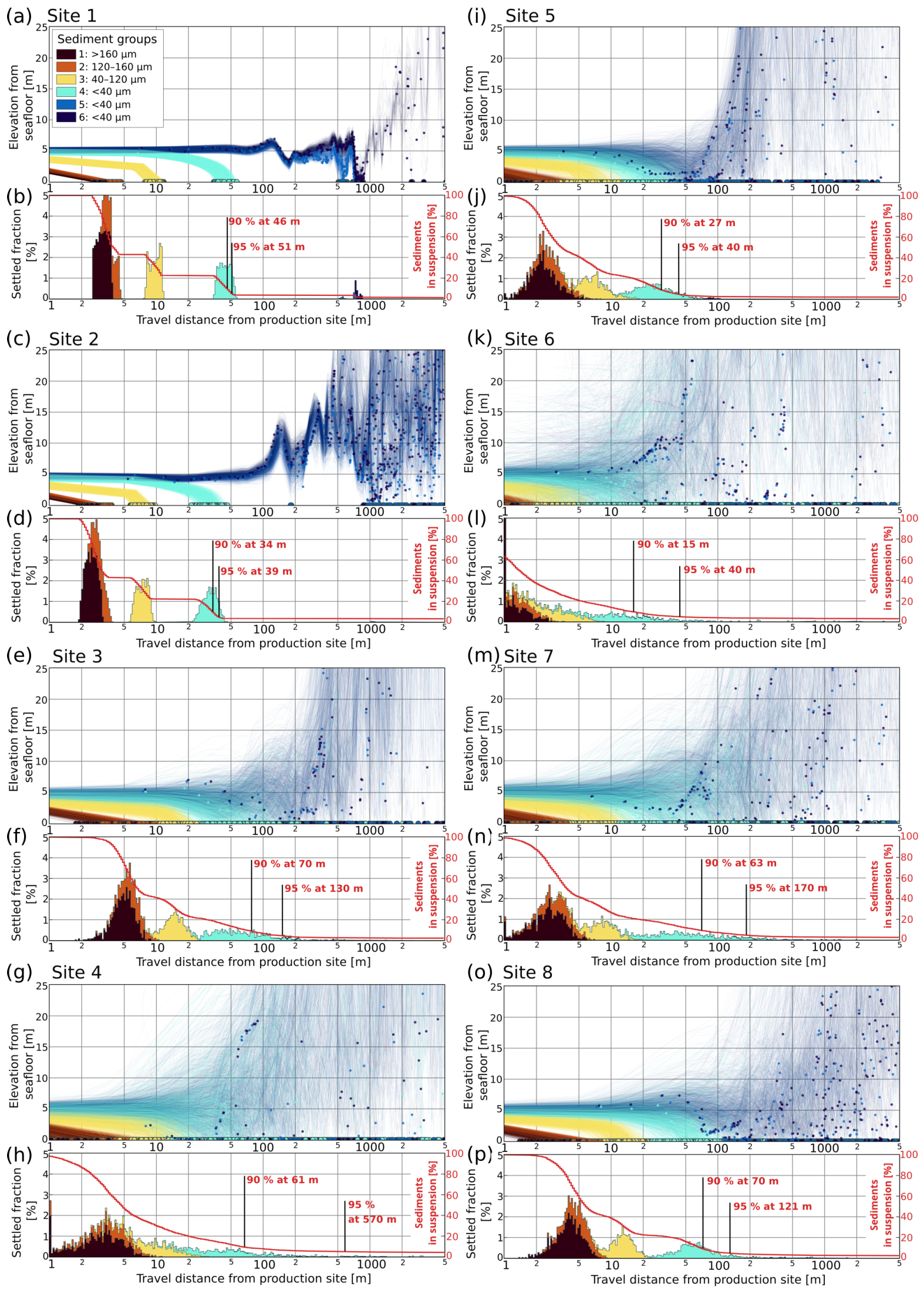
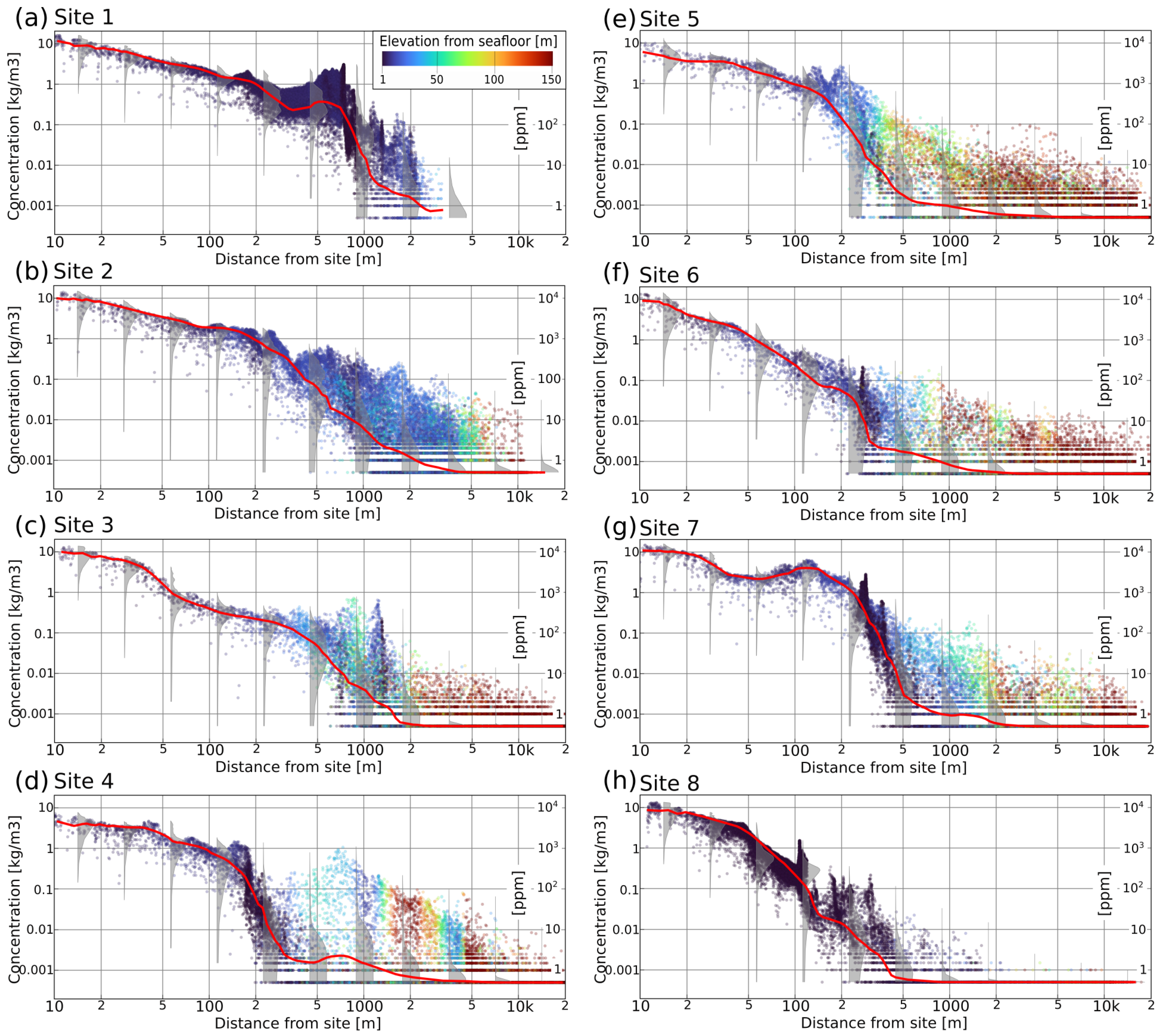
3.2. Particle Spreading

Combining the local mean flow velocities with the particle settling velocities reported for crustal debris [28], allows us to approximate the traveling distance of each sediment group (see Particle Settling Model in Methods for details on the sediment groups definition). We show in Figure 6 the sediment groups that remain in suspension 100 m away (arbitrary) from the release site. We notice that the injection height is a crucial factor affecting the spread of particles. At an injection height of 5 m above the seafloor, particles with a settling velocity equal to or greater than those in group 4 settle within a 100-m radius. When the injection height is at 10 m, particles of group 4 are transported further than 100 m; particles of even lower settling velocities (i.e., groups 5 and 6) stay suspended over most regions of the seamount spreading beyond the vicinity of the injection site. This simplified analysis shows that coarse particles settle at short distances, while finer particles with lower settling velocities can potentially be transported over greater distances.

To obtain a more detailed understanding of how complex flow dynamics affect sediment settling and transport, we conduct numerical experiments in which discrete sets of particles are released and tracked as they move with the computed flow field. This analysis is carried out for eight hypothetical injection sites (see Figure 1 and Figure 4 for injection site locations). At each time step (ca. every 16 min), we release 120 particles (20 particles for each of the 6 sediment groups) in the flow stream over a period of 10 days. This duration allows us to track the particles over several tens of kilometers and statistically assess the variability in the particle trajectories within the turbulent ocean flow. Figure 7 shows the trajectories, distribution, and the fractions of particles remaining in suspension for each of the different sediment groups as a function of distance from the injection sites. The corresponding settled sediment maps are presented as Figure A4, Figure A5, Figure A6, Figure A7, Figure A8, Figure A9, Figure A10, Figure A11 in the Appendix A Section. Overall, we observe a close agreement between the modeled sediment distributions and the predictions made using the mean flow velocity (Figure 6) for the settling distance of the sediment groups 1 to 4, which mainly settle within a 100 m radius. Closer inspection shows that sediment deposition at sites 1, 2, 5, and 8 is characterized by well-defined settling patterns within individual sediment groups, while sediment deposition at sites 3, 4, 6, and 7 exhibits larger variability. These differences are attributed to local hydrodynamic conditions, with sites 1, 2, 5, and 8 being mostly in no/low turbulence areas and sites 3, 4, 6, and 7 in turbulent zones (Figure 4). Interestingly, we still observe that 95% of the plume material settles within 200 m from the injection sites, even in the presence of turbulence. The situation is different for the finest particles in groups 5 and 6, which here is assumed to constitute 3.5% of the total mass. Those only settle in a systematic way close to Site 1, located on the upstream side, slightly away from the escarpments of the seamount, where basal currents are low. For all the other scenarios, the particles in groups 5 and 6 remain mostly in suspension and disperse toward higher levels within the water column (Figure 7). The different behavior of these fine particles can be explained by their lower settling velocities, which make them more susceptible to the effects of turbulence and mixing, thus preventing them from settling to the bottom.

To further investigate the dispersion of sediment groups 5 and 6, we compute their concentration in the water column as a function of water depth and distance to the release site. For this analysis, we have explored an additional release scenario, in which 1 m³ of sediment (assumed equivalent to 1× 10³ kg) is released. Technically, we discretize 35 kg of sediment (corresponding to the 3.5% that represent groups 5 and 6) with 70,000 particles that each represent 0.5 ppm of the volume/mass fraction, randomly distributed within a 1 m³ volume, and released 5 m above the seafloor. We then calculate the sediment concentration for each time step by summing the weights of all neighboring particles present within an enclosed 1 m³ sphere from each particle. We perform this analysis over a period of 6 days which is sufficient to track the development of concentration. The results for all eight hypothetical mining sites are presented in Figure 8, where we plot particle concentrations and the modes of the concentration distributions as functions of the traveled distance. Movie S2 further illustrates the particle dispersion and concentration dynamics at the hypothetical mining Site 4. Within the first 100 m, the fine-grained particles remain close to the seabed (blue markers) and close to each other. In some cases, the local concentration even increases when particles gather in areas of reduced current velocity (Figure 8a,g). Ultimately, a significant concentration drop occurs within a 200 to 1000-m distance when particles become entrained into turbulent zones, causing them to mix and scatter efficiently towards higher elevations from the seafloor (red markers). Beyond the 1000 to 2000-m range, the mode of the concentration distributions falls below 1 ppm, potentially indicating full dilution of the sediment plume into the water column.

4. Discussion and Conclusions

4.1. Lee Wave Dynamics

The presented high-resolution simulations of the flow around a seamount demonstrate that seafloor morphology plays a crucial role in determining the spatial distribution of the turbulent wake channels that develop on the lee side of topographic edifices. These wake channels are an intrinsic feature of flow affected by seamounts, and their intensity scales with background flow velocity.

Our model enables explicit resolution of turbulence using the LES approach, not only preserving the energy balance in the sub-grid space but also preventing the formation of small-scale turbulence. As a result, near-bottom current fluctuations are primarily driven by eddies with characteristic scales of approximately 10 m near the seafloor. While higher-resolution bathymetry and finer mesh discretization could resolve smaller-scale turbulence, computational constraints make this challenging within a single model framework. An alternative approach could involve the use of nested models with varying resolutions, enabling sequential coupling across spatial scales to better capture fine-scale processes. Despite this limitation, the resolution of our model is sufficient to capture key flow dynamics driven by the seamount’s topography, including its influence on the formation of turbulent channels on the lee side (Figure 4). These features are marked by regions of relatively high turbulent kinetic energy, offering valuable insights into potential mixing zones. Importantly, these turbulence maps can be regenerated for a variety of oceanic conditions, accommodating changes in both current direction and amplitude. The stabilization time scale of the turbulent patterns was simulated to be approximately 5 days for the 5 cm/s inlet velocity scenario, starting from laminar flow conditions. This highlights the time required for such structures to develop under changing current conditions. Additionally, the Supplementary Movie S2 effectively illustrates particle dispersion in the water column and clearly shows the scale and strength of lee wave eddies as they form and propagate within the background flow behind the seamount. These findings underscore that, although our model cannot fully resolve turbulence structures in the sub-grid space, it effectively captures the larger-scale dynamics that drive sediment transport and mixing in complex seafloor environments.

4.2. Sediment Interactions with Turbulence

Our simulations show that the importance of these turbulent processes for the spreading of man-made sediment plumes is a function of grain size (and settling velocity). Coarser-grained sediments with settling velocities > ${10}^{-4}$ m/s are modeled to sink rapidly to the seafloor. We here predict that 95% of the sediments settle within 200 m. These results are consistent with in situ experiments from Ref. [3] where 92–98% of sediments settled within the first hundred meters. This can be explained with the majority of sediment plume material having settling velocities that are greater than the vertical component of any local current, meaning that turbulence has limited impact on overall settling distances. However, as discussed in Ref. [6], the deposition pattern within the first few hundred meters can be overprinted by small-scale density currents near the plume release site. Therefore, the sedimentation patterns presented in Figure A4, Figure A5, Figure A6, Figure A7, Figure A8, Figure A9, Figure A10, Figure A11 in the Appendix A Section are only representative for the background flow component of near-field processes but do not capture the full complexity of sediment deposition at the submeter scale. Nevertheless, based on the close agreement between our results and the in situ experiments, we argue that the finite effective settling distance of the plume (95% of the sediments) can be accurately estimated within the distances modeled in our approach.

Smaller sediment particles with settling velocities <${10}^{-4}$ m/s (groups 5 and 6) are likely to remain in suspension over larger distances. As their settling velocities can be orders of magnitude lower than the fluctuations of the background flow, particles can travel over long distances and become entrained into larger scale ocean current eddies. Our simulations show that turbulence can increase the mixing of fine sediment particles, enhancing the dilution of the plume. Within a traveling distance of 2 km from the release site, the concentration of these fine particles drops to sub-ppm levels.

The LES approach inherently filters out turbulence at sub-grid scale, impacting the apparent stability of particles near the release region. In our release scenario of fine sediments, the particles show relatively linear trajectories immediately after release, closely adhering to the local current direction and maintaining a nearly constant elevation above the seafloor. This is visible in Supplementary Movie S2, where particles at this site initially maintain a constant low elevation along the seabed for approximately five hours and 180 m before becoming entrained in turbulence. The turbulent motion subsequently influences their vertical displacement, modulating mainly their elevation and dilution in the water column. This limitation of our model, which filters out the sub-grid turbulence, may lead to an overestimation of the distance at which particles begin interacting with the background turbulence.

Recent studies [30,32] demonstrate that flow turbulence at low shear rates promotes the aggregation of fine particles into larger flocs. At higher shear rates, which our model does not reach, flocs disintegrate. Flocculation primarily occurs at high particle concentrations that are characteristic for the vicinity near release sites and diminishes rapidly once particles disperse into the ocean current. Therefore, we propose that the settling velocities used in our model provide a reasonable first-order estimate for quantifying the dispersal of fine sediment plumes within the ocean current.

4.3. Limitations and Future Work

While our modeling strategy provides important first-order insights into topography-driven turbulence and sediment dispersal, several simplifications highlight promising directions for future development. A primary simplification relates to the large-scale flow dynamics. The neglect of the Coriolis effect prevents our simulated flows from achieving full geostrophic balance. In the North Atlantic, we estimate this could introduce a southward deflection of approximately 10% of the east–west transport distance [33]. While we hypothesize that the regional Lofoten Basin gyre is the dominant forcing, future work should explicitly couple these effects. This could be achieved through nested modeling, embedding our high-resolution LES within a larger-scale ocean circulation model that includes geostrophic and gyre dynamics. Another key area for enhancement is the inclusion of time-varying boundary conditions to represent tidal and seasonal cycles. At depths of 3000 m, internal tides can introduce persistent variability that modulates background currents and enhances vertical mixing over long timescales [18,34]. Incorporating tidally-forced flows, ideally constrained by long-term observational data, would be a valuable step in quantifying their role in shaping sediment plume trajectories. A further limitation lies in the lack of site-specific data, which affects both the representation of the release scenario and the characterization of sediment properties. In the present model, all particles are released within one time step, providing a useful first-order estimate of the dispersal length scale but neglecting variability in the volume, rate, and timing of release, as well as potential operational strategies that may shape input conditions. Similarly, the use of Canary Islands material as a proxy for processed crust offers the best available dataset but may not reflect the mineralogy, density, or particle-size spectrum of Norwegian Sea sediments. Addressing these limitations will require acquisition of site-specific and operationally relevant data, which would enable the formulation of more realistic release scenarios and improve the model.

5. Conclusions

Our analysis demonstrates that high-fidelity, high-resolution modeling of turbulent flow around bathymetric relief provides a powerful approach for assessing the spreading and settling of sediment plumes. The simulations reveal that coarse, heavy particles settle rapidly near the source, with rates governed by their settling velocities, while finer, lighter particles remain suspended, becoming entrained in turbulent flow structures and transported over substantially greater distances. Importantly, the distinction between “settling” and “traveling” sediment mass should not be viewed as a fixed threshold of settling velocities but rather as a continuous transition sensitive to prevailing hydrodynamic conditions, dynamically shaped by background flow and turbulence in the seamount wake. Within our simplified sediment release scenario, turbulence enhances dilution such that fine-particle concentrations decline to sub-ppm levels within approximately 2 km of the release site. This quantification provides valuable first-order estimate constraints for early-stage environmental impact assessments, where reliable dispersal scale estimates remain largely unavailable. Although longer-distance transport results in progressive mixing with ambient seawater and thereby enhances dilution, our results underscore the necessity of carefully characterizing sediment types mobilized by seafloor interventions. Furthermore, it is advisable to minimize mobilization of the finest sediments and to explicitly include turbulent phenomena in hazard assessment frameworks for the spreading of deep-sea sediment plumes.