Finite Element Optimization of 3D Abiotic Glucose Fuel Cells for Implantable Medical Devices
Abstract
1. Introduction
2. Methodology
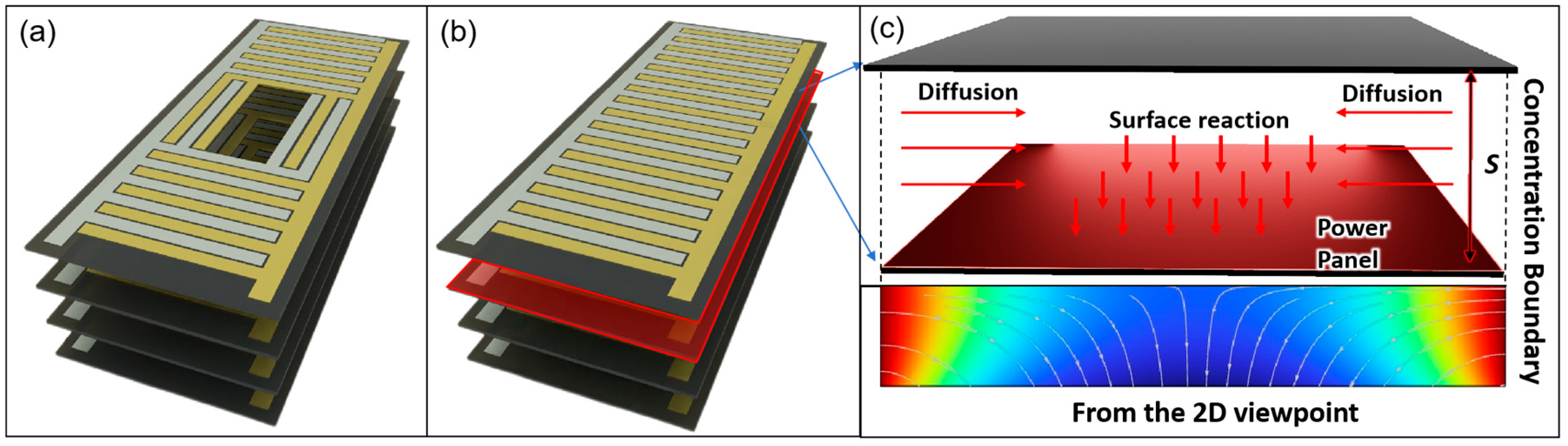
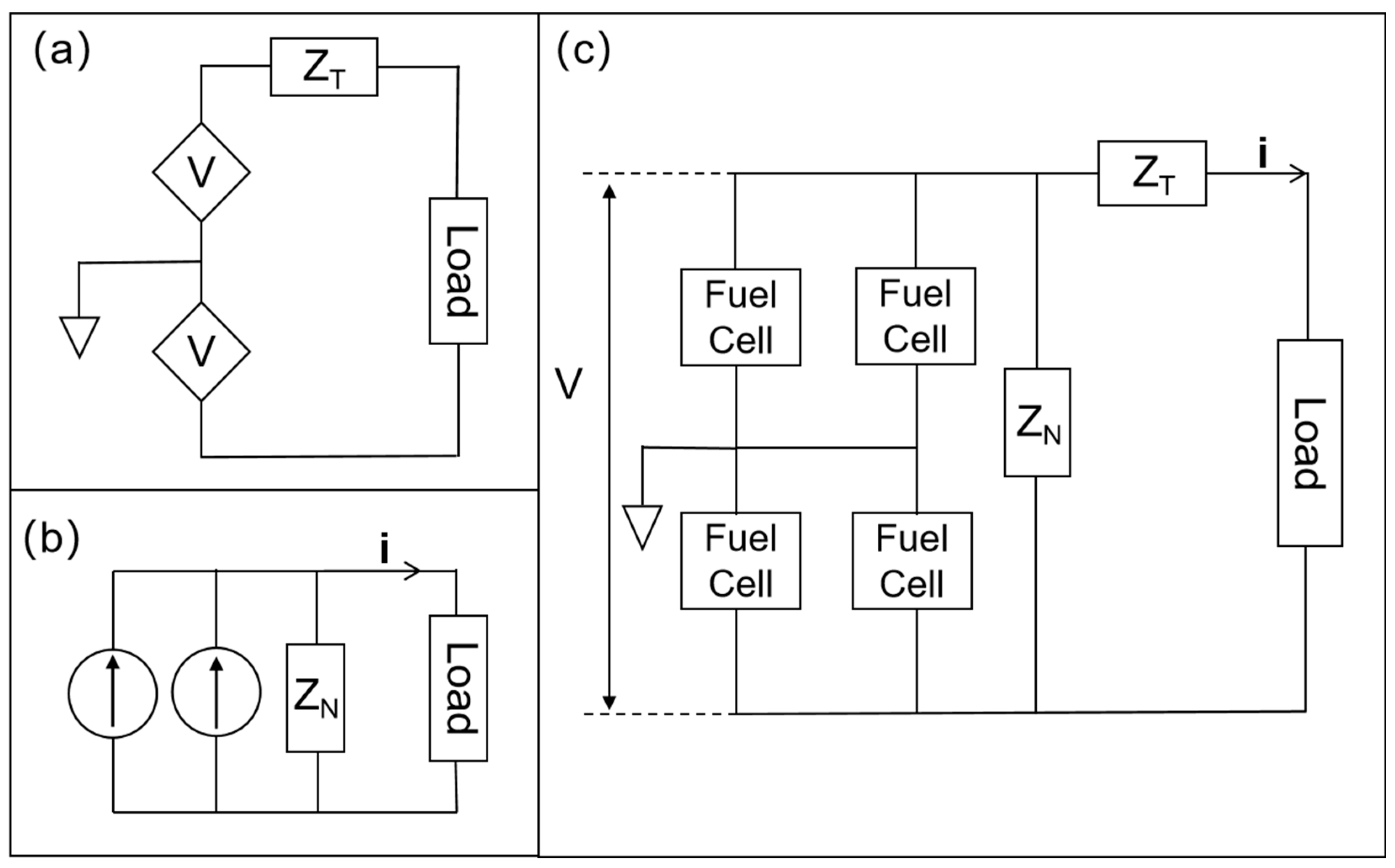
2.1. Simulation Setup
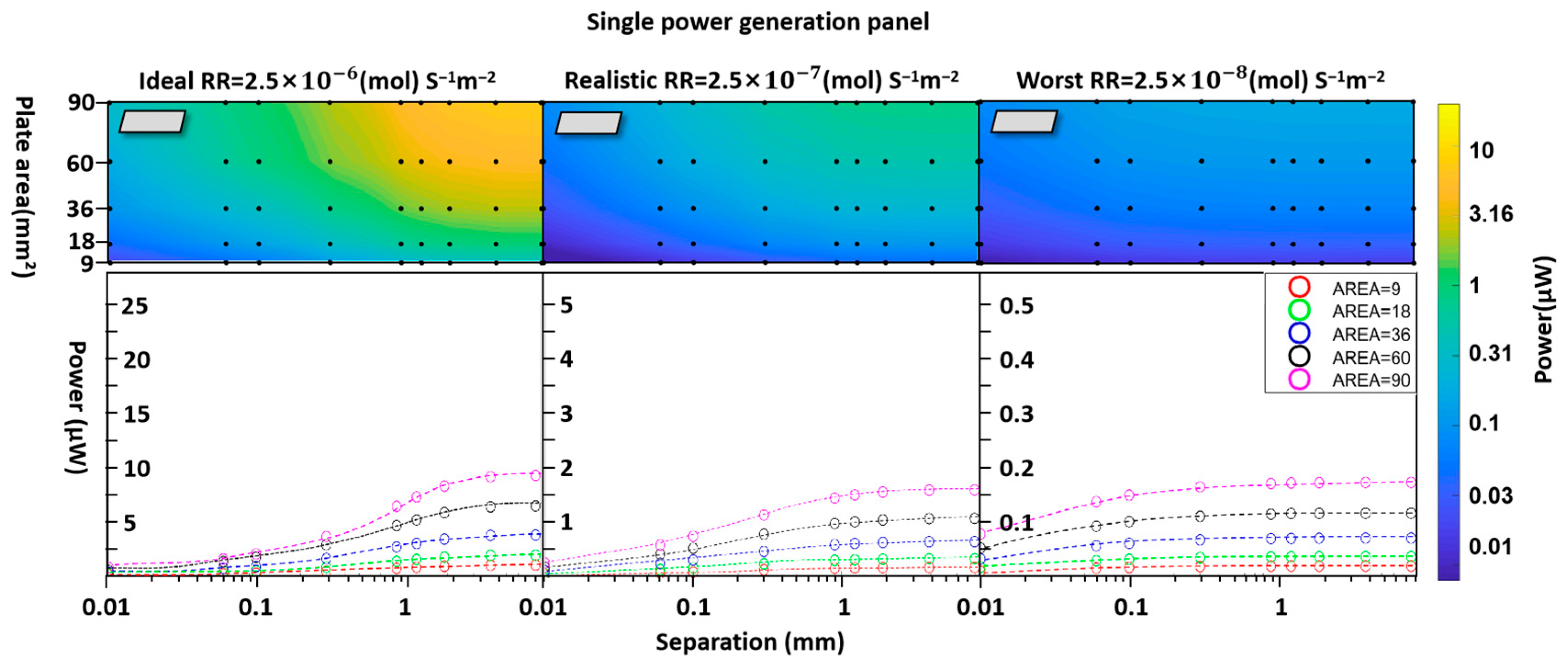
- Blood glucose typically ranges between 3.9 and 6.9 mM, while diffusion into interstitial fluid reduces availability by ~25–30%. Physiological dissolved oxygen in plasma is low (~0.05–0.1 mM), with the majority carried bound to hemoglobin (~9 mM equivalent). In highly vascularized regions, however, hemoglobin unloading continually replenishes the dissolved fraction. Accordingly, we assumed half the arterial oxygen content as an optimistic, perfusion-supported boundary condition to prevent artificial oxygen limitation and to focus on geometric effects. In less-perfused tissues, absolute power would be reduced, but the identified structural trends (optimal spacing, stacking, and geometry) remain valid. We, therefore, set fixed concentrations of 5 mMol L−1 glucose and 4.5 mMol L−1 oxygen at the boundaries of our simulation to be consistent with typical tissue fluid conditions [47,48,49,50].
- The fuel cells are operated at body temperature, 310.15 K.
- The mesh grid was set to ‘extremely fine’.
- The central diffusion cavities do not act as sources of glucose or oxygen but rather serve solely as diffusion pathways.
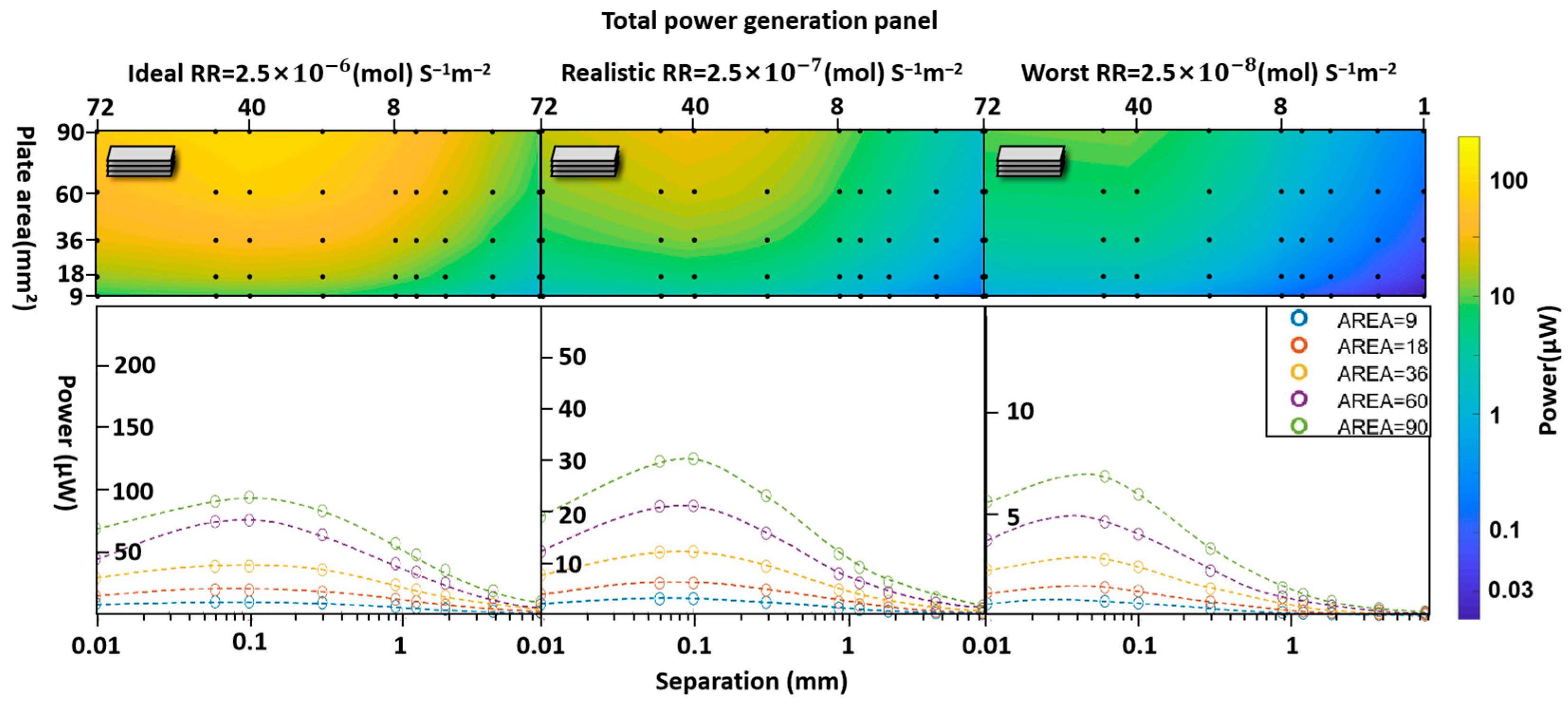
- Surface reaction rate (RR).
- 6.
- Diffusion
- 7.
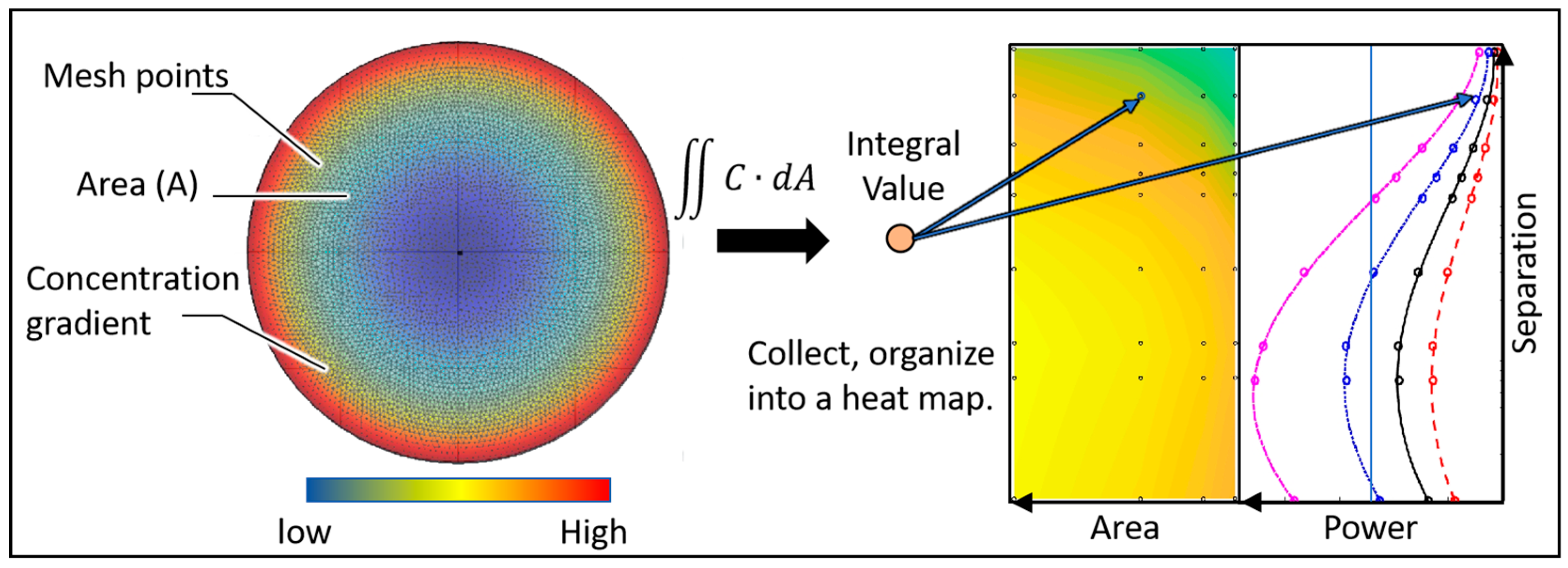
- Integral analysis
2.2. Structural Model
3. Results
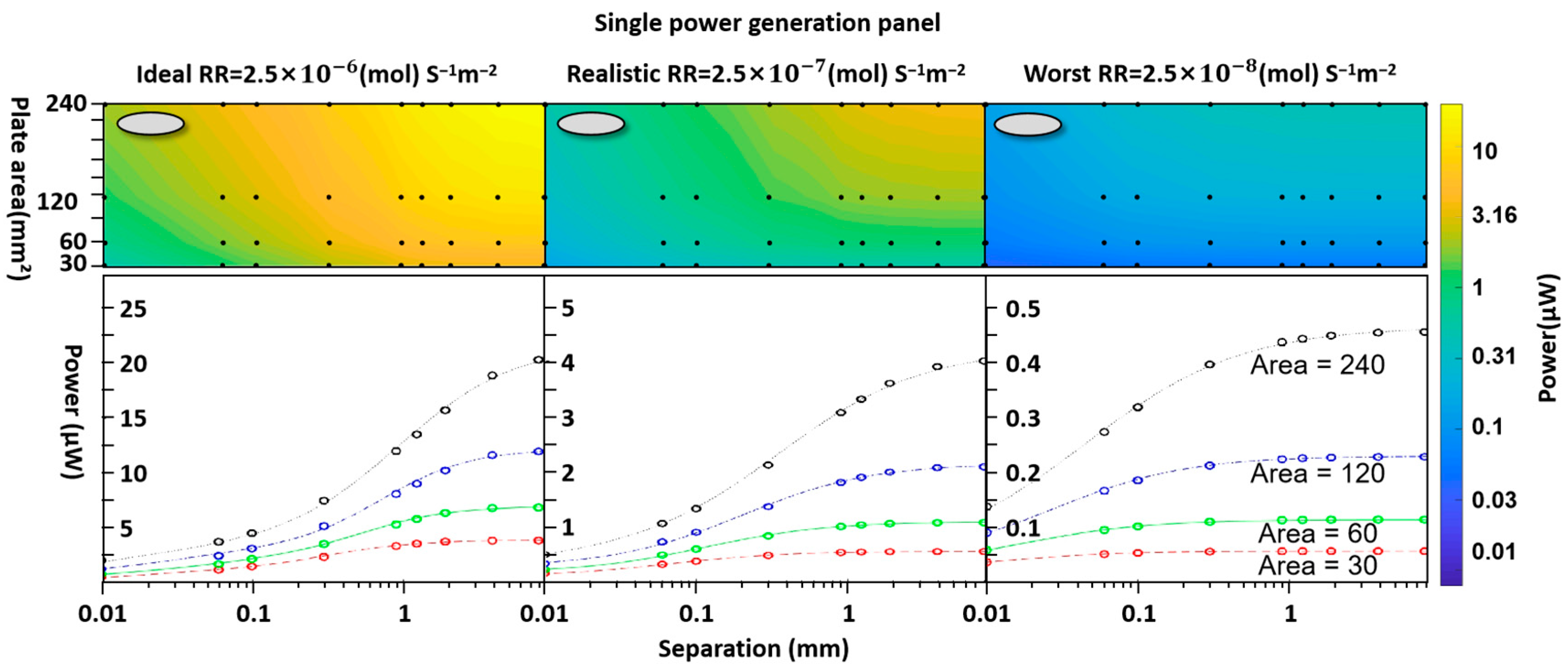
3.1. Individual-Unit Devices
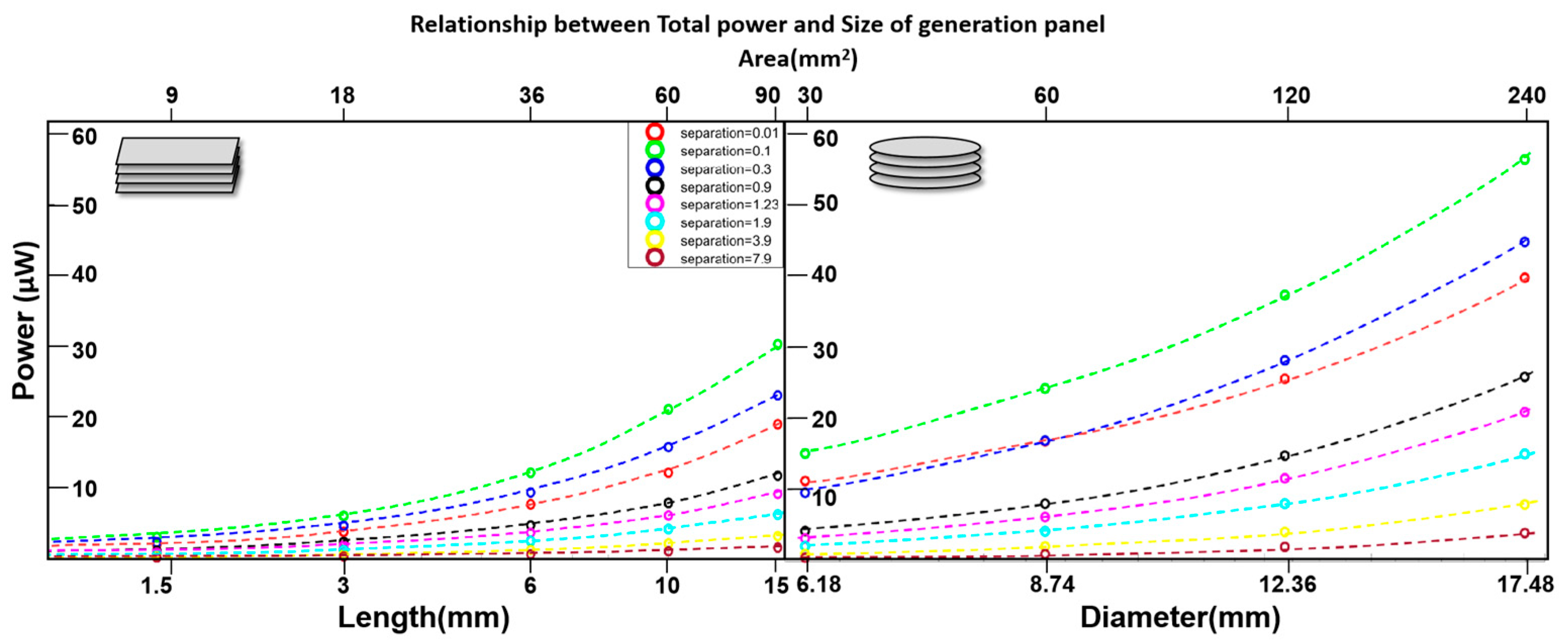
3.2. Multistack Units Without Diffusion Cavities
4. The Effect of Adding Central Diffusion Cavities
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, S.; Sencadas, V.; You, S.S.; Jia, N.Z.; Srinivasan, S.S.; Huang, H.; Ahmed, A.E.; Liang, J.Y.; Traverso, G. Powering Implantable and Ingestible Electronics. Adv. Funct. Mater. 2021, 31, 2009289. [Google Scholar] [CrossRef] [PubMed]
- Goggins, E.; Mitani, S.; Tanaka, S. Clinical perspectives on vagus nerve stimulation: Present and future. Clin. Sci. 2022, 136, 695–709. [Google Scholar] [CrossRef]
- Brinkman, D.J.; Gupta, I.; Matteucci, P.B.; Ouchouche, S.; de Jonge, W.J.; Coatney, R.W.; Salam, T.; Chew, D.J.; Irwin, E.; Yazicioglu, R.F.; et al. Splenic arterial neurovascular bundle stimulation in esophagectomy: A feasibility and safety prospective cohort study. Front. Neurosci. 2022, 16, 1088628. [Google Scholar] [CrossRef]
- Ito, A.; Yamamoto, Y.; Sato, M.; Ikeda, K.; Yamamoto, M.; Fujita, H.; Nagamori, E.; Kawabe, Y.; Kamihira, M. Induction of functional tissue-engineered skeletal muscle constructs by defined electrical stimulation. Sci. Rep. 2014, 4, 4781. [Google Scholar] [CrossRef] [PubMed]
- Cicha, I.; Priefer, R.; Severino, P.; Souto, E.B.; Jain, S. Biosensor-Integrated Drug Delivery Systems as New Materials for Biomedical Applications. Biomolecules 2022, 12, 1198. [Google Scholar] [CrossRef]
- Khadka, B.; Lee, B.; Kim, K.T. Drug Delivery Systems for Personal Healthcare by Smart Wearable Patch System. Biomolecules 2023, 13, 929. [Google Scholar] [CrossRef]
- Joung, Y.H. Development of implantable medical devices: From an engineering perspective. Int. Neurourol. J. 2013, 17, 98–106. [Google Scholar] [CrossRef] [PubMed]
- Wilson, B.S.; Dorman, M.F. Cochlear implants: A remarkable past and a brilliant future. Hear. Res. 2008, 242, 3–21. [Google Scholar] [CrossRef]
- Jacob, M.V.; Bazaka, K. Implantable Devices: Issues and Challenges. Electronics 2012, 2, 1–34. [Google Scholar] [CrossRef]
- Noblett, K.L.; Cadish, L.A. Sacral nerve stimulation for the treatment of refractory voiding and bowel dysfunction. Am. J. Obstet. Gynecol. 2014, 210, 99–106. [Google Scholar] [CrossRef]
- Pavlov, V.A.; Tracey, K.J. Bioelectronic medicine: Preclinical insights and clinical advances. Neuron 2022, 110, 3627–3644. [Google Scholar] [CrossRef]
- Fritz, J.R.; Huston, J.M. Advances in bioelectronic medicine: Noninvasive electrical, ultrasound and magnetic nerve stimulation. Bioelectron. Med. 2019, 2, 143–150. [Google Scholar] [CrossRef]
- Wang, X.; Meng, X.; Zhu, Y.; Ling, H.; Chen, Y.; Li, Z.; Hartel, M.C.; Dokmeci, M.R.; Zhang, S.; Khademhosseini, A. A sub-1V, microwatt power-consumption iontronic pressure sensor based on organic electrochemical transistors. EEE Electron Device Lett. 2021, 42, 46–49. [Google Scholar] [CrossRef]
- Moerke, C.; Wolff, A.; Ince, H.; Ortak, J.; Öner, A. New strategies for energy supply of cardiac implantable devices. Herzschrittmachertherapie Elektrophysiologie 2022, 33, 224–231. [Google Scholar] [CrossRef] [PubMed]
- Khalifa, A.; Lee, S.; Molnar, A.C.; Cash, S. Injectable wireless microdevices: Challenges and opportunities. Bioelectron. Med. 2021, 7, 19. [Google Scholar] [CrossRef]
- Antfolk, C.; Kopta, V.; Farserotu, J.; Decotignie, J.D.; Enz, C. The WiseSkin artificial skin for tactile prosthetics: A power budget investigation. In Proceedings of the 014 8th International Symposium on Medical Information and Communication Technology (ISMICT), Firenze, Italy, 2–4 April 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Katz, D.; Akiyama, T. Pacemaker Longevity: The World’s Longest-Lasting VVI Pacemaker. Ann. Noninvasive Electrocardiol. 2007, 12, 223–226. [Google Scholar] [CrossRef]
- Pfenniger, A.; Jonsson, M.; Zurbuchen, A.; Koch, V.M.; Vogel, R. Energy Harvesting from the Cardiovascular System, or How to Get a Little Help from Yourself. Ann. Biomed. Eng. 2013, 41, 2248–2263. [Google Scholar] [CrossRef] [PubMed]
- Bock, D.C.; Marschilok, A.C.; Takeuchi, K.J.; Takeuchi, E.S. Batteries used to power implantable biomedical devices. Electrochim. Acta 2012, 84, 155–164. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://resonetics.com/sensor-technology-medical-power/medical-batteries/ (accessed on 22 October 2025).
- Hannan, M.A.; Mutashar, S.; Samad, S.A.; Hussain, A. Energy harvesting for the implantable biomedical devices: Issues and challenges. Biomed. Eng. Online 2014, 13, 79. [Google Scholar] [CrossRef]
- Kerzenmacher, S.; Ducrée, J.; Zengerle, R.; von Stetten, F. Energy harvesting by implantable abiotically catalyzed glucose fuel cells. J. Power Sources 2008, 182, 1–17. [Google Scholar] [CrossRef]
- Wei, X.; Liu, J. Power sources and electrical recharging strategies for implantable medical devices. Front. Energy 2008, 2, 1–13. [Google Scholar] [CrossRef]
- The Complete Guide to Medical Device Batteries. Available online: https://Ufinebattery.com (accessed on 22 October 2025).
- Amar, A.B.; Kouki, A.B.; Cao, H. Power approaches for implantable medical devices. Sensors 2015, 15, 28889–28914. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljačić, M. Wireless Power Transfer via Strongly Coupled Magnetic Resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef]
- Magotra, V.K.; Kumar, S.; Kang, T.W.; Inamdar, A.I.; Aqueel, A.T.; Im, H.; Ghodake, G.; Shinde, S.; Waghmode, D.P.; Jeon, H.C. Compost Soil Microbial Fuel Cell to Generate Power using Urea as Fuel. Sci. Rep. 2020, 10, 4154. [Google Scholar] [CrossRef]
- MacVittie, K.; Halámek, J.; Halámková, L.; Southcott, M.; Jemison, W.D.; Lobel, R.; Katz, E. From cyborg lobsters to a pacemaker powered by implantable biofuel cells. Energy Environ. Sci. 2012, 6, 81–86. [Google Scholar] [CrossRef]
- Szczupak, A.; Halámek, J.; Halámková, L.; Bocharova, V.; Alfonta, L.; Katz, E. Living battery—Biofuel cells operating in vivo in clams. Energy Environ. Sci. 2012, 5, 8891–8895. [Google Scholar] [CrossRef]
- Lee, D.Y.; Yun, J.-H.; Bin Park, Y.; Hyeon, J.S.; Jang, Y.; Choi, Y.-B.; Kim, H.-H.; Kang, T.M.; Ovalle, R.; Baughman, R.H.; et al. Two-Ply Carbon Nanotube Fiber-Typed Enzymatic Biofuel Cell Implanted in Mice. IEEE Trans. NanoBiosci. 2020, 19, 333–338. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, M.; Ritzmann, R.E.; Lee, I.; Pollack, A.J.; Scherson, D. An Implantable Biofuel Cell for a Live Insect. J. Am. Chem. Soc. 2012, 134, 1458–1460. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, Y.; Chu, M.; Deng, W.; Tan, Y.; Ma, M.; Su, X.; Xie, Q.; Yao, S. Facile fabrication of network film electrodes with ultrathin Au nanowires for nonenzymatic glucose sensing and glucose/O2 fuel cell. Biosens. Bioelectron. 2014, 52, 105–110. [Google Scholar] [CrossRef]
- Kloke, A.; Ko, C.; Zengerle, R.; Kerzenmacher, S. Porous Platinum Electrodes Fabricated by Cyclic Electrodeposition of PtCu Alloy: Application to Implantable Glucose Fuel Cells. J. Phys. Chem. C 2012, 116, 19689–19698. [Google Scholar] [CrossRef]
- Zhao, Y.; Fan, L.; Hong, B.; Zhang, Y.; Zhang, M.; Que, Q.; Ji, J. Three-dimensional Porous Palladium Foam-like Nanostructures as Electrocatalysts for Glucose Biofuel Cells. Energy Technol. 2016, 4, 249–255. [Google Scholar] [CrossRef]
- Niyazi, A.; Metcalfe, B.; Leese, H.S.; Di Lorenzo, M. One-step polyaniline-platinum nanoparticles grafting on porous gold anode electrodes for high-performance glucose fuel cells. J. Power Sources 2025, 654, 23781. [Google Scholar] [CrossRef]
- Gonzalez-Solino, C.; Metcalfe, B.W.; Lorenzo, M.D. Power generation and autonomous glucose detection with an integrated array of abiotic fuel cells on a printed circuit board. J. Power Sources 2020, 472, 228530. [Google Scholar] [CrossRef]
- Zhiani, M.; Barzi, S.; Ahmadi, A.; Vizza, F.; Gharibi, H.; Azhari, A. Ex vivo energy harvesting by a by-pass depletion designed abiotic glucose fuel cell operated with real human blood serum. J. Power Sources 2022, 521, 230972. [Google Scholar] [CrossRef]
- Sharma, T.; Hu, Y.; Stoller, M.; Feldman, M.; Ruoff, R.S.; Ferrari, M.; Zhang, X. Mesoporous silica as a membrane for ultra-thin implantable direct glucose fuel cells. Lab Chip 2011, 11, 2460–2465. [Google Scholar] [CrossRef]
- Zebda, A.; Cosnier, S.; Alcaraz, J.-P.; Holzinger, M.; Le Goff, A.; Gondran, C.; Boucher, F.; Giroud, F.; Gorgy, K.; Lamraoui, H.; et al. Single glucose biofuel cells implanted in rats power electronic devices. Sci. Rep. 2013, 3, 1516. [Google Scholar] [CrossRef]
- Christwardana, M.; Kim, D.-H.; Chung, Y.; Kwon, Y. A hybrid biocatalyst consisting of silver nanoparticle and naphthalenethiol self-assembled monolayer prepared for anchoring glucose oxidase and its use for an enzymatic biofuel cell. Appl. Surf. Sci. 2018, 429, 180–186. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, L.; Han, Y.; Yu, Y.; Xu, M.; Zhang, X.; Huanh, L.; Dong, S. RGO/Au NPs/N-doped CNTs supported on nickel foam as an anode for enzymatic biofuel cells. Biosens. Bioelectron. 2017, 97, 34–40. [Google Scholar] [CrossRef]
- Hou, C.; Liu, A. An integrated device of enzymatic biofuel cells and supercapacitor for both efficient electric energy conversion and storage. Electrochim. Acta 2017, 245, 303–308. [Google Scholar] [CrossRef]
- Yu, Y.; Xu, M.; Bai, L.; Han, L.; Dong, S. Recoverable hybrid enzymatic biofuel cell with molecular oxygen-independence. Biosens. Bioelectron. 2016, 75, 23–27. [Google Scholar] [CrossRef] [PubMed]
- Oncescu, V.; Erickson, D. A microfabricated low cost enzyme-free glucose fuel cell for powering low-power implantable devices. J. Power Sources 2011, 196, 9169–9175. [Google Scholar] [CrossRef]
- Kerzenmacher, S.; Kräling, U.; Metz, T.; Zengerle, R.; von Stetten, F. A potentially implantable glucose fuel cell with Raney-platinum film electrodes for improved hydrolytic and oxidative stability. J. Power Sources 2011, 196, 1264–1272. [Google Scholar] [CrossRef]
- Köhler, C.; Frei, M.; Zengerle, R.; Kerzenmacher, S. Performance loss of a Pt-based implantable glucose fuel cell in simulated tissue and cerebrospinal fluids. ChemElectroChem 2014, 1, 1895–1900. [Google Scholar] [CrossRef]
- Available online: https://medlineplus.gov/ency/article/003482.htm (accessed on 22 October 2025).
- Available online: https://www.cosinuss.com/en/measured-data/vital-signs/oxygen-saturation/ (accessed on 22 October 2025).
- Collins, J.A.; Rudenski, A.; Gibson, J.; Howard, L.; O’Driscoll, R. Relating oxygen partial pressure, saturation and content: The haemoglobin–oxygen dissociation curve. Breathe 2015, 11, 194–201. [Google Scholar] [CrossRef]
- Available online: https://www.ncbi.nlm.nih.gov/books/NBK538336/?utm_source (accessed on 22 October 2025).
- Lewis, P.M.; Ackland, H.M.; Lowery, A.J.; Rosenfeld, J.V. Restoration of vision in blind individuals using bionic devices: A review with a focus on cortical visual prostheses. Brain Res. 2015, 1595, 51–73. [Google Scholar] [CrossRef]
- Xing, W.; Yin, M.; Lv, Q.; Hu, Y.; Liu, C.; Zhang, J. Oxygen Solubility, Diffusion Coefficient, and Solution Viscosity. In Rotating Electrode Methods and Oxygen Reduction Electrocatalysts; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Bashkatov, A.N.; Genina, E.A.; Sinichkin, Y.P.; Kochubey, V.I.; Lakodina, N.A.; Tuchin, V.V. Glucose and mannitol diffusion in human dura mater. Biophys. J. 2003, 85, 3310–3318. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- La Malfa, F.; Di Lorenzo, M.; Qualtieri, A.; De Vittorio, M.; Rizzi, F.; Desmaële, D. A novel flexible conductive sponge-like electrode capable of generating electrical energy from the direct oxidation of aqueous glucose. In Journal of Physics: Conference Series, Proceedings of the Journal of Physics: Conference Series, Daytona Beach, FL, USA, 4–7 December 2018; IOP Publishing: Philadelphia, PA, USA, 2019; Volume 1407. [Google Scholar] [CrossRef]
- Chen, Y.; Prasad, K.P.; Wang, X.; Pang, H.; Yan, R.; Than, A.; Chan-Park, M.B.; Chen, P. Enzymeless multi-sugar fuel cells with high power output based on 3D graphene–Co3O4 hybrid electrodes. Phys. Chem. Chem. Phys. 2013, 15, 9170–9176. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://www.ciamedical.com/insights/iv-catheter-sizes/ (accessed on 22 October 2025).
- Limperg, T.B.; Novoa, V.Y.; Curlin, H.L.; Veersema, S. 2024. Laparoscopic Trocars: Marketed Versus True Dimensions–A Descriptive Study. J. Minim. Invasive Gynecol. 2024, 31, 304–308. [Google Scholar] [CrossRef]
- Available online: https://www.dipolerfid.com/product/rfid-tags-for-animal-identification (accessed on 22 October 2025).
- Beurskens, N.E.G.; Tjong, F.V.Y.; Knops, R.E. End-of-life management of leadless cardiac pacemaker therapy. Arrhythmia Electrophysiol. Rev. 2017, 6, 129–133. [Google Scholar] [CrossRef]
- Available online: https://newatlas.com/computers/mibmi-text-accuracy/ (accessed on 22 October 2025).
- Drake, R.F.; Kusserow, B.K.; Messinger, S.; Matsuda, S. A tissue implantable fuel cell power supply. ASAIO J. 1970, 16, 199–205. [Google Scholar]
- He, Z.; Yang, X.; Wang, N.; Mu, L.; Pan, J.; Lan, X.; Li, H.; Deng, F. Anti-Biofouling Polymers with Special Surface Wettability for Biomedical Applications. Front. Bioeng. Biotechnol. 2021, 9, 807357. [Google Scholar] [CrossRef] [PubMed]
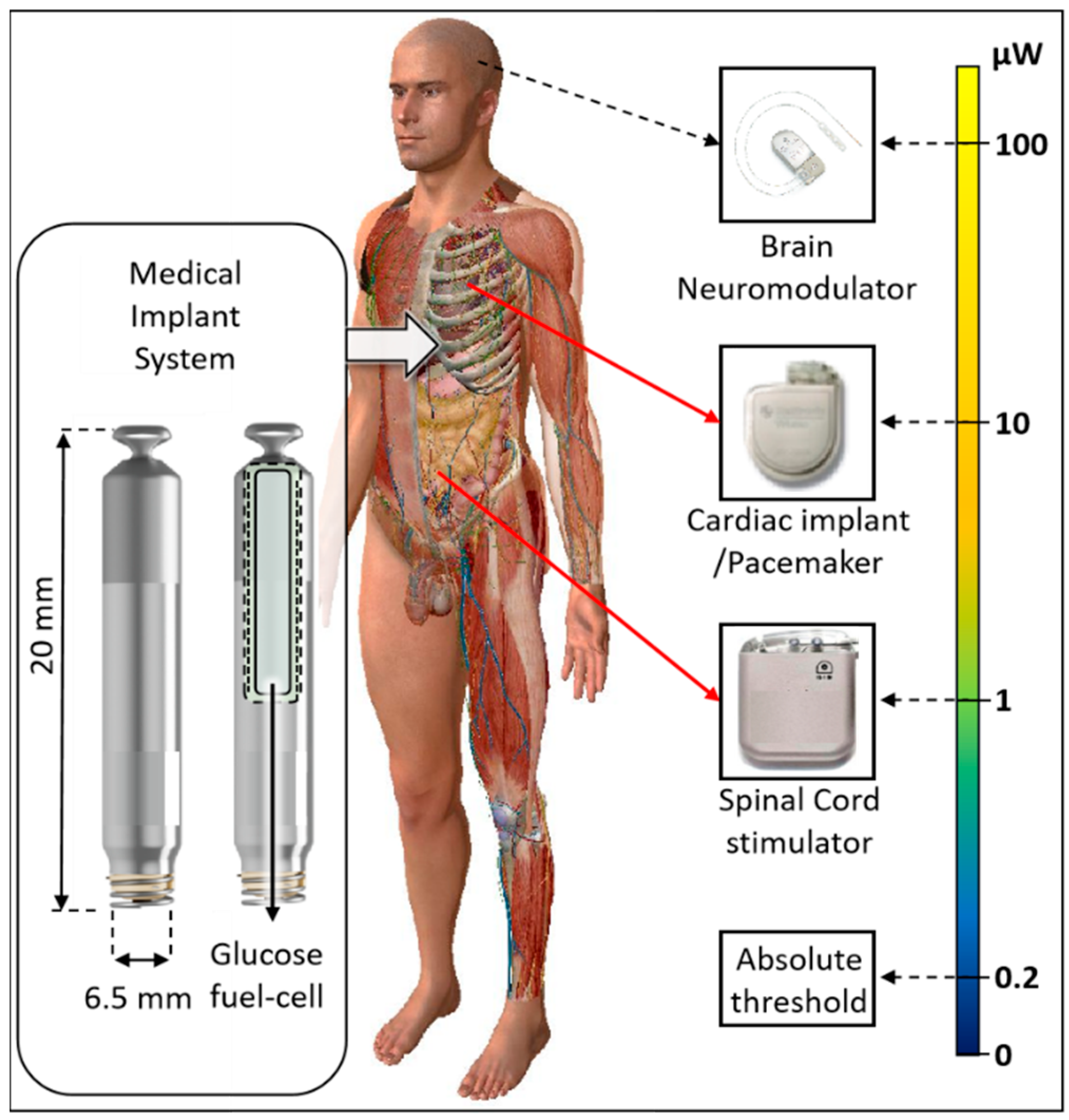
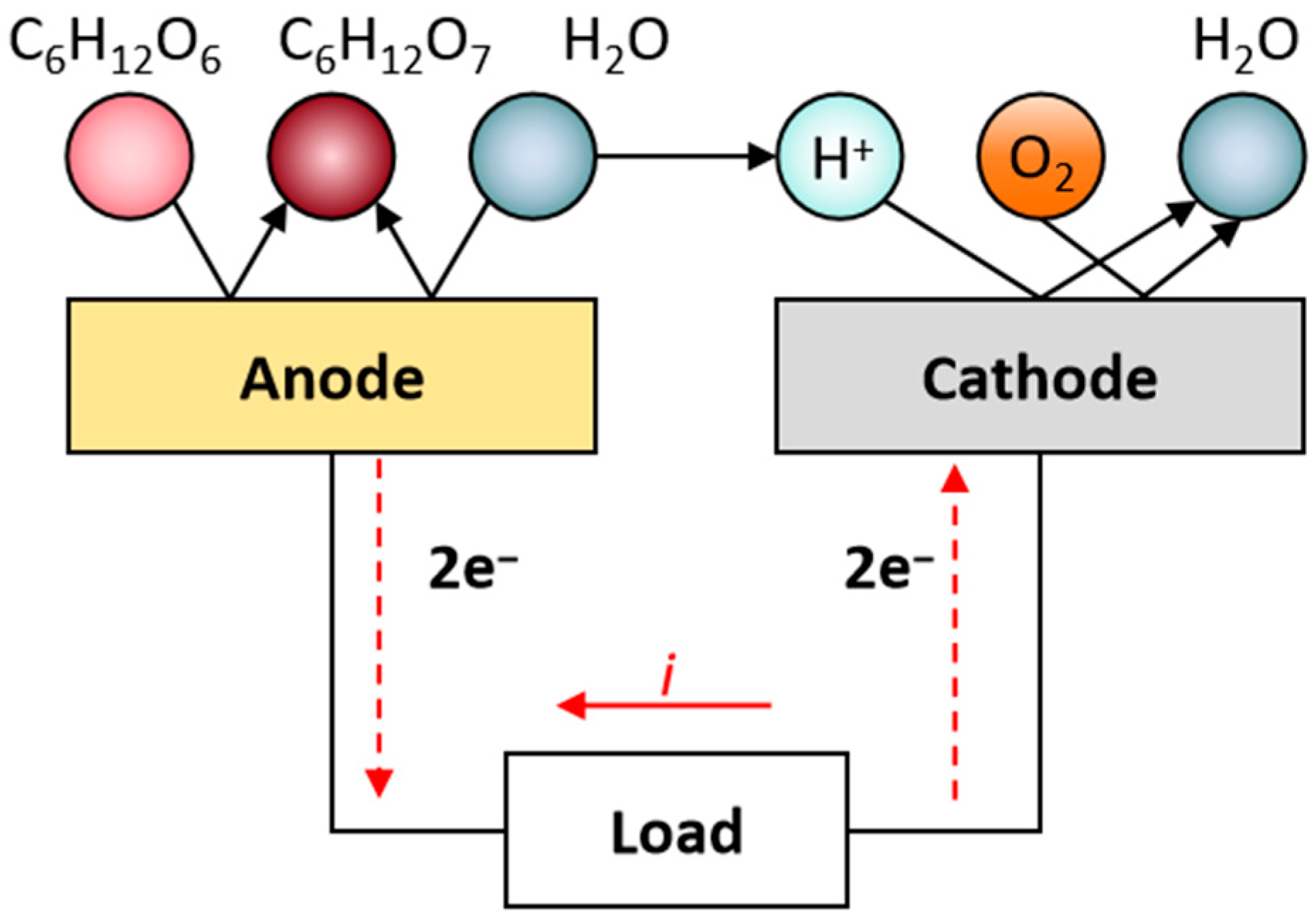
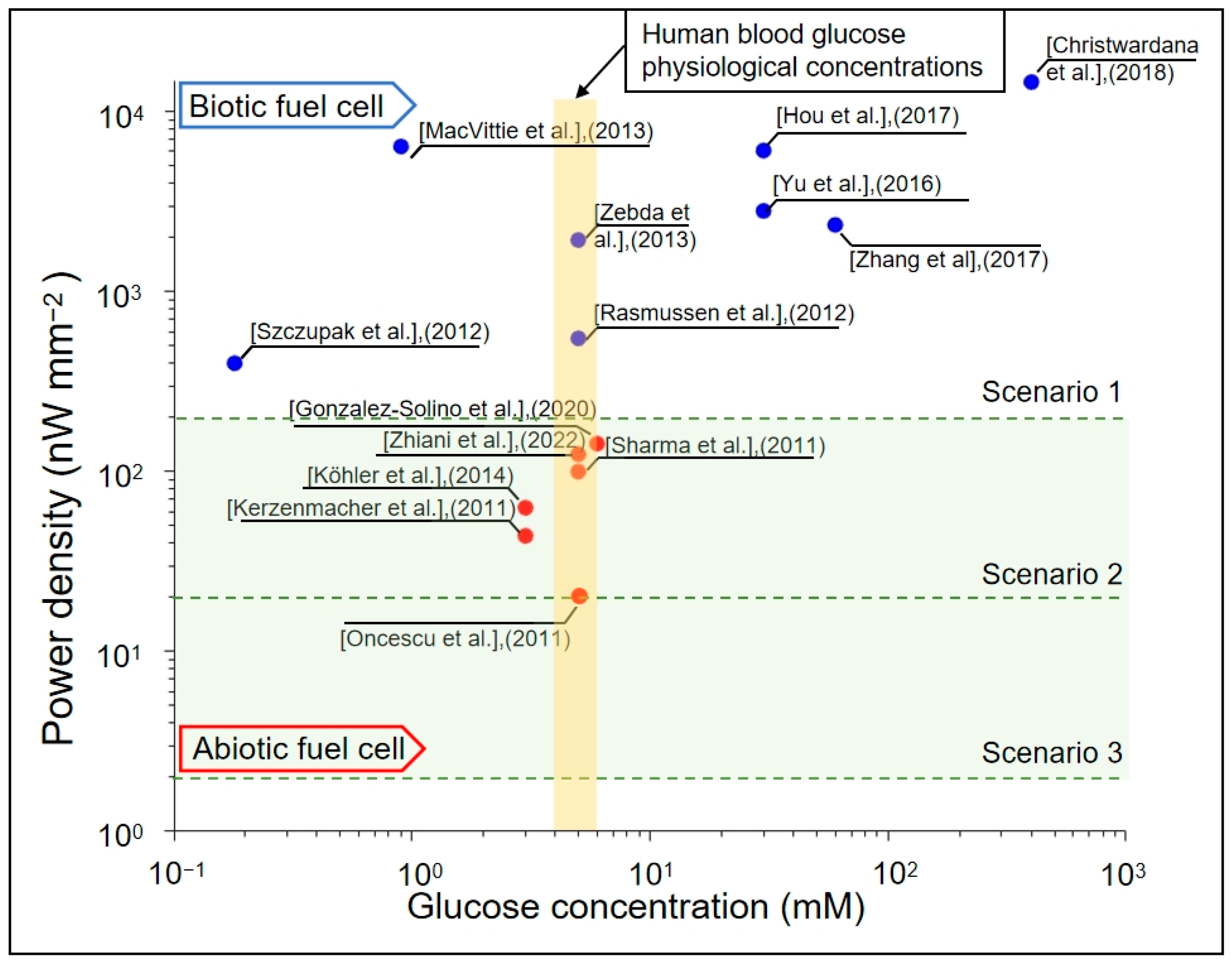
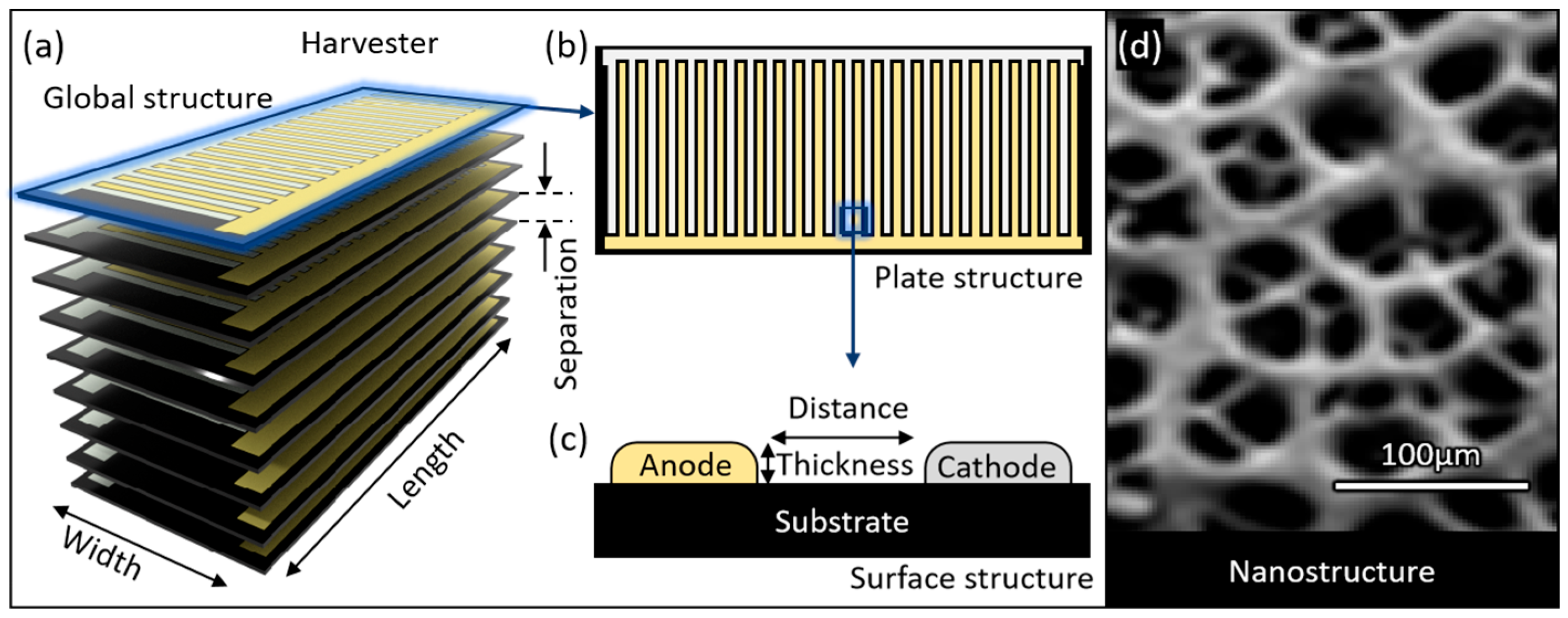
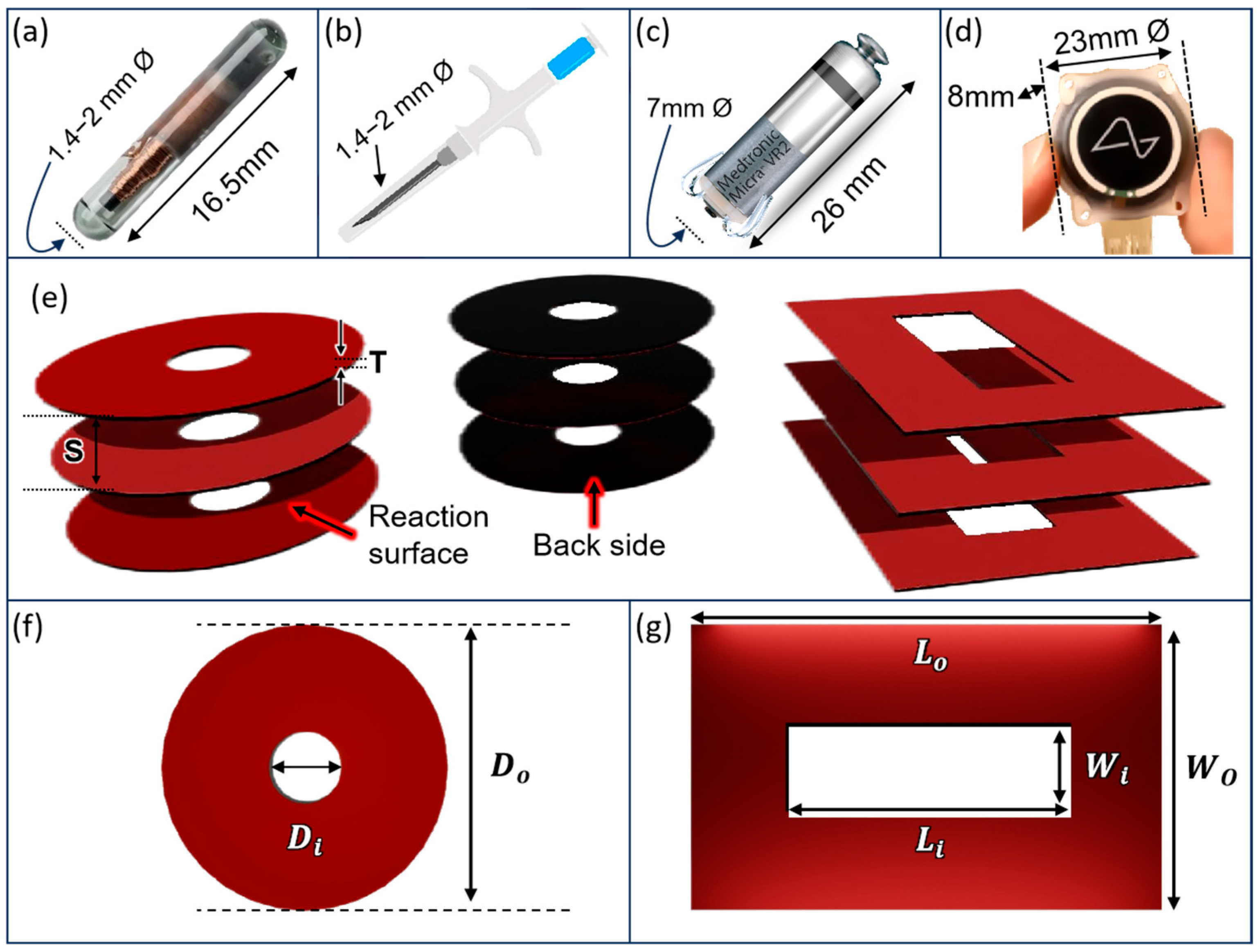



| Implant | Power Range (μW) | Lifetime with a 10 mL Battery | Lifetime with a 1 mL Battery | Lifetime with a 50 µL Battery | Refs. |
|---|---|---|---|---|---|
| Bioelectronic medicine | <10 | >118 years | >11 years | >7 months | [13,15] |
| Pacemaker | ~10–100 | ~11–118 years | ~1–11 years | ~0.6–7 months | [13] |
| Neuro- stimulator | ~100–400 | ~3–11 years | ~0.3–1 year | ~0.1–0.6 months | [14] |
| Sensory prosthetics | >10,000 | Wireless power | Wireless power | Wireless power | [16] |
| Module Parameters | Value | Unit |
|---|---|---|
| Diffusion coefficient | Glucose: 0.9 × 10−9 Oxygen: 3 × 10−9 | m2 s−1 |
| Boundary glucose concentration | 5 | mMol L−1 |
| Boundary oxygen concentration | 4.5 | mMol L−1 |
| Basic surface reaction rate | 2.5 × 10−6 2.5 × 10−7 2.5 × 10−8 | (mol) s−1m−2 |
| Parameter | Values | Unit | |
|---|---|---|---|
| Thickness | T | 0.1 | mm |
| Separation | S | 0.01, 0.06, 0.1, 0.3, 0.9, 1.23, 1.9, 3.9, 7.9 | mm |
| Cylinder | |||
| Outer diameter | 6.18, 8.74, 12.36, 17.48 | mm | |
| Area | A | 30, 60, 120, 240 | mm2 |
| Block without a diffusion cavity | |||
| Width | W | 6 | mm |
| Length | L | 1.5, 3, 6, 10, 15 | mm |
| Area | A | 9, 18, 36, 60, 90 | mm2 |
| Cylinder with a diffusion cavity | |||
| Outer diameter | 8.74 | mm | |
| Inner diameter (cavity) | 1.994, 3.384, 4.37, 5.17 | mm | |
| Area | A | 57, 51, 45, 39, | mm2 |
| Block with a diffusion cavity | |||
| Outer length | 10 | mm | |
| Inner length (cavity) | 3, 6, 7.5, 7 | mm | |
| Outer width | 6 | mm | |
| Inner width (cavity) | 1, 1.5, 2, 3 | mm | |
| Area | A | 57, 51,45, 39 | mm2 |
| Module Parameters | Value | Unit |
|---|---|---|
| Separation | 0.9 | mm |
| Thickness of the generator unit | 0.1 | mm |
| Number of generation units | 8 | |
| Basic surface reaction rate | 2.5 | (mol) s−1m−2 |
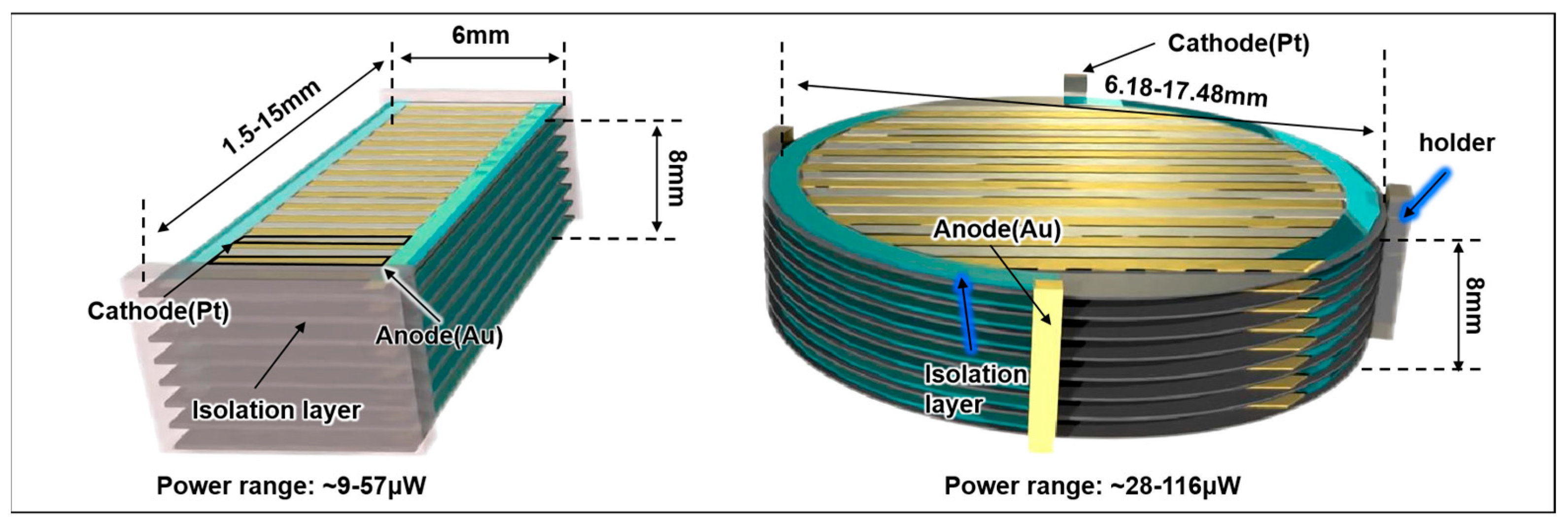
| Pill-shaped device | ||
| Length | 1.5–15 | mm |
| Width | 6 | mm |
| Area | 9–90 | mm2 |
| Total Power (range) | ~9–57 | μW |
| Disc-shaped device | ||
| Diameter | 6.18–17.48 | mm |
| Area | 30–240 | mm2 |
| Total Power range | ~28–116 | μW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Gibson, E.; Di Lorenzo, M.; Degenaar, P. Finite Element Optimization of 3D Abiotic Glucose Fuel Cells for Implantable Medical Devices. Prosthesis 2025, 7, 136. https://doi.org/10.3390/prosthesis7060136
Ma C, Gibson E, Di Lorenzo M, Degenaar P. Finite Element Optimization of 3D Abiotic Glucose Fuel Cells for Implantable Medical Devices. Prosthesis. 2025; 7(6):136. https://doi.org/10.3390/prosthesis7060136
Chicago/Turabian StyleMa, Cong, Elizabeth Gibson, Mirella Di Lorenzo, and Patrick Degenaar. 2025. "Finite Element Optimization of 3D Abiotic Glucose Fuel Cells for Implantable Medical Devices" Prosthesis 7, no. 6: 136. https://doi.org/10.3390/prosthesis7060136
APA StyleMa, C., Gibson, E., Di Lorenzo, M., & Degenaar, P. (2025). Finite Element Optimization of 3D Abiotic Glucose Fuel Cells for Implantable Medical Devices. Prosthesis, 7(6), 136. https://doi.org/10.3390/prosthesis7060136







