In Vitro Comparison of Monolithic Zirconia Crowns: Marginal/Internal Adaptation and 3D-Quantified Preparation Defects Using Air-Driven, Electric-Driven, and Piezoelectric Ultrasonic Handpieces
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethical Approval
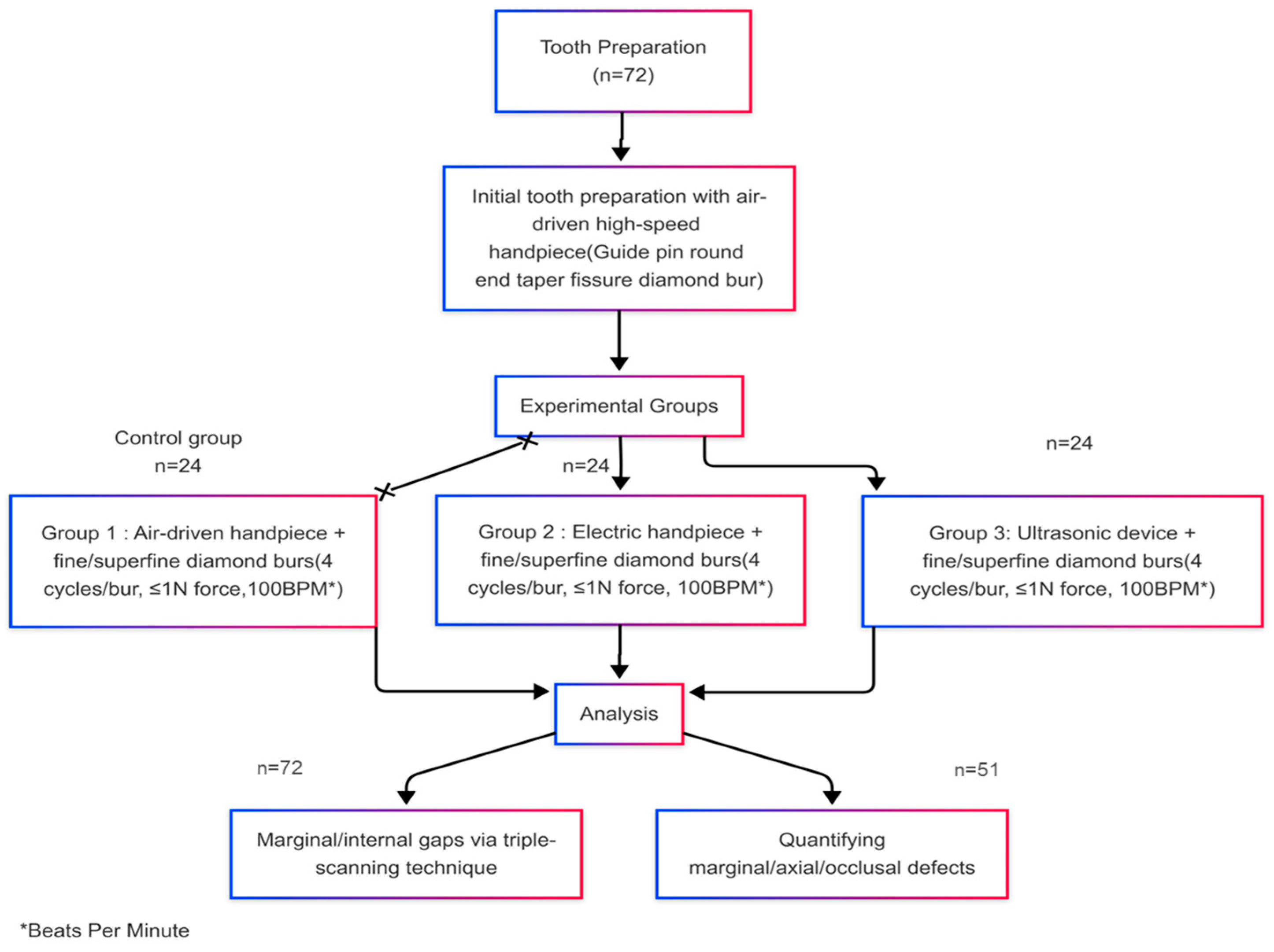
2.2. Study Groups and Sample Size Calculation
2.3. Specimen Preparation and 3D Printing
2.4. Tooth Storage and Mounting
2.5. Tooth Preparation Protocol
2.6. Force Measurement System
2.7. Finishing Procedures
2.8. Digital Scanning and Crown Fabrication
2.9. Crown Scanning and Cementation
2.10. Triple-Scan Analysis for Marginal and Internal Gap Calculation
2.11. Quantifying of the Number of Marginal, Axial, and Occlusal Defects
2.12. Statistical Analysis
3. Results
3.1. Marginal and Internal Gap
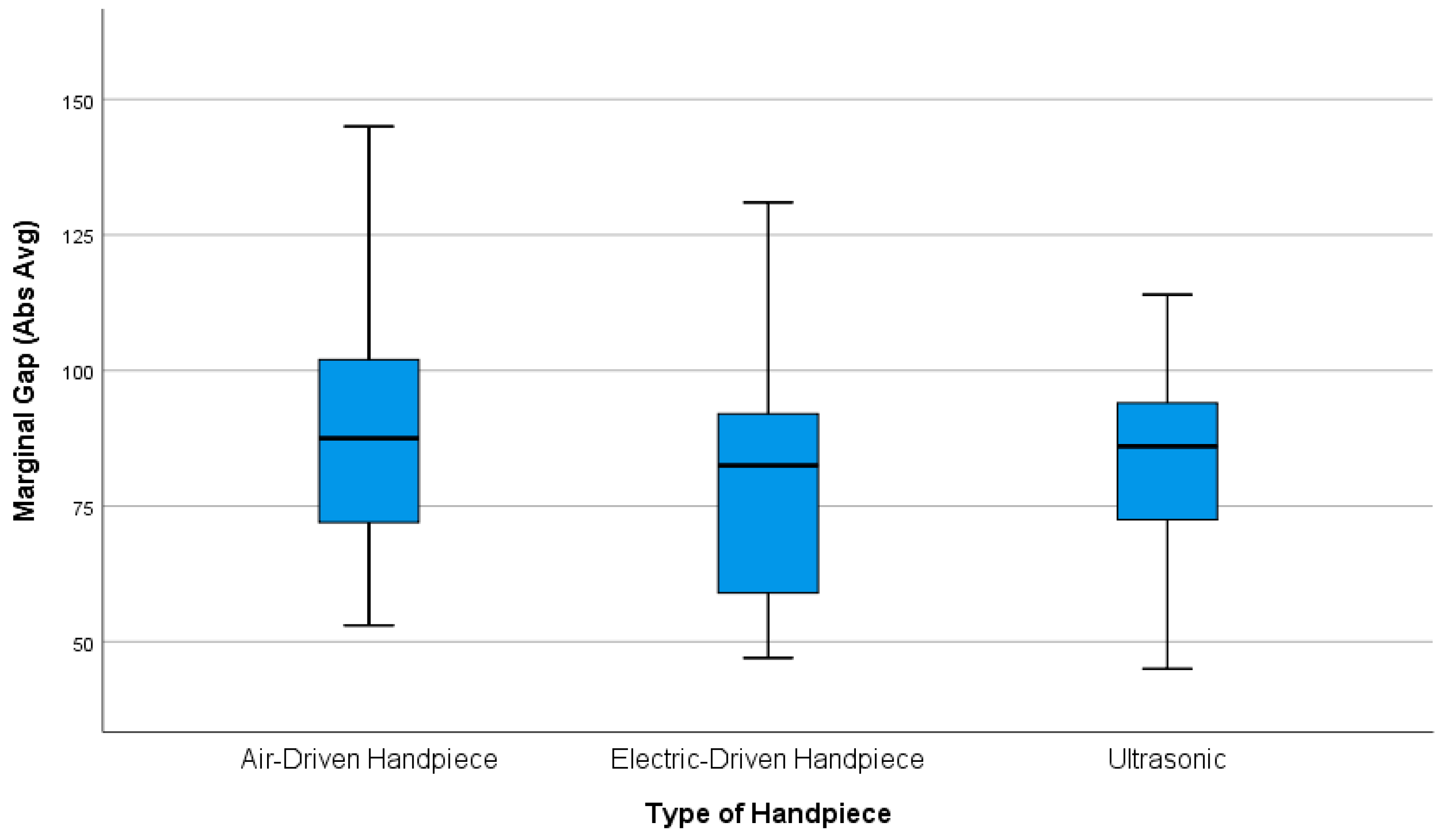
3.1.1. Marginal Gap
- The results indicate that crown preparations with air-driven handpieces have a larger potential for increased marginal gaps than electric-driven handpieces, although this difference did not reach statistical significance as the confidence interval (CI) (−4.44 to 25.60 µm) includes zero (mean difference = 10.583 µm, p = 0.217). The comparison between air-driven handpieces and ultrasonic devices also showed no statistically significant difference (mean difference = 6.625 µm, p = 0.544), in which the confidence interval spanned from (−8.40 to 21.65 µm), while the mean difference between electric-driven handpieces and ultrasonic units was (−3.958 µm); this difference was also not statistically significant (p = 0.803), in which the CI (−18.98 to 11.06 µm) crossed zero.
- Post hoc Dunn’s tests with Bonferroni correction revealed no statistically significant differences between any group pairs (Group 1 vs. Group 2: z = 0.76, uncorrected p = 0.447, adjusted p = 1.341; Group 1 vs. Group 3: z = 0.34, uncorrected p = 0.735, adjusted p = 2.205; Group 2 vs. Group 3: z = −0.42, uncorrected p = 0.674, adjusted p = 2.022; all adjusted p-values > 0.05). The absence of significant z-scores (all z < 0.8) further supports the equivalence of group distributions.
3.1.2. Internal Gap
- The results for the internal gap indicate that crown preparations with air-driven handpieces show no statistically significant difference compared to electric-driven handpieces, as this comparison did not reach statistical significance due to the confidence interval range that includes zero (−1.24 to 21.16 µm, mean difference = 9.958 µm, p-value = 0.091. The comparison between ultrasonic and air-driven handpieces showed a non-significant potential toward smaller internal gaps with air-driven handpieces (mean difference = −2.708 µm, p-value = 0.832), in which the confidence interval (−13.91 to 8.49 µm) included negligible to moderate effects, while the mean difference between electric-driven handpieces and ultrasonic units was −12.667 µm, which was statistically significant, potentially favoring the electric handpiece (p = 0.023), in which the CI (−23.87 to −1.46 µm) did not contain zero, indicating a clinically meaningful effect.
3.2. Marginal, Axial, and Occlusal Defects (Preparation Quality)
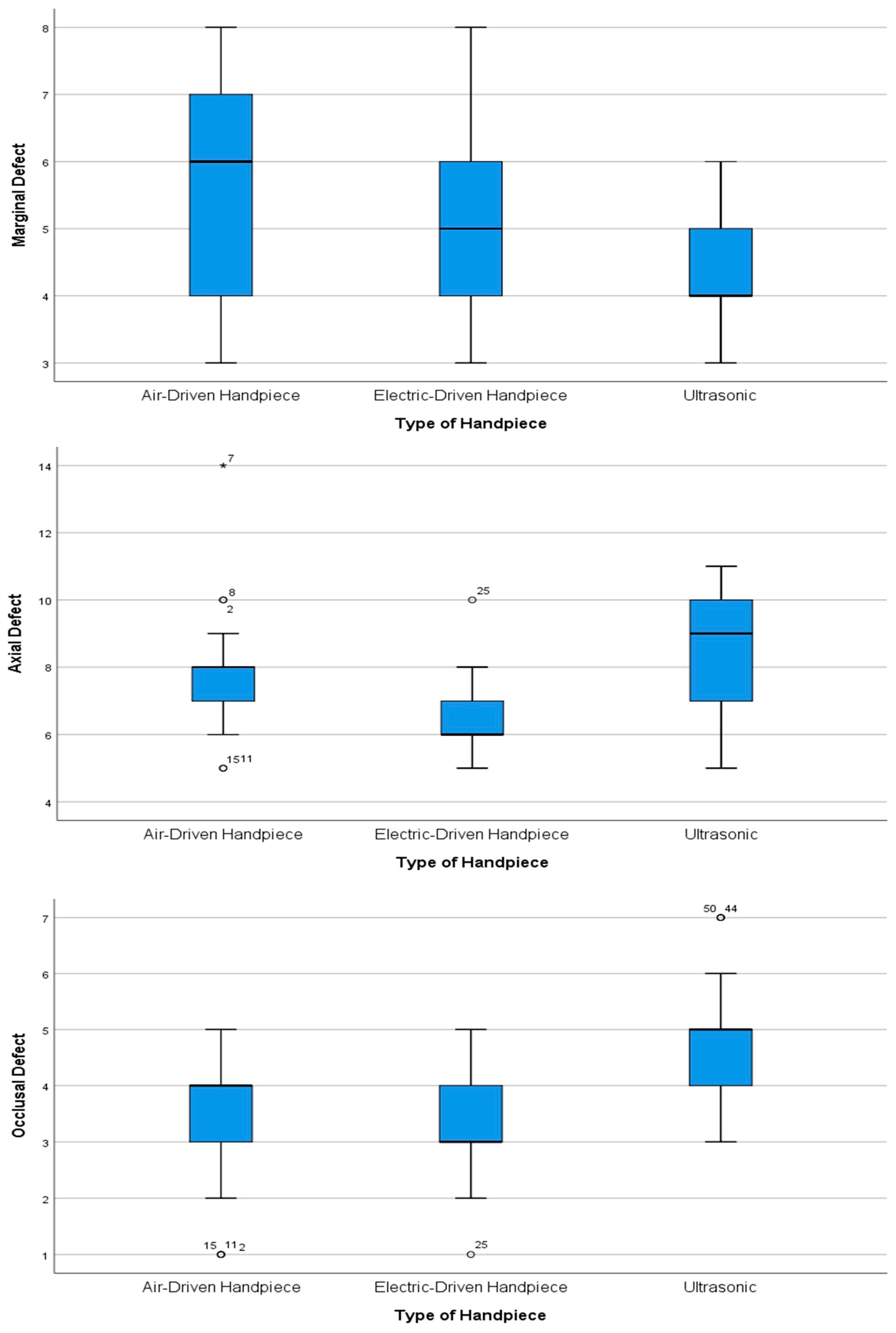
- Marginal defects: The Kruskal–Wallis test showed significant differences between various handpiece types. Dunn’s post hoc test results for marginal defects revealed significant differences between handpiece types (χ2 = 6.617, p = 0.037). The largest difference existed between air-driven (Group 1) and ultrasonic (Group 3) handpieces (Z = 2.485, p = 0.013) with a substantial mean rank difference of (12.38), showing that air-driven units generated significantly more marginal defects—a result that remained significant after Bonferroni correction (p = 0.039). The mean rank difference of (9.06) between electric-driven (Group 2) and ultrasonic handpieces indicated a notable trend (Z = 1.818, p = 0.069), but this difference failed to achieve statistical significance after Bonferroni correction. Air-driven and electric-driven handpieces showed minimal differences in performance (Z = 0.667, p = 0.505) through their small mean rank difference of (3.32), which confirmed their equivalent performance (adjusted p = 1.000). The results demonstrate that ultrasonic handpieces create the fewest marginal defects, while air-driven handpieces generate the most defects, and electric-driven handpieces show results that are similar to both groups.
- Axial defects: The Kruskal–Wallis test showed that there were differences between the types of handpieces (χ2 = 8.410, p = 0.015). Dunn’s post hoc tests showed the following: ultrasonic vs. electric: The ultrasonic handpieces (median = 9, IQR = 7–10) had more defects than the electric handpieces (median = 6, IQR = 6–7; Z = 2.824, p = 0.0047, Bonferroni p = 0.014) with a mean rank difference of (14.205). Ultrasonic vs. air-driven: Although the ultrasonic handpiece had more defects than the air-driven handpieces (median = 7, IQR = 7–8), this was not statistically significant (Z = 0.842, p = 0.400) with a mean rank difference of (4.235). Air-driven vs. electric: There was no significant difference (Z = 1.982, p = 0.047) after Bonferroni correction (p = 0.142), although the air-driven handpiece had more defects with a mean rank difference of (9.971).
- Occlusal defects: The Kruskal–Wallis test revealed significant differences in occlusal defects (χ2 = 11.367, p = 0.003). Dunn’s post hoc test results show that there are significant differences in occlusal defect formation between handpiece types. The most substantial difference exists between electric-driven (Group 2) and ultrasonic (Group 3) handpieces (Z = 3.026, p = 0.00248), with a large mean rank difference of (−15.03), indicating that ultrasonic units produce significantly more occlusal defects—a finding that remains highly significant after Bonferroni correction (p = 0.007). Similarly, air-driven (Group 1) and ultrasonic handpieces show a significant difference (Z = 2.801, p = 0.0051, Bonferroni p = 0.015) with a mean rank difference of (−13.91), though this is slightly less pronounced than the electric–ultrasonic comparison. In contrast, air-driven and electric-driven handpieces reveal minimal difference (Z = 0.225, p = 0.822) with a negligible mean rank difference of (1.12), confirming their comparable performance for occlusal defects. These results collectively establish ultrasonic handpieces as producing significantly more occlusal defects than both air-driven and electric-driven units, while the latter two types show no meaningful difference in occlusal defect formation.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| STL | Standard tessellation language |
| Ra | Average surface roughness |
| Rsk | Skewness of the surface roughness profile (a roughness parameter) |
| HT | High-translucency |
| RMS | Mean root square |
| ABS | Absolute |
| AVG | Average |
| APA | Air particle abrasion |
| UDTs | Ultrasonic diamond tips |
| CAD | Computer-aided design |
| CAM | Computer-aided manufacturing |
| LTD | Low-temperature degradation |
References
- Contrepois, M.; Soenen, A.; Bartala, M.; Laviole, O. Marginal Adaptation of Ceramic Crowns: A Systematic Review. J. Prosthet. Dent. 2013, 110, 447–454. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Monescillo, A.; González-Serrano, C.; González-Serrano, J.; Barbosa, J.M.; López-Suárez, C.; Duarte, S. Effect of Luting Cement and Convergence Angle of the Preparation on the Internal Fit of Zirconia Restorations. Materials 2021, 14, 7858. [Google Scholar] [CrossRef] [PubMed]
- Hamza, T.A.; Sherif, R.M. In Vitro Evaluation of Marginal Discrepancy of Monolithic Zirconia Restorations Fabricated with Different CAD-CAM Systems. J. Prosthet. Dent. 2017, 117, 762–766. [Google Scholar] [CrossRef] [PubMed]
- Rençber Kızılkaya, A.; Kara, A. Impact of Different CAD Software Programs on Marginal and Internal Fit of Provisional Crowns: An In Vitro Study. Heliyon 2024, 10, e24205. [Google Scholar] [CrossRef]
- Farag, E.A.A.; Rizk, A.; Ashraf, R.; Emad Eldin, F. Effect of the scanner type on the marginal gap and internal fit of two monolithic CAD/CAM esthetic crown materials: An in vitro study. Dent. Med. Probl. 2024; Epub ahead of print. [Google Scholar] [CrossRef]
- Morsy, N.; El Kateb, M.; Azer, A.; Fathalla, S. Fit of Zirconia Fixed Partial Dentures Fabricated from Conventional Impressions and Digital Scans: A Systematic Review and Meta-Analysis. J. Prosthet. Dent. 2023, 130, 28–34. [Google Scholar] [CrossRef]
- Abduo, J.; Elseyoufi, M. Accuracy of Intraoral Scanners: A Systematic Review of Influencing Factors. Eur. J. Prosthodont. Restor. Dent. 2018, 26, 101–121. [Google Scholar] [CrossRef]
- Al Hamad, K.Q.; Al-Rashdan, R.B.; Al-Rashdan, B.A.; Baba, N.Z. Effect of Milling Protocols on Trueness and Precision of Ceramic Crowns. J. Prosthodont. 2021, 30, 171–176. [Google Scholar] [CrossRef] [PubMed]
- Al Hamad, K.Q.; Al Rashdan, R.B.; Al Rashdan, B.A.; Al Quran, F.A. Effect of CAD-CAM Tool Deterioration on the Trueness of Ceramic Restorations. J. Prosthet. Dent. 2022, 127, 635–644. [Google Scholar] [CrossRef]
- Renne, W.; McGill, S.T.; Forshee, K.V.; Defee, M.R.; Mennito, A.S. Predicting Marginal Fit of CAD/CAM Crowns Based on the Presence or Absence of Common Preparation Errors. J. Prosthet. Dent. 2012, 108, 310–315. [Google Scholar] [CrossRef]
- McLean, J.W.; Von, F. The Estimation of Cement Film Thickness by an In Vivo Technique. Br. Dent. J. 1971, 131, 107–111. [Google Scholar] [CrossRef]
- Atlas, A.; Isleem, W.; Bergler, M.; Fraiman, H.P.; Walter, R.; Lawson, N.D. Factors Affecting the Marginal Fit of CAD-CAM Restorations and Concepts to Improve Outcomes. Curr. Oral Health Rep. 2019, 6, 277–283. [Google Scholar] [CrossRef]
- Kuper, N.K.; Opdam, N.J.M.; Ruben, J.L.; de Soet, J.J.; Cenci, M.S.; Bronkhorst, E.M.; Huysmans, M.C.D.N.J.M. Gap Size and Wall Lesion Development Next to Composite. J. Dent. Res. 2014, 93 (Suppl. 7), 108S–113S. [Google Scholar] [CrossRef] [PubMed]
- Maske, T.T.; Hollanders, A.C.C.; Kuper, N.K.; Bronkhorst, E.M.; Cenci, M.S.; Huysmans, M.C.D.N.J.M. A Threshold Gap Size for in Situ Secondary Caries Lesion Development. J. Dent. 2019, 80, 36–40. [Google Scholar] [CrossRef]
- Øilo, M.; Schriwer, C.; Flinn, B.; Gjerdet, N.R. Monolithic Zirconia Crowns—Wall Thickness, Surface Treatment and Load at Fracture. Biomater. Investig. Dent. 2019, 6, 13–22. [Google Scholar] [CrossRef]
- Ferraris, F.; Conti, A. Superficial Roughness on Composite Surface, Composite Enamel and Composite Dentin Junctions after Different Finishing and Polishing Procedures. Part I: Roughness after Treatments with Tungsten Carbide vs. Diamond Burs. Int. J. Esthet. Dent. 2014, 9, 184–204. Available online: https://www.quintessence-publishing.com/anz/de/article/852167 (accessed on 4 May 2025).
- Clarke, I.; Aquilia, A.; Bertassoni, L.; Guazzato, M.; Klineberg, I. Surface Roughness of Restoration Margin Preparations: A Comparative Analysis of Finishing Techniques. Int. J. Periodontics Restor. Dent. 2015, 35, 211–218. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wahle, J.J.; Wendt, S.L. Dentinal Surface Roughness: A Comparison of Tooth Preparation Techniques. J. Prosthet. Dent. 1993, 69, 160–164. [Google Scholar] [CrossRef]
- Ayad, M.F. Effects of Tooth Preparation Burs and Luting Cement Types on the Marginal Fit of Extracoronal Restorations. J. Prosthodont. 2009, 18, 145–151. [Google Scholar] [CrossRef]
- Li, Y.Q.; Wang, H.; Wang, Y.J.; Chen, J.H. Effect of Different Grit Sizes of Diamond Rotary Instruments for Tooth Preparation on the Retention and Adaptation of Complete Coverage Restorations. J. Prosthet. Dent. 2012, 107, 86–93. [Google Scholar] [CrossRef]
- Sherawat, S.; Tewari, S.; Duhan, J.; Gupta, A.; Singla, R. Effect of Rotary Cutting Instruments on the Resin-Tooth Interfacial Ultra Structure: An In Vivo Study. J. Clin. Exp. Dent. 2014, 6, e467–e473. [Google Scholar] [CrossRef]
- Jung, M.; Wehlen, L.O.; Klimek, J. Surface Roughness and Bond Strength of Enamel to Composite. Dent. Mater. 1999, 15, 250–256. [Google Scholar] [CrossRef] [PubMed]
- Renne, W.; Wolf, B.; Kessler, R.; McPherson, K.; Mennito, A.S. Evaluation of the Marginal Fit of CAD/CAM Crowns Fabricated Using Two Different Chairside CAD/CAM Systems on Preparations of Varying Quality. J. Esthet. Restor. Dent. 2015, 27, 194–202. [Google Scholar] [CrossRef] [PubMed]
- Geminiani, A.; Abdel-Azim, T.; Ercoli, C.; Feng, C.; Meirelles, L.; Massironi, D. Influence of Oscillating and Rotary Cutting Instruments with Electric and Turbine Handpieces on Tooth Preparation Surfaces. J. Prosthet. Dent. 2014, 112, 51–58. [Google Scholar] [CrossRef]
- Pei, D.; Meng, Y.; Fayed, A.S.; You, Y.; Wu, Z.; Lu, Y. Comparison of Crown Fit and Operator Preferences between Tooth Preparation with Electric and Air-Turbine Handpieces. J. Prosthet. Dent. 2021, 125, 111–116. [Google Scholar] [CrossRef]
- Laufer, B.Z.; Pilo, R.; Cardash, H.S. Surface Roughness of Tooth Shoulder Preparations Created by Rotary Instrumentation, Hand Planing, and Ultrasonic Oscillation. J. Prosthet. Dent. 1996, 75, 4–8. [Google Scholar] [CrossRef]
- Sous, M.; Lepetitcorps, Y.; Lasserre, J.-F.; Six, N. Ultrasonic Sulcus Penetration: A New Approach for Full Crown Preparations. Int. J. Periodontics Restor. Dent. 2009, 29, 277–287. Available online: https://openurl.ebsco.com/EPDB:gcd:3:21544595/detailv2?sid=ebsco:plink:scholar&id=ebsco:gcd:43402418 (accessed on 4 May 2025).
- Ellis, R.; Bennani, V.; Purton, D.; Chandler, N.; Lowe, B. The Effect of Ultrasonic Instruments on the Quality of Preparation Margins and Bonding to Dentin. J. Esthet. Restor. Dent. 2012, 24, 278–285. [Google Scholar] [CrossRef]
- Faus-Matoses, I.; Solá-Ruiz, F. Dental Preparation with Sonic vs High-Speed Finishing: Analysis of Microleakage in Bonded Veneer Restorations. J. Adhes. Dent. 2014, 16, 29–34. [Google Scholar] [CrossRef]
- Sola-Ruiz, M.F.; Faus-Matoses, I.; Del Rio Highsmith, J.; Fons-Font, A. Study of Surface Topography, Roughness, and Microleakage After Dental Preparation with Different Instrumentation. Int. J. Prosthodont. 2014, 27, 530–533. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Aydin, B.; Pamir, T.; Baltaci, A.; Orman, M.N.; Turk, T. Effect of Storage Solutions on Microhardness of Crown Enamel and Dentin. Eur. J. Dent. 2015, 9, 262–266. [Google Scholar] [CrossRef]
- NSK Operation Manual: PanaAir FX Air Turbine; NSK: Kanuma, Japan, 2015; Available online: http://admin.nsk-dental.com/admin/wp-content/uploads/T0457E001.pdf (accessed on 9 May 2025).
- Siegel, S.C.; Von Fraunhofer, J.A. Dental Cutting with Diamond Burs: Heavy-Handed or Light-Touch? J. Prosthodont. 1999, 8, 3–98. [Google Scholar] [CrossRef] [PubMed]
- Rosenstiel, S.F.; Land, M.F.; Fujimoto, J. Contemporary Fixed Prosthodontics, 5th ed.; Elsevier: St. Louis, MO, USA, 2016; pp. 169–208. [Google Scholar]
- Jota. Anhang/Index; Jota AG: Rüti, Switzerland, 2022; p. 311. Available online: https://www.jota.ch/fileadmin/images/Katalog/Anhang_Index_2022_19.07.2022.pdf (accessed on 9 May 2025).
- Shams, R. Dynamic Measurement of the Torque-speed Characteristics of Dental High Speed Air Turbine Handpieces. Aust. Dent. J. 1994, 39, 33–38. [Google Scholar] [CrossRef]
- Li, R.; Chen, H.; Wang, Y.; Sun, Y. Suitability of the Triple-Scan Method with a Dental Laboratory Scanner to Assess the 3D Adaptation of Zirconia Crowns. J. Prosthet. Dent. 2021, 125, 651–656. [Google Scholar] [CrossRef] [PubMed]
- Fasih, P.; Tavakolizadeh, S.; Sedaghat Monfared, M.; Sofi-Mahmudi, A.; Yari, A. Marginal Fit of Monolithic versus Layered Zirconia Crowns Assessed with 2 Marginal Gap Methods. J. Prosthet. Dent. 2023, 130, 250.e1–250.e7. [Google Scholar] [CrossRef]
- Son, K.; Lee, K.B. Marginal and Internal Fit of Ceramic Prostheses Fabricated from Different Chairside CAD/CAM Systems: An In Vitro Study. Appl. Sci. 2021, 11, 857. [Google Scholar] [CrossRef]
- Nawafleh, N.A.; Mack, F.; Evans, J.; Mackay, J.; Hatamleh, M.M. Accuracy and Reliability of Methods to Measure Marginal Adaptation of Crowns and FDPs: A Literature Review. J. Prosthodont. 2013, 22, 419–428. [Google Scholar] [CrossRef] [PubMed]
- Horne, P.; Bennani, V.; Chandler, N.; Purton, D. Ultrasonic Margin Preparation for Fixed Prosthodontics: A Pilot Study. J. Esthet. Restor. Dent. 2012, 24, 201–209. [Google Scholar] [CrossRef]
- Revilla-León, M.; Cascos-Sánchez, R.; Barmak, A.B.; Kois, J.C.; Gómez-Polo, M. The Effect of Different Tooth Preparation Finishing Procedures and Immediate Dentin Sealing on the Scanning Accuracy of Different Intraoral Scanners. J. Dent. 2023, 130, 104431. [Google Scholar] [CrossRef]
- Carbajal Mejía, J.B.; Wakabayashi, K.; Nakamura, T.; Yatani, H. Influence of Abutment Tooth Geometry on the Accuracy of Conventional and Digital Methods of Obtaining Dental Impressions. J. Prosthet. Dent. 2017, 118, 392–399. [Google Scholar] [CrossRef]
- Rapani, A.; Berton, F.; Tramontin, A.; Turco, G.; Marchesi, G.; Di Lenarda, R.; Stacchi, C. Surface Roughness of Enamel and Dentin after Preparation Finishing with Rotary Burs or Piezoelectric Instruments. Prosthesis 2023, 5, 711–720. [Google Scholar] [CrossRef]
- Al-Omari, W.M.; Mitchell, C.A.; Cunningham, J.L. Surface Roughness and Wettability of Enamel and Dentine Surfaces Prepared with Different Dental Burs. J. Oral Rehabil. 2001, 28, 645–650. [Google Scholar] [CrossRef] [PubMed]
- Tuntiprawon, M. Effect of Tooth Surface Roughness on Marginal Seating and Retention of Complete Metal Crowns. J. Prosthet. Dent. 1999, 81, 142–147. [Google Scholar] [CrossRef] [PubMed]
- Øilo, G.; Jørgensen, K.D. The Influence of Surface Roughness on the Retentive Ability of Two Dental Luting Cements. J. Oral Rehabil. 1978, 5, 377–389. [Google Scholar] [CrossRef] [PubMed]
- Gorodovsky, S.; Zidan, O. Retentive Strength, Disintegration, and Marginal Quality of Luting Cements. J. Prosthet. Dent. 1992, 68, 269–274. [Google Scholar] [CrossRef] [PubMed]
- Ayad, M.F.; Rosenstiel, S.F.; Salama, M. Influence of Tooth Surface Roughness and Type of Cement on Retention of Complete Cast Crowns. J. Prosthet. Dent. 1997, 77, 116–121. [Google Scholar] [CrossRef]
- Price, R.B.; Sutow, E.J. Micrographic and Profilometric Evaluation of the Finish Produced by Diamond and Tungsten Carbide Finishing Burs on Enamel and Dentin. J. Prosthet. Dent. 1988, 60, 311–316. [Google Scholar] [CrossRef]
- Vaz, C.C. Ex Vivo Pilot Study on the Performance of Ultrasonic and Rotary Instruments Obtained by the Process of Chemical Vapor Deposition (CVD) in Fixed Prosthodontics. Master’s Thesis, Universidade de Coimbra, Coimbra, Portugal, 2015. [Google Scholar]
- Pecheva, E.; Sammons, R.L.; Walmsley, A.D. The Performance Characteristics of a Piezoelectric Ultrasonic Dental Scaler. Med. Eng. Phys. 2016, 38, 199–203. [Google Scholar] [CrossRef]
- Lea, S.C.; Landini, G. Reconstruction of Dental Ultrasonic Scaler 3D Vibration Patterns from Phase-Related Data. Med. Eng. Phys. 2010, 32, 673–677. [Google Scholar] [CrossRef]
- Frankenberger, R.; Krämer, N.; Lohbauer, U.; Nikolaenko, S.A.; Reich, S.M. Marginal Integrity: Is the Clinical Performance of Bonded Restorations Predictable In Vitro? J. Adhes. Dent. 2007, 9 (Suppl. 1), 107–116. [Google Scholar] [CrossRef]
- Stappert, C.F.J.; Chitmongkolsuk, S.; Silva, N.R.F.A.; Att, W.; Strub, J.R. Effect of Mouth-Motion Fatigue and Thermal Cycling on the Marginal Accuracy of Partial Coverage Restorations Made of Various Dental Materials. Dent. Mater. 2008, 24, 1248–1257. [Google Scholar] [CrossRef]
- Yilmaz, E.Ç.; Sadeler, R. A literature review on chewing simulation and wear mechanisms of dental biomaterials. J. Bio- Tribo-Corros. 2021, 7, 91. [Google Scholar] [CrossRef]
- Stappert, C.F.J.; Denner, N.; Gerds, T.; Strub, J.R. Marginal Adaptation of Different Types of All-Ceramic Partial Coverage Restorations after Exposure to an Artificial Mouth. Br. Dent. J. 2005, 199, 779–783. [Google Scholar] [CrossRef] [PubMed]
- Del Piñal, M.; Lopez-Suarez, C.; Bartolome, J.F.; Volpato, C.A.; Suarez, M.J. Effect of cementation and aging on the marginal fit of veneered and monolithic zirconia and metal-ceramic CAD-CAM crowns. J. Prosthet. Dent. 2021, 125, 323.e1–323.e7. [Google Scholar] [CrossRef] [PubMed]
- Koenig, V.; Douillard, T.; Chevalier, J.; Amiard, F.; Lamy de la Chapelle, M.; Le Goff, S.; Vanheusden, A.; Dardenne, N.; Wulfman, C.; Mainjot, A. Intraoral low-temperature degradation of monolithic zirconia dental prostheses: 5-year results of a prospective clinical study with ex vivo monitoring. Dent. Mater. 2024, 40, 198–209. [Google Scholar] [CrossRef] [PubMed]
- Baldi, A.; Comba, A.; Ferrero, G.; Italia, E.; Michelotto Tempesta, R.; Paolone, G.; Mazzoni, A.; Breschi, L.; Scotti, N. External Gap Progression after Cyclic Fatigue of Adhesive Overlays and Crowns Made with High Translucency Zirconia or Lithium Silicate. J. Esthet. Restor. Dent. 2022, 34, 557–564. [Google Scholar] [CrossRef]
- Wilson, P.R.; Goodkind, R.J.; Delong, R.; Sakaguchi, R. Deformation of Crowns during Cementation. J. Prosthet. Dent. 1990, 64, 601–609. [Google Scholar] [CrossRef]
- Mustafa, R.; Alshali, R.Z.; Silikas, N. The Effect of Desiccation on Water Sorption, Solubility and Hygroscopic Volumetric Expansion of Dentine Replacement Materials. Dent. Mater. 2018, 34, 205–213. [Google Scholar] [CrossRef]
- Wei, Y.J.; Silikas, N.; Zhang, Z.T.; Watts, D.C. Hygroscopic Dimensional Changes of Self-Adhering and New Resin-Matrix Composites during Water Sorption/Desorption Cycles. Dent. Mater. 2011, 27, 259–266. [Google Scholar] [CrossRef]
- Phillips, R.W.; Swartz, M.L.; Lund, M.S.; Moore, B.K.; Vickery, J. In Vivo Disintegration of Luting Cements. J. Am. Dent. Assoc. 1987, 114, 489–492. [Google Scholar] [CrossRef]
- Gemalmaz, D.; Pameijer, C.H.; Latta, M.; Kuybulu, F.; Alcan, T. In Vivo Disintegration of Four Different Luting Agents. Int. J. Dent. 2012, 2012, 831508. [Google Scholar] [CrossRef]

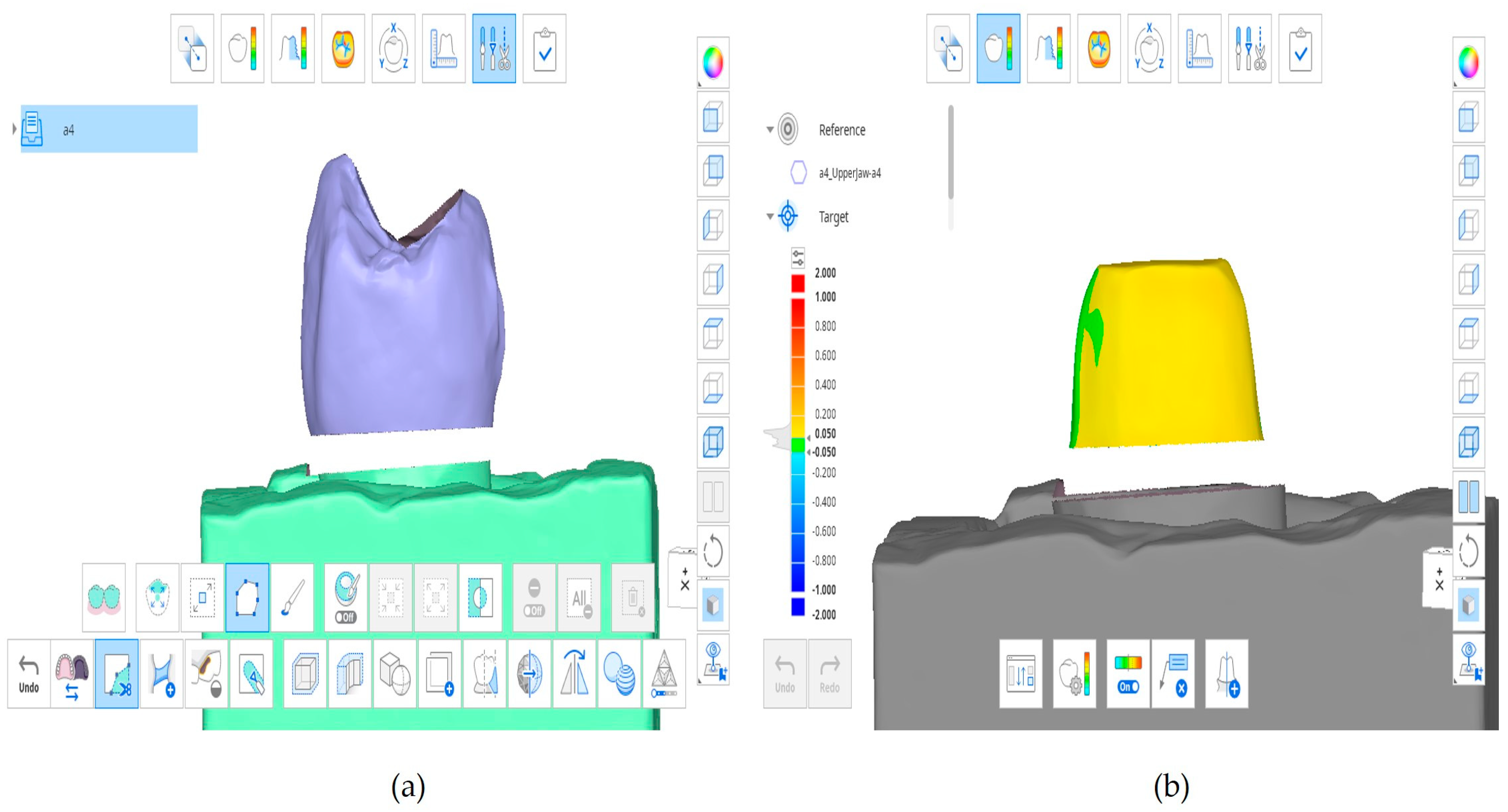



| Defect Type | Visual Cue | Counting Rule | Example from Figure | Subtotal |
|---|---|---|---|---|
| ||||
| Wavy line when looked from the side (Figure 4a) | Entire curvature = 1 defect | Figure 4a (1 sharp curvature) | 1 |
| Isolated peaks (spike), J-shaped margin (lip) | Each spike = 1 defect, each lip = 1 defect | Figure 4b (cluster of 3 spikes) | 3 |
| Hollowing of the finish line periphery when viewed above | Each spot of enamel fracture or gutter = 1 defect | Figure 4c (1 spot of gutter or fracture) | 1 |
| Broken blue segment (discontinuous finish line), C- shaped inward concavity (undercut) | Each broken blue segment = 1 defect, each undercut = 1 defect | Figure 4d (2 interruption spot) | 2 |
| - | - | - | 7 |
| ||||
| Blue spots marked by the software (Figure 4e) | Each blue area = 1 defect | Figure 4e (3 blue depressions) | 3 |
| Red spots marked by the software (Figure 4e) | Each red spot = 1 defect | Figure 4e (4 red spots) | 4 |
| - | - | - | 7 |
| ||||
| Blue spots (Figure 4f) | Each distinct pit = 1 defect | Figure 4f (5 scattered blue concavities, +1 axio-occlusal concavity) | 6 |
| Jagged red edges (Figure 4f) | Each sharp red site = 1 defect | Figure 4f (1 circumferential And 2 surface sharp line angle) | 3 |
| - | - | - | 9 |
| Groups | Total N = 72 | Marginal Gap Abs (Avg) | Marginal Gap RMS | Internal Gap (Axial and Occlusal) Abs (Avg) |
|---|---|---|---|---|
| Group 1: (Air-driven handpiece) | N = 24 | 89.96 ± 25.701 a | 106.21 ± 35.482 a | 71.29 ± 18.534 a,b |
| Group 2: (Electric-driven handpiece) | N = 24 | 79.37 ± 21.032 a | 95.54 ± 20.841 a | 61.33 ± 16.494 a |
| Group 3: (Ultrasonic oscillating handpiece) | N = 24 | 83.33 ± 17.682 a | 98.00 ± 21.516 a | 74.00 ± 13.108 b |
| Sum of Squares | df | Mean Square | F | Sig. | |
|---|---|---|---|---|---|
| Between groups | 1372.528 | 2 | 685.264 | 1.454 | 0.241 |
| Within groups | 32,557.917 | 69 | 471.854 | ||
| Total | 33,930.444 | 71 |
| Independent Samples Kruskal–Wallis Test | Total N | Test Statistic | Degrees of Freedom | Asymptotic Sig. (2-Sided Test) |
|---|---|---|---|---|
| Marginal Gap (RMS) | 72 | 0.578 | 2 | 0.749 |
| Sum of Squares | df | Mean Square | F | Sig. | |
|---|---|---|---|---|---|
| Between Groups | 2135.583 | 2 | 1067.792 | 4.068 | 0.021 * |
| Within groups | 18,110.292 | 69 | 262.468 | ||
| Total | 20,245.875 | 71 |
| Groups | Number of Marginal Defect | Number of Axial Defect | Number of Occlusal Defect |
|---|---|---|---|
| Group 1: (Air-Driven Handpiece) | 6 (4–7) a | 7 (7–8) a,b | 4 (3–4) a |
| Group 2: (Electric-Driven Handpiece) | 5 (4–6) b,a | 6 (6–7) a | 3 (3–4) a |
| Group 3: (Ultrasonic Oscillating Handpiece) | 4 (4–5) b | 9 (7–10) b | 5 (4–5) b |
| Independent Samples Kruskal–Wallis Test | Total N | Test Statistic | Degrees of Freedom | Asymptotic Sig. (2-Sided Test) |
|---|---|---|---|---|
| Marginal Defect | 51 | 6.617 | 2 | 0.037 * |
| Axial Defect | 51 | 8.410 | 2 | 0.015 * |
| Occlusal Defect | 51 | 11.367 | 2 | 0.003 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jadid, R.S.; Al-Zahawi, A.R. In Vitro Comparison of Monolithic Zirconia Crowns: Marginal/Internal Adaptation and 3D-Quantified Preparation Defects Using Air-Driven, Electric-Driven, and Piezoelectric Ultrasonic Handpieces. Prosthesis 2025, 7, 75. https://doi.org/10.3390/prosthesis7040075
Jadid RS, Al-Zahawi AR. In Vitro Comparison of Monolithic Zirconia Crowns: Marginal/Internal Adaptation and 3D-Quantified Preparation Defects Using Air-Driven, Electric-Driven, and Piezoelectric Ultrasonic Handpieces. Prosthesis. 2025; 7(4):75. https://doi.org/10.3390/prosthesis7040075
Chicago/Turabian StyleJadid, Rand Saman, and Abdulsalam Rasheed Al-Zahawi. 2025. "In Vitro Comparison of Monolithic Zirconia Crowns: Marginal/Internal Adaptation and 3D-Quantified Preparation Defects Using Air-Driven, Electric-Driven, and Piezoelectric Ultrasonic Handpieces" Prosthesis 7, no. 4: 75. https://doi.org/10.3390/prosthesis7040075
APA StyleJadid, R. S., & Al-Zahawi, A. R. (2025). In Vitro Comparison of Monolithic Zirconia Crowns: Marginal/Internal Adaptation and 3D-Quantified Preparation Defects Using Air-Driven, Electric-Driven, and Piezoelectric Ultrasonic Handpieces. Prosthesis, 7(4), 75. https://doi.org/10.3390/prosthesis7040075








