EMG and IMU Data Fusion for Locomotion Mode Classification in Transtibial Amputees
Abstract
:1. Introduction
- The fusion of two critical signals, EMG and IMU, significantly enhanced locomotion task classification.
- A comprehensive comparison between two powerful classification models, SVM and LSTM, tailored explicitly for transtibial amputees across a spectrum of locomotion activities.
- A methodology to identify the most representative muscles on the thigh in the gait cycle of individuals with transtibial amputations who use prosthetic sockets on the residual limb was elaborated.
- The use of domain-adaptation techniques to enhance the developed models’ adaptability and robustness, ensuring the models’ reliability and effectiveness across diverse locomotion patterns.
2. Materials and Methods
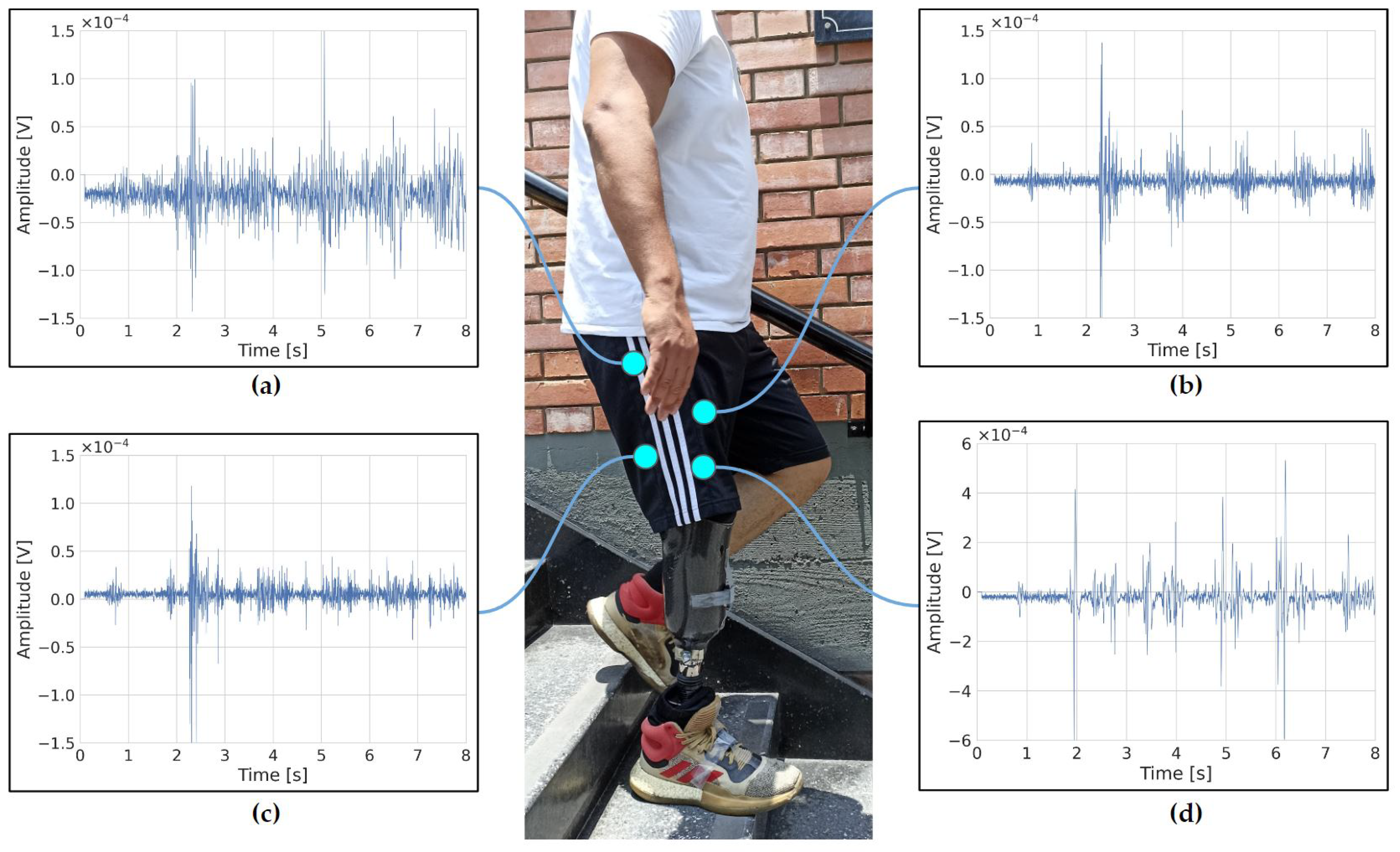
2.1. Experiment Setup
2.2. Experimental Protocol and Tests
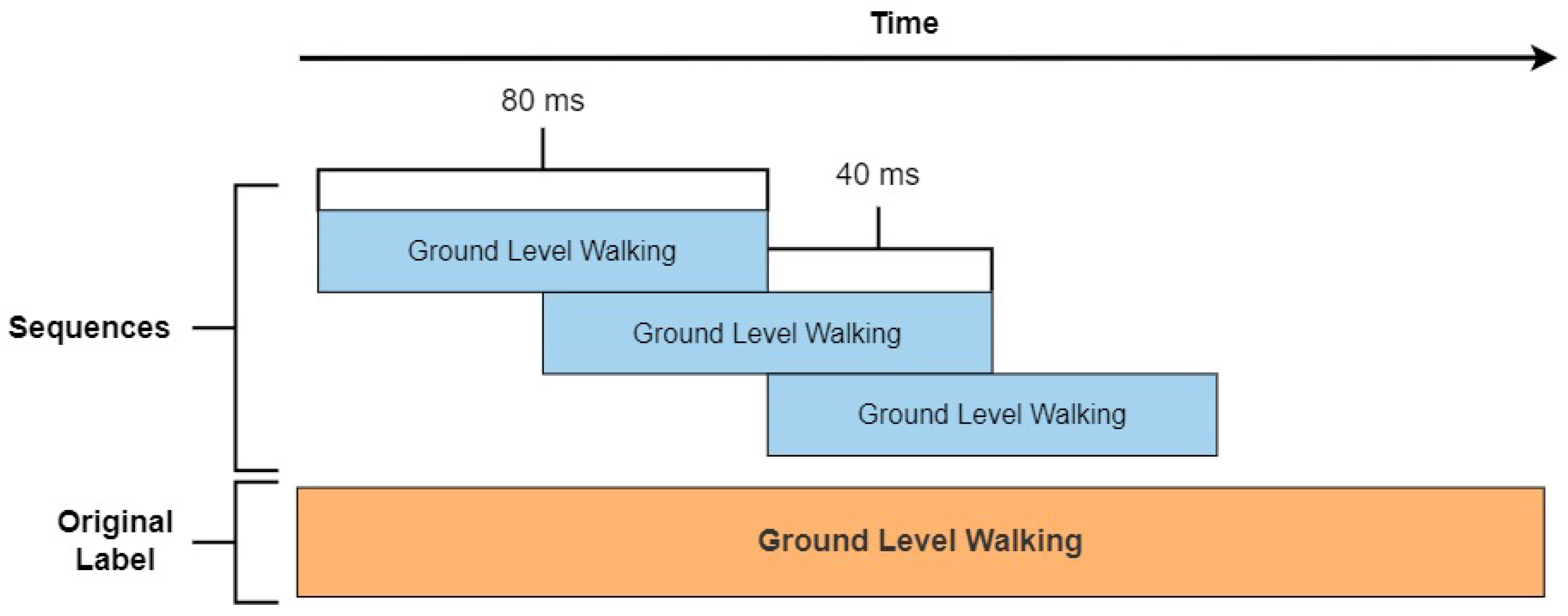
2.3. Data Processing
2.4. System Architecture
2.5. Data Analysis: Performance Metrics
2.6. Hyperparameters
2.6.1. Selection Methodology
2.6.2. Hyperparameters Selected for SVM
2.6.3. Hyperparameters Selected for LSTM
2.7. Domain-Adaptation Techniques
2.8. Statistical Analysis
2.9. Experimental Steps
- Train and test the algorithm on each subject within the non-amputee dataset, meaning the model is trained on 80% of the data from each non-amputee subject and then validated on the remaining 20% of the data from the same subject.
- Train and test on each subject within the amputee data set, using the 80–20 data distribution, similar to the previous item.
- Train and test the algorithm on each subject within the non-amputee dataset, meaning the model is trained on 50% of the data from each non-amputee subject and then validated on the remaining 50% of the data from the same subject.
- Train and test on each subject within the amputee data set, using the 50–50 data distribution, similar to the previous item.
- Train and test on the non-amputee dataset on a subject-independent basis, meaning the models are trained by using the data from all subjects except one in the non-amputee dataset.
- Train and test on the amputee dataset with a subject-independent basis following the same paradigm as the previous step.
- Test the effect of training with non-amputee data and testing on a single amputee subject.
- Test the effect of training with non-amputee data and testing on the entire amputee dataset.
- Evaluate the classification latency assessment of the system.
3. Results
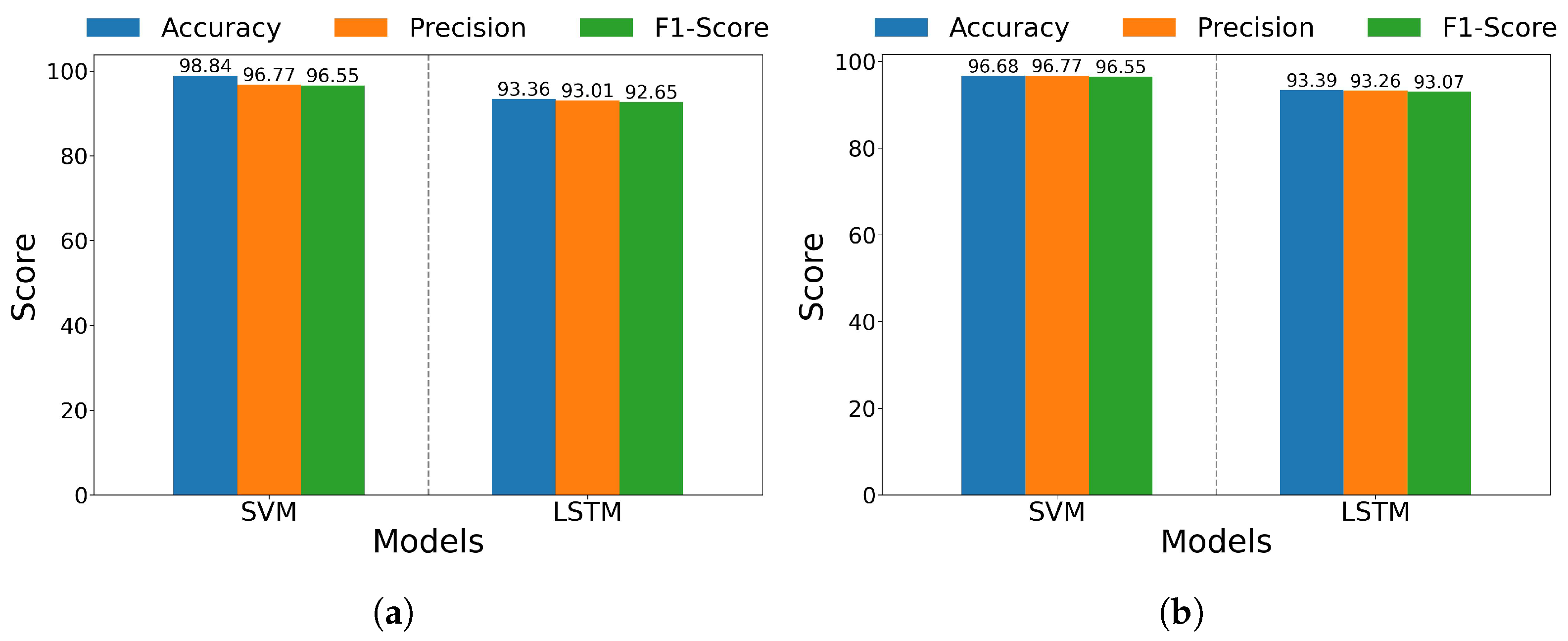
3.1. Within-Subject Evaluation for Non-Amputee and Amputee Datasets
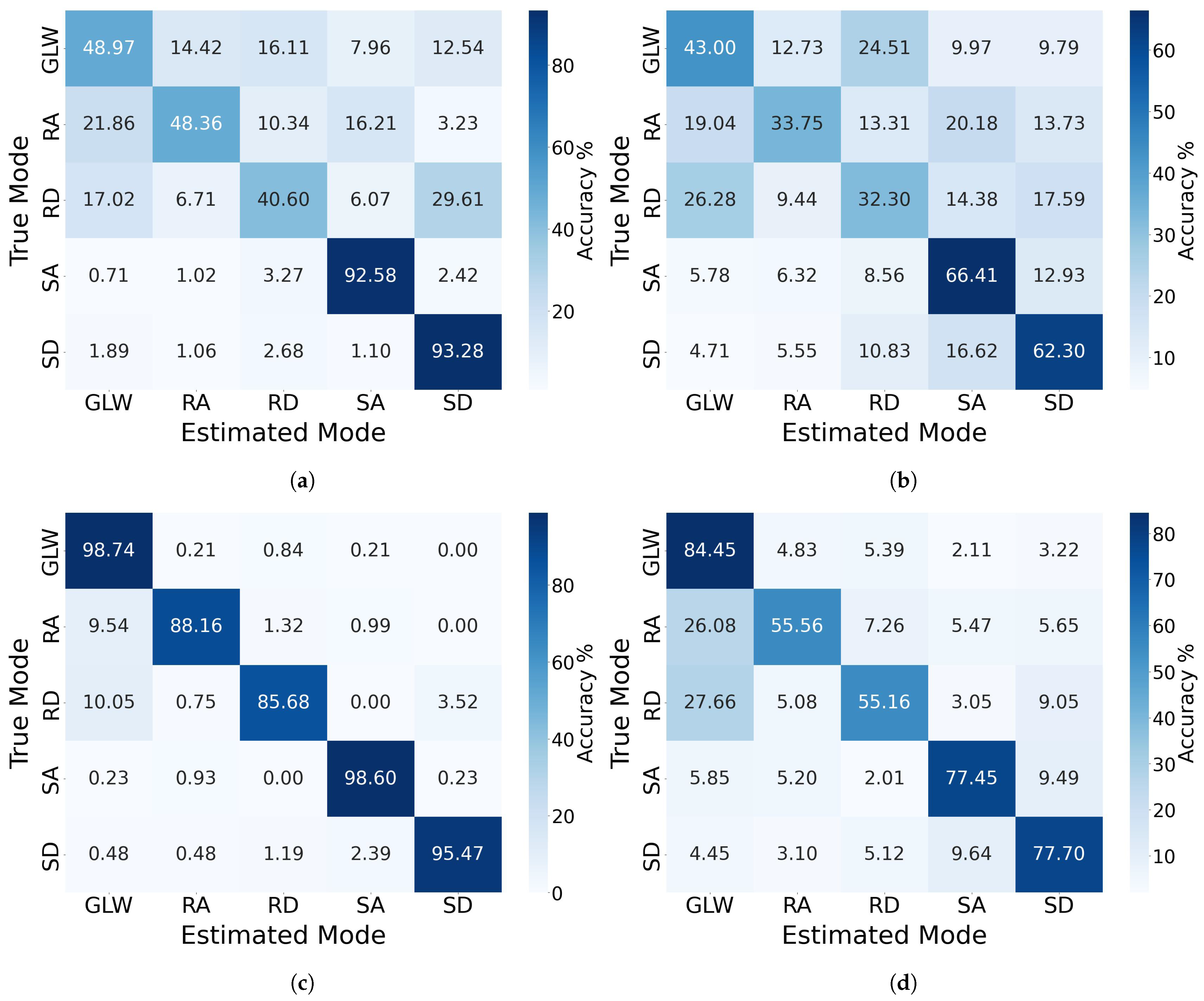
3.2. Cross-Subject Evaluation on Non-Amputee Dataset and Amputee Dataset
3.3. Inter-Population Generalizability
3.4. Classification Latency Assessment
4. Discussion
4.1. Locomotion Modes
4.2. Relevance of Electromyography (EMG), Inertial Measurement Units (IMU), and Data Fusion
4.3. Sensors Positioning
4.4. Architectures of the Algorithms
4.5. Dataset Composition and Its Implications
4.6. Domain-Adaptation in SVM and LSTM Models
4.7. Limitations and Future Outlook
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANOVA | Analysis of variance |
| AL | Adductor longus |
| BF | Biceps femoris |
| Bi-LSTM | Bi-directional long short-term memory |
| CORAL | Correlation alignment |
| EMG | Electromyographic |
| FT | Foot |
| GLW | Ground-level walking |
| HSD | Honest significant difference |
| IMU | Inertial measurement unit |
| LOOCV | Leave-one-out cross-validation |
| LSTM | Long short-term memory |
| RBF | Radial basis function |
| RPA | Ramp ascent |
| RPD | Ramp descent |
| RF | Rectus femoris |
| SSA | Stairs ascent |
| SSD | Stairs descent |
| SVM | Support vector machine |
| TF | Tensor fasciae latae |
| TB | Tibia |
References
- Vázquez, E. Los Amputados y su Rehabilitación. Un Reto Para el Estado; Intersistemas: Ciudad de México (CDMX), Mexico, 2016; p. 5. [Google Scholar]
- Ziegler-Graham, K.; MacKenzie, E.J.; Ephraim, P.L.; Travison, T.G.; Brookmeyer, R. Estimating the prevalence of limb loss in the united states: 2005 to 2050. Arch. Phys. Med. Rehabil. 2008, 89, 422–429. [Google Scholar] [CrossRef]
- Molina, C.S.; Faulk, J. Lower Extremity Amputation; StatPearls Publishing: Treasure Island, FL, USA, 2022. [Google Scholar]
- Su, B.-Y.; Wang, J.; Liu, S.-Q.; Sheng, M.; Jiang, J.; Xiang, K. A CNN-based method for intent recognition using inertial measurement units and intelligent lower limb prosthesis. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1032–1042. [Google Scholar] [CrossRef]
- Farro, L.; Tapia, R.; Bautista, L.; Montalvo, R.; Iriartem, H. Características clínicas y demográficas del paciente amputado. Rev. Med. Hered. 2012, 23, 240–243. [Google Scholar] [CrossRef]
- Miller, J.D.; Beazer, M.S.; Hahn, M.E. Myoelectric walking mode classification for transtibial amputees. IEEE Trans. Biomed. Eng. 2013, 60, 2745–2750. [Google Scholar] [CrossRef]
- Sherrat, F.; Plummer, A.; Iravani, P. Understanding LSTM network behaviour of IMU-based locomotion mode recognition for applications in prostheses and wearables. Sensors 2021, 21, 1264. [Google Scholar] [CrossRef]
- Brantley, J.A.; Luu, T.P.; Nakagome, S.; Contreras-Vidal, J.L. Prediction of lower-limb joint kinematics from surface EMG during overground locomotion. In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017. [Google Scholar]
- Bhakta, K.; Camargo, J.; Young, A.J. Control and experimental validation of a powered knee and ankle prosthetic device. In Proceedings of the ASME 2018 Dynamic Systems and Control Conference, Atlanta, GA, USA, 30 September–3 October 2018. [Google Scholar]
- Simon, A.M.; Finucane, S.B.; Ikeda, A.J.; Cotton, R.J.; Hargrove, L.J. Powered knee and ankle prosthesis use with a K2 level ambulator: A case report. Front. Rehabil. Sci. 2023, 4, 1203545. [Google Scholar] [CrossRef]
- Pi, M. Gait control of robotic leg prosthesis based on motion predictive system. In Proceedings of the International Conference on Advanced Robotics and Mechatronics, Shenzhen, China, 18–21 December 2020. [Google Scholar]
- Zhang, K.; Xiong, C.; Zhang, W.; Liu, H.; Lai, D.; Rong, Y.; Fu, C. Environmental features recognition for lower limb prostheses toward predictive walking. IEEE Trans. Neural Syst. Rehabil. Eng 2019, 27, 465–476. [Google Scholar] [CrossRef]
- Stolyarov, R.; Carney, M.; Herr, H. Accurate heuristic terrain prediction in powered lower-limb prostheses using onboard sensors. IEEE Trans. Biomed. Eng. 2021, 68, 384–392. [Google Scholar] [CrossRef]
- Mazón, D.M.; Groefsema, M.; Lambert, R.B.; Carloni, R. IMU-based classification of locomotion modes, transitions, and gait phases with convolutional recurrent neural networks. Sensors 2022, 22, 8871. [Google Scholar] [CrossRef]
- Barberi, F.; Iberite, F.; Anselmino, E.; Randi, P.; Sacchetti, R.; Gruppioni, E.; Mazzoni, A.; Micera, S. Early decoding of walking tasks with minimal set of EMG channels. J. Neural Eng. 2023, 20, 026038. [Google Scholar] [CrossRef]
- Zhou, C.; Yang, L.; Liao, H.; Liang, B.; Ye, X. Ankle foot motion recognition based on wireless wearable sEMG and acceleration sensors for smart AFO. Sens. Actuator A Phys. 2021, 331, 113025. [Google Scholar] [CrossRef]
- Meng, L.; Pang, J.; Wang, Z.; Xu, R.; Ming, D. The role of surface electromyography in data fusion with inertial sensors to enhance locomotion recognition and prediction. Sensors 2021, 331, 6291. [Google Scholar] [CrossRef]
- Hu, B.; Rouse, E.; Hargrove, L. Benchmark Datasets for bilateral lower-limb neuromechanical signals from wearable sensors during unassisted locomotion in able-bodied individuals. Front. Robot. AI 2018, 5, 14. [Google Scholar] [CrossRef]
- Fleming, A.; Huang, S.; Huang, H. Proportional myoelectric control of a virtual inverted pendulum using residual antagonistic muscles: Toward voluntary postural control. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 1473–1482. [Google Scholar] [CrossRef]
- Huang, S.; Huang, H. Voluntary control of residual antagonistic muscles in transtibial amputees: Reciprocal activation, coactivation, and implications for direct neural control of powered lower limb prostheses. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 85–95. [Google Scholar] [CrossRef]
- Turner, S.; McGregor, A.H. Perceived effect of socket fit on major lower limb prosthetic rehabilitation: A clinician and amputee perspective. Arch. Rehabil. Res. Clin. Transl. 2020, 2, 100059. [Google Scholar] [CrossRef]
- Safari, M.R.; Meier, M.R. Systematic review of effects of current transtibial prosthetic socket designs—Part 1: Qualitative outcomes. J. Rehabil. Res. Dev. 2015, 52, 491–508. [Google Scholar] [CrossRef]
- Trigno Avanti Sensor. Available online: https://delsys.com/trigno-avanti/ (accessed on 11 October 2023).
- Ministerio de Vivienda, Construcción y Saneamiento del Gobierno Peruano. Accesibilidad Para Personas con Discapacidad y de las Personas Adultas Mayores. Available online: https://www.mimp.gob.pe/adultomayor/archivos/Norma_A_120.pdf (accessed on 11 October 2023).
- Nazmi, N.; Abdul Rahman, M.A.; Yamamoto, S.-I.; Ahmad, S.A. Walking gait event detection based on electromyography signals using artificial neural network. Biomed. Signal Process. Control 2018, 47, 334–343. [Google Scholar] [CrossRef]
- Toledo-Pérez, D.C.; Rodríguez, J.; Gómez, R.A.; Martínez, J.F.; Carrasco, J.A. Feature selection algorithms to reduce processing time in classification with SVMs. In Proceedings of the XVII International Engineering Congress, Queretaro, Mexico, 14–18 June 2021. [Google Scholar]
- Trigini, A.; Scattolini, M.; Mengarelli, A.; Fioretti, S.; Morettini, M.; Burattini, L.; Verdini, F. Role of the Window Length for Myoelectric Pattern Recognition in Detecting User Intent of Motion. In Proceedings of the 2022 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Messina, Italy, 22–24 June 2022. [Google Scholar]
- Trigini, A.; Al-Timemy, A.; Verdini, F.; Fioretti, S.; Morettini, M.; Burattini, L.; Mengarelli, A. Decoding transient sEMG data for intent motion recognition in transhumeral amputees. Biomed. Signal Process. Control 2023, 85, 104936. [Google Scholar] [CrossRef]
- Kopke, J.V.; Ellis, M.D.; Hargrove, L.J. Determining User Intent of Partly Dynamic Shoulder Tasks in Individuals with Chronic Stroke Using Pattern Recognition. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 28, 350–358. [Google Scholar] [CrossRef]
- Sarshar, M.; Polturi, S.; Schega, L. Gait Phase Estimation by Using LSTM in IMU-Based Gait Analysis—Proof of Concept. Sensors 2021, 21, 5749. [Google Scholar] [CrossRef]
- Camargo, J.; Flanagan, W.; Csomay-Shanklin, N.; Kanwar, B.; Young, A. A Machine Learning Strategy for Locomotion Classification and Parameter Estimation Using Fusion of Wearable Sensors. IEEE Trans. Biomed. Eng. 2021, 68, 350–358. [Google Scholar] [CrossRef]
- Huang, H.; Zhou, P.; Li, G.; Kuiken, T.A. An Analysis of EMG Electrode Configuration for Targeted Muscle Reinnervation Based Neural Machine Interface. IEEE Trans. Neural Syst. Rehabil. Eng. 2008, 16, 37–45. [Google Scholar] [CrossRef]
- Bruinsma, J.; Carloni, R. IMU-based deep neural network: Prediction of locomotor and transition intentions of an osseointegrated transfemoral amputee. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 1079–1088. [Google Scholar] [CrossRef]
- Putri, F.T.; Caesarendra, W.; Królczyk, G.; Glowacz, A.; Prawibowo, H.; Ismail, R.; Indrawati, R.T. Human walking gait classification utilizing an artificial neural network for the ergonomics study of lower limb prosthetics. Prosthesis 2023, 5, 647–665. [Google Scholar] [CrossRef]
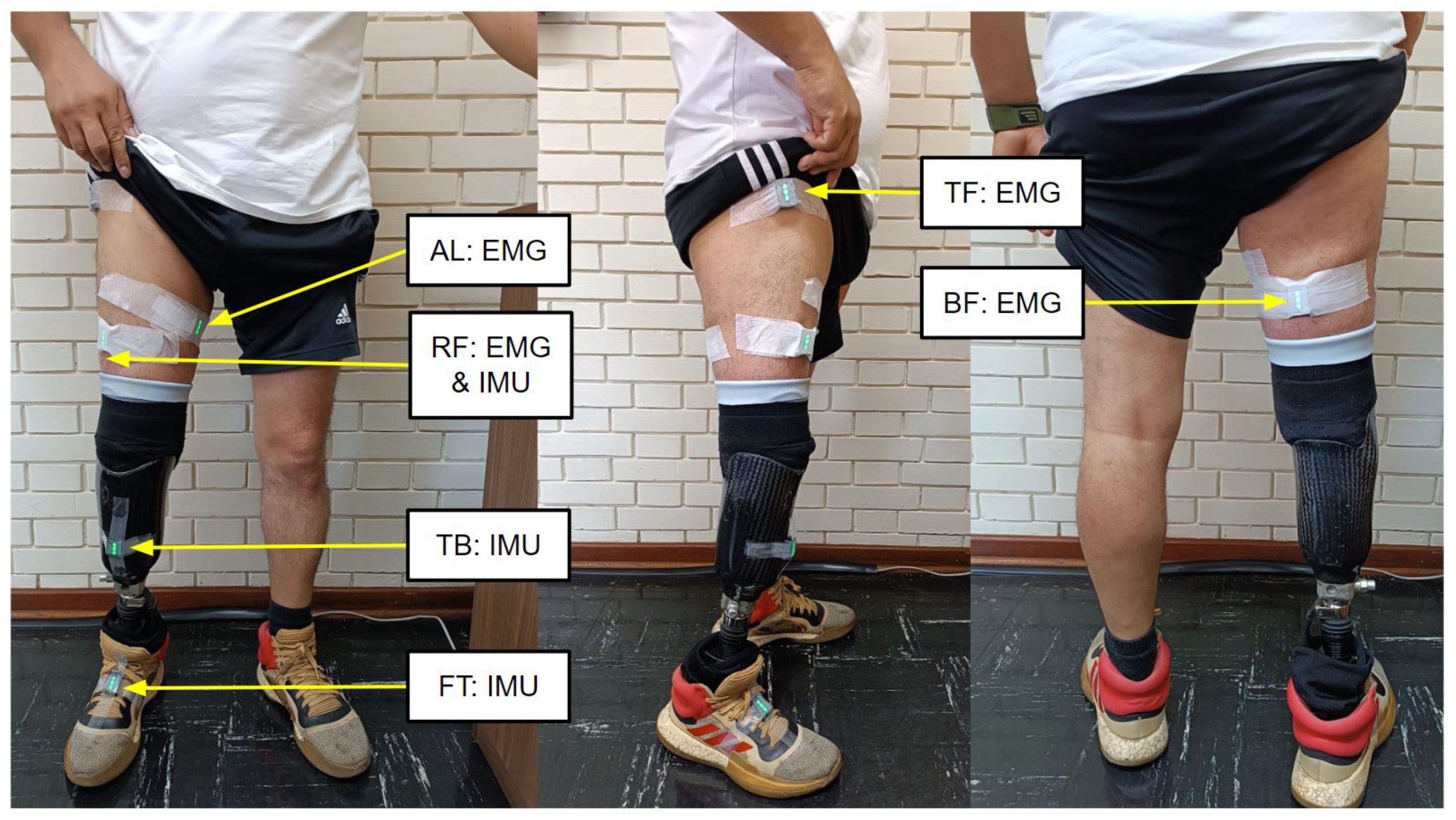




| Participant | Age (Years) | Height (cm) | Weight (kg) | Amputated Side | Year since Amputation | Current Prosthesis |
|---|---|---|---|---|---|---|
| Amputee 01 | 58 | 167 | 66 | Right | 17 years/2006 | Transtibial prosthesis with acrylic sock-type socket with liner and rigid foot |
| Amputee 02 | 50 | 167 | 79 | Left | 5 years/2018 | Transtibial plastic socket type prosthesis without liner and articulated foot |
| Amputee 03 | 24 | 170 | 70 | Right | 1.5 years/2022 | Transtibial fiberglass prosthesis with resin, socket type with liner and articulated foot |
| Amputee 04 | 20 | 174 | 70 | Right | 2 years/2021 | Transtibial carbon fiber socket-type prosthesis with liner and rigid foot |
| Amputee 05 | 41 | 182 | 95 | Right | 12 years/2011 | Transtibial carbon fiber socket-type prosthesis with liner and rigid foot |
| Muscle | Movement |
|---|---|
| Rectus femoris (RF) | With the hip slightly flexed, perform knee extension movements. |
| Biceps femoris (BF) | With the hip slightly extended, perform knee flexion movements, bringing the heel towards the gluteus. |
| Tensor fasciae latae (TF) | Perform hip abduction movements from a natural position. |
| Adductor Longus (AL) | With the feet at hip level, rest the inside edge of the foot against the floor. |
| Subject | Support Vector Machine | Long Short-Term Memory | ||||
|---|---|---|---|---|---|---|
| Accuracy (%) | Precision (%) | F1 Score (%) | Accuracy (%) | Precision (%) | F1 Score (%) | |
| Non-Amputee 01 | 99.20 ± 0.252 | 99.21 ± 0.240 | 99.21 ± 0.244 | 98.48 ± 0.202 | 98.39 ± 0.259 | 98.38 ± 0.187 |
| Non-Amputee 02 | 97.70 ± 0.837 | 97.60 ± 0.760 | 97.22 ± 1.036 | 93.73 ± 0.518 | 92.91 ± 0.690 | 92.43 ± 0.587 |
| Non-Amputee 03 | 97.94 ± 0.813 | 97.92 ± 0.898 | 97.92 ± 0.850 | 95.41 ± 0.538 | 95.48 ± 0.503 | 95.41 ± 0.524 |
| Non-Amputee 04 | 96.82 ± 0.815 | 96.56 ± 0.919 | 96.46 ± 0.934 | 91.40 ± 0.732 | 91.11 ± 0.715 | 90.89 ± 0.791 |
| Non-Amputee 05 | 97.02 ± 1.078 | 97.09 ± 1.018 | 97.00 ± 1.037 | 92.18 ± 0.911 | 92.31 ± 1.155 | 92.13 ± 0.916 |
| Non-Amputee 06 | 94.63 ± 0.253 | 94.57 ± 0.282 | 94.34 ± 0.265 | 90.47 ± 0.945 | 90.50 ± 0.879 | 90.15 ± 1.010 |
| Non-Amputee 07 | 97.69 ± 0.606 | 97.87 ± 0.501 | 97.70 ± 0.639 | 97.03 ± 0.279 | 96.94 ± 0.356 | 96.96 ± 0.278 |
| Non-Amputee 08 | 96.76 ± 0.799 | 96.67 ± 0.863 | 96.11 ± 1.016 | 89.67 ± 0.493 | 88.00 ± 0.944 | 87.62 ± 0.719 |
| Non-Amputee 09 | 96.40 ± 0.741 | 96.27 ± 0.782 | 96.18 ± 0.785 | 94.72 ± 0.482 | 94.40 ± 0.476 | 94.29 ± 0.529 |
| Non-Amputee 10 | 96.41 ± 0.730 | 96.28 ± 0.719 | 95.94 ± 0.833 | 93.14 ± 0.676 | 93.10 ± 0.420 | 92.10 ± 0.821 |
| Non-Amputee 11 | 96.01 ± 0.427 | 95.55 ± 0.512 | 95.34 ± 0.415 | 90.79 ± 0.520 | 90.37 ± 0.849 | 89.62 ± 0.480 |
| Non-Amputee 12 | 97.90 ± 0.914 | 97.86 ± 0.869 | 97.51 ± 1.184 | 94.36 ± 0.660 | 93.35 ± 0.828 | 93.33 ± 0.889 |
| Non-Amputee 13 | 95.97 ± 0.759 | 96.00 ± 0.743 | 95.73 ± 0.766 | 92.34 ± 0.463 | 91.63 ± 0.466 | 91.35 ± 0.609 |
| Non-Amputee 14 | 97.51 ± 0.309 | 97.49 ± 0.325 | 97.37 ± 0.351 | 95.71 ± 0.696 | 95.27 ± 0.725 | 95.09 ± 0.795 |
| Non-Amputee 15 | 96.62 ± 0.684 | 96.46 ± 0.745 | 96.40 ± 0.757 | 92.05 ± 0.588 | 91.94 ± 0.802 | 91.70 ± 0.585 |
| Non-Amputee 16 | 96.77 ± 1.206 | 97.00 ± 1.156 | 96.68 ± 1.285 | 93.00 ± 0.846 | 93.30 ± 0.719 | 92.82 ± 0.930 |
| Non-Amputee 17 | 95.11 ± 0.883 | 94.82 ± 0.843 | 94.66 ± 0.939 | 91.64 ± 0.605 | 90.49 ± 0.844 | 90.72 ± 0.719 |
| Non-Amputee 18 | 96.17 ± 0.605 | 96.09 ± 0.627 | 95.65 ± 0.721 | 93.30 ± 0.470 | 93.41 ± 0.474 | 92.15 ± 0.629 |
| Non-Amputee 19 | 97.34 ± 0.538 | 97.23 ± 0.578 | 96.79 ± 0.709 | 92.91 ± 0.358 | 92.36 ± 0.481 | 91.42 ± 0.401 |
| Non-Amputee 20 | 96.90 ± 0.340 | 96.80 ± 0.388 | 96.71 ± 0.352 | 94.80 ± 0.434 | 94.87 ± 0.517 | 94.47 ± 0.454 |
| Non-Amputee Average | 98.84 ± 0.679 | 96.77 ± 0.688 | 96.55 ± 0.756 | 93.36 ± 0.571 | 93.01 ± 0.655 | 92.65 ± 0.643 |
| Amputee 01 | 95.47 ± 0.869 | 95.46 ± 0.901 | 95.19 ± 0.985 | 91.38 ± 0.301 | 91.16 ± 0.445 | 90.87 ± 0.367 |
| Amputee 02 | 95.31 ± 0.722 | 95.39 ± 0.700 | 95.31 ± 0.662 | 91.31 ± 0.494 | 91.25 ± 0.485 | 91.03 ± 0.436 |
| Amputee 03 | 96.83 ± 0.532 | 97.18 ± 0.559 | 96.70 ± 0.591 | 94.33 ± 0.470 | 94.03 ± 0.629 | 93.96 ± 0.512 |
| Amputee 04 | 97.05 ± 0.465 | 97.13 ± 0.506 | 96.98 ± 0.479 | 94.22 ± 0.299 | 94.36 ± 0.286 | 94.03 ± 0.315 |
| Amputee 05 | 98.72 ± 0.447 | 98.67 ± 0.429 | 98.57 ± 0.436 | 95.69 ± 0.418 | 95.51 ± 0.414 | 95.47 ± 0.463 |
| Amputee Average | 96.68 ± 0.607 | 96.77 ± 0.619 | 96.55 ± 0.631 | 93.39 ± 0.396 | 93.26 ± 0.452 | 93.07 ± 0.419 |
| Subject | Support Vector Machine | Long Short-Term Memory | ||||
|---|---|---|---|---|---|---|
| Accuracy (%) | Precision (%) | F1 Score (%) | Accuracy (%) | Precision (%) | F1 Score (%) | |
| Non-Amputee 01 | 98.93 ± 0.423 | 98.96 ± 0.419 | 98.93 ± 0.433 | 98.17 ± 0.319 | 98.03 ± 0.336 | 98.04 ± 0.342 |
| Non-Amputee 02 | 96.88 ± 0.673 | 96.64 ± 0.671 | 96.18 ± 0.733 | 93.66 ± 0.462 | 93.21 ± 0.478 | 92.32 ± 0.610 |
| Non-Amputee 03 | 97.48 ± 1.428 | 97.49 ± 1.386 | 97.42 ± 1.459 | 95.37 ± 0.702 | 95.44 ± 0.640 | 95.36 ± 0.683 |
| Non-Amputee 04 | 94.70 ± 1.371 | 94.24 ± 1.503 | 94.07 ± 1.493 | 91.91 ± 0.178 | 91.70 ± 0.258 | 91.41 ± 0.188 |
| Non-Amputee 05 | 96.04 ± 0.781 | 96.20 ± 0.714 | 95.90 ± 0.818 | 91.94 ± 0.285 | 92.16 ± 0.370 | 91.91 ± 0.285 |
| Non-Amputee 06 | 91.69 ± 1.379 | 91.69 ± 1.481 | 91.21 ± 1.364 | 89.93 ± 0.470 | 89.94 ± 0.647 | 89.57 ± 0.481 |
| Non-Amputee 07 | 96.48 ± 0.812 | 96.78 ± 0.894 | 96.42 ± 0.928 | 96.63 ± 0.398 | 96.53 ± 0.400 | 96.56 ± 0.399 |
| Non-Amputee 08 | 94.44 ± 1.223 | 94.20 ± 1.164 | 93.13 ± 1.640 | 88.57 ± 0.612 | 87.52 ± 0.664 | 85.99 ± 0.961 |
| Non-Amputee 09 | 95.32 ± 0.935 | 95.17 ± 0.892 | 94.97 ± 1.025 | 94.91 ± 0.161 | 94.68 ± 0.117 | 94.47 ± 0.190 |
| Non-Amputee 10 | 95.24 ± 0.734 | 95.05 ± 0.632 | 94.53 ± 0.799 | 93.83 ± 0.783 | 93.58 ± 0.660 | 92.95 ± 0.919 |
| Non-Amputee 11 | 93.48 ± 1.463 | 92.90 ± 2.043 | 92.34 ± 1.828 | 91.31 ± 0.752 | 90.61 ± 0.744 | 90.20 ± 0.876 |
| Non-Amputee 12 | 97.25 ± 1.248 | 97.09 ± 1.317 | 96.65 ± 1.567 | 95.40 ± 0.744 | 94.89 ± 0.762 | 94.72 ± 0.933 |
| Non-Amputee 13 | 94.36 ± 1.058 | 94.14 ± 1.294 | 93.76 ± 1.266 | 92.52 ± 0.421 | 91.99 ± 0.320 | 91.70 ± 0.498 |
| Non-Amputee 14 | 95.93 ± 0.683 | 95.90 ± 0.694 | 95.62 ± 0.765 | 95.65 ± 0.528 | 95.21 ± 0.500 | 95.11 ± 0.512 |
| Non-Amputee 15 | 95.73 ± 0.861 | 95.47 ± 0.890 | 95.42 ± 0.920 | 91.89 ± 0.774 | 91.69 ± 0.951 | 91.60 ± 0.868 |
| Non-Amputee 16 | 94.65 ± 1.318 | 94.87 ± 1.256 | 94.30 ± 1.510 | 92.98 ± 0.969 | 92.98 ± 1.183 | 92.86 ± 0.950 |
| Non-Amputee 17 | 94.19 ± 1.239 | 94.20 ± 1.291 | 93.56 ± 1.493 | 91.01 ± 0.542 | 89.75 ± 0.701 | 89.92 ± 0.604 |
| Non-Amputee 18 | 94.82 ± 0.712 | 94.72 ± 0.865 | 94.05 ± 0.757 | 93.39 ± 0.321 | 93.03 ± 0.430 | 92.11 ± 0.271 |
| Non-Amputee 19 | 95.88 ± 0.579 | 95.74 ± 0.659 | 95.00 ± 0.688 | 92.63 ± 0.725 | 91.75 ± 0.752 | 91.23 ± 0.757 |
| Non-Amputee 20 | 95.80 ± 0.967 | 95.60 ± 1.025 | 95.42 ± 1.049 | 94.94 ± 0.641 | 94.98 ± 0.596 | 94.61 ± 0.702 |
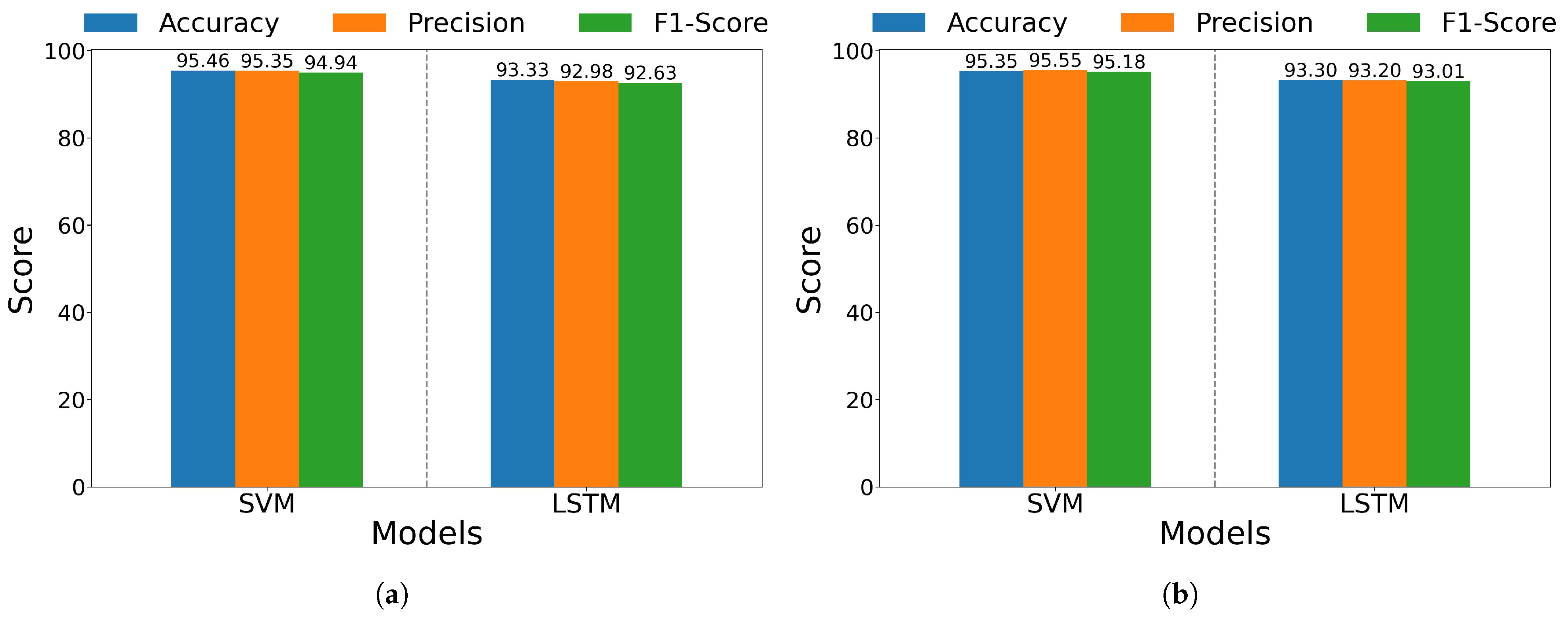
| Non-Amputee Average | 95.46 ± 0.994 | 95.35 ± 1.055 | 94.94 ± 1.127 | 93.33 ± 0.539 | 92.98 ± 0.575 | 92.63 ± 0.601 |
| Amputee 01 | 93.85 ± 2.275 | 94.07 ± 2.150 | 93.50 ± 2.489 | 91.41 ± 0.929 | 91.21 ± 1.024 | 90.98 ± 1.010 |
| Amputee 02 | 93.58 ± 1.121 | 93.77 ± 1.228 | 93.70 ± 1.048 | 90.82 ± 0.618 | 90.89 ± 0.687 | 90.59 ± 0.632 |
| Amputee 03 | 95.84 ± 1.300 | 96.34 ± 1.016 | 95.52 ± 1.486 | 94.47 ± 0.249 | 94.17 ± 0.326 | 94.06 ± 0.278 |
| Amputee 04 | 95.82 ± 0.264 | 95.96 ± 0.346 | 95.72 ± 0.265 | 94.18 ± 0.641 | 94.25 ± 0.789 | 94.04 ± 0.689 |
| Amputee 05 | 97.67 ± 1.058 | 97.61 ± 1.075 | 97.45 ± 1.107 | 95.63 ± 0.530 | 95.48 ± 0.543 | 95.37 ± 0.531 |
| Amputee Average | 95.35 ± 1.204 | 95.55 ± 1.163 | 95.18 ± 1.279 | 93.30 ± 0.593 | 93.20 ± 0.674 | 93.01 ± 0.628 |
| Group Subject | Support Vector Machine | Long Short-Term Memory | |||||
|---|---|---|---|---|---|---|---|
| Accuracy(%) | Precision (%) | F1 Score (%) | Accuracy(%) | Precision (%) | F1 Score (%) | ||
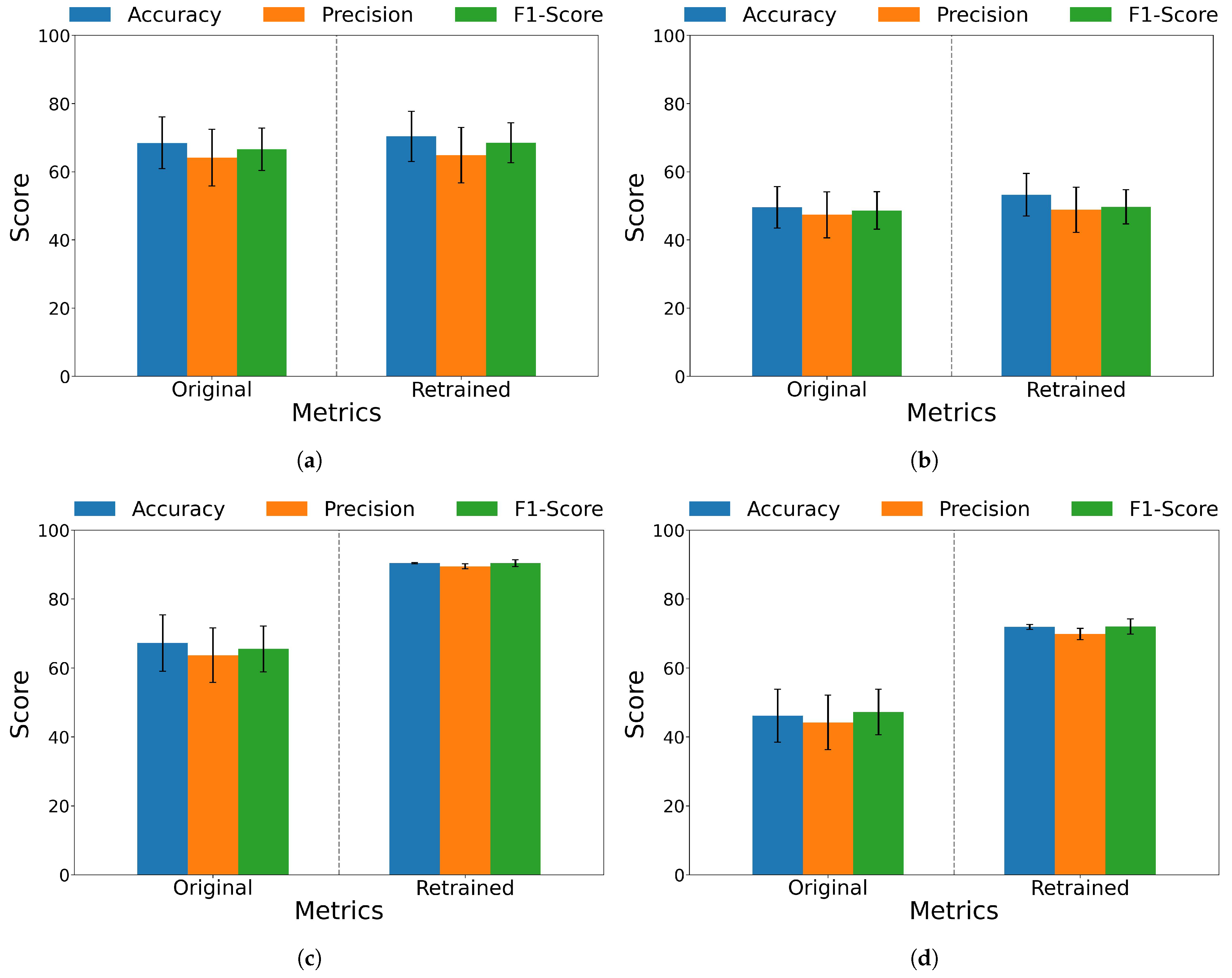
| Amputee Group | Before | 49.52 ± 6.06 | 47.33 ± 6.75 | 48.61 ± 5.48 | 46.16 ± 7.69 | 44.21 ± 7.92 | 47.22 ± 6.63 |
| After | 53.22 ± 6.22 | 48.84 ± 6.65 | 49.68 ± 5.02 | 71.86 ± 0.67 | 69.83 ± 1.61 | 72.00 ± 2.19 | |
| Non-amputee Group | Before | 68.45 ± 7.59 | 64.13 ± 8.33 | 66.57 ± 6.26 | 67.22 ± 8.16 | 63.67 ± 7.90 | 65.52 ± 6.64 |
| After | 70.37 ± 7.38 | 64.83 ± 8.10 | 68.52 ± 5.94 | 90.37 ± 0.18 | 89.45 ± 0.75 | 90.36 ± 1.03 | |
| Support Vector Machine | Long Short-Term Memory | |||||
|---|---|---|---|---|---|---|
| Accuracy (%) | Precision (%) | F1 Score (%) | Accuracy (%) | Precision (%) | F1 Score (%) | |
| Before | 43.14 | 43.04 | 42.73 | 45.86 | 45.81 | 45.68 |
| After | 45.71 | 45.83 | 45.32 | 73.07 | 76.16 | 72.75 |
| Support Vector Machine | Long Short-Term Memory | |||||
|---|---|---|---|---|---|---|
| Accuracy (%) | Precision (%) | F1 Score (%) | Accuracy (%) | Precision (%) | F1 Score (%) | |
| Before | 43.60 | 43.82 | 43.07 | 45.21 | 46.38 | 44.30 |
| After | 44.23 | 43.94 | 44.02 | 70.57 | 71.81 | 69.30 |
| Model | Average Latency (ms) |
|---|---|
| Support Vector Machine | 19.84 |
| Long Short-Term Memory | 37.07 |
| Author/Year | Muscle | Locomotion Modes | Participants | Accuracy |
|---|---|---|---|---|
| Miller et al., 2013 [6] | Tibialis anterior, medial gastrocnemius, vastus lateralis, biceps femoris | Ground-level walking, ramp ascent, ramp descent, stairs ascent, stairs descent | 5 non-amputees, 5 transtibial amputees | 94.7%, 97.9% |
| Meng et al., 2021 [17] | Rectus femoris, vastus lateralis, biceps femoris, semitendinosus, tibialis anterior, medial gastrocnemius, lateral gastrocnemius | Ground-level walking, ramp ascent, ramp descent, stairs ascent, stairs descent, standing, sitting | 10 non-amputees | 98.0% |
| Barberi et al., 2023 [15] | Adductor longus, rectus femoris, biceps femoris, tensor fasciae latae | Ground-level walking, ramp ascent, ramp descent, stairs ascent, stairs descent | 13 transfemoral amputees | 94.0% |
| Present study | Adductor longus, rectus femoris, biceps femoris, tensor fasciae latae | Ground-level walking, ramp ascent, ramp descent, stairs ascent, stairs descent | 20 non-amputees, 5 transtibial amputees | 98.8%, 96.7% |
| Author/Year | Dataset | Data Acquisition | Architectures of the Algorithms | Machine Learning Method | Accuracy |
|---|---|---|---|---|---|
| Bruinsma et al., 2021 [33] | Transfemoral amputee | IMU | RNNs + 4× GRU + 2× dense layers | LDA | 93.0% |
| RNNs + 4× LSTM + 2× dense layers | LDA | 90.0% | |||
| BiLSTM | 99.8% | ||||
| SVM | 90.4% | ||||
| Zhou et al., 2021 [16] | Ankle–foot motion | EMG + IMU | BiLSTM layer + dense layer + Softmax | ANN | 94.7% |
| Decision tree (DT) | 74.5% | ||||
| Naive Bayes (NB) | 82.5% | ||||
| Mazon et al., 2022 [14] | Transfemoral amputee | IMU | 2× ReLU + Dropout + 2× dense layer + Softmax | LSTM | 95.0% |
| Putri et al., 2023 [34] | Transtibial amputee | EMG | Hidden | ANN | 96.0% |
| Present study | Transtibial amputees | EMG + IMU | Lineal kernel, 2nd order poly kernel | SVM | 98.8% |
| BiLSTM + Dropout + BiLSTM + Dropout + ReLU + Softmax | LSTM | 93.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzales-Huisa, O.A.; Oshiro, G.; Abarca, V.E.; Chavez-Echajaya, J.G.; Elias, D.A. EMG and IMU Data Fusion for Locomotion Mode Classification in Transtibial Amputees. Prosthesis 2023, 5, 1232-1256. https://doi.org/10.3390/prosthesis5040085
Gonzales-Huisa OA, Oshiro G, Abarca VE, Chavez-Echajaya JG, Elias DA. EMG and IMU Data Fusion for Locomotion Mode Classification in Transtibial Amputees. Prosthesis. 2023; 5(4):1232-1256. https://doi.org/10.3390/prosthesis5040085
Chicago/Turabian StyleGonzales-Huisa, Omar A., Gonzalo Oshiro, Victoria E. Abarca, Jorge G. Chavez-Echajaya, and Dante A. Elias. 2023. "EMG and IMU Data Fusion for Locomotion Mode Classification in Transtibial Amputees" Prosthesis 5, no. 4: 1232-1256. https://doi.org/10.3390/prosthesis5040085
APA StyleGonzales-Huisa, O. A., Oshiro, G., Abarca, V. E., Chavez-Echajaya, J. G., & Elias, D. A. (2023). EMG and IMU Data Fusion for Locomotion Mode Classification in Transtibial Amputees. Prosthesis, 5(4), 1232-1256. https://doi.org/10.3390/prosthesis5040085








