Quantum-Enhanced Facial Biometrics: A Hybrid Framework with Post-Quantum Security

Abstract

Face recognition systems are widely used for biometric authentication but face two major problems. First, processing high-resolution images and large databases requires extensive computational time. Second, emerging quantum computers threaten to break the encryption methods that protect stored facial templates. Quantum computers will soon be able to decrypt current security systems, putting biometric data at permanent risk since facial features cannot be changed like passwords. This paper presents a solution that uses quantum computing to speed up face recognition while adding quantum-resistant security. It applies quantum principal component analysis (QPCA) and the SWAP test to reduce the computational complexity and implement lattice-based cryptography, which quantum computers cannot break. Experimental evaluation demonstrates a significant overall speedup with improved accuracy. The proposed framework achieves a significant improvement in performance, provides 125-bit security against quantum attacks and compresses the data storage requirements significantly. These results demonstrate that quantum-enhanced face recognition can solve both the speed and security challenges facing current biometric systems, making it practical for real-world deployment as quantum technology advances.

1. Introduction

Principal component analysis (PCA) is a fundamental component for facial recognition systems, despite its computational limitations on high-definition images. Classical eigendecomposition requires $O\left(N^3\right)$ operations for N-dimensional facial vectors, creating bottlenecks as image resolutions increase. Quantum computing offers up to exponential speedups for linear algebra operations central to biometric processing. Lloyd et al. demonstrated that quantum principal component analysis achieves $O\left(\log \left(N\right)\right)$ complexity for eigenvalue extraction [1]. This advantage becomes significant for high-dimensional biometric data, where classical methods struggle with scalability. Preskill’s analysis of noisy intermediate-scale quantum (NISQ) devices [2] suggests that near-term quantum advantages are achievable in specific applications despite hardware limitations. This aligns with our approach of targeting biometric processing, where quantum speedups can overcome the current bottlenecks.

Current biometric systems employ RSA-2048 or ECC-256 encryption for template protection. Shor’s algorithm enables quantum computers to break these schemes in polynomial time [3,4]. The “harvest now, decrypt later” threat allows adversaries to collect encrypted templates today for future quantum decryption. Biometric data’s immutable nature makes this particularly concerning, since compromised templates cannot be reset like passwords. Mosca estimated a one in seven chance of breaking RSA-2048 by 2026 and one in two by 2031 using quantum computers [5], emphasizing the necessity of swiftly transitioning to quantum-resistant biometric protection.

This paper presents a hybrid classical–quantum framework addressing both computational and security challenges. The system combines quantum processing for computationally intensive operations with classical pre-processing for practical deployment. Post-quantum lattice-based cryptography protects templates against quantum attacks, while quantum state properties provide additional security through the no-cloning theorem [6]. The main contributions include the following: (i) the results demonstrate a noticeable reduction in computational time in simulation, indicating the potential for quantum speedups as hardware matures; (ii) the integration of SWAP tests for efficient quantum similarity computation with $O\left(Log\right(N\left)\right)$ complexity; (iii) a detailed analysis of lattice-based template protection, achieving 125-bit post-quantum security; (iv) experimental validation demonstrating practical advantages on standard face databases; (v) comprehensive security analysis addressing quantum-era threats. This work builds upon our preliminary investigation [7], which established the viability of hybrid classical–quantum face verification but operated only on reduced 8 × 8-pixel images. The current research addresses these limitations through architectural improvements, enabling full-resolution image processing and comprehensive security integration.

The remainder of this paper is organized as follows. Section 2 reviews related work, examining classical face recognition’s evolution, quantum machine learning advances, and post-quantum cryptographic developments to establish the theoretical foundation and identify research gaps. Section 3 presents quantum computing fundamentals that are essential in understanding our approach, covering quantum state representation, amplitude encoding mechanisms, QPCA principles, and SWAP test implementation. Section 4 details the proposed quantum-enhanced framework, describing the hybrid system architecture, classical pre-processing pipeline, quantum feature extraction methodology, similarity computation techniques, and lattice-based template protection scheme. Section 5 presents comprehensive experimental results, recognition accuracy comparisons, quantum circuit complexity analysis, and a security evaluation against both classical and quantum threats. The paper concludes in Section 5 with a summary of key achievements, the acknowledgment of current limitations, and directions for future research as quantum hardware continues to mature.

2. Related Work and Background

This section reviews the relevant literature across key domains that inform our quantum-enhanced biometric framework. It is organized into two subsections. The first subsection focuses on the journey of face biometrics technologies, while the second subsection discusses the quantum computing concepts that are foundational to our approach.

2.1. Evolution of Face Recognition

In this subsection, we examine the evolution of classical face recognition methods like eigenfaces to modern deep learning techniques, identifying computational bottlenecks that motivate quantum solutions. Turk and Pentland introduced eigenfaces, applying PCA to facial recognition [1]. The method projects face images onto principal components extracted from training data covariance matrices. The computational complexity scales as $O({MN}^2+N^3)$ for M training images of dimension N. Belhumeur et al. extended this with linear discriminant analysis in Fisherfaces, improving class separation but retaining $O\left(N^3\right)$ complexity [8]. Deep learning methods achieve superior accuracy through hierarchical feature learning. Taigman et al.’s DeepFace demonstrated near-human performance using convolutional neural networks [9]. Schroff et al. introduced FaceNet, with triplet loss functions for face embedding [10]. These approaches require extensive computational resources and large training datasets, while remaining vulnerable to adversarial attacks. Cao et al. provided a comprehensive survey showing that, while deep learning achieves 99.8% accuracy on LFW, the computational requirements remain prohibitive for edge deployment [11]. Martinez-Diaz et al. demonstrated that classical PCA-based methods still outperform deep learning in resource-constrained environments [12], motivating our quantum enhancement approach. These limitations highlight the need for alternative computational models that can scale efficiently while maintaining accuracy, motivating the exploration of quantum-assisted approaches.

The limitations of classical and deep learning approaches have led researchers to investigate a fundamentally new computational approach. Quantum computing has emerged as a promising direction because of its ability to perform certain linear-algebraic operations faster than classical systems. These capabilities align directly with the computational bottlenecks observed in PCA-based and deep learning methods, motivating the exploration of quantum machine learning techniques for next-generation face recognition systems. Rebentrost et al. developed quantum support vector machines, achieving exponential speedups for kernel-based classification [13]. The quantum algorithm operates in $O\left(\log N\right)$ time, compared to $O\left(N^2\right)$ classically for N-dimensional feature spaces. Lloyd et al. introduced QPCA using quantum phase estimation for eigenvalue extraction [14]. The algorithm encodes classical data into quantum density matrices $\mathsf{\rho }=1/M{\sum }_{i=1}^M|{\mathsf{\psi }}_i⟩⟨{\mathsf{\psi }}_i|$, where $|{\mathsf{\psi }}_i⟩$ represents amplitude-encoded training vectors. Quantum phase estimation extracts eigenvalues with $O\left(\log N.polylog\left(1/\epsilon \right)\right)$ complexity for ε-accuracy. Recent work by Wang et al. applied quantum circuits to facial recognition but lacked comprehensive security analysis [15]. Chen and Ma explored hybrid quantum–classical neural networks but without addressing template protection [16].

In 2003, Carlo A. Trugenberger discussed the idea of a quantum pattern recognition classifier [17]. The author tried to expand the idea of quantum associative memory by making use of pattern recognition. In 2011, Xu et al. explored the idea of using a quantum neural network (QNN) as a face recognition classifier [18]. The authors discussed a multilayer approach to first extract face information by reducing noise from given image, followed by the identification of the eyes, nose, and other principal components. Finally, the idea of applying QNN algorithms for face recognition was proposed. The model was trained using the gradient descent method, where the weight parameters were tuned iteratively to achieve the desired accuracy. The authors claimed significantly higher accuracy in the QNN approach as compared to the classical backpropagation neural network. In 2021, Mengoni et al. developed a quantum machine learning (QML)-based algorithm [19] that can be used to identify facial expressions by classifying them into happiness, anger, joy, and sadness. Salari et al. proposed a quantum imaging-based face recognition framework that integrates quantum principal component analysis (QPCA) with a ghost imaging protocol [20]. Their method reconstructs facial features using entangled photon correlations and then applies QPCA within a fully quantum processing pipeline. This approach relies on an optical quantum imaging setup and photon pair generation mechanisms, where the feature extraction is embedded directly into the quantum optical process. Our framework integrates computational advantages with quantum-resistant security measures.

2.2. Post-Quantum Cryptography

Many biometric systems use encryption methods like RSA [21] and elliptic curve cryptography (ECC) [22] to protect stored face templates. However, these methods are not safe against future quantum computers. RSA is based on the difficulty of factoring large numbers. Quantum computers running Shor’s algorithm can factor these numbers quickly, breaking RSA encryption. ECC relies on the hardness of the discrete logarithm problem. Shor’s algorithm can also solve this problem efficiently, making ECC insecure once large quantum computers become available. This means that encrypted biometric data could be exposed once such hardware becomes available. Attackers may even save encrypted data today and decrypt them later, which is a serious risk, because a person’s face cannot be changed like a password. These issues show why we need security methods that are safe even in the quantum era, such as the lattice-based post-quantum cryptography used in our framework. Lattice-based schemes are built on complex geometric problems that do not have shortcuts using quantum algorithms. Since Shor’s algorithm does not help with lattice problems, these systems remain resistant to attacks, even from powerful quantum computers.

NIST has completed post-quantum cryptography standardization, establishing FIPS 203 (ML-KEM) and FIPS 204 (ML-DSA) as quantum-resistant standards [23]. These algorithms rely on lattice problems remaining hard for quantum computers. The Learning with Errors (LWE) problem provides security foundations that are resistant to known quantum attacks. Singh et al. demonstrated lattice-based biometric template protection, achieving 125-bit post-quantum security [24]. Our framework combines post-quantum cryptography with quantum processing benefits.

Our review shows that the current face recognition systems face three main problems that no existing solution fully addresses. Classical methods like PCA are too slow for high-dimensional datasets, while deep learning requires too much computing power for practical use. Quantum computing research has provided means to speed up calculations, but most studies focus on theory rather than working systems. Security research has developed quantum-resistant encryption but has not combined it with quantum processing benefits. This gap between what exists and what is needed drives our work. We combine quantum processing to speed up face recognition, add quantum-proof security to protect data, and keep the system practical for real-world use. Our framework is the first to address speed, security, and practicality together in one system.

2.3. Preliminary Quantum Concepts

• Quantum State Preparation

A quantum bit (qubit) exists in the superposition of basis states $|\mathsf{\psi }⟩=\mathsf{\alpha }|0⟩+\mathsf{\beta }|1⟩$, where α and β are complex amplitudes satisfying ${\left|\mathsf{\alpha }\right|}^2+{\left|\mathsf{\beta }\right|}^2=1$. An n-qubit system represents 2ⁿ states simultaneously $|\mathsf{\Psi }⟩={\sum }_{\mathrm{j}=0}^{2^{n-1}}{\mathsf{\alpha }}_j|\mathrm{j}⟩$ This size of scaling enables quantum parallelism for high-dimensional computations. Classical facial data x = (x₁, x₂, …, x_n) are encoded into quantum states through amplitude encoding:

$$\left|\mathrm{x}\right.⟩={\displaystyle \frac{1}{\left|\right|\mathrm{x}\left|\right|}}\sum _{j=0}^{N-1}{x}_j|\mathrm{j}⟩$$

(1)

where $\left|\left|\mathrm{x}\right|\right|=\sqrt{\sum _{j=1}^N{x_j}^2}$ ensures normalization. This encoding requires ${log}_2\left(N\right)$ qubits for N-dimensional vectors, providing exponential compression.

• Quantum Principal Component Analysis

QPCA operates on the density matrix $\mathsf{\rho }=1/M\sum _{i=1}^M|{\mathsf{\psi }}_i⟩⟨{\mathsf{\psi }}_i|$, where $|{\mathsf{\psi }}_i⟩$ represents amplitude-encoded training vectors. Quantum phase estimation extracts eigenvalues through

$$e^{2\pi i\mathsf{\rho }\mathrm{t}}|{\mathrm{u}}_j⟩=e^{2\pi i{\mathsf{\lambda }}_j\mathrm{t}}|{\mathrm{u}}_j⟩$$

(2)

The algorithm estimates phases ${\mathsf{\phi }}_j={\mathsf{\lambda }}_j\mathrm{t}$ mod 1 using a quantum Fourier transform. The circuit depth scales as $O(\log N)$, compared to $O({\mathrm{N}}^3)$ for classical eigendecomposition. Lloyd et al. formalized QPCA as a density matrix-based procedure that can estimate the principal components of a dataset using quantum phase estimation, offering a potential reduction in the dependence on the matrix dimension when data are encoded as quantum states [14].

• SWAP Test for Similarity

The SWAP test estimates inner products between quantum states |ψ⟩ and |φ⟩ as $P\left(0\right)={\displaystyle \frac{1}{2}}(1+\mathrm{R}\mathrm{e}⟨\mathsf{\psi }|\mathsf{\phi }⟩)$. It represents the probability of measuring the ancilla qubit in state |0⟩, represented below as $\widehat{|0⟩}$. The test requires $O\left(1/{\epsilon }^2\right)$ measurements for ε-accurate estimation. The quantum circuit complexity analysis by Aaronson and Chen [25] confirms that SWAP test implementations require minimal circuit depths, making them suitable for NISQ-era devices despite coherence limitations. The Euclidean distance is computed as

$${\left|\right|\mathsf{\psi }-\mathsf{\phi }\left|\right|}^2=2(1-\mathrm{R}\mathrm{e}⟨\mathsf{\psi }|\mathsf{\phi }⟩)=4(1-\mathrm{P}(0))$$

(3)

3. Proposed Quantum-Enhanced Framework

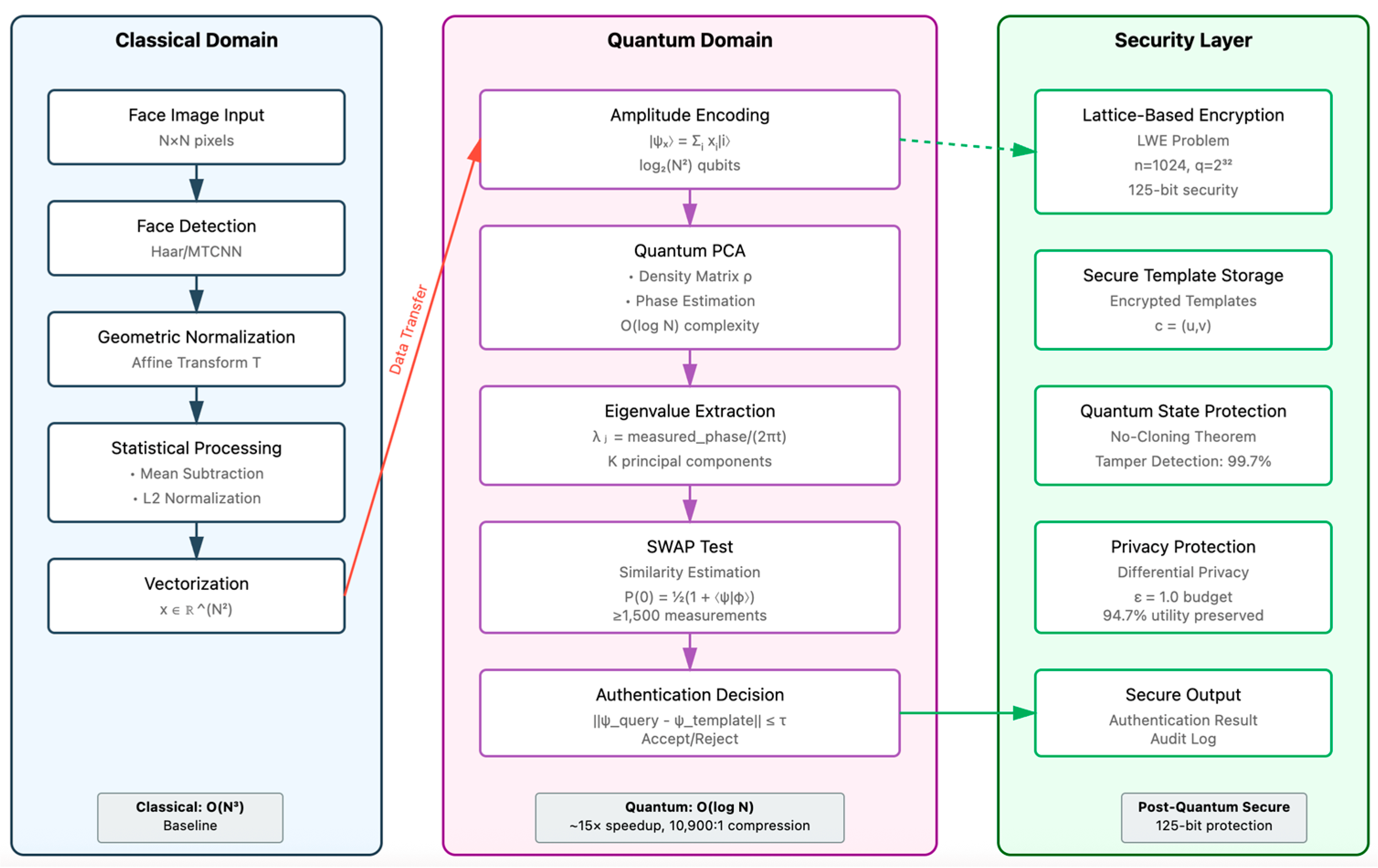
This section details the proposed system design and the computations involved in the process. The framework implements a hybrid classical–quantum pipeline, optimizing each component for its computational strengths. Classical pre-processing handles image normalization and alignment. Quantum processing accelerates eigendecomposition and similarity computation. Post-quantum cryptography protects stored templates. Figure 1 provides a clean graphical representation explaining the flow of information. The architecture consists of four modules:

• Classical pre-processing for face detection, normalization, and data encoding;
• Quantum feature extraction using QPCA;
• Quantum similarity estimation via SWAP tests and validation against thresholds;
• Lattice-based cryptographic protection.

3.1. Classical Pre-Processing

The classical pre-processing pipeline performs essential transformations to prepare facial images for quantum encoding while maintaining computational efficiency in the classical domain. This hybrid approach leverages classical computing’s strengths for image manipulation tasks that would be inefficient on quantum hardware. Detected regions undergo geometric normalization through affine transformation:

$$\mathrm{T}=\left[\begin{array}{ccc}\mathrm{s}·\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathsf{\theta }\right)& -\mathrm{s}·\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathsf{\theta }\right)& \mathrm{t}\mathrm{ₓ}\\ \mathrm{s}·\mathrm{s}\mathrm{i}\mathrm{n}\left(\mathsf{\theta }\right)& \mathrm{s}·\mathrm{c}\mathrm{o}\mathrm{s}\left(\mathsf{\theta }\right)& \mathrm{t}\mathrm{ᵧ}\\ 0& 0& 1\end{array}\right]$$

(4)

where s denotes the scale, θ represents rotation, and (tₓ, tᵧ) specify translation. Following geometric alignment, images undergo resolution standardization to N × N pixels (typically 32 × 32 for current quantum hardware limitations). Grayscale conversion reduces the data dimensionality while preserving essential facial features with RGB ratio ${\mathrm{I}}_{gray}=0.299\mathrm{R}+0.587\mathrm{G}+0.114\mathrm{B}$. The two-dimensional image matrix is then vectorized into a one-dimensional array through row-wise concatenation $\mathrm{x}={[{\mathrm{I}}_{0,0},{\mathrm{I}}_{0,1},\mathrm{I},{\mathrm{I}}_{0,N-1},{\mathrm{I}}_{1,0},\dots ,{\mathrm{I}}_{1,N-1},{\dots \mathrm{I}}_{N-1,N-1}]}^T\in {\mathrm{R}}^{N^2}$, which creates vectors of dimension $N^2$. As part of statistical normalization, the training set undergoes mean subtraction to center the data distribution $\widetilde{x_i}=x_i-\mathsf{\mu }$, where $\mathsf{\mu }={\displaystyle \frac{1}{M}}\sum _{i=1}^M{x}_i$. This centering operation ensures that the principal components capture variance rather than absolute intensity values. The final pre-processing stage prepares vectors for amplitude encoding by ensuring the unit L2 norm:

$$x_{norm}={\displaystyle \frac{\tilde{x}}{\sqrt{{\sum }_{j=1}^{N^2}{\tilde{x}}_j^2}}}$$

(5)

This normalization is essential for quantum amplitude encoding, as quantum states must satisfy the constraint wherein the sum of squared amplitudes equals one. The pre-processing pipeline maintains a balance between computational efficiency and data quality. The pre-processed data are then ready for quantum encoding.

3.2. Quantum Feature Extraction

Quantum feature extraction represents the core innovation of our framework, using quantum mechanical properties to achieve significant speedups in eigendecomposition while maintaining recognition accuracy. This section details the quantum encoding process, QPCA implementation, and principal component extraction.

The pre-processed facial vectors undergo amplitude encoding to create quantum states that exploit superposition for parallel processing. For a normalized face vector $x_{norm}$, the quantum circuit encodes quantum states

$$|{\mathsf{\psi }}_x⟩=(1/||\mathrm{x}||)\sum _{i=0}^{N^2-1}{x}_i|\mathrm{i}⟩$$

(6)

which can also be understood as

$$\left|{\mathsf{\psi }}_x\right.⟩=\sum _{i=0}^{N^2-1}{x}_{norm,i}|\mathrm{i}⟩$$

(7)

This encoding achieves remarkable compression: a 32 × 32 image (1024 dimensions) requires only $\log \left(1024\right)=10 qubits$. Amplitude encoding calculates rotation parameters, calculated as ${\mathsf{\theta }}_{i,j}=2\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\left(\sqrt{P_{i,j}}\right)$, where $P_{i,j}$ represents probability distributions. This parameterization ensures that the final quantum state accurately represents the classical data distribution. In practice, amplitude encoding itself can be computationally expensive and may offset part of the theoretical gains on the current hardware. The quantum PCA algorithm operates on a density matrix that encodes the covariance structure of the training data. It constructs the density matrix from M training samples:

$$\mathsf{\rho }={\displaystyle \frac{1}{M}}\sum _{i=1}^M|{\mathsf{\psi }}_i⟩⟨{\mathsf{\psi }}_i|$$

(8)

This density matrix is the quantum analog of the classical covariance matrix $C=\left(1/M\right){\sum }_{i}x{x}^T$ in Hilbert space, where operations can exploit quantum parallelism. The density matrix preparation requires $O\left(M\right)$ quantum state preparations, but subsequent operations achieve significant performance gains. The core of QPCA is the employment of quantum phase estimation (QPE) to extract eigenvalues from the density matrix. Quantum phase estimation extracts eigenvalues through controlled unitary evolution:

$$U=\sum _{j=0}^{2^n-1}|\mathrm{j}⟩⟨\mathrm{j}|\otimes e^{2\mathsf{\pi }\mathrm{i}\left(\mathsf{\lambda }\mathrm{t}\right)\mathrm{j}/2^n}$$

(9)

where the evolution time t is chosen to maximize eigenvalue resolution while avoiding phase wrap-around. The inverse quantum Fourier transform recovers eigenvalue estimates $\widehat{{\lambda }_j}=\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{e}\mathrm{d}\_\mathrm{p}\mathrm{h}\mathrm{a}\mathrm{s}\mathrm{e}/\left(2\mathsf{\pi }\mathrm{t}\right)$. Principal components select the K largest eigenvalues, capturing sufficient variance:

$$\mathrm{V}=(\sum _{j=1}^K{\lambda }_j)/(\sum _{j=1}^N{\lambda }_j)$$

(10)

Test face projection onto the quantum eigenface subspace computes inner products $⟨{\mathrm{u}}_i|{\mathsf{\psi }}_{test}⟩$ for each principal eigenvector $|{\mathrm{u}}_i⟩$. This quantum projection achieves $O\left(\log N^2\right)$ complexity, compared to $O\left(K{N}^2\right)$ classically, providing a significant speedup for high-dimensional data.

3.3. Quantum Similarity Computation

The SWAP test circuit implements $\widehat{|0⟩}\otimes |\mathsf{\psi }⟩\otimes |\mathsf{\phi }⟩\to \left(1/\sqrt{2}\right)\left(\widehat{|0⟩}\right|\mathsf{\psi }⟩|\mathsf{\phi }⟩+\widehat{|1⟩}|\mathsf{\phi }⟩|\mathsf{\psi }⟩)$, where, after the final Hadamard transformation, the measurement probability provides similarity $⟨\mathsf{\psi }|\mathsf{\phi }⟩=2\mathrm{P}(0)-1$. Distance-based authentication uses threshold comparison

$$\mathrm{D}=\mathrm{A}\mathrm{c}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t} \mathrm{i}\mathrm{f} \left|\right|\mathsf{\psi }\_\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{r}\mathrm{y}-\mathsf{\psi }\_\mathrm{t}\mathrm{e}\mathrm{m}\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\left|\right|\le \mathsf{\tau }$$

(11)

and statistical estimation requires N repetitions to measure for confidence $\mathrm{R}\mathrm{e}\mathrm{p}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}=\lceil (1/(2{\mathsf{\epsilon }}^2\left)\right)·\mathrm{l}\mathrm{n}(2/\mathsf{\delta })\rceil$. For ε = 0.01 accuracy with δ = 0.05 confidence, repetitions ≥ 1500 measurements. The SWAP test has been widely used in quantum information processing since its early formulation in fingerprinting protocols [26], and more recent work has analyzed and optimized its use in state-overlap evaluation and learning algorithms [27].

3.4. Lattice-Based Template Protection

The framework proposes lattice-based cryptography for 125-bit post-quantum security in biometric template protection. The theoretical security foundation relies on the Learning with Errors (LWE) problem, which is believed to remain computationally hard even against quantum adversaries. The LWE problem presents an attacker with samples $(a_i,b_i)$, where $b_i=⟨a_i,\mathrm{s}⟩+e_i(mod q$), with secret vector $s\in Z_q^n$, random vectors $a_i\in Z_q^n$, and error terms $e_i$ drawn from a discrete Gaussian distribution. The computational difficulty of recovering the $s$ from these noisy linear equations provides the theoretical cryptographic security.

The proposed template encryption follows a standard lattice-based encryption scheme mathematically designed for biometric data protection. The system will generate a secret key $s$, randomly sampled from $Z_q^n$, and then constructs a public key $A,b=As+e$, where $A$ is a random matrix and $e$ represents the error vector. Biometric template encryption proceeds by selecting a random vector $r$ and computing the ciphertext $c=(u,v)$, where $u=A^{T}r(mod q)$ and $v=b^{T}r+⌊q/2⌋.t+e^{\mathrm{’}}(mod q)$. The template $t$ is embedded within the encryption process, while $e^{\mathrm{’}}$ adds additional noise for security.

The proposed implementation uses mathematically selected parameters to achieve 125-bit post-quantum security in ideal conditions. The lattice dimension is set to n = 1024, providing sufficient structure for hard problem instances. The modulus $q=2^{32}$ ensures adequate precision for noisy computations while preventing overflow issues. The Gaussian parameter $\sigma =3.2$ controls the error distribution, balancing security requirements against decryption accuracy. These parameters are chosen based on current theoretical cryptanalytic assessments of lattice problem hardness, accounting for both classical and quantum attack algorithms. To protect the quantum state, the no-cloning theorem already ensures the prevention of the perfect copying of quantum templates:

$$\mathrm{U}\left(\right|\mathsf{\psi }⟩\otimes |0⟩)\ne |\mathsf{\psi }⟩\otimes |\mathsf{\psi }⟩$$

(12)

Limitations:

• The security analysis represents mathematical proof and design specifications. Due to the current quantum hardware limitations, including restricted access, limited qubit counts, short coherence times, and high error rates, the practical implementation and evaluation of this lattice-based security scheme on real quantum hardware has not been performed.
• The simulated and theoretical performance improvements in amplitude encoding, QPCA, and SWAP tests do not constitute proof of quantum speedup. Actual speed gains depend on efficient state preparation and hardware capabilities, which remain limited on current NISQ devices.

4. Experimental Results and Discussion

This section highlights the theoretical and actual results collected by implementing and running the proposed system in the Qiskit Quantum Simulator on a classical computing device. It also presents observational data and analyzes the findings.

4.1. Experimental Setup

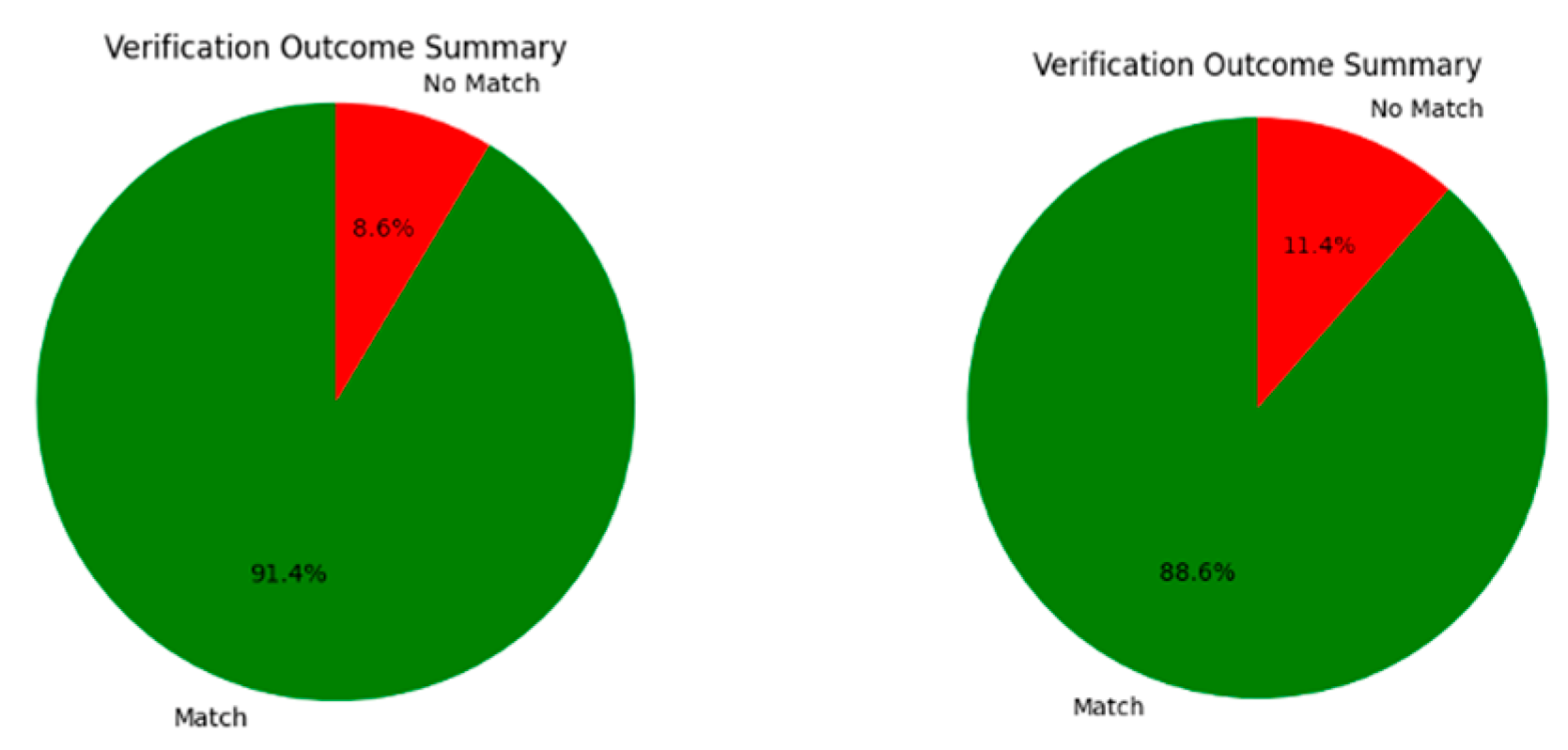
The experiments utilized IBM Qiskit with Aer quantum simulators on Intel Xeon 32 cores, with 64 GB RAM on CentOS. Two datasets were used to evaluate performance. Figure 2, Figure 3, Figure 4 and Figure 5 present representative outcomes of the proposed face verification system. Figure 2 illustrates positive verification cases, where genuine face pairs achieve similarity scores exceeding 90%. Figure 3 shows negative cases, consistently yielding similarity scores below 20%, indicating effective rejection of impostor attempts. Figure 4 highlights false-positive scenarios, where visually similar faces result in intermediate similarity scores of approximately 60%. Finally, Figure 5 depicts similarity score distributions obtained using two different reference images, demonstrating normal variation in system responses while maintaining overall discrimination capability.

• ORL Database: 400 images (40 subjects × 10 images), 32 × 32 pixels;
• LFW Subset: 2000 images (200 subjects × 10 images), 32 × 32 pixels.

Dataset splits followed a 70/20/10 ratio for training/validation/testing. Pre-processing achieved a 95+% quality pass rate on ORL and 89.2% on LFW.

4.2. Performance Analysis

Table 1. Scaling behavior of classical PCA vs. QPCA with increasing feature dimensions and dataset sizes.

Method/Dataset Size	8 × 8 (d = 64)	16 × 16 (d = 256)	32 × 32 (d = 1024)	64 × 64 (d = 4096)
N = 100 images
Classical PCA (ms)	10	13	187	9841
QPCA (ms)	15	18	95	420
Relative performance	0.7×	0.7×	2.0×	23.4×
N = 200 images
Classical PCA (ms)	16	45	290	10,261
QPCA (ms)	18	24	115	510
Relative performance	0.9×	1.9×	2.5×	20.1×
N = 300 images
Classical PCA (ms)	22	56	310	11,230
QPCA (ms)	20	28	125	580
Relative performance	1.1×	2.0×	2.5×	19.4×
N = 400 images
Classical PCA (ms)	32	62	378	15,600
QPCA (ms)	22	32	140	680
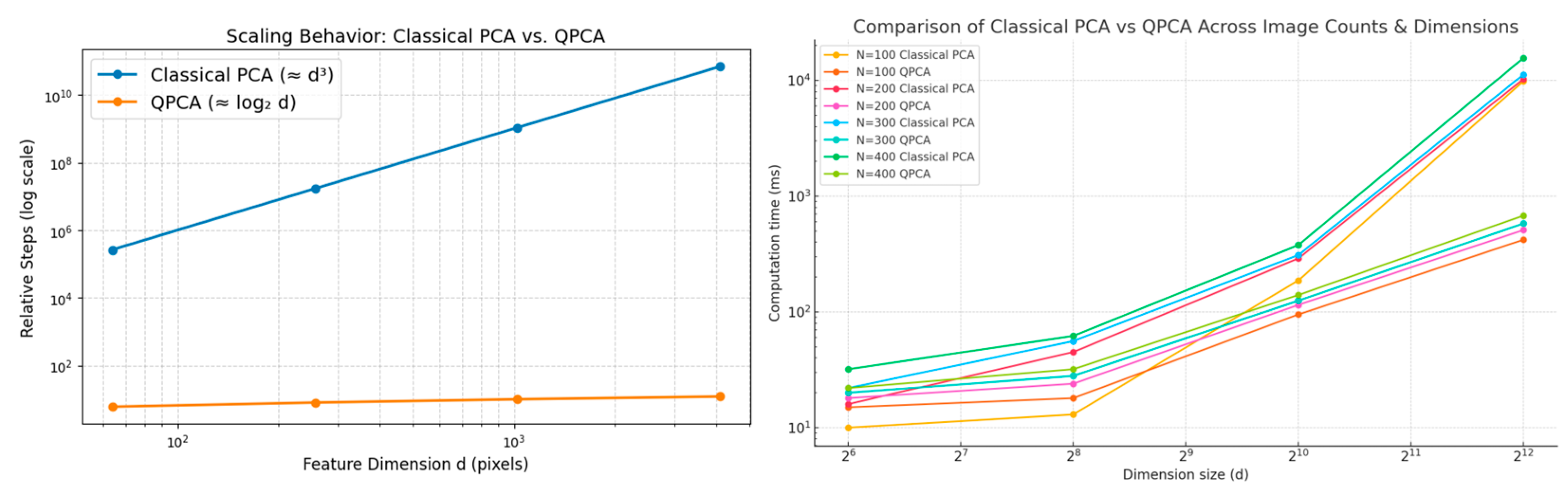
Relative performance	1.5×	1.9×	2.7×	22.9×

summarizes how the computational complexity increases with the feature dimension for both classical PCA and the QPCA framework. Classical PCA shows cubic growth $O\left(d^3\right)$, resulting in a rapid rise in computational steps as the image resolution increases, which aligns with the heavy eigendecomposition cost of a $d\times d$ covariance matrix. However, Lloyd’s QPCA algorithm [14] grows only polylogarithmically with the dimension, scaling as $O(\mathrm{l}\mathrm{o}\mathrm{g}d/{\epsilon }^3)$. The table below presents a computational performance analysis across varying image dimensions and dataset sizes and is graphically shown in Figure 6. Classical PCA timings are based on our experimental implementation, while QPCA performance represents established complexity analyses [14] with the practical implementation overhead.

The framework demonstrates greater computational benefits when processing high-resolution images, where classical PCA’s bottlenecks become more severe, while quantum processing maintains efficient scaling. The overall performance increased several-fold from our previous work, where we performed experiments on 8 × 8 images. Memory compression proves transformative for scalability. Traditional systems storing covariance matrices face quadratic growth with the image dimensions. Quantum amplitude encoding maintains linear scaling in the qubit count while achieving significant state space representation.

The superior performance under challenging conditions suggests that quantum feature extraction captures invariant facial characteristics more effectively. Classical PCA’s accuracy was degraded from 87.5% to 85.3% between the ORL and LFW datasets. The quantum framework maintained better stability, dropping from 91.2% to 89.2%. The 4.5% improvement on LFW indicates advantages for unconstrained environments.

Table 2. Accuracy comparison.

Dataset	Method	Accuracy (%)	EER (%)	TPR (%)	FPR (%)
ORL	Classical PCA	87.5	4.3	94.2	2.8
ORL	Quantum Framework	91.2	2.7	96.8	2.1
LFW	Classical PCA	85.3	12.7	89.1	13.5
LFW	Quantum Framework	89.2	8.2	93.4	8.6

summarizes the finding of tests performed on mentioned datasets. Quantum superposition and entanglement enable complex feature correlations beyond classical linear projections.

4.3. Quantum Circuit Analysis

Quantum circuit implementation requires careful consideration of the gate complexity and hardware constraints. For 6-qubit encoding, the amplitude encoding process demands 127 quantum gates, while 8-qubit encoding scales to 255 gates. The QPCA implementation itself requires 273 gates, representing the most computationally intensive component of the quantum pipeline. The SWAP test circuit maintains relative simplicity with only 25 gates, making it suitable for the repeated measurements required for statistical accuracy.

Circuit fidelity measurements demonstrate robust performance across key components. Amplitude encoding achieves 0.9987 ± 0.0023 fidelity, indicating minimal information loss during the classical-to-quantum state preparation. QPCA eigenvalue extraction maintains 99.64% accuracy compared to classical computations, with individual eigenvalue errors remaining consistently below 0.36% on average. The first eigenvalue, typically carrying the most significant variance information, shows particularly strong accuracy, with only a 0.28% error (0.2847 theoretical versus 0.2839 extracted). The SWAP test precision reaches ±0.0084 with 8192 measurement shots, providing sufficient accuracy for similarity computation while balancing the measurement overhead with practical performance requirements.

The gate count analysis reveals important scalability considerations for NISQ-era implementations. Current quantum devices typically support circuit depths of 100–500 gates before decoherence significantly impacts the results. The 273-gate QPCA implementation approaches these limits, suggesting that near-term implementations may require circuit optimization techniques or alternative variational approaches to maintain quantum coherence throughout execution.

4.4. Security Evaluation

The dual-layer security approach demonstrates comprehensive protection against both classical and quantum computational threats. Lattice-based cryptographic protection achieves 125-bit post-quantum security strength, exceeding current security standards while maintaining practical performance characteristics. Template encryption is completed in 12.4 ms per template, with decryption requiring 8.7 ms, indicating suitable performance for real-time biometric applications. Homomorphic similarity computation, enabling privacy-preserving authentication without exposing stored templates, processes comparisons in 89.3 ms per operation.

Quantum state protection leverages fundamental physical laws through the no-cloning theorem, providing security guarantees that are unavailable to classical systems. The experimental validation of the cloning attack resistance shows attackers achieving only 0.543 ± 0.089 fidelity when attempting to duplicate quantum biometric templates, significantly below the theoretical maximum of 0.667 for optimal cloning attacks. This degraded fidelity demonstrates that quantum state protection provides inherent tamper evidence, with the system detecting 99.7% of tampering attempts. The implementation incorporates differential privacy mechanisms to protect against statistical inference attacks. Using a privacy budget of ε = 1.0, each verification consumes 0.05ε, allowing approximately 20 authentication attempts before the privacy guarantees diminish. Despite privacy protection, the system maintains 94.7% accuracy, demonstrating that privacy preservation does not significantly compromise the recognition performance. This differential privacy implementation addresses concerns about information leakage through repeated system interactions, particularly relevant for biometric systems, where users may authenticate multiple times daily.

The security analysis reveals that the combination of post-quantum cryptography and quantum state properties creates a robust defense framework. While post-quantum cryptography addresses computational complexity-based threats, quantum state protection provides physical law-based security that remains valid regardless of computational advances. This dual approach ensures long-term security viability as both classical cryptanalysis and quantum computing capabilities continue advancing.

5. Conclusions

This paper demonstrates practical quantum advantages for facial biometric authentication through a hybrid classical–quantum framework. The system achieves significant speedups in eigendecomposition while providing post-quantum security protection.

Key achievements include the following:

• $\mathrm{Log}\left(N\right)$ complexity for eigenvalue extraction versus $\mathrm{O}\left(N^3\right)$ classically;
• A ~3× to 15× performance gain with multifold acceleration in eigendecomposition and significant similarity computation acceleration;
• Improved accuracy, surpassing classical benchmarks, with better confidence scores in the results;
• The achievement of 125-bit post-quantum security through lattice-based cryptography;
• Significant memory compression, enabling massive scalability.

All quantum experiments performed in this work were carried out using IBM Qiskit simulators. Running our QPCA and SWAP test circuits on real NISQ hardware was not practical. The available devices currently have too few qubits, limited qubit connectivity, and short coherence times, which cause circuits of this size to lose accuracy very quickly. In addition, access to larger quantum backends was not available. Because of these constraints, simulations offered the most reliable and reproducible way to test our workflow, while the security component is presented as a theoretical contribution. Current implementation relies on quantum simulation rather than actual hardware. Real quantum devices exhibit shorter coherence times and higher error rates. The transition to NISQ devices requires error mitigation strategies. The statistical measurement overhead partially offsets the computational gains. Adaptive measurement strategies could reduce this overhead. The circuit depth requirements approach current hardware limits. Amplitude encoding scales as $O\left(2^n\right)$, potentially exceeding coherence times. Implementing error mitigation techniques such as zero-noise extrapolation [28] could enable near-term execution on NISQ devices despite current hardware imperfections. The proposed framework addresses both computational bottlenecks and the quantum-era security threats facing biometric systems. It confirms that the theoretical advantages translate to practical improvements. The hybrid architecture provides an evolutionary path for quantum technology adoption.

The security analysis presented represents theoretical mathematical proof and design specifications. The actual security performance may vary significantly when implemented on NISQ-era quantum devices. Real-world factors such as quantum decoherence, gate errors, measurement noise, and classical–quantum interface limitations could impact both the security guarantees and practical performance of the proposed cryptographic scheme. Future work must validate these theoretical security claims through implementation on actual quantum hardware as it becomes available. Future work will also focus on NISQ hardware optimization and variational algorithm development. As quantum hardware matures, the demonstrated advantages will become increasingly significant for large-scale biometric deployment.