Many-Body Effects in a Molecular Quantum NAND Tree
Abstract
1. Introduction
2. From NAND Trees to Quantum Transport
3. Many-Body Quantum Transport Theory
3.1. Lanczos Method for Green’s Functions
3.2. Molecular Hamiltonian
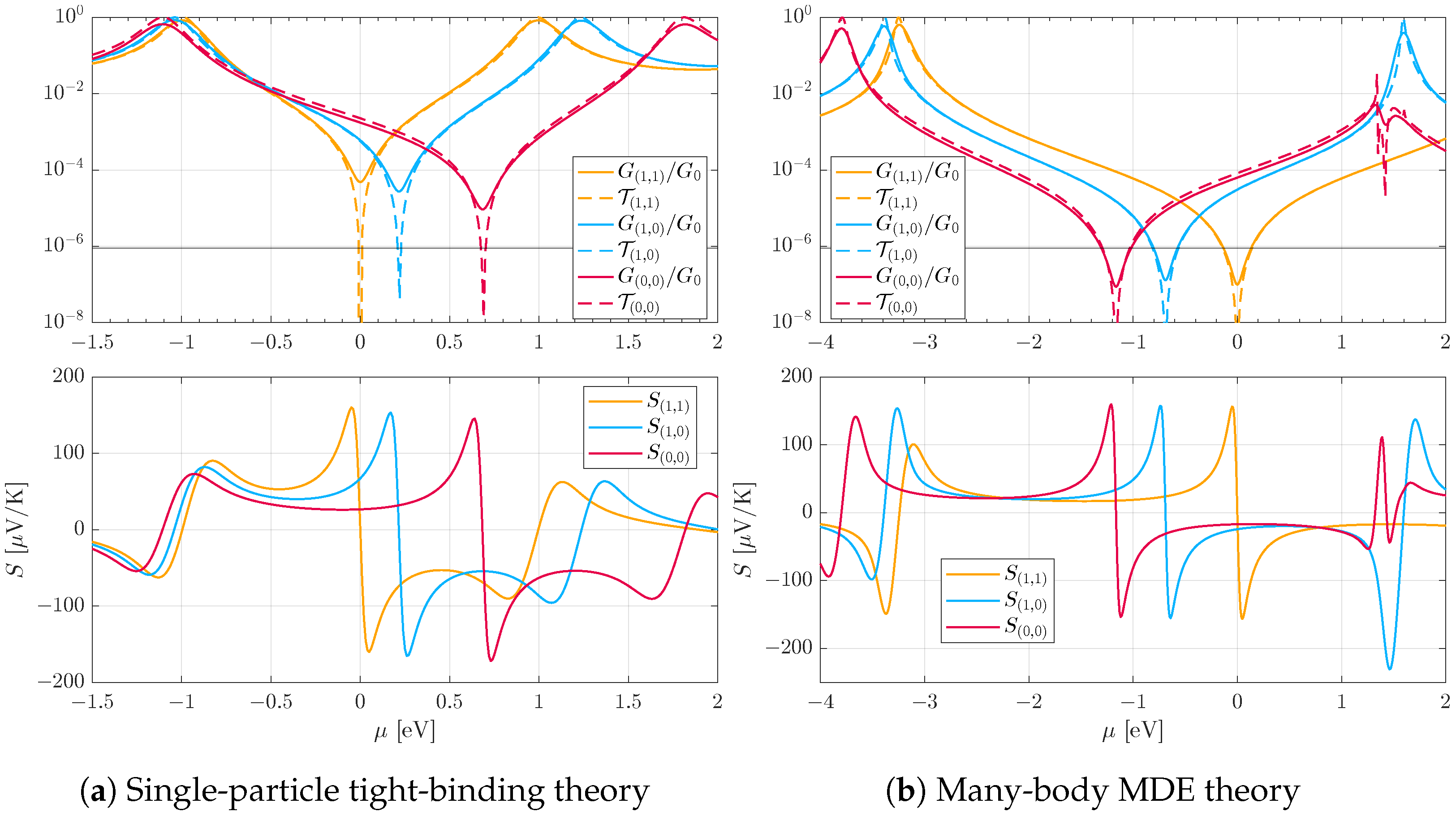
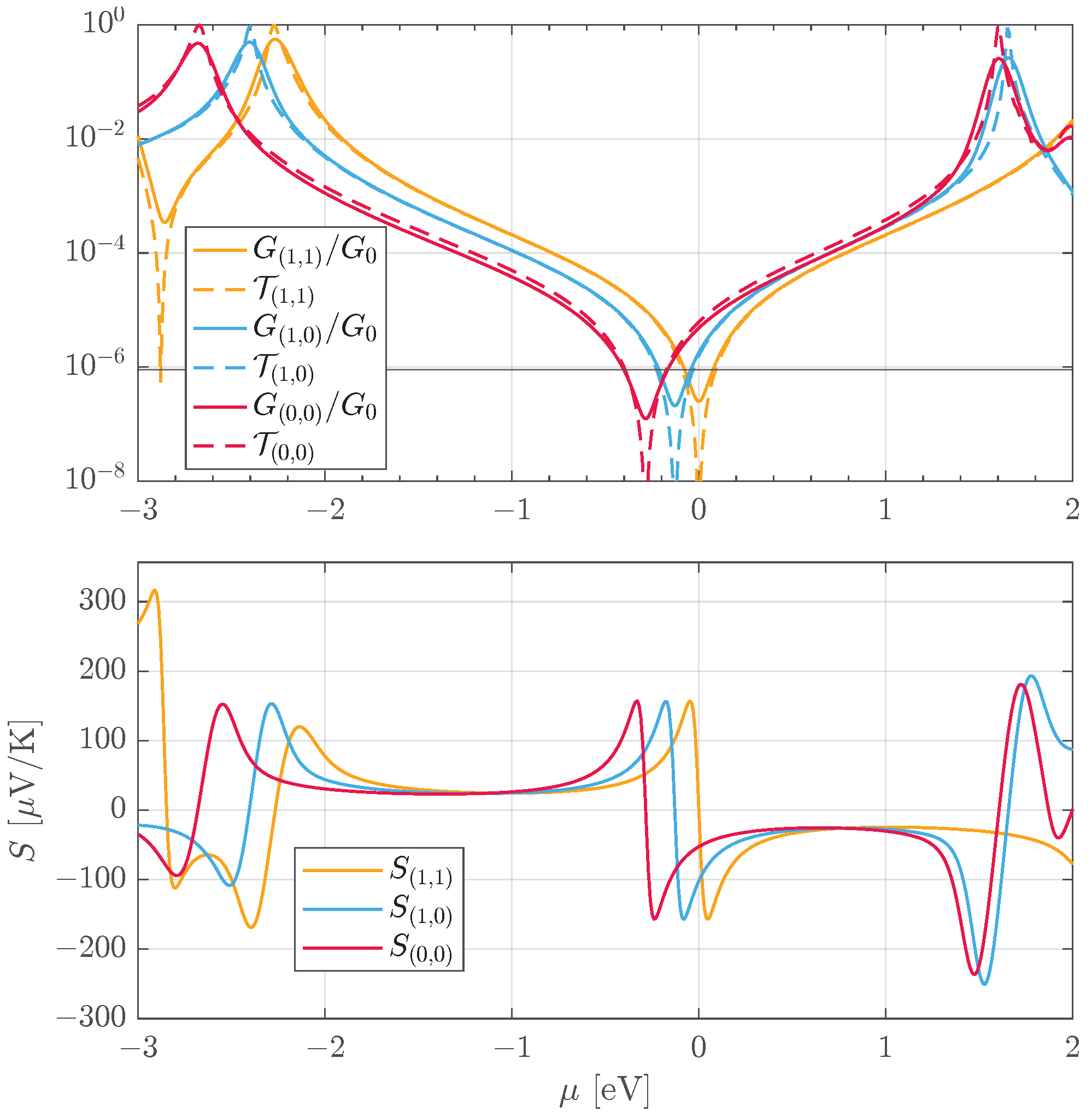
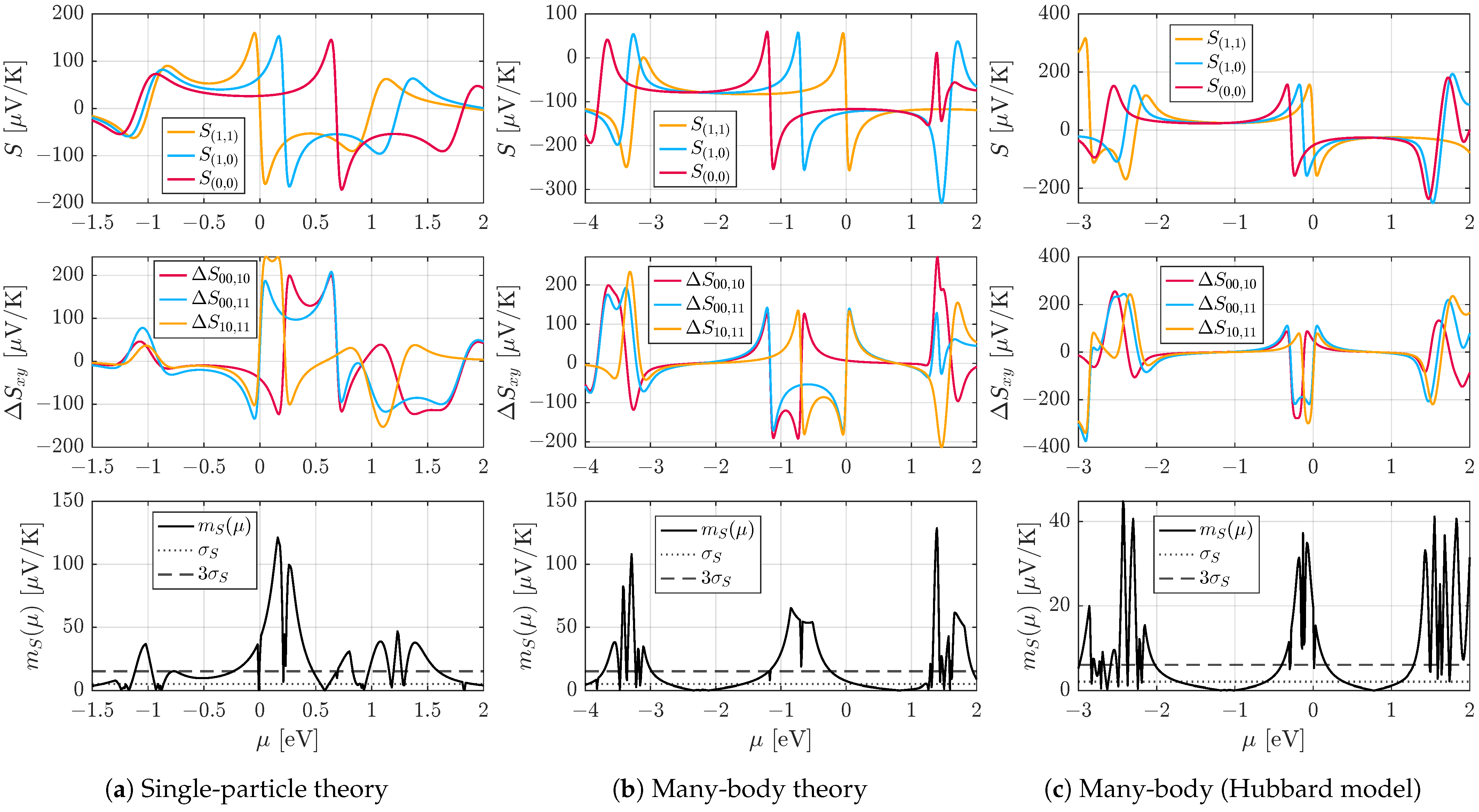
4. Results
Thermopower Discrimination of Logic States
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Influence of σ-System Transport
References
- Deutsch, D.; Jozsa, R. Rapid solution of problems by quantum computation. Proc. R. Soc. Lond. A 1992, 439, 553–558. [Google Scholar]
- Shor, P.W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 1999, 41, 303–332. [Google Scholar] [CrossRef]
- Childs, A.M. Universal Computation by Quantum Walk. Phys. Rev. Lett. 2009, 102, 180501. [Google Scholar] [CrossRef]
- Childs, A.M.; Gosset, D.; Webb, Z. Universal computation by multiparticle quantum walk. Science 2013, 339, 791–794. [Google Scholar] [CrossRef]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quantum Inf. Process. 2012, 11, 1015–1106. [Google Scholar] [CrossRef]
- Childs, A.M.; Strouse, D. Levinson’s theorem for graphs. J. Math. Phys. 2011, 52, 082102. [Google Scholar] [CrossRef]
- Childs, A.M.; Gosset, D. Levinson’s theorem for graphs II. J. Math. Phys. 2012, 53, 102207. [Google Scholar] [CrossRef]
- Whitfield, J.D.; Rodríguez-Rosario, C.A.; Aspuru-Guzik, A. Quantum stochastic walks: A generalization of classical random walks and quantum walks. Phys. Rev. A 2010, 81, 022323. [Google Scholar] [CrossRef]
- Farhi, E.; Gutmann, S. Quantum computation and decision trees. Phys. Rev. A 1998, 58, 915. [Google Scholar] [CrossRef]
- Farhi, E.; Goldstone, J.; Gutmann, S. A Quantum Algorithm for the Hamiltonian NAND Tree. arXiv 2007, arXiv:quant-ph/0702144. [Google Scholar] [CrossRef]
- Hoyer, P.; Spalek, R. Lower Bounds on Quantum Query Complexity. arXiv 2005, arXiv:quant-ph/0509153. [Google Scholar] [CrossRef]
- Saks, M.; Wigderson, A. Probabilistic Boolean decision trees and the complexity of evaluating game trees. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science (SFCS 1986), Toronto, ON, Canada, 27–29 October 1986; pp. 29–38. [Google Scholar]
- Tsuji, Y.; Estrada, E.; Movassagh, R.; Hoffmann, R. Quantum interference, graphs, walks, and polynomials. Chem. Rev. 2018, 118, 4887–4911. [Google Scholar] [CrossRef] [PubMed]
- Namarvar, O.F.; Giraud, O.; Georgeot, B.; Joachim, C. Quantum Hamiltonian Computing protocols for molecular electronics Boolean logic gates. Quantum Sci. Technol. 2019, 4, 035009. [Google Scholar] [CrossRef]
- Baytekin, H.T.; Akkaya, E.U. A molecular NAND gate based on Watson- Crick base pairing. Org. Lett. 2000, 2, 1725–1727. [Google Scholar] [CrossRef]
- Erbas-Cakmak, S.; Kolemen, S.; Sedgwick, A.C.; Gunnlaugsson, T.; James, T.D.; Yoon, J.; Akkaya, E.U. Molecular logic gates: The past, present and future. Chem. Soc. Rev. 2018, 47, 2228–2248. [Google Scholar] [CrossRef]
- Kompa, K.; Levine, R. A molecular logic gate. Proc. Natl. Acad. Sci. USA 2001, 98, 410–414. [Google Scholar] [CrossRef]
- Evers, F.; Korytár, R.; Tewari, S.; van Ruitenbeek, J.M. Advances and challenges in single-molecule electron transport. Rev. Mod. Phys. 2020, 92, 035001. [Google Scholar] [CrossRef]
- Jensen, P.W.; Jin, C.; Dallaire-Demers, P.L.; Aspuru-Guzik, A.; Solomon, G.C. Molecular realization of a quantum NAND tree. Quantum Sci. Technol. 2019, 4, 015013. [Google Scholar] [CrossRef]
- Soe, W.H.; Manzano, C.; Renaud, N.; de Mendoza, P.; De Sarkar, A.; Ample, F.; Hliwa, M.; Echavarren, A.M.; Chandrasekhar, N.; Joachim, C. Manipulating molecular quantum states with classical metal atom inputs: Demonstration of a single molecule NOR logic gate. ACS Nano 2011, 5, 1436–1440. [Google Scholar] [CrossRef]
- Joachim, C.; Renaud, N.; Hliwa, M. The different designs of molecule logic gates. Adv. Mater. 2012, 24, 312–317. [Google Scholar] [CrossRef] [PubMed]
- Renaud, N.; Joachim, C. Design and stability of NOR and NAND logic gates constructed with three quantum states. Phys. Rev. A 2008, 78, 062316. [Google Scholar] [CrossRef]
- Joachim, C.; Gimzewski, J.; Aviram, A. Electronics using hybrid-molecular and mono-molecular devices. Nature 2000, 408, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Dridi, G.; Julien, R.; Hliwa, M.; Joachim, C. The mathematics of a quantum Hamiltonian computing half adder Boolean logic gate. Nanotechnology 2015, 26, 344003. [Google Scholar] [CrossRef]
- Dridi, G.; Namarvar, O.F.; Joachim, C. Qubits and quantum Hamiltonian computing performances for operating a digital Boolean 1/2-adder. Quantum Sci. Technol. 2018, 3, 025005. [Google Scholar] [CrossRef]
- Joachim, C.; Duchemin, I.; Fiurášek, J.; Cerf, N. Hamiltonian logic gates: Computing inside a molecule. Int. J. Nanosci. 2005, 4, 107–118. [Google Scholar] [CrossRef]
- Bergfield, J.P.; Solomon, G.C.; Stafford, C.A.; Ratner, M.A. Novel quantum interference effects in transport through molecular radicals. Nano Lett. 2011, 11, 2759–2764. [Google Scholar] [CrossRef]
- Barr, J.D.; Stafford, C.A. On Transmission Node Structure in Interacting Systems. arXiv 2013, arXiv:1303.3618. [Google Scholar] [CrossRef]
- Pedersen, K.G.; Strange, M.; Leijnse, M.; Hedegård, P.; Solomon, G.C.; Paaske, J. Quantum interference in off-resonant transport through single molecules. Phys. Rev. B 2014, 90, 125413. [Google Scholar] [CrossRef]
- Arroyo, C.R.; Tarkuc, S.; Frisenda, R.; Seldenthuis, J.S.; Woerde, C.H.; Eelkema, R.; Grozema, F.C.; van der Zant, H.S. Signatures of Quantum Interference Effects on Charge Transport Through a Single Benzene Ring. Angew. Chem. 2013, 125, 3234–3237. [Google Scholar] [CrossRef]
- Guédon, C.M.; Valkenier, H.; Markussen, T.; Thygesen, K.S.; Hummelen, J.C.; van der Molen, S.J. Observation of quantum interference in molecular charge transport. Nat. Nanotechnol. 2012, 7, 305–309. [Google Scholar] [CrossRef]
- Li, Y.; Buerkle, M.; Li, G.; Rostamian, A.; Wang, H.; Wang, Z.; Bowler, D.R.; Miyazaki, T.; Xiang, L.; Asai, Y.; et al. Gate controlling of quantum interference and direct observation of anti-resonances in single molecule charge transport. Nat. Mater. 2019, 18, 357–363. [Google Scholar] [CrossRef]
- Liu, J.; Huang, X.; Wang, F.; Hong, W. Quantum interference effects in charge transport through single-molecule junctions: Detection, manipulation, and application. Acc. Chem. Res. 2018, 52, 151–160. [Google Scholar] [CrossRef]
- Nairz, O.; Arndt, M.; Zeilinger, A. Quantum interference experiments with large molecules. Am. J. Phys. 2003, 71, 319–325. [Google Scholar] [CrossRef]
- Aradhya, S.V.; Meisner, J.S.; Krikorian, M.; Ahn, S.; Parameswaran, R.; Steigerwald, M.L.; Nuckolls, C.; Venkataraman, L. Dissecting contact mechanics from quantum interference in single-molecule junctions of stilbene derivatives. Nano Lett. 2012, 12, 1643–1647. [Google Scholar] [CrossRef]
- Wang, X.; Bennett, T.L.; Ismael, A.; Wilkinson, L.A.; Hamill, J.; White, A.J.; Grace, I.M.; Kolosov, O.V.; Albrecht, T.; Robinson, B.J.; et al. Scale-up of room-temperature constructive quantum interference from single molecules to self-assembled molecular-electronic films. J. Am. Chem. Soc. 2020, 142, 8555–8560. [Google Scholar] [CrossRef]
- Liu, S.X.; Ismael, A.K.; Al-Jobory, A.; Lambert, C.J. Signatures of room-temperature quantum interference in molecular junctions. Acc. Chem. Res. 2023, 56, 322–331. [Google Scholar] [CrossRef] [PubMed]
- Bergfield, J.P.; Stafford, C.A. Many-body theory of electronic transport in single-molecule heterojunctions. Phys. Rev. B 2009, 79, 245125. [Google Scholar] [CrossRef]
- Bergfield, J.P.; Solis, M.A.; Stafford, C.A. Giant thermoelectric effect from transmission supernodes. ACS Nano 2010, 4, 5314–5320. [Google Scholar] [CrossRef] [PubMed]
- Bennett, R.X.; Hendrickson, J.R.; Bergfield, J.P. Quantum Interference Enhancement of the Spin-Dependent Thermoelectric Response. ACS Nano 2024, 18, 11876–11885. [Google Scholar] [CrossRef]
- Erdogan, E.; Bergfield, J.P. When Dephasing Fails: Thermodynamic Consequences of Decoherence Models in Quantum Transport. arXiv 2025, arXiv:2508.20343. [Google Scholar] [CrossRef]
- Miao, R.; Xu, H.; Skripnik, M.; Cui, L.; Wang, K.; Pedersen, K.G.; Leijnse, M.; Pauly, F.; Waarnmark, K.; Meyhofer, E.; et al. Influence of quantum interference on the thermoelectric properties of molecular junctions. Nano Lett. 2018, 18, 5666–5672. [Google Scholar] [CrossRef] [PubMed]
- Bergfield, J.P. Identifying Quantum Interference Effects from Joint Conductance–Thermopower Statistics. Nano Lett. 2024, 24, 15110–15117. [Google Scholar] [CrossRef] [PubMed]
- Hamill, J.M.; Ismael, A.; Al-Jobory, A.; Bennett, T.L.; Alshahrani, M.; Wang, X.; Akers-Douglas, M.; Wilkinson, L.A.; Robinson, B.J.; Long, N.J.; et al. Quantum interference and contact effects in the thermoelectric performance of anthracene-based molecules. J. Phys. Chem. C 2023, 127, 7484–7491. [Google Scholar] [CrossRef] [PubMed]
- Finch, C.M.; García-Suárez, V.M.; Lambert, C.J. Giant thermopower and figure of merit in single-molecule devices. Phys. Rev. B 2009, 79, 033405. [Google Scholar] [CrossRef]
- Ke, S.H.; Yang, W.; Baranger, H.U. Quantum-interference-controlled molecular electronics. Nano Lett. 2008, 8, 3257–3261. [Google Scholar]
- Cardamone, D.M.; Stafford, C.A.; Mazumdar, S. Controlling quantum transport through a single molecule. Nano Lett. 2006, 6, 2422–2426. [Google Scholar] [CrossRef]
- Hansen, T.; Solomon, G.C.; Andrews, D.Q.; Ratner, M.A. Interfering pathways in benzene: An analytical treatment. J. Chem. Phys. 2009, 131, 194704. [Google Scholar] [CrossRef]
- Markussen, T.; Stadler, R.; Thygesen, K.S. The relation between structure and quantum interference in single molecule junctions. Nano Lett. 2010, 10, 4260–4265. [Google Scholar] [CrossRef]
- Solomon, G.C.; Andrews, D.Q.; Goldsmith, R.H.; Hansen, T.; Wasielewski, M.R.; Van Duyne, R.P.; Ratner, M.A. Quantum Interference in Acyclic Systems: Conductance of Cross-Conjugated Molecules. J. Am. Chem. Soc. 2008, 130, 17301–17308. [Google Scholar] [CrossRef]
- Solomon, G.C.; Andrews, D.Q.; Van Duyne, R.P.; Ratner, M.A. Electron transport through conjugated molecules: When the π system only tells part of the story. ChemPhysChem 2009, 10, 257–264. [Google Scholar] [CrossRef]
- Lunde, A.M.; Flensberg, K. On the Mott formula for the thermopower of non-interacting electrons in quantum point contacts. J. Phys. Condens. Matter 2005, 17, 3879. [Google Scholar] [PubMed]
- Bergfield, J.P.; Stafford, C.A. Thermoelectric Signatures of Coherent Transport in Single-Molecule Heterojunctions. Nano Lett. 2009, 9, 3072–3076. [Google Scholar] [CrossRef] [PubMed]
- Bergfield, J.P. Quantum Interference Supernodes, Thermoelectric Enhancement, and the Role of Dephasing. Entropy 2025, 27, 1000. [Google Scholar] [CrossRef]
- Inui, S.; Stafford, C.A.; Bergfield, J.P. Emergence of Fourier’s law of heat transport in quantum electron systems. ACS Nano 2018, 12, 4304–4311. [Google Scholar] [CrossRef]
- Solomon, G.C.; Bergfield, J.P.; Stafford, C.A.; Ratner, M.A. When “small” terms matter: Coupled interference features in the transport properties of cross-conjugated molecules. Beilstein J. Nanotechnol. 2011, 2, 862–871. [Google Scholar] [CrossRef]
- Meir, Y.; Wingreen, N.S. Landauer formula for the current through an interacting electron region. Phys. Rev. Lett. 1992, 68, 2512. [Google Scholar] [CrossRef]
- Imry, Y.; Landauer, R. Conductance viewed as transmission. In More Things in Heaven and Earth; Springer: Berlin/Heidelberg, Germany, 1999; pp. 515–525. [Google Scholar]
- Haug, H.; Jauho, A.P. Solid-State Sciences. In Quantum Kinetics in Transport and Optics of Semiconductors; Springer: Berlin/Heidelberg, Germany, 1996; Volume 123. [Google Scholar]
- Stefanucci, G.; Van Leeuwen, R. Nonequilibrium Many-Body Theory of Quantum Systems: A Modern Introduction; Cambridge University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Cuniberti, G.; Fagas, G.; Richter, K. Introducing Molecular Electronics: A Brief Overview; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Brisker, D.; Cherkes, I.; Gnodtke, C.; Jarukanont, D.; Klaiman, S.; Koch, W.; Weissman, S.; Volkovich, R.; Toroker, M.C.; Peskin, U. Controlled electronic transport through branched molecular conductors. Mol. Phys. 2008, 106, 281–287. [Google Scholar] [CrossRef]
- Baym, G. Self-Consistent Approximations in Many-Body Systems. Phys. Rev. 1962, 127, 1391–1401. [Google Scholar] [CrossRef]
- Anderson, P.W. Localized Magnetic States in Metals. Phys. Rev. 1961, 124, 41–53. [Google Scholar] [CrossRef]
- Kozik, E.; Ferrero, M.; Georges, A. Nonexistence of the Luttinger-Ward Functional and Misleading Convergence of Skeleton Diagrammatic Series for Hubbard-Like Models. Phys. Rev. Lett. 2015, 114, 156402. [Google Scholar] [CrossRef] [PubMed]
- Vučičević, J.; Wentzell, N.; Ferrero, M.; Parcollet, O. Practical consequences of the Luttinger-Ward functional multivaluedness for cluster DMFT methods. Phys. Rev. B 2018, 97, 125141. [Google Scholar] [CrossRef]
- Lanczos, C. An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. J. Res. Natl. Bur. Stand. 1950, 45, 255–282. [Google Scholar] [CrossRef]
- Barr, J.D.; Stafford, C.A.; Bergfield, J.P. Effective field theory of interacting π electrons. Phys. Rev. B 2012, 86, 115403. [Google Scholar] [CrossRef]
- Mori, H. A continued-fraction representation of the time-correlation functions. Prog. Theor. Phys. 1965, 34, 399–416. [Google Scholar] [CrossRef]
- Barford, W. Electronic and Optical Properties of Conjugated Polymers; OUP Oxford: Oxford, UK, 2005; Volume 129. [Google Scholar]
- Purcell, W.P.; Singer, J.A. A brief review and table of semiempirical parameters used in the Hueckel molecular orbital method. J. Chem. Eng. Data 1967, 12, 235–246. [Google Scholar] [CrossRef]
- Ohno, K. Some remarks on the Pariser-Parr-Pople method. Theor. Chim. Acta 1964, 2, 219–227. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle–Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z=11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system, version 6.0. WIRES Comput. Mol. Sci. 2025, 15, e70019. [Google Scholar] [CrossRef]
- Neese, F. An improvement of the resolution of the identity approximation for the formation of the Coulomb matrix. J. Comp. Chem. 2003, 24, 1740–1747. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Bykov, D.; Petrenko, T.; Izsak, R.; Kossmann, S.; Becker, U.; Valeev, E.; Neese, F. Efficient implementation of the analytic second derivatives of Hartree-Fock and hybrid DFT energies: A detailed analysis of different approximations. Molec. Phys. 2015, 113, 1961–1977. [Google Scholar] [CrossRef]
- Helmich-Paris, B.; de Souza, B.; Neese, F.; Izsák, R. An improved chain of spheres for exchange algorithm. J. Chem. Phys. 2021, 155, 104109. [Google Scholar] [CrossRef] [PubMed]
- Rankin, D.W. CRC Handbook of Chemistry and Physics; Lide, D.R., Ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Reddy, P.; Jang, S.Y.; Segalman, R.A.; Majumdar, A. Thermoelectricity in molecular junctions. Science 2007, 315, 1568–1571. [Google Scholar] [CrossRef]
- Evangeli, C.; Gillemot, K.; Leary, E.; Gonzalez, M.T.; Rubio-Bollinger, G.; Lambert, C.J.; Agrait, N. Engineering the thermopower of C60 molecular junctions. Nano Lett. 2013, 13, 2141–2145. [Google Scholar] [CrossRef]
- Rincón-García, L.; Evangeli, C.; Rubio-Bollinger, G.; Agraït, N. Thermopower measurements in molecular junctions. Chem. Soc. Rev. 2016, 45, 4285–4306. [Google Scholar] [CrossRef]
- Solomon, G.C.; Andrews, D.Q.; Hansen, T.; Goldsmith, R.H.; Wasielewski, M.R.; Van Duyne, R.P.; Ratner, M.A. Understanding quantum interference in coherent molecular conduction. J. Chem. Phys. 2008, 129, 054701. [Google Scholar] [CrossRef]
- Van Veen, F.H.; Ornago, L.; Van Der Zant, H.S.; El Abbassi, M. Benchmark study of alkane molecular chains. J. Phys. Chem. C 2022, 126, 8801–8806. [Google Scholar] [CrossRef]
- Guo, S.; Hihath, J.; Diez-Perez, I.; Tao, N. Measurement and Statistical Analysis of Single-Molecule Current–Voltage Characteristics, Transition Voltage Spectroscopy, and Tunneling Barrier Height. J. Am. Chem. Soc. 2011, 133, 19189–19197. [Google Scholar]
- Li, X.; He, J.; Hihath, J.; Xu, B.; Lindsay, S.M.; Tao, N. Conductance of single alkanedithiols: Conduction mechanism and effect of molecule- electrode contacts. J. Am. Chem. Soc. 2006, 128, 2135–2141. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Pobelov, I.; Wandlowski, T.; Bagrets, A.; Arnold, A.; Evers, F. Charge transport in single Au| alkanedithiol| Au junctions: Coordination geometries and conformational degrees of freedom. J. Am. Chem. Soc. 2008, 130, 318–326. [Google Scholar] [CrossRef] [PubMed]
- Haiss, W.; Martiín, S.; Leary, E.; Zalinge, H.v.; Higgins, S.J.; Bouffier, L.; Nichols, R.J. Impact of junction formation method and surface roughness on single molecule conductance. J. Phys. Chem. C 2009, 113, 5823–5833. [Google Scholar] [CrossRef]
- Venkataraman, L.; Klare, J.E.; Tam, I.W.; Nuckolls, C.; Hybertsen, M.S.; Steigerwald, M.L. Single-molecule circuits with well-defined molecular conductance. Nano Lett. 2006, 6, 458–462. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bergfield, J.P. Many-Body Effects in a Molecular Quantum NAND Tree. Quantum Rep. 2025, 7, 45. https://doi.org/10.3390/quantum7040045
Bergfield JP. Many-Body Effects in a Molecular Quantum NAND Tree. Quantum Reports. 2025; 7(4):45. https://doi.org/10.3390/quantum7040045
Chicago/Turabian StyleBergfield, Justin P. 2025. "Many-Body Effects in a Molecular Quantum NAND Tree" Quantum Reports 7, no. 4: 45. https://doi.org/10.3390/quantum7040045
APA StyleBergfield, J. P. (2025). Many-Body Effects in a Molecular Quantum NAND Tree. Quantum Reports, 7(4), 45. https://doi.org/10.3390/quantum7040045






