Abstract
We present a topologically protected teleportation protocol based on projective parity measurements between spatially separated Majorana zero modes (MZMs), eliminating the need for dynamic braiding. Unlike conventional teleportation schemes, our method preserves logical information through nonlocal encoding and suppresses decoherence exponentially with Majorana separation. We provide a rigorous mathematical framework that includes six theorems and a lemma, proving fidelity bounds, no entropy increase under ideal QND parity measurement under quantum non-demolition (QND) measurements, and compliance with the no-cloning theorem. We demonstrate that all correction operations lie within the Clifford group, enabling efficient, fault-tolerant implementation. Furthermore, we outline a scalable architecture for multi-qubit teleportation and relate our framework to recent experimental advances in quantum-dot-based Kitaev chains and superconducting nanowire platforms. These results position Majorana-based teleportation as a thermodynamically stable and experimentally viable approach to scalable quantum information transfer. All operations discussed are Clifford-only; achieving universality requires non-Clifford resources and lies outside our scope.
1. Introduction
Quantum teleportation is a foundational protocol in quantum information science that transfers an unknown quantum state between distant parties using shared entanglement and classical communication [1,2,3]. It relies on quantum entanglement and classical communication and has been demonstrated across several platforms—including photonic systems, trapped ions, and superconducting circuits—spanning both discrete-variable and continuous-variable regimes—with recent work achieving logical-level teleportation using transversal gates and lattice surgery [3,4,5,6]. Despite these advances, reliable high-fidelity teleportation over long distances and in noisy environments remains a central challenge for scalable quantum networks [3,7,8] and, in the near term, motivates architectures that minimize error-correction overhead in the NISQ regime [9].
The standard teleportation protocol suffers from vulnerabilities to decoherence and environmental noise, especially when implemented in systems that store quantum information locally [3,7,8,10]. These imperfections not only reduce fidelity but also require elaborate quantum error correction techniques, which can limit scalability and increase resource overhead [11,12,13].
Majorana fermions, originally proposed in high-energy physics and now realized as quasiparticles in condensed matter systems, present a transformative opportunity [14,15,16,17,18,19]. These exotic states of matter are their own antiparticles and exhibit non-Abelian statistics, making them fundamentally different from conventional fermions or bosons [20,21]. In one-dimensional topological superconductors, Majorana zero modes (MZMs) appear at the ends of topological superconducting wires and can be used to encode qubits in a nonlocal manner [14].
MZMs provide an alternative route: qubits can be encoded nonlocally at the ends of topological superconducting wires, offering protection against local noise via fermion-parity conservation [14,16,20,22,23]. Experiments on hybrid superconductor–semiconductor devices have reported phase-coherent transport through “Majorana islands” consistent with nonlocal encoding [24], while theory and device studies show that hybridization-induced splittings—and associated error rates—can be exponentially suppressed with increasing separation relative to the coherence length [25]. In parallel, the statistical and computational framework of non-Abelian anyons underpins the appeal of Majorana platforms for fault-tolerant operations [20].
This topological encoding offers intrinsic protection against certain local decoherence channels: hybridization-induced splittings (and associated error processes) can be exponentially suppressed by increasing MZM separation relative to the coherence length, consistent with both theory and experiment [16,25,26].
From a thermodynamic and information-theoretic viewpoint, parity-preserving (QND) measurements need not increase system entropy, providing a principled basis for low-dissipation state transfer when ideal conditions hold [2,23]. Complementing device-level progress, emulation studies have realized Majorana-encoded teleportation primitives on gate-model hardware by mapping Kitaev-chain dynamics to spin circuits [14], helping to clarify resource requirements and control strategies that inform future experiments on true topological hardware [14,24,27].
In this work we analyze Majorana-based teleportation protocols that leverage nonlocal encoding and parity operations to enhance robustness against local noise. We explore how their nonlocal properties and topological protection can enable teleportation protocols that are naturally resistant to decoherence and errors. We outline how these ingredients can be used to implement teleportation primitives within the encoded space, discuss realistic constraints and error budgets, and survey experimental progress and architectural proposals toward scalable implementations [18,28].
2. Majorana Fermions and Topological Qubits
Majorana fermions, first theorized by Ettore Majorana in 1937 [29], are unique in that they are their own antiparticles [30]. While elementary Majorana particles have not been found in high-energy physics, condensed matter systems—particularly topological superconductors—have provided platforms where Majorana zero modes (MZMs) can emerge as quasiparticle excitations. These modes appear at the ends of 1D nanowires in a topologically nontrivial superconducting phase, such as those made from indium arsenide (InAs) or indium antimonide (InSb) coupled to conventional superconductors like aluminum (Al).
What makes MZMs exceptional is that they obey non-Abelian exchange statistics, unlike typical fermions or bosons. This means that braiding two MZMs—a process of adiabatically exchanging their positions—does not just permute their labels but enacts a unitary transformation on the quantum state of the system. The result of braiding depends on the order in which the exchanges are performed, which provides a method for performing quantum gates that are inherently fault-tolerant.
A topological qubit can be constructed using four MZMs, typically located at the ends of two nanowires or within a Y-junction geometry. The logical qubit states |0⟩ and |1⟩ are encoded in the fermionic parity—the occupation number—of the paired Majorana modes. Importantly, this qubit is nonlocally encoded, meaning that no single local measurement can collapse the entire state. This nonlocality is a major reason why Majorana qubits exhibit natural resistance to local decoherence, as any environmental noise affecting one end of the wire does not have access to the complete quantum information.
Furthermore, the system is protected by a superconducting energy gap, which suppresses thermal excitations that could disturb the quantum state. If the device operates at sufficiently low temperatures (typically < 100 mK), and the system remains within the topological phase, the encoded quantum information can persist for remarkably long times [15,31].
This makes Majorana-based qubits fundamentally different from conventional superconducting qubits (like transmons) or photonic qubits. In standard qubits, coherence times are limited by charge noise, photon loss, or material imperfections. In contrast, topological protection means that quantum information in a Majorana qubit is effectively “hidden” from most sources of decoherence.
These features have inspired topological quantum computing architectures, notably pursued by Microsoft’s Station Q and several academic collaborations [32]. In such architectures, computation is carried out by braiding MZMs and measuring their joint parity. Notably, braiding operations are geometric rather than dynamic, meaning that they depend on the path taken, not the speed or exact timing—offering further immunity to control noise.
In practical devices, braiding operations—which are essential for implementing non-Abelian quantum gates in Majorana-based systems—typically require Y-shaped or X-shaped junction geometries where three or more semiconductor-superconductor nanowires meet at a central node. These junctions allow for the controlled exchange or coupling of multiple spatially separated MZMs through the modulation of gate voltages or tunneling amplitudes. The Y-shape geometry enables the selective tuning of hybridization between pairs of MZMs while keeping others isolated, effectively implementing parity measurements or braids in a topologically protected subspace. These configurations are necessary to go beyond linear nanowire systems, as linear chains do not support topologically nontrivial braiding operations without overlap, and hence lack universality. Recent experimental designs and proposals have demonstrated how T-junctions, tri-junctions, and Y-networks allow for the manipulation of MZMs without violating parity conservation or inducing decoherence, thereby supporting nonlocal qubit manipulations essential for fault-tolerant topological quantum computing [33,34].
The non-Abelian anyon nature of Majoranas also opens the possibility for exotic forms of quantum entanglement and nonlocal quantum gates, which are ideal for quantum teleportation schemes where maintaining coherence and entanglement across long distances is essential [20].
In short, Majorana fermions offer not only a promising route to building a fault-tolerant quantum computer, but also a uniquely stable substrate for long-lived entangled states, robust qubits, and high-fidelity quantum teleportation. Their realization represents a convergence of condensed matter physics, quantum information science, and materials engineering at the frontier of next-generation technology. The measurement-only teleportation protocol replaces geometric braiding with sequences of joint-parity measurements, but it does not circumvent the Ising-anyon universality limit: the gate set realized here is Clifford-only. We make no claim of implementing non-Clifford gates (e.g., T or π/8) or magic-state distillation; those resources are outside the scope of this work (see Appendix A, Theorem A4).
3. Preserving Coherence via Topological Protection
In this work we distinguish two notions: decoherence suppression and entropy preservation. Decoherence suppression refers to the exponential protection of off-diagonal logical coherences achieved by nonlocal (topological) encoding and separation (see Equation (17)). Entropy preservation refers to the statement under ideal QND parity measurements when and no residual system–meter entanglement remains (Theorems A5 and A6). Outside these ideal conditions (e.g., finite visibility, leakage, meter back-action), one generally has . Our entropy statements are therefore operational and limited to the specified QND regime, whereas decoherence suppression concerns the encoding and device-level parameters.
The stability of MZMs against decoherence and local disturbances arises from a two-fold physical mechanism. The total decoherence rate scales as as shown in Lemma A1 (see Equation (A14)), where local operators acting on a single Majorana mode are proven to commute with the logical parity operator. First, the system is protected by a bulk energy gap (Δ) in the topological superconducting phase. This energy gap separates the ground state manifold—which hosts the MZMs—from higher-energy excitations. As long as external perturbations remain smaller than this gap, they cannot drive the system out of its topological phase or excite unwanted quasiparticles.
Second, and crucially, the logical qubit is encoded nonlocally in the fermionic parity of two spatially separated MZMs. Defining a Dirac fermion as, the occupation number n = c†c determines the qubit states |0⟩ and |1⟩. Local operations acting on only one Majorana operator cannot change this parity; only simultaneous perturbations to both γ1 and γ2 can affect the logical state. Therefore, even if a local error disturbs one part of the system, it does not collapse or decohere the encoded quantum information. This nonlocal encoding acts as a passive error-protection mechanism. In combination with the energy gap, it provides exponential suppression of decoherence as the Majorana separation L increases. The total decoherence rate scales as Γ, where ξ is the superconducting coherence length. This is shown in Lemma A1 (see Equation (A3)), where local operators acting on a single Majorana mode are proven to commute with the logical parity operator.
Thus, the topological protection of MZMs is due to both the presence of an energy gap that prevents excitation and a nonlocal qubit structure that shields the encoded state from local noise.
To clarify the distinction made in this manuscript, we note that ‘entropy preservation’ and ‘decoherence suppression’ refer to related but physically distinct concepts. Decoherence refers to the loss of quantum coherence due to entanglement with the environment, resulting in the decay of off-diagonal terms in the system’s density matrix. In contrast, entropy exchange refers to thermodynamic information flow—specifically, the increase in von Neumann entropy due to energy and disorder transferred between the system and its surroundings.
In topological systems based on MZMs, decoherence is suppressed due to the nonlocal encoding of qubits in the fermionic parity of spatially separated MZMs. This encoding renders the logical qubit immune to local perturbations. Meanwhile, entropy exchange is limited because operations such as braiding, and parity measurement are non-dissipative and often quantum non-demolition (QND) in nature. These operations preserve the system’s total entropy by avoiding direct energy exchange with the environment. Thus, although related, entropy preservation arises from thermodynamic isolation, while decoherence suppression arises from topological encoding and symmetry constraints.
To describe the protection mechanism mathematically, we consider the Kitaev chain Hamiltonian [14]:
This model supports MZMs at the ends of a 1D chain in the topological phase (). The Majorana operators are defined as and . In this phase, edge-localized MZMs and emerge with zero energy, separated by an energy gap Δ.
The logical qubit is encoded in the nonlocal fermionic mode , with number operator . The qubit states are and . The associated parity operator is .
The stability arises because local perturbations cannot change the nonlocal parity: [ for local operators . Hence, the overlap . Moreover, the decoherence rate due to hybridization of the two Majoranas scales as , where L is their separation and ξ is the superconducting coherence length. Thus, topological protection arises from both the spectral gap that suppresses excitations and the nonlocal encoding that renders logical operations immune to local errors.
One of the most pressing challenges in quantum information science is maintaining the coherence of quantum states over time. Decoherence—caused by unavoidable interactions with the surrounding environment—leads to the loss of quantum information and ultimately limits the performance of quantum computers and communication networks. In conventional qubit systems, such as superconducting transmons or trapped ions, quantum information is localized in physical degrees of freedom (like current or spin), which makes them vulnerable to even minimal environmental disturbances [10,34,35].
Since Majorana fermions encode information nonlocally using the joint parity of two spatially separated MZMs located at opposite ends of a topological superconducting nanowire, if local noise—say, an electric field fluctuation or phonon interaction—affects only one end of the wire, it does not collapse the quantum state or cause a bit-flip. The quantum information is not stored at one end but rather distributed across the two ends. Consequently, only a correlated disturbance affecting both MZMs simultaneously could compromise the qubit’s logical state—a scenario that is exponentially less likely to occur. See Lemma A1 in Appendix A for a formal proof that logical states encoded in Majorana qubits are immune to local operators.
This structural feature acts as a passive error correction mechanism. Unlike traditional qubit systems that rely on active error correction codes (requiring additional overhead in terms of qubits and gate operations), Majorana qubits have error suppression built into the physical substrate itself. This form of topological protection makes them attractive for any protocol that relies on maintaining entangled states for extended periods, especially teleportation [27].
Another coherence-preserving aspect of Majorana systems is the adiabatic braiding of Majorana modes to perform quantum operations. In most quantum computers, logical gates require precise timing and control of interactions between qubits, which can introduce errors. In contrast, braiding operations in Majorana systems depend only on the topology of the path—not the timing or shape of the trajectory—making them inherently robust to timing jitter or slow control signal noise. If the system is kept in the ground state and transitions are avoided across the superconducting energy gap, the braiding operation completes a well-defined unitary transformation.
This robustness has profound implications for quantum teleportation. A standard quantum teleportation protocol involves a Bell-state measurement and classical communication of the outcome to reconstruct the original state. In traditional systems, this measurement step typically collapses the state and is subject to fidelity loss due to imperfect entanglement or decoherence during measurement. In a Majorana-based system, teleportation can be implemented via projective parity measurements that do not destroy the logical qubit and can be made fault-tolerant through topological encoding [27].
Moreover, Majorana qubits maintain their coherence for longer durations compared to standard qubits. This enables long-range entangled resource states—essential for teleportation—to be prepared ahead of time and stored without rapidly degrading. Studies suggest that even in environments with thermal noise or fluctuating magnetic fields, topologically encoded information can be preserved if the system stays below a certain energy threshold and within the topological phase.
Recent research has also introduced the concept of “measurement-only” topological quantum computation, where all quantum operations are implemented using sequences of parity measurements, and no actual braiding is needed [36,37].
Recent research has introduced “measurement-only” topological quantum computation, in which braiding transformations are affected by sequences of topological-charge (parity) measurements, so no physical braiding is required [28,36,37]. This paradigm further reduces operational complexity and makes teleportation not only feasible but efficient and programmable. In this scheme, qubit teleportation is effectively equivalent to moving the logical qubit from one Majorana pair to another, without physically transporting any particles—minimizing decoherence during the process.
Lastly, Majorana-based teleportation is resilient even in partially decohered or “mixed” quantum states. While standard teleportation protocols suffer from fidelity loss when entanglement is imperfect, the topological entanglement structure of Majorana systems ensures that some forms of noise can be naturally filtered or rendered ineffective. This leads to higher average teleportation fidelities even under non-ideal conditions.
In summary, topological protection provides a quantum shield for information encoded in Majorana systems. By preventing local disturbances from collapsing qubits, ensuring robustness to gate errors, and enabling non-destructive teleportation protocols, topological qubits represent a paradigm shift in how quantum coherent.
4. Teleportation Using Majorana Fermions
Quantum teleportation transmits an unknown quantum state from one party (Alice) to another (Bob) using two key resources: a shared entangled state and a classical communication channel. Majorana-based protocols adapt this model by encoding each logical qubit in spatially separated Majorana zero modes (e.g., , for Alice and , for Bob) and using parity measurements as the core operation. Figure 1 (minimal 4-MZM case) illustrates the entanglement-generation primitive: a joint parity measurement of and projects the system into an entangled state . This entangled pair provides the quantum channel. The full teleportation protocol—which uses this AB resource together with classical messages and applies the appropriate parity-conditioned correction on a third encoded qubit —is shown in Figure 2.
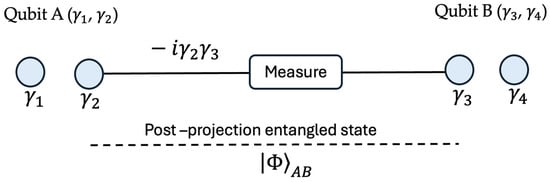
Figure 1.
Entanglement distribution protocol using topological (Majorana-based) qubits. Alice holds a logical qubit encoded in the pair , , while Bob holds another qubit encoded in , . A joint fermionic parity measurement between and (via ) is performed. This operation projects the system into an entangled state shared between the two topological qubit halves, thereby distributing entanglement across spatially separated regions. Dashed line indicates the post-projection entanglement resource (a Bell link) between Qubits A and B, i.e., the state . It’s a conceptual correlation, not a physical wire or coupling.
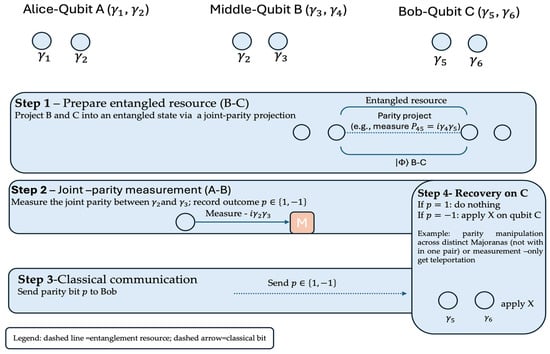
Figure 2.
Protocol flow for Majorana-based, measurement-only teleportation. Step 1: prepare an entangled resource between () and () via a joint-parity projection (e.g., measure ). Step 2: perform a joint-parity measurement on (measure ) and record the outcome . Solid arrow (Step 2): the physical coupling path used to perform the joint-parity measurement on (i.e., you momentarily turn on a tunnel/hybridization to read out the operator ). Boxed “M”: the parity meter/readout (e.g., quantum-dot/transmon/charge sensor) that performs a projective measurement giving the outcome . Step 3: send to Bob over a classical channel. Step 4: apply the Pauli correction on C: if do nothing, if apply . In our architecture is realized by parity manipulation across distinct Majoranas or by measurement-only gate teleportation; braiding within a single pair cannot implement (see Section 4 and Theorem A4). Ideal QND readout underlying Steps 2–3 is the regime addressed by Theorems A5 and A6.
In this teleportation scheme, Qubit A is the logical input qubit initially held by Alice. Qubit B is an ancillary system that participates in parity measurements but does not receive the teleported state. Qubit C is held by Bob and ultimately receives the teleported quantum information after corrections. As shown in Figure 1, the parity projection between (Alice) and (Bob) generates entanglement between topological qubits nonlocally. This allows teleportation to proceed via measurement-only logic.
Unlike conventional teleportation protocols, which rely on Bell-state measurements and classical corrections sensitive to decoherence and timing delays, Majorana-based teleportation uses topologically protected parity measurements between nonlocally encoded qubits. This section presents a mathematical formulation of the protocol, highlighting its robustness to noise and suitability for measurement-only quantum computation.
In the simplest Majorana teleportation scheme, consider three logical qubits, each encoded in a pair of MZMs:
- Qubit A (the state to be teleported),
- Qubit B (entangled with Qubit C), and
- Qubit C (held by the receiver, Bob).
Teleportation proceeds through the following topologically protected steps:
- Entanglement Preparation: Qubits B and C are entangled via a joint parity operation. In practice, this is achieved by coupling the MZMs through a controlled tunneling interaction or via an auxiliary quantum dot. The resulting state encodes shared fermionic parity between the two qubit pairs. This process is formally described in Theorem A1 in Appendix A, which shows that parity projections preserve logical coherence and entangle MZMs deterministically.
- Projective Measurement: Alice performs a joint parity measurement between Qubit A and Qubit B. This measurement entangles the unknown state of A with B and collapses the system into a superposition conditioned on the measured parity. Unlike a conventional Bell measurement, this step can be done non-destructively in Majorana systems using charge sensing or interferometry.
- Classical Communication: The result of the parity measurement is transmitted to Bob via a classical channel. Because Majorana-based gates are Clifford operations, the necessary correction is typically a Pauli operation (X, Y, or Z) or a controlled-phase gate, depending on the measurement outcome.
- Recovery Operation: Bob applies the correction to Qubit C, effectively reconstructing the original state of Qubit A. Importantly, the information has now been relocated—not copied—to a new topological region, satisfying the no-cloning theorem, supported by Theorem A2 while completing the teleportation.
See Theorem A3 in Appendix A for a mathematical formulation of topological protection under parity-based teleportation.
Protocol setup. We consider three logical qubits: A holds the unknown state to be teleported; B is the entangled ancilla (shared resource); C is Bob’s receiver qubit. Each logical qubit is encoded nonlocally by a pair of Majorana zero modes (MZMs):
Qubit A: , Qubit B: , Qubit C: .
- Encoding and algebra
The Majorana operators satisfy:
Define Dirac fermions for each pair (so that ):
Logical Z for each qubit is its pair parity,
with logical basis
For qubit B, the vacuum/occupied states are
A product basis state for is, e.g.,
- Step 1: Prepare entanglement between B and C
Use a joint parity projection to prepare the logical Bell state
e.g., by projecting an inter-pair parity (one convenient choice in this layout is)
(Physically, the parity projection is implemented by interferometric or charge-sensing readout; see [28,37,38,39,40,41]).
- Step 2: Joint parity measurement between A and B
Alice holds
She measures the link parity
Let be the projectors. Acting on the initial state
the selective post-measurement state is
(With a Bell resource, 1 for each outcome).
- Step 3: Classical communication and correction rule
Alice sends the one-bit outcome to Bob. The required correction on is a logical Pauli conditioned on :
One implementation in this geometry is the parity-generated operation
- Step 4: Recovery on C
Bob applies and discards :
Equivalently, for pure states,
Notes. (i) The operations used here are Clifford (see Theorem A4); no non-Clifford gates are assumed. (ii) When the outcome is not used (no feed-forward), the map on C reduces to dephasing in the basis; with feed-forward, the channel is the identity on the logical subspace.
Thus, the quantum information originally encoded in Qubit A has been relocated to Qubit C—not cloned—satisfying the no-cloning theorem and completing the teleportation, as proven in Theorem A2 and Equation (A9), which shows the reduced state at the sender becomes maximally mixed after teleportation.
In our teleportation protocol, Alice performs a joint parity measurement between Majorana modes and , using the operator . The projection operator is defined in Equation (A1) in Appendix A. While belongs to Qubit B (which is entangled with Qubit C), this operation does not require Alice to control the full logical state of Qubit B. As shown in Figure 2 (Step 1), we prepare a B–C resource by a joint-parity projection (e.g., ). In Majorana-based systems, it is physically feasible to couple two Majorana modes—even from different devices—via an intermediate quantum dot or superconducting island. This setup enables a joint parity measurement without collapsing the full entangled state.
Such measurements are non-demolition and topologically protected, acting only on the parity degree of freedom. They have been well-established in the literature as primitives for measurement-only topological quantum computation. For example, Vijay, Haah, and Fu (2016) proposed a dimensional hierarchy of quasiparticles based on such parity projections [37]. Similarly, Karzig et al. (2017) detailed scalable architectures in which joint parity measurements using quantum dots mediate topologically robust logical operations [28].
Therefore, although Alice performs a measurement involving , she does so through an accessible and non-destructive mechanism that operates at the level of Majorana parity, not full qubit manipulation.
In conventional teleportation protocols, the Bell pair ∣Φ+⟩ used for entanglement is subject to environmental decoherence. If Bob must wait for Alice’s measurement result before applying a correction, any delay may degrade the quantum state fidelity during that window [10,42]. In standard teleportation, Bob’s ability to recover the original state is fully dependent on receiving Alice’s classical outcome. This forces a synchronization bottleneck and prevents parallel computation [1,43].
This model of teleportation avoids direct exposure of the quantum state to environmental noise. Moreover, the non-local encoding of Majorana qubits ensures that even if one MZM suffers a local perturbation during the protocol, the full quantum information can still be recovered. Additionally, the entire process can be conducted without physically moving qubits, reducing the risk of control-induced decoherence.
In certain architectures, such as measurement-only topological quantum computing, teleportation is the central primitive. Rather than implementing quantum gates by dynamically braiding MZMs, operations are simulated through a network of teleportation steps. By measuring joint parities in a specific sequence, one can effectively move and manipulate quantum states across a Majorana qubit network without ever exposing the encoded information to a noisy channel. This “braiding without braiding” approach, proposed by Vijay and Fu in 2016, underlines how teleportation in a Majorana system is not merely a communication protocol but a computational engine [37].
Topological qubits based on Majorana fermions also provide a unique opportunity to explore entropy-preserving quantum operations. Mathematically, this suppression can be understood as conservation of entropy under parity-preserving QND operations, as proven in Theorem A5. Unlike standard qubits where entropy increases rapidly due to environmental coupling, the joint parity of spatially separated MZMs allows for an effective suppression of entropy production at the local level. This is because decoherence pathways are constrained by the topological nature of the encoding, limiting entropy exchange with the environment. Entanglement entropy between subsystems in a topological quantum circuit remains stable over longer durations, enabling more accurate teleportation fidelity under noise. These features make Majorana systems not just physically robust, but thermodynamically efficient carriers of quantum information, aligning with the core mission of entropy-sensitive quantum computation [23,44,45]. This is made precise in Theorem A6, which shows no entropy increase under ideal QND parity measurement under quantum non-demolition parity measurements, as formally derived in Equation (A23), where the von Neumann entropy is shown to be preserved under parity projective measurement.
Another significant advantage of Majorana-based teleportation is its compatibility with error detection and correction. Since the parity measurements project the system into a known subspace, any unexpected outcome (e.g., forbidden parity) can be flagged as an error. This enables passive detection of certain fault types during the teleportation sequence, offering further protection to quantum information.
Furthermore, Majorana-based teleportation protocols are scalable and modular. Unlike conventional qubit systems, where longer chains of qubits and entangled pairs suffer from exponential fidelity loss, the topological robustness of Majorana qubits allows entangled states to be maintained and distributed across larger distances or arrays [20]. This scalability is essential for building quantum repeaters, distributed quantum computing networks, or even the foundations of a quantum internet. Parity manipulation across distinct Majoranas using island-mediated tunnel links is exactly the mechanism proposed in Majorana box-qubit architectures [46].
5. Experimental Milestones (2020–2025)
The last five years have witnessed rapid progress in demonstrating the physical feasibility of Majorana-based quantum teleportation. From early signatures of teleportation-like behavior to prototype quantum hardware designed specifically for Majorana qubit control, the field has matured from theoretical speculation to engineering reality. The following table summarizes key experimental and theoretical milestones.
Table 1 summarizes selected developments in the field, from the first phase-coherent teleportation through Majorana islands (2020) to recent device-level demonstrations and proposals relevant to scalable topological architectures. It includes both hardware milestones and foundational theoretical advances, providing a chronological perspective on progress toward stable, error-resilient quantum teleportation using Majorana zero modes [9,22,27,30,32].

Table 1.
Major experimental and theoretical milestones in Majorana-based quantum teleportation (2020–2025).
6. Advantages over Standard Qubit Approaches
Majorana-based systems offer a compelling suite of advantages that set them apart from conventional quantum computing and communication platforms. While standard qubit technologies—such as superconducting transmons, trapped ions, and photonic qubits—have shown promising developments in speed, gate fidelity, and scaling, they remain fundamentally limited by their sensitivity to decoherence and noise. In contrast, topologically encoded Majorana qubits inherently mitigate many of these challenges due to their nonlocal and fault-tolerant structure. This section outlines the critical benefits of using Majorana fermions in quantum teleportation and beyond:
- Extended Coherence Times via Nonlocal Encoding. One of the most significant advantages of Majorana-based qubits is their exceptionally long coherence times. Unlike conventional qubits, which store information in localized degrees of freedom, Majorana qubits encode quantum information in the joint parity of two spatially separated zero modes. This encoding prevents local perturbations—like stray electric fields or background noise—from collapsing the qubit state, allowing entangled Majorana pairs to persist far longer [21].
- Built-In Error Protection at the Hardware Level. Topological qubits serve as physical error-correcting codes. Their architecture suppresses both bit-flip and phase-flip errors without requiring active correction cycles. This greatly enhances reliability for quantum teleportation protocols and simplifies the system architecture [28,38].
- Resilience in Noisy and Mixed-State Environments. Teleportation using standard qubits degrades rapidly under environmental noise. In contrast, studies have shown that Majorana qubits can maintain high-fidelity teleportation even when the entangled resource is partially decohered or in a mixed state—greatly enhancing potential in practical applications.
- Deterministic, Topologically Protected Operations. Operations using Majorana qubits—such as braiding or parity measurements—are topologically protected and deterministic. They are immune to small control inaccuracies, unlike pulse-driven gates in other qubit types, making them particularly attractive for repeatable and high-fidelity teleportation [19].
- Reduced Overhead for Error Correction. Unlike conventional systems that require extensive redundancy and syndrome detection, Majorana qubits embed error resilience into their hardware. Teleportation protocols thus become simpler and more scalable, requiring fewer physical qubits per logical operation [40].
- Scalability and Modular Design. Topological qubit networks can be laid out modularly using repeating nanowire segments and Y-junctions. This design lends itself naturally to teleportation circuits, distributed computing, and fault-tolerant quantum networks—forming a promising architecture for the future quantum internet [33].
In summary, the stability, robustness, and design flexibility of Majorana qubits offer a clear path forward for reliable and efficient quantum teleportation systems.
7. Experimental and Physical Realization of Majorana-Based Quantum Teleportation
Recent advances in topological quantum materials and hybrid semiconductor–superconductor systems have enabled the experimental and physical realization of quantum teleportation using MZMs. In this approach, quantum information is encoded nonlocally in pairs of MZMs at the ends of superconducting nanowires, such as InAs or InSb wires with epitaxially grown Al or Nb shells. Under suitable magnetic fields and gate voltages, these nanowires support topologically protected zero-energy modes that can be used to encode qubits through their fermionic parity [33,42].
To initiate the teleportation protocol, an unknown quantum state is prepared in a topological qubit consisting of two MZMs (). In parallel, an entangled state is generated between two other topological qubits: one held by Alice () and the other by Bob (). Physically, this entangled Bell-like state
is produced by initializing a fixed total parity over a shared superconducting Coulomb Island or through coherent tunneling across a controlled capacitive link between distant nanowires [16,38].
The teleportation process begins when Alice performs a joint parity measurement between one Majorana from her unknown qubit () and one from the entangled pair (γ4). This sequence is illustrated schematically in Figure 3, showing the layout of Alice’s and Bob’s qubits, the parity measurement via a quantum dot, and the corrective operation on Bob’s side.
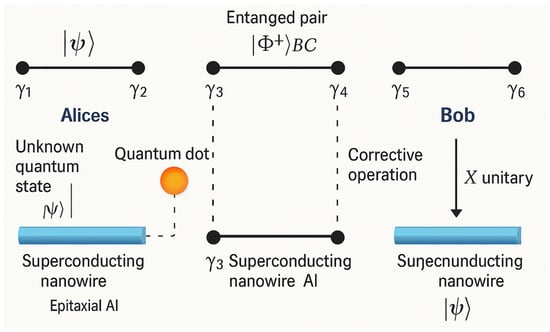
Figure 3.
Experimental setup for Majorana-based quantum teleportation. Alice holds an unknown quantum state encoded in two Majorana zero modes ( at the ends of a superconducting nanowire (InAs/Al). An entangled parity pair is generated between Alice’s auxiliary qubit (4) and Bob’s qubit (). A quantum dot is used to perform a joint parity measurement between Alice’s unknown state and the entangled resource. The parity-dependent outcome is read non-destructively using charge sensing or microwave dispersive shift and communicated to Bob via a classical channel. Bob applies a corrective Pauli-X operation if needed, recovering the original quantum state on his side.
This measurement is implemented using a quantum dot or a superconducting microwave resonator coupled to both MZMs. The energy level of the dot or the resonator response shifts depending on the joint parity of the two Majoranas. A nearby charge sensor (e.g., quantum point contact or single-electron transistor) or dispersive readout enables non-demolition readout of the parity eigenvalue (+1 or −1) [39,47].
Based on this measurement, Alice sends a single classical bit (even or odd parity outcome) to Bob over a conventional communication channel. If the outcome is even, Bob takes no action. If it is odd, Bob performs a corrective Pauli-X (bit-flip) operation on his Majorana qubit ().
Implementation of . The Pauli-X correction cannot be achieved by braiding within a single Majorana pair (which preserves parity). Instead, is implemented by parity manipulation across distinct Majoranas—e.g., by temporarily enabling a parity-changing tunnel/coupling between different pairs or by measurement-only gate teleportation that conditions on joint parity outcomes [16,28,38]. This is consistent with our Appendix A proof that single-pair braiding preserves parity and thus cannot flip the qubit’s logical occupation.
The Pauli-X correction shown in Equation (12) cannot be implemented by braiding operations within a single pair of Majorana modes, such as and . Braiding two Majoranas within the same fermionic mode (i.e., forming the same Dirac fermion) does not alter the occupation number of the fermionic mode, and therefore cannot flip the logical qubit state. This is because such braiding operations preserve the fermionic parity and effectively induce only phase transformations within the fixed-parity subspace.
In other words, the Hilbert space of a single fermionic mode, defined by , consists of the states and . The parity operator has eigenvalues ±1, and any unitary generated by braiding within the , pair commutes with P, and hence cannot change the parity—i.e., it cannot flip the qubit. To implement an effective Pauli-X gate, which does flip the parity (i.e., maps ), one must couple MZMs from different qubit pairs or introduce an ancillary parity degree of freedom through projective measurement or measurement-based gate teleportation. For example, a controlled Pauli-X can be implemented by measuring the joint parity and conditioning on the result. This form of logic is consistent with measurement-only topological quantum computation schemes [47].
Therefore, while braiding is an essential tool for generating non-Abelian operations, Pauli-X corrections in Majorana-based teleportation must be applied using parity manipulation between distinct Majorana pairs, not within a single pair.
To verify teleportation, Bob measures the state of his qubit by converting fermion parity into charge and using quantum state tomography. Repeating this process for multiple input states and bases allows the construction of the teleported density matrix. The fidelity of teleportation is computed as
where F→1 when parity is accurately measured and corrected [40,41].
Theoretical models predict that the decoherence/hybridization error rate scales as Γ in Equation (17), where Δ is the superconducting gap, L is the MZM separation, and ξ is the coherence length [40].
Feasibility & error budget: end-to-end teleportation fidelity ≳ (parity-readout fidelity) × exp(−2L/ξ) as bounded in Theorem A3; device-level factors (finite T, charge noise, quasiparticle poisoning, disorder) renormalize prefactors and effective ξ; Equation (17) is an ideal-limit expression. This exponential suppression is supported by experimental observations in nanowire-based devices, where coherence times of Majorana states appear significantly extended compared to conventional charge qubits [47]. The fidelity is suppressed exponentially with MZM separation and gap as formalized in Theorem A3 and Equation (A12), which bounds fidelity.
Our finite-temperature parity-readout model uses Gaussian hypothesis testing for the readout misclassification probability, includes Poissonian quasiparticle poisoning during the integration window, and adds a hybridization term , following standard treatments [16,18,25,26,28,32]. We model the joint-parity measurement as a binary hypothesis test on a continuous readout with Gaussian statistics conditioned on the parity eigenvalue . The temperature-dependent signal amplitude scales as , while the noise standard deviation is (dominated by amplifier noise plus a small thermal component). The optimal threshold yields a misclassification probability
During the integration window , quasiparticle poisoning is treated as a Poisson process with rate , giving in the small-rate limit. If poisoning occurs, we conservatively take the outcome fidelity to be . The effective readout fidelity is then
Finally, we fold in hybridization as a parity-flip/dephasing channel with weight , giving the conservative multiplicative bound
which captures the expected trends: improves with and , but degrades with and overly short (SNR-limited). See Table 2 for the corresponding error-budget parameters [16,18,25,26,28,32]. It provides a compact way to translate device-level parameters into a predicted teleportation fidelity band for experimental planning.

Table 2.
Dominant error channels for a single teleportation shot and how they combine in our conservative bound. See Refs. [16,18,25,26,28,32].
Device Limitations. Equation (17) is an ideal-limit expression for topological suppression. In practical devices, several effects renormalize the prefactor and the effective suppression length: finite temperature (thermally activated quasiparticles), charge/phase noise (fluctuations of couplings and readout), quasiparticle poisoning (setting a floor ), and disorder-induced subgap states (reducing Δ and enlarging an effective coherence length ). Operationally, one should read Equation (17) as , with determined by device engineering. Our claims are therefore asymptotic/ideal; practical rates depend on the realized , poisoning times, and readout fidelity.
While current efforts focus on teleporting single logical qubits, the same architecture can, in principle, be scaled up to enable the teleportation of macroscopic quantum information. To achieve this, one would:
- Encode a complex quantum object—e.g., a mesoscopic system or register—into an array of nonlocal Majorana qubits.
- Perform multi-qubit parity measurements between the object’s logical qubits and shared entangled parity states distributed across devices or regions.
- Use correlated classical bits from these measurements to guide corrections on the receiving side.
- Reconstruct the full macroscopic state in the receiver’s device without moving any physical particles.
This approach requires careful management of parity conservation across multiple nonlocal encodings but offers the revolutionary possibility of teleporting entire many-body quantum states without loss of coherence. Because Majorana qubits are protected from local errors, this type of teleportation would preserve global entanglement in a way that is currently impossible with fragile photonic or spin systems.
Such a protocol would build directly upon the measurement-only framework proposed by Vijay, Haah, and Fu [37] and extended in networked architectures by Karzig et al. [28]. With coherent coupling and distributed parity readout, a macroscopic teleportation scheme could redefine the scope of long-distance quantum communication and distributed quantum computing.
Entanglement and the Challenge of Distance. An important conceptual point arises in considering whether distant teleportation using Majorana systems necessarily requires the sharing of an entangled state—particularly in the form of a photon-mediated entangled pair, such as through absorption and emission of photons. In traditional quantum teleportation protocols, entanglement is distributed between sender and receiver, often using photons as carriers of nonlocal quantum correlations. However, in the Majorana-based architecture developed here, quantum information is transferred via joint parity measurement and classical communication, without physically transporting entangled particles. The nonlocality is embedded in the parity-conserving structure of the topological system itself.
Still, the question of how to physically realize distant entanglement, especially across cryogenic boundaries or between separate hardware platforms, remains a key challenge. One possible avenue is to mediate the entanglement of two spatially separated Majorana systems (e.g., and ) using an entangled photon link, wherein the photon couples to the parity degree of freedom via engineered cavity-QED or spin-photon interfaces. This remains an open area of exploration and may bridge the topological and photonic realms. Alternatively, the model developed in this work may circumvent the need for pre-shared entanglement by exploiting measurement-based teleportation over fixed parity manifolds.
Ultimately, the boundary between topological parity transfer and conventional entanglement distribution warrants deeper investigation. We acknowledge that further clarification—both theoretical and experimental—is required to fully understand the interplay between Majorana parity dynamics and photonic entanglement in long-distance quantum state transfer.
Figure 4 illustrates two complementary approaches to teleportation in Majorana-based quantum systems. In the left panel, an entangled photon pair establishes a nonlocal quantum link between γ4 (on Alice’s chip) and γ5 (on Bob’s chip), enabling the remote sharing of an entangled Majorana parity state. This hybrid architecture supports long-distance quantum information transfer while preserving topological protection, an essential feature for scalable and fault-tolerant quantum networks [19]. The right panel shows a fully local, measurement-based teleportation scheme in which Alice performs a joint parity measurement between γ2 (from her input qubit) and γ4 (from the entangled pair), using a quantum dot or resonator. The result is sent classically to Bob, who applies a Pauli-X correction to his qubit (γ5–γ6), thereby completing the teleportation without physically moving any quantum particle. Both approaches demonstrate how Majorana systems leverage topological encoding and parity-preserving operations to enable robust, decoherence-resistant quantum communication.
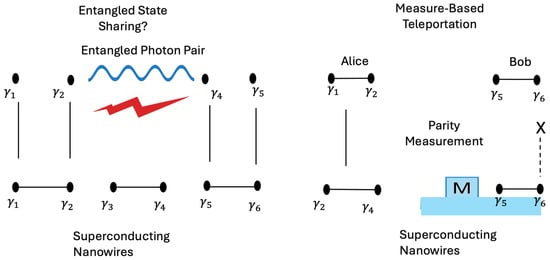
Figure 4.
Entangled Photon Sharing vs. Measurement-Based Teleportation in Majorana Systems. (Left) A schematic illustrating how an entangled photon pair can mediate a nonlocal entangled state between spatially separated Majorana modes γ4 (Alice) and γ5 (Bob). Alice’s unknown qubit is encoded in γ1–γ2, while Bob’s target qubit resides in γ5–γ6. This hybrid architecture combines superconducting nanowires and optical links to establish long-distance entanglement without physical proximity. Blue waves: entangled photon pair used to share a Bell state. Red lightning: classical heralding/communication signal from photon detection. (Right) A standard measurement-based Majorana teleportation protocol. Alice performs a joint parity measurement between γ2 (her qubit) and γ4 (her entangled pair), using a quantum dot or resonator (M). She sends the parity outcome via a classical channel, and Bob applies a Pauli-X correction to γ5–γ6 if needed. Throughout, topological protection is maintained by encoding information nonlocally in fermion parity.
For example, a minimal realization of the Kitaev chain was demonstrated in coupled quantum dots [48], showcasing the feasibility of engineering topological superconducting phases in nanoscale systems. Building on this foundation, enhanced stability was achieved in three-site quantum dot chains [49,50], illustrating the robustness of such architectures against environmental decoherence and fabrication imperfections. These developments enable precise control over MZM hybridization and fermionic parity, both of which are critical ingredients for implementing reliable quantum teleportation protocols.
Additional experimental evidence has supported the presence of both edge and bulk Majorana states in quantum dot arrays [51], further validating the topological nature of these engineered systems. Complementing these observations, theoretical models have captured nontrivial fusion phenomena in extended dot networks [52], providing important insights into the manipulation of non-Abelian excitations. Taken together, these advances suggest that quantum-dot arrays not only serve as promising and scalable platforms for hosting MZMs but also constitute a practical and tunable medium for executing the parity-based measurements required in topological quantum teleportation. Moreover, demonstrating a full Majorana-based teleportation protocol remains a near-term research goal; ongoing efforts report ingredients such as parity readout and non-local correlations, but a complete implementation is future work.
8. Discussion: Limitations and the Challenge of Macroscopic Teleportation
While Majorana-based quantum teleportation presents a robust and theoretically sound method for transmitting quantum information with topological protection, extending such a protocol to macroscopic or biological systems faces fundamental limitations. The teleportation described in this framework is restricted to the transfer of quantum states, not physical matter. MZMs only exist under cryogenic conditions—typically in the millikelvin range—required to stabilize the topological superconducting phase [28]. These ultra-cold temperatures are essential for maintaining the superconducting topological phase that hosts non-Abelian quasiparticles and enables fermionic parity encoding. As such, all operations involving Majorana-based qubits—preparation, entanglement, parity measurement, and correction—must be performed in cryogenic environments.
Teleportation in this context operates by encoding quantum information into the parity of spatially separated MZMs. A joint parity measurement and classical communication suffice to transfer the quantum state between distant nodes without moving any physical qubit. However, teleporting a macroscopic object would require mapping every degree of freedom of that system—including position, spin, and vibrational states—into a quantum register with exceptional isolation from the environment. Biological systems decohere rapidly at room temperature, on the order of femtoseconds, making them fundamentally incompatible with the required quantum coherence lifetimes [53].
Even for engineered systems, several critical challenges must still be addressed before Majorana-based teleportation can be deployed in scalable quantum networks:
- Engineering Stable Majorana Modes: A key requirement is the reproducible and scalable generation of MZMs in solid-state nanowires. Although signatures of MZMs have been observed, reliably creating topological superconducting phases with stable zero-energy modes remains a materials and fabrication challenge [15,16,53]. Future work must focus on heterostructure refinement, disorder reduction, and high-fidelity control.
- Gate Set Limitations—Non-Universality of Ising Anyons: Majorana-based qubits support Clifford operations through braiding, but this gate set is insufficient for universal quantum computation. Realizing non-Clifford gates requires ancillary operations like magic state distillation, which adds significant overhead [54]. Hybrid approaches that embed Majoranas into more universal quantum architectures are a promising direction.
- Interfacing with Photonic Systems for Long-Distance Teleportation: Since Majorana qubits are hosted in cryogenic environments, achieving long-distance teleportation will require hybrid interfaces between photonic qubits and Majorana modes. Such interfaces are in early stages of development and remain a major bottleneck for integrating Majorana systems into quantum communication networks [55].
- Experimental Readout and Control: Joint parity measurements are central to Majorana teleportation, but current methods such as tunneling spectroscopy and charge sensing lack the required fidelity and scalability. Advances in quantum-dot coupling, resonator-based readout, and measurement-only control architectures are needed to reliably access and manipulate fermionic parity [56].
- System-Level Scalability and Fault-Tolerant Architectures: Although topological protection offers intrinsic noise suppression, it does not eliminate the need for active error correction. Realizing scalable teleportation requires modular architectures that support parallel operation, fault-tolerant correction, and compatibility with quantum memory and networking protocols [28].
In this sense, while Majorana teleportation is a powerful tool for transferring quantum information within cryogenic, engineered environments, it does not enable teleportation of physical or biological objects as imagined in science fiction. The cold environment is not the fundamental limiting factor—the real issue is that such complex systems cannot be coherently and completely mapped into a quantum information architecture without destroying the very structure we aim to preserve.
Thus, the scope of Majorana-based teleportation is best understood as a platform for transferring quantum logic, not classical matter. It holds promise for distributed quantum computing, error-resilient communication between superconducting qubit nodes, and potentially teleporting many-body quantum states engineered within cold, coherent systems—but not for transferring warm, living, or structurally complex matter across space.
Future Outlook. The path forward is promising. Theoretical work has laid a rigorous foundation for Majorana teleportation protocols, and experimental advances in nanowire engineering, parity readout, and measurement-based logic are falling into place. Over the next decade, we expect to see this architecture applied to quantum repeater systems, topological quantum networks, and robust quantum error correction. While macroscopic teleportation of physical matter remains unattainable due to decoherence and scalability limits, Majorana-based teleportation of many-body quantum states in engineered systems could become a practical and powerful building block for scalable quantum technology.
9. Conclusions
The development of quantum teleportation protocols using Majorana fermions represents a transformative step toward building robust, scalable, and fault-tolerant quantum systems. Unlike conventional approaches that are vulnerable to environmental noise and require extensive error correction, Majorana-based systems offer intrinsic protection through topological encoding. This nonlocal nature enables stable quantum information transfer—even under decoherence—making them ideal candidates for next-generation quantum networks.
Over the last five years, both theoretical proposals and experimental achievements have laid a strong foundation for the realization of teleportation using Majorana zero modes. From phase-coherent transport experiments to quantum simulations and prototype hardware, the building blocks are coming into place.
However, substantial challenges remain. Creating scalable arrays of Majorana qubits, integrating them with photonic systems, and expanding their computational universality will require multidisciplinary collaboration across physics, materials science, and quantum engineering.
Despite these hurdles, the trajectory is clear: Majorana fermions have the potential to solve one of quantum computing’s greatest challenges—decoherence. By leveraging their exotic topological properties, we move closer to realizing not only stable quantum teleportation but also the infrastructure for a global quantum internet. This work provides a Clifford-level teleportation primitive in a measurement-only Majorana architecture; universality would require additional non-Clifford resources provided externally.
Author Contributions
Conceptualization, H.T.C.; methodology, H.T.C., D.E. and T.D.; investigation, D.E.; writing—original draft preparation, H.T.C.; writing—review and editing, T.D. and D.E.; supervision, H.T.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research supported by internal research funding and external funding by Department of Education: Fund #: P120A230072 and P031S240353.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Formal Theorems and Proofs in Majorana-Based Teleportation
Overview: This appendix rigorously presents the formal theorems and corresponding proofs relevant to measurement-only teleportation using Majorana zero modes (MZMs). All operations are assumed to act within the topologically protected logical subspace of non-Abelian anyons in a 1D topological superconductor [14]. Notation follows standard conventions in fermionic quantum information.
Let each logical qubit be encoded in a pair of MZMs: , and ,, such that the associated Dirac fermion is defined by: with logical states:
Preliminaries (measurement model used below). We model a non-selective, ideal QND measurement of the joint parity by the Lüders instrument .
Under the commuting assumption , the entropy property and identity action of are proved later (see Theorem A5, Equations (A18) and (A19)). We now analyze the selective outcome explicitly (projector action, normalization, and parity-conditioned Clifford correction).
Theorem A1.
Parity-Based Entanglement is Unitary on Logical Subspace
Statement: A projective parity measurement between Majorana qubits A and B preserves the logical subspace and can be interpreted as a unitary transformation followed by a known Pauli correction.
Proof of Theorem A1.
Let qubit A be encoded in Majorana modes , and qubit B in . The Dirac fermion operators are defined as: , . The logical basis states are: . A general two-qubit logical state is: . We now perform a parity measurement between (from A) and (from B) , using the operator:
with projectors:
The variable represents the measured eigenvalue (outcome) of the fermionic parity operator .
Let us apply to :
To compute this, use the fact that and . Thus:
Substitute back into the expression:
This is an unnormalized state. To normalize, compute the norm:
So, the normalized state is:
This procedure is consistent with the general rule for post-measurement states:
where is the projector onto the parity eigenspace and is the normalized post-measurement state. Up to a known phase, this is a unitary transformation of the original state within the logical subspace. A Pauli or correction (depending on measurement outcome) recovers the standard entangled form. Hence, the parity projection acts unitarily on the logical subspace, modulo a known correction. □
Theorem A2.
No-Cloning in Majorana-Based Teleportation
Statement: The teleportation process collapses the original qubit to a maximally mixed state, ensuring compliance with the quantum no-cloning theorem.
Proof of Theorem A2.
Consider teleportation of a qubit state from site A to site C via projective parity measurements. After applying correction at C, the state is reconstructed. However, the parity measurement collapses A’s state, resulting in a maximally mixed reduced state:
This ensures that no duplicate copy exists at A after the process, in full compliance with the quantum no-cloning theorem.
Let the initial state of the three-qubit system (A: source, B: ancilla, C: target) be:
This is a product of the input qubit and a maximally entangled Bell pair.
Apply joint parity measurements between A and B, and between B and C. These parity projections collapse the system onto an entangled subspace, transferring the quantum state from A to C up to a Pauli correction: where = and is an unentangled residual state.
To confirm that cloning does not occur, trace out B and C:
The reduced density matrix at site A is maximally mixed, regardless of .
Meanwhile, the output state at C is pure: . This demonstrates that although the quantum state has been reconstructed at C, no information remains at A. The process destroys the original and does not violate the no-cloning theorem. □
Theorem A3.
Measurement-Only Teleportation is Topologically Protected
Statement: The teleportation of a Majorana-encoded qubit using only joint parity measurements and Pauli corrections operates entirely within the topologically protected code space and is robust to local decoherence.
Proof of Theorem A3.
Teleporting qubit A () to qubit C () through an entangled pair B (,) involves only joint parity projections and Clifford corrections. The entire protocol remains within the topologically encoded code space.
Because MZMs are spatially separated by distance , and the system is protected by a superconducting gap , the fidelity is bounded as:
This implies robustness to thermal fluctuations and local decoherence, thus demonstrating the topological protection of the teleportation protocol. □
Lemma A1.
Local Operators Cannot Distinguish Logical States
Statement: Any operator acting on a single Majorana mode commutes with the logical parity and cannot distinguish between and .
Proof of Lemma A1.
Consider a qubit encoded using the Dirac fermion . The logical states are:
Let be a Hermitian operator that acts only on i.e., with no dependence on . Then:
Now consider the specific case . Observe:
Thus, maps , but it does not distinguish them—it flips the states rather than measuring them.
To see this more formally, consider the expectation values:
So, while (e.g., ) may transform logical states, it cannot extract information about which logical state the system is in. Therefore, no observable constructed from a single Majorana mode can resolve the logical basis—a signature of nonlocal encoding. □
Theorem A4.
Correction Operations Lie in the Clifford Group
Statement: All Pauli corrections resulting from parity measurement outcomes are elements of the Clifford group.
Proof of Theorem A4.
Consider a teleportation protocol involving three Majorana qubits A, B, and C, encoded using pairs of Majorana zero modes: , . The logical states are eigenstates of the Dirac occupation number operator , corresponding to even and odd fermion parity respectively.
The teleportation proceeds via two joint parity measurements:
- . Each has eigenvalues , yielding four possible combinations of outcomes. These projections collapse the total state into one of four correlated subspaces.
Let the initial state be:
After parity measurements, the resulting state (before correction) is of the form: where depends on the parity outcomes.
Since these correction operators are from the Pauli group , and the Pauli group is preserved under conjugation by Clifford gates, it follows that:
- The set of operations involved in this teleportation protocol (i.e., joint parity measurements and Pauli corrections) lies within the Clifford group .
By definition, the Clifford group is: Since each Pauli operator (including measurement-induced corrections) satisfies this property, we conclude: . Therefore, the entire teleportation protocol can be described by Clifford operations. □
Theorem A5.
Entropy Conservation Under Repeated QND Parity Measurements
Statement: For a state that is diagonal in the parity basis, repeated quantum non-demolition (QND) measurements with commuting parity operators do not increase entropy: .
Let be a parity operator with projectors
Assume the state ρ is diagonal in the parity basis (equivalently, ). An ideal, non-selective QND parity measurement is described by the Lüders map
Then the von Neumann entropy is invariant:
Proof.
Since , we also have . Decompose . Because ==0, the cross terms vanish and . Hence the Lüders map leaves the state unchanged, , so , proving Equation (A19). □
Theorem A6.
Entropy Invariance After Ideal QND Parity Measurement
Statement: Let be the state of a system encoded in the parity subspace of two spatially separated Majorana zero modes , , and let be the fermionic parity operator. Consider a non-selective, ideal QND parity measurement of (implemented by a pointer model with no residual system–meter entanglement, or equivalently by the Lüders instrument). Assume (i.e., is block-diagonal in the parity basis). Then the post-measurement state satisfies
where is the von Neumann entropy.
Proof.
Let the parity operator be
Its projectors onto the parity eigenspaces are
Because , is block-diagonal in the parity basis and can be written as
A non-selective ideal QND measurement of PPP updates the state by the Lüders rule,
Comparing Equations (A22) and (A23) gives , hence . □
Remark A1.
Outside the ideal QND conditions (e.g., if or residual system–meter correlations remain), the general statement is , not equality.
Physical Interpretation:
- The QND parity measurement does not extract or disturb quantum coherence within the parity eigenspace.
- The measurement apparatus does not entangle with the system, and hence no entropy is transferred to the environment.
- Since Majorana qubits are encoded in parity subspaces, the information is immune not just to local perturbations (decoherence) but also to entropy leakage.
Summary: This result shows that Majorana parity measurements are thermodynamically reversible in ideal QND settings, enabling quantum logic operations that preserve entropy. This contrasts with conventional measurement models, where entropy increases due to wavefunction collapse or entanglement with the measuring device.
References
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge Univ. Press: Cambridge, UK, 2000. [Google Scholar]
- Pirandola, S.; Eisert, J.; Weedbrook, C.; Furusawa, A.; Braunstein, S.L. Advances in quantum teleportation. Nat. Photonics 2015, 9, 641–652. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.W.; Mattle, K.; Eibl, M.; Weinfurter, H.; Zeilinger, A. Experimental quantum teleportation. Nature 1997, 390, 575–579. [Google Scholar] [CrossRef]
- Riebe, M.; Häffner, H.; Roos, C.F.; Hänsel, W.; Benhelm, J.; Lancaster, G.P.T.; Körber, T.W.; Becher, C.; Schmidt-Kaler, F.; James, D.F.V.; et al. Deterministic quantum teleportation with atoms. Nature 2004, 429, 734–737. [Google Scholar] [CrossRef]
- Furusawa, A.; Sørensen, J.L.; Braunstein, S.L.; Fuchs, C.A.; Kimble, H.J.; Polzik, E.S. Unconditional quantum teleportation. Science 1998, 282, 706–709. [Google Scholar] [CrossRef]
- Sangouard, N.; Simon, C.; De Riedmatten, H.; Gisin, N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 2011, 83, 33–80. [Google Scholar] [CrossRef]
- Wehner, S.; Elkouss, D.; Hanson, R. Quantum internet: A vision for the road ahead. Science 2018, 362, eaam9288. [Google Scholar] [CrossRef]
- Ryan-Anderson, C.; Brown, N.C.; Baldwin, C.H.; Dreiling, J.M.; Foltz, C.; Gaebler, J.P.; Gatterman, T.M.; Hewitt, N.; Holliman, C.; Horst, C.V.; et al. High-fidelity teleportation of a logical qubit using transversal gates and lattice surgery. Science 2024, 385, 1327–1331. [Google Scholar] [CrossRef] [PubMed]
- Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Fowler, A.G.; Mariantoni, M.; Martinis, J.M.; Cleland, A.N. Surface codes: Towards practical large-scale quantum computation. Phys. Rev. A 2012, 86, 032324. [Google Scholar] [CrossRef]
- Terhal, B.M. Quantum error correction for quantum memories. Rev. Mod. Phys. 2015, 87, 307–346. [Google Scholar] [CrossRef]
- Litinski, D. A Game of Surface Codes. Quantum 2019, 3, 128. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Physics-Uspekhi 2001, 44, 131–136. [Google Scholar] [CrossRef]
- Mourik, V.; Zuo, K.; Frolov, S.M.; Plissard, S.R.; Bakkers, E.P.A.M.; Kouwenhoven, L.P. Signatures of Majorana fermions in hybrid superconductor–semiconductor nanowire devices. Science 2012, 336, 1003–1007. [Google Scholar] [PubMed]
- Albrecht, S.M.; Higginbotham, A.P.; Madsen, M.; Kuemmeth, F.; Jespersen, T.S.; Nygård, J.; Krogstrup, P.; Marcus, C.M. Exponential protection of zero modes in Majorana islands. Nature 2016, 531, 206–209. [Google Scholar] [CrossRef] [PubMed]
- Aguado, R. Majorana quasiparticles in condensed matter. Riv. Nuovo Cimento 2017, 40, 523–593. [Google Scholar]
- Prada, E.; San-Jose, P.; de Moor, M.W.; Geresdi, A.; Lee, E.J.; Klinovaja, J.; Loss, D.; Nygård, J.; Aguado, R.; Kouwenhoven, L.P. From Andreev to Majorana bound states in hybrid superconductor–semiconductor nanowires. Nat. Rev. Phys. 2020, 2, 575–594. [Google Scholar] [CrossRef]
- Beenakker, C.W.J. Search for Majorana fermions in superconductors. Annu. Rev. Condens. Matter Phys. 2013, 4, 113–136. [Google Scholar] [CrossRef]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083–1159. [Google Scholar] [CrossRef]
- Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 2012, 75, 076501. [Google Scholar] [CrossRef]
- Esposito, M.; Harbola, U.; Mukamel, S. Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 2009, 81, 1665–1702. [Google Scholar] [CrossRef]
- Goold, J.; Huber, M.; Riera, A.; del Rio, L.; Skrzypczyk, P. The role of quantum information in thermodynamics—A topical review. J. Phys. A Math. Theor. 2016, 49, 143001. [Google Scholar] [CrossRef]
- Whiticar, A.M.; Fornieri, A.; O’Farrell, E.C.T.; Drachmann, A.C.C.; Wang, T.; Thomas, C.; Gronin, S.; Kallaher, R.; Gardner, G.C.; Manfra, M.J.; et al. Coherent transport through a Majorana island in an Aharonov–Bohm interferometer. Nat. Commun. 2020, 11, 3212. [Google Scholar] [CrossRef]
- Cheng, M.; Lutchyn, R.M.; Das Sarma, S. Topological protection of Majorana qubits. Phys. Rev. B 2012, 85, 165124. [Google Scholar] [CrossRef]
- Rainis, D.; Loss, D. Majorana qubit decoherence by quasiparticle poisoning. Phys. Rev. B 2012, 85, 174533. [Google Scholar] [CrossRef]
- Huang, H.-L.; Narożniak, M.; Liang, F.; Zhao, Y.; Castellano, A.D.; Gong, M.; Wu, Y.; Wang, S.; Lin, J. Emulating quantum teleportation of a Majorana zero mode qubit. Phys. Rev. Lett. 2021, 126, 090502. [Google Scholar] [CrossRef]
- Karzig, T.; Knapp, C.; Lutchyn, R.M.; Bonderson, P.; Hastings, M.B.; Nayak, C.; Alicea, J.; Flensberg, K.; Plugge, S.; Oreg, Y.; et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. Phys. Rev. B 2017, 95, 235305. [Google Scholar] [CrossRef]
- Majorana, E. Teoria simmetrica dell’elettrone e del positrone. Il Nuovo C. 1937, 14, 171–184. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, L. Topologically protected teleportation using Ising anyons. Quantum Inf. Process. 2022, 21, 107. [Google Scholar]
- Oreg, Y.; Refael, G.; von Oppen, F. Helical liquids and Majorana bound states in quantum wires. Phys. Rev. Lett. 2010, 105, 177002. [Google Scholar] [CrossRef]
- Aasen, D.; Aghaee, M.; Alam, Z.; Andrzejczuk, M.; Antipov, A.; Astafev, M.; Avilovas, L.; Barzegar, A.; Bauer, B.; Becker, J.; et al. Roadmap to fault tolerant quantum computation using topological qubit arrays. arXiv 2025, arXiv:2502.12252. [Google Scholar]
- Pandey, B.; Kaushal, N.; Alvarez, G.; Dagotto, E. Majorana zero modes in Y-shape interacting Kitaev wires. npj Quantum Mater. 2023, 8, 51. [Google Scholar] [CrossRef]
- Aasen, D.; Hell, M.; Mishmash, R.V.; Higginbotham, A.; Danon, J.; Leijnse, M.; Jespersen, T.S.; Folk, J.A.; Marcus, C.M.; Flensberg, K.; et al. Milestones Toward Majorana-Based Quantum Computing. Phys. Rev. X 2016, 6, 031016. [Google Scholar] [CrossRef]
- Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, T.P.; Gustavsson, S.; Oliver, W.D. A quantum engineer’s guide to superconducting qubits. Appl. Phys. Rev. 2019, 6, 021318. [Google Scholar] [CrossRef]
- Bonderson, P.; Freedman, M.; Nayak, C. Measurement-Only Topological Quantum Computation. Phys. Rev. Lett. 2008, 101, 010501. [Google Scholar] [CrossRef]
- Vijay, S.; Haah, J.; Fu, L. A new kind of topological quantum order: A dimensional hierarchy of quasiparticles built from stationary excitations. Phys. Rev. B 2016, 94, 235446. [Google Scholar] [CrossRef]
- Gharavi, K.; Hoving, D.; Baugh, J. Readout of Majorana parity states using a quantum dot. Phys. Rev. B 2016, 94, 155417. [Google Scholar] [CrossRef]
- Van Heck, B.; Akhmerov, A.R.; Hassler, F.; Burrello, M.; Beenakker, C.W.J. Coulomb-assisted braiding of Majorana fermions in a Josephson junction array. New J. Phys. 2012, 14, 035019. [Google Scholar] [CrossRef]
- Bonderson, P.; Freedman, M.; Nayak, C. Measurement-only topological quantum computation via anyonic interferometry. Ann. Phys. 2009, 324, 787–826. [Google Scholar] [CrossRef]
- Lutchyn, R.M.; Bakkers, E.P.A.M.; Kouwenhoven, L.P.; Krogstrup, P.; Marcus, C.M.; Oreg, Y. Majorana zero modes in superconductor–semiconductor heterostructures. Nat. Rev. Mater. 2018, 3, 52–68. [Google Scholar] [CrossRef]
- Schlosshauer, M. Decoherence and the Quantum-to-Classical Transition; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Gottesman, D.; Kitaev, A.; Preskill, J. Encoding a qubit in an oscillator. Phys. Rev. A 2001, 64, 012310. [Google Scholar] [CrossRef]
- Vinjanampathy, S.; Anders, J. Quantum thermodynamics. Contemp. Phys. 2016, 57, 545–579. [Google Scholar] [CrossRef]
- Allahverdyan, A.E.; Balian, R.; Nieuwenhuizen, T.M. Understanding quantum measurement from the solution of dynamical models. Phys. Rep. 2013, 525, 1–166. [Google Scholar] [CrossRef]
- Plugge, S.; Rasmussen, A.; Egger, R.; Flensberg, K. Majorana box qubits. New J. Phys. 2017, 19, 012001. [Google Scholar] [CrossRef]
- Deng, M.-T.; Vaitiekėnas, S.; Hansen, E.B.; Danon, J.; Leijnse, M.; Flensberg, K.; Nygård, J.; Krogstrup, P.; Marcus, C.M. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 2016, 354, 1557–1562. [Google Scholar] [CrossRef] [PubMed]
- Bravyi, S.; Kitaev, A. Universal quantum computation with ideal Clifford gates and noisy ancillas. Phys. Rev. A 2005, 71, 022316. [Google Scholar] [CrossRef]
- Dvir, T.; Wang, G.; van Loo, N.; Liu, C.-X.; Mazur, G.P.; Bordin, A.; Haaf, S.L.D.T.; Wang, J.-Y.; van Driel, D.; Zatelli, F.; et al. Realization of a minimal Kitaev chain in coupled quantum dots. Nature 2023, 614, 445–450. [Google Scholar] [CrossRef]
- Liu, C.X.; Dvir, T.; Zatelli, F.; Ten Haaf, S.L.; van Driel, D.; Wang, G.; Van Loo, N.; Zhang, Y.; Wolff, J.C.; Van Caekenberghe, T. Enhanced Majorana stability in a three-site Kitaev chain. Nat. Nanotechnol. 2025, 20, 726–731. [Google Scholar] [CrossRef] [PubMed]
- ten Haaf, S.L.D.; Zhang, Y.; Wang, Q.; Bordin, A.; Liu, C.-X.; Kulesh, I.; Sietses, V.P.M.; Prosko, C.G.; Xiao, D.; Thomas, C.; et al. Observation of edge and bulk states in a three-site Kitaev chain. Nature 2025, 641, 890–895. [Google Scholar] [CrossRef]
- Pandey, B.; Okamoto, S.; Dagotto, E. Nontrivial fusion of Majorana zero modes in interacting quantum-dot arrays. Phys. Rev. Res. 2024, 6, 033314. [Google Scholar] [CrossRef]
- Liu, D.E.; Cheng, M.; Lutchyn, R.M. Probing Majorana physics in quantum-dot shot-noise experiments. Phys. Rev. B 2015, 91, 081405. [Google Scholar] [CrossRef]
- van Loo, A.F.; Fedorov, A.; Lalumière, K.; Sanders, B.C.; Blais, A.; Wallraff, A. Photon-mediated interactions between distant artificial atoms. Science 2013, 342, 1494–1496. [Google Scholar] [CrossRef] [PubMed]
- Clarke, D.J.; Alicea, J.; Shtengel, K. Exotic circuit elements from zero-modes in hybrid superconductor–quantum-Hall systems. Nat. Phys. 2014, 10, 877–882. [Google Scholar] [CrossRef]
- Das Sarma, S.; Freedman, M.; Nayak, C. Majorana zero modes and topological quantum computation. npj Quantum Inf. 2015, 1, 15001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).