A Review on Models and Applications of Quantum Computing

Abstract

This manuscript is intended for readers who have a general interest in the subject of quantum computation and provides an overview of the most significant developments in the field. It begins by introducing foundational concepts from quantum mechanics—such as superposition, entanglement, and the no-cloning theorem—that underpin quantum computation. The primary computational models are discussed, including gate-based (circuit) quantum computing, adiabatic quantum computing, measurement-based quantum computing and the quantum Turing machine. A selection of significant quantum algorithms are reviewed, notably Grover’s search algorithm, Shor’s factoring algorithm, and Quantum Singular Value Transformation (QSVT), which enables efficient solutions to linear algebra problems on quantum devices. To assess practical performance, we compare quantum and classical implementations of support vector machines (SVMs) using several synthetic datasets. These experiments offer insight into the capabilities and limitations of near-term quantum classifiers relative to classical counterparts. Finally, we review leading quantum programming platforms—including Qiskit, PennyLane, and Cirq—and discuss their roles in bridging theoretical models with real-world quantum hardware. The paper aims to provide a concise yet comprehensive guide for those looking to understand both the theoretical foundations and applied aspects of quantum computing.

1. Introduction

Quantum computing finds its roots in the realization that information is fundamentally physical and must obey the laws of quantum mechanics. This idea was expressed when a reversible Turing machine governed by a quantum–mechanical Hamiltonian was described [1]. Richard Feynman observed that classical computers cannot efficiently simulate quantum systems and proposed the concept of a quantum simulator to overcome this boundary [2]. Later, David Deutsch formally proposed the idea of universal quantum computer, showing that quantum parallelism could at its core solve certain problems that are beyond reach of any classical Turing machine [3]. Regardless of these theoretical advancements, practical quantum hardware remained unreachable until the past decade, when improvements in qubit control, coherence time, and error mitigation led the way to Noisy Intermediate-scale Quantum (NISQ) era hardware. This hardware is characterized by systems with tens of to a few hundred qubits that lack full error correction but can perform nontrivial quantum behavior [4]. Currently, NISQ systems allow experimental discoveries of quantum algorithms in chemistry, optimization, and machine learning, even as researchers try to overcome noise and scalability problems. Industry and academia have already applied NISQ devices to simulate small molecules’ electronic structure, enabling potential breakthroughs in drug discovery and materials science by evaluating ground-state energies more efficiently than classical methods [5]. At the same time, combinatorial optimization problems, such as graph partitioning and portfolio optimization, have been tackled using the quantum approximate optimization algorithm (QAOA). This is a hybrid quantum classical approach which is particularly well suited for NISQ hardware [4,6]. Along with classical approaches, quantum machine learning can be advanced with variational quantum algorithms (VQAs) offering flexible frameworks for tasks such as classification and clustering by parametrizing quantum circuits and training them using classical optimizers [7]. On the quantum networking side, experimental distributed quantum computing was realized across an optical link between two modules separated by two meters. Grover’s search algorithm was executed as the first fully distributed quantum algorithm using quantum gate teleportation [8]. Existing review papers on quantum computing offer valuable insights into the field’s theoretical foundations, applications, and challenges. Gill et al. [9,10] provide a broad taxonomy and systematic review, emphasizing future directions across various domains. Paudel et al. [11] focus on energy applications, highlighting quantum simulations’ potential, while Rietsche et al. [12] outline quantum computing layers and application areas. Putranto et al. [13] analyze the quantum start-up ecosystem, and the Qiskit paper [14] details software tools for quantum computing. However, these reviews have limitations; they often lack comprehensive case studies, focus narrowly on specific sectors, omit detailed experimental comparisons, or are software-centric without broad industry analysis. The novelty of this review lies in its integration of theoretical foundations, computational models, core algorithms, and a detailed case study comparing quantum and classical SVMs using synthetic datasets. This experimental approach provides empirical insights into capabilities and limitations, addressing a gap in practical performance evaluation. Limitations include its reliance on simulated quantum data and lack of access to fault-tolerant hardware. The review spans works from the 1980s to recent advancements, providing a comprehensive historical and contemporary analysis. This paper is intended for a diverse audience, including researchers and students in computational science seeking a comprehensive understanding of quantum computing’s theoretical and practical aspects, engineers and developers interested in quantum software platforms and hardware applications, and industry professionals in fields like chemistry, optimization, and machine learning looking to explore quantum-enhanced solutions. The inclusion of a detailed case study and software ecosystem analysis makes it particularly valuable for practitioners aiming to bridge theory and real-world implementation.

2. Theoretical Foundations

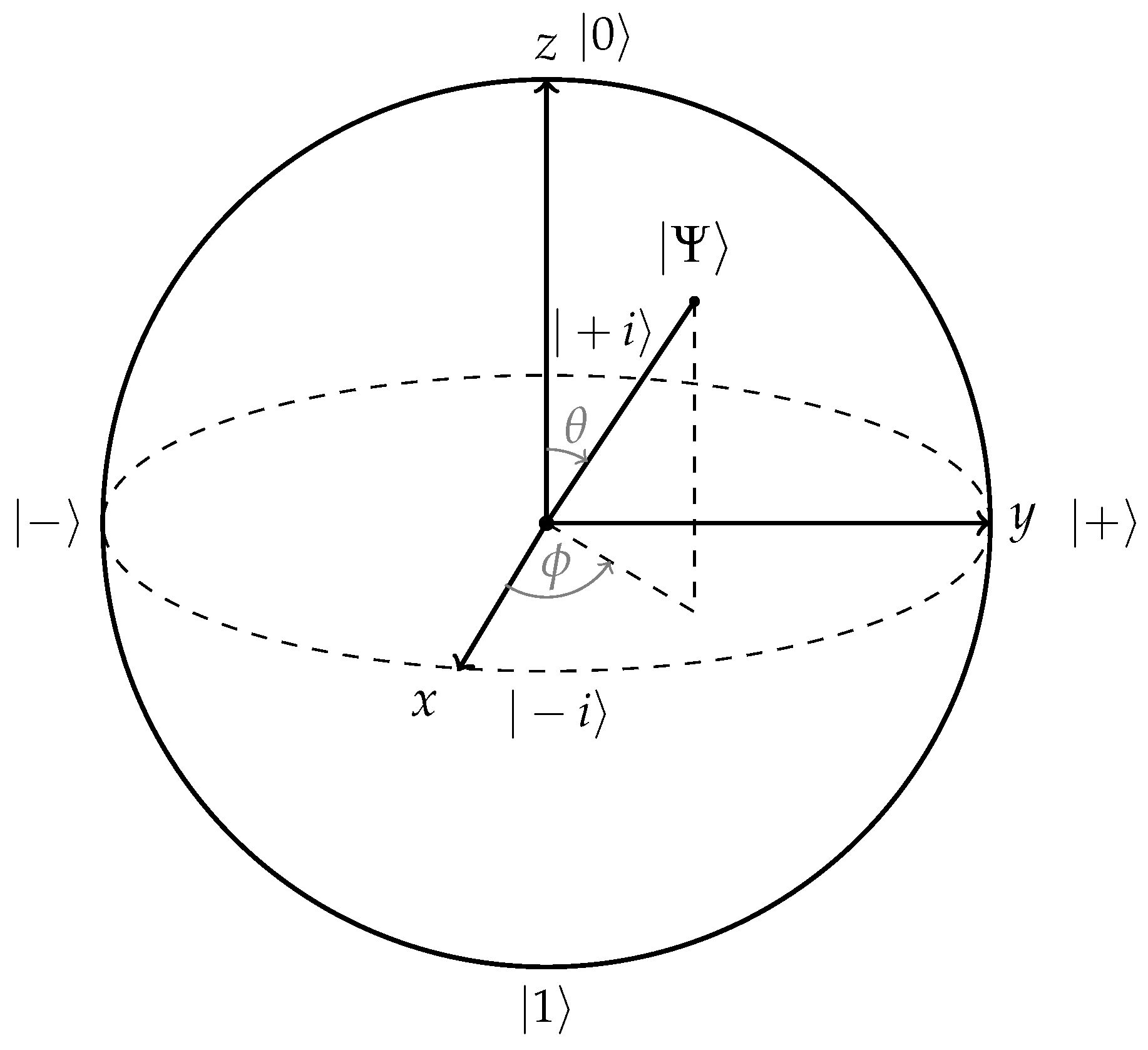
2.1. Qubits and Superposition

In classical computing we fundamentally distinguish two mutually exclusive physical states, which follow classical laws of physics, but with the development of quantum mechanics, we have an alternative view. What if these states can exist simultaneously? For a moment this could be counterintuitive; however, along with other things, quantum mechanics breaks boundaries. Imagine a solid barrier with two narrow, parallel slits cut into it; on one side of the barrier is placed an emitting device and on the other side is a capturing screen (image). The device starts to emit electrons towards the barrier one at a time; in terms of classical physics it is expected that the particle should pass either through the first or second slit. Eventually the screen should have two lines (projections of slits); however, instead, a dotted diffraction pattern is observed. This experiment shows the duality principle of electrons being both waves and particles. The interference pattern expresses a fundamental concept in quantum mechanics, the superposition. When a single electron approaches the slits, it does not pass through one of them. Instead it exists in a superposition and passes through both of them at the same time. The wave nature makes the electron interfere with itself. The detector device can be placed right before the slit entrance, to observe particles before they enter the slit. Surprisingly, while emitting several electrons, two lines are observed on the screen. This indicates that while an electron is being watched or measured, it collapses into one definite path, either the first or second slit, and behaves like a classical particle [15].

The mathematical definition of a quantum bit (qubit) in Dirac’s notation is as follows:

$$|\psi \rangle =\alpha |0\rangle +\beta |1\rangle ,$$

(1)

where $\alpha$ and $\beta$ are complex numbers and

$${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1.$$

(2)

(1) is a linear combination of states, otherwise known as the superposition of a state. Here the values of $\alpha$ and $\beta$ are called amplitudes of states and their modulus squares define the probability that after measurement, the state will collapse to the state $|0\rangle$ or $|1\rangle$. Naturally, the reader may come up with the questions of why the amplitude of a state is a complex number and why we should take its modulus square as a probability of the measuring state. First, the amplitudes are defined as complex numbers because the sum of two real numbers between 0 and 1 will always be greater than each of these numbers; in the case of complex numbers, it is not necessary that the sum is greater. In other words, complex numbers enable us to manipulate state probabilities not only by increasing but also by decreasing them, which in the case of real numbers is not possible [16]. To answer the second question, Born’s Rule states that the square of the magnitude of a particle’s wave function gives the probability density of finding the particle at a particular position when a measurement is made

$$P\left(a\right)={\left|\langle a|\mathrm{\Psi }\rangle \right|}^2,$$

(3)

where $\langle a|\mathrm{\Psi }\rangle$ is the inner product between the state $|a\rangle$ and the quantum state $|\mathrm{\Psi }\rangle$, which represents the system’s state before measurement. The idea of using the $L_2$ norm is important in the context of probability, as it should be in the range from 0 to 1. More importantly it satisfies the Schrödinger wave function equation:

$$iћ{\displaystyle \frac{\partial }{\partial t}}\mathrm{\Psi }(\mathbf{x},t)=\widehat{H}\mathrm{\Psi }(\mathbf{x},t),$$

(4)

where $\mathrm{\Psi }(\mathbf{x},t)$ is the wave function, $\widehat{H}$ is the Hamiltonian operator, and ћ is the reduced Planck constant and after arbitrary transformations the amplitude remains normalized [15]. Geometrically it is interpreted that the qubit’s state should be normalized to the length 1. In Figure 1 the unit vector $|\mathrm{\Psi }\rangle$ represents the state vector of a single qubit system (for obvious reasons it is not possible to represent a multi-qubit system in 3D space). The Bloch sphere maps a qubit’s state to a point on a unit sphere. The standard form $|\psi \rangle =cos(\theta /2)|0\rangle +e^{i\varphi }sin(\theta /2)|1\rangle$ uses $\theta /2$ to ensure that as $\theta$ goes from 0 to $\pi$, the state moves smoothly from $|0\rangle$ (north pole) to $|1\rangle$ (south pole) without repeating. A simpler form, $cos\theta |0\rangle +e^{i\varphi }sin\theta |1\rangle$, would cause a problem: at $\theta =\pi$, it gives $-|0\rangle$, which is equivalent to $|0\rangle$ (since global phase does not affect measurements), not $|1\rangle$. This would map the sphere twice, wasting space and misplacing states. The $\theta /2$ factor fixes this, making the sphere’s geometry match the qubit’s states perfectly, with opposite points representing orthogonal states like $|0\rangle$ and $|1\rangle$. Here, intuitively, if the vector is in the upper sphere, then with higher probability it will collapse into the basis state $|0\rangle$.

2.2. Entanglement

Another phenomenon of quantum physics which is hardly explained from a classical perspective is qubit entanglement. Given two qubits, all possible states of a system are

$$|00\rangle ,|01\rangle ,|10\rangle ,|11\rangle$$

(5)

or equivalently

$$|0\rangle ,|1\rangle ,|2\rangle ,|3\rangle .$$

Suppose that the first qubit is in an equally likely superposition,

$${\displaystyle \frac{|0\rangle +|1\rangle }{\sqrt{2}}}$$

(6)

and the second qubit is in the base state $|0\rangle$; then their combined state is a tensor product of individual states:

$${\displaystyle \frac{|0\rangle +|1\rangle }{\sqrt{2}}}\otimes |0\rangle ={\displaystyle \frac{|00\rangle +|10\rangle }{\sqrt{2}}}.$$

(7)

These qubits are separable as we can take out $|0\rangle$. Let us introduce a binary function called CNOT which negates qubits depending on controlled qubits. In other words, with highly controlled qubits, the target qubit is flipped. This function (actually the gate, covered in the next sections), applied to (7), evaluates the state as follows:

$${\displaystyle \frac{|00\rangle +|10\rangle }{\sqrt{2}}}\stackrel{\mathrm{CNOT}}{\to }{\displaystyle \frac{|00\rangle +|11\rangle }{\sqrt{2}}}.$$

(8)

Mathematically, the new state is not separable; no common qubits can be taken out. Physically this means that while measuring one of the qubits, the other also collapses into a definite state. For example, if the first bit is measured and it is 1, then without looking into the content of the second qubit, it can be stated that it is also 1; the same applies for the 0 state. It is proven that even if the qubits are separated in the distance, they still remain entangled. Examples of separable states include all computational basis states (5), as well as product superpositions such as (7) or

$$|1\rangle \otimes {\displaystyle \frac{|0\rangle -|1\rangle }{\sqrt{2}}},$$

(9)

in general form

$$\begin{array}{cc}\hfill & (\alpha |0\rangle +\beta |1\rangle )\otimes (\gamma |0\rangle +\delta |1\rangle )=\hfill \\ \hfill & \left(\alpha \gamma \right)|00\rangle +\left(\alpha \delta \right)|01\rangle +\left(\beta \gamma \right)|10\rangle +\left(\beta \delta \right)|11\rangle .\hfill \end{array}$$

(10)

where ${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1$ and ${\left|\gamma \right|}^2+{\left|\delta \right|}^2=1$. On the other hand, a state is entangled if it cannot be factorized into a product of states of its individual subsystems. The canonical maximally entangled states for two qubits are the Bell states:

$$|{\mathrm{\Phi }}^{\pm }\rangle ={\displaystyle \frac{|00\rangle \pm |11\rangle }{\sqrt{2}}},|{\mathrm{\Psi }}^{\pm }\rangle ={\displaystyle \frac{|01\rangle \pm |10\rangle }{\sqrt{2}}}.$$

(11)

With this definition, if a quantum state is entangled, it exhibits correlations between its subsystems that cannot be explained by any local, classical means and are a direct result of the quantum entanglement. From a statistical perspective, entanglement can be described using the density matrix formalism. The density matrix unifies key quantum properties, namely, entanglement, coherence, and entropic uncertainty, and provides alternative state representation. The density matrix $\rho$, satisfying $Tr\left(\rho \right)={\sum }_i\langle i\left|\rho \right|i\rangle =1$, describes a system’s state, both for single qubits and multi-qubit systems. A pure state, similar to a single qubit (6) or a two-qubit Bell state (11), is a fully known quantum state with no uncertainty, represented by

$$\rho =|\psi \rangle \langle \psi |$$

(12)

and satisfying $Tr\left({\rho }^2\right)=1$. In contrast, a mixed state, caused by noise or incomplete knowledge, is an ensemble of pure states:

$$\rho =\sum _i{p}_i|{\psi }_i\rangle \langle {\psi }_i|$$

(13)

where $p_i$ are probabilities representing the likelihood of the system being in each pure state $|{\psi }_i\rangle$ with $Tr\left({\rho }^2\right)<1$, indicating uncertainty. A separable state or any product state is independent and can be written as a tensor product, ${\rho }_{AB}={\rho }_A\otimes {\rho }_B$. However, entangled states, such as the maximally entangled Bell states (11), link qubits; therefore, measuring one instantly affects the other, and ${\rho }_{AB}\ne {\rho }_A\otimes {\rho }_B$. In case of an entangled pair, the individual qubits states can be expressed by the reduced density matrix ${\rho }_A$ or ${\rho }_B$ as subsystems. The main advantage of the density matrix formalism is that it allows us to describe entangled states and their subsystems, whereas using the state vector representation, the individual qubit states are uncertain and correlated and therefore cannot be written. For example, for two-qubit system in the state $|{\mathrm{\Phi }}^{+}\rangle$, the density matrix is given by

$$\begin{array}{cc}\hfill {\rho }_{AB}& =|{\mathrm{\Phi }}^{+}\rangle \langle {\mathrm{\Phi }}^{+}|=\hfill \\ \hfill & {\displaystyle \frac{1}{2}}(|00\rangle \langle 00|+|00\rangle \langle 11|+|11\rangle \langle 00|+|11\rangle \langle 11|)\hfill \end{array}$$

(14)

or in matrix form:

$${\rho }_{AB}={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}1& 0& 0& 1\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 1& 0& 0& 1\end{array}\right]$$

(15)

Using the reduced density matrix, the individual qubit state can be expressed as ${\rho }_A=T{r}_B\left({\rho }_{AB}\right)$, and it is obtained by summing over B’s states using the partial trace, averaging over B to isolate A’s state:

$${\rho }_A={\mathrm{Tr}}_B\left({\rho }_{AB}\right)={\displaystyle \frac{1}{2}}\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$

(16)

This ${\rho }_A$ becomes mixed ($Tr\left({\rho }_A^2\right)<1$) for entangled states, unlike pure separable states. In open systems, noise affects ${\rho }_{AB}$ via the master equation:

$${\displaystyle \frac{d\rho }{dt}}=-{\displaystyle \frac{i}{ћ}}[H,\rho ]+\mathcal{L}\left(\rho \right),$$

(17)

where H drives qubit–resonator coupling and $\mathcal{L}\left(\rho \right)$ models noise, namely, amplitude damping and dephasing [17,18]. This causes entanglement to oscillate, decay, or revive under detuning, which is a frequency mismatch between qubits and resonators.

The ability to preserve superpositions is measured by the coherence $L_1$-norm $C_{L_1}\left(\rho \right)={\sum }_{i\ne j}\left|{\rho }_{ij}\right|$, where ${\rho }_{ij}$ are off-diagonal elements. Noise reduces these elements, making ${\rho }_{AB}$ more classical and less quantum. This loss is connected to entropic uncertainty, which measures unpredictability in measuring two properties, like spin in X and Z directions. It is given by

$$H\left(X\right|B)+H\left(Z\right|B)\ge {log}_2{\displaystyle \frac{1}{c}}+S\left(A\right|B),$$

(18)

where $H\left(X\right|B)=S\left({\rho }_{XB}\right)-S\left({\rho }_B\right)$ is the conditional entropy. $H\left(X\right|B)$ quantifies uncertainty in measuring observable X on qubit A given access to qubit B’s state, with ${\rho }_{XB}$ denoting the joint state after measuring X [19]. Here, $S\left(\rho \right)=-Tr\left(\rho {log}_2\rho \right)$ is the von Neumann entropy, measuring disorder in $\rho$. The term c is compatibility, indicating how much X and Z overlap, and $S\left(A\right|B)=S\left({\rho }_{AB}\right)-S\left({\rho }_B\right)$ decreases with entanglement, tightening the uncertainty bound. Noise diminishes entanglement and coherence, at the same time increasing entropy and uncertainty. However, detuning can revive these quantum features by preserving ${\rho }_{AB}$’s structure. This relationship, encoded in $\rho$, is essential for robust quantum computation. The discussion of entanglement has primarily focused on its theoretical formalisms. Another crucial aspect concerns the generation and control of entanglement in practice, particularly through nonlinear interactions in physical systems. In quantum physics, nonlinear processes are interactions between quantum systems, such as qubits, resonators, and oscillators, where a small change in one system causes large, complex, or unpredictable effects in another. Nonlinear processes in quantum entanglement provide powerful mechanisms both for generating and controlling entangled states on optical, mechanical, and hybrid platforms. The main method for entangled photon generation is the second-order ${\chi }^2$ process known as spontaneous parametric down-conversion (SPDC), where a high-energy pump photon is converted inside a nonlinear crystal into two lower-energy photons whose properties are quantum-correlated [20,21]. Recent integrated implementations achieve high-brightness, narrow-band emission in CMOS-compatible devices [22]. Theoretical advances now enable nonperturbative treatment of SPDC in the high-gain regime, expanding its applicability to on-chip and multimode scenarios [23]. Beyond ${\chi }^2$ interactions, third-order (${\chi }^3$) Kerr nonlinearities have been harnessed to mediate deterministic entangling gates in photonic circuits [24] and to enhance bipartite entanglement in hybrid magnon–photon systems [25], while Duffing-type mechanical nonlinearities can increase steady-state entanglement in optomechanical setups [26]. Advances in engineered materials, including ultrathin van der Waals heterostructures [27] and nanophotonic platforms [28], have significantly boosted nonlinear interaction strengths, enabling brighter and more scalable entanglement sources. Comprehensive theoretical frameworks that incorporate multimode structure and mode-matching considerations [29] are increasingly essential for accurately modeling and optimizing these nonlinear entanglement processes.

2.3. No-Cloning Theorem

Copying is one of the fundamental operations in computer science; however, surprisingly, quantum mechanics does not allow such operation [30,31]. Suppose that we have a given state, $|\psi \rangle ={\displaystyle \frac{|00\rangle +|11\rangle }{\sqrt{2}}}$. Clearly, if the first qubit is 0, then the second qubit is also evaluated to 0 (the same for the case with 1). However, what if the state of the second qubit is also an arbitrary state? Suppose that we have the arbitrary two qubit system state

$$|\psi \rangle \otimes |e\rangle$$

Then applying some function, U (which can be treated as Hamiltonian applied to a state), the content of the second qubit will be evaluated to the content of the first qubit or equivalently

$$U|\psi \rangle \otimes |e\rangle =|\psi \rangle \otimes |\psi \rangle .$$

(19)

Now let us show that it is not possible to come up with such a Hamiltonian, U. Assuming that there is such a Hamiltonian, U, and the states $|{\psi }_1\rangle ,|{\psi }_2\rangle$, then the following must hold:

$$U|{\psi }_1\rangle \otimes |e\rangle =|{\psi }_1\rangle \otimes |{\psi }_1\rangle$$

(20)

$$U|{\psi }_2\rangle \otimes |e\rangle =|{\psi }_2\rangle \otimes |{\psi }_2\rangle$$

(21)

Next, let us define the linear superposition

$$|\varphi \rangle =\alpha |{\psi }_1\rangle +\beta |{\psi }_2\rangle$$

Applying the U Hamiltonian,

$$U|\varphi \rangle \otimes |e\rangle =U(\alpha |{\psi }_1\rangle +\beta |{\psi }_2\rangle )\otimes |e\rangle$$

Then, by linearity,

$$U|\varphi \rangle \otimes |e\rangle =\alpha U|{\psi }_1\rangle \otimes |e\rangle +\beta U|{\psi }_2\rangle \otimes |e\rangle .$$

Substituting (20) and (21),

$$U|\varphi \rangle \otimes |e\rangle =\alpha |{\psi }_1\rangle \otimes |{\psi }_1\rangle +\beta |{\psi }_2\rangle \otimes |{\psi }_2\rangle$$

(22)

but if cloning were truly possible, then the state should be

$$|\varphi \rangle \otimes |\varphi \rangle =(\alpha |{\psi }_1\rangle +\beta |{\psi }_2\rangle )\otimes (\alpha |{\psi }_1\rangle +\beta |{\psi }_2\rangle )$$

$$\begin{array}{c}\hfill ={\alpha }^2|{\psi }_1\rangle \otimes |{\psi }_1\rangle +\alpha \beta |{\psi }_1\rangle \otimes |{\psi }_2\rangle \\ \hfill +\beta \alpha |{\psi }_2\rangle \otimes |{\psi }_1\rangle +{\beta }^2|{\psi }_2\rangle \otimes |{\psi }_2\rangle \end{array}$$

which contradicts (22). This expression includes the cross-terms $\alpha \beta |{\psi }_1\rangle \otimes |{\psi }_2\rangle$ and $\beta \alpha |{\psi }_2\rangle \otimes |{\psi }_1\rangle$, which are absent in (22). For these expressions to be equivalent for arbitrary $|{\psi }_1\rangle$ and $|{\psi }_2\rangle$, the tensor product would need to exhibit a commutative isomorphism, meaning that the order of states in the tensor product (e.g., $|{\psi }_1\rangle \otimes |{\psi }_2\rangle$ vs. $|{\psi }_2\rangle \otimes |{\psi }_1\rangle$) would not affect the result. However, quantum mechanics does not permit such commutativity for arbitrary states, leading to a contradiction. Thus, no unitary U can clone arbitrary quantum states, proving the no-cloning theorem. This limitation poses a significant challenge in quantum computing, where manipulating quantum states is central. Unlike classical computing, where data can be duplicated for backups or checkpoints, the inability to clone quantum states prevents such operations, complicating error correction and state recovery during computations. At the same time, this limitation can be leveraged for certain quantum protocols, such as Quantum Secure Direct Communication (QSDC), a protocol for securely transmitting messages without a separate key exchange; quantum states are encoded into the polarization of photons and transported via optical fibers [32]. Recent advancements in QSDC demonstrate its potential for secure communication using photonic qubits. A device-independent QSDC protocol, utilizing high-efficiency single-photon sources and a heralded entanglement architecture, achieves secure communication over distances approximately six times longer than those of earlier protocols, with efficiency improved by a factor of 600 [33]. Additionally, a hybrid entanglement-based QSDC protocol combines continuous and discrete variable encoding, leveraging simple linear optical elements to enhance communication efficiency and fidelity, maintaining security for bit error rates below 0.073 [34]. Unlike classical systems, where data duplication is straightforward, the no-cloning constraint in quantum computing leads to novel approaches to error correction and state management.

3. Quantum Computation Models

3.1. Gate Model

Operations on qubits are performed by some model of computation, which aligns with quantum mechanics rules. As in classical computing, quantum computing also defines a gate model of computation [35]. First, all the operations should be performed by unitary operators, meaning that $U{U}^{†}=I$. This states that every operation is reversible, which is a fundamental rule in quantum mechanics [36]. In the context of logical operations on qubits (logical gates), this reversibility implies that for a given set of output qubit states, it is possible to unambiguously recover the input set of qubit states. Unitarity ensures that during time the total probability of the system is preserved and no information is lost while performing operations. The most essential gate is the Hadamard gate, a single-qubit gate, H, which is defined as

$$H={\displaystyle \frac{1}{\sqrt{2}}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]$$

(23)

This gate is the first step in quantum circuit design as it creates an equally likely superposition state given the initial qubit

$$\begin{array}{cc}\hfill H|0\rangle & ={\displaystyle \frac{1}{\sqrt{2}}}\left(\right|0\rangle +|1\rangle ),\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill H|1\rangle & ={\displaystyle \frac{1}{\sqrt{2}}}\left(\right|0\rangle -|1\rangle )\hfill \end{array}$$

(25)

for $|0\rangle$, $|1\rangle$ basis states, respectively. It is easy to verify that the gate is unitary and reversible, $H{H}^{†}=I$. The phase shift operator is the next building block. It is defined as

$$R_{\theta }=\left[\begin{array}{cc}1& 0\\ 0& e^{i\theta }\end{array}\right]$$

(26)

or, equivalently,

$$R_{\theta }|0\rangle =|0\rangle ,R_{\theta }|1\rangle =e^{i\theta }|1\rangle$$

(27)

This operator shifts the phase of the state; on the Bloch sphere (Figure 1), the change affects the $\varphi$ angle, leaving $\theta$ the same. After applying phase shift, the probability does not change; however, the state is modified in phase. The Pauli-X gate is a basic single-qubit operation, which is known as the quantum NOT gate. It flips the state of a qubit from $|0\rangle$ to $|1\rangle$ and vice versa:

$$X=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right],X|0\rangle =|1\rangle ,X|1\rangle =|0\rangle .$$

(28)

Geometrically, on the Bloch sphere, the Pauli-X gate represents a rotation by $\pi$ radians around the X-axis. Next is the CNOT gate which was mentioned earlier in the entanglement discussion. Given two qubit inputs, the first qubit acts as a controlling qubit and the second as a target qubit in the computational basis $\left\{\right|0\rangle ,|1\rangle \}$. However, the designation of control and target qubits can depend on the basis used. For example, in the Hadamard-transformed basis $\left\{\right|+\rangle ,|-\rangle \}$, the roles interchange, the state of the second qubit remains unchanged, while the state of the first qubit is flipped based on the state of the second qubit. In practice, this basis dependence is accounted for by carefully designing quantum circuits in the standard computational basis, where the control and target roles are well defined and transform to other bases only when necessary through additional gates like Hadamard gates applied before and after CNOT. In a matrix form, CNOT is defined:

$$\mathrm{CNOT}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 1& 0\end{array}\right],$$

(29)

When the first qubit is $|1\rangle$, the second qubit is flipped; otherwise, it remains unchanged. Alternatively, CNOT can be interpreted as the XOR of qubits written as target qubits:

$$\mathrm{CNOT}\left(|a\rangle \otimes |b\rangle \right)=|a\rangle \otimes |a\oplus b\rangle$$

(30)

The general controlled-U gate is defined as follows. If the control qubit is $|0\rangle$, the unitary U is not applied; otherwise, the gate is applied to the target qubit:

$$|0\rangle \otimes |x\rangle \mapsto |0\rangle \otimes |x\rangle ,|1\rangle \otimes |x\rangle \mapsto |1\rangle \otimes U|x\rangle .$$

(31)

The Toffoli gate is an extended version of CNOT with three input qubits. Given three input bits, if the first two are $|1\rangle$, then the last is flipped; otherwise, it remains the same.

$$|x,y,z\rangle \mapsto |x,y,z\oplus (x·y)\rangle .$$

(32)

and the corresponding 8 × 8 matrix is

$$\mathrm{Toffoli}=\left[\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 0& 1& 0\end{array}\right].$$

(33)

3.2. Quantum Adiabatic Model

The quantum adiabatic model (QAM) of computation is based on adiabatic theory [37]. Given a quantum system described by the Schrödinger Equation (4), the theory states that if the system starts in the ground state ${\mathrm{\Psi }}_I$ of an initial Hamiltonian, $H_I$, at time $t=0$ and the Hamiltonian changes sufficiently slowly to $H_T$ at time $t=T$, then the system will remain in the ground state of the final Hamiltonian $H_T$. The function of $H\left(t\right)$ can be formulated as

$$H\left(t\right)=(1-{\displaystyle \frac{t}{T}})H_I+{\displaystyle \frac{t}{T}}{H}_T.$$

(34)

This method of computation is generally used in optimization problems where the optimal solution is hard to find. The first general algorithm was demonstrated on the 3-SAT problem [38]. Later, it was shown that the adiabatic model is polynomially equivalent to gate model [39]. However, the main challenge is how slowly the Hamiltonian must evolve to ensure that the system reaches the optimal final state. This requirement poses practical difficulties in implementing adiabatic quantum systems [40]. The formal computational cost of the adiabatic algorithm is determined by the total evolution time T, which scales as $T\sim 1/{\mathrm{\Delta }}_{min}^2$, where ${\mathrm{\Delta }}_{min}$ is the minimal spectral gap along the Hamiltonian path, to ensure that the system remains in the ground state with high probability [41]. This cost is intimately connected to the spectral gap, as the adiabatic theorem requires the evolution to be sufficiently slow relative to ${\mathrm{\Delta }}_{min}$, specifically satisfying $T\gg {max}_t\left|{\displaystyle \frac{dH}{dt}}\right|/{\mathrm{\Delta }}_{min}^2$, where smaller gaps necessitate longer times to avoid excitations [41,42]. In the context of simulating a quantum circuit with L gates using the adiabatic model, the minimal gap scales as ${\mathrm{\Delta }}_{min}\sim {\pi }^2/\left[8{(L+1)}^2\right]$ for large L, leading to a polynomial evolution time, $T\sim \mathrm{poly}\left(L\right)$, that establishes polynomial equivalence between the adiabatic and gate models [43]. The Hamiltonian must evolve slowly enough to maintain adiabaticity, with the required slowness inversely proportional to the square of the spectral gap, posing challenges when ${\mathrm{\Delta }}_{min}$ closes exponentially for hard optimization instances [44]. Key drawbacks of the QAM include exponentially small spectral gaps in problems with first-order phase transitions, leading to prohibitively long evolution times, sensitivity to decoherence and thermal noise that can excite the system out of the ground state, and classical simulability in certain regimes, such as one-dimensional systems with constant gaps or stoquastic Hamiltonians without a sign problem [41,45]. Suggestions to mitigate these drawbacks involve shortcuts to adiabaticity via counter-diabatic driving to suppress transitions, diabatic annealing protocols that allow controlled excitations for faster convergence, variational quantum adiabatic algorithms (VQAAs) that optimize nonlinear paths using gradient-based methods to reduce time by factors of ∼10 while maintaining high fidelity, and reinforcement learning to design adaptive Hamiltonian schedules that enhance success probabilities, as demonstrated for the 3-SAT and Grover search problems [42,44,46,47].

3.3. Measurement-Based Quantum Computation

Measurement-based quantum computation (MBQC), also known as one-way quantum computation, is a model of quantum processing where universal computation is achieved through adaptive single-qubit measurements in a pre-entangled multi-qubit resource state, rather than sequential unitary gates. In MBQC, computation starts with a special quantum state called a cluster state, which is a grid of qubits all tangled together in a highly organized way, created by applying specific controlled-phase gates to a starting state where all qubits are in a $|+\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(\right|0\rangle +|1\rangle )$ state. Mathematically, a cluster state on a lattice is defined by stabilizers, which are rules like

$$K\left(a\right)={\sigma }_x^{\left(a\right)}\prod _{b\in \mathrm{nbgh}\left(a\right)}{\sigma }_z^{\left(b\right)}{|\mathrm{\Phi }\rangle }_C={|\mathrm{\Phi }\rangle }_C,$$

(35)

where ${\sigma }_x$ and ${\sigma }_z$ are Pauli operators and $\mathrm{nbgh}\left(a\right)$ are neighboring qubits on the grid; this setup ensures the qubits are deeply entangled, meaning that their states are interconnected [48,49]. Computation takes the following process; each qubit, one by one, is measured in a specific basis, and these measurements control the quantum state for performing calculations, with results adjusted using simple corrections (applying ${\sigma }_x$ or ${\sigma }_z$ based on random measurement outcomes) to obtain the desired answer [50]. MBQC’s advantages are the following: it is used for systems with photons or trapped ions where creating entanglement upfront is easier than applying gates repeatedly, it can perform many operations at once to speed things up (certain calculations collapse nearly instantly), and it works with error-correcting codes to protect against mistakes [51]. However, there are downsides; a huge number of qubits are used (sometimes thousands more than those in other methods), measurements destroy the state and, therefore, a new one needs to be created each time, and choosing the right measurement angles in noisy conditions is tricky [49]. Compared to the gate model, MBQC simplifies hardware needs but uses more qubits; unlike adiabatic quantum computing, MBQC is faster but sensitive to measurement errors [52]. Recent advancements make MBQC even more promising; for example, new methods use continuous-variable systems (like light waves) with special error-correcting codes (GKP codes) to achieve fault tolerance with a squeezing threshold of 12.7 dB, meaning that they can handle errors well in photonic systems [53]. Other advances include efficient designs using color-code states for simpler hardware [54], low-overhead error correction with Gaussian operations [55], and even combining MBQC with machine learning to generate complex data patterns [56]. These developments show MBQC’s potential in future quantum computers, especially for systems where measurements are easier than gates, though it still needs work to reduce qubit demands and handle noise effectively [50].

3.4. Quantum Turing Machine

With an advancement in quantum mechanics, researchers began rethinking the Church–Turing thesis. The thesis states that each problem, naturally regarded as computable, can be simulated by a Turing machine. Furthermore, the universal Turing machine showed that a single machine could simulate any other Turing machine. However, a question arose: whether this classical model was sufficient when considering the physical world, which is governed by quantum mechanics. Eventually, a new formulation of the Church–Turing thesis was proposed accounting quantum mechanics, which states that “Every finitely realizable physical system can be perfectly simulated by a universal model computing machine operating by finite means [3]”. Deutsch [3] defines a finite processor which consists of two-state observables, $\left\{{\widehat{n}}_i\right\}$. The tape is infinite with the two-state observables $\left\{{\widehat{m}}_i\right\}$. The computation is fixed in time, T, during which the processor and finite part of the memory tape interact. The observable $\left\{\widehat{x}\right\}$ represents the address of the tape at which the reading head is currently located. The state of the machine is determined by the superposition $|x,n,m\rangle$ which is in the composite Hilbert space of $\mathcal{H}={\mathcal{H}}_{\mathrm{control}}\otimes {\mathcal{H}}_{\mathrm{tape}}\otimes {\mathcal{H}}_{\mathrm{head}}$. The transition, as in the Turing machine, is the evolution of the quantum state governed by a unitary operator, U, which acts on the entire system, namely, the control, tape, and head. It is crucial to note that two consecutive states cannot be identical after non-trivial evolution of the system. Moreover, the state should not be observed before the end of computation as it will collapse and remaining transformations would not be possible to resume. To signal that the computation is halted, a separate bit is needed in the processor ${\widehat{n}}_0$. If the program is valid, then $n_0$ is set to 1 to indicate halting; otherwise, no interaction is needed. Therefore, periodically observing this qubit, we can determine when to measure the state and finish the computation. Later, Berstein and Vizari [57] proposed a widely accepted formal definition of the quantum Turing machine (QTM) as follows:

$$M=(Q,\mathrm{\Sigma },\delta ,q_0,q_{\mathrm{accept}},q_{\mathrm{reject}},\mathcal{H})$$

(36)

where

• Q is a finite set of internal (control) states;
• $\mathrm{\Sigma }$ is a finite tape alphabet containing a blank symbol, #;
• $\delta$ is the transition function, a map defining amplitudes of transitions:

  $$\delta :Q\times \mathrm{\Sigma }\times Q\times \mathrm{\Sigma }\times \{L,R\}\to \mathbb{C}$$
• $q_0\in Q$ is the initial state;
• $q_{\mathrm{accept}}\in Q$ is the accepting state;
• $q_{\mathrm{reject}}\in Q$ is the rejecting state ($q_{\mathrm{accept}}\ne q_{\mathrm{reject}}$);
• $\mathcal{H}$ is the Hilbert space spanned by basis states:

  $$|q,x,h\rangle$$

  where $q\in Q$, $x\in {\mathrm{\Sigma }}^{\mathbb{Z}}$ is the tape content, and $h\in \mathbb{Z}$ is the position of the head.

The major difference between Deutsch’s proposal is that this a QTM allows the U operator and system state to be defined by complex numbers rather than positive reals. Furthermore, Bounded-error Quantum Polynomial (BQP) time class of decision problems was introduced, which is the quantum equivalent of classical Bounded-error Probabilistic Polynomial (BPP) time. Additionally, a universal QTM was shown, capable of simulating any other QTM machine with only polynomial slowdown [57].

4. Quantum Algorithms

4.1. Quantum Search

Classically, we are bound linearly to find some element in an arbitrary array, which means that we should look through each element and compare it with our sample. However, in quantum settings, this can be performed more effectively. For simplicity, $N=2^n$; in other words, with N elements, they are encoded by n qubits. Let us define a function, $f:{\{0,1\}}^n\to \{0,1\}$, such that there exists exactly one binary string, $x_0$, for wich $f\left(x_0\right)=1$, and for the rest, $x\ne x_0$, $f\left(x\right)=0$. The general idea of the algorithm is to amplify the target state amplitude and measure it. First, the superposition of n qubits is prepared by applying the Hadamard gate to each qubit. Then, applying the phase inversion or $U_f$ gate, the amplitude of the desired state is inverted:

$$U_f|x\rangle |t\rangle =|x\rangle |t\oplus f\left(x\right)\rangle$$

(37)

where $f\left(x\right)$ encodes desired target state. After this operation, all the amplitudes remain unchanged except the target’s, which is inverted. If the measurement is conducted at this point, it will not be possible to differentiate the target since, although it became inverted, the probability of measuring it remains equally likely compared with that of bad states. The next step is to apply a diffusion operator or inversion about the mean. This operator is defined as

$$D=2|\psi \rangle \langle \psi |-I$$

(38)

where $|\psi \rangle$ is the equal superposition state:

$$|\psi \rangle ={\displaystyle \frac{1}{\sqrt{N}}}\sum _{x=0}^{N-1}|x\rangle$$

(39)

The effect of this operator is that all amplitudes are inverted around the mean. As a result, our target amplitude is amplified and the bad states’ amplitudes are shrinked. However, applying these two operators once does not guarantee that after measurement the desired state will collapse. It was proven that approximately $\sqrt{N}$ iterations should be performed to amplify the target state, making the algorithm $\mathcal{O}\left(\sqrt{N}\right)$ complex [58]. Later, a multiple-target approach was shown which extends quantum search with the possibility of multiple targets present in array; in this case the number iterations becomes smaller and overall complexity becomes $\mathcal{O}\left(\sqrt{N/t}\right)$ where t is the number of solutions [59]. Moreover, it was proven that any quantum algorithm needs at least $\mathrm{\Omega }\left(\sqrt{N}\right)$ queries to solve the unstructured search problem, with N elements [60].

4.2. Quantum Factoring

Number factoring is the cornerstone of modern cryptography; more precisely, the absence of effective factoring algorithms makes encryption algorithms work. With the development of quantum computing, one of the most influential algorithms is Shor’s factorization algorithm which is exponentially faster than existing classical algorithms, ensuring, at least by now, theoretical quantum speedup [61]. Although Shor’s algorithm is complex in its mathematical formulation, the actual quantum routine is what makes it efficient. Given a number, N, composed of prime factors, p and q, the task is to efficiently find prime factors, knowing only N. The algorithm begins by choosing an arbitrary number, a, such that

$$1<a<N\mathrm{and}gcd(a,N)=1,$$

(40)

meaning that a does not have common factors with N. Next, with

$$a^r\equiv 1modN,$$

(41)

the main task becomes to find the minimum order r. If the order can be found, using the facts that

$$a^r-1=(a^{r/2}+1)(a^{r/2}-1)$$

(42)

and

$$a^r\equiv 1modN$$

(43)

it follows that

$$(a^{r/2}+1)(a^{r/2}-1)\equiv 0modN,$$

(44)

which means that N divides this product. Therefore, calculating the greatest common divisor (GCD),

$$gcd\left(a^{r/2}\pm 1,N\right)$$

(45)

can reveal the prime factor. The classical bottleneck is the computation of the order r which can take time up to $\mathcal{O}(rlogN)$ where r can be up to N, which is impractical for large N. However, in quantum settings there is a method of order finding which boosts the process dramatically. Quantum order finding is implemented as follows: The first register initialized with $|0\rangle$ handles the superposition of m qubits; in this register the number of qubits represents the precision of our calculations. The second register has $n=\lceil logN\rceil$ qubits initialized with $|1\rangle$, to represent the output of the function $f\left(x\right)=a^{x}modN$, which takes values in the range $\{0,1,\dots ,N-1\}$. After initializing the system, the quantum state is prepared as follows:

$${|0\rangle }^{\otimes m}{|1\rangle }^{\otimes n}\stackrel{H^{\otimes m}}{\to }{\displaystyle \frac{1}{\sqrt{2^m}}}\sum _{x=0}^{2^m-1}|x\rangle |1\rangle$$

(46)

The modular exponentiation unitary $U_f$ is defined as

$$U_f:|x\rangle |1\rangle \mapsto |x\rangle |a^{x}modN\rangle$$

(47)

and applied to the state

$${\displaystyle \frac{1}{\sqrt{2^m}}}\sum _{x=0}^{2^m-1}|x\rangle |a^{x}modN\rangle$$

(48)

Without going into details of the quantum Fourier transform, after applying it, the state has the form

$${\displaystyle \frac{1}{\sqrt{2^{m}r}}}\sum _{s=0}^{r-1}\sum _{k=0}^{2^m-1}{e}^{2\pi isk/r}|k\rangle |u_s\rangle ,$$

(49)

where $|u_s\rangle$ is an eigenstate of the modular exponentiation unitary operator $U_f$ and s represents different frequencies ranging from 0 to $r-1$. After applying the inverse quantum Fourier transform, the registers evolve to the state

$${\displaystyle \frac{1}{\sqrt{r}}}\sum _{s=0}^{r-1}|s/r\rangle |u_s\rangle .$$

(50)

At this point, measuring the state will give a number, s, which is close to a rational multiple of $2^n/r$. This is because the quantum Fourier transform of the first register of n qubits (where 2n is the register size) resolves frequencies associated with the period r, producing peaks at multiples of 2n/r in the measurement probabilities. Finally, using continued fractions, the value $s/2^n$ can be approximated, based on the fact that

$${\displaystyle \frac{s}{2^n}}\approx {\displaystyle \frac{k}{r}}$$

(51)

where k is some integer. Therefore the smallest value of r among possible candidates can be determined. As described previously, using the classical Euclidean algorithm for computing the GCD, the prime factors of N can be extracted. It should be noted that if the randomly chosen a does not have even order, or if the resulting r does not lead to a successful factorization, then the entire process is repeated. Since the set of valid a values is exponentially large (up to $N-1$), the probability of eventually finding an appropriate a is high. The complexity of this algorithm is $\mathcal{O}\left({log}^{3}N\right)$, which demonstrates an exponential speedup compared to the best-known classical factoring algorithms. Although the result is groundbreaking, the practical implementation of this algorithm requires a multi-qubit reliable quantum system and error-correction techniques for scaling [62]. Using Shor’s algorithm to break traditional cryptographic schemes like RSA can be done with 20 million noisy qubits; RSA-2048 could be factored in as little as 8 h [63].

4.3. Quantum Singular Value Transformation

In classical linear algebra, Singular Value Decomposition (SVD) is a matrix factorization method which decomposes an arbitrary matrix, A, as

$$A=US{V}^{†},$$

(52)

where U is a unitary matrix of left singular vectors, S is a diagonal matrix of singular values, and $V^{†}$ is the conjugate transpose of a unitary matrix of right singular vectors. Alternatively, the matrix can be written in sum form as

$$A=\sum _{i=1}^r{s}_i{u}_i{v}_i^{†},$$

(53)

where $s_i$ are the singular values, and ${\mathbf{u}}_i,{\mathbf{v}}_i$ are the left and right singular vectors, respectively. These singular values encode how the matrix stretches or compresses input vectors. Classically, to apply a function, f, to A, it is necessary to decompose A and apply the function to its singular values which is a computationally expensive task. In a novel quantum approach, it is shown that the function f can be applied without explicitly calculating the singular values [64]. First, the matrix A must be embedded into a larger unitary matrix, U, a process known as block encoding, typically in the form

$$U=\left[\begin{array}{cc}A/\alpha & ·\\ ·& ·\end{array}\right].$$

(54)

Since quantum circuits cannot directly encode arbitrary functions, the target function must be approximated. This is achieved using Chebyshev polynomial approximation, where any continuous function, f, can be written as

$$f\left(x\right)\approx \sum _{k=0}^d{a}_k{T}_k\left(x\right),$$

(55)

where $T_k\left(x\right)$ are the Chebyshev polynomials. The result is a polynomial, $P\left(x\right)$, of the degree d that approximates $f\left(x\right)$ over a bounded interval. This is implemented through a sequence of quantum gates generated by a series of phases, $\{{\varphi }_1,{\varphi }_2,\dots {\varphi }_d\}$. It is proven that computing these phases has the complexity $\mathcal{O}(d^3·\mathrm{poly}(d/ϵ))$ [65]. The general procedure to construct the f function is as follows. After classically computing the phase sequence, the combined operator is defined as

$$U_{\mathrm{QSVT}}=P_0\left({\varphi }_1\right)U{P}_0\left({\varphi }_2\right)U^{†}\dots ,$$

(56)

where $P_0\left({\varphi }_i\right)$ is a conditional phase gate that applies a phase shift only when the ancilla qubits are in the $|0\dots 0\rangle$ state, ensuring that the transformation targets the encoded A block. Depending on the parity of d, if d is even, then the final gate that is applied is $U^{†}$; otherwise, it is U. This gate encodes the polynomial $P\left(A\right)$, that is,

$$U_{\mathrm{QSVT}}\approx f\left(A\right),$$

(57)

and can then be applied to a general $|\varphi \rangle$ input state. The complexity of the algorithm depends on several factors: the degree d of the target function approximation, the cost of block-encoding A, and the cost of preparing the initial state $|\varphi \rangle$. Quantum Singular Value Transformation (QSVT) offers a powerful route to exponential speedups for a wide range of linear algebra problems. However, the actual performance gain depends critically on the structure of the problem and the output required. One of the most important applications of this algorithm is matrix inversion. Defining a function, $f=1/x$, constrained over a domain of nonzero singular values, it is possible to efficiently calculate the polynomial approximation using QSVT. Moreover, QSVT is a core method in quantum machine learning, namely in the implementation of quantum principal component analysis and quantum support vector machines [64]. Additionally, a dequantized version was proposed which demonstrates that for low-degree polynomial transformations, QSVT can be efficiently simulated classically with arbitrarily small constant precision [66].

5. Quantum Machine Learning

5.1. Quantum Hopfield Networks

One influential work in Artificial Intelligence is the associative memory model introduced by Hopfield [67]. The model is a neural network with fully connected neurons. The weights are symmetric and binary, meaning that the weight going from neuron i to j is the same as that from j to i with values $\{-1,1\}$. The energy function is defined as follows

$$E=-{\displaystyle \frac{1}{2}}\sum _{i\ne j}{w}_{ij}{s}_i{s}_j+\sum _i{\theta }_i{s}_i,$$

(58)

where $w_{ij}$ is the weight between neurons i and j, $s_i$ is the state of neuron i, and ${\theta }_i$ is the threshold for neuron i. The objective is to minimize the energy and drive the system into a stable configuration. The network learns using the Hebbian learning rule,

$$w_{ij}={\displaystyle \frac{1}{P}}\sum _{\mu =1}^P{\xi }_i^{\mu }{\xi }_j^{\mu },w_{ii}=0,$$

(59)

where P is the number of patterns to be stored, and ${\xi }_i^{\mu }$ is the i-th bit of the $\mu$-th pattern. It is proven that if there are N neurons, the maximum number of storable patterns is approximately $0.138N$ [68]. Once patterns are selected, the Hebbian rule is applied to compute $w_{ij}$; then the network can recover a noisy version of a stored pattern. Quantum Hopfield networks extend the classical idea by encoding weights and neuron states in the amplitudes of quantum states [69]. The quantum Hebbian learning rule defines the weight matrix W as

$$W={\displaystyle \frac{1}{P}}\sum _{\mu =1}^P|{\xi }^{\mu }\rangle \langle {\xi }^{\mu }|,$$

(60)

where $|{\xi }^{\mu }\rangle$ are the quantum states representing patterns. A pattern state, $|{\xi }^{\mu }\rangle$, is prepared using the encoding

$$|{\xi }^{\mu }\rangle ={\displaystyle \frac{1}{|{\xi }^{\mu }|}}\sum _{i=1}^d{\xi }_i^{\mu }|i\rangle ,$$

(61)

where d is the length and $|{\xi }^{\mu }|$ denotes the Euclidean (L₂) norm of the pattern, defined as $|{\xi }^{\mu }|=\sqrt{{\sum }_{i=1}^d{\left({\xi }_i^{\mu }\right)}^2}$. The pattern retrieval problem is reduced to solving the linear system $Ax=b$, where A is constructed from W and a regularization term, and b is the input pattern vector. The solution vector x approximates the stored pattern. This system is solved using the Harrow–Hassidim–Lloyd algorithm [70], involving quantum phase estimation, controlled rotations, and inverse phase estimation, to approximate $A^{-1}b$. Then the output state $|x\rangle$ is measured to retrieve the pattern. Due to the probabilistic nature of quantum measurement, multiple runs may be necessary for high-confidence recovery. The quantum algorithm has a runtime complexity of

$$\mathcal{O}\left(\mathrm{poly}(P,logd,1/ϵ,1/\mu )\right),$$

(62)

where $ϵ$ is the desired error tolerance, $\mu$ is the condition number of the matrix, and d is the pattern size. For comparison, the best-known classical matrix inversion algorithm [71] has the complexity

$$\mathcal{O}\left(\mathrm{poly}(d,1/\sqrt{\mu },log(1/ϵ),s)\right),$$

(63)

where s is the sparsity of the matrix. Therefore, the quantum approach offers exponential speedup in the dimensionality d. Additionally, there are quantum versions with neuron embedding directly in qubits [72], using quantum search [73]. Moreover, the usage of quantum annealing was shown to address memory recall as an energy minimization task, where the stored patterns are mapped to low-energy levels [74].

5.2. Quantum Support Vector Machines (QSVMs)

Support vector machines (SVMs) are widely used supervised learning algorithms for classification and regression tasks [75]. The central idea is to find the optimal hyperplane in a given dataset that separates classes. Given the labeled samples ${\left\{(x_i,y_i)\right\}}_{i=1}^n$, where $x_i\in {\mathbb{R}}^d$ and $y_i\in \{-1,+1\}$, the algorithm constructs a hyperplane characterized by $w\in {\mathbb{R}}^d$ and $b\in \mathbb{R}$ such that

$$y_i(w^T{x}_i+b)\ge 1\forall i.$$

(64)

The margin distance between the hyperplane and the nearest points (support vectors) is maximized by minimizing

$$\underset{w,b}{min}{\displaystyle \frac{1}{2}}{\parallel w\parallel }^2.$$

(65)

This is known as the primal optimization form of the SVM, which can be applied to linearly separable data. If the data are nonlinear, the optimization problem becomes

$$max\sum _{i=1}^n{\alpha }_i-{\displaystyle \frac{1}{2}}\sum _{i,j}{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)$$

(66)

with the following constraints:

$$0\le {\alpha }_i\le C,\sum _i{\alpha }_i{y}_i=0,$$

(67)

where $K(x_i,x_j)=\langle \varphi \left(x_i\right),\varphi \left(x_j\right)\rangle$ is the kernel function. The kernel function is used to map data into a higher dimensional space using a feature map, $\varphi$, where separation may be possible. There are three major kernel families, namely, linear, $K(x,x^{\prime })=x^T{x}^{\prime }$, polynomial, $K(x,x^{\prime })={(x^T{x}^{\prime }+c)}^d$, and Gaussian or radial base function (RBF), $K(x,x^{\prime })=exp(-\gamma \parallel x-x^{\prime }{\parallel }^2)$ [76]. Quantum support vector machines (QSVMs) are defined based on quantum kernel methods to find solutions in high-dimensional feature spaces [77]. The kernel function is defined by the inner product of quantum states:

$$K(x_i,x_j)={\left|\langle \varphi \left(x_i\right)|\varphi \left(x_j\right)\rangle \right|}^2.$$

(68)

The key advantage is that this kernel captures complex relationships in the data that might be inaccessible in the classical domain. The kernel measures the similarity between data points after encoding them into a quantum state using a quantum feature map. The classical input x is encoded by applying the $U\left(x\right)$ circuit feature map such that

$$|\varphi \left(x\right)\rangle =U_{\varphi }\left(x\right)|0\rangle ,$$

(69)

where $|0\rangle$ is the initial quantum state, and $U\left(x\right)$ is a parameterized circuit that encodes specific x using data-dependent rotations and entanglement. $K(x_i,x_j)$ is computed using either the overlap test or the SWAP test [78]. The overlap test prepares the state

$$U^{†}\left(x_i\right)U\left(x_j\right)|0\rangle ,$$

(70)

and the probability of measuring $|0\rangle$ gives an estimate of the inner product $|\langle \varphi \left(x_i\right)|\varphi \left(x_j\right)\rangle {|}^2$. The circuit is repeated R times to estimate the probability of returning to the $|0\rangle$ state. The SWAP test prepares identical quantum registers, $\left|\varphi \right(x_i)\rangle$ and $\left|\varphi \right(x_j)\rangle$, and applies the Hadamard → controlled-SWAP → Hadamard gate sequence to an ancilla qubit; then the ancilla is measured. Controlled-SWAP is a three-qubit gate that conditionally swaps the states of two target qubits depending on the state of a control qubit. In the case of multi-qubit quantum states, the CSWAP operation is applied in parallel across all corresponding qubit pairs. The goal is to fetch the probability of the ancilla qubit collapsing to $|0\rangle$. To estimate the probability, we iterate the circuit multiple times to obtain the count. Using the SWAP test identity

$$|\langle \varphi \left(x_i\right)|\varphi \left(x_j\right)\rangle {|}^2=2P\left(0\right)-1,$$

(71)

the $K(x_i,x_j)$ value is defined. Finally, the SVM dual problem is solved using the quantum kernel classically, making this algorithm a hybrid, both classical and quantum. As the optimization problem solver is the same in both computations, in terms of complexity, the kernel estimation running time should be considered. For the classical version, depending on the kernel type, the complexity is $\mathcal{O}(n^2·k\left(d\right))$ where d is the dimension of the feature space, and $k\left(d\right)$ is a function of cost for a specific kernel; it should be noted that most of the classical kernels are $\mathcal{O}\left(d\right)$. In quantum settings, the complexity is $\mathcal{O}(n^2·R·d_q)$ where R is the number of iterations for probability estimation and $d_q$ is the depth of a quantum circuit, which is usually polynomial in data size. The classical algorithm is efficient in the case of low-dimensional feature space and a small number of samples. In contrast, the potential advantage of the quantum version is that it can operate in high-dimensional spaces that may be computationally infeasible using classical methods. Another quantum SVM approach reformulates the SVM problem as least squares optimization, eventually reducing it to the task of solving a linear system of equations [79]. This system is then solved using the HHL quantum algorithm [70], allowing for potential exponential speedup under certain conditions.

6. Software Ecosystem

Quantum computing software provides a bridge between theoretical and practical applications. It is a critical layer in research and development of quantum algorithms which enables the development, testing, and execution of quantum algorithms on both simulated and physical quantum devices. Currently, advancements in quantum software development include high-level programing frameworks, low-level compilers, simulators, and domain-specific libraries, namely, machine learning, financial, and optimization problem libraries. Quantum software can generally be categorized based on its abstraction level and functional scope. At the highest level, there are software development kits (SDKs) that enable native scientific interfaces for building and executing quantum circuits. One widely used SDK is Qiskit, developed by IBM [14]. Qiskit provides various functionalities for quantum algorithm development including transpilation, simulation, and optimization. Qiskit supports the Python programming language interface and can be integrated with IBM’s quantum hardware. It has a specialized module for machine learning algorithms that supports designing methods such as quantum neural networks, quantum kernel methods, and variational quantum algorithms. PennyLane is another high-level SDK, designed by Xanadu [80]. In contrast, PennyLane stresses a wider range of integrations, giving one interface for various simulators and quantum hardware vendors. The design and implementation are particularly well suited for machine learning applications supporting state-of-the-art machine learning methods. Another notable SDK is Cirq, developed by Google, which is optimized to support near-term quantum devices and provides full control over quantum gates [81]. Amazon Bracket offers an SDK that is capable of running on various backends, both simulated and real. In contrast to these high-level frameworks, low-level solutions offer more specific control over quantum circuit compilation [82]. ProjectQ is developed taking into account modular architecture that highlights compiler optimization [83]. Q# is a domain specific language which is integrated in the Azure Quantum Development Kit, supporting a strong type of checking and simulation environment [84]. Quantum simulators are an important layer in the development lifecycle of quantum algorithms by enabling the emulation of quantum behavior on classical hardware. Qiskit Aer is a quantum state vector simulator which simulates the evolution of quantum states with high accuracy using a noise-aware simulation technique which injects parameterized amounts of noise into a system that reflects real gate and measurement errors. ITensor is a C++ library for tensor network calculations, primarily designed for many efficient noise-free quantum body system simulations using tensor contraction techniques [85]. Another class of quantum software supports quantum annealing, which is a model focused on quantum tunneling to find low-energy configurations of a cost function used in optimization problems [86]. The most famous software ecosystem of quantum annealers is offered by D-Wave Systems. Their Ocean SDK provides Python tools for problem formulation, embedding, and execution on D-Wave quantum annealers. It is designed to support quadratic unconstrained binary optimization problems and hybrid quantum–classical pipelines. Quantum annealers are specifically useful for applications in logistics, finance, and machine learning such as clustering and sampling. Quantum machine learning encompasses quantum computing and machine learning algorithms that try to utilize quantum advantages in data processing and model training. Qiskit provides a dedicated module for machine learning that integrates essential tools for implementing quantum classifiers, regressors and other algorithms. PennyLane offers similar capabilities with more emphasis on optimization through interfaces with PyTorch and TensorFlow.

6.1. Case Study: QSVM vs. Classical SVM

This case study explores the performance of a classical SVM versus a QSVM on various synthetic binary classification datasets, highlighting their capabilities in handling different data complexities. The datasets were generated using scikit-learn functions and split into training (80%) and testing (20%) sets. The linearly separable dataset consisted of 100 samples with two features, created with two centers and a cluster standard deviation of 1.0, resulting in well-separated clusters. The nonlinearly separable dataset had 100 samples and noise of 0.1 and was scaled by 10 for larger values, producing interlocking crescent shapes. The overlapping dataset employed 100 samples, two features, and two centers but a higher cluster standard deviation of 3.0, leading to significant class overlap. The high-dimensional dataset featured 100 samples across 10 dimensions (7 informative, 3 redundant), introducing complexity through higher feature space. Finally, the imbalanced dataset also featured 100 samples with two features but had the class weights [0.9, 0.1] and was scaled by 10, resulting in a majority class dominating a sparse minority (as illustrated in Figure 2).

The classical SVM pipeline leverages scikit-learn’s SVC class. For linear and simple cases, it uses a linear kernel by default, but for nonlinear scenarios like moon-shaped data, it employs a Radial Basis Function (RBF) kernel to implicitly map data into a higher-dimensional space via the kernel trick, enabling curved decision boundaries. The process involves fitting the model using training data, predicting using test data, and evaluating metrics, namely, accuracy, precision, recall, and F1-score.

In contrast, the quantum SVM pipeline integrates quantum computing elements using Qiskit’s tools on a simulated backend. Processing begins by scaling features to the [0, $\pi$] range to suit quantum encoding and then applies a ZZFeatureMap (with four repetitions) to embed classical data into a quantum Hilbert space [14,87]. (68) is used for state overlap estimation, a kernel matrix representing quantum similarities. This matrix is then fed into a classical SVC for training and prediction, mirroring the classical evaluation metrics. The key difference lies in the kernel computation; the classical RBF uses mathematical approximations in Euclidean space, while the QSVM exploits quantum superposition and entanglement for potentially more expressive feature maps in exponentially larger spaces, though it was simulated here classically, which limited true quantum advantages.

Analyzing the results, the classical SVM consistently outperformed the QSVM across all datasets on the test sets (

Table 1. Dataset generation parameters and classification results.

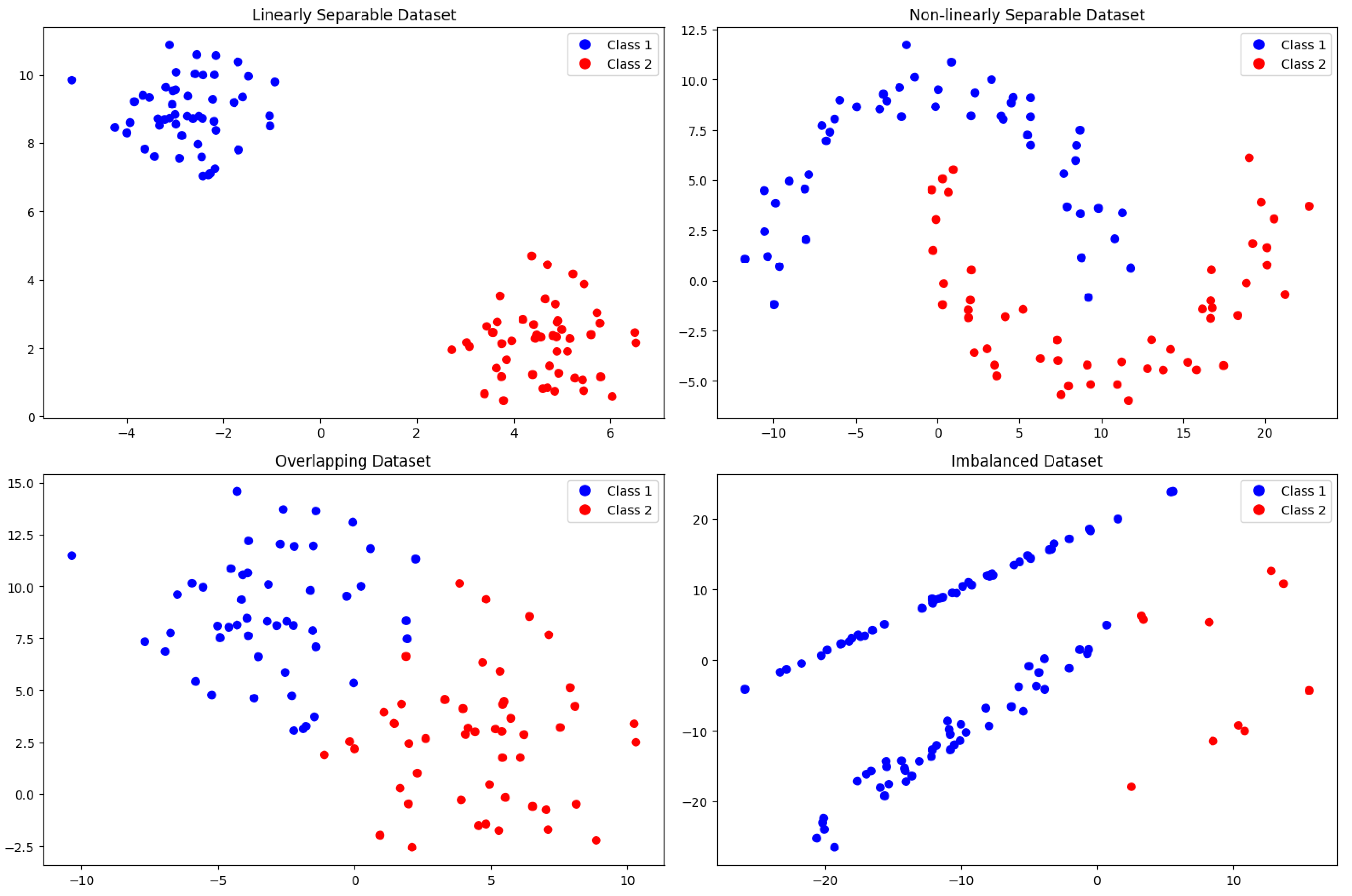
Dataset	Generation Parameters			Classical SVM Metrics
	Samples/Features	Key Params	Split (Train/Test)	Acc	Prec	Rec	F1
Linearly Separable	100/2	centers = 2, cluster_std = 1.0	80/20	1.00	1.00	1.00	1.00
Nonlinearly Separable	100/2	noise = 0.1, scaled ×10	80/20	1.00	1.00	1.00	1.00
Overlapping	100/2	centers = 2, cluster_std = 3.0	80/20	0.95	0.90	1.00	0.94
High-Dimensional	100/10	informative = 7, redundant = 3	80/20	0.75	0.54	1.00	0.70
Imbalanced	100/2	weights = [0.9, 0.1], scaled ×10	80/20 (strat.)	1.00	1.00	1.00	1.00
Dataset				Quantum SVM Metrics
				Acc	Prec	Rec	F1
Linearly Separable				0.85	0.80	0.88	0.84
Nonlinearly Separable				0.80	0.62	0.83	0.71
Overlapping				0.45	0.37	0.33	0.35
High-Dimensional				0.30	0.30	1.00	0.46
Imbalanced				0.70	0.85 *	0.70 *	0.76 *

* Weighted metrics for imbalanced dataset.

). For the linearly separable data, classical achieved perfect scores, while the QSVM dropped to 0.85 accuracy, possibly due to quantum encoding overhead introducing noise in simulation. On nonlinear data, classical again perfected at 1.0, leveraging the RBF effectively, but the QSVM yielded 0.80 accuracy with lower precision (0.625), indicating challenges in capturing nonlinearities via the ZZFeatureMap. Overlapping data resulted in classical being at 0.95 accuracy versus the QSVM’s poor 0.45, highlighting the QSVM’s sensitivity to noise and overlap. In high-dimensional space, classical managed 0.75 accuracy, but QSVM’s plummeted to 0.30, struggling with the 10-feature encoding into qubits. For imbalanced data, classical perfected at 1.0, while the QSVM (with class weights) reached 0.70 weighted accuracy, better handling minority recall but overall being inferior.

The classical SVM’s advantages include robustness, efficiency on small datasets, and mature implementations, yielding high performance without specialized hardware, making it practical for real-world use. However, it may scale poorly in high dimensions due to computational costs of kernel matrices. The QSVM offers potential advantages in theoretically handling complex, high-dimensional data via quantum speedup, as seen in slightly better recall in some cases (e.g., 1.0 in high dimensions), suggesting promise for entangled patterns which are unfeasible classically. Disadvantages include simulation limitations introducing errors, higher computational demands (even when simulated), sensitivity to scaling and feature mapping choices, and current immaturity leading to lower metrics (0.3–0.85 accuracy), underscoring that true benefits may emerge only on fault-tolerant quantum hardware for larger datasets. Overall, while the classical SVM excels in this study, the QSVM hints at future potential for intractable problems, warranting further optimization like advanced feature maps or hybrid approaches.

6.2. Limitations

Quantum software faces numerous challenges. One of the core challenges is scalability. Current quantum devices are constrained in terms of qubit count, coherence times, and gate fidelity, which restricts the size and complexity of models that can be executed. Existing approaches can soften current hardware limitations while still using quantum components [88]. Another major field for development is parallel software and hardware design. Optimizing quantum circuits for specific hardware characteristics is essential to maximize performance. Advancements in quantum compilers, transpilers, and error mitigation techniques will be crucial in this regard [7].

7. Conclusions and Future Prospects

Quantum computing has made outstanding theoretical progress in computer science, with demonstrated advantages in tasks such us search, factorization, and quantum-enhanced machine learning. However, current quantum devices posses significant limitations. Among major problems are short qubit coherence time, low gate fidelity, and limited qubit systems. These limitations make scaling quantum algorithms to reliably solve practical problems extremely difficult. As a result, implementation of algorithms like Shor’s still remain on paper. Other problematic aspects are the development of error correction codes and fault-tolerant quantum architectures. These problems remain active research topics as fault-tolerant computing requires a significantly large amount of physical qubits, which remains a hardware bottleneck.

While quantum computing provides (at least on paper) exponential speedups in particular problems, NP-complete problems still remain intractable in general. Current advancements suggest that quantum computing will not solve all computational problems but rather complement classical computing in hybrid systems. Such systems already show tangible results in optimization, chemistry, and machine learning.

In the future, it is likely that the standard of computational systems will be hybrid machines, where quantum processors act as accelerators for specific subroutines, while classical processors handle the overall orchestration and post-processing. This mixed relationship between classical and quantum devices will define the next era of computational innovation, enabling robust solutions in domains where neither system alone would be sufficient.