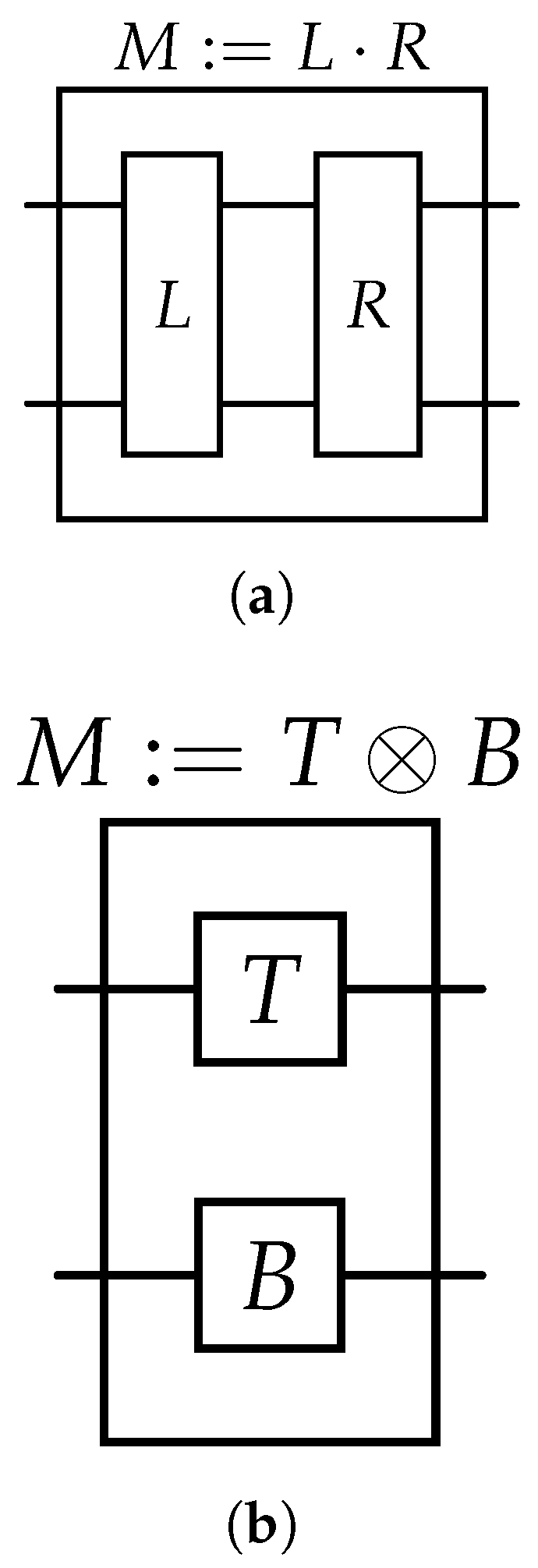HHL Algorithm for Tensor-Decomposable Matrices

Abstract

We use the HHL algorithm to retrieve a quantum state holding the algebraic normal form (ANF) of a Boolean function. Unlike the standard HHL applications, we do not describe the cipher as an exponentially big system of equations. Rather, we perform a set of small matrix inversions which correspond to the Boolean Möbius transform. This creates a superposition holding information about the ANF in the form $|{\mathcal{A}}_f⟩={\displaystyle \frac{1}{C}}{\sum }_{I=0}^{2^n-1}{c}_I|I⟩$, where $c_I$ is the coefficient of the ANF and C is a scaling factor. The procedure has a time complexity of $\tilde{\mathcal{O}}(n)$ for a Boolean function with n-bit input. We also propose two approaches by which some information about the ANF can be extracted from such a state. Next, we use a similar approach, the Dual Boolean Möbius transform, to compute the preimage under the algebraic transition matrix. We show that such a matrix is well-suited for the HHL algorithm when the attacker gets oracle access in the Q2 setting to the Boolean function.

1. Introduction

The most successful quantum algorithms rely on the quantum computer’s ability to efficiently switch between different representations of a function. Then, a measurement in the corresponding basis delivers information about some structural property of the function. The most prominent example, a measurement in the Fourier basis, can extract information about the periodicity of the function and allows breaking schemes like the RSA. Similarly, the algorithm proposed in [1] uses the Fourier transform over the ${(\mathbb{Z}/2\mathbb{Z})}^n$ to find the parity basis representation [2]. In this paper, we want to follow a similar approach, however, in a different setting. We begin with an easy-to-prepare yet exponentially big quantum state. Next, we perform a quantum basis change, which in a classical setting is costly, and retrieve meaningful information about the function.

The HHL algorithm, proposed in 2009 by [3], is a quantum procedure that computes the preimage of a given input. Unlike the classical approaches, it does not linearly depend on the size of the matrix. Rather, its runtime is defined by the sparseness and condition number of the matrix, and only logarithmically by the matrix size. Since most of the modern ciphers can be described as some form of exponentially big equation system, the idea of using HHL to cryptanalyse ciphers came forward [4] and was quickly followed by other publications. However, the common factor was always the abuse of the logarithmic speed-up in the runtime of the HHL algorithm.

In this paper, we will also tackle an exponentially big input $\overrightarrow{b}$. In contrast to the standard approaches of HHL-based cryptanalysis, we will consider matrices of a special form. We prove that, if the matrix M can be decomposed into a tensor product $M=M_1\otimes M_2\otimes \dots \otimes M_n$, then computing the pre-image can be significantly sped up. On classical computers, pre-image computation can be done in polynomial time in regard to the vector’s size. Only in the case when the input $\overrightarrow{b}$ can likewise be decomposed into the following tensor product:

$$\begin{array}{c}\hfill \overrightarrow{b}=\overrightarrow{b_1}\otimes \overrightarrow{b_2}\otimes \dots \otimes \overrightarrow{b_n},\end{array}$$

are we able to obtain a subpolynomial runtime. Here, the sizes of $\overrightarrow{b_i}$’s must match the sizes of corresponding matrices $M_i$ for each $i\in 1,\dots ,n$. If such a decomposition of $\overrightarrow{b}$ is unknown, or even impossible, the fastest known classical approximation algorithm is the conjugate gradient method, with a runtime of $\mathcal{O}\left(Ns\sqrt{\kappa }{log}_2({\displaystyle \frac{1}{ϵ}})\right)$. In our approach, we do not need a vector decomposition to perform the HHL algorithm, allowing a runtime advantage over classical computers. We summarize this observation in the following Theorem:

Theorem 1.

Let $M={⨂}_{i=1}^t{M}_i$ be a horizontal decomposition of a Hermitian matrix M. Further, for all $i=1,\dots ,t$, let $M_i\in {\mathbb{C}}^{N_i\times N_i}$ be a Hermitian matrix with ${\kappa }_i$ its condition number and $s_i$ its sparseness. The time complexity of the vertical HHL from Theorem 2 for the matrix M is:

$$\begin{array}{c}\hfill \tilde{\mathcal{O}}\left(t·(\underset{i}{max}{\kappa }_i·s_i·\mathit{poly}(log{N}_i))\right)\end{array}$$

Based on the above Theorem, our approach is next applied to a cryptographically significant matrix corresponding to the Boolean Möbius transform. The transform allows transition between the algebraic normal form (ANF) of a Boolean function and its truth table (TT). We decided to decompose this matrix as, in its composed form, it has high sparsity (one full column). Applying the standard HHL algorithm in such a scenario would be counterproductive, as the runtime would be comparable to the gradient approach ($\tilde{\mathcal{O}}\left(N\right)$, where N is the number of rows in the matrix. Instead, we decompose the Möbius transform into a tensor product of n small sub-matrices ($2\times 2$ before Booleanization) and achieve a runtime of $\tilde{\mathcal{O}}(n)$ with $N=2^n$.

By capturing the truth table in the superposition and computing its preimage under the Boolean Möbius transform, we manage to encapsulate the algebraic normal form of a Boolean function f under attack in the quantum register. The result is as follows:

$$\begin{array}{c}\hfill |{\mathcal{A}}_f\rangle ={\displaystyle \frac{1}{\sqrt{\mathrm{hw}\left({\mathcal{A}}_f\right)}}}\sum _{I=0}^{2^n-1}{c}_I|I\rangle \end{array}$$

where $c_I$ is the binary coefficient of the monomial $x^I$. $|{\mathcal{A}}_f\rangle$ can be used to both retrieve the ANF of the function, as well as to estimate its Hamming weight. We also use the technique introduced in [5] to extract information about a Boolean function using the algebraic transition matrices (ATMs).

A standard requirement in quantum computation is the unitarity of evolutions applied to the qubits. We employ the HHL algorithm to allow inversion of non-unitary matrices. The HHL algorithm is a well-established framework suitable for this operation. However, in the Boolean Möbius transform setting, the procedure could be adjusted. As the Möbius transform is self-inverse, we do not need to compute the preimage. Instead, computing the image under the transform delivers the same result.

We introduce the notation in Section 1.2. Section 2 focuses on the HHL algorithm. We estimate the runtime and present how to Booleanize a matrix and how the HHL algorithm is used in cryptanalysis. In Section 3, we discuss our new approach to applying HHL to a tensor product. The final section concludes with the proof of Theorem 1. Section 4 shows how to apply the tensor approach to a specific function—the Boolean Möbius transform. We define the Boolean Möbius transform and its tensor decomposition. We explain why it is better to apply the algorithm to decomposed matrices and how to generate the input quantum state. Finally, we describe the result of our algorithm. In Section 5 we elaborate on the cryptographic use-cases of the Boolean Möbius transform. We show how the transform can be used to analyse the algebraic normal form of a Boolean function.

1.1. State-of-the-Art of HHL in Cryptanalysis

The cryptographic appeal of the HHL algorithm is clear. Most modern ciphers are characterized by complex equation systems needed to describe them. The first attempt was introduced in [4], and used the so-called Macaulay matrix—an exponentially big and sparse matrix which can be solved for the Boolean solution of a polynomial system. The next proposal targeted the NTRU system [6] and used the HHL algorithm to solve a polynomial system with noise [7]. Finally, in [8], the Grain-128 and Grain-128a ciphers were cryptanalysed using techniques based on [4,7]. Ref. [9] suggested improvements upon the above papers, and proved a lower-bound on the condition number of the Macaulay matrix approach. In [10], two systems of equations for AES-128, one over $GF\left(2\right)$ and another over $GF\left(2^8\right)$ based on the BES construction introduced in [11], were analysed under the HHL algorithm.

1.2. Notation

We will shortly introduce the common notation used throughout this paper. A function $f:{\mathbb{F}}_2^n⟶{\mathbb{F}}_2$ is called a Boolean function. It is known that each Boolean function f has a polynomial representation $f\left(x\right)\in {\mathbb{F}}_2[x_1,\dots ,x_n]$ [2]. For an index set $I\subseteq \{1,2,\dots ,n\}$, we define $x^I:={\prod }_{i\in I}{x}_i$. We also define $c_I\in {\mathbb{F}}_2$ as the coefficient of the term $x^I$, and will sometimes switch to the notation where the index is the decimal number defined by the binary interpretation of I. For a Boolean function $f\left(x\right)={\sum }_{I\in \left[n\right]}{c}_I{x}^I$, the Algebraic Normal Form (ANF) of f is ${\mathcal{A}}_f:=(c_0,\dots ,c_{2^n-1})$. The representation of f in the ANF is unique and defines the function f. Moreover, we can compute the coefficients $c_I$’s as follows:

$$c_I=\sum _{supp\left(x\right)\subseteq I}f\left(x\right),$$

(1)

where $supp\left(x\right):=\{i:x_i\ne 0\}$ [2]. In other words, we can compute the coefficient $c_I$ by adding (over ${\mathbb{F}}_2$) the images of all inputs dominated by I (cf. to precursor sets defined in [5]).

The Hamming weight of a Boolean vector $x\in {\mathbb{F}}_2^n$ is denoted as $\mathrm{hw}\left(x\right)$, and it is the number of non-zero entries. The degree of a coefficient can be computed using the Hamming weight:

$$\begin{array}{c}\hfill deg\left(c_I\right)=\mathrm{hw}\left(I\right)\end{array}$$

The truth table of a Boolean function f is a binary vector ${\mathcal{T}}_f\in {\mathbb{F}}_2^{2^n}$ defined as ${\mathcal{T}}_f=\left(f\left(0\right),f\left(1\right),\dots ,f(2^n-1)\right)$.

A vectorial Boolean function is defined as $F:{\{0,1\}}^n\to {\{0,1\}}^m$ for $n,m\in \mathbb{N}$. Further, for all $0\le i\le m-1$, $F_i:{\{0,1\}}^n\to \{0,1\}$ is a Boolean function and the projection of F to the ith component. A projection of a string s to its i’th component will be denoted by ${s|}_i$.

By $H_1={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{cc}1& 1\\ 1& -1\end{array}\right)$ we denote the Hadamard gate, and by $H_n={⨂}_{i=1}^n{H}_1$ its n-fold tensor product. The E is an identity matrix. In the cases where the size of the identity matrix is not explicitly stated, the index j indicates the size of the matrix $E_j\in {\mathbb{C}}^{2^j\times 2^j}$.

2. HHL Algorithm

The HHL algorithm, named after the authors Harrow, Hassidim, and Lloyd, is one of the new tools in the quantum toolbox used for cryptanalysis. It was first proposed in [3] as an efficient algorithm to solve exponentially big systems of linear equations, outperforming any classical algorithm. Its cryptographic significance was quickly discovered, and [4] proposed the first attack scenario. Since then, a series of cryptographic publications have considered the HHL setting.

We introduce two problems closely related to the HHL algorithm:

Problem 1.

Given a Hermitian matrix $M\in {\mathbb{C}}^{2^n\times 2^n}$ and an input state $\overrightarrow{b}\in {\mathbb{C}}^{2^n}$ with $\overrightarrow{b}=(b_0,\dots ,b_{2^n-1})$ find the state $\overrightarrow{x}$ such that:

$$\begin{array}{c}\hfill M·\overrightarrow{x}=\overrightarrow{b}\end{array}$$

We can also reframe this into the quantum setting as follows:

Problem 2.

Given a Hermitian matrix $M\in {\mathbb{C}}^{2^n\times 2^n}$ and an input state

$$\begin{array}{c}\hfill |b\rangle =\sum _{i=0}^{2^n-1}{b}_i|i\rangle \end{array}$$

with $\overrightarrow{b}=(b_0,\dots ,b_{2^n-1})\in {\mathbb{C}}^{2^n}$ find the state $|x\rangle ={\sum }_{i=0}^{2^n-1}{x}_i|i\rangle$ such that:

$$\begin{array}{c}\hfill M·\overrightarrow{x}=\overrightarrow{b}\end{array}$$

with $\overrightarrow{x}=(x_0,\dots ,x_{2^n-1})\in {\mathbb{C}}^{2^n}$.

The HHL algorithm solves Problem 2. To compute the pre-image of $\overrightarrow{b}$, we need to represent the vector as a quantum register $|b\rangle ={\sum }_{i=0}^{N-1}{b}_i|i\rangle$. Then, M is transformed into a unitary operator $e^{iMn}$, and the operator is applied to $|b\rangle$ using the Hamiltonian simulation technique [12]. This is equivalent to decomposing $|b\rangle$ to an eigenbasis of M and determining the corresponding eigenvalues. The register after this transformation is in the following state:

$$\begin{array}{c}\hfill \sum _{j=0}^{N-1}{\beta }_j|u_j\rangle |{\lambda }_j\rangle \end{array}$$

where $|b\rangle ={\sum }_{j=0}^{N-1}{\beta }_j|u_j\rangle$, ${\left\{u_j\right\}}_{j=0,\dots ,N-1}$ is the eigenbasis and ${\lambda }_j$’s are the corresponding eigenvalues. Using an additional ancilla register, we perform a rotation conditioned on the value of ${\lambda }_j$ to obtain the following state:

$$\begin{array}{c}\hfill \sum _{j=0}^{N-1}{\beta }_j|u_j\rangle |{\lambda }_j\rangle \stackrel{\mathrm{ancilla}\mathrm{register}}{\overbrace{\left(\sqrt{1-{\displaystyle \frac{C^2}{{\lambda }_j^2}}}|0\rangle +{\displaystyle \frac{C}{{\lambda }_j}}|1\rangle \right)}}\end{array}$$

We finish with a measurement of the ancilla register. If $|1\rangle$ is observed, the eigenvalues $|{\lambda }_j\rangle$ of the matrix M are inverted, and the register ends in the following state:

$$C·\sum _{j=0}^{N-1}{\beta }_j{\lambda }_j^{-1}|u_j\rangle =M^{-1}|b\rangle =|x\rangle$$

(2)

2.1. HHL Runtime

In [3], the authors show how to run the HHL algorithm for a matrix $M\in {\mathbb{C}}^{N\times N}$ in time $\tilde{\mathcal{O}}\left({\kappa }^2·s^2·\mathrm{poly}(logN)\right)$, where s is the sparseness of the matrix M, $\kappa$ is its condition number, and N is the size. The $\tilde{\mathcal{O}}(·)$ notation suppresses all slowly-growing parameters (logarithmic with respect to $s,\kappa$ or $logN$). The algorithm requires that M is either efficiently row-computable, or an access to the oracle which returns the indices of non-zero matrix entries for each row. The phase estimation (PE) step is responsible for a significant portion of the runtime of the HHL. For an s-sparse matrix, the PE takes $\tilde{\mathcal{O}}(logN{s}^2)$ computations. We observe that, after the rotation conditioned on ${\lambda }_j$, we have only a certain probability of observing the ancilla register in a state $|1\rangle$. However, since the constant C from Equation (2) is of magnitude $\mathcal{O}(1/\kappa )$, with $\mathcal{O}(\kappa )$ applications of the amplitude amplification algorithm [13] we can lower the probability of the undesired measurement to a negligible value. Ref. [14] improved the HHL algorithm by lowering the condition number dependence from quadratic to almost linear. Ref. [15] proposed a further improvement to achieve the runtime as follows:

$$\begin{array}{c}\hfill \tilde{\mathcal{O}}(\kappa ·s·\mathrm{poly}(logN))\end{array}$$

This will be the complexity that we will use in this paper. Nevertheless, since the values $s,\kappa$ of the matrices we propose are constant, the choice of the implementation should not have much influence on the feasibility of the algorithm we develop.

2.2. HHL over Finite Fields

The HHL algorithm in its initial form is defined for matrices and vectors over $\mathbb{C}$. Since most of the cryptographic constructions use finite field arithmetic, the question of whether HHL can be adapted to this setting came forward. In this part, we want to present a set of rules which describe how to transform an equation system M over a finite field ${\mathbb{F}}_2$ to an equation system over $\mathbb{C}$ as required by the HHL algorithm. Most of the reductions were proposed in [7]. The result will be an equation system over $\mathbb{C}$ which shares the solution with the original system. We will call the resulting system the Booleanization of M, and the $\mathbb{C}$-matrix corresponding to the system a Booleanized matrix. The total sparseness of a matrix is the number of non-zero entries in all of its rows and columns.

Reduction from Boolean Equations to Equations over $\mathbb{C}$

For a given set of Boolean functions $\mathcal{F}=\{f_1,\dots ,f_m\}\subseteq {\mathbb{F}}_2\left[\mathbb{X}\right]$ with n variables, we want to find a system ${\mathcal{F}}_{\mathbb{C}}=\{f_1^{\prime },\dots ,f_{m^{\prime }}^{\prime }\}\subseteq \mathbb{C}[\mathbb{X},\mathbb{Z}]$, such that when $(\widehat{\mathbb{X}},\widehat{\mathbb{Z}})$ is a solution to ${\mathcal{F}}_{\mathbb{C}}=0$, then $\widehat{\mathbb{X}}$ is a solution of $\mathcal{F}=0$. To do this, we will define a new set of variables $\mathbb{Z}=\{z_1,\dots ,z_m\}$ and $m+n$ new quadratic equations as follows:

$$\begin{array}{cc}{f}_i(x_1,\dots ,x_n)-z_i=0\hfill & \hfill \hspace{1em}\forall i=1,\dots ,m\end{array}$$

(3)

$$\begin{array}{cc}{z}_i/2\in \mathbb{Z}\hfill & \hfill \hspace{1em}\forall i=1,\dots ,m\end{array}$$

(4)

$$\begin{array}{cc}{x}_j-x_j^2=0\hfill & \hfill \hspace{1em}\forall j=1,\dots ,n\end{array}$$

(5)

The first two sets of equations guarantee that the value of $f_i\left(\widehat{\mathbb{X}}\right)=0mod2$. This represents the Boolean addition logic in the original system $\mathcal{F}$. The last equation guarantees that the only possible values of $x_1,\dots ,x_n$ are from ${\mathbb{F}}_2$. An important observation here is also that $\forall i=1,\dots ,m0\le z_i\le \#f_i$.

Next, we need to present $z_i$’s in a form usable by the quantum computer. Each $z_i$ will be represented in its binary form with $log(\#f_i)$ bits:

$$\begin{array}{c}\hfill z_i=\sum _{b=0}^{log\#f_i}{2}^b{z}_{i_b}\end{array}$$

However, since Equation (4) holds, we know $\forall 1\le i\le m:z_{i_0}=0$. This means we actually only consider the following representation:

$$\begin{array}{c}\hfill z_i=\sum _{b=1}^{log\#f_i}{2}^b{z}_{i_b}\end{array}$$

We need to incorporate this into the equation system mentioned above in the following way:

$$\begin{array}{ccc}\hfill & f_i(x_1,\dots ,x_n)-\sum _{b=1}^{log\#f_i}{2}^b{z}_{i_b}=0\hfill & \hfill \forall i=1,\dots ,m\\ \hfill & z_{i_b}-z_{i_b}^2=0\hfill & \hfill \forall i=1,\dots ,m,\forall b=1,\dots ,log\#f_i\\ \hfill & x_j-x_j^2=0\hfill & \hfill \forall j=1,\dots ,n\end{array}$$

Similarly, as in (5), the equation $z_{i_b}-z_{i_b}^2=0$ forces the values of $z_{i_b}\in {\mathbb{F}}_2$. The additional equations mentioned in this section increase the number of needed variables from n to $n+m·log\#f_i$ and the number of equations from m to $m·(1+log\#f_i)+n$. Thus, in the $\tilde{\mathcal{O}}$ notation, the runtime of the HHL remains the same for $n\sim m$.

Finally, the HHL algorithm requires the input matrix to be Hermitian. The resulting Booleanized matrix corresponding to the system ${\mathcal{F}}_{\mathbb{C}}$ is not. Luckily, we can use the procedure proposed by the original authors of the HHL algorithm to cover this case [3]. The technique uses the property that for an arbitrary matrix M that is not Hermitian, we can construct a new matrix $C_M$:

$$\begin{array}{c}\hfill C_M:=\left(\begin{array}{cc}0& M\\ M^{†}& 0\end{array}\right),\end{array}$$

The newly constructed matrix $C_M$ will be Hermitian and a valid HHL input. Here, the $M^{†}$ is the conjugate transpose of M. We finish this section with a Lemma characterizing the setting and the runtime of the HHL algorithm:

Lemma 1.

([3,15]). Let $M\in {\mathbb{C}}^{2^n\times 2^n}$ be a Hermitian matrix and $|b\rangle \in {\mathbb{C}}^{2^n}$ be a quantum state. We denote the application of the HHL with the matrix M to a state $|b\rangle$ as:

$$\begin{array}{c}\hfill HH{L}_M\left(|b\rangle \right)=|x\rangle \end{array}$$

The result $|x\rangle$ is a quantum state which solves Problem 2 and the procedure takes $\tilde{\mathcal{O}}(\kappa ·s·poly(log(N)))$ time.

3. HHL for Tensors of Matrices

Usually, when considering the use-case of HHL, we want to leverage the exponential speed-up in regard to the size of the matrix. This is the natural direction, as that is the obvious runtime difference between the HHL and the classical approach. The hindrance is, however, that, even though the matrix can be exponentially big, it should not have too many entries. In fact, a matrix with a single full column eliminates the potential use of the HHL (cf. Section 2.1).

In this section, we present an approach to overcome the above-mentioned obstacles for a special set of matrices. We prove that if for a matrix M we are given a tensor decomposition $M=M_1\otimes M_2\otimes \dots \otimes M_n$, where each $M_i$ is again Hermitian and has a small size, applying the HHL approach to each $M_i$ has a low runtime and delivers the same result. In some cases, our algorithm computes the preimage of a quantum state $|b\rangle$ under the matrix M exponentially faster than the standard HHL approach. A similar technique is a building block of known quantum algorithms, among others, Shor’s or Simon’s algorithm. For these two algorithms, instead of applying a matrix $H_n$ to an n-long register $|x\rangle$, we apply $H_1$ to each of n qubits of $|x\rangle$.

We start with a simple Lemma saying that applying a vertical/tensor (cf. Figure 1) decomposition of a unitary matrix $U={⨂}_{i=1}^t{U}_i$ to quantum sub-registers results in the same state as applying the matrix U to the whole register:

Lemma 2.

Let $U_1,\dots ,U_t$ be unitary matrices with $U_i\in {\mathbb{C}}^{n_i\times n_i}$. Further, let $|x_1\rangle ,\dots ,|x_t\rangle$ be the corresponding quantum states with $|x_i\rangle \in {\mathbb{C}}^{n_i}$. Then:

$$\begin{array}{c}\hfill \left(\underset{i=1}{\overset{t}{⨂}}{U}_i\right)·\left(\underset{i=1}{\overset{t}{⨂}}|x_i\rangle \right)=\underset{i=1}{\overset{t}{⨂}}(U_i·|x_i\rangle ).\end{array}$$

This result is unsurprising and is the reason for most quantum algorithms’ efficiency. However, we will generalize the argument to show that this equality also holds for non-unitary matrices.

Lemma 3.

Let $M_1,\dots ,M_t$ be matrices and $E_1,\dots ,E_t$ be identity matrices with $M_i,E_i\in {\mathbb{C}}^{n_i\times n_i}$ and $M={⨂}_{i=1}^t{M}_i$ and $|x\rangle \in {\mathbb{C}}^{{\prod }_{i=0}^t{n}_i}$. Then:

$$\begin{array}{c}\hfill M·|x\rangle =\prod _{j=1}^t\left(\underset{i=1}{\overset{j-1}{⨂}}{E}_i\otimes M_j\otimes \underset{i=j+1}{\overset{t}{⨂}}{E}_i\right)·|x\rangle \end{array}$$

Proof. 

Since both the product and the tensor of two matrices are matrices again, it suffices to show this property for two matrices. The rest follows from the associativity of matrix products. Let $M_1,E_1\in {\mathbb{C}}^{n_1\times n_1}$, $M_2,E_2\in {\mathbb{C}}^{n_2\times n_2}$. Further, let $M=M_1\otimes M_2$. Then, by standard tensor properties, we know the following:

$$\begin{array}{cc}\hfill (M_1\otimes E_2)·(E_1\otimes M_2)& =(M_1·E_1)\otimes (M_2·E_2)\hfill \\ \hfill & =M_1\otimes M_2\hfill \\ \hfill & =M\hfill \end{array}$$

Since $(M_1\otimes E_2)·(E_1\otimes M_2)$ is indifferent to M, it does not make a difference which one we apply to a vector $|x\rangle$.    □

Again, this is a simple fact from linear algebra, but it will constitute a major stepping stone for our algorithm. We want to highlight that the vector $M·|x\rangle$ from Lemma 3 does not have to be a valid quantum state even if $|x\rangle$ is. Since the matrix M is not unitary, it means the result does not have to be normed.

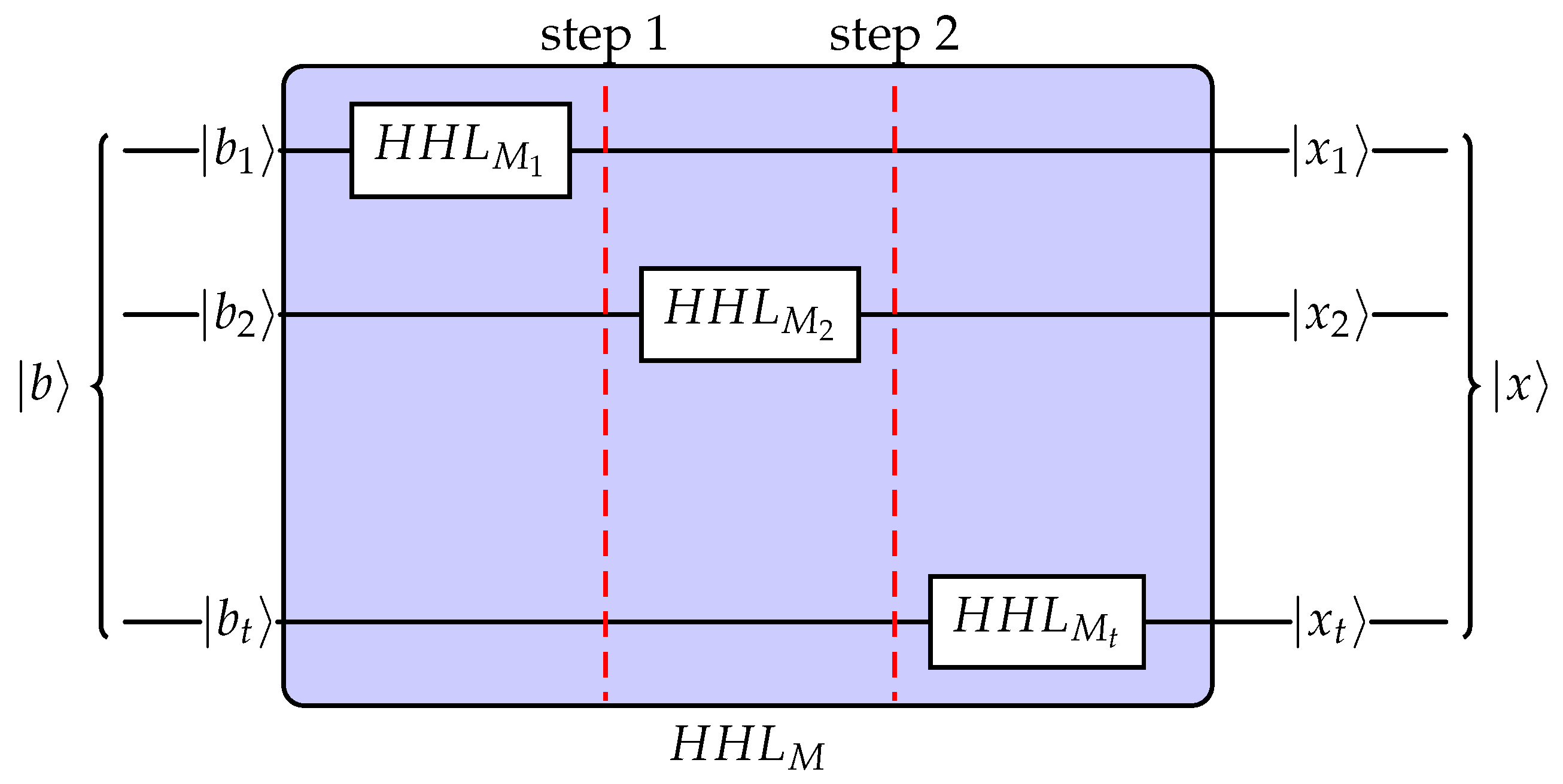
We will now use the observation from Lemma 3 to build a procedure to solve Problem 2 for a matrix $M\in {\mathbb{C}}^{2^n\times 2^n}$ with the property $M={⨂}_{i=1}^t{M}_i$. Instead of applying HHL to the whole matrix M, we will consider its vertical decomposition and apply HHL to the sub-matrices. We highlight that finding such a decomposition is an NP-hard problem [16], but we assume it is given to us. The idea is depicted in Figure 2. The resulting state will be identical to that of HHL applied to the matrix M.

We begin with a Lemma showing that, for a simple-structured tensor product (a tensor product of mostly diagonal matrices), applying the HHL algorithm on the combined state or the horizontal decomposition delivers the same result and has almost identical runtime.

Lemma 4.

Let $M\in {\mathbb{C}}^{N\times N}$ be a Hermitian matrix and $HH{L}_M$ be the HHL algorithm from Lemma 1. Further, let M have the following structure:

$$\begin{array}{c}\hfill M=\underset{i=1}{\overset{j-1}{⨂}}{E}_i\otimes M_j\otimes \underset{i=j+1}{\overset{t}{⨂}}{E}_i\end{array}$$

for a Hermitian $M_j$. Here, $E_i$’s are identity matrices of appropriate dimension. Then, for a given input $|b\rangle$, the following equality holds:

$$\begin{array}{c}\hfill HH{L}_M|b\rangle =\underset{i=1}{\overset{j-1}{⨂}}{E}_i\otimes HH{L}_{M_j}\otimes \underset{i=j+1}{\overset{t}{⨂}}{E}_i|b\rangle \end{array}$$

Proof. 

For a matrix $M={⨂}_{i=1}^{j-1}{E}_i\otimes M_j\otimes {⨂}_{i=j+1}^t{E}_i$, the HHL algorithm first uses the Hamiltonian simulation technique to apply $e^{iMn}$ to the register $|b\rangle$. Observe that we can rewrite M as follows:

$$\begin{array}{cc}\hfill M& =\underset{i=1}{\overset{j-1}{⨂}}{E}_i\otimes M_j\otimes \underset{i=j+1}{\overset{t}{⨂}}{E}_i\hfill \\ & =E_1\otimes M_j\otimes E_2\hfill \end{array}$$

for $E_1={⨂}_{i=1}^{j-1}{E}_i$ and $E_2={⨂}_{i=j+1}^t{E}_i$. Then, the following equality holds:

$$\begin{array}{cc}\hfill e^M& =e^{E_1\otimes M_j\otimes E_2}\hfill \\ \hfill & =\sum _{j=0}^{\infty }{\displaystyle \frac{{(E_1\otimes M_j\otimes E_2)}^j}{j!}}\hfill \\ \hfill & ={(E_1\otimes M_j\otimes E_2)}^0+(E_1\otimes M_j\otimes E_2)+{\displaystyle \frac{1}{2}}{(E_1\otimes M_j\otimes E_2)}^2+\dots \hfill \\ \hfill & =(E_1^0\otimes M_j^0\otimes E_2^0)+(E_1\otimes M_j\otimes E_2)+{\displaystyle \frac{1}{2}}(E_1^2\otimes M_j^2\otimes E_2^2)+\dots \hfill \\ \hfill & =(E_1\otimes M_j^0\otimes E_2)+(E_1\otimes M_j\otimes E_2)+(E_1\otimes {\displaystyle \frac{1}{2}}{M}_j^2\otimes E_2)+\dots \hfill \\ \hfill & =E_1\otimes \left(M_j^0+M_j+{\displaystyle \frac{1}{2}}{M}_j^2+\dots \right)\otimes E_2\hfill \\ \hfill & =E_1\otimes e^{M_j}\otimes E_2\hfill \end{array}$$

As the remaining steps of the HHL algorithm do not depend on the matrix M, the claim follows.    □

Because of the simple structure of M from Lemma 4, the runtime of $HH{L}_M$ will be $\tilde{\mathcal{O}}\left({\kappa }_{M_j}·s_{M_j}·poly(logN)\right)$. This accounts for an overhead of $\tilde{\mathcal{O}}(logN)$ when compared to $HH{L}_{M_j}$ (under the assumption that $E_i$’s and $M_j$ are of relatively similar size).

Theorem 2.

Let $M={⨂}_{i=1}^t{M}_i$ be a vertical decomposition of a Hermitian M. Given $M_i$’s are Hermitian matrices as well, let $HH{L}_M$ and $HH{L}_{M_i}$ be the unitary HHL algorithm circuit for a matrix M and $M_i$, respectively. Then for all quantum states $|b\rangle$:

$$\begin{array}{c}\hfill HH{L}_M|b\rangle =\prod _{j=1}^t\left(\underset{i=1}{\overset{j-1}{⨂}}{E}_i\otimes HH{L}_{M_j}\otimes \underset{i=j+1}{\overset{t}{⨂}}{E}_i\right)|b\rangle \end{array}$$

and the result is a valid quantum state $|x\rangle$ from Problem 2.

Proof. 

Let $HH{L}_M$ and $HH{L}_{M_i}$ be the unitary circuit which implements the application of the HHL algorithm with input matrix M and $M_i$, respectively. Then, by the Lemmas 3 and 4, the following constructions are equal:

$$\begin{array}{cc}\hfill HH{L}_M& =\prod _{j=1}^t\left(HH{L}_{({⨂}_{i=1}^{j-1}{E}_i\otimes M_j\otimes {⨂}_{i=j+1}^t{E}_i)}\right)\hfill \\ \hfill & =\prod _{j=1}^t\left(\underset{i=1}{\overset{j-1}{⨂}}{E}_i\otimes HH{L}_{M_j}\otimes \underset{i=j+1}{\overset{t}{⨂}}{E}_i\right)\hfill \end{array}$$

Further, since ${\prod }_{j=1}^t\left({⨂}_{i=1}^{j-1}{E}_i\otimes HH{L}_{M_j}\otimes {⨂}_{i=j+1}^t{E}_i\right)$ is a valid quantum circuit, the output of the algorithm is a proper quantum state. Finally, as described in Section 2, the output of the algorithm is a vector $|x\rangle$ such that the following is true:

$$\begin{array}{c}\hfill A·\overrightarrow{x}=\overrightarrow{b}\end{array}$$

This is exactly the solution to Problem 2.    □

As the vertical construction is well-parallelizable, the runtime of the vertical HHL will be upper bound by the complexity of the most time-intensive inversion.

Theorem 3.

Let $M={⨂}_{i=1}^t{M}_i$ be a horizontal decomposition of a Hermitian matrix M. Further, for all $i=1,\dots ,t$, let $M_i\in {\mathbb{C}}^{N_i\times N_i}$ be a Hermitian matrix with ${\kappa }_i$ its condition number and $s_i$ its sparseness. The time complexity of the vertical HHL from Theorem 2 for the matrix M is:

$$\begin{array}{c}\hfill \tilde{\mathcal{O}}\left(t·\left(\underset{i}{max}{\kappa }_i·s_i·\mathit{poly}(log{N}_i)\right)\right)\end{array}$$

Proof. 

The time complexity of applying each $HH{L}_{M_i}$ on a subregister is upper-bound by applying the most cost-intensive one. As presented in Section 2.1, this corresponds to a time complexity as follows:

$$\begin{array}{c}\hfill \tilde{\mathcal{O}}\left(\underset{i}{max}{\kappa }_i·s_i·\mathrm{poly}(log{N}_i)\right)\end{array}$$

(6)

Further, applying $E_i$ to any subregister is equivalent to not evolving the register in any way. Therefore in each step, we apply $HH{L}_{M_i}$ to one of the subregisters and leave the other registers constant. Since we need to invert t sub-matrices, we have t steps, each upper-bound by Equation (6). This results in the runtime as follows:

$$\begin{array}{c}\hfill \tilde{\mathcal{O}}\left(t·(\underset{i}{max}{\kappa }_i·s_i·\mathrm{poly}(log{N}_i))\right)\end{array}$$

In our analysis, we implicitly hide the fact that, as mentioned in Section 2.1, in the HHL algorithm we need to perform a measurement of the ancilla register which, with a certain probability, might fail. However, using the amplitude amplification we can boost the probability of measuring the correct state to be almost 1 in $\mathcal{O}({\kappa }_i)$ steps for each HHL-subroutine. In [13], the authors describe a method how to slow the rotation down, when the amplitude of the correct state is big enough. In fact, for each subroutine, with $\mathcal{O}({\max }_i{\kappa }_i)$ steps we can obtain a probability of measuring the incorrect state upper-bound by ${\displaystyle \frac{1}{2t}}$. Then, for the state $|x\rangle$, which is the result of the vertical HHL algorithm, the probability of measuring at least a single $|0\rangle$ can be lower-bound by the following:

$$\begin{array}{cc}\hfill Pr\left({\displaystyle \frac{M|x\rangle }{\langle x|M^{†}M|x\rangle }}\ne {|1\rangle }^{\otimes t}\right)& \le \sum _{i=1}^{t}Pr\left({\displaystyle \frac{M|x\rangle }{\langle x|M^{†}M|x\rangle }}\ne \left(\underset{j=1}{\overset{i-1}{⨂}}|1\rangle \right)|0\rangle \left(\underset{j=i+1}{\overset{t}{⨂}}|1\rangle \right)\right)\hfill \\ \hfill & \le {\displaystyle \frac{1}{2t}}+\dots +{\displaystyle \frac{1}{2t}}\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}\hfill \end{array}$$

Therefore, with at least ${\displaystyle \frac{1}{2}}$ probability the vertical HHL algorithm will succeed. It should be noted that the ancilla registers indicate when one of the matrix inversions has failed.    □

Finally, we want to highlight that, in our considerations, all the subroutines $HH{L}_{M_j}$ are not executed at the exact same time. Instead, they are sequentially applied to each of the registers. We believe that simultaneously applying all the routines would not drastically change the result and could lead to a speed-up factor of $\tilde{\mathcal{O}}(t)$ compared to Theorem 3. We keep it as future research to formally prove the claim.

4. HHL for Möbius Transform

In this section, we introduce the Boolean Möbius transform, a building block of many cryptanalytical tools. Further, we present how the method from Section 3 can be used for the Möbius transform.

4.1. Möbius Transform of Boolean Functions

The Boolean Möbius transform is the mapping $\mu :{\mathbb{F}}_2^{2^n}\to {\mathbb{F}}_2^{2^n}$. It acts as the bijective transform between the ANF of a Boolean function f, and its truth table ${\mathcal{T}}_f$. It is defined in the following way:

$$\begin{array}{c}\hfill \forall x\in {\mathbb{F}}_2^n:f\left(x\right)=\underset{I\in {\mathbb{F}}_2^n}{⨁}\mu \left(f\right)\left(I\right)x^I,\end{array}$$

where $\mu \left(f\right)$ is the Boolean function defined through the coefficients [17] (cf. Equation (1)). For a Boolean function f, we can compute its Möbius transform in terms of matrices.

Claim 1.

 Let $T_n$ be a Boolean matrix recursively defined as:

1.

$\hspace{1em}{T}_1=\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)$

2.

$\hspace{1em}{T}_n=\left(\begin{array}{cc}{T}_{n-1}& O_{n-1}\\ T_{n-1}& T_{n-1}\end{array}\right)$

where $O_{n-1}$ is a $2^{n-1}\times 2^{n-1}$ 0-matrix.

For a Boolean function f, $T_n$ can serve as the Möbius transform acting on the truth table ${\mathcal{T}}_f$ and the corresponding ANF as follows:

• $\mu \left({\mathcal{A}}_f\right)={\mathcal{T}}_f$
• $\mu \left({\mathcal{T}}_f\right)={\mathcal{A}}_f$.

A direct consequence is that $T_n$ is self-inverse.

The above claim is thoroughly discussed in [18,19]. As a consequence, we can describe the Möbius transform as a tensor product of polynomial terms:

Lemma 5.

We can describe $T_n$ using the tensor product as:

$$\begin{array}{c}\hfill T_n=T_1\otimes T_{n-1}\end{array}$$

Proof. 

Using the definition of tensor products for matrices, we have the following:

$$\begin{array}{cc}\hfill T_1\otimes T_{n-1}& =\left(\begin{array}{cc}1·T_{n-1}& 0·T_{n-1}\\ 1·T_{n-1}& 1·T_{n-1}\end{array}\right)\hfill \\ & =\left(\begin{array}{cc}{T}_{n-1}& O_{n-1}\\ T_{n-1}& T_{n-1}\end{array}\right)\hfill \\ & =T_n\hfill \end{array}$$

   □

Lemma 6.

Let ${\mathcal{T}}_f\in {\mathbb{F}}_2^{2^n}$ be the truth table of a Boolean function f. Then we can compute the algebraic normal form of f as:

$$\begin{array}{c}\hfill {\mathcal{A}}_F=T_n{\mathcal{T}}_f=\prod _{j=1}^t\left(\underset{i=1}{\overset{j-1}{⨂}}{E}_1\otimes T_1\otimes \underset{i=j+1}{\overset{t}{⨂}}{E}_1\right){\mathcal{T}}_f\end{array}$$

Proof. 

By Claim 1 and Lemma 5, we know $T_n$ can be described as follows:

$$\begin{array}{c}\hfill T_n=\underset{i=1}{\overset{n}{⨂}}{T}_1\end{array}$$

Further, by Lemma 3, we know that the constructions are equivalent:

$$\begin{array}{c}\hfill \prod _{j=1}^t\left(\underset{i=1}{\overset{j-1}{⨂}}{E}_1\otimes T_1\otimes \underset{i=j+1}{\overset{t}{⨂}}{E}_1\right){\mathcal{T}}_f=\left(\underset{i=1}{\overset{n}{⨂}}{T}_1\right){\mathcal{T}}_f=T_n{\mathcal{T}}_f\end{array}$$

Finally, by using Claim 1, we know that $T_n{\mathcal{T}}_f={\mathcal{A}}_f$ proving the statement.    □

Example 1.

Let $f(X_1,X_2)=X_1\oplus X_1{X}_2$. Then, the truth table of f is ${\mathcal{T}}_f=\left(\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right)$. We will compute the ANF of f using the procedure mentioned in Lemma 6:

$$\begin{array}{cc}\hfill T_2{\mathcal{T}}_f& =(T_1\otimes E_1)·(E_1\otimes T_1){\mathcal{T}}_f\hfill \\ \hfill & =\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 1& 0& 1& 0\\ 0& 1& 0& 1\end{array}\right)·\left(\begin{array}{cccc}1& 0& 0& 0\\ 1& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 1& 1\end{array}\right)\left(\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right)\hfill \\ \hfill & =\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 1& 0& 1& 0\\ 0& 1& 0& 1\end{array}\right)\left(\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right)\hfill \\ \hfill & =\left(\begin{array}{c}0\\ 1\\ 0\\ 1\end{array}\right)\hfill \\ \hfill & ={\mathcal{A}}_f\hfill \end{array}$$

We highlight that the formula for the ANF of f from Lemma 6 resembles the formula mentioned in Theorem 2. We will next show that by using the HHL algorithm we can mimic the application of $T_n$ and the result will be a quantum state which represents the ${\mathcal{A}}_f$.

4.2. Möbius Transform Using HHL

In this section, we show how to tackle a specific initialization of Problem 2. We will compute the preimage of the matrix $T_n$ describing the Möbius transform.

Problem 3.

Given a matrix $T_n\in {\mathbb{F}}_2^{2^n\times 2^n}$ defined in Claim 1, and an input state

$$\begin{array}{c}\hfill |b\rangle =\sum _{i=0}^{2^n-1}{b}_i|i\rangle \end{array}$$

with $\overrightarrow{b}=(b_0,\dots ,b_{2^n-1})\in {\mathbb{C}}^{2^n}$, find the state $|x\rangle ={\sum }_{i=0}^{2^n-1}{x}_i|i\rangle$ such that:

$$\begin{array}{c}\hfill T_n·\overrightarrow{x}=\overrightarrow{b}\end{array}$$

As we have seen in Section 2, inverting the matrix $T_n$ would solve Problem 3. However, we cannot simply apply the HHL algorithm for matrix $T_n$ to an arbitrary register $|b\rangle$. First, observe that $T_n$ is defined as an ${\mathbb{F}}_2$-matrix, while HHL operates over $\mathbb{C}$. Instead, we need to use the reduction mentioned in Section 2.2 to create a different matrix ${\mathrm{\Gamma }}_n$, which delivers the same result as $T_n$ over ${\mathbb{F}}_2$. We need additional variables and equations to force the solution to be an ${\mathbb{F}}_2$-vector and ensure that the addition modulo 2 is correct. It must be noted that this procedure will expand the size of the matrix only polynomially.

Second, the HHL algorithm requires the matrix to be inverted to be Hermitian. The resulting matrix ${\mathrm{\Gamma }}_n$ is not. We can use the procedure already mentioned in Section 2 by [3]. The main idea is that, for an arbitrary matrix M that is not Hermitian, we can construct a new matrix $C_M$:

$$\begin{array}{c}\hfill C_M: =\left(\begin{array}{cc}0& M\\ M^{†}& 0\end{array}\right),\end{array}$$

and the matrix $C_M$ will be Hermitian. Since, for our target matrix ${\mathrm{\Gamma }}_n$, all the entries are real, it is clear that ${\mathrm{\Gamma }}_n^{†}={\mathrm{\Gamma }}_n^T$. No conjugation needs to be calculated to provide oracle access to ${\mathrm{\Gamma }}_n^{†}$. Instead, we now also need the column-oracle of the matrix (cf. Section 2.1). The reason for this is the observation that the bottom rows of $C=\left(\begin{array}{cc}0& {\mathrm{\Gamma }}_n\\ {\mathrm{\Gamma }}_n^{†}& 0\end{array}\right)$ are in fact the rows of ${\mathrm{\Gamma }}_n^{†}={\mathrm{\Gamma }}_n^T$, which are actually the columns of ${\mathrm{\Gamma }}_n$. For matrices of exponentially big sparsity, this is an additional requirement.

Further, the input vector must be adjusted. While, for ${\mathrm{\Gamma }}_n$, the input was a vector of the form $\overrightarrow{b}$, for the new matrix C we need the vector $\tilde{b}:=\left(\begin{array}{c}\overrightarrow{b}\\ 0\end{array}\right)$. Also, the output will have a different form, $\tilde{x}:=\left(\begin{array}{c}0\\ \overrightarrow{x}\end{array}\right)$, due to the following:

$$\begin{array}{cc}\hfill C·\tilde{x}& =\left(\begin{array}{cc}0& {\mathrm{\Gamma }}_n\\ {\mathrm{\Gamma }}_n^{†}& 0\end{array}\right)·\left(\begin{array}{c}0\\ \overrightarrow{x}\end{array}\right)\hfill \\ & =\left(\begin{array}{c}{\mathrm{\Gamma }}_n·\overrightarrow{x}\\ 0\end{array}\right)\hfill \\ & =\left(\begin{array}{c}\overrightarrow{b}\\ 0\end{array}\right)\hfill \\ & =\tilde{b}\hfill \end{array}$$

(7)

There is one problem when we try to apply this approach to the matrix $T_n$. The sparsity plays a crucial role in the runtime of the HHL. As the Boolean Möbius transform always has one full column, the sparseness of $T_n$ is exponential:

$$\begin{array}{c}\hfill s\left(T_n\right)=2^n.\end{array}$$

We will overcome the runtime implications of the high sparsity of $T_n$ as input to HHL using the decomposition technique.

4.3. Booleanized $T_n$ vs. Booleanized $T_1$

To overcome the exponentially big runtime of $HH{L}_{T_n}$, we will instead call the HHL with the Boolean Möbius transform for each single qubit. Again, we want to highlight that the HHL algorithm requires a Hermitian matrix, which neither $T_1$ nor $T_n$ are. In the construction above, we Booleanized the matrix $T_n$ to guarantee that the addition is performed modulo 2 and the solution is an ${\mathbb{F}}_2$-vector. However, it is not guaranteed that the matrix ${\mathrm{\Gamma }}_n$ can be decomposed into a tensor of small matrices.

Instead, for the vertical HHL, we will first decompose the matrix $T_n$, and then perform the Booleanization on each sub-matrix $T_1$. Refs. [7,8] mentioned a set of additional or alternative equations, which when incorporated into the equation system, allow ${\mathbb{F}}_2$-computation. In the example below, we present one candidate for such a matrix.

Example 2.

Using the techniques mentioned in Section 2.2, we contruct a matrix ${\mathrm{\Gamma }}_1^{\prime }\in {\mathbb{C}}^{5\times 5}$. For $a,b\in {\mathbb{F}}_2$, the preimage under ${\mathrm{\Gamma }}_1^{\prime }$ of the vector $\overrightarrow{b}=\left(\begin{array}{c}{b}_0\\ b_1\\ 0\\ 0\\ 0\end{array}\right)$ has the form:

$$\begin{array}{c}\hfill \overrightarrow{x}=\left(\begin{array}{c}{T}_1^{-1}\left(\begin{array}{c}{b}_0\\ b_1\end{array}\right){|}_0\\ T_1^{-1}\left(\begin{array}{c}{b}_0\\ b_1\end{array}\right){|}_1\\ \ast \\ \ast \\ \ast \end{array}\right)=\left(\begin{array}{c}{T}_1^{-1}\left(\begin{array}{c}{b}_0\\ b_1\end{array}\right)\\ \ast \\ \ast \\ \ast \end{array}\right)\end{array}$$

We define ${\mathrm{\Gamma }}_1^{\prime }$ as:

$$\begin{array}{c}\hfill {\mathrm{\Gamma }}_1^{\prime }=\left(\begin{array}{ccccc}1& 0& 0& 0& 0\\ -2& -2& 2& 1& 1\\ 1& 0& 0& 1& 0\\ 0& 1& 0& 0& 1\\ 0& 1& 0& 0& -1\end{array}\right)\end{array}$$

(8)

such, that:

$$\begin{array}{ccccc}\hfill & {\mathrm{\Gamma }}_1^{\prime }\left(\begin{array}{c}\mathit{0}\\ \mathit{0}\\ 0\\ 0\\ 0\end{array}\right)=\left(\begin{array}{c}\mathit{0}\\ \mathit{0}\\ 0\\ 0\\ 0\end{array}\right),\hfill & \hfill {\mathrm{\Gamma }}_1^{\prime }\left(\begin{array}{c}\mathit{1}\\ \mathit{0}\\ 1\\ 1\\ 0\end{array}\right)=\left(\begin{array}{c}\mathit{1}\\ \mathit{1}\\ 0\\ 0\\ 0\end{array}\right),& {\mathrm{\Gamma }}_1^{\prime }\left(\begin{array}{c}\mathit{0}\\ \mathit{1}\\ 1\\ 0\\ 1\end{array}\right)=\left(\begin{array}{c}\mathit{0}\\ \mathit{1}\\ 0\\ 0\\ 0\end{array}\right),\hfill & \hfill {\mathrm{\Gamma }}_1^{\prime }\left(\begin{array}{c}\mathit{1}\\ \mathit{1}\\ 1\\ 1\\ 1\end{array}\right)=\left(\begin{array}{c}\mathit{1}\\ \mathit{0}\\ 0\\ 0\\ 0\end{array}\right)\end{array}$$

The construction uses a handful of extra qubits for each HHL application, however, the number of needed qubits will stay polynomial in terms of the size of the register holding the state $|b\rangle$. The matrix must be Hermitianized before being plugged into the HHL (see Equation (7)). The result will be a matrix ${\mathrm{\Gamma }}_1$. We want to highlight that the sparsity in Example 2 does not depend on the number n:

$$\begin{array}{c}\hfill s\left({\mathrm{\Gamma }}_1\right)=5\end{array}$$

and the condition number ${\kappa }_{{\mathrm{\Gamma }}_1}$ is constant.

With the machinery in place, we can solve Problem 3 using the algorithm from Theorem 2. Further, we can estimate the runtime of the algorithm:

Theorem 4.

Let $T_n={⨂}_{i=1}^n{T}_1$ be a horizontal decomposition of $T_n$. Further, let ${\mathrm{\Gamma }}_1\in {\mathbb{C}}^{\mathcal{O}\left(1\right)\times \mathcal{O}\left(1\right)}$ be the Booleanized version of $T_1$. Then, using the vertical HHL algorithm with input ${\mathrm{\Gamma }}_1$, for an arbitrary quantum state $|b\rangle$, we can solve Problem 3 in $\tilde{\mathcal{O}}(n)$ time.

Proof. 

As seen in Theorem 1, for a matrix decomposition $M={⨂}_{i=1}^t{M}_i$, the runtime is as follows:

$$\begin{array}{c}\hfill \tilde{\mathcal{O}}\left(t·(\underset{i}{max}{\kappa }_i·s_i·\mathrm{poly}(log{N}_i))\right)\end{array}$$

In our case, all $M_i$’s correspond to the Booleanized version of the $T_1$ matrix. We can use the techniques mentioned in Section 2.2 to create a Booleanized ${\mathrm{\Gamma }}_1$. All the reduction steps keep the sparsity, the condition number, and the size of the resulting matrix polynomial in terms of the size of $T_1$ [7]. Let $s_{{\mathrm{\Gamma }}_1},{\kappa }_{{\mathrm{\Gamma }}_1},N_{{\mathrm{\Gamma }}_1}$ be the sparsity, condition number, and size of the matrix ${\mathrm{\Gamma }}_1$, respectively. Plugging the values into the upper-bound, we obtain the collected runtime for the algorithm:

$$\begin{array}{c}\hfill \tilde{\mathcal{O}}\left(t·(\underset{i}{max}{\kappa }_i·s_i·\mathrm{poly}(log{N}_i))\right)=\tilde{\mathcal{O}}\left(n·({\kappa }_{{\mathrm{\Gamma }}_1}·s_{{\mathrm{\Gamma }}_1}·log(N_{{\mathrm{\Gamma }}_1}))\right)=\tilde{\mathcal{O}}\left(n\right)\end{array}$$

Keeping in mind that Problem 3 is an initialization of Problem 2, as well as Theorem 4 is an initialization of Theorem 2, the claim follows.    □

4.4. How to Generate Input

We propose two approaches to generate the input $|b\rangle$ as described in Problem 3. They will consider two different settings and target different encryption scheme types. We first introduce the Q1 model, the more realistic yet less powerful one. In Q1 model, the attacker has access to a quantum computer and some classical oracle. This is the standard model used for Shor’s or Grover’s algorithm. In the Q2 model, we assume a quantum oracle to which the attacker has access. A quantum oracle allows superposition queries. While this attack scenario is based on a very strong assumption, it might still lead to interesting insights into ciphers structure [20,21].

Our Q1 attack will target plaintext-independent constructions, like classical stream ciphers or block ciphers in counter-mode with fixed IVs. Since for a fixed cipher f and a fixed IV value we can build a deterministic classical circuit, we are also able to build its unitary version $U_f$ [22]. Using $U_f$ and an equally distributed superposition of all states, we can prepare the following state in polynomial time:

$$\begin{array}{c}\hfill |x\rangle |y\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}\sum _{i=0}^{2^n-1}|i\rangle |f\left(i\right)\rangle .\end{array}$$

Now, when we measure a $|1\rangle$ in the second register, only values i for which $f\left(i\right)=1$ will remain with a non-zero amplitude in the superposition:

$$\begin{array}{c}\hfill |x\rangle |y\rangle ={\displaystyle \frac{1}{\sqrt{\mathrm{hw}\left({\mathcal{T}}_f\right)}}}\sum _{\begin{array}{c}i=0\\ f\left(i\right)=1\end{array}}^{2^n-1}|i\rangle |1\rangle .\end{array}$$

The register $|x\rangle$ has now exactly the desired form of $|b\rangle$ from Problem 3, and each $b_i$ corresponds to the bit output for a given key i. Obviously, the $|1\rangle$ measurement only happens with a certain probability. However, as in the cryptographic setting, we mostly work with functions that are almost balanced [2], and we expect the probability to measure the desired state to be fairly high. For a Boolean function f, the said probability is the ratio of the Hamming weight of ${\mathcal{T}}_f$ and the size of its truth table, as it is for a balanced function $\frac{1}{2}$. We show the exact procedure in Algorithm 1.

Algorithm 1: Q1 model input preparation for Problem 3

Input: Quantum implementation $U_f$ of a keyed cipher $f:{\{0,1\}}^n\to \{0,1\}$

$\mathbf{1} |x\rangle |y\rangle \leftarrow {|0\rangle }^{\otimes n}|0\rangle$;

$\mathbf{2} |x\rangle |y\rangle \leftarrow H_n|x\rangle |y\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}{\sum }_{i=0}^{2^n-1}|i\rangle |0\rangle$;

$\mathbf{3} |x\rangle |y\rangle \leftarrow U_f|x\rangle |y\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}{\sum }_{i=0}^{2^n-1}|i\rangle |f\left(i\right)\rangle$;

$\mathbf{4}$ Measure register $|y\rangle$;

$\mathbf{5}$ If $|y\rangle ==|0\rangle$ go to step 1;

$\mathbf{6}$ return $|x\rangle$;

Output: $|b\rangle ={\sum }_{i=0}^{2^n-1}{b}_i|i\rangle$, where $b_i$ is the value of $f\left(i\right)$ scaled by the factor      ${\displaystyle \frac{1}{\sqrt{\mathrm{hw}\left({\mathcal{T}}_f\right)}}}$ to produce a valid quantum state.

In the Q2 model, we can perform a similar trick to retrieve the superposition of all outputs of a function with a fixed key. The superposition, however, encapsulates the possible inputs to an encryption function with a secret key. Especially in the case where there are weak keys, this might allow retrieving some additional information about the key and some encrypted plaintext. The Q2 attack resembles the previous one and is presented in Algorithm 2.

Algorithm 2: Q2 model input preparation for Problem 3

Input: Quantum oracle ${\mathcal{O}}_{f_k}$ for a cipher $f_k:{\{0,1\}}^n\to \{0,1\}$

$\mathbf{1} |x\rangle |y\rangle \leftarrow {|0\rangle }^{\otimes n}|0\rangle$;

$\mathbf{2} |x\rangle |y\rangle \leftarrow H_n|x\rangle |y\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}{\sum }_{i=0}^{2^n-1}|i\rangle |0\rangle$;

$\mathbf{3} |x\rangle |y\rangle \leftarrow U_{f_k}|x\rangle |y\rangle ={\displaystyle \frac{1}{\sqrt{2^n}}}{\sum }_{i=0}^{2^n-1}|i\rangle |f_k\left(i\right)\rangle$;

$\mathbf{4}$ Measure register $|y\rangle$;

$\mathbf{5}$ If $|y\rangle ==|0\rangle$ go to step 1;

$\mathbf{6}$ return $|x\rangle$;

Output: $|b\rangle ={\sum }_{i=0}^{2^n-1}{b}_i|i\rangle$, where $b_i$ is the value of $f_k\left(i\right)$ scaled by the factor      ${\displaystyle \frac{1}{\sqrt{\mathrm{hw}\left({\mathcal{T}}_{f_k}\right)}}}$ to produce a valid quantum state.

5. Cryptographic Use-Case

In this section, we want to use the HHL algorithm for Möbius transform to perform cryptanalysis of Boolean functions. We begin with an approach that allows creating the state $|{\mathcal{A}}_f\rangle$, which might be polynomially reconstructible for sparse functions.

5.1. Retrieving the Algebraic Normal Form

In Section 4.2, we showed how to generate the input corresponding to the ${\mathcal{T}}_f$ for a Boolean function f. The procedure runs in polynomial time and the result is a vector of the following form:

$$\begin{array}{c}\hfill |{\mathcal{T}}_f\rangle ={\displaystyle \frac{1}{\sqrt{\mathrm{hw}\left({\mathcal{T}}_f\right)}}}\sum _{\begin{array}{c}i=0\\ f\left(i\right)=1\end{array}}^{2^n-1}|i\rangle ={\displaystyle \frac{1}{\sqrt{\mathrm{hw}\left({\mathcal{T}}_f\right)}}}·{\mathcal{T}}_f\end{array}$$

We also showed how to construct the matrix input ${\mathrm{\Gamma }}_1$ for the HHL algorithm, which corresponds to the Boolean Möbius transform. The matrix is sparse and of low condition number and a constant size. The HHL algorithm would take constant time to run for a single instance of ${\mathrm{\Gamma }}_1$, and $\tilde{\mathcal{O}}\left(n\right)$ time to apply the Möbius transform to the whole register (cf. Theorem 4).

As seen in Section 4.1, applying $T_n$ to the vector ${\mathcal{T}}_f$ results in a vector which describes the algebraic normal form of the function f. A similar result is obtained when the vertical HHL algorithm with ${\mathrm{\Gamma }}_1$ input is applied to the register $|{\mathcal{T}}_f\rangle$.

Theorem 5.

Let $HH{L}_{{\mathrm{\Gamma }}_n}$ be the vertical application of $HH{L}_{{\mathrm{\Gamma }}_1}$ to n qubits:

$$\begin{array}{c}\hfill HH{L}_{{\mathrm{\Gamma }}_n}|b\rangle |ancilla\rangle :=\prod _{j=1}^n\left(\underset{i=1}{\overset{j-1}{⨂}}{E}_1\otimes HH{L}_{{\mathrm{\Gamma }}_1}\otimes \underset{i=j+1}{\overset{n}{⨂}}{E}_1\right)|b\rangle |ancilla\rangle \end{array}$$

The ancilla register is needed to cover for the special Booleanized construction of ${\mathrm{\Gamma }}_1$. Then, applying the $HH{L}_{{\mathrm{\Gamma }}_n}$ to the state $|{\mathcal{T}}_f\rangle$ results in the following register:

$$\begin{array}{c}\hfill HH{L}_{{\mathrm{\Gamma }}_n}|{\mathcal{T}}_f\rangle |ancilla\rangle =|{\mathcal{A}}_f\rangle |ancilla\rangle =\left({\displaystyle \frac{1}{\sqrt{hw\left({\mathcal{A}}_f\right)}}}·{\mathcal{A}}_f\right)|ancilla\rangle \end{array}$$

With an additional measurement of some helper register we can obtain the pure state $|{\mathcal{A}}_f\rangle$.

Proof. 

As seen in Theorem 4, applying the vertical HHL approach with ${\mathrm{\Gamma }}_1$ input allows for computing of the preimage of the input vector $|b\rangle$. The result is equivalent to the preimage of $\overrightarrow{b}$ under the Boolean Möbius transformation $T_n$. As seen in Claim 1, the result is a vector ${\mathcal{A}}_f$ holding the algebraic normal form of f scaled by a factor dependent on the superposition. Finally, we can discard the ancilla register (or perform some additional conditional measurement) and only consider the register $|{\mathcal{A}}_f\rangle$. □

The resulting register corresponds to the vector description of the ANF of f, scaled by a factor. The important observation is that only the coefficients which are one have a non-zero amplitude.

5.1.1. Sparse ANF Representation

Classically, reconstruction of an unknown Boolean function is a difficult problem. One of the approaches can be obtained from the learning theory and is based on the Fourier spectrum [2]. One can also use the Formula (1) mentioned in Section 1.2 to reveal the ANF. While obtaining the coefficients of low degree coefficients is not problematic, the complexity grows exponentially with the degree of the coefficient. On the other hand, if the degree of the coefficient is too high, it affects a small number of possible outputs and has a low influence on the truth table of the function.

When considering the result of the algorithm described in Theorem 5, we want to highlight that the state $|{\mathcal{A}}_f\rangle$ is an equally distributed superposition of all the base states which contribute to the ANF. Upon measurement, we obtain any of the ANF’s active (non-zero) coefficients with the same probability. The difference, opposing the classical scenario, is that the number of steps we need for each coefficient is independent of the coefficient’s degree. Especially for Boolean functions with sparse representation (polynomial number of coefficients with respect to n) and many high-order coefficients, the ANF reconstruction can be significantly sped up. Simple measurements can be combined with techniques like amplitude amplification to guarantee that the whole ANF is properly recovered in polynomial time [13].

In the Q1 model, retrieving the ${\mathcal{A}}_f$ can give us information about the secret key that is being used to generate some bit-stream. By combining information from multiple Boolean functions (e.g., multiple one-bit projections generated by the stream cipher) we could build a polynomial-size equation system which can be solved for the secret key. The ANF obtained in the Q2 model does not give us direct information about the key, but could be used to decrypt future ciphertexts.

5.1.2. Estimating the Number of Terms

In some cases, especially when $\mathrm{hw}\left({\mathcal{A}}_f\right)$ is super-polynomial, we might consider other properties of f rather than its ANF. The state $|{\mathcal{A}}_f\rangle$ allows us to estimate the number of non-zero coefficients in the algebraic normal form of the Boolean function. We can achieve this using a technique called Quantum Amplitude Estimation [13].

Quantum amplitude estimation deals with a problem connected to the Grover’s algorithm setting. However, instead of searching for an $\{x\in X:f(x)=1\}$, we are interested in the size of said set. Similarly, as in Grover’s algorithm, the algorithm divides the space into two subspaces following some indicator function f:

$$\begin{array}{c}\hfill |\Psi \rangle =|{\Psi }_1\rangle +|{\Psi }_0\rangle \end{array}$$

We call $|{\Psi }_1\rangle$ the good components and $|{\Psi }_0\rangle$ the bad components. We want to estimate the probability of measuring a good component. To achieve it, the algorithm uses the famous Grover’s operator combined with phase estimation. After [13] was published, other potential candidates to solve the same problem were constructed [23,24,25].

We begin with a straightforward observation that the state $|{\mathcal{A}}_f\rangle$ is an equal superposition of all states which correspond to the non-zero coefficients of ${\mathcal{A}}_f$. This means that the amplitudes of $|{\mathcal{A}}_f\rangle$ are only zeros and ones scaled by a factor of ${\displaystyle \frac{1}{\sqrt{\mathrm{hw}\left({\mathcal{A}}_f\right)}}}$. If we were able to estimate the amplitude of one of the active entries, we could determine the Hamming weight $\mathrm{hw}\left({\mathcal{A}}_f\right)$. This is exactly the sparsity of the function f. Further, since all non-zero amplitudes are equal, we just need to find the amplitude of a single element from the ANF (e.g., by measuring $|{\mathcal{A}}_f\rangle$ we find the element from ${\mathcal{A}}_f$ and subsequently estimate its amplitude). Sometimes, we might not be interested in finding the exact number but rather proving that it is above a certain threshold. Since most of the amplitude estimation algorithms have their runtime dependent on an error threshold, we could verify if the amplitude is only smaller than some value, which guarantees the desired ANF sparseness.

We could iterate the above ideas to prove additional properties. By carefully choosing the function used for amplitude estimation, we could check how many higher-order terms are in the ANF. The good states (as defined in [13]) could be the terms with a degree greater than some threshold. This task would take exponential time in the classical scenario, but could be efficiently performed on a quantum computer.

5.1.3. Comparison to Classical Approaches

Retrieving the algebraic normal form of a Boolean function is a concept closely related to computational learning theory. In the classical scenario, given a set of samples of the form ${\left(x,f\left(x\right)\right)}_{x\in \mathcal{S}}$, we want to compute a function $\tilde{f}$ such that the following is true:

$$\begin{array}{c}\hfill \underset{x\in {\{0,1\}}^n}{Pr}\left(\tilde{f}\left(x\right)=f\left(x\right)\right)\ge c\end{array}$$

for some non-negligible constant c. Obviously, reconstructing the original function f would solve this problem. However, since higher-order terms of ${\mathcal{A}}_f$ only influence a few outputs, ignoring terms with orders bigger than some predetermined value t might be beneficial. How many such high-order terms might be ignored depends on the value of c.

In [2], a learning approach is proposed, which relies on determining the Fourier coefficients of f instead of its ANF. As there are $2^n$ such coefficients, and computing each one is not a trivial task; for bigger n-values, this is not a manageable approach. The corollary below estimates the runtime of such an approach for a specific set of with total influence bounded by some value t.

Corollary 1

([2]). Let $\mathit{I}\left(f\right)$ be the total influence of a Boolean function f, defined as:

$$\begin{array}{c}\hfill \mathit{I}\left(f\right)=\sum _{S\subseteq \left[n\right]}\left|S\right|\widehat{f}{\left(S\right)}^2,\end{array}$$

where $\widehat{f}\left(S\right)$ are the Fourier coefficients of f.

For $t\ge 1$, let $\mathcal{C}=\{f:{\{-1,1\}}^n\to \{-1,1\}|\mathit{I}\left(f\right)\le t\}$. Then $\mathcal{C}$ is learnable from random examples with error ϵ in time $n^{\mathcal{O}(t/ϵ)}$.

An alternate approach would be learning the actual ANF coefficients of the function f. As mentioned in Section 1.2, the formula for a coefficient of the term $x^I$ is as follows:

$$\begin{array}{c}\hfill c_I=\sum _{supp\left(x\right)\subseteq I}f\left(x\right).\end{array}$$

So, to compute a coefficient of order $deg\left(I\right)=t$, we need to evaluate the function f at $2^t$ inputs and add them together. For higher-order terms, the number of computational steps is thus $\mathcal{O}\left(2^t\right)$.

In comparison, our approach depends solely on n and the Hamming weight of the algebraic normal form of f. The high-order coefficients are as easy to determine as the low-order terms. Furthermore, we are not aware of any classical algorithm other than trivial counting, which determines the Hamming weight of the ANF of a function.

Historically, certain sparse but high-order functions were used in cryptography. A famous example, the Toyocrypt cipher, was attacked in [26]. Even though the polynomial used there was not secret, some of the currently used ciphers may use functions with sparse polynomial representation.

5.2. Algebraic Transition Matrix

Another approach using a concept closely related to the Boolean Möbius Transform was proposed in [5]. For a vectorial Boolean function $F:{\{0,1\}}^n\to {\{0,1\}}^m$, ref. [5] define a linear operator mapping from ${\delta }_x$ to ${\delta }_{F\left(x\right)}$, where ${\delta }_x$ is the Kronecker delta function. The operator is called a transition matrix:

Definition 1

(Transition matrix [5]). Let $\mathbb{K} \text{be a field and let} F:{\mathbb{F}}_2^n\to {\mathbb{F}}_2^m$ be a vectorial Boolean function. Define $T^F:{\mathbb{K}}^{{\mathbb{F}}_2^n}\to {\mathbb{K}}^{{\mathbb{F}}_2^m}$ as the unique linear operator that maps ${\delta }_x$ to ${\delta }_{F\left(x\right)}$. The transition matrix of F is the coordinate representation of $T^F$ with respect to the Kronecker delta bases of ${\mathbb{K}}^{{\mathbb{F}}_2^n}$ and ${\mathbb{K}}^{{\mathbb{F}}_2^m}$.

The transition matrix has a set of useful properties which allow combining smaller transformations to a bigger, more complex one [5]. However, in this paper, we will not focus on those and rather will show that, in the Q2 model, we can obtain oracle access to the transition matrix.

Example 3

([5]). Consider a function $F:{\mathbb{F}}_2^2\to {\mathbb{F}}_2^2$ defined as

$$\begin{array}{c}\hfill F(x_1,x_2)=(F_1(x_1,x_2),F_2(x_1,x_2))\mapsto (x_2+1,x_1+x_1{x}_2)\end{array}$$

The truth table of such a function is as follows:

$$\begin{array}{cc}\hfill F:& (0,0)\mapsto (1,0)\hfill \\ \hfill & (1,0)\mapsto (1,1)\hfill \\ \hfill & (0,1)\mapsto (0,0)\hfill \\ \hfill & (1,1)\mapsto (0,0)\hfill \end{array}$$

The transition matrix $T^F$ is then: as follows

$$T^F=\begin{array}{cc}& \begin{array}{cccc}(0,0)& (1,0)& (0,1)& (1,1)\end{array}\\ \begin{array}{c}(0,0)\\ (1,0)\\ (0,1)\\ (1,1)\end{array}& ( \begin{array}{cccc}0& 0& 1& 1\\ 1& 0& 1& 1\\ 0& 0& 0& 0\\ 0& 1& 0& 0\end{array} )\end{array}$$

We want to highlight that, given a column index i, the only non-zero entry appears in the $F\left(i\right)$’th row. If we allow superposition queries to the function F (as is assumed in the Q2 model), we have a quantum column-oracle for the transition matrix. To obtain the row-oracle which, given a row index, returns the indices of non-zero entries in that row, we additionally need an oracle for the $F^{-1}$ function. For a permutation, the oracle acts as a bijection. However, as seen in the example above, this must not be the case in general. With some assumptions about the maximal number of elements $\nu$ that map to the same value, we can still solve this problem with a bigger output register. We also want to highlight that such a matrix is well-suited for the HHL algorithm—the sparseness and condition number can be upper-bound by $s=\mathcal{O}\left(\nu \right)=\kappa$. Especially for F, which is a permutation, the runtime of HHL with $T^F$ is $\tilde{\mathcal{O}}(n+m)$.

While the transition matrix is not necessarily useful in the HHL setting, they are a building block of a more interesting construction. We will first introduce a dual to the Boolean Möbius transform, as defined in [5], and then use it to build an algebraic transition matrix.

Definition 2

(Dual Boolean (binary) Möbius Transformation [5]). The dual Boolean Möbius transformation of a Boolean function $f\in {\mathbb{F}}_2^{{\mathbb{F}}_2^n}$ is the Boolean function ${\mathcal{P}}_n\left(f\right)=\tilde{f}\in {\mathbb{F}}_2^{{\mathbb{F}}_2^n}$, where $\tilde{f}\left(u\right)$ is the coordinate of f corresponding to ${\pi }_u$ in the precursor basis. The precursor basis vectors ${\pi }_u$ are the indicator function of precursor sets:

$$\begin{array}{c}\hfill {\pi }_u={\mathbb{1}}_{\left\{supp\right(x)\subseteq u\}}\end{array}$$

The matrix representation of ${\mathcal{P}}_n$ has the following form:

$$\begin{array}{c}\hfill {\mathcal{P}}_n={\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)}^{\otimes n}\end{array}$$

Observe that the dual Boolean Möbius transform ${\mathcal{P}}_n$ is actually the transpose of $T_n$ defined in Section 4.1. By techniques similar to the ones mentioned above, we can also Booleanize ${\mathcal{P}}_n$. With the definitions above, we can finally introduce the algebraic transition matrices:

Definition 3

(Algebraic Transition Matrix [5]). Let $F:{\mathbb{F}}_2^n\to {\mathbb{F}}_2^m$ be a vectorial Boolean function. Define $A^F:{\mathbb{F}}_2^{{\mathbb{F}}_2^n}\to {\mathbb{F}}_2^{{\mathbb{F}}_2^m}$ as the dual Boolean Möbius transformation of $T^F$. That is:

$$\begin{array}{c}\hfill A^F={\mathcal{P}}_m{T}^F{\mathcal{P}}_n^{-1}\end{array}$$

The algebraic transition matrix of F is the coordinate representation of $T^F$ with respect to the precursor bases of ${\mathbb{F}}_2^{{\mathbb{F}}_2^n}$ and ${\mathbb{F}}_2^{{\mathbb{F}}_2^m}$.

The algebraic transition matrix can be computed as a horizontal decomposition of three matrices, two dual Möbius transforms and a transition matrix. We observe that like the Boolean Möbius transform, its dual is self-inverse. So in fact, we can compute $A^F$ as follows:

$$\begin{array}{c}\hfill A^F={\mathcal{P}}_m{T}^F{\mathcal{P}}_n\end{array}$$

The HHL algorithm for each of those matrices runs in time $\mathcal{O}(m+n)$. The two dual transforms can be vertically decomposed (cf. Figure 1b) using the technique from Section 4.2, while $T^F$ is well-suited for HHL as we argued above. We can combine the three HHL routines by straight concatenation:

$$\begin{array}{c}\hfill HH{L}_{A^F}|b\rangle =HH{L}_{{\mathcal{P}}_m}\circ HH{L}_{T^F}\circ HH{L}_{{\mathcal{P}}_n}|b\rangle \end{array}$$

As a result, we can compute the preimage of a quantum state $|b\rangle$ under the algebraic transition matrix in polynomial time by combining the classical HHL algorithm with the vertical HHL.

5.2.1. Interpretation of ATMs Mappings

The algebraic transition matrix gives us deep insights into the vectorial Boolean function which is being investigated. In [5], the authors show that, for $I=(i_1,\dots ,i_m)$, $J=(j_1,\dots ,j_n)$, the matrix $A^F$ following holds:

$$\begin{array}{c}\hfill {\left(A^F\right)}_{(I,J)}=1\iff {\mathcal{A}}_{\left({\prod }_{k=1}^m{F}_k^{i_k}\right)}{|}_J=1,\end{array}$$

where ${\mathcal{A}}_{\left({\prod }_{k=1}^m{F}_k^{i_k}\right)}{|}_J$ is the Jth coefficient $c_J$ of the algebraic normal form of the Boolean function f as defined in Section 1.2.

Using the HHL algorithm does not give us direct access to the algebraic transition matrix. However, ref. [5] comes with a theorem which explains the result of multiplying $A^F$ by some vector $g\in {\mathbb{F}}_2^{{\mathbb{F}}_2^m}$:

Theorem 6

(Property of Algebraic Transition Matrices [5]). Let $F:{\mathbb{F}}_2^n\to {\mathbb{F}}_2^m$ be a vectorial Boolean function and $A^F$ its algebraic transition matrix. Further, let $g:{\mathbb{F}}_2^m\to {\mathbb{F}}_2$ be a Boolean function with m inputs. Then:

$$\begin{array}{c}\hfill {\mathcal{A}}_{g\circ F}={\left(A^F\right)}^T{\mathcal{A}}_g\end{array}$$

In other words, for a given Boolean function of the form $h=g\circ F$, using the HHL algorithm with input matrix $A^F$ and a vector $|h\rangle$, we can find the state $|g\rangle$ which encapsulates the searched function.

Example 4

([5]). Consider a function $F:{\mathbb{F}}_2^2\to {\mathbb{F}}_2^2$ defined as follows

$$\begin{array}{c}\hfill F(x_1,x_2)=(F_1(x_1,x_2),F_2(x_1,x_2))\mapsto (x_2+1,x_1+x_1{x}_2)\end{array}$$

The algebraic transition matrix $A^F$ is then as follows:

$$A^F=\begin{array}{cc}& \begin{array}{cccc}1& x_1& x_2& x_1{x}_2\end{array}\\ \begin{array}{c}1\\ F_1\\ F_2\\ F_1·F_2\end{array}& \left(\begin{array}{cccc}1& 0& 0& 0\\ 1& 0& 1& 0\\ 0& 1& 0& 1\\ 0& 1& 0& 1\end{array}\right)\end{array}$$

The rows correspond to products of the projection functions $F_i$’s, while the columns indicate whether the coefficient of each $x^I$ is one or zero.

The algebraic transition matrix also allows quick computation of the Boolean function obtained by composition of F with any Boolean function. For example for the Boolean function $g(x_1,x_2)=x_1+x_2$, we can compute $g\circ F$:

$$\begin{array}{cc}\hfill {\left(A^F\right)}^T·{\mathcal{A}}_g& ={\left(\begin{array}{cccc}1& 0& 0& 0\\ 1& 0& 1& 0\\ 0& 1& 0& 1\\ 0& 1& 0& 1\end{array}\right)}^T\left(\begin{array}{c}0\\ 1\\ 1\\ 0\end{array}\right)\hfill \\ & =\left(\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right)\hfill \\ & =1+x_1+x_2+x_1{x}_2\hfill \\ & =g\circ F\hfill \end{array}$$

A possible attack scenario includes finding a Boolean form to compute the value of each $x_i$ from the output of the function F. For example, to find the formula for $x_1$, the input vector to the HHL algorithm would have to be as follows:

$$|b⟩=\left(\begin{array}{c}0\\ 1\\ 0\\ ⋮\\ 0\\ ⋮\\ 0\end{array}\right)\begin{array}{c}1\\ x_1\\ x_2\\ \\ x_i{x}_2\\ \\ \prod _{i=1}^m{x}_i\end{array}$$

We highlight that the matrix to be inverted is not $A^F$, but ${\left(A^F\right)}^T$. This is not a problem as we can just switch the row- and column-oracles to obtain the transpose of the matrix $T^F$ and use the following fact:

$$\begin{array}{cc}\hfill {\left(A^F\right)}^T& ={\left({\mathcal{P}}_m{T}^F{\mathcal{P}}_n\right)}^T\hfill \\ \hfill & ={\mathcal{P}}_n^T·{\left(T^F\right)}^T·{\mathcal{P}}_m^T\hfill \\ \hfill & ={\mathcal{P}}_n·{\left(T^F\right)}^T·{\mathcal{P}}_m\hfill \end{array}$$

For each low-order term $x^I$, we can use the techniques used in Section 5.1.2 to verify whether the preimage has a small Hamming weight. If such an input is found, there exists a sparse Boolean function that allows the computation of the value of $x^I$. We can recover such a function and use it to deduce the values of $x_i$ for $i\in I$. For example, we can use the fact that if $x^I=1$, then $\forall i\in I$ follows $x_i=1$.

5.2.2. Comparison to Classical Approaches

In the classical setting, to find a formula to compute certain bits, the attacker would have to analyze the ciphers algebraic properties. The concept is similar to algebraic cryptanalysis, where the cipher is rewritten as a set of equations for which the solution is the secret key [27].

We are, however, not interested in building a huge equation system, but rather want to find a function which, combined with the original function, leaks secret bits. The idea resembles the concept of annihilators, introduced in [26]. An annihilator of a Boolean function $f\left(x\right):{\mathbb{F}}_2^n\to {\mathbb{F}}_2$ is another Boolean function $g\left(x\right):{\mathbb{F}}_2^n\to {\mathbb{F}}_2$ such that the following is true:

$$\begin{array}{c}\hfill f\left(x\right)·g\left(x\right)=0\forall x\in {\mathbb{F}}_2^n\end{array}$$

The annihilators allow reducing the degree of algebraic equations and, as a consequence, finding some of the secret key bits used in encryption. In our approach, we are rather interested in analyzing a vectorial Boolean function $F\left(x\right):{\mathbb{F}}_2^n\to {\mathbb{F}}_2^m$ using a Boolean function $g\left(x\right):{\mathbb{F}}_2^m\to {\mathbb{F}}_2$ such that the following is true:

$$\begin{array}{c}\hfill g\circ F\left(x\right)=x^I\forall x\in {\mathbb{F}}_2^n,\end{array}$$

but the desired outcome is similar.

6. Conclusions

In this paper, we have shown how tensor-decomposable matrices can be used in the HHL setting to improve the runtime of the linear system solving algorithm proposed in [3]. We have proven that a vertical decomposition has a direct influence on the run-time, and in the quantum setting allows preimage computation even if the input to be inverted is not tensor-decomposable. This is a direct improvement over the classical computation.

Next, we have shown a polynomial-time procedure to create a quantum state which describes the algebraic normal form of a Boolean function f. The register has the form $|{\mathcal{A}}_f\rangle ={\sum }_{i=0}^{2^n-1}{\displaystyle \frac{1}{\sqrt{\mathrm{hw}\left({\mathcal{A}}_f\right)}}}·{\mathcal{A}}_f$, where ${\mathcal{A}}_f$ represents the coefficient vector of f. We further show how $|{\mathcal{A}}_f\rangle$ could be used to extract some information about the ANF. In most straightforward scenarios, a distinguisher attack could be performed to differentiate a cryptographic function from a random function. The Hamming weight of the ANF of a random function will be roughly $N/2$. Meanwhile, a cryptographic function is likely to deviate from this value. The attack could also be used as a testing method for new ciphers. It would allow a quicker verification of the sparsity of ANF representations.

We show how a construct called an algebraic transition matrix can be used in the HHL setting to improve the cryptanalysis of Boolean functions. By using the polynomial-time HHL algorithm for all three parts of the horizontal decomposition of $A^F$, with specific input, we can find formulas for the values of the key used in the encryption process.

We finally point to the fact that the Boolean Möbius transform $T_n$ is self-inverse. Therefore, it is not necessary to compute the preimage under the Möbius transformation. We could compute the value $T_n·|b\rangle$ and obtain the same result. We would not have to invert the eigenvalue ${\lambda }_k$, but use it as a factor. It remains an open question how significantly such an alteration improves the runtime. We believe that, for some use cases, it might pose an interesting question.