Towards a Multiqudit Quantum Processor Based on a 171Yb+ Ion String: Realizing Basic Quantum Algorithms
Abstract
1. Introduction
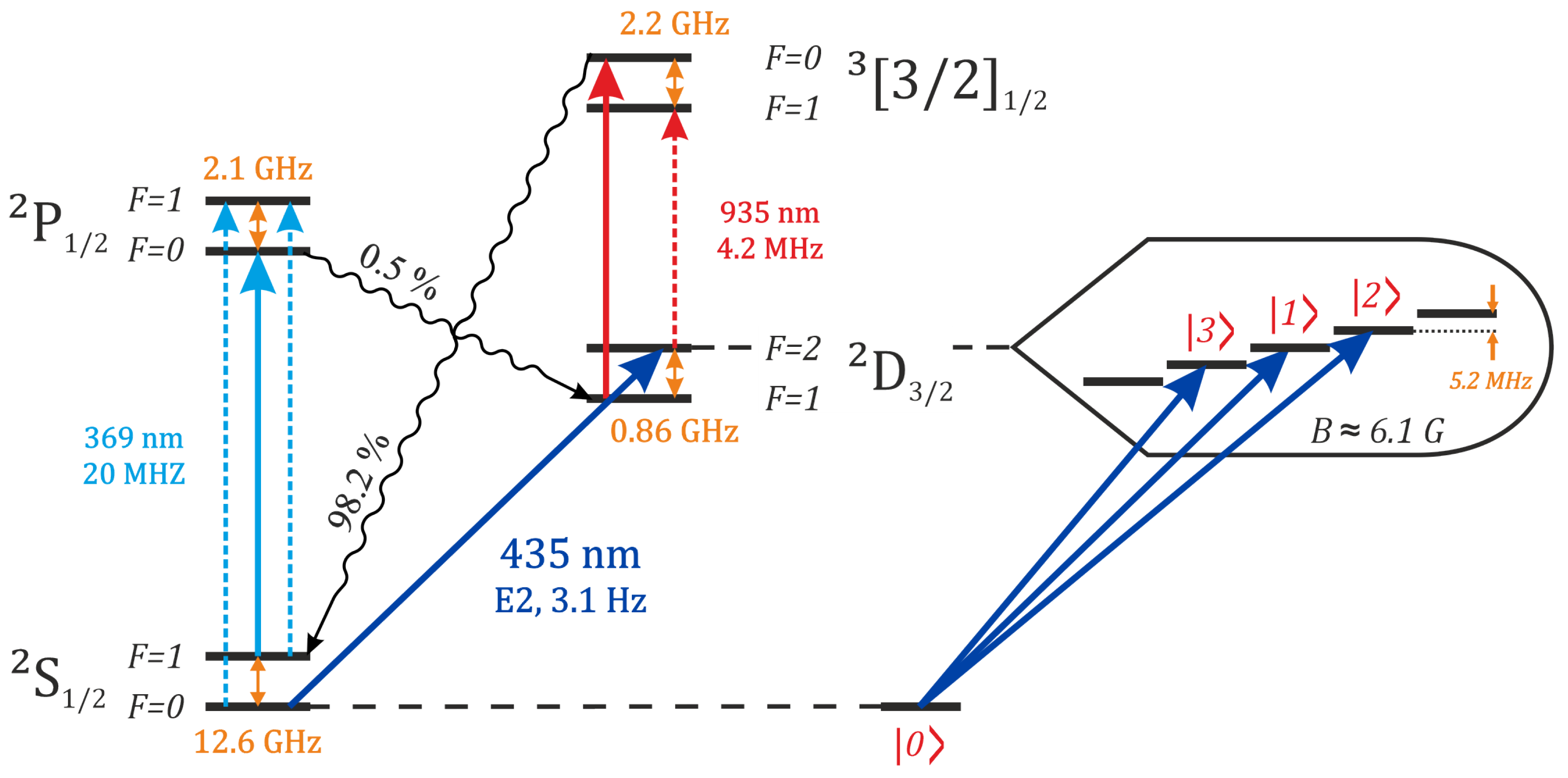
2. Qudits Encoded in Ions
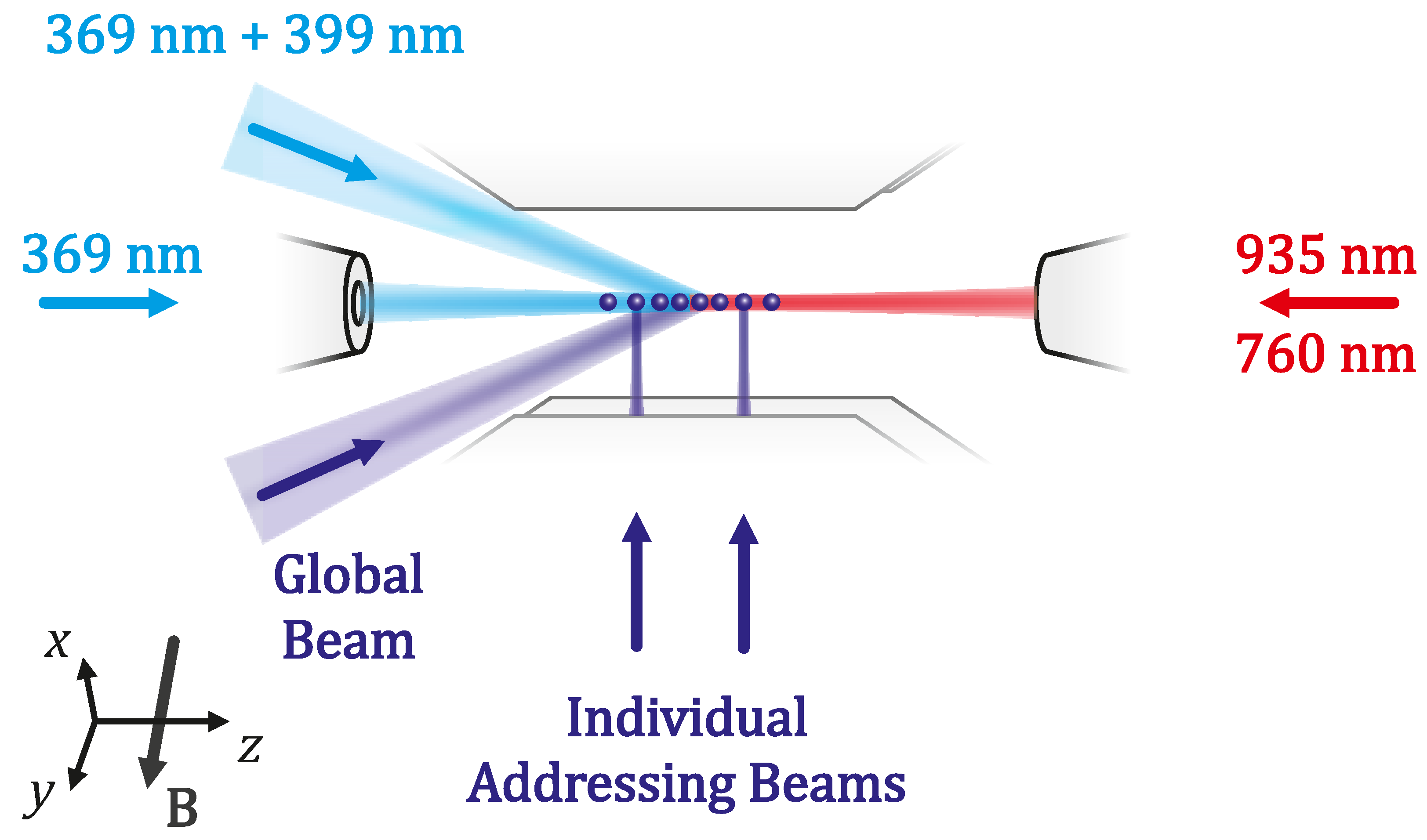
3. Eight-Qudit Quantum Processor
4. Components Benchmarking
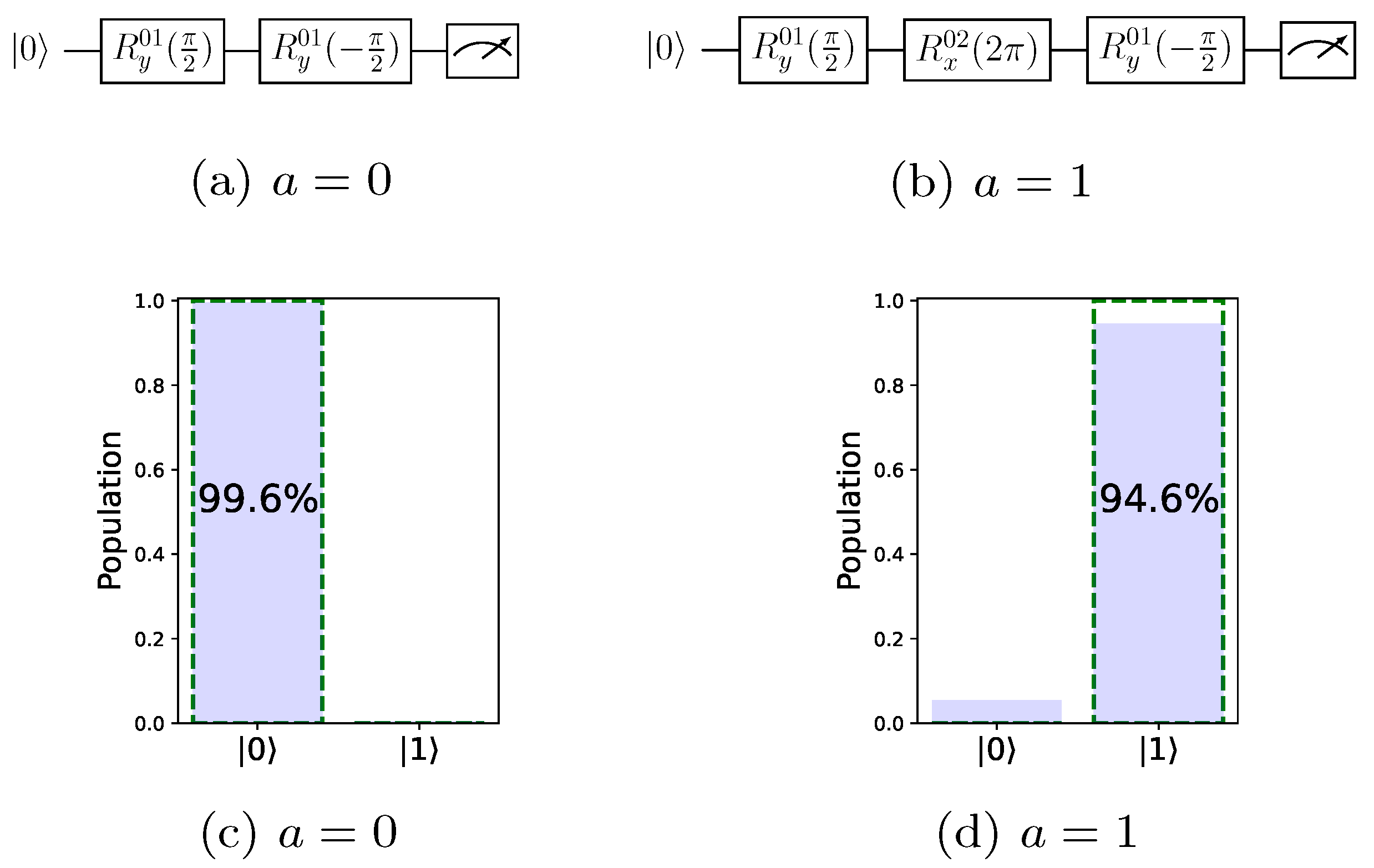
4.1. Single-Qudit Gates
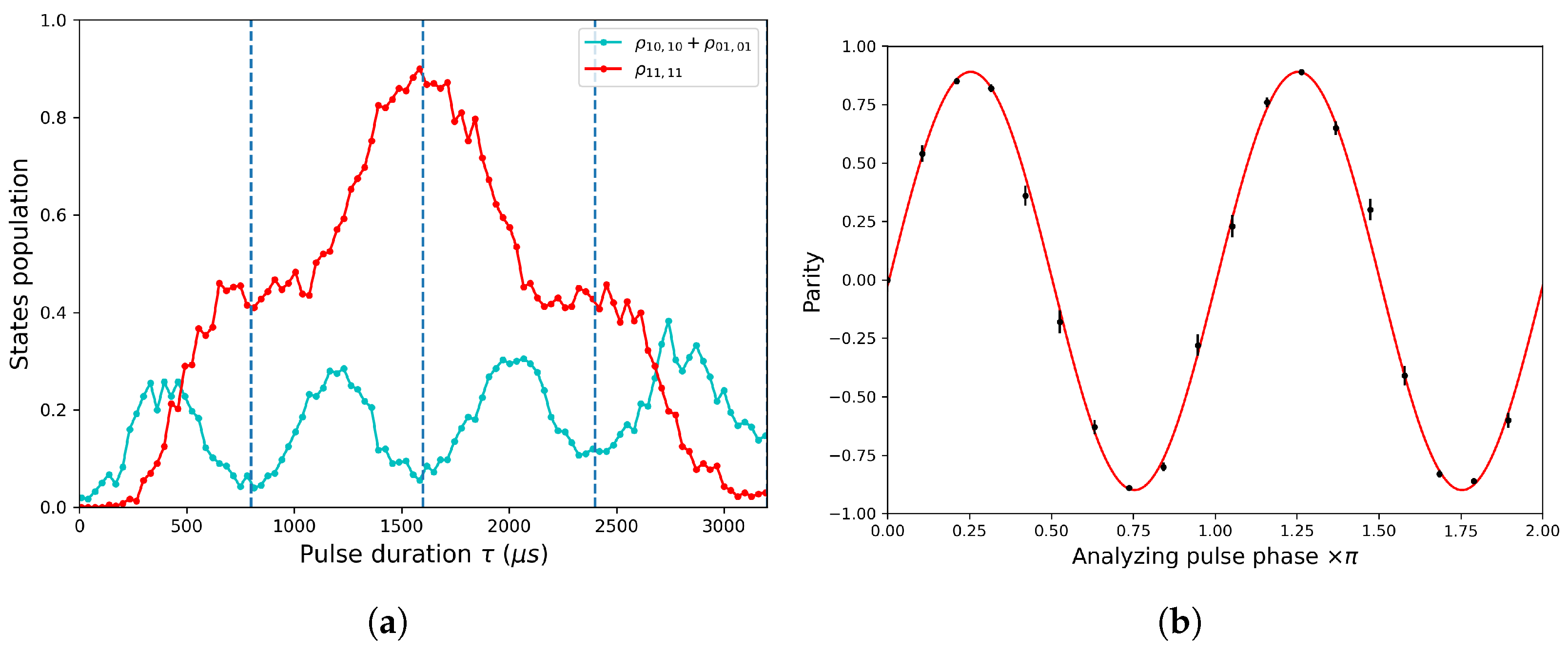
4.2. Two-Qudit Gate Benchmarking
4.3. Coherence Time
5. Realization of Quantum Algorithms
5.1. Algorithmic Benchmarking in the Qubit Regime
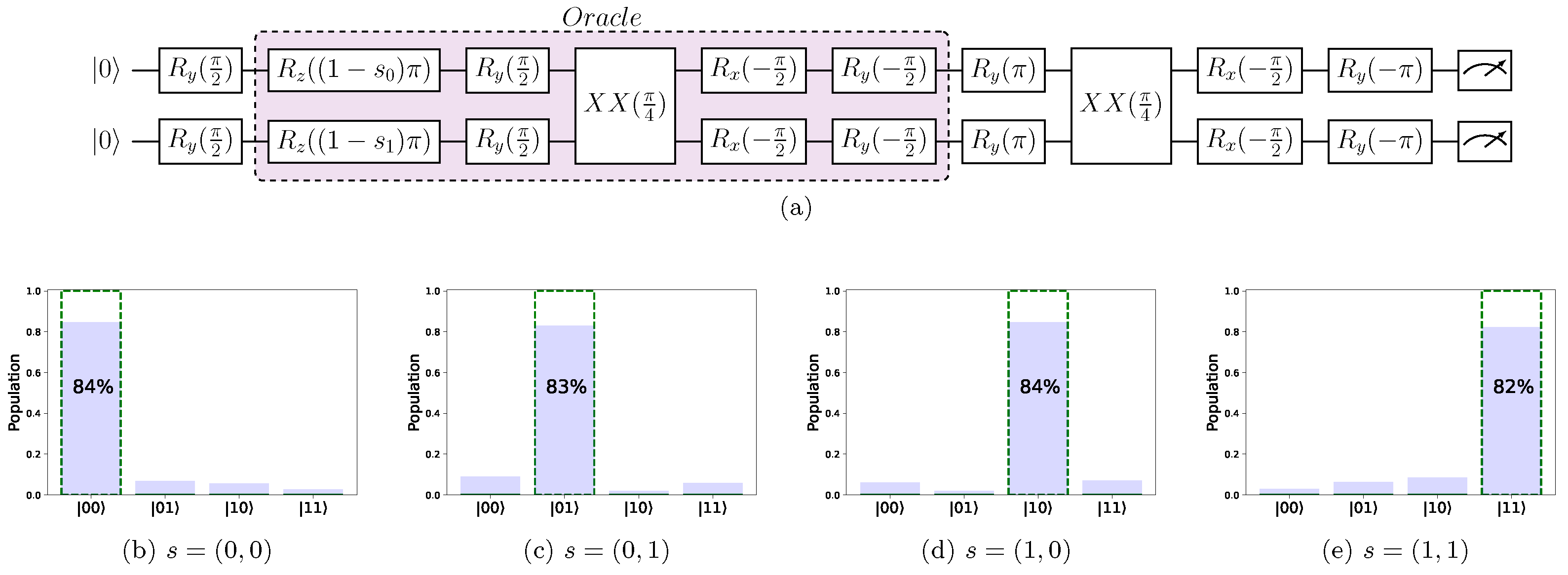
5.1.1. Two-Qubit Bernstein–Vazirani Algorithm
5.1.2. Two-Qubit Grover’s Algorithm
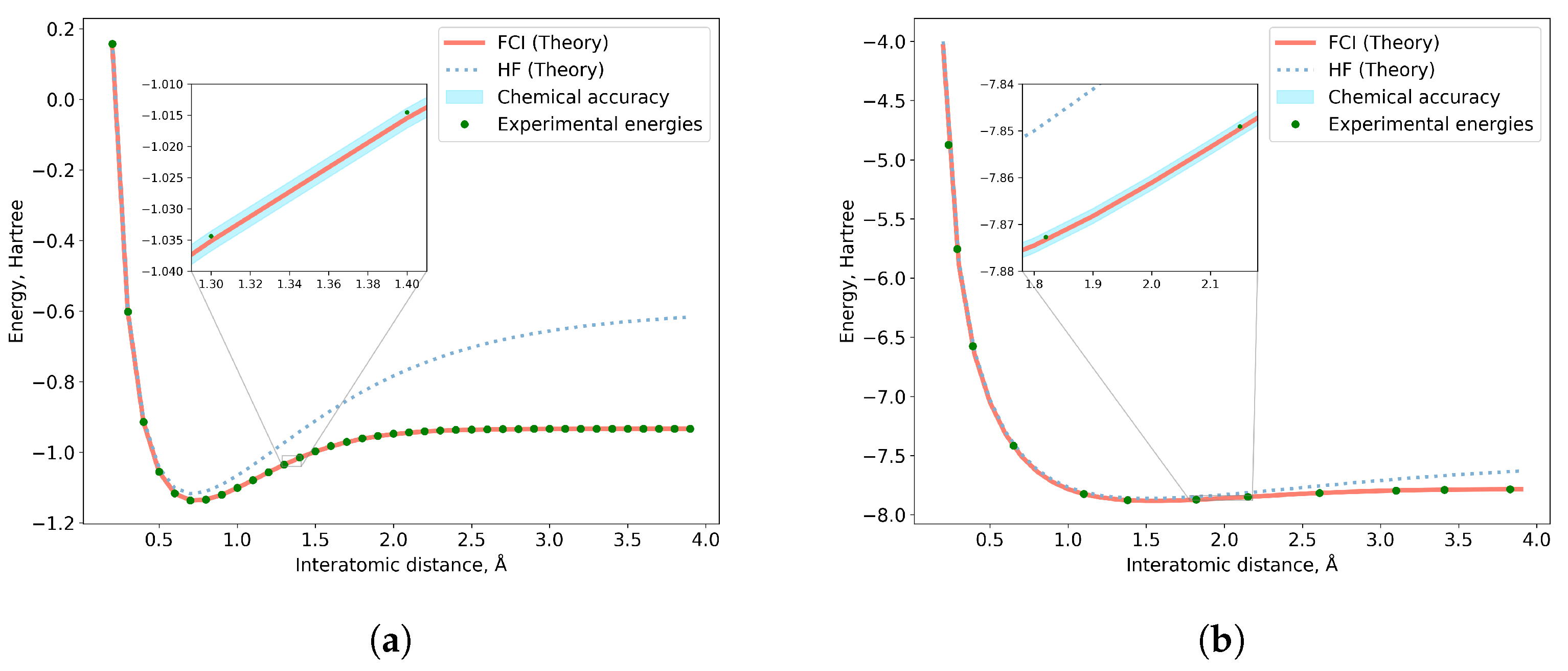
5.1.3. Quantum Chemistry: H2 and LiH Simulations
5.2. Algorithmic Benchmarking in Ququart Regime
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cirac, J.I.; Zoller, P. Quantum Computations with Cold Trapped Ions. Phys. Rev. Lett. 1995, 74, 4091–4094. [Google Scholar] [CrossRef] [PubMed]
- Monroe, C.; Meekhof, D.M.; King, B.E.; Itano, W.M.; Wineland, D.J. Demonstration of a Fundamental Quantum Logic Gate. Phys. Rev. Lett. 1995, 75, 4714–4717. [Google Scholar] [CrossRef] [PubMed]
- Gulde, S.; Riebe, M.; Lancaster, G.P.T.; Becher, C.; Eschner, J.; Häffner, H.; Schmidt-Kaler, F.; Chuang, I.L.; Blatt, R. Implementation of the Deutsch–Jozsa algorithm on an ion-trap quantum computer. Nature 2003, 421, 48–50. [Google Scholar] [CrossRef]
- Schmidt-Kaler, F.; Häffner, H.; Riebe, M.; Gulde, S.; Lancaster, G.P.T.; Deuschle, T.; Becher, C.; Roos, C.F.; Eschner, J.; Blatt, R. Realization of the Cirac–Zoller controlled-NOT quantum gate. Nature 2003, 422, 408–411. [Google Scholar] [CrossRef]
- Fedorov, A.K.; Gisin, N.; Beloussov, S.M.; Lvovsky, A.I. Quantum computing at the quantum advantage threshold: A down-to-business review. arXiv 2022, arXiv:2203.17181. [Google Scholar]
- Blatt, R.; Roos, C.F. Quantum simulations with trapped ions. Nat. Phys. 2012, 8, 277–284. [Google Scholar] [CrossRef]
- Monz, T.; Nigg, D.; Martinez, E.A.; Brandl, M.F.; Schindler, P.; Rines, R.; Wang, S.X.; Chuang, I.L.; Blatt, R. Realization of a scalable Shor algorithm. Science 2016, 351, 1068–1070. [Google Scholar] [CrossRef]
- Wright, K.; Beck, K.M.; Debnath, S.; Amini, J.M.; Nam, Y.; Grzesiak, N.; Chen, J.S.; Pisenti, N.C.; Chmielewski, M.; Collins, C.; et al. Benchmarking an 11-qubit quantum computer. Nat. Commun. 2019, 10, 5464. [Google Scholar] [CrossRef]
- Chiaverini, J.; Leibfried, D.; Schaetz, T.; Barrett, M.D.; Blakestad, R.B.; Britton, J.; Itano, W.M.; Jost, J.D.; Knill, E.; Langer, C.; et al. Realization of quantum error correction. Nature 2004, 432, 602–605. [Google Scholar] [CrossRef]
- Schindler, P.; Barreiro, J.T.; Monz, T.; Nebendahl, V.; Nigg, D.; Chwalla, M.; Hennrich, M.; Blatt, R. Experimental Repetitive Quantum Error Correction. Science 2011, 332, 1059–1061. [Google Scholar] [CrossRef]
- Stricker, R.; Vodola, D.; Erhard, A.; Postler, L.; Meth, M.; Ringbauer, M.; Schindler, P.; Monz, T.; Müller, M.; Blatt, R. Experimental deterministic correction of qubit loss. Nature 2020, 585, 207–210. [Google Scholar] [CrossRef] [PubMed]
- Egan, L.; Debroy, D.M.; Noel, C.; Risinger, A.; Zhu, D.; Biswas, D.; Newman, M.; Li, M.; Brown, K.R.; Cetina, M.; et al. Fault-tolerant control of an error-corrected qubit. Nature 2021, 598, 281–286. [Google Scholar] [CrossRef]
- Erhard, A.; Poulsen Nautrup, H.; Meth, M.; Postler, L.; Stricker, R.; Stadler, M.; Negnevitsky, V.; Ringbauer, M.; Schindler, P.; Briegel, H.J.; et al. Entangling logical qubits with lattice surgery. Nature 2021, 589, 220–224. [Google Scholar] [CrossRef]
- Postler, L.; Heuβen, S.; Pogorelov, I.; Rispler, M.; Feldker, T.; Meth, M.; Marciniak, C.D.; Stricker, R.; Ringbauer, M.; Blatt, R.; et al. Demonstration of fault-tolerant universal quantum gate operations. Nature 2022, 605, 675–680. [Google Scholar] [CrossRef]
- Ryan-Anderson, C.; Brown, N.C.; Allman, M.S.; Arkin, B.; Asa-Attuah, G.; Baldwin, C.; Berg, J.; Bohnet, J.G.; Braxton, S.; Burdick, N.; et al. Implementing Fault-tolerant Entangling Gates on the Five-qubit Code and the Color Code. arXiv 2022, arXiv:2208.01863. [Google Scholar]
- Paetznick, A.; da Silva, M.P.; Ryan-Anderson, C.; Bello-Rivas, J.M.; III, J.P.C.; Chernoguzov, A.; Dreiling, J.M.; Foltz, C.; Frachon, F.; Gaebler, J.P.; et al. Demonstration of logical qubits and repeated error correction with better-than-physical error rates. arXiv 2024, arXiv:2404.02280. [Google Scholar]
- Yamamoto, K.; Duffield, S.; Kikuchi, Y.; Ramo, D.M. Demonstrating Bayesian Quantum Phase Estimation with Quantum Error Detection. arXiv 2023, arXiv:2306.16608. [Google Scholar] [CrossRef]
- System Model h2. Available online: https://www.quantinuum.com/products-solutions/quantinuum-systems/system-model-h2 (accessed on 6 April 2025).
- Arute, F.; Arya, K.; Babbush, R.; Bacon, D.; Bardin, J.C.; Barends, R.; Biswas, R.; Boixo, S.; Brandao, F.G.S.L.; Buell, D.A.; et al. Quantum supremacy using a programmable superconducting processor. Nature 2019, 574, 505–510. [Google Scholar] [CrossRef]
- Wu, Y.; Bao, W.S.; Cao, S.; Chen, F.; Chen, M.C.; Chen, X.; Chung, T.H.; Deng, H.; Du, Y.; Fan, D.; et al. Strong Quantum Computational Advantage Using a Superconducting Quantum Processor. Phys. Rev. Lett. 2021, 127, 180501. [Google Scholar] [CrossRef]
- Xue, X.; Russ, M.; Samkharadze, N.; Undseth, B.; Sammak, A.; Scappucci, G.; Vandersypen, L.M.K. Quantum logic with spin qubits crossing the surface code threshold. Nature 2022, 601, 343–347. [Google Scholar] [CrossRef]
- Madzik, M.T.; Asaad, S.; Youssry, A.; Joecker, B.; Rudinger, K.M.; Nielsen, E.; Young, K.C.; Proctor, T.J.; Baczewski, A.D.; Laucht, A.; et al. Precision tomography of a three-qubit donor quantum processor in silicon. Nature 2022, 601, 348–353. [Google Scholar] [CrossRef] [PubMed]
- Noiri, A.; Takeda, K.; Nakajima, T.; Kobayashi, T.; Sammak, A.; Scappucci, G.; Tarucha, S. Fast universal quantum gate above the fault-tolerance threshold in silicon. Nature 2022, 601, 338–342. [Google Scholar] [CrossRef]
- Zhong, H.S.; Wang, H.; Deng, Y.H.; Chen, M.C.; Peng, L.C.; Luo, Y.H.; Qin, J.; Wu, D.; Ding, X.; Hu, Y.; et al. Quantum computational advantage using photons. Science 2020, 370, 1460–1463. [Google Scholar] [CrossRef]
- Madsen, L.S.; Laudenbach, F.; Askarani, M.F.; Rortais, F.; Vincent, T.; Bulmer, J.F.F.; Miatto, F.M.; Neuhaus, L.; Helt, L.G.; Collins, M.J.; et al. Quantum computational advantage with a programmable photonic processor. Nature 2022, 606, 75–81. [Google Scholar] [CrossRef] [PubMed]
- Ebadi, S.; Wang, T.T.; Levine, H.; Keesling, A.; Semeghini, G.; Omran, A.; Bluvstein, D.; Samajdar, R.; Pichler, H.; Ho, W.W.; et al. Quantum phases of matter on a 256-atom programmable quantum simulator. Nature 2021, 595, 227–232. [Google Scholar] [CrossRef]
- Scholl, P.; Schuler, M.; Williams, H.J.; Eberharter, A.A.; Barredo, D.; Schymik, K.N.; Lienhard, V.; Henry, L.P.; Lang, T.C.; Lahaye, T.; et al. Quantum simulation of 2D antiferromagnets with hundreds of Rydberg atoms. Nature 2021, 595, 233–238. [Google Scholar] [CrossRef] [PubMed]
- Henriet, L.; Beguin, L.; Signoles, A.; Lahaye, T.; Browaeys, A.; Reymond, G.O.; Jurczak, C. Quantum computing with neutral atoms. Quantum 2020, 4, 327. [Google Scholar] [CrossRef]
- Graham, T.M.; Song, Y.; Scott, J.; Poole, C.; Phuttitarn, L.; Jooya, K.; Eichler, P.; Jiang, X.; Marra, A.; Grinkemeyer, B.; et al. Multi-qubit entanglement and algorithms on a neutral-atom quantum computer. Nature 2022, 604, 457–462. [Google Scholar] [CrossRef]
- Monroe, C.; Kim, J. Scaling the Ion Trap Quantum Processor. Science 2013, 339, 1164–1169. [Google Scholar] [CrossRef]
- Bruzewicz, C.D.; Chiaverini, J.; McConnell, R.; Sage, J.M. Trapped-ion quantum computing: Progress and challenges. Appl. Phys. Rev. 2019, 6, 021314. [Google Scholar] [CrossRef]
- Wang, P.; Luan, C.Y.; Qiao, M.; Um, M.; Zhang, J.; Wang, Y.; Yuan, X.; Gu, M.; Zhang, J.; Kim, K. Single ion qubit with estimated coherence time exceeding one hour. Nat. Commun. 2021, 12, 233. [Google Scholar] [CrossRef] [PubMed]
- Gaebler, J.P.; Tan, T.R.; Lin, Y.; Wan, Y.; Bowler, R.; Keith, A.C.; Glancy, S.; Coakley, K.; Knill, E.; Leibfried, D.; et al. High-Fidelity Universal Gate Set for 9Be+ Ion Qubits. Phys. Rev. Lett. 2016, 117, 060505. [Google Scholar] [CrossRef]
- Brown, K.R.; Chiaverini, J.; Sage, J.M.; Häffner, H. Materials challenges for trapped-ion quantum computers. Nat. Rev. Mater. 2021, 6, 892–905. [Google Scholar] [CrossRef]
- Krutyanskiy, V.; Canteri, M.; Meraner, M.; Krcmarsky, V.; Lanyon, B.P. Multimode ion-photon entanglement over 101 kilometers of optical fiber. PRX Quantum 2024, 5, 020308. [Google Scholar] [CrossRef]
- Stephenson, L.J.; Nadlinger, D.P.; Nichol, B.C.; An, S.; Drmota, P.; Ballance, T.G.; Thirumalai, K.; Goodwin, J.F.; Lucas, D.; Ballance, C.J. High-Rate, High-Fidelity Entanglement of Qubits Across an Elementary Quantum Network. Phys. Rev. Lett. 2020, 124. [Google Scholar] [CrossRef]
- Kielpinski, D.; Monroe, C.; Wineland, D.J. Architecture for a large-scale ion-trap quantum computer. Nature 2002, 417, 709–711. [Google Scholar] [CrossRef]
- Pino, J.M.; Dreiling, J.M.; Figgatt, C.; Gaebler, J.P.; Moses, S.A.; Allman, M.S.; Baldwin, C.H.; Foss-Feig, M.; Hayes, D.; Mayer, K.; et al. Demonstration of the trapped-ion quantum CCD computer architecture. Nature 2021, 592, 209–213. [Google Scholar] [CrossRef] [PubMed]
- Farhi, E.; Gutmann, S. Analog analogue of a digital quantum computation. Phys. Rev. A 1998, 57, 2403–2406. [Google Scholar] [CrossRef]
- Kessel’, A.R.; Ermakov, V.L. Multiqubit spin. J. Exp. Theor. Phys. Lett. 1999, 70, 61–65. [Google Scholar] [CrossRef]
- Kessel’, A.R.; Ermakov, V.L. Physical implementation of three-qubit gates on a separate quantum particle. J. Exp. Theor. Phys. Lett. 2000, 71, 307–309. [Google Scholar] [CrossRef]
- Kessel, A.R.; Yakovleva, N.M. Implementation schemes in NMR of quantum processors and the Deutsch-Jozsa algorithm by using virtual spin representation. Phys. Rev. A 2002, 66, 062322. [Google Scholar] [CrossRef]
- Muthukrishnan, A.; Stroud, C.R. Multivalued logic gates for quantum computation. Phys. Rev. A 2000, 62, 052309. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Bremner, M.J.; Dodd, J.L.; Childs, A.M.; Dawson, C.M. Universal simulation of Hamiltonian dynamics for quantum systems with finite-dimensional state spaces. Phys. Rev. A 2002, 66, 022317. [Google Scholar] [CrossRef]
- Wang, X.; Sanders, B.C.; Berry, D.W. Entangling power and operator entanglement in qudit systems. Phys. Rev. A 2003, 67, 042323. [Google Scholar] [CrossRef]
- Klimov, A.B.; Guzmán, R.; Retamal, J.C.; Saavedra, C. Qutrit quantum computer with trapped ions. Phys. Rev. A 2003, 67, 062313. [Google Scholar] [CrossRef]
- Bagan, E.; Baig, M.; Muñoz Tapia, R. Minimal measurements of the gate fidelity of a qudit map. Phys. Rev. A 2003, 67, 014303. [Google Scholar] [CrossRef]
- Vlasov, A.Y. Algebra of quantum computations with higher dimensional systems. In Proceedings of the First International Symposium on Quantum Informatics; Ozhigov, Y.I., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA USA, 2003; Volume 5128, pp. 29–36. [Google Scholar] [CrossRef]
- Greentree, A.D.; Schirmer, S.G.; Green, F.; Hollenberg, L.C.L.; Hamilton, A.R.; Clark, R.G. Maximizing the Hilbert Space for a Finite Number of Distinguishable Quantum States. Phys. Rev. Lett. 2004, 92, 097901. [Google Scholar] [CrossRef]
- O’Leary, D.P.; Brennen, G.K.; Bullock, S.S. Parallelism for quantum computation with qudits. Phys. Rev. A 2006, 74, 032334. [Google Scholar] [CrossRef]
- Ralph, T.C.; Resch, K.J.; Gilchrist, A. Efficient Toffoli gates using qudits. Phys. Rev. A 2007, 75, 022313. [Google Scholar] [CrossRef]
- Lanyon, B.P.; Weinhold, T.J.; Langford, N.K.; O’Brien, J.L.; Resch, K.J.; Gilchrist, A.; White, A.G. Manipulating Biphotonic Qutrits. Phys. Rev. Lett. 2008, 100, 060504. [Google Scholar] [CrossRef]
- Ionicioiu, R.; Spiller, T.P.; Munro, W.J. Generalized Toffoli gates using qudit catalysis. Phys. Rev. A 2009, 80, 012312. [Google Scholar] [CrossRef]
- Ivanov, S.S.; Tonchev, H.S.; Vitanov, N.V. Time-efficient implementation of quantum search with qudits. Phys. Rev. A 2012, 85, 062321. [Google Scholar] [CrossRef]
- Li, B.; Yu, Z.H.; Fei, S.M. Geometry of Quantum Computation with Qutrits. Sci. Rep. 2013, 3, 2594. [Google Scholar] [CrossRef]
- Kiktenko, E.O.; Fedorov, A.K.; Man’ko, O.V.; Man’ko, V.I. Multilevel superconducting circuits as two-qubit systems: Operations, state preparation, and entropic inequalities. Phys. Rev. A 2015, 91, 042312. [Google Scholar] [CrossRef]
- Kiktenko, E.; Fedorov, A.; Strakhov, A.; Man’ko, V. Single qudit realization of the Deutsch algorithm using superconducting many-level quantum circuits. Phys. Lett. A 2015, 379, 1409–1413. [Google Scholar] [CrossRef]
- Song, C.; Su, S.L.; Wu, J.L.; Wang, D.Y.; Ji, X.; Zhang, S. Generation of tree-type three-dimensional entangled states via adiabatic passage. Phys. Rev. A 2016, 93, 062321. [Google Scholar] [CrossRef]
- Frydryszak, A.; Jakóbczyk, L.; Lugiewicz, P. Determining quantum correlations in bipartite systems—From qubit to qutrit and beyond. J. Phys. Conf. Ser. 2017, 804, 012016. [Google Scholar] [CrossRef]
- Bocharov, A.; Roetteler, M.; Svore, K.M. Factoring with qutrits: Shor’s algorithm on ternary and metaplectic quantum architectures. Phys. Rev. A 2017, 96, 012306. [Google Scholar] [CrossRef]
- Gokhale, P.; Baker, J.M.; Duckering, C.; Brown, N.C.; Brown, K.R.; Chong, F.T. Asymptotic Improvements to Quantum Circuits via Qutrits. In Proceedings of the 46th International Symposium on Computer Architecture (ISCA ’19), Phoenix, AZ, USA, 22–26 June 2019; pp. 554–566. [Google Scholar] [CrossRef]
- Luo, Y.H.; Zhong, H.S.; Erhard, M.; Wang, X.L.; Peng, L.C.; Krenn, M.; Jiang, X.; Li, L.; Liu, N.L.; Lu, C.Y.; et al. Quantum Teleportation in High Dimensions. Phys. Rev. Lett. 2019, 123, 070505. [Google Scholar] [CrossRef]
- Low, P.J.; White, B.M.; Cox, A.A.; Day, M.L.; Senko, C. Practical trapped-ion protocols for universal qudit-based quantum computing. Phys. Rev. Res. 2020, 2, 033128. [Google Scholar] [CrossRef]
- Jin, Z.; Gong, W.J.; Zhu, A.D.; Zhang, S.; Qi, Y.; Su, S.L. Dissipative preparation of qutrit entanglement via periodically modulated Rydberg double antiblockade. Opt. Express 2021, 29, 10117–10133. [Google Scholar] [CrossRef] [PubMed]
- Neeley, M.; Ansmann, M.; Bialczak, R.C.; Hofheinz, M.; Lucero, E.; O’Connell, A.D.; Sank, D.; Wang, H.; Wenner, J.; Cleland, A.N.; et al. Emulation of a Quantum Spin with a Superconducting Phase Qudit. Science 2009, 325, 722–725. [Google Scholar] [CrossRef] [PubMed]
- Lanyon, B.P.; Barbieri, M.; Almeida, M.P.; Jennewein, T.; Ralph, T.C.; Resch, K.J.; Pryde, G.J.; O’Brien, J.L.; Gilchrist, A.; White, A.G. Simplifying quantum logic using higher-dimensional Hilbert spaces. Nat. Phys. 2009, 5, 134–140. [Google Scholar] [CrossRef]
- Fedorov, A.; Steffen, L.; Baur, M.; da Silva, M.P.; Wallraff, A. Implementation of a Toffoli gate with superconducting circuits. Nature 2012, 481, 170–172. [Google Scholar] [CrossRef]
- Mischuck, B.E.; Merkel, S.T.; Deutsch, I.H. Control of inhomogeneous atomic ensembles of hyperfine qudits. Phys. Rev. A 2012, 85, 022302. [Google Scholar] [CrossRef]
- Peterer, M.J.; Bader, S.J.; Jin, X.; Yan, F.; Kamal, A.; Gudmundsen, T.J.; Leek, P.J.; Orlando, T.P.; Oliver, W.D.; Gustavsson, S. Coherence and Decay of Higher Energy Levels of a Superconducting Transmon Qubit. Phys. Rev. Lett. 2015, 114, 010501. [Google Scholar] [CrossRef]
- Svetitsky, E.; Suchowski, H.; Resh, R.; Shalibo, Y.; Martinis, J.M.; Katz, N. Hidden two-qubit dynamics of a four-level Josephson circuit. Nat. Commun. 2014, 5, 5617. [Google Scholar] [CrossRef]
- Braumüller, J.; Cramer, J.; Schlör, S.; Rotzinger, H.; Radtke, L.; Lukashenko, A.; Yang, P.; Skacel, S.T.; Probst, S.; Marthaler, M.; et al. Multiphoton dressing of an anharmonic superconducting many-level quantum circuit. Phys. Rev. B 2015, 91, 054523. [Google Scholar] [CrossRef]
- Kues, M.; Reimer, C.; Roztocki, P.; Cortés, L.R.; Sciara, S.; Wetzel, B.; Zhang, Y.; Cino, A.; Chu, S.T.; Little, B.E.; et al. On-chip generation of high-dimensional entangled quantum states and their coherent control. Nature 2017, 546, 622–626. [Google Scholar] [CrossRef]
- Godfrin, C.; Ferhat, A.; Ballou, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W.; Balestro, F. Operating Quantum States in Single Magnetic Molecules: Implementation of Grover’s Quantum Algorithm. Phys. Rev. Lett. 2017, 119, 187702. [Google Scholar] [CrossRef]
- Sawant, R.; Blackmore, J.A.; Gregory, P.D.; Mur-Petit, J.; Jaksch, D.; Aldegunde, J.; Hutson, J.M.; Tarbutt, M.R.; Cornish, S.L. Ultracold polar molecules as qudits. New J. Phys. 2020, 22, 013027. [Google Scholar] [CrossRef]
- Pavlidis, A.; Floratos, E. Quantum-Fourier-transform-based quantum arithmetic with qudits. Phys. Rev. A 2021, 103, 032417. [Google Scholar] [CrossRef]
- Rambow, P.; Tian, M. Reduction of circuit depth by mapping qubit-based quantum gates to a qudit basis. arXiv 2021, arXiv:2109.09902. [Google Scholar]
- Chi, Y.; Huang, J.; Zhang, Z.; Mao, J.; Zhou, Z.; Chen, X.; Zhai, C.; Bao, J.; Dai, T.; Yuan, H.; et al. A programmable qudit-based quantum processor. Nat. Commun. 2022, 13, 1166. [Google Scholar] [CrossRef]
- Nikolaeva, A.S.; Kiktenko, E.O.; Fedorov, A.K. Decomposing the generalized Toffoli gate with qutrits. Phys. Rev. A 2022, 105, 032621. [Google Scholar] [CrossRef]
- Nikolaeva, A.S.; Kiktenko, E.O.; Fedorov, A.K. Generalized Toffoli Gate Decomposition Using Ququints: Towards Realizing Grover’s Algorithm with Qudits. Entropy 2023, 25, 387. [Google Scholar] [CrossRef] [PubMed]
- Barenco, A.; Bennett, C.H.; Cleve, R.; DiVincenzo, D.P.; Margolus, N.; Shor, P.; Sleator, T.; Smolin, J.A.; Weinfurter, H. Elementary gates for quantum computation. Phys. Rev. A 1995, 52, 3457–3467. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.Q.; Wei, H.R.; Kwek, L.C. Low-Cost Fredkin Gate with Auxiliary Space. Phys. Rev. Appl. 2020, 14, 054057. [Google Scholar] [CrossRef]
- Baker, J.M.; Duckering, C.; Chong, F.T. Efficient Quantum Circuit Decompositions via Intermediate Qudits. In Proceedings of the 2020 IEEE 50th International Symposium on Multiple-Valued Logic (ISMVL), Miyazaki, Japan, 9–11 November 2020; pp. 303–308. [Google Scholar] [CrossRef]
- Kiktenko, E.O.; Nikolaeva, A.S.; Xu, P.; Shlyapnikov, G.V.; Fedorov, A.K. Scalable quantum computing with qudits on a graph. Phys. Rev. A 2020, 101, 022304. [Google Scholar] [CrossRef]
- Liu, W.Q.; Wei, H.R.; Kwek, L.C. Universal Quantum Multi-Qubit Entangling Gates with Auxiliary Spaces. Adv. Quantum Technol. 2022, 5, 2100136. [Google Scholar] [CrossRef]
- Galda, A.; Cubeddu, M.; Kanazawa, N.; Narang, P.; Earnest-Noble, N. Implementing a Ternary Decomposition of the Toffoli Gate on Fixed-Frequency Transmon Qutrits. arXiv 2021, arXiv:2109.00558. [Google Scholar]
- Gu, X.; Allcock, J.; An, S.; Liu, Y.x. Efficient multi-qubit subspace rotations via topological quantum walks. arXiv 2021, arXiv:2111.06534. [Google Scholar]
- Nikolaeva, A.S.; Zalivako, I.V.; Borisenko, A.S.; Semenin, N.V.; Galstyan, K.P.; Korolkov, A.E.; Kiktenko, E.O.; Khabarova, K.Y.; Semerikov, I.A.; Fedorov, A.K.; et al. Scalable improvement of the generalized Toffoli gate realization using trapped-ion-based qutrits. arXiv 2024, arXiv:2407.07758. [Google Scholar]
- Monz, T.; Kim, K.; Hänsel, W.; Riebe, M.; Villar, A.S.; Schindler, P.; Chwalla, M.; Hennrich, M.; Blatt, R. Realization of the Quantum Toffoli Gate with Trapped Ions. Phys. Rev. Lett. 2009, 102, 040501. [Google Scholar] [CrossRef] [PubMed]
- Chu, J.; He, X.; Zhou, Y.; Yuan, J.; Zhang, L.; Guo, Q.; Hai, Y.; Han, Z.; Hu, C.K.; Huang, W.; et al. Scalable algorithm simplification using quantum AND logic. Nat. Phys. 2023, 19, 126–131. [Google Scholar] [CrossRef]
- Nikolaeva, A.S.; Kiktenko, E.O.; Fedorov, A.K. Efficient realization of quantum algorithms with qudits. arXiv 2021, arXiv:2111.04384. [Google Scholar] [CrossRef]
- Kiktenko, E.O.; Nikolaeva, A.S.; Fedorov, A.K. Realization of quantum algorithms with qudits. arXiv 2023, arXiv:2311.12003. [Google Scholar]
- Chicco, S.; Allodi, G.; Chiesa, A.; Garlatti, E.; Buch, C.D.; Santini, P.; De Renzi, R.; Piligkos, S.; Carretta, S. Proof-of-Concept Quantum Simulator Based on Molecular Spin Qudits. J. Am. Chem. Soc. 2023, 146, 1053–1061. [Google Scholar] [CrossRef]
- Tacchino, F.; Chiesa, A.; Sessoli, R.; Tavernelli, I.; Carretta, S. A proposal for using molecular spin qudits as quantum simulators of light–matter interactions. J. Mater. Chem. C 2021, 9, 10266–10275. [Google Scholar] [CrossRef]
- Vezvaee, A.; Earnest-Noble, N.; Najafi, K. Quantum simulation of Fermi-Hubbard model based on transmon qudit interaction. arXiv 2024, arXiv:2402.01243. [Google Scholar]
- Popov, P.P.; Meth, M.; Lewestein, M.; Hauke, P.; Ringbauer, M.; Zohar, E.; Kasper, V. Variational quantum simulation of U(1) lattice gauge theories with qudit systems. Phys. Rev. Res. 2024, 6, 013202. [Google Scholar] [CrossRef]
- Calajó, G.; Magnifico, G.; Edmunds, C.; Ringbauer, M.; Montangero, S.; Silvi, P. Digital Quantum Simulation of a (1+1)D SU(2) Lattice Gauge Theory with Ion Qudits. PRX Quantum 2024, 5, 040309. [Google Scholar] [CrossRef]
- Meth, M.; Haase, J.F.; Zhang, J.; Edmunds, C.; Postler, L.; Steiner, A.; Jena, A.J.; Dellantonio, L.; Blatt, R.; Zoller, P.; et al. Simulating 2D lattice gauge theories on a qudit quantum computer. arXiv 2024, arXiv:2310.12110. [Google Scholar]
- Ringbauer, M.; Meth, M.; Postler, L.; Stricker, R.; Blatt, R.; Schindler, P.; Monz, T. A universal qudit quantum processor with trapped ions. Nat. Phys. 2022, 18, 1053–1057. [Google Scholar] [CrossRef]
- Aksenov, M.A.; Zalivako, I.V.; Semerikov, I.A.; Borisenko, A.S.; Semenin, N.V.; Sidorov, P.L.; Fedorov, A.K.; Khabarova, K.Y.; Kolachevsky, N.N. Realizing quantum gates with optically addressable Yb+ 171 ion qudits. Phys. Rev. A 2023, 107, 052612. [Google Scholar] [CrossRef]
- Hill, A.D.; Hodson, M.J.; Didier, N.; Reagor, M.J. Realization of arbitrary doubly-controlled quantum phase gates. arXiv 2021, arXiv:2108.01652. [Google Scholar]
- Roy, T.; Li, Z.; Kapit, E.; Schuster, D.I. Realization of two-qutrit quantum algorithms on a programmable superconducting processor. arXiv 2022, arXiv:2211.06523. [Google Scholar]
- Low, P.J.; White, B.; Senko, C. Control and Readout of a 13-level Trapped Ion Qudit. arXiv 2023, arXiv:2306.03340. [Google Scholar]
- Zalivako, I.V.; Borisenko, A.S.; Semerikov, I.A.; Korolkov, A.E.; Sidorov, P.L.; Galstyan, K.P.; Semenin, N.V.; Smirnov, V.N.; Aksenov, M.D.; Fedorov, A.K.; et al. Continuous dynamical decoupling of optical 171Yb+ qudits with radiofrequency fields. Front. Quantum Sci. Technol. 2023, 2, 1228208. [Google Scholar] [CrossRef]
- Zalivako, I.; Semerikov, I.; Borisenko, A.; Smirnov, V.; Vishnyakov, P.; Aksenov, M.; Sidorov, P.; Kolachevsky, N.; Khabarova, K. Improved Wavelength Measurement of 2S1/2→2P1/2 and 2D3/2→3[3/2]1/2 Transitions in Yb+. J. Russ. Laser Res. 2019, 40, 375–381. [Google Scholar] [CrossRef]
- Quantinuum H-Series Quantum Computer Accelerates Through 3 More Performance Records for Quantum Volume. Available online: https://www.quantinuum.com/news/quantinuum-h-series-quantum-computer-accelerates-through-3-more-performance-records-for-quantum-volume-217-218-and-219 (accessed on 6 April 2025).
- Moses, S.A.; Baldwin, C.H.; Allman, M.S.; Ancona, R.; Ascarrunz, L.; Barnes, C.; Bartolotta, J.; Bjork, B.; Blanchard, P.; Bohn, M.; et al. A Race-Track Trapped-Ion Quantum Processor. Phys. Rev. X 2023, 13, 041052. [Google Scholar] [CrossRef]
- Letokhov, V.S.; Ol’shanii, M.A.; Ovchinnikov, Y.B. Laser cooling of atoms: A review. Quantum Semiclassical Opt. J. Eur. Opt. Soc. Part B 1995, 7, 5–40. [Google Scholar] [CrossRef]
- Schreck, F.; Druten, K.v. Laser cooling for quantum gases. Nat. Phys. 2021, 17, 1296–1304. [Google Scholar] [CrossRef]
- Monroe, C.; Meekhof, D.M.; King, B.E.; Jefferts, S.R.; Itano, W.M.; Wineland, D.J.; Gould, P. Resolved-sideband Raman cooling of a bound atom to the 3D zero-point energy. Phys. Rev. Lett. 1995, 75, 4011–4014. [Google Scholar] [CrossRef] [PubMed]
- Pogorelov, I.; Feldker, T.; Marciniak, C.D.; Postler, L.; Jacob, G.; Krieglsteiner, O.; Podlesnic, V.; Meth, M.; Negnevitsky, V.; Stadler, M.; et al. Compact Ion-Trap Quantum Computing Demonstrator. PRX Quantum 2021, 2, 020343. [Google Scholar] [CrossRef]
- McKay, D.C.; Wood, C.J.; Sheldon, S.; Chow, J.M.; Gambetta, J.M. Efficient Z gates for quantum computing. Phys. Rev. A 2017, 96, 022330. [Google Scholar] [CrossRef]
- Nikolaeva, A.S.; Kiktenko, E.O.; Fedorov, A.K. Universal quantum computing with qubits embedded in trapped-ion qudits. arXiv 2023, arXiv:2302.02966. [Google Scholar] [CrossRef]
- Mølmer, K.; Sørensen, A. Multiparticle Entanglement of Hot Trapped Ions. Phys. Rev. Lett. 1999, 82, 1835–1838. [Google Scholar] [CrossRef]
- Sørensen, A.; Mølmer, K. Quantum Computation with Ions in Thermal Motion. Phys. Rev. Lett. 1999, 82, 1971–1974. [Google Scholar] [CrossRef]
- Sørensen, A.; Mølmer, K. Entanglement and quantum computation with ions in thermal motion. Phys. Rev. A 2000, 62, 022311. [Google Scholar] [CrossRef]
- Knill, E.; Leibfried, D.; Reichle, R.; Britton, J.; Blakestad, R.B.; Jost, J.D.; Langer, C.; Ozeri, R.; Seidelin, S.; Wineland, D.J. Randomized benchmarking of quantum gates. Phys. Rev. A 2008, 77, 012307. [Google Scholar] [CrossRef]
- Benhelm, J.; Kirchmair, G.; Roos, C.F.; Blatt, R. Towards fault-tolerant quantum computing with trapped ions. Nat. Phys. 2008, 4, 463–466. [Google Scholar] [CrossRef]
- Nakav, H.; Finkelstein, R.; Peleg, L.; Akerman, N.; Ozeri, R. Effect of fast noise on the fidelity of trapped-ion quantum gates. Phys. Rev. A 2023, 107, 042622. [Google Scholar] [CrossRef]
- Kolodzie, N.; Mirgorodskiy, I.; Nölleke, C.; Schmidt, P.O. Ultra-low frequency noise external cavity diode laser systems for quantum applications. Opt. Express 2024, 32, 29781. [Google Scholar] [CrossRef] [PubMed]
- Mai, X.; Zhang, L.; Lu, Y. High-Fidelity Detection on 171Yb+ Qubit via 2D3/2 Shelving. arXiv 2024, arXiv:2402.18868. [Google Scholar]
- Nazarova, T.; Lisdat, C.; Riehle, F.; Sterr, U. Low-frequency-noise diode laser for atom interferometry. J. Opt. Soc. Am. B 2008, 25, 1632–1638. [Google Scholar] [CrossRef]
- Akerman, N.; Navon, N.; Kotler, S.; Glickman, Y.; Ozeri, R. Universal gate-set for trapped-ion qubits using a narrow linewidth diode laser. New J. Phys. 2015, 17, 113060. [Google Scholar] [CrossRef]
- Blumel, R.; Grzesiak, N.; Pisenti, N.; Wright, K.; Nam, Y. Power-optimal, stabilized entangling gate between trapped-ion qubits. arXiv 2021, arXiv:1905.09292. [Google Scholar] [CrossRef]
- Bernstein, E.; Vazirani, U. Quantum Complexity Theory. SIAM J. Comput. 1997, 26, 1411–1473. [Google Scholar] [CrossRef]
- Grover, L.K. A Fast Quantum Mechanical Algorithm for Database Search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing (STOC ’96), Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar] [CrossRef]
- Grover, L.K. Quantum Mechanics Helps in Searching for a Needle in a Haystack. Phys. Rev. Lett. 1997, 79, 325–328. [Google Scholar] [CrossRef]
- Bennett, C.H.; Bernstein, E.; Brassard, G.; Vazirani, U. Strengths and Weaknesses of Quantum Computing. SIAM J. Comput. 1997, 26, 1510–1523. [Google Scholar] [CrossRef]
- Bharti, K.; Haug, T. Iterative quantum-assisted eigensolver. Phys. Rev. A 2021, 104, L050401. [Google Scholar] [CrossRef]
- Bharti, K.; Haug, T. Quantum-assisted simulator. Phys. Rev. A 2021, 104, 042418. [Google Scholar] [CrossRef]
- Haug, T.; Bharti, K. Generalized Quantum Assisted Simulator. Quantum Sci. Technol. 2022, 7, 045019. [Google Scholar] [CrossRef]
- Bharti, K.; Haug, T.; Vedral, V.; Kwek, L.C. Noisy intermediate-scale quantum algorithm for semidefinite programming. Phys. Rev. A 2022, 105, 052445. [Google Scholar] [CrossRef]
- Hehre, W.J.; Stewart, R.F.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. I. Use of Gaussian Expansions of Slater-Type Atomic Orbitals. J. Chem. Phys. 1969, 51, 2657–2664. [Google Scholar] [CrossRef]
- Seeley, J.; Richard, M.; Love, P. The Bravyi-Kitaev transformation for quantum computation of electronic structure. J. Chem. Phys. 2012, 137, 224109. [Google Scholar] [CrossRef]
- Jordan, P.; Wigner, E.P. About the Pauli exclusion principle. Eur. Phys. J. A 1928, 47, 631–651. [Google Scholar]
- Bravyi, S.; Gambetta, J.M.; Mezzacapo, A.; Temme, K. Tapering off qubits to simulate fermionic Hamiltonians. arXiv 2017, arXiv:1701.08213. [Google Scholar]


| Mechanism | Gate Error (%) | |
|---|---|---|
| Estimated | Measured | |
| Two-Qudit Gate | ||
| Spontaneous decay () | ||
| Slow laser frequency fluctuations () | ||
| Fast laser phase noise | ||
| Other a | ||
| SPAM | ||
| Total (including SPAM) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zalivako, I.V.; Nikolaeva, A.S.; Borisenko, A.S.; Korolkov, A.E.; Sidorov, P.L.; Galstyan, K.P.; Semenin, N.V.; Smirnov, V.N.; Aksenov, M.A.; Makushin, K.M.; et al. Towards a Multiqudit Quantum Processor Based on a 171Yb+ Ion String: Realizing Basic Quantum Algorithms. Quantum Rep. 2025, 7, 19. https://doi.org/10.3390/quantum7020019
Zalivako IV, Nikolaeva AS, Borisenko AS, Korolkov AE, Sidorov PL, Galstyan KP, Semenin NV, Smirnov VN, Aksenov MA, Makushin KM, et al. Towards a Multiqudit Quantum Processor Based on a 171Yb+ Ion String: Realizing Basic Quantum Algorithms. Quantum Reports. 2025; 7(2):19. https://doi.org/10.3390/quantum7020019
Chicago/Turabian StyleZalivako, Ilia V., Anastasiia S. Nikolaeva, Alexander S. Borisenko, Andrei E. Korolkov, Pavel L. Sidorov, Kristina P. Galstyan, Nikita V. Semenin, Vasilii N. Smirnov, Mikhail A. Aksenov, Konstantin M. Makushin, and et al. 2025. "Towards a Multiqudit Quantum Processor Based on a 171Yb+ Ion String: Realizing Basic Quantum Algorithms" Quantum Reports 7, no. 2: 19. https://doi.org/10.3390/quantum7020019
APA StyleZalivako, I. V., Nikolaeva, A. S., Borisenko, A. S., Korolkov, A. E., Sidorov, P. L., Galstyan, K. P., Semenin, N. V., Smirnov, V. N., Aksenov, M. A., Makushin, K. M., Kiktenko, E. O., Fedorov, A. K., Semerikov, I. A., Khabarova, K. Y., & Kolachevsky, N. N. (2025). Towards a Multiqudit Quantum Processor Based on a 171Yb+ Ion String: Realizing Basic Quantum Algorithms. Quantum Reports, 7(2), 19. https://doi.org/10.3390/quantum7020019






