Analysis of D-Wave Topologies with k-Hop-Based Graph Metrics

Abstract

In this paper, we present a graph-based analysis of the topology of D-Wave quantum computers, focusing on the Pegasus, Chimera, and Zephyr architectures. We investigate these topologies under different parameter settings using k-hop-based graph metrics. Each of these architectures comprises distinct subgraphs in which qubits are interconnected according to specific patterns dictated by their implementation. Our study pursues two primary objectives. First, we analyze the structural properties of the Chimera, Pegasus, and Zephyr topologies, examining their scalability and connectivity characteristics. Second, we evaluate the behavior of graph-based density and redundancy metrics within these architectures. The inherent symmetries of these quantum hardware designs provide a unique opportunity to systematically assess the effectiveness of these metrics across varying connectivity patterns. By leveraging these symmetries, our findings not only enhance the understanding of these topological structures but also offer deeper insights into the reliability and applicability of the proposed metrics in the broader context of quantum hardware design.

1. Introduction

The modeling and analysis of the topology of different computer systems (e.g., quantum computer topologies) is an interdisciplinary field integrating computer science, physics, and mathematics. Quantum topologies inherently rely on mathematical foundations drawn from graph theory, whereby abstract topological structures describing quantum systems can be effectively represented as directed or undirected graphs. Typically, such topological representations incorporate probabilistic elements and structural constraints derived from quantum mechanical properties [1,2,3,4,5]. Quantum computing architectures have significantly diversified in recent years, notably including circuit-based quantum computers, measurement-based quantum computers, topological quantum computers, and quantum annealers [6,7,8]. Circuit-based quantum computers typically consist of qubits arranged linearly or in grid configurations, where quantum gates are applied sequentially to perform computations [9]. Measurement-based quantum computing employs initial highly entangled states, performing computations through measurements on selected qubits, and can be implemented using linear optics or spin chains [10,11]. Topological quantum computers leverage lattice topologies to encode and protect quantum information, providing enhanced fault tolerance [12,13]. Quantum annealers, such as D-Wave systems, utilize specialized graph-based architectures designed for optimization problems, where interactions between qubits solve complex computational challenges [14,15,16]. Analyzing these quantum architectures involves traditional measurement-based graph metrics such as centrality measures and clustering coefficients [17,18,19,20,21,22,23,24,25]. Measurement-based metrics include distance-based metrics (eccentricity), centrality-based metrics (degree centrality, closeness centrality, betweenness centrality, eigenvector centrality, eccentricity centrality), and connection-based metrics (degree of a node, number of edges, degree distribution). However, classical metrics generally become computationally intensive and less interpretable for large quantum graphs [26,27]. Thus, recent advancements have proposed quantum-specific metrics explicitly designed for evaluating quantum connectivity, redundancy, and error resilience in quantum hardware [28,29,30,31]. Furthermore, hybrid quantum–classical network approaches have increasingly emphasized optimizing quantum connectivity in combination with classical computing nodes, significantly enhancing both scalability and computational efficiency [32,33,34]. Recent advances in quantum graph embedding methods have improved the mapping of optimization problems onto quantum processors, increasing embedding accuracy and computational performance [35,36,37]. The k-hop-based type of analysis has been applied extensively across various domains within computer science, including social networks, ontologies, software verification, data mining, bioinformatics, complex optimization problems, machine learning, artificial intelligence, and cyber–physical systems. The goal of k-hop-based algorithms is to reduce the search space by combining local and global search procedures, thereby mitigating the explosion in exponential complexity. In addition, these metrics effectively represent local–global properties inherent in complex problems. Significant research has focused on k-hop reachability queries in directed graphs, efficient indexing methods [38,39], graph neural networks for fundamental property identification [40,41], and minimum-cost k-hop spanning tree problems [5]. Moreover, parallel key/value-based processing for large-scale graphs [42] and enhanced partition-based methods for spatial data mining leveraging k-hop neighborhoods have also emerged [43]. Quantum topology [44] explores topological properties of quantum mechanical systems, including knots, links, and their invariants. These topological invariants have applications in physics [45], biology [46], and computer science [47]. Another relevant study area is topological quantum field theory, which is invariant under topology changes [48]. Throughout this manuscript, we intentionally use the term ‘topology’ to denote abstract graph-based structures and their connectivity properties within quantum annealing processors, following established quantum computing conventions [49,50,51]. We distinguish this explicitly from ‘topography’, which is primarily related to spatial or physical qubit arrangements on quantum hardware [52]. Different topologies possess unique strengths and weaknesses depending on the applied quantum algorithms and available technology [10,50,53].

The remainder of the paper is organized as follows: Section 2 introduces the definitions and methodology of the proposed k-hop-based metrics, reviews related work, and summarizes key previous results; Section 3 presents a detailed analysis of the Chimera, Pegasus, and Zephyr topologies using these metrics; finally, Section 4 concludes our findings and outlines potential directions for future research.

2. Previous and Related Work

There are many metrics for characterizing networks and topologies, most of which are either global or local. Local metrics consider only the immediate neighbors of the observed nodes, while global graph metrics describe the overall structure of the graph. Our metrics represent the environment of the nodes (subgraph), and as such are interpreted in the space between purely local and purely global metrics.

In our previous work, we focused on wireless sensor networks and defined some globally local and locally global graph-based metrics.

We introduced several density-based and redundancy-based metrics interpreted in a k-hop environment [54]:

• Weighted Communication Graph Density ($\mathcal{WCGD}$)
• Relative Communication Graph Density ($\mathcal{RCGD}$)
• Weighted Relative Communication Graph Density ($\mathcal{WRCGD}$)
• Communication Graph Redundancy (value-based) (${\mathcal{CGR}}_{vb}$)
• Weighted Communication Graph Redundancy (size-based) (${\mathcal{WCGR}}_{sb}$) and (value-based) (${\mathcal{WCGR}}_{vb}$).

Density-based metrics ($\mathcal{WCGD}$,$\mathcal{RCGD}$,$\mathcal{WRCGD}$) are mathematically based on spanning trees, while redundancy-based metrics (${\mathcal{CGR}}_{vb}$,${\mathcal{WCGR}}_{sb}$,${\mathcal{WCGR}}_{vb}$) are based on cliques.

• Density-based metrics

• Density-based metrics of a graph refer to a given k-hop distance (weighted density) and relate to the to the overall structure of the graph (relative density).

• Redundancy-based metrics

• Metrics that analyze the redundancy of a graph refer to redundant or over-connected structures between links. They describe the topological robustness of the graph.

• Definitions of k-hop-based metrics

• u: The candidate node.
• k: The number of hops.
• $\mathcal{N}$, $\mathcal{V}$: The number of nodes and edges of graph $\mathcal{G}$.
• ${\mathcal{N}}^{\left[k\right]}\left(u\right)$,${\mathcal{V}}^{\left[k\right]}\left(u\right)$: The number of nodes and edges of graph ${\mathcal{G}}^{\left[k\right]}\left(u\right)$.
• $\mathcal{C}l$, $\mathcal{M}$: The set of maximum cliques of graph $\mathcal{G}$ and the cardinality of this set.
• $\mathcal{C}{l}^{\left[k\right]}\left(u\right)$, ${\mathcal{M}}^{\left[k\right]}\left(u\right)$: The set of maximal cliques of graph ${\mathcal{G}}^{\left[n\right]}\left(u\right)$ and the cardinality of this set.
• ${\mathcal{T}}^{\left[k\right]}\left(u\right)$, $\mathcal{T}$: The number of edges of the minimum cost spanning tree of graph ${\mathcal{G}}^{\left[k\right]}\left(u\right)$ and $\mathcal{G}$; note that in the case of a communication graph, we have $\mathcal{T}=\mathcal{N}-1$ regardless of whether the graph is directed or undirected.
• s: The spreading factor, which is a technical value used to enlarge small differences in the metrics; in this article, we set $s=2.71$.
• $cs$: The clique size, for which the minimum value is 2.

In addition, we defined two global metrics, namely, the average clique size and average value of cliques, as follows:

$$\overline{\mathcal{CL}}={\displaystyle \frac{1}{\mathcal{M}}}\sum _{i=1}^{\mathcal{M}}{\left|\mathcal{C}{l}_i\right|}_{>=cs},\overline{{\mathcal{CL}}_V}={\displaystyle \frac{1}{\mathcal{M}}}\sum _{i=1}^{\mathcal{M}}{\displaystyle \frac{{\left|\mathcal{C}{l}_i\right|}_{>=cs}}{\mathcal{N}}}{s}^{{\displaystyle \frac{|\mathcal{C}{l}_i{|}_{>=cs}}{\overline{\mathcal{CL}}}}}.$$

(1)

Weighted Communication Graph Density:

$${\mathcal{WCGD}}^{\left[k\right]}\left(u\right)=s^{{\displaystyle \frac{{\mathcal{V}}^{\left[k\right]}\left(u\right)}{{\mathcal{T}}^{\left[k\right]}\left(u\right)}}}{\displaystyle \frac{{\mathcal{N}}^{\left[k\right]}\left(u\right)}{\mathcal{N}}}.$$

(2)

Relative Communication Graph Density:

$${\mathcal{RCGD}}^{\left[k\right]}\left(u\right)=s^{{\displaystyle \frac{{\mathcal{CGD}}^{\left[k\right]}\left(u\right)}{\mathcal{CGD}}}}=s^{{\displaystyle \frac{{\mathcal{V}}^{\left[k\right]}\left(u\right)\mathcal{T}}{{\mathcal{T}}^{\left[k\right]}\left(u\right)\mathcal{V}}}}.$$

(3)

Weighted Relative Communication Graph Density:

$${\mathcal{WRCGD}}^{\left[k\right]}\left(u\right)=s^{{\displaystyle \frac{{\mathcal{V}}^{\left[k\right]}\left(u\right)\mathcal{T}}{{\mathcal{T}}^{\left[k\right]}\left(u\right)\mathcal{V}}}}{\displaystyle \frac{{\mathcal{N}}^{\left[k\right]}\left(u\right)}{\mathcal{N}}}.$$

(4)

Communication Graph Redundancy (value-based):

$${{\mathcal{WCGR}}_{sb}}^{\left[k\right]}\left(u\right)={{\mathcal{CGR}}_{sb}}^{\left[k\right]}\left(u\right){\displaystyle \frac{{\mathcal{N}}^{\left[k\right]}\left(u\right)}{\mathcal{N}}}.$$

(5)

Weighted Communication Graph Redundancy (size-based):

$${{\mathcal{CGR}}_{vb}}^{\left[k\right]}\left(u\right)={\mathcal{M}}^{\left[k\right]}\left(u\right)\sum _{i=1}^{{\mathcal{M}}^{\left[k\right]}\left(u\right)}{\displaystyle \frac{|\mathcal{C}{l}^{\left[k\right]}{\left(u\right)}_i{|}_{>=cs}}{{\mathcal{N}}^{\left[k\right]}\left(u\right)}}{s}^{{\displaystyle \frac{|\mathcal{C}{l}^{\left[k\right]}{\left(u\right)}_i{|}_{>=cs}}{{\overline{\mathcal{CL}}}^{\left[k\right]}\left(u\right)}}}.$$

(6)

Weighted Communication Graph Redundancy (value-based):

$${{\mathcal{WCGR}}_{vb}}^{\left[k\right]}\left(u\right)={\displaystyle \frac{1}{{{\mathcal{CGR}}_{vb}}^{\left[k\right]}\left(u\right)}}{\displaystyle \frac{{\mathcal{N}}^{\left[k\right]}\left(u\right)}{\mathcal{N}}}.$$

(7)

• Correlation Analysis

The result of the correlation analysis (classical and k-hop-based graph metrics) can be seen in

Table 1. Correlations between classical and k-hop-based metrics ($k=3$).

	${\mathcal{WCGD}}^{\left[\mathit{k}\right]}$	${\mathcal{RCGD}}^{\left[\mathit{k}\right]}$	${\mathcal{WRCGD}}^{\left[\mathit{k}\right]}$	${\mathcal{WCGR}}_{\mathit{sb}}^{\left[\mathit{k}\right]}$	${\mathcal{CGR}}_{\mathit{vb}}^{\left[\mathit{k}\right]}$	${\mathcal{WCGR}}_{\mathit{vb}}^{\left[\mathit{k}\right]}$
Clustering coeff.	0.12	0.03	−0.20	0.03	−0.24	−0.19
Eccentricity	−0.27	−0.18	−0.55	−0.30	−0.56	−0.51
Betweenness c.	0.18	0.07	0.36	0.14	0.38	0.29
Degree c.	0.46	0.55	0.63	0.56	0.54	0.62
Closeness c.	0.38	0.25	0.63	0.34	0.67	0.54
Eigenvector c.	0.72	0.55	0.52	0.52	−0.26	0.59

.

The bolded values in Table 1 indicate the highest absolute correlation values, emphasizing particularly strong relationships between the k-hop-based metrics and classical graph metrics. The conceptual interpretation of the metric values in random graphs following a binomial distribution is analyzed by examining the 3-hop neighborhood of all vertices. If a metric shows a higher than average value, according to the interpretations of classical metrics, we can concluded the following:

In the case of spanning tree-based metrics:

• There is an average/high probability of many direct connections.
• There is an average/high probability of neighbors with a large number of degrees.
• There is a weak/average probability of a central location.
• There is a weak probability of a high geodesic distance from any other node.

In the case of clique-based metrics:

• There is an average probability of many direct connections.
• There is an average/high probability of neighbors with a large number of degrees.
• There is an average probability of a central location.
• There is a weak probability of a high geodesic distance from any other node.

In addition, we have briefly described how these metrics can be used to rank vertices (nodes).

• Correlation analysis of k-hop metrics and classical graph measures from a quantum topology perspective

• ${\mathcal{WCGD}}^{\left[k\right]}$ and Degree Centrality: This relatively strong correlation suggests that the k-hop-based density effectively reflects the degree distribution of nodes, which can be particularly relevant in highly connected graphs such as those of the Pegasus and Zephyr topologies.
  ${\mathcal{WRCGD}}^{\left[k\right]}$ and Closeness Centrality: The weighted relative density metric is closely related to graphs’ global accessibility characteristics, which can help to optimize quantum topologies by maximizing accessible pathways.
• ${\mathcal{RCGD}}^{\left[k\right]}$ and Clustering Coefficient: This indicates that the relative density is minimally influenced by local clustering, making it unsuitable for modeling purely local graph features.
  ${\mathcal{WCGR}}_{sb}^{\left[k\right]}$ and Clustering Coefficient: Size-based redundancy also shows a weak correlation with the clustering coefficient, suggesting that this metric primarily reflects global patterns rather than local ones.
• WRCGD[k] ${\mathcal{WRCGD}}^{\left[k\right]}$ and Eccentricity: The negative correlation indicates that the k-hop-based density decreases as eccentricity increases, meaning that nodes farther apart contribute less to density metrics.
  ${\mathcal{CGR}}_{vb}^{\left[k\right]}$ and Eigenvector Centrality: This negative relationship suggests that value-based redundancy does not emphasize the global dominance of nodes within the graph structure.

• Optimal k-hop environment for quantum topology analysis

It is not easy to define the size of the environmental parameter k or to determine whether the size of the subgraph defined in this way provides sufficient information about the environment of a given vertex. Here, we justify the use of a k-hop environment through some illustrative examples. In D-Wave’s quantum computers, quantum bits are arranged in a special physical topology defined by the internal interconnection structure of the system. The study of the 3-hop environment for a given quantum bit provides sufficient insight into the interaction potential of that quantum bit with its direct and indirect neighbors.

Quantum decoherence is when a quantum system loses its coherence, i.e., the phases of the superposition states of individual quantum bits become disconnected. Possible causes of this include temperature noise, electromagnetic interference, or the states of other quantum bits in the immediate environment of the quantum well [55]. Such interactions with the environment are nonlocal, i.e., they are not limited to immediate neighbors, meaning that they can also affect more distant quantum bits. The strength of the quantum decoherence decreases exponentially with the distance; the further away one qubit is from another, the weaker the interaction. Beyond a 3-hop distance these interactions become practically negligible. Of course, a 2-hop or 4-hop environment can also be investigated, depending on the topology; in some cases, a 2-hop environment may only be suitable for representing features that are too local, while a 4-hop environment may already significantly increase the number of vertices/interactions to be investigated, especially in high-degree topologies, adding significant computational cost and complexity.

Beyond the effects of quantum decoherence, the 3-hop neighborhood of quantum bits provides a sufficient framework for describing the interplay between local and global properties in quantum systems. Quantum entanglement is inherently a local phenomenon, with its probability declining rapidly as the spatial distance increases [56]. The 3-hop distance is often the limit at which the effect of entanglement is no longer detectable, as the interactions between indirect quantum bits are weakened. Spin systems or quantum magnets can exhibit local dynamical phase transitions where interactions at a certain distance no longer dominate [57,58]. The 3-hop distance often covers the interaction boundaries in these cases as well. Thus, we believe that this distance provides a balance between the study of local and global interactions. For a system with a dense topology, this depth is sufficient to reveal the complex behavior of the system while not becoming unmanageably complex. Of course, a 3-hop depth can be a lot in certain cases; for example, the connectivity density and layout of the Zephyr topology studied in this paper means that a 3-hop depth environment already contains a significant fraction of quantum bits. We note beforehand that in this case the study of a 2-hop environment may be sufficient; however, we will cover this in a future paper.

• Classical graph metrics

In our other previous paper [59], we focused on graph-based analysis of the topology of D-Wave quantum computers. The Pegasus, Chimera, and Zephyr topologies were generated with different parameters, which we examined using classical-based graph metrics. We worked with the average values of the metrics interpreted on the graphs, as we were interested in the characteristics demonstrated by these metrics.

Classical graph metrics such as degree centrality, closeness centrality, betweenness centrality, ${\mathcal{RCGD}}^{\left[3\right]}$ similarity, and eigenvector centrality can provide valuable insights into the structure and properties of graphs. However, they have several limitations:

• Metrics such as betweenness and closeness centrality have high computational complexity, making them impractical for very large graphs [60,61].
• Metrics can be affected by the density of the graph. For example, in very dense or very sparse graphs, some centrality measures might not apply. In our previous paper [59], we focused on graph-based analysis of the topology of D-Wave quantum computers. We examined Pegasus, Chimera, and Zephyr topologies generated with different parameters using classical-based graph metrics. We worked with the average values of the metrics interpreted on the graphs, as we were interested in the characteristics shown by these metrics. Classical graph metrics such as degree centrality, closeness centrality, betweenness centrality, and eigenvector centrality can provide valuable insights into the structure and properties of graphs as well as meaningful distinctions between nodes [62].
• Many metrics were originally designed for undirected graphs, and may not apply straightforwardly to directed graphs [63].
• Centrality measures can be significantly affected by the presence of outlier nodes, which may not be representative of the overall network [64].
• Many classical metrics assume that all nodes have similar roles or functions, which is not always true in heterogeneous networks where nodes represent different entities or functions [65].
• Classical metrics may not effectively capture the nuances of complex network structures such as modularity, community structure, or hierarchical organization [66].

• Baseline models and comparative analysis in quantum topology research

The comparative analysis of novel methodologies against established baseline models is crucial in validating and interpreting their effectiveness. Existing research has typically employed classical graph metrics such as degree centrality, betweenness centrality, closeness centrality, eigenvector centrality, and clustering coefficients to evaluate quantum computing topologies, including D-Wave’s Chimera, Pegasus, and Zephyr architectures [49,50,67,68,69]. Additionally, recent studies have introduced quantum-specific metrics tailored specifically to quantum annealers in order to assess connectivity, redundancy, and optimization efficiency [14,23,25,68,70]. These metrics often focus on evaluating quantum annealing performance concerning optimization problems, energy landscape characteristics, or the effects of qubit connectivity on computational efficiency.

Moreover, advanced comparative studies have utilized metrics derived from quantum information theory and statistical mechanics, including entanglement entropy, mutual information, and spin glass order parameters, providing deeper insights into quantum topological structures and annealing dynamics [71,72,73,74]. In particular, recent research employing entanglement-based metrics has demonstrated significant potential for identifying critical connectivity patterns and predicting quantum annealing performance in complex quantum hardware topologies [75,76].

In contrast, our work introduces novel k-hop-based graph metrics explicitly designed for analyzing quantum hardware topologies by effectively bridging local and global connectivity information. By explicitly considering neighborhoods within a k-hop distance, our proposed metrics provide more nuanced and detailed insights into redundancy, density, and fault tolerance, addressing limitations associated with purely classical metrics [67,68]. Future research will extend our comparative analysis by systematically benchmarking our proposed k-hop metrics against both classical baseline metrics and advanced quantum-specific metrics, offering a comprehensive evaluation of their effectiveness in quantum hardware analysis.

• D-Wave quantum computers and topological developments

D-Wave quantum computers are among the most advanced quantum annealing devices currently available. They are designed to solve optimization problems efficiently using a graph-based qubit connectivity structure. Over the years, significant advancements have been made in their architectural design and computational capabilities, leading to the development of the Chimera, Pegasus, and Zephyr topologies. These innovations directly impact the performance and scalability of quantum annealers.

One of the earliest comprehensive evaluations of quantum annealing performance on D-Wave systems in comparison with classical optimization algorithms was presented in [77]. This study demonstrated that quantum annealers may outperform specific classical heuristics on certain problem instances, emphasizing the critical role of topological connectivity in computational efficiency. Subsequent work provided empirical evidence for the scaling advantages of quantum annealers in large-scale graph problems, particularly when leveraging advanced connectivity structures such as Pegasus and Zephyr [78]. A detailed review of the underlying mechanisms of quantum annealing, including the role of open-system quantum dynamics in performance enhancement, was offered in [79]. This analysis further supports the importance of understanding the topological properties of D-Wave architectures to enable more effective algorithmic implementation. The ongoing development of D-Wave architectures highlights the central importance of graph-based connectivity in quantum computing. Building upon these prior contributions, the present study introduces k-hop-based graph metrics to assess and compare the structural properties of different topologies. The conclusions drawn [77,78,79] collectively underscore the relevance of this approach, as they point to the necessity for more refined graph-theoretic metrics to systematically evaluate the efficiency of quantum annealing.

• Recent advances in quantum topologies and graph metrics

Quantum computing architectures continue to evolve rapidly, with several novel topologies and analytical methods emerging in recent years. These advancements focus significantly on improving scalability, fault tolerance, and graph-based analysis metrics, all of which are relevant for optimization and error mitigation strategies in quantum computing devices [80,81,82]. Recently, Microsoft unveiled the Majorana 1, a topological quantum processor powered by topological qubits, marking a transformative leap toward practical quantum computing [80]. This new design facilitates efficient error-correction implementations due to higher connectivity and locality properties. The structural advantages of topological qubits particularly benefit fault-tolerant quantum computations and enable compact representations of quantum circuits. Another innovative development is the Hyperion project led by Nu Quantum, which aims to advance distributed quantum computing by demonstrating efficient qubit interconnects [82]. This approach allows quantum error correction schemes to be encoded directly into the hardware architecture, thereby enhancing computational throughput under decoherence conditions. This design allows for significantly richer connectivity patterns than traditional lattice structures, providing a substantial advantage in executing complex quantum algorithms. Novel metrics have also been proposed from a graph-theoretical perspective. A notable advancement is the Quantum Robustness Metric (QRM), specifically designed to assess structural fault-tolerance through dynamic connectivity properties within quantum graphs. This metric offers refined tools for topology optimization in the presence of operational quantum noise, greatly benefiting hardware validation processes. Additionally, Spectral Quantum Graph Theory (SQGT) has emerged as a robust analytical framework that exploits spectral properties of adjacency matrices to analyze quantum connectivity, supporting scalability predictions for large quantum processor architectures. It has proven particularly effective in characterizing quantum hardware in terms of entanglement distributions and error propagation. Several algorithms leveraging graph-theoretical frameworks have recently gained prominence in the context of quantum optimization, particularly in improving the embedding of problem graphs onto quantum annealing hardware. Quantum graph embedding techniques aim to enhance the fidelity of the mapping between logical and physical qubits while minimizing chain lengths and resource overhead. Recent work has demonstrated that quantum annealing-based node embedding can exploit graph structures to improve embedding efficiency [83]. Variational quantum algorithms have also been used to generate compact graph embeddings through parameterized quantum circuits, enabling more effective use of hardware resources [84,85]. In addition, scalable heuristic methods for minor embedding have been proposed for sparse hardware topologies with tens of thousands of nodes, showing significant improvements in embedding quality and hardware utilization [86]. By effectively optimizing graph embeddings, this method significantly mitigates the performance bottlenecks often encountered in large-scale quantum annealers. In parallel, developments involving hybrid topologies such as the Helios configuration have merged classical–quantum hybrid interconnectivity, showing improved flexibility in solving large-scale optimization problems through quantum–classical cooperative graph processing [87]. Hybrid architectures enable enhanced computational performance by strategically integrating classical computing nodes into quantum networks. Finally, recent theoretical insights have provided a deeper understanding of the complexity classes associated with graph-based quantum computing. Particularly noteworthy is the formal proof establishing tighter upper bounds for complexity in quantum topologies by utilizing graph isomorphism verification algorithms, thereby refining theoretical constraints for topology designers [88,89]. These insights allow for better theoretical predictions of the limits of quantum computational scalability. Advancements in recent years have highlighted substantial progress in topology design as well as in analytical methodologies, indicating promising avenues for future integration of quantum computing hardware and software.

3. Topology Analysis

In this article, we focus on D-Wave processor topologies. D-Wave’s processors work with quantum annealing, which they use to solve optimization problems. D-Wave’s quantum annealing processors are structured on the basis of the Chimera, Pegasus, and Zephyr graph topologies [49,50,51]. In general, these topologies (graphs) consist of different subgraphs depending on the implementation, in which the qubits are connected in a specific pattern. On the entire chip, these subgraphs are repeated with varying degrees of interconnectedness, resulting in a highly interconnected and modular architecture. These topologies are optimized for optimization problems such as the Ising model and the quadratic unconstrained binary optimization (QUBO) problem. D-Wave’s processors are not universal, and may not be suitable for other types of quantum algorithms that require different types of connectivity or topology [68,69,70].

3.1. Chimera

The Chimera two-dimensional lattice graph ${\mathcal{C}}_{M,N,L}$ is an $\mathcal{M}$ x $\mathcal{N}$ grid of Chimera tiles, and implements the topology of D-Wave 2000Q systems. The Chimera titles ${\mathcal{K}}_{L,L}$ are complete bipartite graphs. A Chimera graph contains a particularly nice clique minor, making the triangle embedding uniform and near-optimal [49,67].

The degree number distribution of the Chimera graph is not probabilistic, instead following a discrete deterministic distribution with a nature that depends in part on the right-heterogeneity of the topology. Regardless of the parameters, in general it can be said that the vertices of the graph can be classified into two groups according to their number of vertices, that is, interior vertices and edge vertices. The best way to characterize the graph is that the degree number distribution is close to a delta distribution, with variation (4–5) at the edges. This degree distribution close to the delta distribution allows algorithms optimized for the structure of the Chimera graph to work efficiently, as the uniform connectivity pattern facilitates the embedding of the problem [49,67].

The following configurations were used on Chimera-based D-Wave processors: ${\mathcal{C}}_{l·n,l·n,l}$, where $n\in {\mathbf{N}}^{+}$ and $l=4$. In the ${\mathcal{C}}_{12,12,4}$ configuration, the processor can use 1152 qubits. The Chimera graphs were examined under different configurations from ${\mathcal{C}}_{2,2,4}$ to ${\mathcal{C}}_{16,16,4}$ with L values of 4 and 8.

Within the analyzed interval, the average number of neighbors of each vertex is from 6 to $6.875$, while the average degrees of vertices is from 10 to $11.75$. Let $f_C(M,N,L)$ be a function for representing a Chimera graph $G(V,E)$ as a function of V + E. The value set of $f_C$ is then provided by the average values of one of the previously defined classical or k-hop-based metrics.

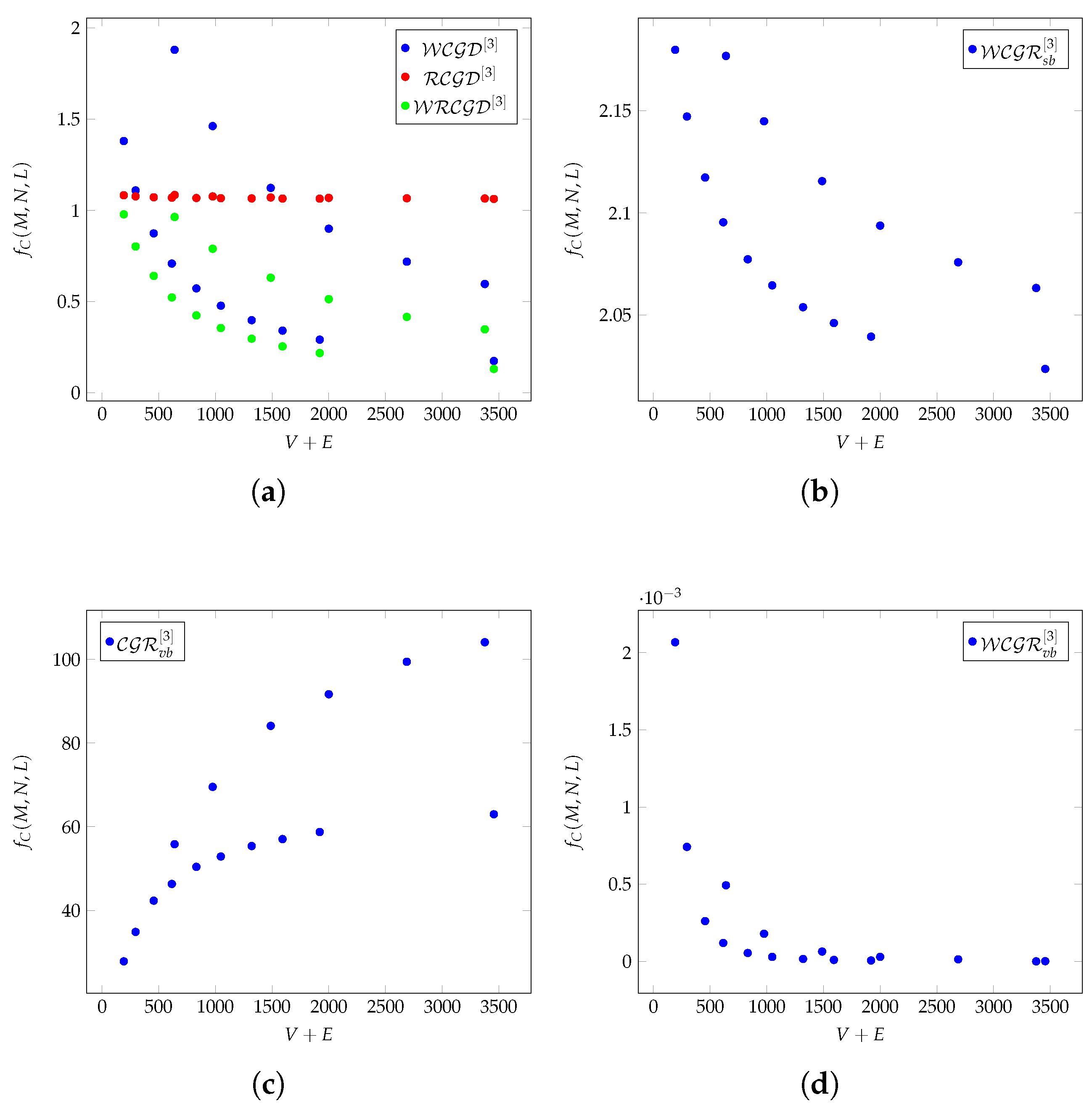
The parameters N and M primarily define the characteristic of the function, while L defines the offset of $f_C$ on the y-axis. Figure 1a–d shows the $f_C$ functions of the k-hop-based metrics as functions of $V+E$ for different Chimera graphs.

Figure 1a presents the behavior of ${\mathcal{WCGD}}^{\left[3\right]}$, ${\mathcal{RCGD}}^{\left[3\right]}$, and ${\mathcal{WRCGD}}^{\left[3\right]}$ as a function of graph size. The ${\mathcal{RCGD}}^{\left[3\right]}$ values remain relatively stable across different graph sizes, indicating that the relative communication density metric does not exhibit significant variation with increasing graph complexity. In contrast, ${\mathcal{WCGD}}^{\left[3\right]}$ and ${\mathcal{WRCGD}}^{\left[3\right]}$ show a more variable pattern, with noticeable fluctuations, particularly in smaller graphs, before settling into a decreasing trend as the graph grows larger. This suggests that the influence of weighted density measures is more pronounced in smaller graphs and gradually diminishes as the graph structure expands. These results indicate that ${\mathcal{RCGD}}^{\left[3\right]}$ is a reliable measure of relative density regardless of graph size, while ${\mathcal{WCGD}}^{\left[3\right]}$ and ${\mathcal{WRCGD}}^{\left[3\right]}$ are more sensitive to local structural variations, especially in smaller networks. This distinction is particularly relevant for quantum-inspired topologies, where the balance between local connectivity and global graph density influences computational performance and information flow.

In Figure 1b, it can be seen that the redundancy of the graph increases faster than the number of vertices (V) and edges (E) as the value of ${{\mathcal{WCGR}}_{sb}}^{\left[3\right]}$ increases. The L value defines the unit cell size in the Chimera topology, affecting connectivity patterns and redundancy properties. The ${{\mathcal{WCGR}}_{sb}}^{\left[3\right]}$ metric has a decreasing trend, meaning that the ${{\mathcal{WCGR}}_{sb}}^{\left[3\right]}$ value gradually decreases as the graph size increases. In larger Chimera graphs, the effect of weighted redundancy becomes more uniform.

Figure 1c shows that the ${{\mathcal{CGR}}_{vb}}^{\left[3\right]}$ metric shows a strong upward trend, meaning that the clustering redundancy grows as the graph size ($V+E$) increases The ${{\mathcal{CGR}}_{vb}}^{\left[3\right]}$ metric that measures the redundancy of local and global connection patterns in a graph. It specifically examines the repetition and density of connection patterns between nodes. If ${{\mathcal{CGR}}_{vb}}^{\left[3\right]}$ increases, this means that more nodes are involved in dense and repetitive clustering patterns. Larger values of ${{\mathcal{CGR}}_{vb}}^{\left[3\right]}$ indicate that as the Chimera topology expands, it maintains and strengthens connectivity, which is a key property for quantum error correction.

Figure 1d shows that the ${{\mathcal{WCGR}}_{vb}}^{\left[3\right]}$ values decrease sharply as the total number of vertices and edges ($V+E$) increases. This suggests that weighted redundancy is significantly reduced in larger Chimera-based quantum graphs. Initial high values indicate that weighted links contribute strongly to redundancy in small Chimera graphs. As the graph expands, ${{\mathcal{WCGR}}_{vb}}^{\left[3\right]}$ drops exponentially, reaching nearly zero at the largest $V+E$ values. This suggests that as the Chimera topology scales, the contribution of individual weighted connections to the global redundancy diminishes, making the structure less robust in terms of weighted redundancy. The sharp decline in ${{\mathcal{WCGR}}_{vb}}^{\left[3\right]}$ suggests that Chimera graphs become structurally sparser in a weighted redundancy sense. This has direct implications for embedding quantum algorithms, as redundancy is often required in order to maintain fault tolerance.

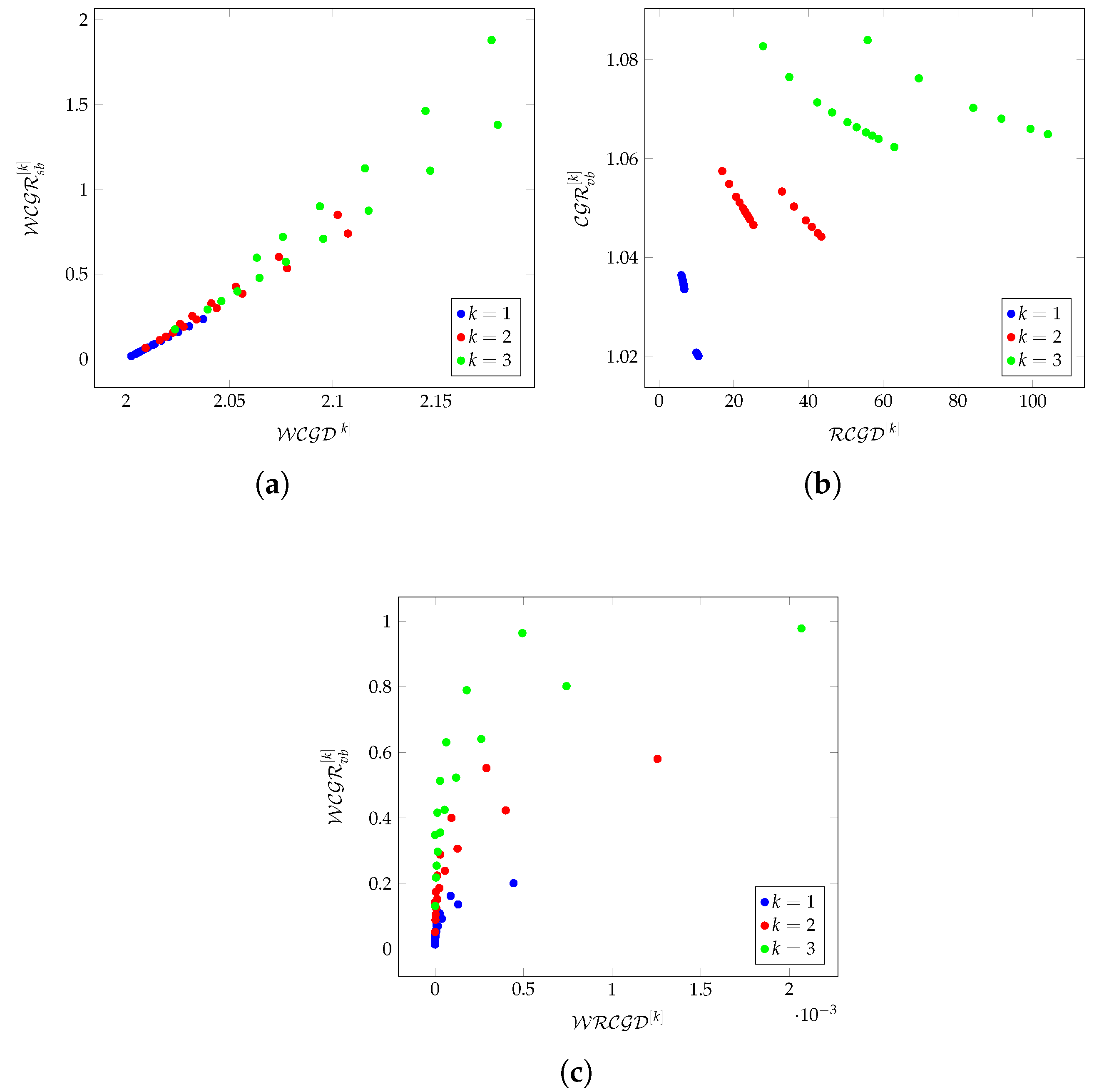
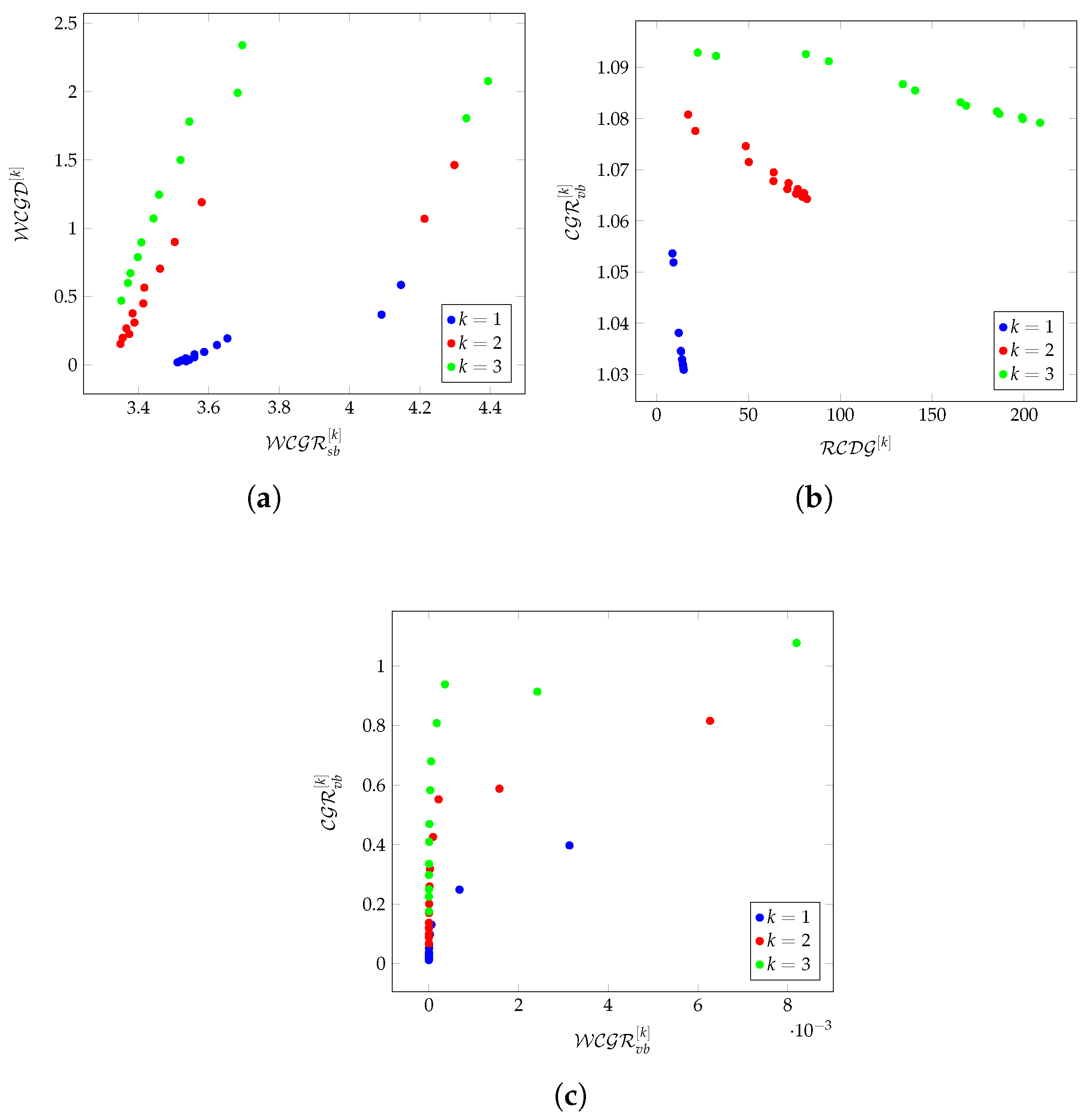
Figure 2a–c shows the relationships between individual k-hop-based metrics on Chimera graphs.

Figure 2a shows the following:

• For $k=1$, the relationship between ${\mathcal{WCGD}}^{\left[k\right]}$ and ${\mathcal{WCGR}}_{sb}^{\left[k\right]}$ is linear.
• For $k=2$ and $k=3$, the lower part of the data follows a linear relationship for Chimera graph generation with $l=2$.
• For $l=4$, the trend deviates slightly upward, suggesting that in these cases the redundancy metric does not scale perfectly linearly with the density.

When the relationship between ${\mathcal{WCGD}}^{\left[k\right]}$ and ${\mathcal{WCGR}}_{sb}^{\left[k\right]}$ is linear, this means that:

• As graph density increases, redundancy grows at a constant rate.
• There are no sudden phase transitions or structural changes; every additional increase in density results in a fixed rise in redundancy.
• The network structure is likely to be well-balanced and predictable, and adding edges or nodes is unlikely to introduce complexity beyond simple proportional scaling.
• In linear regions, adding new quantum connections results in proportional improvements in fault tolerance, meaning that error correction strategies can be systematically scaled.
• The efficiency of quantum embedding remains stable, as there are no unexpected nonlinear effects.

If ${\mathcal{WCGR}}_{sb}^{\left[k\right]}$ and ${\mathcal{WCGD}}^{\left[k\right]}$ follow a polynomial trend (as seen in $l=4$ cases for $k=2$ and $k=3$), then this suggests that:

• Adding new connections will result in a disproportionately high increase in redundancy.
• Certain structural changes in the graph (e.g., higher connectivity patterns or increased clustering) will enhance redundancy at a faster than linear rate.
• After a certain point, additional density does not significantly contribute to redundancy growth.
• There is a possibility of network bottlenecks in which new connections are not effectively utilized.
• Polynomial relationships may indicate sudden structural shifts in the network that could either improve error tolerance (superlinear case) or lead to inefficiencies (sublinear case).
• If the increase in redundancy is nonlinear, embedding quantum circuits could become more complex due to non-trivial connectivity patterns.

In Figure 2b it can be seen that ${\mathcal{CGR}}_{vb}^{\left[k\right]}$ decreases as the relative density ${\mathcal{RCGD}}^{\left[k\right]}$ increases. This trend is observed across all three of the Chimera, Pegasus, and Zephyr topologies, suggesting a fundamental structural property of these graphs.

When a graph has lower ${\mathcal{RCGD}}^{\left[k\right]}$ values (less dense connectivity), more redundant pathways are needed, leading to higher ${\mathcal{CGR}}_{vb}^{\left[k\right]}$. As ${\mathcal{RCGD}}^{\left[k\right]}$ increases, direct paths become more dominant, reducing the need for alternative redundant paths. If a topology is optimized for high-density communication, then redundancy is inherently lower, as most nodes are already well connected. In sparse graphs, redundancy is higher because paths have to be more flexible in order to compensate for missing direct connections. High-density networks use fewer redundant pathways, optimizing quantum routing for efficiency, while low-density networks rely on alternative paths, requiring redundancy to maintain fault tolerance.

A strong negative correlation (linear decrease) suggests that redundancy is an inverse function of density, meaning that denser regions of a quantum processor require fewer redundant pathways. For quantum annealers, denser connectivity may reduce overhead in implementing error correction mechanisms. For quantum error correction and optimization, this suggests that redundancy is mainly needed in lower-density areas where connectivity is weaker.

Figure 2c shows the following:

• The observed logarithmic trend implies that ${{\mathcal{WCGR}}_{vb}}^{\left[k\right]}$ grows at a progressively slower rate as ${\mathcal{WRCGD}}^{\left[k\right]}$ increases; redundancy still increases as density grows, but at a diminishing rate.
• Beyond a certain point, adding more connectivity does not significantly improve redundancy. This suggests a form of ‘redundancy saturation’, meaning that additional connectivity no longer contributes meaningfully to extra redundancy in highly-connected networks.
• In the early stages of increasing ${\mathcal{WRCGD}}^{\left[k\right]}$, there is a rapid rise in ${{\mathcal{WCGR}}_{vb}}^{\left[k\right]}$; this means that small increases in connectivity initially provide large gains in redundancy.
• As ${\mathcal{WRCGD}}^{\left[k\right]}$ continues to increase, the growth in redundancy slows down. This suggests that at high-density levels, additional connections mostly reinforce existing pathways rather than introducing new redundancy.
• If ${{\mathcal{WCGR}}_{vb}}^{\left[k\right]}$ becomes saturated logarithmically, the quantum error correction benefits decrease after a certain connectivity level. This suggests that increasing connectivity beyond an optimal threshold is unnecessary for maximizing fault tolerance.
• Logarithmic growth indicates that scaling connectivity does not require proportional increases in redundancy. This is good for large-scale quantum systems, where efficient routing and embedding must be balanced with density and redundancy.

Examining the ${\mathcal{C}}_{8,8,4}$ graph in more detail, the redundancy of the entire graph is $5.77$ and the average value of the cliques is $8.4\times {10}^3$.

Table 2. Average values of classical metrics in 1-hop to 3-hop environments of vertices.

	N. of Vertices	N. of Edges
1-hop	$6.75$	$11.5$
2-hop	$25.25$	$66.5$
3-hop	63	226

shows how the average number of vertices and edges in each vertex environment increases as a function of the hop number. In this graph, the number of vertices is 512 and the number of edges is 2944. In a 3-hop environment, on average $12.3$% of all vertices can be reached from custom vertices, and the environments contain $7.7$% of all edges on average.

Table 3. Average values of density-based and redundancy-based metrics in 1-hop to 3-hop environments of vertices.

k	Density-Based Metrics			Redundancy-Based Metrics
	${\mathcal{WCGD}}^{\left[\mathbf{k}\right]}$	${\mathcal{RCGD}}^{\left[\mathbf{k}\right]}$	${\mathcal{WRCGD}}^{\left[\mathbf{k}\right]}$	${\mathcal{WCGR}}_{\mathit{sb}}^{\left[\mathbf{k}\right]}$	${\mathcal{CGR}}_{\mathit{vb}}^{\left[\mathbf{k}\right]}$	${\mathcal{WCGR}}_{\mathit{vb}}^{\left[\mathbf{k}\right]}$
1	0.0159	1.0335	0.0136	2.0025	6.7474	$1\times {10}^{-7}$
2	0.0641	1.0465	0.0517	2.0094	25.2405	$4.3\times {10}^{-7}$
3	0.1745	1.0623	0.1309	2.0236	62.9765	$1.04\times {10}^{-6}$

shows the average values of density-based and redundancy-based metrics in 1-hop to 3-hop environments of vertices.

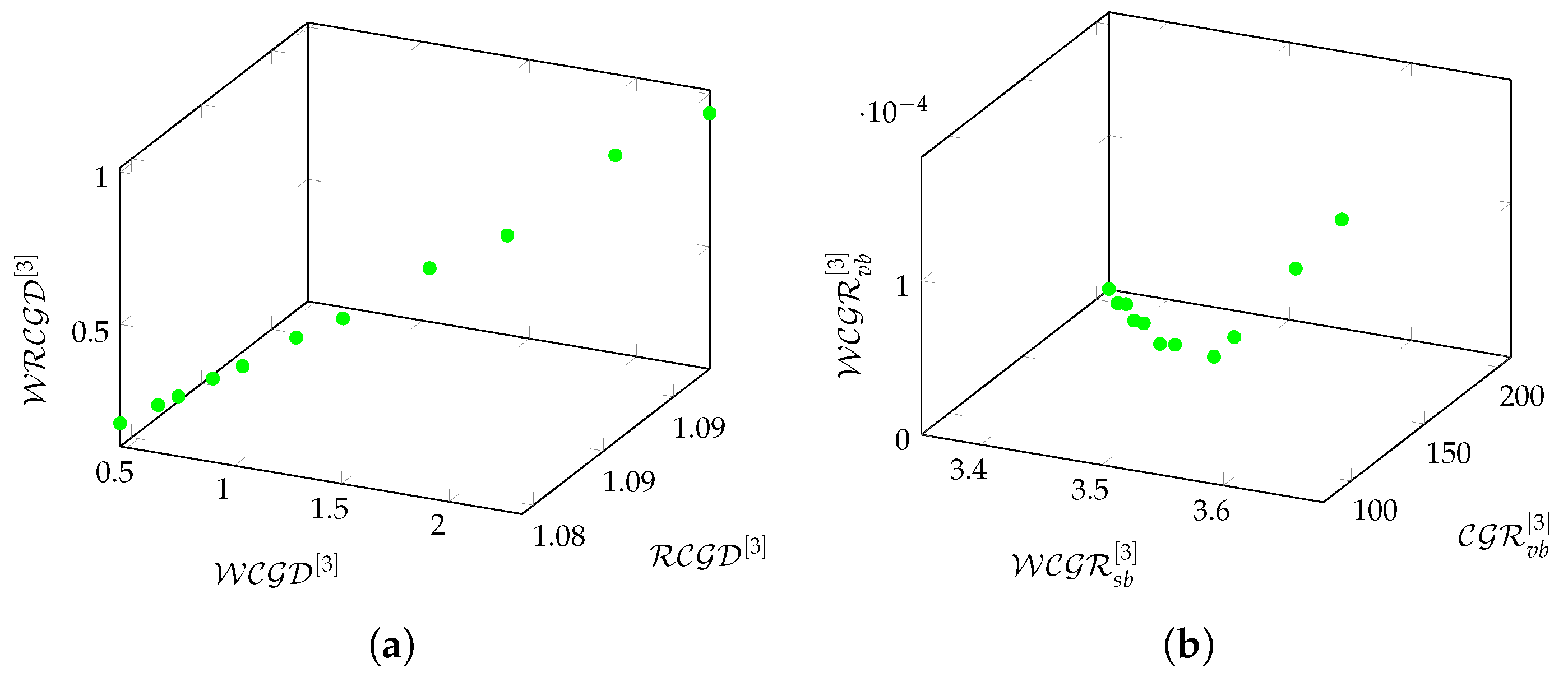
Figure 3a,b shows the relationships between the average values of density-based and redundancy-based metrics on Chimera graphs in a 3-hop environment.

Figure 3a shows the relationship between ${\mathcal{WCGD}}^{\left[3\right]}$, ${\mathcal{RCGD}}^{\left[3\right]}$, and ${\mathcal{WRCGD}}^{\left[3\right]}$. The differences between density-based metrics reflect sensitivity levels. It can be seen that ${\mathcal{WCGD}}^{\left[3\right]}$ decreases more rapidly than ${\mathcal{RCGD}}^{\left[3\right]}$ and ${\mathcal{WRCGD}}^{\left[3\right]}$, since it compensates less for the thinning of the links. This confirms that the relative density of connections decreases as the graph size increases. Figure 3b shows the relationship between ${{\mathcal{WCGR}}_{sb}}^{\left[3\right]}$, ${{\mathcal{CGR}}_{vb}}^{\left[3\right]}$, and ${{\mathcal{WCGR}}_{vb}}^{\left[3\right]}$. The size-based redundancy (${{\mathcal{WCGR}}_{sb}}^{\left[3\right]}$) shows faster growth than the value-based metrics (${{\mathcal{CGR}}_{vb}}^{\left[3\right]}$, ${{\mathcal{WCGR}}_{vb}}^{\left[3\right]}$). This difference indicates stronger scaling of size-based metrics, while value-based metrics reflect finer patterns.

3.2. Pegasus

The Pegasus topology is a variation of the Chimera architecture. In this topology, each tile has eight qubits arranged in a square, and each qubit is connected to its four nearest neighbors by couplers. The couplers are essentially connections between qubits. One of the important features of the Pegasus topology is that it also has longer-range couplers that connect qubits between adjacent tiles.

In Pegasus, the number of quantum bits depends on their position in the graph; here too, we distinguish between inner and outer quantum bits. The degree of the graphs is higher than for Chimera, as Pegasus maintains more connections between quantum bits. The degree number distribution is not uniform, as in this topology the quantum bits are located in different positions and the number of neighbors is position-dependent. The degree number distribution is truncated normal-like.

Pegasus is suitable for performing more complex calculations than Chimera-based processors because it allows for more complex interactions between qubits. The Pegasus topology is designed to provide high connectivity and flexibility. Thus, Pegasus-based processors support a wider range of quantum algorithms than earlier ones. As in Chimera, the qubit orientations in Pegasus are vertical or horizontal [50,90]. The maximum degree of the ${\mathcal{P}}_M$ graph is 15. The number of vertices depends on multiple parameters: u, w, k, and z respectively represent the orientation, tile offset, qubit offset, and parallel tile offset.

By definition, ${\mathcal{P}}_0$ consists of some disconnected components and contains $8(M-1)$ qubits. The size of the main processor fabric is $24M(M-1)-8(M-1)$, while the size of the full disconnected graph is $24M(M-1)$. A Pegasus graph that retains the basic characteristics of Chimera can also be created; in this case, the size of the graph is $24{(M-1)}^2$, with ${\mathcal{P}}_8$ containing 1344 qubits and 1288 in the main fabric. Pegasus graphs were examined under different configurations from ${\mathcal{P}}_2$ to ${\mathcal{P}}_8$.

Within the analyzed interval, the average number of neighbors of each vertex is from $8.66$ to $14.67$, while the average degrees of the vertices are from $15.33$ to $27.34$. Let $f_P\left(M\right)$ be a function for representing a Pegasus graph $G(V,E)$ as a function of V + E. The value set of $f_P$ is provided by the average values of one of the previously defined classical or k-hop-based metrics.

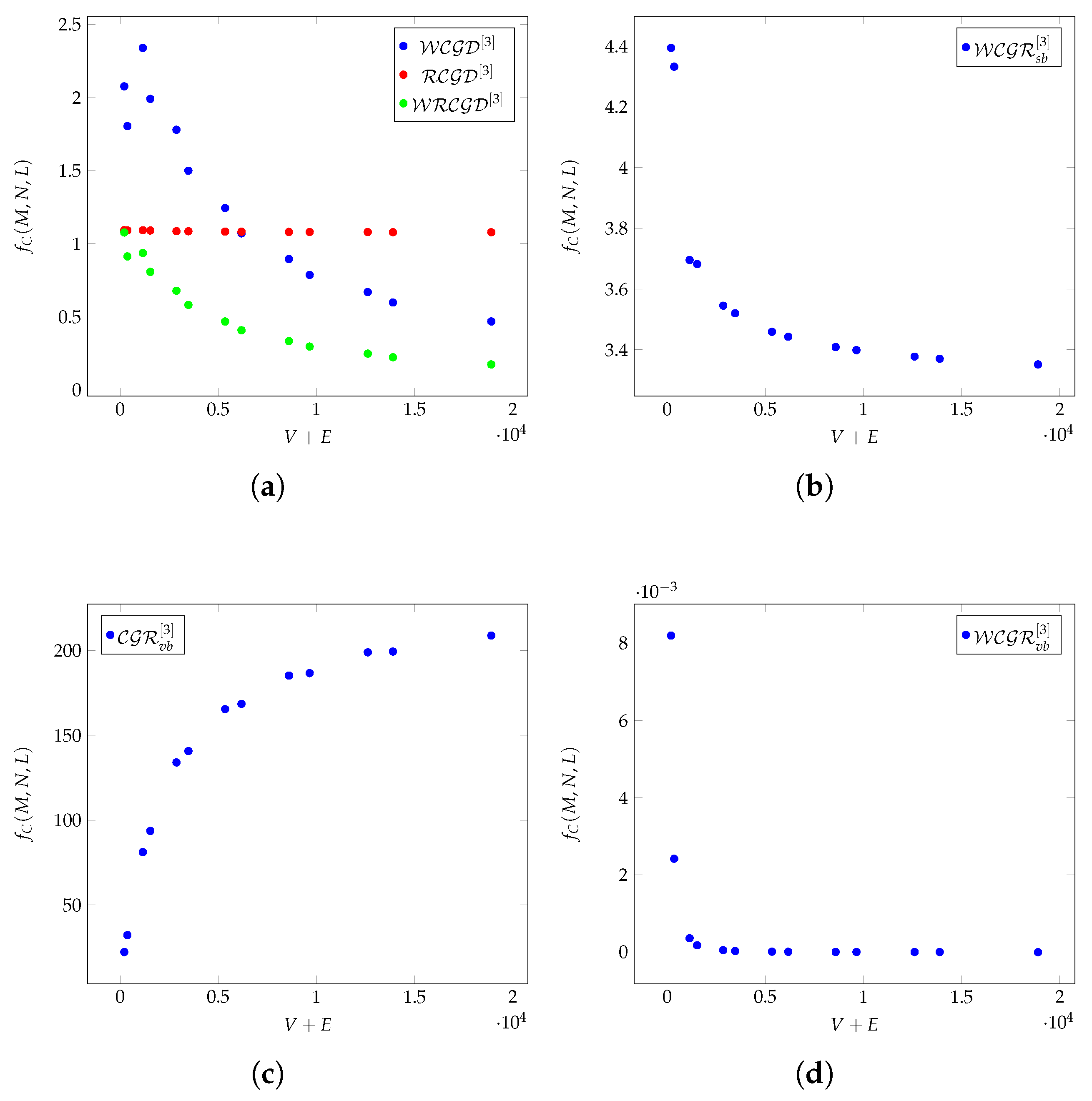
Figure 4a–d shows the $f_P$ functions of k-hop-based metrics as functions of $V+E$ for different Pegasus graphs. Figure 4a presents the behavior of ${\mathcal{WCGD}}^{\left[3\right]}$, ${\mathcal{RCGD}}^{\left[3\right]}$, and ${\mathcal{WRCGD}}^{\left[3\right]}$ as functions of the graph size. It can be seen that ${\mathcal{RCGD}}^{\left[3\right]}$ remains relatively stable across all graph sizes, maintaining values close to $1.08$–$1.09$. This suggests that the relative communication density is not highly sensitive to changes in graph size. In addition, ${\mathcal{WCGD}}^{\left[3\right]}$ and ${\mathcal{WRCGD}}^{\left[3\right]}$ exhibit decreasing trends as the graph grows larger. Initially, ${\mathcal{WCGD}}^{\left[3\right]}$ reaches higher values ($2.3$ at $V+E=1152$) compared to Chimera (see Figure 1a), indicating stronger weighted communication density in smaller Pegasus graphs. In smaller graphs, ${\mathcal{WCGD}}^{\left[3\right]}$ is more volatile, displaying fluctuations similar to Chimera but with higher peak values. It can be seen that ${\mathcal{WRCGD}}^{\left[3\right]}$ also follows a decreasing pattern, starting from $1.08$ at $V+E=208$ and gradually declining towards $0.17$ at $V+E=18896$, suggesting that the weighted relative communication density becomes less significant in larger graphs, with higher initial ${\mathcal{WCGD}}^{\left[3\right]}$ values in Pegasus and ${\mathcal{WCGD}}^{\left[3\right]}$ for small graph sizes compared to Chimera. This suggests that the local connectivity in Pegasus is initially denser, likely due to its more interconnected structure. While both topologies show declines in these metrics, Pegasus exhibits a steeper decrease in the ${\mathcal{WCGD}}^{\left[3\right]}$ and ${\mathcal{WRCGD}}^{\left[3\right]}$ values, meaning that the impact of weighted density metrics diminishes more significantly than in Chimera as the graph grows. The ${\mathcal{RCGD}}^{\left[3\right]}$ values remain stable in both topologies, suggesting that the relative communication density is not highly topology-dependent.

Figure 4b shows a decreasing trend, i.e., as the graph size increases, the size-weighted redundancy decreases. Initially (for small graphs), the values of ${{\mathcal{WCGR}}_{sb}}^{\left[3\right]}$ are much higher than for Chimera (see Figure 1b), suggesting that the Pegasus topology is more locally redundant at smaller scales. Pegasus is initially more redundant, which could be useful for fault-tolerant qubit communication. The decrease in redundancy is more stable, which could indicate that topological organization is more efficient at larger scales.

Figure 4c shows a rapid increase in the ${{\mathcal{CGR}}_{vb}}^{\left[3\right]}$ metric, suggesting that as the Pegasus graph grows, its redundancy expands. Pegasus starts at a slightly lower ${{\mathcal{CGR}}_{vb}}^{\left[3\right]}$ value but surpasses Chimera significantly (see Figure 1c) as the graph size increases. The final ${{\mathcal{CGR}}_{vb}}^{\left[3\right]}$ values in Pegasus are nearly twice as high, indicating that it maintains higher redundancy at larger scales. Compared to Chimera, Pegasus maintains a more structured and high-redundancy topology, which is beneficial for quantum hardware optimization.

Figure 4d shows that the ${{\mathcal{WCGR}}_{vb}}^{\left[3\right]}$ metric drops significantly as the Pegasus graph expands. Compared to Chimera (see Figure 1d), Pegasus initially has higher weighted redundancy, but this advantage diminishes quickly as the system scales.

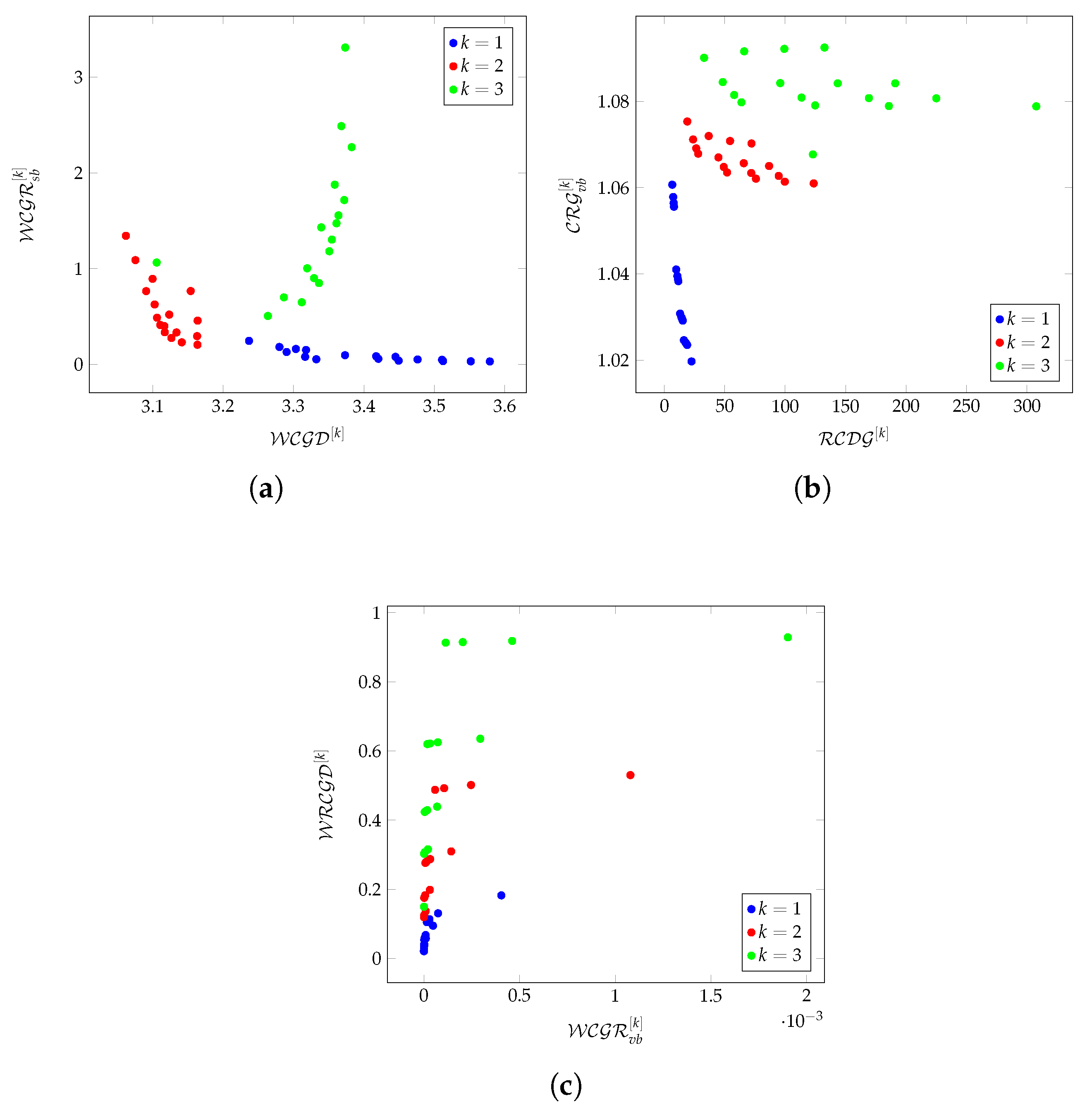
Figure 5a–c shows the relationships between custom k-hop-based metrics on Pegasus graphs.

Figure 5a shows the following:

• Unlike the Chimera graph (see Figure 2a), where different l values ($l=2$, $l=4$) cause deviations from linearity, the Pegasus graph maintains a strictly linear relationship between ${\mathcal{WCGD}}^{\left[k\right]}$ and ${\mathcal{WCGR}}_{sb}^{\left[k\right]}$ regardless of the hop depth ($k=1$, $k=2$, $k=3$).
• The Pegasus graph expands in a highly regular and predictable manner. Each additional connection preserves the same proportional redundancy increase, meaning that there are no sudden structural shifts or saturation points.
• The topology does not introduce emergent clustering behaviors that would alter the redundancy scaling. This means that error correction and optimization techniques can be applied consistently without needing to account for nonlinear effects.

Figure 5c shows the logarithmic trend, implying that ${{\mathcal{WCGR}}_{vb}}^{\left[k\right]}$ grows at a progressively slower rate as ${\mathcal{WRCGD}}^{\left[k\right]}$ increases. The redundancy still increases as density grows, but at a diminishing rate. Beyond a certain point, adding more connectivity does not significantly improve redundancy. This suggests a form of ‘redundancy saturation’, meaning that additional connectivity no longer contributes meaningfully to extra redundancy in highly connected networks.

Examining the ${\mathcal{P}}_8$ graph in more detail, the redundancy of the entire graph is 13.69 and the average value of the cliques is $2.16\times {10}^{-6}$.

Table 4. Average values of classical metrics in 1-hop to 3-hop environments of vertices.

	N. of Vertices	N. of Edges
1-hop	$14.67$	$60.21$
2-hop	$81.76$	$741.38$
3-hop	$208.8$	$2311.7$

shows how the average number of vertices and edges in each vertex environment increases as a function of the hop number. In this graph, the number of vertices is 1288 and the number of edges is 17,608. In a 3-hop environment, on average of $16.2$% of all vertices can be reached from custom vertices, and the custom environments contain $13.1$% of all edges on average.

Table 5. Average values of density-based and redundancy-based k-hop metrics in 1-hop to 3-hop environments of vertices.

k	${\mathcal{WCGD}}^{\left[\mathit{k}\right]}$	${\mathcal{RCGD}}^{\left[\mathit{k}\right]}$	${\mathcal{WRCGD}}^{\left[\mathit{k}\right]}$	${\mathcal{WCGR}}_{\mathit{sb}}^{\left[\mathit{k}\right]}$	${\mathcal{CGR}}_{\mathit{vb}}^{\left[\mathit{k}\right]}$	${\mathcal{WCGR}}_{\mathit{vb}}^{\left[\mathit{k}\right]}$
1	0.0173	1.0309	0.0117	3.5113	14.6667	$1.00\times {10}^{-8}$
2	0.1527	1.0642	0.0677	3.3490	81.7421	$1.56\times {10}^{-7}$
3	0.4691	1.0791	0.1753	3.3513	208.7459	$3.64\times {10}^{-6}$

shows the average values of density-based and redundancy-based metrics in 1-hop to 3-hop environments of vertices.

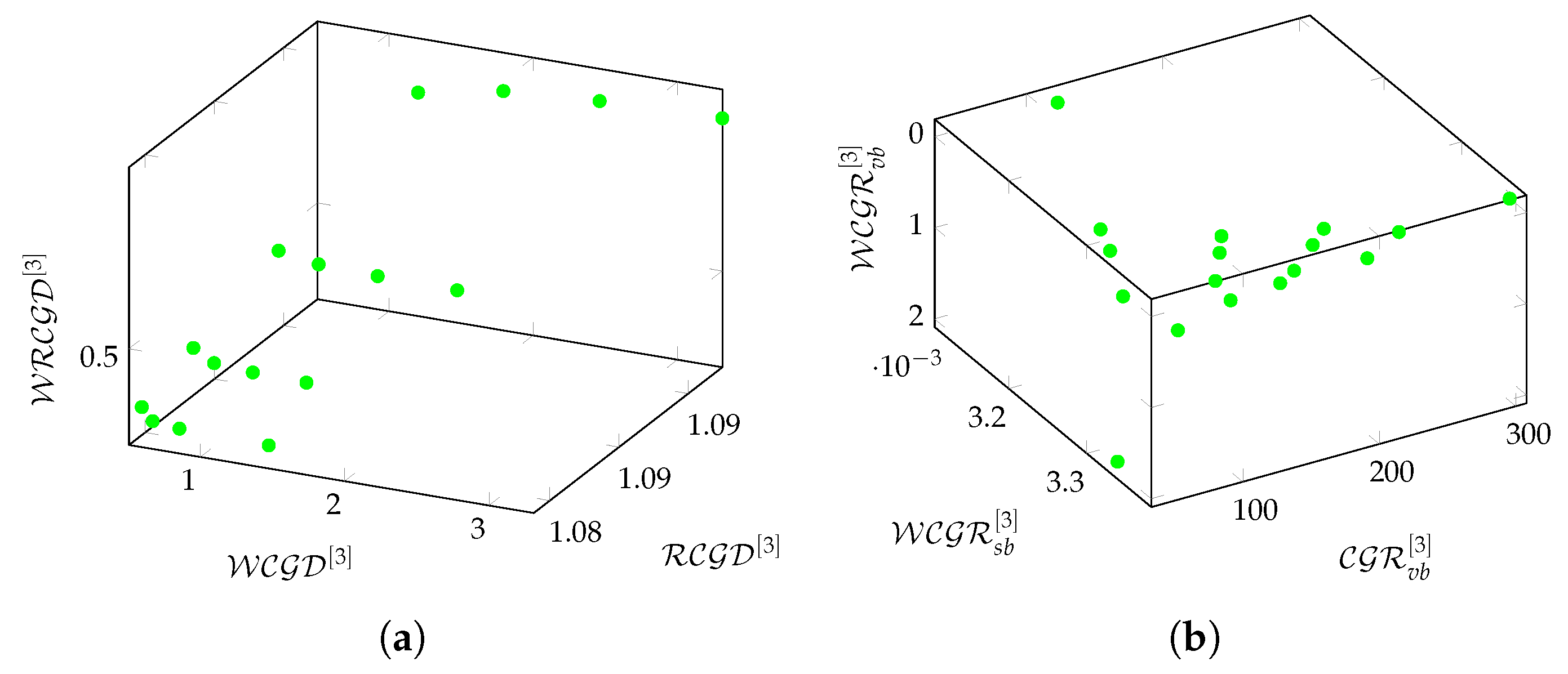
Figure 6a,b shows the relationships between density-based and redundancy-based metrics on Pegasus graphs in a 3-hop environment.

Figure 6a shows the relationship between ${\mathcal{WCGD}}^{\left[3\right]}$, ${\mathcal{RCGD}}^{\left[3\right]}$, and ${\mathcal{WRCGD}}^{\left[3\right]}$. While all three density indices decrease, the values for Pegasus are higher than those for Chimera. Pegasus preserves density better, which is a result of its more complex topology. Figure 6b shows the relationship between ${{\mathcal{WCGR}}_{sb}}^{\left[k\right]}$, ${{\mathcal{CGR}}_{vb}}^{\left[k\right]}$, ${{\mathcal{WCGR}}_{vb}}^{\left[k\right]}$. It can be seen that (${{\mathcal{WCGR}}_{sb}}^{\left[k\right]}$) grows faster than the value-based metrics, which is a consequence of the higher number of degrees.

3.3. Zephyr

Zephyr provides the topology of D-Wave’s latest-generation processors. In Zephyr, as in Pegasus and Chimera, the qubits are oriented either vertically or horizontally. The Zephyr topology includes the basic coupler types of both Chimera and Pegasus, with two odd couplers, two external couplers, and sixteen internal couplers. The degree number distribution of the Zephyr topology is not random, instead depending on the position of the qubits. Similar to Pegasus, the degree number distribution of Zephyr follows a determinate location-dependent pattern. In this topology, the nominal length and degree of qubits are 16 and 20, respectively. The two basic parameters of the Zephyr graph ${\mathcal{Z}}_{M,T}$ are M (grid parameter) and T (tile parameter). The maximum degree of this graph is $4T+4$, and the number of nodes is $4TM(2+1)$ [51,68].

The number of edges depends on parameter settings:

$${\mathcal{Z}}_{M,T}=\{\begin{array}{ll}2T((8T+8)M^2-2M-3,\hfill & \mathrm{if} \mathrm{M}>1,\\ 2T(8T+3),\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\mathrm{.}\hfill \end{array}$$

The Zephyr index of a vertex in a Zephyr lattice depends on multiple parameters: u, w, k, j, and z respectively represent the orientation, perpendicular block (major) offset, qubit index (secondary offset), shift identifier (minor offset), and parallel tile offset. The ${\mathcal{Z}}_{3,1}$ graph consists of 84 vertices and 540 edges, while the ${\mathcal{Z}}_{3,2}$ graph contains 168 and 1656, respectively. The Zephyr graphs were examined under different configurations from ${\mathcal{Z}}_{2,1}$ to ${\mathcal{Z}}_{5,5}$.

Within the analyzed interval, the average number of neighbors of each vertex is from $6.7$ to $22.582$, while the average degrees of vertices are from $11.44$ to $43.16$ Let $f_Z(M,T)$ be a function for representing a Zephyr graph $G(V,E)$ as a function of V + E. The value set of $f_Z$ is provided by the average values of the k-hop-based metrics.

Figure 7a–d shows the $f_Z(M,T)$ functions of k-hop-based metrics as functions of $V+E$ for different Zephyr graphs.

Figure 7a presents the behavior of ${\mathcal{WCGD}}^{\left[3\right]}$, ${\mathcal{RCGD}}^{\left[3\right]}$, and ${\mathcal{WRCGD}}^{\left[3\right]}$ as functions of graph size. It can be seen that ${\mathcal{RCGD}}^{\left[3\right]}$ remains stable across different graph sizes, similar to the trends seen in the Chimera and Pegasus topologies. This confirms that the relative communication density metric is largely independent of graph size. In addition, ${\mathcal{WCGD}}^{\left[3\right]}$ shows extreme fluctuations in smaller graphs (e.g., $V+E=2608$ with ${\mathcal{WCGD}}^{\left[3\right]}$$\simeq 3.31$), indicating that weighted communication density behaves more unpredictably in the Zephyr topology. As the graph size increases, ${\mathcal{WCGD}}^{\left[3\right]}$ stabilizes, though it remains higher compared to Chimera (see Figure 1a) and Pegasus (see Figure 4a) in some cases. While ${\mathcal{WRCGD}}^{\left[3\right]}$ follows a decreasing trend, similar to Pegasus and Chimera, the initial values are notably high ($0.92$ at $V+E=268$), suggesting that weighted relative communication is more prominent in small Zephyr graphs. Next, ${\mathcal{WCGD}}^{\left[3\right]}$ exhibits larger fluctuations in small graphs compared to Chimera and Pegasus. Across all three topologies, ${\mathcal{RCGD}}^{\left[3\right]}$ remains relatively stable, reinforcing its robustness as a metric. In Zephyr, the ${\mathcal{WRCGD}}^{\left[3\right]}$ values remain higher for longer graph sizes, whereas in Chimera and Pegasus the decline is more pronounced. The Zephyr topology exhibits higher local weighted density fluctuations, making it structurally distinct from Chimera and Pegasus. The ${\mathcal{WCGD}}^{\left[3\right]}$ metric is more unstable in Zephyr, likely due to the denser connectivity pattern and the presence of highly interconnected regions. ${\mathcal{RCGD}}^{\left[3\right]}$ remains a reliable metric across all topologies, suggesting its potential for universal applicability in quantum-inspired graphs.

Figure 7b shows that the ${{\mathcal{WCGR}}_{sb}}^{\left[3\right]}$ metric remains relatively stable across different graph sizes, fluctuating around an average value of $3.34$. Unlike Chimera (see Figure 1b) and Pegasus (see Figure 4b), Zephyr does not exhibit a strong decreasing trend, instead maintaining a more constant level of ${{\mathcal{WCGR}}_{sb}}^{\left[3\right]}$. The stability of ${{\mathcal{WCGR}}_{sb}}^{\left[3\right]}$ suggests that Zephyr’s connectivity structure preserves redundancy more consistently, which could be beneficial for quantum computations requiring stable interconnectivity. In larger graphs (e.g., $V+E>$ 10000), ${{\mathcal{WCGR}}_{sb}}^{\left[3\right]}$ remains within a narrow range, indicating that redundancy levels do not degrade significantly with graph growth. The stability of ${{\mathcal{WCGR}}_{sb}}^{\left[3\right]}$ in Zephyr suggests that it maintains a more consistent level of interconnectivity, which may be beneficial for quantum computations requiring stable and predictable connectivity. In quantum hardware, maintaining high and stable clustering redundancy could improve fault tolerance and error correction strategies.

Figure 7c shows that the ${{\mathcal{CGR}}_{vb}}^{\left[3\right]}$ metric exhibits a general increasing trend, indicating that as the Zephyr graph’s clustering redundancy strengthens as it expands. Choosing the Zephyr configuration significantly impacts the behavior of ${{\mathcal{CGR}}_{vb}}^{\left[3\right]}$, with higher m and n values leading to stronger clustering redundancy at large scales. Configurations such as ${\mathcal{Z}}_{5,4}$ and ${\mathcal{Z}}_{5,5}$ achieve the highest ${{\mathcal{CGR}}_{vb}}^{\left[3\right]}$ values, making them ideal for quantum network architectures that require high redundancy and fault tolerance. Lower-order configurations (e.g., ${\mathcal{Z}}_{2,2}$, ${\mathcal{Z}}_{3,3}$) maintains a more controlled and gradual increase in redundancy, which could be beneficial for applications that require optimized connectivity over scalability. Higher ${{\mathcal{CGR}}_{vb}}^{\left[3\right]}$ means stronger interconnectivity, which is essential for fault-tolerant quantum computing. Zephyr exhibits the strongest clustering redundancy, with stepwise increases suggesting structural transitions. Pegasus provides stable and predictable redundancy expansion (see Figure 4c), making it ideal for balanced quantum network architectures. Chimera is more localized in redundancy growth, with less scalability in clustering properties (see Figure 1c). As shown in Figure 7d, ${{\mathcal{WCGR}}_{vb}}^{\left[3\right]}$ grows exponentially, similar to ${{\mathcal{WCGR}}_{sb}}^{\left[3\right]}$, but is more sensitive to weighted relationships. Compared to Pegasus, Zephyr shows slightly better growth, indicating the exploitation of weighted redundancy. All three topologies exhibit a strong decreasing trend in ${{\mathcal{WCGR}}_{vb}}^{\left[3\right]}$, indicating that the metric becomes less relevant as graph size increases. Pegasus starts with the highest initial ${{\mathcal{WCGR}}_{vb}}^{\left[3\right]}$ ($0.0082$ at $V+E=208$) but declines rapidly (see Figure 4d), meaning that initial structured connectivity weakens significantly as the graph expands. Zephyr exhibits the smoothest decline (see Figure 7d), suggesting a more stable redundancy structure over large scales. Chimera starts lower and decreases gradually (see Figure 1d), which indicates different underlying redundancy behavior compared to Pegasus and Zephyr. Pegasus initially maintains the highest ${{\mathcal{WCGR}}_{vb}}^{\left[3\right]}$, meaning that it retains more of the measured redundancy in small-scale graphs. Zephyr’s smooth decline suggests that its large-scale structure stabilizes faster, making it potentially more predictable in large quantum network implementations. Chimera’s more gradual decrease suggests a more balanced redundancy structure, which may impact quantum hardware design choices for error correction strategies.

Examining the ${\mathcal{Z}}_{5,5}$ graph in more detail, the average values of the classical metrics of degree centrality, betweenness centrality, closeness centrality, eccentricity, and clustering coefficient in 1-hop to 3-hop environments are naturally the same: $0.0196$, $0.0033$, $0.2154$, $8.836$, and $0.1187$, respectively. The redundancy of the entire graph is $21.62$, and the average value of the cliques is $3.18\times {10}^{-6}$.

In this graph, the number of vertices is 1100 and the number of edges is 23,740. In the 3-hop environment, an average of $27.9$% of all vertices can be reached from custom vertices, and the custom environments contain $22.4$% of all edges on average.

Table 6. Average numbers of vertices and edges in 1-hop to 3-hop environments of vertices in graphs ${\mathcal{Z}}_{5,1}$ through ${\mathcal{Z}}_{5,5}$.

Hop	${\mathcal{Z}}_{5,1}$		${\mathcal{Z}}_{5,2}$		${\mathcal{Z}}_{5,3}$
	Vertices	Edges	Vertices	Edges	Vertices	Edges
1-hop	8.03	14.07	11.67	21.34	15.31	62.87
2-hop	28.09	134.18	51.98	357.89	75.87	687.93
3-hop	63.94	364.04	124.92	1072.72	185.89	2138.07
Hop	${\mathcal{Z}}_{\mathbf{5},\mathbf{4}}$		${\mathcal{Z}}_{\mathbf{5},\mathbf{5}}$
	Vertices	Edges	Vertices	Edges
1-hop	18.94	79.96	22.58	97.05
2-hop	99.76	1124.31	123.65	1667
3-hop	246.85	3560.10	307.82	5338.70

shows how the average numbers of vertices and edges in each vertex environment increases as a function of the hop number.

Table 7. Average values of density-based and redundancy-based k-hop metrics in 1-hop to 3-hop environments of vertices for graphs ${\mathcal{Z}}_{5,1}$ through ${\mathcal{Z}}_{5,5}$.

Graph	k	${\mathcal{WCGD}}^{\left[\mathit{k}\right]}$	${\mathcal{RCGD}}^{\left[\mathit{k}\right]}$	${\mathcal{WRCGD}}^{\left[\mathit{k}\right]}$	${\mathcal{WCGR}}_{\mathit{sb}}^{\left[\mathit{k}\right]}$	${\mathcal{CGR}}_{\mathit{vb}}^{\left[\mathit{k}\right]}$	${\mathcal{WCGR}}_{\mathit{vb}}^{\left[\mathit{k}\right]}$
${\mathcal{Z}}_{5,1}$	1	0.0541	1.0555	0.0380	3.3323	8.0244	$2.8\times {10}^{-6}$
	2	0.2056	1.0678	0.1370	3.1634	28.0510	$9.2\times {10}^{-6}$
	3	0.5068	1.0797	0.3156	3.2635	63.8723	$2.13\times {10}^{-5}$
${\mathcal{Z}}_{5,2}$	1	0.0400	1.0383	0.0276	3.4493	11.6637	$5.2·{10}^{-7}$
	2	0.2313	1.0635	0.1260	3.1411	51.9446	$2.1\times {10}^{-6}$
	3	0.6497	1.0790	0.3073	3.3117	124.8359	$5.25\times {10}^{-6}$
${\mathcal{Z}}_{5,3}$	1	0.0353	1.0291	0.0239	3.5124	15.3011	$1.8\times {10}^{-7}$
	2	0.2767	1.0620	0.1223	3.1264	75.8364	$8.9\times {10}^{-7}$
	3	0.8502	1.0789	0.3045	3.3362	185.7993	$2.3\times {10}^{-6}$
${\mathcal{Z}}_{5,4}$	1	0.0329	1.0235	0.0220	3.5518	18.9379	$9.6·{10}^{-8}$
	2	0.3366	1.0613	0.1205	3.1170	99.7278	$5\times {10}^{-7}$
	3	1.1184	1.0788	0.3032	3.3510	246.7626	$1.13\times {10}^{-6}$
${\mathcal{Z}}_{5,5}$	1	0.0315	1.0196	0.0209	3.57895	22.5746	$8.18\times {10}^{-8}$
	2	0.4123	1.0609	0.1194	3.1106	123.6190	$3.2\times {10}^{-7}$
	3	1.4744	1.0788	0.3024	3.3610	307.7261	$8.4\times {10}^{-7}$

shows the average values of density-based and redundancy-based metrics in 1-hop to 3-hop environments of vertices.

Figure 8a–c shows the relationships between custom k-hop-based metrics on Zephyr graphs.

Figure 8a shows the following:

• For $k=1$ and $k=2$, the relationship between ${\mathcal{WCGD}}^{\left[k\right]}$ and ${\mathcal{WCGR}}_{sb}^{\left[k\right]}$ shows a decreasing trend. This suggests that redundancy does not increase proportionally to density as the graph expands; instead, the network becomes less redundant relative to its density.
• For $k=3$, the trend deviates from linearity and shows an increasing pattern, meaning that in larger graphs the redundancy rises instead of following the previously observed decreasing trend. This deviation is significant because nearly all nodes in the graph are reachable at $k=3$, meaning that the observed behavior is not just a local effect but a property of the entire graph.
• In smaller k-hop environments, connectivity is still constrained by local structures. As the graph grows, the additional nodes contribute more to density than redundancy, meaning that even though there are more connections, they are not necessarily redundant. This suggests that local connectivity optimizations may not necessarily improve global redundancy.
• At $k=3$, the entire graph is nearly reachable, meaning that we are no longer observing only local effects but rather a global property of the graph. The increase in ${\mathcal{WCGR}}_{sb}^{\left[k\right]}$ at $k=3$ suggests that redundancy mechanisms in the network structure become dominant at the global level. This could mean that graph expansion beyond a certain point shifts the balance from local sparsity to a highly interconnected global structure.
• Because almost all nodes are accessible, redundancy starts to grow nonlinearly, instead of decreasing as it does with smaller k values. This could indicate a phase transition in which the graph shifts from localized connectivity constraints to a more fully connected network.

Local connectivity does not guarantee increasing redundancy, meaning that short-range couplings in a quantum system may not inherently improve fault tolerance. Optimizations at these levels should focus on increasing redundancy through additional pathways rather than just increasing density.

Redundancy increases beyond a threshold, meaning that after a network reaches a certain scale it becomes more robust. This could suggest that full-scale quantum networks may need to operate at a global level rather than just optimizing local structures. Nonlinearity in redundancy at large scales could also mean that certain quantum algorithms might benefit from global connectivity rather than purely local interactions.

Figure 8c shows a logarithmic trend, implying that ${{\mathcal{WCGR}}_{vb}}^{\left[k\right]}$ grows at a progressively slower rate as ${\mathcal{WRCGD}}^{\left[k\right]}$ increases.

Figure 9a,b shows the relationships between density-based and redundancy-based metrics on Zephyr graphs in a 3-hop environment.

Figure 9a shows the relationship between ${\mathcal{WCGD}}^{\left[3\right]}$, ${\mathcal{RCGD}}^{\left[3\right]}$, and ${\mathcal{WRCGD}}^{\left[3\right]}$. It can be seen that size-based redundancies grow faster than value-based redundancies. While similar to Pegasus, Zephyr shows better performance. Figure 9b shows the relationship between ${{\mathcal{WCGR}}_{sb}}^{\left[k\right]}$, ${{\mathcal{CGR}}_{vb}}^{\left[k\right]}$, and ${{\mathcal{WCGR}}_{vb}}^{\left[k\right]}$. Again, ${{\mathcal{WCGR}}_{sb}}^{\left[k\right]}$ grows faster than the value-based metrics, which is a consequence of the higher number of degrees.

4. Conclusions and Future Work

In this paper, we conduct a graph-based analysis of the topology of D-Wave quantum computers, focusing on the Chimera, Pegasus, and Zephyr architectures across various configurations. In our analysis, we examine Chimera topologies ranging from ${\mathcal{C}}_{16,16,4}$, Pegasus topologies from ${\mathcal{P}}_2$ to ${\mathcal{P}}_8$, and Zephyr topologies from ${\mathcal{Z}}_{2,1}$ to ${\mathcal{Z}}_{5,5}$. Our primary focus is on the use of average values of graph-based metrics to identify key structural characteristics and limitations of these topologies. We explored the structural properties of the Chimera, Pegasus, and Zephyr quantum processor topologies using k-hop-based graph metrics, focusing on both density-based and redundancy-based measures. The results reveal fundamental differences in how these topologies scale and maintain connectivity, providing insights into their potential efficiency in quantum computing applications. Our findings indicate that Pegasus exhibits a strictly linear relationship between connectivity and redundancy, making it the most predictable topology in terms of scalability. In contrast, Chimera deviates from linearity, particularly in redundancy-related metrics, suggesting structural constraints that impact connectivity growth. Zephyr, on the other hand, demonstrates the most balanced behavior, maintaining high connectivity while preserving stable redundancy without excessive overhead. This suggests that Zephyr is structurally optimized to support robust connectivity while avoiding unnecessary redundancy. One of the most significant results is our observation of a logarithmic growth pattern of redundancy with increasing density. This implies that beyond a certain density threshold, additional connectivity offers diminishing returns in terms of redundancy improvement. This finding has crucial implications for quantum hardware design, as it suggests that excessive interconnectivity does not necessarily enhance fault tolerance beyond a critical point.

Overall, these results highlight the importance of selecting the appropriate topology for quantum computing applications. While Zephyr appears to provide the most efficient tradeoff between connectivity and redundancy, further research is needed to explore how quantum circuits can be optimally embedded onto Zephyr using cliques, bicliques, and high-dimensional lattice structures. Additionally, future studies should examine how topological transformations influence computational efficiency in quantum annealing and fault-tolerant quantum computing. We hope that this study can provide a foundation for further optimizations in quantum hardware design, ensuring that quantum processors scale efficiently while maintaining robust connectivity and fault tolerance.