Practitioners’ Rule of Thumb for Quantum Volume

Abstract

Quantum volume (QV) is a widely recognized metric for assessing the practical capabilities of quantum computers, as it provides an estimate of the largest quantum circuit that can be reliably executed. However, measuring QV on a real device requires comparing experimental outcomes with ideal theoretical results—a process that rapidly becomes computationally expensive. By examining the cumulative impact of errors in two-qubit gates, we present a simple, accessible `rule of thumb’ that relates the quantum volume directly to the average error rate of native gates. Our formula shows a strong agreement with experimental data from leading quantum computing platforms, including both superconducting and trapped-ion systems. This straightforward model offers a clear, intuitive guideline for predicting quantum hardware performance, enabling more informed decisions regarding circuit design and resource allocation.

1. Introduction

In recent years, the scientific community working with quantum computers has grown dramatically. While some researchers aim to contribute to the physical realization of these machines, others are interested in their practical applications. In particular, quantum computers hold promise for simulating complex quantum systems relevant to chemistry, condensed-matter and high-energy physics, and more. These researchers, whom we may refer to as “practitioners”, often need to know whether a given computer is able to run a quantum circuit that they have in mind, before bearing the burden of actually running it. A naive answer to this question considers whether the quantum computer has a sufficient number of quantum bits (qubits) to run the target circuit. This condition is, however, not sufficient for successfully running the circuit: quantum computers are highly susceptible to time-dependent noise, leading to decay and dephasing, and are generally limited to quantum circuits with fewer qubits than the number of available ones. The answer to this question also depends on the number of gates that need to be applied to each qubit, or the “circuit depth”, as well as the connectivity of the circuit. Further, the number of required measurements should also be taken into consideration.

To help practitioners navigate the world of quantum computers, IBM proposed a single parameter, the quantum volume (QV), which determines the size of the largest circuit that can be successfully run on the computer [1,2]. Its formal definition involves square circuits, i.e., circuits with a depth equal to the number of qubits N (see Figure 1 for $N=4$). A quantum computer is said to have a quantum volume of $2^N$ if it runs square circuits of size N with a success rate larger than 50%. This quantity is measured according to the experimental probability of obtaining a bitstring whose overlap with the ideal quantum state is larger than the median value. From a practitioner’s perspective, $N_{\max }={\log }_2\mathrm{QV}$ can be identified with the maximal (linear) size of the circuit that can be run.

This approach fits well with our own experience: since 2020, we have performed ten research projects involving actual calculations on quantum computers [3,4,5,6,7,8,9,10,11,12] by major manufacturers such as IBM, IonQ, (Honeywell) Quantinuum, and Rigetti. These projects involved the simulation of many-body quantum effects such as nonlocality, topology, time crystals, phase transitions, thermodynamics, caustics, and more. We generally found that $N_{\max }$ is indeed a good way to predict the success rate of a quantum computer. We had access to the quantum computers with a QV of $2^5$ to $2^6$ and, indeed, were able to successfully simulate quantum protocols with up to 6 qubits and a comparable circuit depth. Quantum circuits requiring a larger number of gates produced unreliable results and, in general, were not reported in the published papers.

In spite of the usefulness of QV, determining its values is often a computationally hard task, which will become more and more challenging as quantum computers improve their performance: To probe the QV, one has to run a large number of circuits and obtain a large number of shots (bitstrings). Next, for each experimentally observed bitstring, one needs to numerically compute its overlap with the output of the ideal quantum circuit. This calculation needs to be performed without errors using a state-vector representation of the states and requires exponentially large classical resources. In addition, the QV may depend on the specific circuits tested, on the precise calibration of the device, on error mitigation techniques, and more. A recent cross-sectional study found significant deviations between the QV declared by the manufacturers and that observed by users, where, in general, the former was larger than the latter [13].

2. Materials and Methods

The goal of this work is to provide a simple relation between QV and a basic property of the quantum computer, namely the average error of native gates, which we denote by $ϵ$. To achieve this goal, we developed an estimate for the fidelity, by applying several simplifying approximations: First, we neglected the errors introduced by single-qubit gates, which are usually at least one order of magnitude smaller than two-qubit errors. Next, we neglected state-preparation and measurement errors that do not scale with the circuit depth. Finally, we neglected correlations between errors in different gates and assumed that the total fidelity is given by the product of the fidelity of each gate, $(1-ϵ)$. The validity of the latter approximation has been studied, for example, in the quantum supremacy experiment by Google [14], where it was found to be in excellent agreement with the experimental findings. We ended up with a compact formula for the fidelity of a circuit with n native two-qubit gates:

$$\begin{array}{c}\hfill F={(1-ϵ)}^n.\end{array}$$

(1)

We can further simplify this expression using a Taylor expansion in $ϵ$, leading to $F\approx 1-nϵ$. This approximation, while not exact, will allow us to provide a simple expression for the QV.

The definition of QV refers to square circuits with N qubits and N layers of $N/2$ random two-qubit gates each, for a total of $N_{2q}=N^2/2$ two-qubit gates. When running on the quantum computer, the random gates need to be compiled using native gates, usually CNOT or CZ gates. A naive approach to compile such a circuit involves three native gates for each two-qubit gate, and this number can be reduced using more advanced methods. For our estimation of the quantum volume, we assume a ratio of 1:2 between two-qubit gates in the circuit and native gates in the actual implementation. This leads to a total of $n=2N_{2q}=N^2$ native gates and an estimated total fidelity of $F\approx 1-N^2ϵ$.

3. Results

The quantum volume can now be evaluated by finding the largest square circuit whose total fidelity is larger than 50%, or $F>0.5$. Using the approximation developed above, we find

$$\begin{array}{cc}\hfill {\log }_2\mathrm{QV}=& ⌊\sqrt{{\displaystyle \frac{0.5}{ϵ}}}⌋.\hfill \end{array}$$

(2)

Equation (2) represents the main finding of this paper and offers a simple relation between the two-qubit gate error $ϵ$ and the quantum volume QV.

To verify the validity of our approach, we compare the results of Equation (2) with the experimental QV reported by several manufacturers, for both superconducting and trapped-ion quantum computers (see Figure 2 and

Table 1. Two-qubit error and logarithmic quantum volume for different technologies: a comparison between some reported experimental results and eq:logQV.

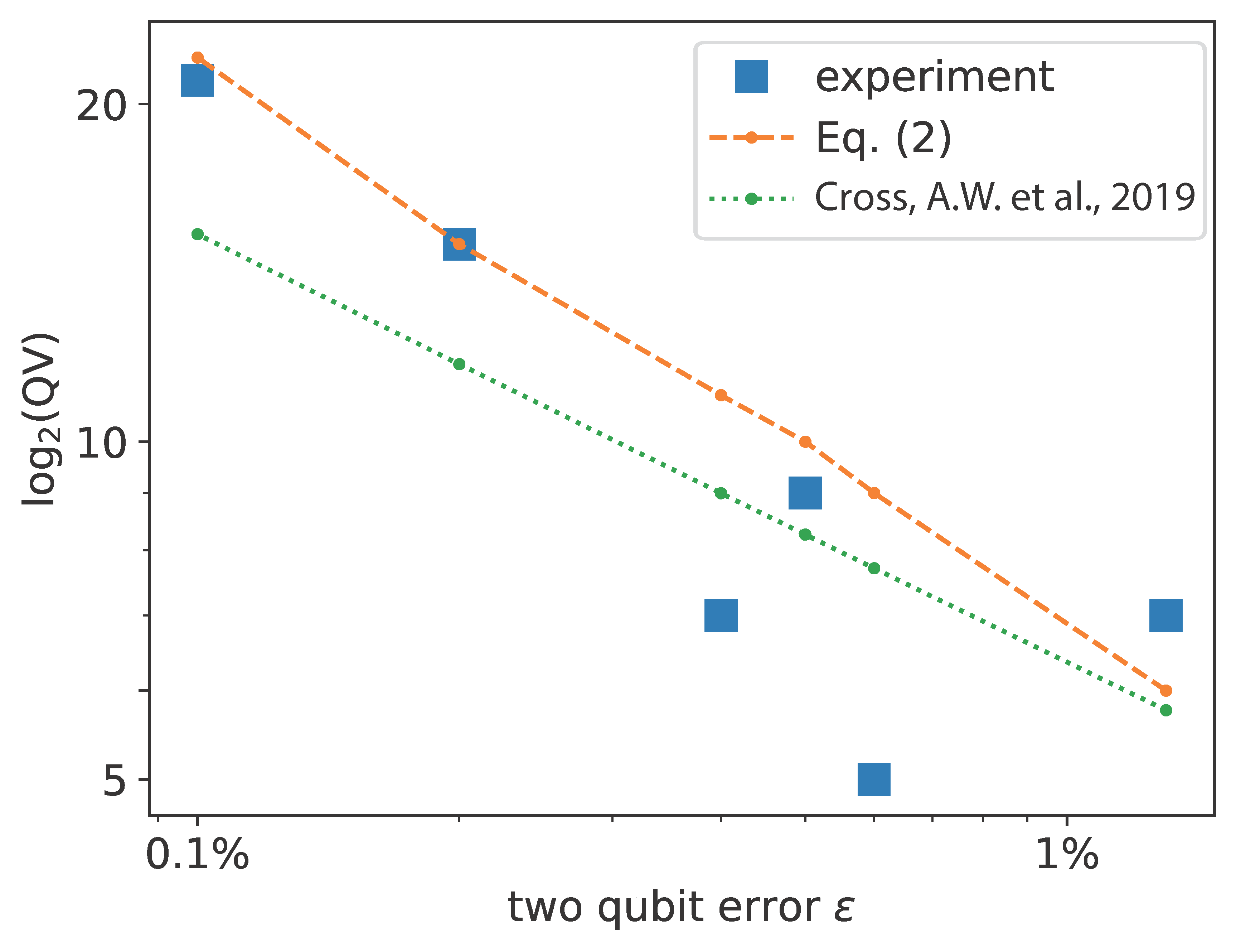
$\mathit{ϵ}$	${\text{log}}_2$ QV (Exp.)	${\text{log}}_2$ QV (Equation (2))	Technology	Company	Year	Ref.
0.1%	21	22	trapped ions	Quantinuum	2024	[15,16]
0.2%	15	15	trapped ions	Quantinuum	2022	[17]
0.4%	7	10	trapped ions	Honeywell	2020	[18]
0.5%	9	10	supercond. circuits	IBM	2022	[19]
0.6%	5	9	supercond. circuits	IBM	2020	[18]
1.3%	7	6	trapped ions	AQT	2023	[20]

). For older systems, our approach over-estimates the actual quantum volume, presumably due single-qubit-gate errors, measurement errors, and limited connectivity that were neglected in our approach. For the largest values reported so far, we obtain a quantitative agreement. In Figure 2, we also report the numerical solution of an expression $N_{\max }^2=1/\left(a\sqrt{N_{\max }}+b\right)$ with $a=1.29$ and $b=-0.45$, derived in Ref [2] by noisy simulations of quantum computers with a two-dimensional connectivity. As expected, our closed-form expression, Equation (2), delivers a better fit for quantum computers with all-to-all connectivity. Thanks to its simplicity, our approach allows us to predict future trends of the QV. Due to the square-root dependence of ${\log }_2\mathrm{QV}$ on $ϵ$, it will be extremely challenging to improve this number beyond a few tens. For example, reaching ${\log }_2\mathrm{QV}=100$ would require $ϵ=5\times {10}^{-5}$, which is beyond the reach of current technologies.

4. Discussion

A key result of our analysis is that near-term quantum computers are not expected to reach a quantum volume of $2^{100}$. A natural question, then, is determining how to reconcile this prediction with the recent announcement by IBM [21] to have matched the $100\times 100$ challenge [22], by successfully running a circuit with 5000 gates, using a three-9-digit-precision (albeit, $ϵ\sim 0.1\%$) quantum computer. To answer this question, one needs to consider two key ingredients: (i) in analogy to the IBM utility experiment [23], the $100\times 100$ challenge focuses on expectation values of local observables, rather than on overlaps of the final state, which decay much slower as a function of the circuit depth; (ii) the latest results by IBM involve advanced error mitigation methods, which significantly improve the precision of local observables, albeit at the cost of running a larger number of quantum circuits. These findings indicate a possible pathway to reaching the best results from a quantum computer, through the choice of an appropriate target function and the combination of heavy circuit redundancy and classical post-processing.