Continuum Limit of the Green Function in Scaled Affine ${\phi }_4^4$ Quantum Euclidean Covariant Relativistic Field Theory

Abstract

Through path integral Monte Carlo computer experiments, we prove that the affine quantization of the ${\phi }_4^4$-scaled Euclidean covariant relativistic scalar field theory is a valid quantum field theory with a well-defined continuum limit of the one- and two-point functions. Affine quantization leads to a completely satisfactory quantization of field theories in situations involving scaled behavior, leading to an unexpected term, ${\hslash }^2/{\phi }^2$, which arises only in the quantum aspects.

1. Introduction

It is well known that ${\phi }_4^4$ quantum Euclidean covariant relativistic field theory, when quantized through canonical (Dirac [1]) quantization (CQ), is trivial since its corresponding renormalized theory tends to become a free theory in the continuum limit [2,3,4,5,6].

Recently, J. R. Klauder [7,8,9,10,11] noticed that this difficulty can be overcome by using a different kind of quantization method, namely affine quantization (AQ).

In a sequel of recent papers [12,13,14,15,16,17,18,19,20,21,22], we proved that, through path integral Monte Carlo (PIMC), affine quantization is able to make the ${\phi }_4^4$ theory non-trivial. A crucial point left unanswered in these papers is the validity of the continuum limit at the level of the one- and two-point functions.

The aim of the present work is to show that, as we approach the continuum on the computer, the one- and two-point functions converge to well-defined results. In other words, we prove the validity of the continuum limit for the field theory quantized through affine quantization.

Our result could prove to be important in the physics of the standard model, where the long-standing problem of the triviality of canonical quantum ${\phi }^4$ theory is crucial for particle physics, as it undermines the Higgs mechanism. It is also very important for progress in quantum gravity, where the role of the field is played by the metric tensor, which must be positive definite [20].

2. Field Theory Formulation

For a scalar field, $\phi$, with spatial degrees of freedom $x=(x_1,x_2,\dots ,x_s)$ and canonical momentum $\pi \left(x\right)$, the classical affine variables are $\kappa \left(x\right)\equiv \pi \left(x\right)\phi \left(x\right)$ and $\phi \left(x\right)\ne 0$. The reason we insist that $\phi \left(x\right)\ne 0$ is that if $\phi \left(x\right)=0$, then $\kappa \left(x\right)=0$, regardless of the value of $\pi \left(x\right)$.

We then introduce the classical Hamiltonian expressed in affine variables. This leads us to the following:

$$\begin{array}{c}\hfill \mathcal{H}(\kappa ,\phi )=\int \{\frac{1}{2}[\kappa {\left(x\right)}^2\phi {\left(x\right)}^{-2}+{(\nabla \phi \left(x\right))}^2+m^2\phi {\left(x\right)}^2]+g\phi {\left(x\right)}^r\}{d}^{s}x,\end{array}$$

(1)

where r is a positive, even integer and $g\ge 0$ is the bare coupling constant, such that for $g\to 0$, we fall into the free field theory. With these variables, we do not let $\phi \left(x\right)=\infty$; otherwise, $\phi {\left(x\right)}^{-2}=0$, which is not fair to $\kappa \left(x\right)$, and as we have already observed, we must forbid $\phi \left(x\right)=0$, which would admit $\phi {\left(x\right)}^{-2}=\infty$, creating an undetermined kinetic term. Therefore, the AQ bounds $0<\phi \left(x\right)<\infty$ forbid any triviality [12,13,14,15,16,17,18,19,20,21,22], which is otherwise possible for CQ [2,3,4,5].

The quantum affine operators are the scalar field $\widehat{\phi }\left(x\right)=\phi \left(x\right)$ and the dilation operator, $\widehat{\kappa }\left(x\right)=[\widehat{\phi }\left(x\right)\widehat{\pi }\left(x\right)+\widehat{\pi }\left(x\right)\widehat{\phi }\left(x\right)]/2$ where the momentum operator is $\widehat{\pi }\left(x\right)=-i\hslash \delta /\delta \phi \left(x\right)$. Accordingly, for the self-adjoint kinetic term, $\widehat{\kappa }\left(x\right)\widehat{\phi }{\left(x\right)}^{-2}\widehat{\kappa }\left(x\right)=\widehat{\pi }{\left(x\right)}^2+(3/4)\hslash \delta {\left(0\right)}^{2s}\phi {\left(x\right)}^{-2}$ (note that the factor $3/4$, which applies when $\phi >0$, should be replaced by a factor of 2 if $\left|\phi \right|>0$ [17]); thus, one finds the following for the quantum Hamiltonian operator:

$$\begin{array}{c}\hfill \widehat{H}(\widehat{\kappa },\widehat{\phi })=\int \left\{\frac{1}{2}[\widehat{\pi }{\left(x\right)}^2+{(\nabla \phi \left(x\right))}^2+m^2\phi {\left(x\right)}^2]+g\phi {\left(x\right)}^r+\frac{3}{8}{\hslash }^2\frac{\delta {\left(0\right)}^{2s}}{\phi {\left(x\right)}^2}\right\}{d}^{s}x.\end{array}$$

(2)

The affine action is found by adding time, $x_0=ct$, where c is the constant speed of light and t denotes the Euclidean imaginary time; thus, $\mathcal{S}={\int }_0^{\beta }Hd{x}_0$, where H is the semi-classical Hamiltonian corresponding to that of Equation (2) (see Appendix A).

$$\begin{array}{c}\hfill \mathcal{S}\left[\phi \right]={\int }_0^{\beta }d{x}_0{\int }_{L^s}{d}^{s}x\left\{\frac{1}{2}\left[{\displaystyle \sum _{\mu =0}^s}{\left(\frac{\partial \phi \left(x\right)}{\partial x_{\mu }}\right)}^2+m^2\phi {\left(x\right)}^2\right]+g\phi {\left(x\right)}^r+\frac{3}{8}\hslash \frac{\delta {\left(0\right)}^{2s}}{\phi {\left(x\right)}^2}\right\},\end{array}$$

(3)

where we employ an abuse of notation by using x for $(x_0,x_1,x_2,\dots ,x_s)$ and $\beta =1/k_{B}T$, with $k_B$ denoting Boltzmann’s constant and T denoting the absolute temperature. In this work, we will set $\beta =L$.

The vacuum expectation value of an observable $\mathcal{O}\left[\phi \right]$ is then given by the following expression:

$$\begin{array}{c}\hfill \langle \mathcal{O}\rangle =\frac{\int \mathcal{O}\left[\phi \right]exp(-\mathcal{S}[\phi \left]\right)\mathcal{D}\phi \left(x\right)}{\int exp(-\mathcal{S}[\phi \left]\right)\mathcal{D}\phi \left(x\right)},\end{array}$$

(4)

where the functional integrals are calculated on a lattice using the PIMC method, as will be explained later on.

The theory considers a real scalar field, $\phi$, taking the value, $\phi \left(x\right)$, at each site, x, on a periodic n-dimensional lattice, where $n=s+1$ denotes the space-time dimensions, of lattice spacing a, the ultraviolet cutoff, exhibiting spatial periodicity with $L=Na$ and temporal periodicity with $\beta =Na$. The field path is a closed loop on an n-dimensional closed surface of an $(n+1)$-dimensional $\beta$-periodic cylinder of radius L: an $(n+1)$-dimensional torus. We use a lattice formulation of the AQ field theory in Equation (3) (also studied in Equation (8) of [12]), and additionally apply the scaling transformations $\phi \to a^{-s/2}\phi$ and $g\to a^{s(r-2)/2}g$; these adjustments are necessary to eliminate the divergent Dirac delta factor $\delta \left(0\right)=a^{-1}$ in the continuum limit as $a\to 0$. The affine action for the field (in the primitive approximation [23]) is then approximated by the following:

$$\begin{array}{c}\hfill \frac{S\left[\phi \right]}{a}=\frac{1}{2}\left\{{\displaystyle \sum _{x,\mu }}{a}^{-2}{[\phi \left(x\right)-\phi (x+e_{\mu })]}^2+m^2{\displaystyle \sum _x}\phi {\left(x\right)}^2\right\}+{\displaystyle \sum _x}\left[g\phi {\left(x\right)}^r+\frac{3}{8}{\displaystyle \frac{{\hslash }^2}{\phi {\left(x\right)}^2}}\right],\end{array}$$

(5)

where $e_{\mu }$ is a vector of length a in the $+\mu$ direction with $\mu =0,1,2,\dots ,s$. We will have $\mathcal{S}\approx S$.

In this work, we are interested in reaching the continuum limit by keeping $Na$ fixed while allowing $N\to \infty$, at a fixed volume of $L^s$.

We perform a PIMC [23,24,25,26] calculation for the AQ field theory described by the action of Equation (5) in natural Planck units $c=\hslash =k_B=1$. Specifically, we study the $s=3$ and $r=4$ case. We calculate the renormalized coupling constant, $g_R$, and mass, $m_R$, defined in Equations (11) and (13) of [12], respectively, measuring them in the PIMC through vacuum expectation values, like in Equation (4).

In particular,

$$\begin{array}{c}\hfill m_R^2=\frac{p_0^2\langle |\tilde{\phi }\left(p_0\right){|}^2\rangle }{\langle \tilde{\phi }{\left(0\right)}^2\rangle -\langle |\tilde{\phi }\left(p_0\right){|}^2\rangle },\end{array}$$

(6)

and at zero momentum,

$$\begin{array}{c}\hfill g_R=\frac{3{\langle \tilde{\phi }{\left(0\right)}^2\rangle }^2-\langle \tilde{\phi }{\left(0\right)}^4\rangle }{{\langle \tilde{\phi }{\left(0\right)}^2\rangle }^2},\end{array}$$

(7)

where $\tilde{\phi }\left(p\right)=\int d^{n}x{e}^{ip·x}\phi \left(x\right)$ is the Fourier transform of the field, and we choose the 4-momentum, $p_0$, with one spatial component equal to $2\pi /Na$, and all other components equal to zero.

We also calculate the one-point, two-point-, and two-point connected functions, respectively, given by the following:

$$\begin{array}{ccc}\hfill V& =& {\displaystyle \sum _x}\langle \phi \left(x\right)\rangle /N^n,\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill D\left(z\right)& =& {\displaystyle \sum _x}\langle \phi \left(x\right)\phi (x+z)\rangle /N^n,\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill D_c\left(z\right)& =& {\displaystyle \sum _x}(\langle \phi \left(x\right)\phi (x+z)\rangle -{\langle \phi \left(x\right)\rangle }^2)/N^n=D\left(z\right)-V^2.\hfill \end{array}$$

(10)

By construction, these are periodic functions, $D\left(z\right)=D(z+L)$, of period L. Moreover, since the action $\mathcal{S}$ contains only even powers of the field, these functions must be symmetric with respect to $z=L/2$, namely, $D\left(z\right)=D(L-z)$.

3. The Scaling

We work with a scaled field ${\phi }^{\prime }\left(x\right)$, related to the variable $\phi \left(x\right)$, used for example in [12], by

$$\begin{array}{c}\hfill \phi \left(x\right)=a^{-3/2}{\phi }^{\prime }\left(x\right).\end{array}$$

(11)

In other words, we re-normalize the bare field. This can be compared with the standard renormalization formula, as follows:

$$\begin{array}{c}\hfill \phi \left(x\right)=Z^{1/2}{\phi }^{\mathrm{ren}}\left(x\right).\end{array}$$

(12)

${\phi }^{\mathrm{ren}}\left(x\right)$ is referred to as the renormalized field and Z is called the renormalization constant. In this language, we set $Z=a^{-3}$.

At the same time, we rescale the coupling constant with

$$\begin{array}{c}\hfill g=a^3{g}^{\prime }.\end{array}$$

(13)

In the Standard Model, the various coupling constants also need to be renormalized for the continuum limit to exist, but the renormalization is not simply given by a power of the lattice spacing. Instead, it needs to carefully be tuned to the cutoff and the couplings. In the perturbation theory of canonical ${\phi }^4$, the bare coupling constant can be expressed in terms of the renormalized one, order by order. The result consists of a series that starts with $g^{\mathrm{ren}}$:

$$\begin{array}{c}\hfill g=g^{\mathrm{ren}}+c_2{\left(g^{\mathrm{ren}}\right)}^2+c_3{\left(g^{\mathrm{ren}}\right)}^3+\dots \end{array}$$

(14)

The standard renormalization procedure is based on the fact that the Fourier transform of the renormalized two-point function contains a pole at $p^2=M^2$, where M is the physical mass of the particle. The renormalization constant, Z, is chosen such that the residue of this pole is equal to 1. In particular, this ensures that ${\phi }^{\mathrm{ren}}\left(x\right)$ and $\phi \left(x\right)$ as well as $g^{\mathrm{ren}}$ and g have the same dimensions. Note that our rescaling, (11) and (13), instead changes the dimensions of these objects.

In our first case study below, we will see that the expectation value, $\langle {\phi }^{\prime }\left(x\right)\rangle$, tends to a constant when N becomes large. This means that the expectation value of the unscaled field, $\langle \phi \left(x\right)\rangle$, tends to infinity in proportion to $N^{3/2}$ [12,14].

As we are holding $g^{\prime }$ constant, the unscaled coupling constant, g, tends to zero in proportion to $1/N^3$. This suggests that, for the parameter values we consider, the connected Green’s functions of the unscaled model tend to be those of a free scalar field.

4. Numerical Results

Our PIMC simulations use the Metropolis algorithm [24,25] to calculate the ensemble average of Equation (4), which is an $N^n$-multidimensional integral. The simulation starts from the initial condition, $\phi \left(x\right)=ϵ>0$, for all lattice points, x, with $ϵ$ denoting a small positive number. One PIMC step consists of a random displacement of each one of the $N^n$ field values, $\phi \left(x\right)$, as follows:

$$\begin{array}{c}\hfill \phi \to \phi +(2\eta -1)\delta ,\end{array}$$

(15)

where $\eta$ is a uniform pseudo-random number in $[0,1]$ and $\delta$ is the amplitude of the displacement. Each one of these $N^n$ moves is accepted if $exp(-\Delta S)>\eta$, where $\Delta S$ is the change in the action due to the move (it can be efficiently calculated, considering how the kinetic part and the potential part change by the displacement of a single $\phi \left(x\right)$) and is rejected otherwise. The amplitude, $\delta$, is chosen in such a way as to have acceptance ratios as close as possible to $1/2$, and is kept constant during the evolution of the simulation. One simulation consists of M PIMC steps. The statistical error on the average $\langle \mathcal{O}\rangle$ will then depend on the correlation time necessary to decorrelate the property $\mathcal{O}$, ${\tau }_{\mathcal{O}}$, and will be determined as $\sqrt{{\tau }_{\mathcal{O}}{\sigma }_{\mathcal{O}}^2/\left(M{N}^n\right)}$, where ${\sigma }_{\mathcal{O}}^2$ is the intrinsic variance for $\mathcal{O}$.

We use a lattice comprising up to $N^n={25}^4=\mathrm{390,625}$ points ($N=25$) and up to $M=2\times {10}^6$, corresponding to $M{N}^n$ PIMC displacement moves.

4.1. First Case Study

In our simulation, we first choose the following case study: $m=g=L=\beta =1$ and $ϵ={10}^{-10}$.

Notice that the minima of the two symmetric potential wells in the semi-classical Hamiltonian density described by the function, $f\left(\phi \right)=\frac{1}{2}{\phi }^2+{\phi }^4+\frac{3}{8}{\phi }^{-2}$, are at ${\phi }_{\pm }=\pm 2^{-1/2}\approx \pm 0.707107$. From our Monte Carlo simulations (see

Table 1. Renormalized mass, $m_R$, renormalized coupling constant, $g_R$, and one-point value (vacuum expectation value of the field) $V={\sum }_x\langle \phi \left(x\right)\rangle /N^n$ for $n=3+1$, $m=g=L=\beta =1$ and $N=L/a=4,7,13,25$. In our PIMC simulations, we use Equations (4) and (5).

N	${\mathit{m}}_{\mathit{R}}$	${\mathit{g}}_{\mathit{R}}$	V
4	0.1421 (2)	2.01178 (2)	0.7501 (4)
7	0.0602 (1)	2.001129 (4)	0.7339 (2)
13	0.0224 (2)	1.999894 (5)	0.7216 (2)
25	0.0084 (1)	2.000048 (4)	0.7148 (3)

), it seems that the vacuum expectation value of the field (one-point value), $V={\sum }_x\langle \phi \left(x\right)\rangle /N^n$, tends to the values in the continuum limit, $a=1/N\to 0$. Note that in some of our previous works [16,18,19], where, instead of keeping the bare mass, m, constant, we tuned it to have a constant renormalized mass, $m_R$, and found $V=0$ in all cases. This is due to the fact that as N increases, so does the necessary bare mass, which keeps a constant $m_R$. Thus, the two symmetric potential wells in the semi-classical Hamiltonian density have minima that tend to zero, and one experiences tunneling of the potential barrier at $\phi =0$.

In

Table 2. Renormalized mass, $m_R$, renormalized coupling constant, $g_R$, and one-point value (vacuum expectation value of the field) $V={\sum }_x\langle \phi \left(x\right)\rangle /N^n$ for $n=3+1$, $g=L=\beta =1$, $m=\sqrt{N}/L$ and $N=L/a=4,7,13,25$. In our PIMC simulations, we use Equations (4) and (5).

N	${\mathit{m}}_{\mathit{R}}$	${\mathit{g}}_{\mathit{R}}$	V
4	0.1461 (2)	2.01199 (2)	0.6672 (4)
7	0.0627 (1)	2.001154 (4)	0.5992 (3)
13	0.02463 (5)	1.999844 (2)	0.5169 (2)
25	0.00867 (5)	2.000069 (7)	0.4359 (3)

, we show the values of the renormalized mass, $m_R$, and coupling constant, $g_R$, at increasing values of $N=1/a$. We see that in the continuum limit, ${lim}_{a\to 0}{m}_R=0$, and ${lim}_{a\to 0}{g}_R=2$, meaning that ${lim}_{a\to 0}\langle \tilde{\phi }{\left(0\right)}^4\rangle /{\langle \tilde{\phi }{\left(0\right)}^2\rangle }^2=1$.

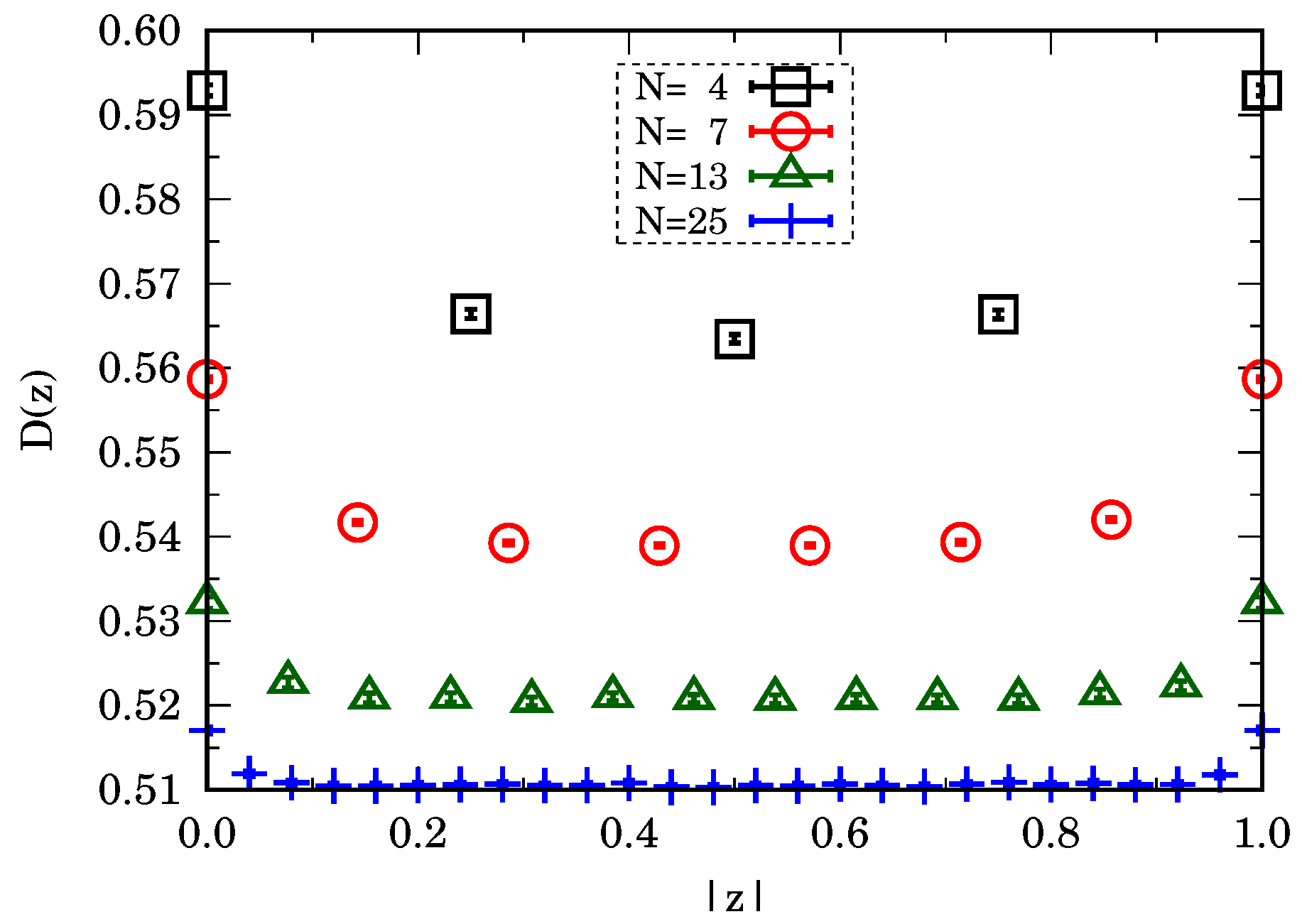
In Figure 1, we show $D\left(z\right)$ at increasing values of $N=1/a$. From the plot of the simulation data, we see that the function is symmetric with respect to $z=1/2$, as expected since the action only contains even powers in the field.

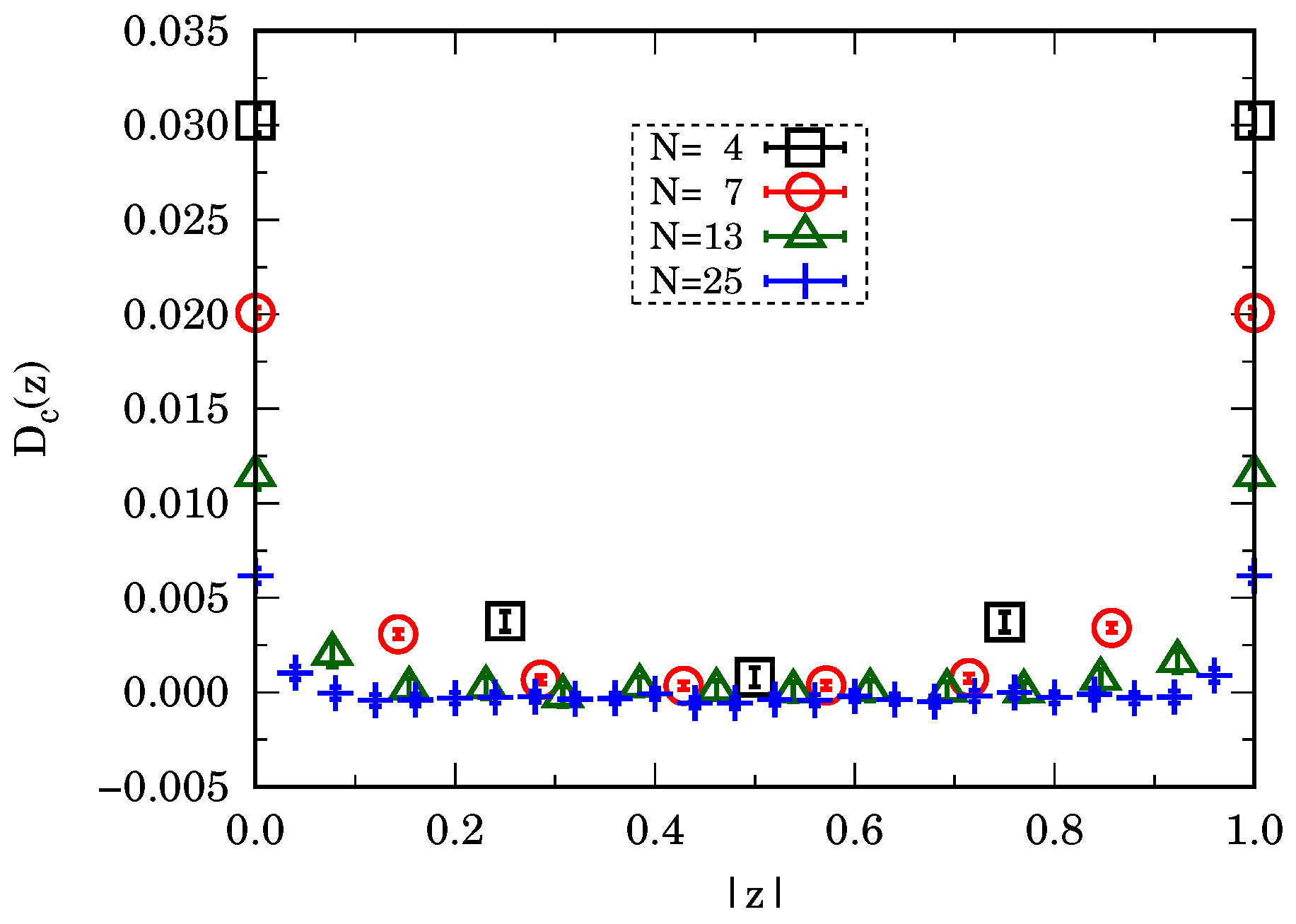
In Figure 2, we show $D_c\left(z\right)$ at increasing values of $N=1/a$. From the plot of the simulation data, we see that ${lim}_{a\to 0}D(1/2)=0$. The width of the spike of $D_c\left(z\right)$ at $z=0$ seems to be related to the value of the renormalized mass, $m_R$.

Alternatively, we could adjust, at each change in N, the value of the bare mass, m, to have a fixed value for the renormalized mass, $m_R$. This would result in a convergence toward a unique two-point connected function in the continuum limit, $N\to \infty$. We did not adopt this strategy because numerically tuning the bare mass to maintain the same value for the renormalized mass at each N proves problematic. This is what we did in some of our previous papers [12,13,16,17,18,19,20,21,22]. As explained in those works, keeping the renormalized mass constant is extremely cumbersome due to the unavoidable systematic numerical error that one faces. It would then have been extremely difficult to achieve a reasonable comparison between the two-point functions at different values of N.

4.2. Second Case Study

For the parameter values we just used, the box plays a crucial role: the bare Compton wavelength ($1/m$) is equal to the size, L, of the box. For the box to be a purely technical device introduced to regularize the theory, it must be large compared to the correlation length of the model. At the same time, the lattice spacing must be small compared to it:

$$\begin{array}{c}\hfill 1/L\ll m\ll 1/a.\end{array}$$

(16)

Therefore, next, we consider the study case with $g=L=\beta =1$, $m=\sqrt{N}/L$ and $ϵ={10}^{-10}$, which should be much less affected by the presence of the box than the previous choice, $m=1/L$.

Notice that the minima of the two symmetric potential wells in the semi-classical Hamiltonian density, described by $f\left(\phi \right)=\frac{1}{2}{m}^2{\phi }^2+{\phi }^4+\frac{3}{8}{\phi }^{-2}$, ${\phi }_{\pm }\left(m\right)$, are such that

$$\begin{array}{c}\hfill {\phi }_{\pm }\left(m\right)=\pm 3^{1/4}{\left(2m\right)}^{-1/2}+\mathrm{O}\left(m^{-7/2}\right)\mathrm{for}m\gg 1.\end{array}$$

(17)

So, with our choice of $m=\sqrt{N}$, in the continuum limit, we find

$$\begin{array}{c}\hfill {\displaystyle \underset{N\to \infty }{lim}}\langle \phi \rangle ={\displaystyle \underset{N\to \infty }{lim}}{\phi }_{+}\left(\sqrt{N}\right)=0,\end{array}$$

(18)

which is in agreement with the results in Refs. [12,13,16,18,19,20,21,22].

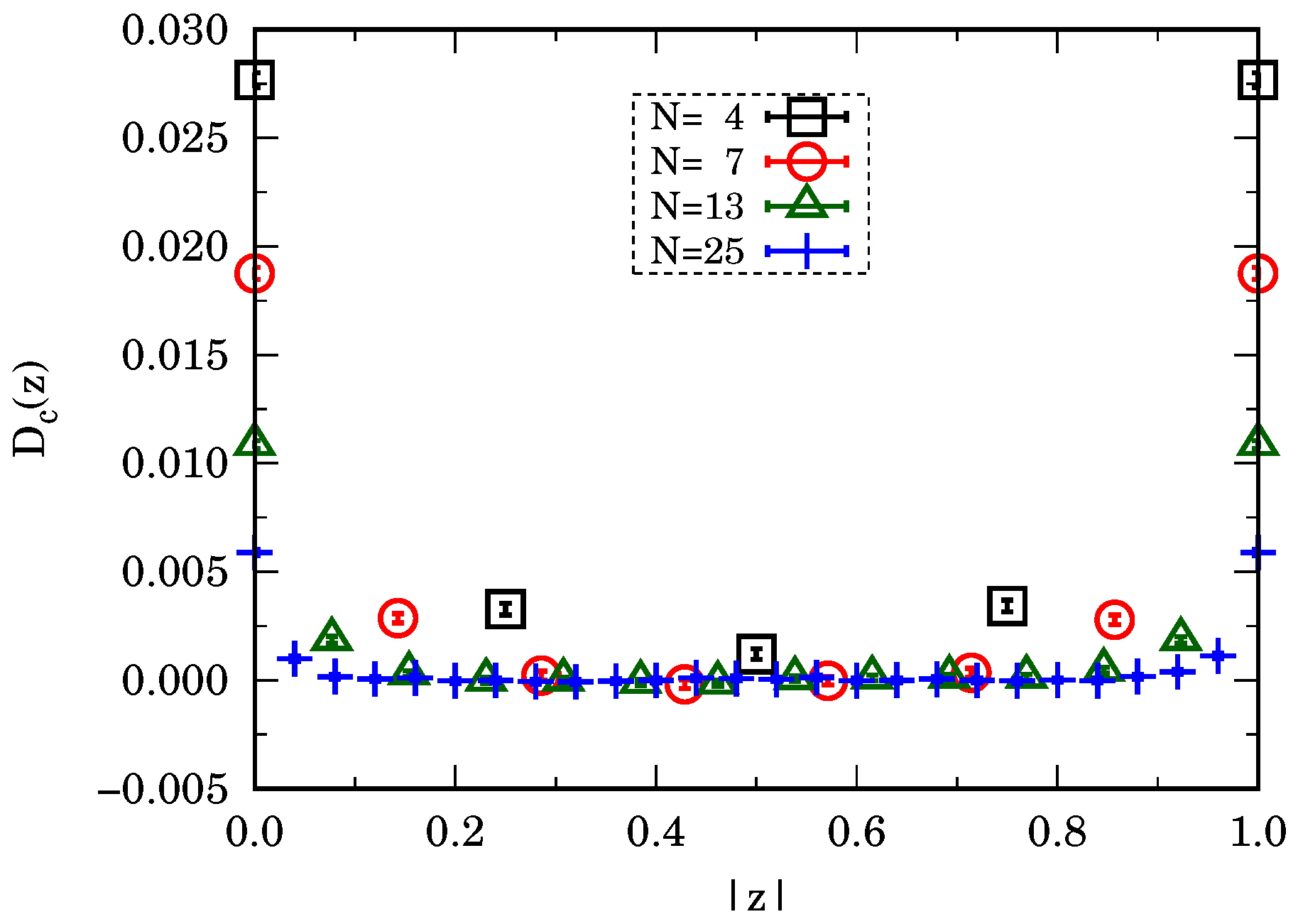
From Figure 3, we see the continuum limit, $N\to \infty$, of the scaled two-point connected function, where, with the abuse of notation, we drop the prime from $D_c$, which was adopted rigorously in Section 3. With respect to reference [14] (see Figure 3 there), which deals with the unscaled free field case, and $D_c\left(0\right)$, which increases with the increasing N, we see how scaling has the effect of letting the value of $D_c^{\prime }\left(0\right)$ decrease with increasing N, as shown in Figure 3, as ${\phi }^{\prime }=\phi /N^{3/2}$ and $D_c^{\prime }=D_c/N^3$. It is only by tuning the bare mass, m, to have a constant renormalized mass, $m_R$, for each N, that we would find true convergence. Unfortunately, this procedure is not easily accomplished numerically since for each N we would have to make several test runs with different values of m in order to find the value that keeps $m_R$ approximately constant. This procedure was nonetheless carried out in the following works [12,13,16,18,19,20,21,22].

5. Conclusions

In this paper, we denote $\pi \left(x\right)$ by $k\left(x\right)/\phi \left(x\right)$. To ensure proper values for $\pi \left(x\right)$, it is necessary to restrict $0<\phi \left(x\right)<\infty$ as well as $0\le \left|k\right(x\left)\right|<\infty$. Indeed, such a symbol change can treat Hamiltonian densities with an interaction, $\phi {\left(x\right)}^4$. This leads to a completely satisfactory quantization of field theories using situations that involve scaled behavior leading to an unexpected, ${\hslash }^2/\phi {\left(x\right)}^2$, which arises only in quantum aspects. Indeed, it is fair to claim that this symbol change leads to valid field theory quantization.

With respect to reference [14], which deals with the free field case, here, we repeat that analysis but for the ${\phi }^4$ interacting case.

We prove through path-integral Monte Carlo computer experiments that the affine quantization of the ${\phi }_4^4$-scaled Euclidean covariant relativistic field theory is a well-defined quantum field theory, with a well-defined continuum limit of the one- and two-point functions (the Green’s function).

The simple pseudo-potential, $\propto {\hslash }^2/{\phi }^2$, stemming from the affine quantization procedure [9], does not disturb the continuum limit, as we prove here; moreover, it can render the ${\phi }_4^4$ theory non-trivial, which is known to be trivial [2] when treated with the more commonly known canonical quantization [1].