A Schrödinger Equation for Evolutionary Dynamics
Abstract
:1. Introduction
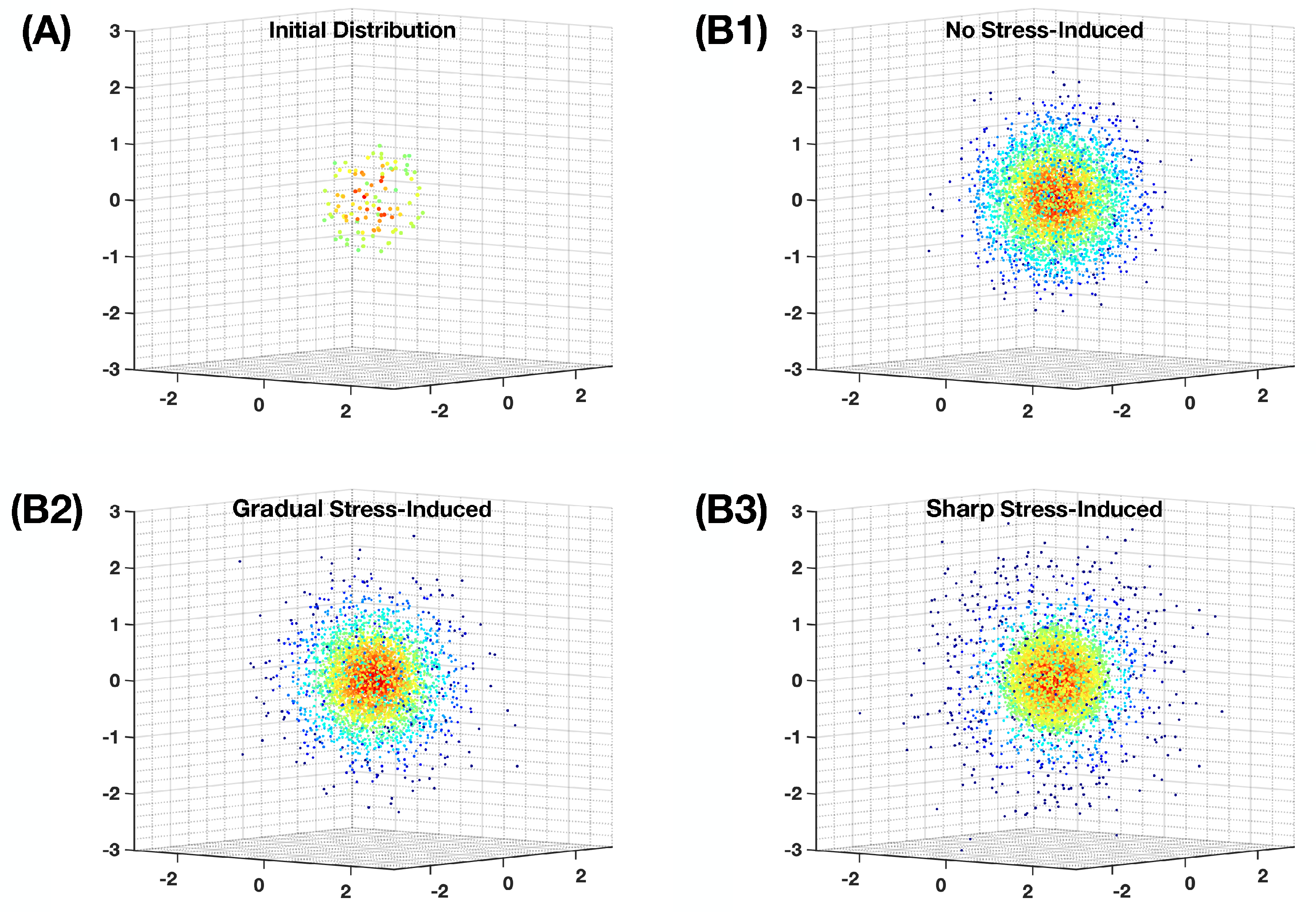
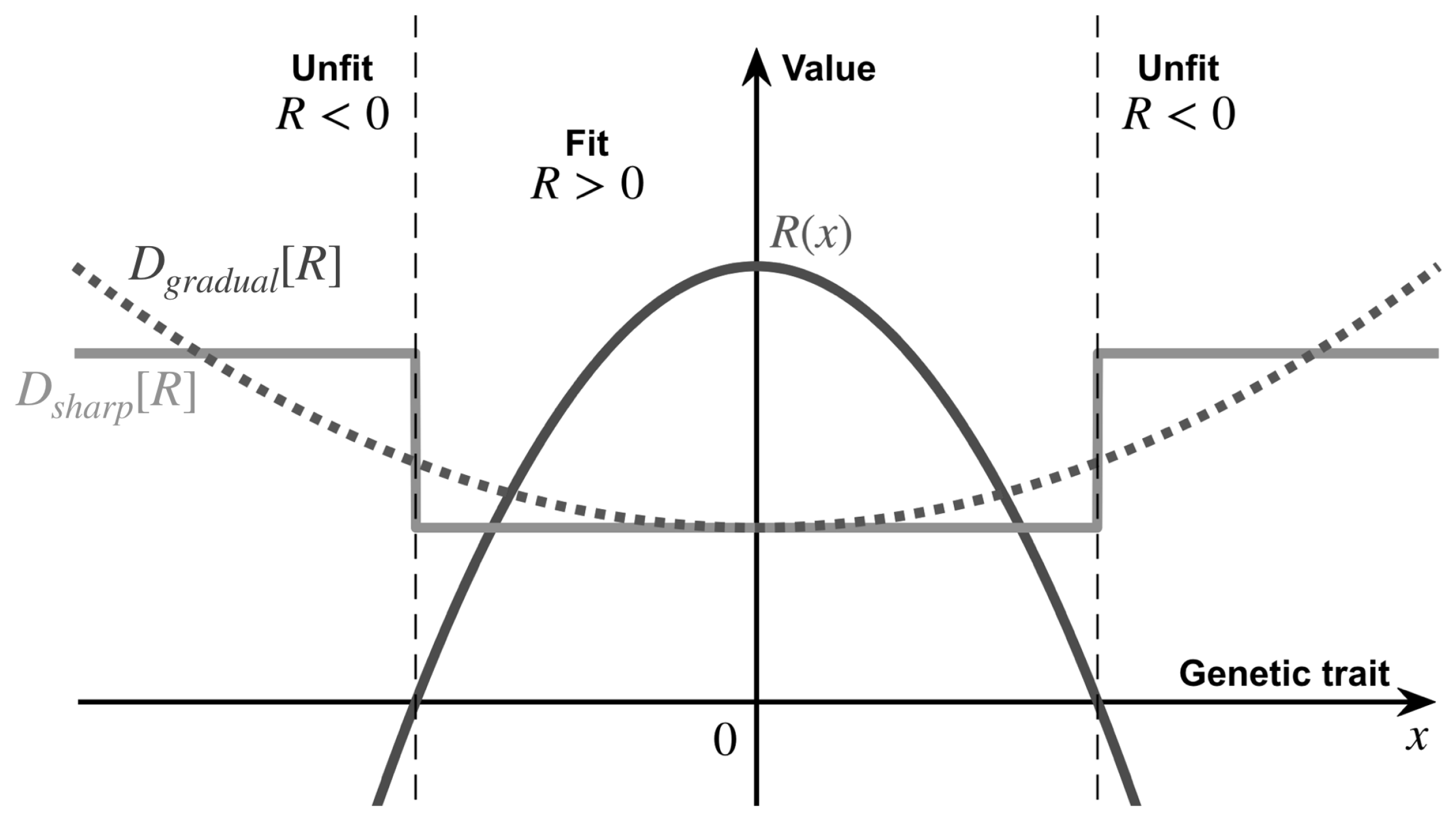
2. Evolutionary Landscape and Ecological Influence
3. An Analogy to the Schrödinger Equation
4. Applying the Rayleigh–Schrödinger Perturbation Theory to Stress-Induced Mutagenesis
4.1. A Gradual Change
4.2. A Sharp Change
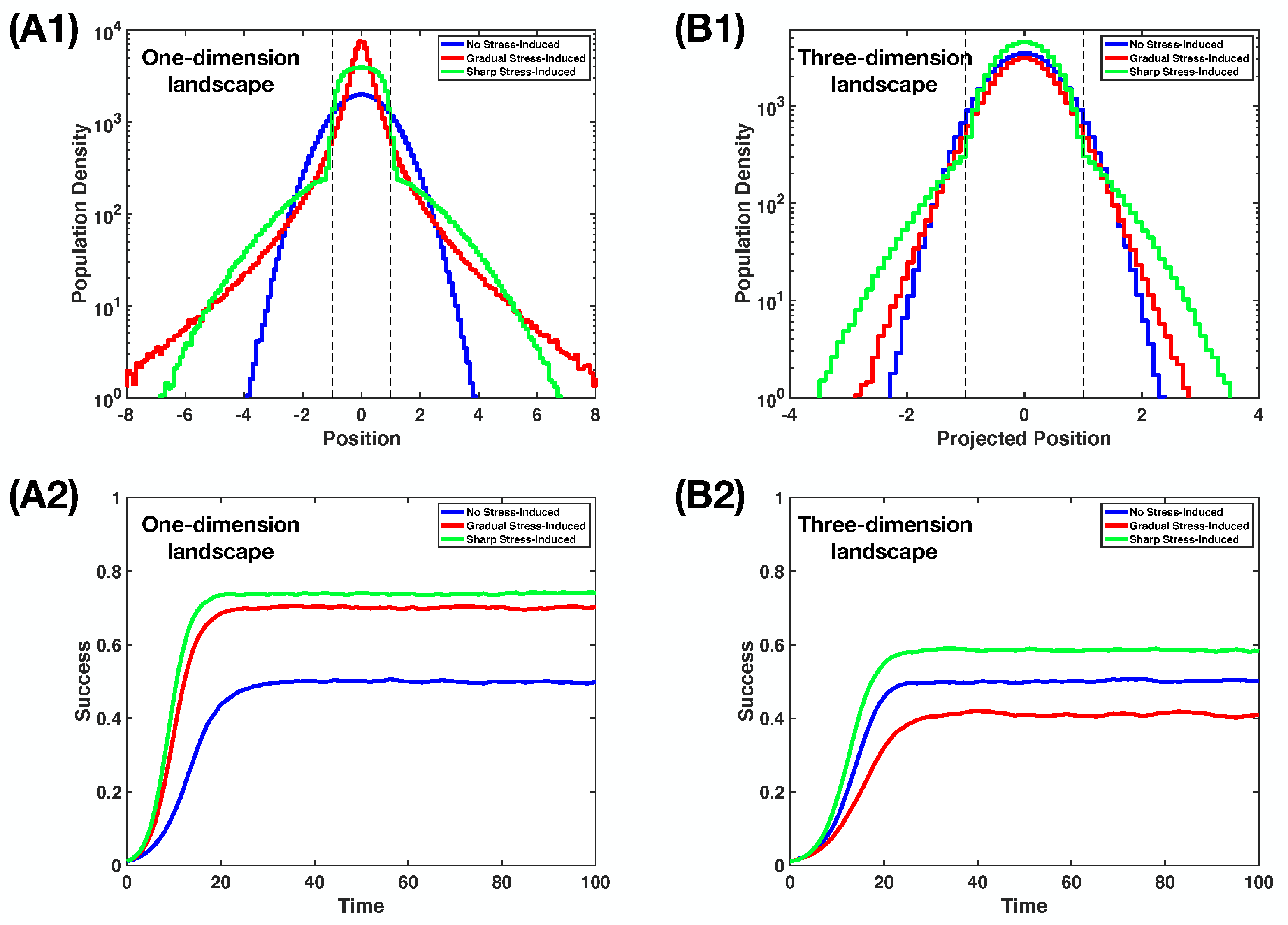
4.3. A Comparison between Two Stress-Induced Mutagenesis Regimes
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Summary of All Mathematical Quantities
- t: time.
- : position (a genomic configuration) in the abstract -dimensional fitness landscape.
- : population density on the landscape, which has the unit of population number per unit volume (equal to a unit length to the power ).
- : effective diffusivity in the landscape, which has the unit of unit length squared (to the power 2) per unit time.
- : the maximum growth rate of the sub-population located at position in the landscape, which has the unit of inverse unit time.
- K: carrying capacity, which has the unit of population number.
- S: success, which is the ratio between the total population number and the carrying capacity K; therefore, it is a dimensionless quantity.
Appendix B. Estimations of Stationary Population Success
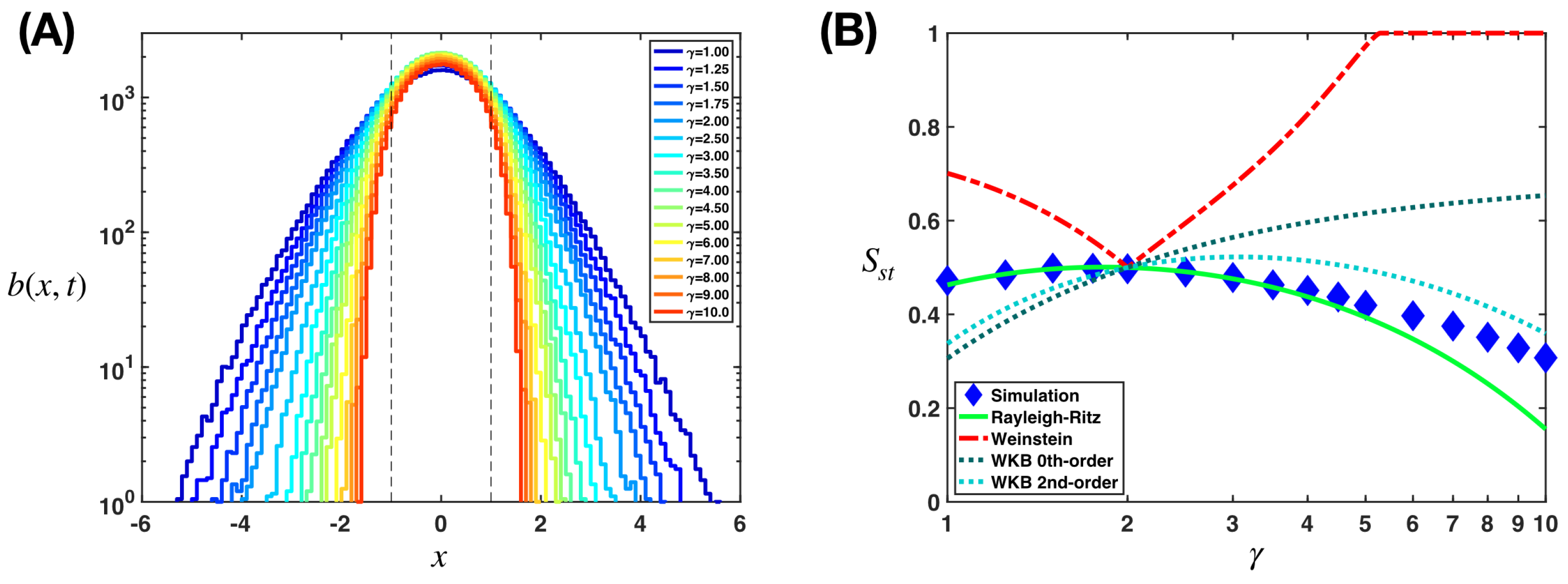
Appendix B.1. Application of the Rayleigh–Ritz Variational Method
Appendix B.2. Application of the Weinstein Method
Appendix B.3. Application of the Wentzel–Kramers–Brillouin Approximation
Appendix C. Simulation of the Non-Homogeneous Random Walk on the Landscape
Appendix D. Perturbative Corrections
Appendix D.1. With Perturbed Hamiltonian Contains
Appendix D.2. With Perturbed Hamiltonian Contains
Appendix D.3. With Perturbed Hamiltonian Contains Heaviside Function
References
- Darwin, C. On the Origin of Species, 1859; Routledge: London, UK, 2004. [Google Scholar]
- Dawkins, R. The Selfish Gene; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Waddington, C.H. Evolutionary adaptation. Perspect. Biol. Med. 1959, 2, 379–401. [Google Scholar] [CrossRef]
- Rose, M.R.; Lauder, G.V. Adaptation; Academic Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Endler, J.A. Natural Selection in the Wild; Number 21; Princeton University Press: Princeton, NJ, USA, 1986. [Google Scholar]
- Nevo, E. Genetic variation in natural populations: Patterns and theory. Theor. Popul. Biol. 1978, 13, 121–177. [Google Scholar] [PubMed]
- Tsoularis, A.; Wallace, J. Analysis of logistic growth models. Math. Biosci. 2002, 179, 21–55. [Google Scholar] [CrossRef] [PubMed]
- Getz, W.M. A unified approach to multispecies modeling. Nat. Resour. Model. 1991, 5, 393–421. [Google Scholar] [CrossRef]
- Getz, W.M. A metaphysiological approach to modeling ecological populations and communities. In Frontiers in Mathematical Biology; Springer: Berlin/Heidelberg, Germany, 1994; pp. 411–442. [Google Scholar]
- Bjedov, I.; Tenaillon, O.; Gerard, B.; Souza, V.; Denamur, E.; Radman, M.; Taddei, F.; Matic, I. Stress-induced mutagenesis in bacteria. Science 2003, 300, 1404–1409. [Google Scholar] [CrossRef]
- Fitzgerald, D.M.; Hastings, P.; Rosenberg, S.M. Stress-induced mutagenesis: Implications in cancer and drug resistance. Annu. Rev. Cancer Biol. 2017, 1, 119–140. [Google Scholar] [PubMed]
- Conrad, M. The geometry of evolution. BioSystems 1990, 24, 61–81. [Google Scholar] [CrossRef]
- Zhang, Q.; Lambert, G.; Liao, D.; Kim, H.; Robin, K.; Tung, C.k.; Pourmand, N.; Austin, R.H. Acceleration of emergence of bacterial antibiotic resistance in connected microenvironments. Science 2011, 333, 1764–1767. [Google Scholar] [CrossRef]
- Risken, H.; Caugheyz, T. The Fokker-Planck Equation: Methods of Solution and Application. J. Appl. Mech. 1991, 58, 860. [Google Scholar] [CrossRef]
- Wright, S. The Roles of Mutation, Inbreeding, Crossbreeding, and Selection in Evolution. In Proceedings of the Sixth International Congress of Genetics; 1932; pp. 356–366. Available online: http://www.esp.org/books/6th-congress/facsimile/#:~:text=The%20Proceedings%20of%20the%20Sixth,as%20president%20of%20the%20congress (accessed on 16 March 2023).
- Vincent, T.L.; Brown, J.S. Evolutionary Game Theory, Natural Selection, and Darwinian Dynamics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Kimura, M. Diffusion models in population genetics. J. Appl. Probab. 1964, 1, 177–232. [Google Scholar] [CrossRef]
- Sergey, G. Fitness Landscapes and the Origin of Species (MPB-41); Princeton University Press: Princeton, NJ, USA, 2004. [Google Scholar]
- Schrödinger, E. Quantisierung als eigenwertproblem. Ann. Phys. 1926, 385, 437–490. [Google Scholar] [CrossRef]
- Popov, V. Imaginary-Time Method in Quantum Mechanics and Field Theory. Phys. At. Nucl. 2005, 68. [Google Scholar] [CrossRef]
- Bloch, F. Über die quantenmechanik der elektronen in kristallgittern. Z. Phys. 1929, 52, 555–600. [Google Scholar] [CrossRef]
- Heidari, H.; Karamati, M.R.; Motavalli, H. Tumor growth modeling via Fokker–Planck equation. Phys. A Stat. Mech. Its Appl. 2022, 596, 127168. [Google Scholar] [CrossRef]
- Fung, L. Analogy between streamers in sinking spheroids, gyrotactic plumes and chemotactic collapse. J. Fluid Mech. 2023, 961, A12. [Google Scholar] [CrossRef]
- Armstrong, S.; Mourrat, J.C. Variational Methods for the Kinetic Fokker-Planck Equation. 2019. Available online: https://hal.science/hal-02144896/ (accessed on 16 March 2023).
- Rozenman, G.G.; Bondar, D.I.; Schleich, W.P.; Shemer, L.; Arie, A. Observation of Bohm trajectories and quantum potentials of classical waves. Phys. Scr. 2023, 98, 044004. [Google Scholar] [CrossRef]
- Rodrigues Gonçalves, M.; Rozenman, G.G.; Zimmermann, M.; Efremov, M.A.; Case, W.B.; Arie, A.; Shemer, L.; Schleich, W.P. Bright and dark diffractive focusing. Appl. Phys. B 2022, 128, 51. [Google Scholar] [CrossRef]
- Williams, M.B. Deducing the consequences of evolution: A mathematical model. J. Theor. Biol. 1970, 29, 343–385. [Google Scholar] [CrossRef]
- Mayr, E. What Evolution Is; Basic Books: New York, NY, USA, 2001. [Google Scholar]
- Imasheva, A. Environmental stress and genetic variation in animal populations. Genetika 1999, 35, 421–431. [Google Scholar]
- Hoffmann, A.A.; Hercus, M.J. Environmental stress as an evolutionary force. Bioscience 2000, 50, 217–226. [Google Scholar] [CrossRef]
- Phan, T.V.; Morris, R.J.; Lam, H.T.; Hulamm, P.; Black, M.E.; Bos, J.; Austin, R.H. Emergence of Escherichia coli critically buckled motile helices under stress. Proc. Natl. Acad. Sci. USA 2018, 115, 12979–12984. [Google Scholar] [CrossRef] [PubMed]
- Cirz, R.T.; Chin, J.K.; Andes, D.R.; de Crécy-Lagard, V.; Craig, W.A.; Romesberg, F.E. Inhibition of mutation and combating the evolution of antibiotic resistance. PLoS Biol. 2005, 3, e176. [Google Scholar] [CrossRef] [PubMed]
- Bos, J.; Zhang, Q.; Vyawahare, S.; Rogers, E.; Rosenberg, S.M.; Austin, R.H. Emergence of antibiotic resistance from multinucleated bacterial filaments. Proc. Natl. Acad. Sci. USA 2015, 112, 178–183. [Google Scholar] [CrossRef] [PubMed]
- Foster, P.L. Stress-induced mutagenesis in bacteria. Crit. Rev. Biochem. Mol. Biol. 2007, 42, 373–397. [Google Scholar] [CrossRef] [PubMed]
- Pribis, J.P.; Zhai, Y.; Hastings, P.; Rosenberg, S.M. Stress-Induced Mutagenesis, Gambler Cells, and Stealth Targeting Antibiotic-Induced Evolution. mBio 2022, 13, e01074-22. [Google Scholar] [CrossRef]
- Govindaraj Vaithinathan, A.; Vanitha, A. WHO global priority pathogens list on antibiotic resistance: An urgent need for action to integrate One Health data. Perspect. Public Health 2018, 138, 87–88. [Google Scholar] [CrossRef]
- Rayleigh, L. On the dynamical theory of gratings. Proc. R. Soc. London Ser. A Contain. Pap. Math. Phys. Character 1907, 79, 399–416. [Google Scholar]
- Ritz, W. Über eine neue Methode zur Lösung Gewisser Variationsprobleme der Mathematischen Physik. J. Die Reine Angew. Math. 1909. Available online: https://www.degruyter.com/document/doi/10.1515/crll.1909.135.1/html?lang=de (accessed on 16 March 2023). [CrossRef]
- Cohen, M.; Feldmann, T. Rayleigh-Schrodinger perturbation theory with a non-Hermitian perturbation. J. Phys. B At. Mol. Phys. 1982, 15, 2563. [Google Scholar] [CrossRef]
- Phan, T.V.; Wang, G.; Do, T.K.; Kevrekidis, I.G.; Amend, S.; Hammarlund, E.; Pienta, K.; Brown, J.; Liu, L.; Austin, R.H. It doesn’t always pay to be fit: Success landscapes. J. Biol. Phys. 2021, 47, 387–400. [Google Scholar] [CrossRef]
- An, J.H.; Goo, E.; Kim, H.; Seo, Y.S.; Hwang, I. Bacterial quorum sensing and metabolic slowing in a cooperative population. Proc. Natl. Acad. Sci. USA 2014, 111, 14912–14917. [Google Scholar] [CrossRef]
- Mooney, J.A.; Pridgen, E.M.; Manasherob, R.; Suh, G.; Blackwell, H.E.; Barron, A.E.; Bollyky, P.L.; Goodman, S.B.; Amanatullah, D.F. Periprosthetic bacterial biofilm and quorum sensing. J. Orthop. Res. 2018, 36, 2331–2339. [Google Scholar] [CrossRef] [PubMed]
- Wu, A.; Liao, D.; Tlsty, T.D.; Sturm, J.C.; Austin, R.H. Game theory in the death galaxy: Interaction of cancer and stromal cells in tumour microenvironment. Interface Focus 2014, 4, 20140028. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Phulpoto, I.A.; Zhang, G.; Yu, Z. Acceleration of emergence of E. coli antibiotic resistance in a simulated sublethal concentration of copper and tetracycline co-contaminated environment. Amb Express 2021, 11, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ram, Y.; Hadany, L. Stress-induced mutagenesis and complex adaptation. Proc. R. Soc. Biol. Sci. 2014, 281, 20141025. [Google Scholar] [CrossRef]
- Murray, C.J.; Ikuta, K.S.; Sharara, F.; Swetschinski, L.; Aguilar, G.R.; Gray, A.; Han, C.; Bisignano, C.; Rao, P.; Wool, E.; et al. Global burden of bacterial antimicrobial resistance in 2019: A systematic analysis. Lancet 2022, 399, 629–655. [Google Scholar] [CrossRef]
- Kemp, S.A.; Collier, D.A.; Datir, R.P.; Ferreira, I.A.; Gayed, S.; Jahun, A.; Hosmillo, M.; Rees-Spear, C.; Mlcochova, P.; Lumb, I.U.; et al. SARS-CoV-2 evolution during treatment of chronic infection. Nature 2021, 592, 277–282. [Google Scholar] [CrossRef]
- Kontsevich, M.; Segal, G. Wick rotation and the positivity of energy in quantum field theory. Q. J. Math. 2021, 72, 673–699. [Google Scholar] [CrossRef]
- van Dommelen, L. Fundamental Quantum Mechanics for Engineers. 2007. Available online: https://www.semanticscholar.org/paper/Quantum-mechanics-for-engineers.-Dommelen/2eb883af5ccb0d0bdd9f0d10009c4a7151c9c339 (accessed on 16 March 2023).
- Rosen, G. Theoretical significance of the condition δ = 2μ in bacterial chemotaxis. Bull. Math. Biol. 1983, 45, 151–153. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Lectures on Quantum Mechanics; Courier Corporation: North Chelmsford, MA, USA, 2001; Volume 2. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Elsevier: Amsterdam, The Netherlands, 2013; Volume 3. [Google Scholar]
- Griffiths, D.J.; Schroeter, D.F. Introduction to quantum mechanics; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Sakurai, J.J.; Commins, E.D. Modern Quantum Mechanics, revised ed.; Addison-Wesley: Boston, MA, USA, 1995. [Google Scholar]
- Weinstein, D. Modified ritz method. Proc. Natl. Acad. Sci. USA 1934, 20, 529–532. [Google Scholar] [CrossRef]
- Lee, J. The upper and lower bounds of the ground state energies using the variational method. Am. J. Phys. 1987, 55, 1039–1040. [Google Scholar] [CrossRef]
- Temple, G. The theory of Rayleigh’s principle as applied to continuous systems. Proc. R. Soc. London Ser. Contain. Pap. Math. Phys. Character 1928, 119, 276–293. [Google Scholar]
- Pollak, E. A tight lower bound to the ground-state energy. J. Chem. Theory Comput. 2019, 15, 4079–4087. [Google Scholar] [CrossRef] [PubMed]
- Wentzel, G. Eine verallgemeinerung der quantenbedingungen für die zwecke der wellenmechanik. Z. Phys. 1926, 38, 518–529. [Google Scholar] [CrossRef]
- Kramers, H.A. Wellenmechanik und halbzahlige Quantisierung. Z. Phys. 1926, 39, 828–840. [Google Scholar] [CrossRef]
- Brillouin, L. La mécanique ondulatoire de Schrödinger: Une méthode générale de resolution par approximations successives”, Comptes Rendus de l’Academie des Sciences 183, 24 U26 (1926) HA Kramers. Wellenmechanik Halbzählige Quantisierung Zeit. Phys. 1926, 39, U840. [Google Scholar]
- Karnakov, B.M.; Krainov, V.P. WKB Approximation in Atomic Physics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Voros, A. The return of the quartic oscillator. The complex WKB method. Ann. l’IHP Phys. Théorique 1983, 39, 211–338. [Google Scholar]
- Balian, R.; Parisi, G.; Voros, A. Discrepancies from asymptotic series and their relation to complex classical trajectories. Phys. Rev. Lett. 1978, 41, 1141. [Google Scholar] [CrossRef]
- Gabai, B.; Yin, X. Exact quantization and analytic continuation. J. High Energy Phys. 2023, 2023, 1–33. [Google Scholar] [CrossRef]
- Ito, K.; Marino, M.; Shu, H. TBA equations and resurgent Quantum Mechanics. J. High Energy Phys. 2019, 2019, 1–45. [Google Scholar] [CrossRef]
- Dorey, P.; Tateo, R. Anharmonic oscillators, the thermodynamic Bethe ansatz and nonlinear integral equations. J. Phys. A Math. Gen. 1999, 32, L419. [Google Scholar] [CrossRef]
- Voros, A. Airy function-exact WKB results for potentials of odd degree. J. Phys. A Math. Gen. 1999, 32, 1301. [Google Scholar] [CrossRef]
- Vraničar, M.; Robnik, M. Accuracy of the WKB approximation: The case of general quartic potential. Prog. Theor. Phys. Suppl. 2000, 139, 214–233. [Google Scholar] [CrossRef]
- Olver, F. The generalized exponential integral. In Proceedings of the Approximation and Computation: A Festschrift in Honor of Walter Gautschi: Proceedings of the Purdue Conference, West Lafayette, IN, USA, 2–5 December 1993; Springer: Berlin/Heidelberg, Germany, 1994; pp. 497–510. [Google Scholar]
- Pham, K.T.; Nguyen, D.M.; Tran, D.V.; Ao, V.D.; Tran, H.D.; Do, T.K.; Phan, T.V. Stress-Induced Mutagenesis Can Further Boost Population Success in Static Ecology. arXiv 2023, arXiv:2303.09084. [Google Scholar]
- Arnold, S.J. Morphology, performance and fitness. Am. Zool. 1983, 23, 347–361. [Google Scholar] [CrossRef]
- Bukkuri, A.; Pienta, K.J.; Austin, R.H.; Hammarlund, E.U.; Amend, S.R.; Brown, J.S. A life history model of the ecological and evolutionary dynamics of polyaneuploid cancer cells. Sci. Rep. 2022, 12, 13713. [Google Scholar] [CrossRef]
- Cunningham, J.J.; Gatenby, R.A.; Brown, J.S. Evolutionary dynamics in cancer therapy. Mol. Pharm. 2011, 8, 2094–2100. [Google Scholar] [CrossRef]
- Staňková, K.; Brown, J.S.; Dalton, W.S.; Gatenby, R.A. Optimizing cancer treatment using game theory: A review. JAMA Oncol. 2019, 5, 96–103. [Google Scholar] [CrossRef] [PubMed]
- Vincent, T.L.; Brown, J.S. The evolution of ESS theory. Annu. Rev. Ecol. Syst. 1988, 19, 423–443. [Google Scholar] [CrossRef]
- Elsasser, W.M. The Physical Foundation of Biology: An Analytical Study; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Dawkins, R. The Blind Watchmaker: Why the Evidence of Evolution Reveals a Universe without Design; WW Norton & Company: New York, NY, USA, 1996. [Google Scholar]
- Bhattacharjee, T.; Datta, S.S. Bacterial hopping and trapping in porous media. Nat. Commun. 2019, 10, 2075. [Google Scholar] [CrossRef] [PubMed]
- Phan, T.V.; Morris, R.; Black, M.E.; Do, T.K.; Lin, K.C.; Nagy, K.; Sturm, J.C.; Bos, J.; Austin, R.H. Bacterial route finding and collective escape in mazes and fractals. Phys. Rev. X 2020, 10, 031017. [Google Scholar] [CrossRef]
- Fu, X.; Kato, S.; Long, J.; Mattingly, H.H.; He, C.; Vural, D.C.; Zucker, S.W.; Emonet, T. Spatial self-organization resolves conflicts between individuality and collective migration. Nat. Commun. 2018, 9, 2177. [Google Scholar] [CrossRef]
- Langhoff, P.; Epstein, S.; Karplus, M. Aspects of time-dependent perturbation theory. Rev. Mod. Phys. 1972, 44, 602. [Google Scholar] [CrossRef]
- Dykhne, A. Quantum transitions in the adiabatic approximation. Sov. Phys. JETP 1960, 11, 411. [Google Scholar]
- Casas, F.; Oteo, J.; Ros, J. Floquet theory: Exponential perturbative treatment. J. Phys. A Math. Gen. 2001, 34, 3379. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, G.; Huang, M.X. New exact quantization condition for toric Calabi-Yau geometries. Phys. Rev. Lett. 2015, 115, 121601. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Phan, T.V.; Li, S.; Wombacher, M.; Qu, J.; Peng, Y.; Chen, G.; Goldman, D.I.; Levin, S.A.; Austin, R.H.; et al. Emergent field-driven robot swarm states. Phys. Rev. Lett. 2021, 126, 108002. [Google Scholar] [CrossRef]
- Phan, T.V.; Wang, G.; Liu, L.; Austin, R.H. Bootstrapped motion of an agent on an adaptive resource landscape. Symmetry 2021, 13, 225. [Google Scholar] [CrossRef]
- Wang, G.; Phan, T.V.; Li, S.; Wang, J.; Peng, Y.; Chen, G.; Qu, J.; Goldman, D.I.; Levin, S.A.; Pienta, K.; et al. Robots as models of evolving systems. Proc. Natl. Acad. Sci. USA 2022, 119, e2120019119. [Google Scholar] [CrossRef]
- Balakrishnan, V. All about the Dirac delta function (?). Resonance 2003, 8, 48–58. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ao, V.D.; Tran, D.V.; Pham, K.T.; Nguyen, D.M.; Tran, H.D.; Do, T.K.; Do, V.H.; Phan, T.V. A Schrödinger Equation for Evolutionary Dynamics. Quantum Rep. 2023, 5, 659-682. https://doi.org/10.3390/quantum5040042
Ao VD, Tran DV, Pham KT, Nguyen DM, Tran HD, Do TK, Do VH, Phan TV. A Schrödinger Equation for Evolutionary Dynamics. Quantum Reports. 2023; 5(4):659-682. https://doi.org/10.3390/quantum5040042
Chicago/Turabian StyleAo, Vi D., Duy V. Tran, Kien T. Pham, Duc M. Nguyen, Huy D. Tran, Tuan K. Do, Van H. Do, and Trung V. Phan. 2023. "A Schrödinger Equation for Evolutionary Dynamics" Quantum Reports 5, no. 4: 659-682. https://doi.org/10.3390/quantum5040042
APA StyleAo, V. D., Tran, D. V., Pham, K. T., Nguyen, D. M., Tran, H. D., Do, T. K., Do, V. H., & Phan, T. V. (2023). A Schrödinger Equation for Evolutionary Dynamics. Quantum Reports, 5(4), 659-682. https://doi.org/10.3390/quantum5040042





