Abstract
Quantum teleportation is the name of a problem: How can the real-valued parameters encoding the state at Alice’s location make their way to Bob’s location via shared entanglement and only two bits of classical communication? Without an explanation, teleportation appears to be a conjuring trick. Investigating the phenomenon with Schrödinger states and reduced density matrices shall always leave loose ends because they are not local and complete descriptions of quantum systems. Upon demonstrating that the Heisenberg picture admits a local and complete description, Deutsch and Hayden rendered its explanatory power manifest by revealing the trick behind teleportation, namely, by providing an entirely local account. Their analysis is re-exposed and further developed.
1. Introduction
In the context of the recent Nobel Prize of physics, the Scientific American published [1] an article titled “The Universe Is Not Locally Real, and the Physics Nobel Prize Winners Proved It”. I could dedicate my piece to the fact that we do not “prove” such claims in science or to the fact that the universe is real. Instead, I will address the question of locality, which creates tremendous confusion in the community of quantum foundations. The key message that I want to advocate is that quantum systems can be described in a local and complete way, and we should do so.
Since Bell [2], the term locality, more often seen negated, has come to mean compatibility with an underlying explanation by local hidden variables. However, local hidden variables are only one way in which locality can be instantiated, whose full generality is captured by Einstein’s locality [3]: “the real factual situation of system A is independent of what is done with the system B, which is spatially separated from the former.” Scientific theories are tentative descriptions of the real factual situation; thus, Einstein’s locality can be lifted (and slightly generalized) into a criterion for theories: The description of system A is independent of what is performed with system B, which is dynamically isolated from the former.
If Alice and Bob share an entangled pair of particles in a pure state, the reduced density matrices provide a local mode of description. Indeed, an action by Bob on his quantum system shall alter its density matrix, but Alice’s remains unchanged. However, reduced density matrices are not a complete mode of description, a sufficient definition of which is that the distribution of any joint measurement can be computed from the individual descriptions. The object that encompasses the distribution of any joint measurement is the global state vector, which cannot be retrieved from the reduced density matrices since too much information has been traced out.
The global state vector can also serve as a mode of description in which both Alice and Bob take it as the description of their own system. It is complete; however, it is not local, for if Bob makes a local change to his quantum system, it alters its description, which is fine, but it also alters the description of Alice’s system. We seem to be stuck in a dichotomy: quantum systems are described either locally or completely, and the appropriate description is chosen based on the problem at hand.
However, this dichotomy was proven false in 2000 by Deutsch and Hayden [4], who showed that the Heisenberg picture admits descriptors, which fulfill both Einstein’s locality and completeness. To insist, Bob’s action on his system alters its descriptor but leaves the descriptor of Alice’s system invariant; moreover, the global state vector can be recovered from the pair of descriptors. Note that the existence of such a local mode of description in quantum theory makes the theory local: the existence of non-local ways in which the theory can be expressed is irrelevant. (Terminology-wise, that the wave function is not a local and complete description has been referred to as its nonseparability [5,6]. Descriptors are a separable account, and therefore, quantum theory is separable.)
In the more recent literature, there are two other approaches to what can be called quantum locality: the proposals of Raymond-Robichaud. Evolution matrices [7] are framed within the quantum formalism. Noumenal states [8], on the other hand, take a more general approach, as they apply to a class of theories for which operations form a group. Since quantum theory qualifies, noumenal states can be instantiated in quantum theory. I proved [9] all these modes of description to be formally equivalent, and investigated some of the consequences of embracing these modes of description as an account of reality.
We have been inundated with numerous alternative approaches to quantum theory, and it may appear that I am advocating yet another. However, that is not what it is. The proposal by Deutsch and Hayden hinges on previous work by Gottesman on the Heisenberg representation of quantum computers [10], i.e., the Heisenberg picture of quantum theory applied to networks of qubits. This picture is the way in which the theory was discovered [11] in 1925, with the usual dynamical variables being promoted to dynamical operators. Consequently, what I shall present here is not about interpretation; it is about the mathematical formalism of quantum theory. It is the Heisenberg picture of unitary quantum theory.
If one finds that locality and completeness are not good enough reasons to adopt Heisenberg-picture descriptors as our tentative best account of quantum systems, then how they can be put to work might be more persuasive. To demonstrate the explanatory power of Heisenberg-picture descriptors, I delve into a problem; the problem of teleportation [12]. How can the real-valued parameters encoding the state at Alice’s location make their way to Bob’s location via shared entanglement and only two bits of classical communication?
In this piece, I re-expose and further develop Deutsch and Hayden’s solution. If teleportation felt like a magic trick, they unveiled it. After an overview of teleportation in the Schrödinger picture (Section 2) and of Heisenberg-picture descriptors (Section 3), teleportation is revisited in the light of descriptors (Section 4). Then, it is argued that more than two real-valued parameters are “teleported,” as descriptors also encompass counterfactual descriptive elements (Section 5). A conclusion (Section 6) and a discussion (Section 7) follow.
2. The Usual Take on Teleportation
The teleportation protocol—whose textbook appearance is displayed in Figure 1—starts by preparing a pair of entangled qubits in the state, which is then shared between Alice and Bob. (The four Bell states are and .) Then, or in the meantime, Alice prepares a qubit in the state to be teleported, . Alice might put her personal diary into and , as there is plenty of room in and ; being complex numbers, they can encode infinitely many bits. Since all qubits involved are initiated in their state, Alice’s preparation is seen as an operation U, which takes to . She then performs a Bell measurement between her shared entangled state and her prepared qubit. It yields two classical bits of output that she communicates to Bob over a classical communication channel, such as a telephone. Bob then manipulates his qubit in accordance with the two bits that he receives. He will, or not, apply the X gate; and he will, or not, apply the Z gate. After Bob’s processing of his system, its corresponding state is . The very fact that a phenomenon is called “teleportation” underlines its puzzlement:
Let me insist that and , in principle, contain infinitely many bits, but only two classical bits are communicated.
How do α and β make their way from Alice to Bob?

Figure 1.
Teleportation in a yet-to-be-defined quantum–classical dualistic theory.
To review the computation in the Schrödinger picture, it is expositive to re-express the global state after and have been prepared. Calling this time and disregarding normalization,
Expressing in such a way helps to verify the rest of the protocol; the Bell measurement distinguishes the four possible terms and provides the information about which correction needs to be performed on Bob’s system to recover . Verifying that the protocol achieves the purported functionality does not amount to explaining how it works. If the flexibility in the way can be expressed is useful for the verification of the protocol, it is disastrous to provide an explanation of the transmission of and , for the mathematical equality between an expression describing and at Alice’s location and an expression displaying them to be at Bob’s location annihilates the hopes to locate the information accurately in the state vector.
Importantly, embracing unitary quantum theory does not lead to much progress. In fact, records of the measurement outcome can be appended as displayed in Figure 2. In this quantum setting, the state vector evolves according to
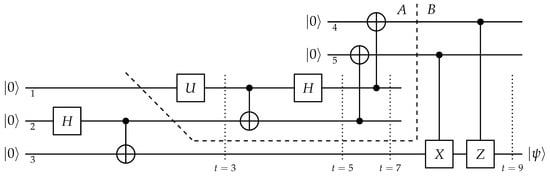
Figure 2.
Teleportation in unitary quantum theory.
On the question of the apparent instantaneous transfer in teleportation, what inhibits progress is the Schrödinger picture, for full unitarity does not change the fact that in , and can freely jump around the state vector. Therefore, on Schrödinger’s stage, the local transfer remains unseeable, and one might be fooled by the suggestion that and really are teleported. Heisenberg takes us backstage.
3. Heisenberg-Picture Descriptors
In this section, I present an overview of how descriptors work. For a thorough exposition, see [13]. A reader who prefers avoiding this section—perhaps due to its more elaborate mathematical content—can have a glance at Equation (2), accept the action of gates on descriptors as given by Equations (5), (6) and (8), and proceed to the following section.
In the Heisenberg picture, observables evolve in time while the state remains constant and conveniently set to in the context of quantum computational networks. In front of the uncountable number of observables that evolve in time, the tempting thought is to give up on Heisenberg-picture descriptions. Fortunately, the algebra of observables admits a generating set, i.e., a set of operators that multiplicatively generate a basis of all operators. This generating set can be chosen such that only a few operators act non-trivially on each system. These operators are then encompassed into a single object, the descriptor of the system, which evolves in time and can be used to calculate any time-evolved observable of that system. Similarly, any time-evolved observable that pertains to a collection of systems can be obtained from the descriptors of those systems. To connect with the more familiar language of the Schrödinger picture, the descriptors corresponding to a collection of systems permit the reconstruction of the density matrix of this collection of systems. In particular, the global density matrix can be obtained from all individual descriptors.
3.1. Qubit Descriptors
Consider a network of n qubits, whose ith qubit is denoted . At time 0, the descriptor of can be expressed as the pair of operators acting on
where and are Pauli matrices, and is the identity on . A third descriptor component, , can be obtained as . Descriptors evolve as observables do; namely, if U denotes the evolution operator of what happens to the whole network between time 0 and time t, then
where the U acts on both components of . Time evolution preserves the algebra of descriptors, which, in the context of qubits, is the Pauli algebra,
Suppose that between the discrete times and t, only one gate is performed, whose matrix representation on the whole network is denoted . Therefore, , where V consists of all gates from time 0 to . The evolution of descriptors can also be expressed in a step-by-step fashion,
where is the -component object that encodes the descriptor of each qubit at the corresponding time and is a fixed operator-valued function of some components of its argument. The function satisfies the defining equation , which is guaranteed to exist by the generative ability of the components of . More precisely, any linear operator can be expressed as a polynomial in the matrices , , …, , , and is one such polynomial. The expressions (3) and (4) for the evolution of can be recognized equivalent:
The second equality follows because in each term of the polynomial , products of components that are surrounded by and V will have their inner s and Vs cancelled, leaving only the outer ones, which can be factorized outside of the polynomial to retrieve the first line.
3.2. Locality and Completeness
The locality of the descriptors is due to the fact that if the gate acts only on qubits of the subset , then its functional representation shall only depend on components of , for . Therefore, for any , the descriptor commutes with , and thus remains unchanged between times and t: the description of system A is independent of what is performed with system B, which is dynamically isolated from the former. Einstein’s criterion, generalized as above with dynamical isolation instead of spatial separation, stresses that the locality of the mode of description is inherited from the locality of interactions. If, in spacetime, the interactions are constrained by a lightcone structure, the descriptors inherit the constraint, and spatially separated systems shall be described independently of what is performed on the other.
When the constant reference vector is also taken into account, the descriptors are complete. The expectation value of any observable that concerns only qubits of I can be determined by the descriptors . This can be seen more clearly at time 0, where an observable on the qubits of a subset is, like a gate , a linear operator that acts non-trivially only on the qubits of I. Again, any such operator can be generated additively and multiplicatively by the components of , with . So, there exists a polynomial such that . Therefore,
(Again, in a term that consists of a product of various components, the inner s and Us cancel out, and the outer s and Us can be factored out of the polynomial.) Since the elements of the density matrix can be computed as the expectation value of an appropriate operator, the density matrix of the joint subsystems in I can be obtained from . In what follows, we shall only be interested in computing the reduced density matrix of one qubit from its descriptor. The reduced density matrix of qubit at time t can be expressed in the Pauli basis, like any hermitian matrix of trace one, as
From the trace relations of Pauli matrices, the components are
The second equality comes from that is, as a super-operator, the adjoint of , and the rightmost equality follows from the cyclicity of the trace. That is not tracked in time is no problem since it can be computed as .
3.3. The Action of Gates
For concrete calculations in a network that admits a fixed set of gates, it is convenient to find the action that each gate has on the descriptors. The matrix representation of the Hadamard gate applied to (and the identity elsewhere) can be expressed as
which defines its functional representation . From Equation (4), and using the algebra of operators at time to simplify the right-hand side, one finds , or more elaborately,
Therefore, the Hadamard gate switches the components of the descriptor on which it acts (regardless of how these components are expressed in terms of Pauli operators at time ). Abstracting away the time at which the gate occurs, the action of is specified by
In a like manner, the action of the Cnot can be found to be
where the label c refers to the control qubit and the label t, to the target qubit. The z-component of the control is copied onto the z-component of the target, while the x-component of the target is copied onto the x-component of the control (regardless of what those components are at that time). The action of the controlled-Z gate can be found from
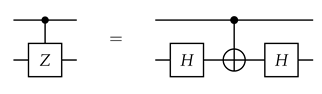 .
.
 .
.In the teleportation protocol, Alice’s preparation consists of a generic one-qubit gate U, which maps to . Such a generic transformation of can be expressed as the exponentiation of a generator, or alternatively, it can be parametrized with Euler angles as
Note that and are parametrized, as in the first column of U, with respect to . Since Alice’s preparation involves an action only on , it can be expressed as in Equation (7) where the components of replace and . This thus defines the functional representation of from which the action can be computed,
Sparing the detailed expressions, and denote two functions that depend on the operators , and on the parameters (and therefore on and ).
4. The Heisenberg Picture of Teleportation
Teleportation is now revisited in the Heisenberg picture. Descriptors are such a local description of quantum systems, that a computation in a network can be carried out by writing the descriptors directly on each qubit wire, as in Figure 3.
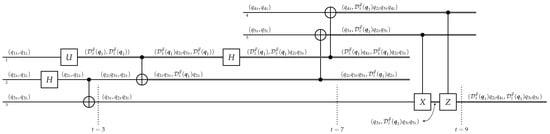
Figure 3.
The descriptors in quantum teleportation. The computation starts with all qubits properly initialized to , which, for conciseness, is denoted without time dependence as . When entering a gate, the components of the input are shuffled into the output in accordance with the action of the gate, which is prescribed by Equations (5), (6) and (8). The information flow of the parameters and , encoded in , is highlighted in dark grey, with the wires thickened. It spreads locally in the network through the interactions, and, as can be seen, the “classical” bits are responsible for carrying the parameters encoding Alice’s system over to Bob’s location.
The correspondence with the famous result in the Schrödinger picture can be verified by computing the reduced density matrix of at time 9, . It is expressed by
where the fixed Heisenberg state. Because
only differ by operators that have eigenvalues 1 with respect to ,
Therefore, the state vector that corresponds to Bob’s descriptor after his correction is .
4.1. Locally Inaccessible Information
To articulate the localization of information, Deutsch and Hayden did not require a quantitative notion of information. Instead, they coined and worked with the following criteria:
- (i)
- A system is deemed to contain information about a parameter if (though not necessarily only if) the probability of some outcome of some measurement on alone depends on ;
- (ii)
- A system is deemed to contain no information about if there exists a complete description of that satisfies Einstein’s criterion and is independent of .
Following these criteria, Deutsch and Hayden realized that there is such a thing as locally inaccessible information, namely, information that is present in a system but does not affect the probability of any outcome of any possible measurement on that system alone. Notably, in the communication channel used in teleportation, and are locally inaccessible. Indeed, the collection of systems , and at time 7 contains information about and since, as the rest of the protocol shows, the parameters can crop up in the probability distributions of some measurement brought about only by those systems. However, by (ii), and do not reside in , for is independent of them. Therefore, and are located in and , notwithstanding their associated density matrix proportional to the identity. Being locally inaccessible, the information about and that is carried in and remains unaffected by measurements, and thus it remains unaffected by decoherence. This observation has prompted Deutsch and Hayden to realize the tradeoff between local accessibility and robustness to decoherence in information transfer.
4.2. On the Classicality of the Bits
The discoverers of teleportation pointed out in the first sentence of their abstract that the process relies on “purely classical information”. However, as a potential critique might have it, the use of the quantum bits and as a communication channel contradicts the requirement that classical bits are to be utilized. Not only does this, prima facie, undermine the very purpose of teleportation by seemingly having a quantum channel already in place, but it appears to be a flagrant category mistake: classical and quantum bits are of a fundamentally different kind, one might argue.
The claim of “purely classical information” is the crucial element in the conjuring trick’s setup. Let us not be fooled by it, for there is no such thing, fundamentally, as purely classical information: either quantum theory holds universally, or it does not, but in the latter case, an explanatory theory about a boundary of its domain of validity is required. Everett’s proposal [14] was that although measurement interactions seem to impose a boundary on the domain of unitary quantum theory, they do not. The key to unraveling teleportation is to accept that, by the same token, classical information also does not push against the domain of unitary quantum theory; rather, it is absorbed by it. For a unified theory, the primary concern is to explain “purely classical information” in terms of quantum systems [15,16] and not vice versa. Whatever it is that we view as purely classical information is instantiated in physical systems, which, after all, satisfy quantum theory.
Yet, it can be argued that, indeed, the two bits are classical, according to explanations of what “classical” can mean within quantum theory. First, as illustrated in Figure 4, a nearby environment can be modeled to decohere the two qubits on the basis that has been selected by the measurement interaction. The environment contains at least the logical space of two qubits, whose descriptors and are given by some generic representation of the Pauli algebra, i.e., they need not be initialized as in Equation (2). When the environment is affected by the records and , the records are also affected: the x-components of the environment reach the x-components of the records. However, these operators do not make it any further towards because the interactions that follow involve the records as control qubits, and so only pass on their z-components. Therefore, a decohering environment does not prevent teleportation; the transfer is robust to decoherence, a distinguishing property of classical communication.
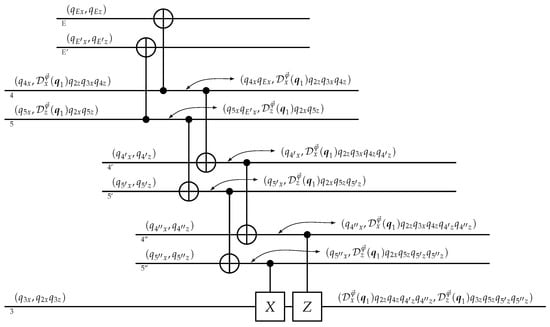
Figure 4.
A telephone.
Second, I suggested that the classical communication channel could be thought to be a telephone, but in the protocol displayed in Figure 3, the records and are physically brought to Bob’s location. In usual classical communication channels, precise (quantum) systems are seldom sent from one location to another; rather, the information is transmitted through a chain reaction that occurs in a collection of quantum systems. Therefore, a telephone, or more generally, the relevant degrees of freedom in classical communication, can be modeled by a chain reaction that involves the prepared systems , , , , and generically many others. See Figure 4 for the calculation, which yields a final descriptor with dependencies on . If the telephone line is properly initialized with descriptors of the form (2), the operators appended to the final descriptor do not affect the expectation values in (9) because they have eigenvalue 1 with respect to ; the Schrödinger state corresponding to after the process remains . Thus, not only is the information transfer robust to decoherence, but it is realizable in a chain reaction that resembles classical communication.
Note, moreover, that decoherence can occur everywhere in the telephone line without inhibiting the transfer of and on Bob’s final descriptor. As a final remark: where is Bob? Is he not supposed to receive the communication and act on in accordance with the received bits? Yes, but this is taken into account in the generically many other systems involved in the communication line. No special assumptions are required to include Bob in Figure 4, only his ability to manipulate systems mechanically and decoherently, like any other parts of the communication line.
4.3. Explaining the Information Transfer
So, how do and make their way from Alice’s location to Bob’s? The Copenhagen tradition would have it due to the collapse of the state vector, which has prompted many to view the transfer as instantaneous, through action at a distance. Jozsa suggested that “nonlocal influences” allow them to “fly across the entanglement” [17]. For Penrose, the entangled pair has a channel that “proceeds into the past” [18] and into the future again. In the Bohmian theory, the “transfer is mediated by the nonlocal quantum potential” [19]. Vaidman suggests that “the nonlocality of Everett’s world is the basis of the teleportation of quantum information” [20]. (As Popescu mentioned [21], these worlds should be called “Lev’s worlds”, for they extend arbitrarily far in space and are constructed from so-called “macroscopic objects” in a “definite classically described state” [22], but no signs of such concepts at the fundamental level can be found in Everett’s writings.) Most proponents of unitary quantum theory in the Schrödinger picture do not resign to such extravagant conjectures, for they do not attempt to amend quantum theory. Braunstein argued that “the quantum information is ‘hidden’ within the correlations between the system and the environment while being wholly absent from any of the individual subsystems” [23], and Timpson wrote that “global rather than local properties are being used to carry information” [24]. These proposals are confined by the unfulfillment of Einstein’s criterion of locality by the global state vector, which prevents the localization of the parameters in the Schrödinger picture. However, they can be localized in the Heisenberg picture. According to Deutsch and Hayden, the information about and is transported “simply, prosaically, in the qubits and as they traveled from A to B”.
5. Counterfactual Elements of Reality
Despite being expressed in terms of two complex numbers, the state prepared at Alice’s location, , contains only two free (real) parameters due to the constraints imposed by normalization and the irrelevance of the phase factor. The latter can be considered by demanding that , which also fixes through normalization, so viewed in this way, the second free parameter is the phase of , . Alice’s preparation U, however, is a generic one-qubit gate, which, as parameterized by in Equation (7), contains three free parameters. (In fact, a generic element of contains four free parameters. However, since , , which almost amounts to quotiating the global phase of the unitary operator. “Almost”, because there remains a ambiguity due to a possible factor , which leaves the determinant equal to 1 while being a non-trivial global phase. However, the possibility for this factor can be avoided by suitable constraints on the domain of .) Since U can be expressed as
where and are the amplitudes of the prepared state, and the extra parameter , of the unit norm, labels a one-parameter family of states that are legitimate images of under U: each of the are orthogonal to . Therefore, the descriptor’s components and that depend on can alternatively be thought to depend on , and . Since the descriptor of at time 9 also carries the dependency on , a question arises: has η also reached to Bob’s location?
The Instrumentalist Temptation
Deutsch and Hayden’s criteria remain silent on the question of the localization of . Indeed, even if all systems are collected at some time after the preparation, there exists no measurement on the network as a whole whose distribution of outcomes would depend on . Therefore, fails to fulfill criterion (i), even if is taken to be the network as a whole. A tempting view is to dismiss the existence of all that is oblivious from experiments, which embodies the instrumentalist attitude, namely, the consideration of scientific theories as mere tools for predictions. In spite of Deutsch and Hayden’s warning “(though not necessarily only if)”, which insists that criterion (i) is only sufficient, instrumentalism would also demand it be necessary in a strong sense; namely, it might demand that if the distribution of some measurement outcomes on alone is independent of , then is not a descriptive element of . Not only would be deemed to be absent from the system, but and , too, could not be thought to be localized in and as they are transferred. The Heisenberg-picture description would vanish, for what remains after the instrumentalist’s mutilation would be informationally equivalent to the global state, and Raymond-Robichaud ([7], Section 4) showed that any attempt to build a local and complete description of quantum systems from the state vector alone must fail. (In Timpson’s terminology [25], the instrumentalist’s mutilation amounts to shifting from the ontological to the conservative interpretation of Heisenberg-picture descriptors. In Raymond-Robichaud’s [7], from noumenal to phenomenal states.)
In his thesis, Everett criticizes instrumentalism [14]:
It is necessary to say a few words about a view which is sometimes expressed, the idea that a physical theory should contain no elements which do not directly correspond to observables. This position seems to be founded on the notion that the only purpose of a theory is to serve as a summary of known data, and overlooks the second major purpose, the discovery of totally new phenomena. The major motivation for this viewpoint appears to be the desire to construct perfectly “safe” theories which will never be open to contradiction. Strict adherence to such a philosophy would probably seriously stifle the progress of physics.
To embrace the full power of Heisenberg-picture descriptors is not merely to view them as another way to think of quantum theory, which may be convenient in some cases—for instance, to make sense of teleportation. Nor is it a tool whose sole purpose is to make predictions. It is to consider them as an account of reality. The reality captured by the descriptors is larger than that captured by the universal state vector [9,26,27]. In particular, it has room for . The descriptive elements which, like , lie in Heisenberg-picture descriptions but not in the Schrödinger state are globally inaccessible (not just locally). They reside in the multiverse, yet, in some unobservable sector, for only the sector which is singled out by the Heisenberg state is amenable to observations. The unobservable sector encompasses and, more generally, all that resides in the global unitary operator that embodies the dynamics and yet is beyond the “column” selected by the Heisenberg state. All of it is counterfactual descriptive elements of reality; it accounts for what would be accessible had some prior operation been performed. In the teleportation setting, would have cropped up in the distributions had been rotated anyhow except around the Z-axis before being prepared with U.
6. Conclusions
The solution by Deutsch and Hayden to the problem of teleportation provides a probe into the classical realm, which signals that it is much deeper than expected. In fact, it is even deeper than expected from the Schrödinger picture of unitary quantum theory. Anyone who takes for granted that communication between Alice and Bob involves “purely classical information” is fooled by teleportation. The classical realm is quantum; a classical communication channel is one that is robust to decoherence and realizable in a chain reaction in quantum systems.
Explaining classical communication from some interaction within quantum systems might seem radical at first glance. However, the opposite is true. If one posits that quantum theory does not universally hold, then one must explain where its boundary resides and why. The proposal here simply follows Everett’s program to take the quantum theory seriously and, in the absence of the need to introduce a boundary to its domain of applicability, consider it universal.
Unitarity does not fully clarify the explanation of teleportation in the Schrödinger picture. The explanation presented here is only possible in the Heisenberg picture of unitary quantum theory. Those accustomed to unitary quantum theory (i.e., Everettian quantum theory) shall see arguments for adopting and further developing the Heisenberg picture. However, those who are still agnostic about how to “interpret” quantum theory—namely, still deciding whether unitary quantum theory needs to be truncated, merged with another theory, or completed in some way—will see in the proposed explanation of teleportation arguments for both the Heisenberg picture and for unitary quantum theory, as their conjunction solves the problem of the locality of information transfer in teleportation. Progress can be assessed by the problems that are solved. When I explained the teleportation protocol in the Heisenberg picture to Gilles Brassard, one of the discoverers of the phenomenon, he right away told me that it was the most satisfactory elucidation of teleportation that he had ever heard. I hope that this piece can have a similar effect on you.
Teleportation is not the only phenomenon whose apparent non-locality has been puzzling. Heisenberg-picture descriptors also make locality manifest in superdense coding [13] and in the Aharanov–Bohm effect [28].
I shall conclude with a brief reflection on Lev’s problem, why is Everettian quantum theory not in the consensus? Deutsch wrote [29]
Some people may enjoy conjuring tricks without ever wanting to know how they work. Similarly, during the twentieth century, most philosophers, and many scientists, took the view that science is incapable of discovering anything about reality. Starting from empiricism, they drew the inevitable conclusion (which would nevertheless have horrified the early empiricists) that science cannot validly do more than predict the outcomes of observations, and that it should never purport to describe the reality that brings those outcomes about. This is known as instrumentalism.
The prevalence of instrumentalism might be a part of the explanation as to why Everettian quantum theory is not in the consensus. The denial of taking a theory seriously as a tentative account of reality also denies a proper investigation of its consequences. Moreover, satisfaction with mere predictions entails satisfaction with conjuring tricks: why should we strive for an explanation of teleportation when we already have a theory that predicts Bob’s observations after the protocol?
7. Discussion
- Lev Vaidman:
- If I understand correctly, the story, your story, is about the universe. When we talk about teleportation, we talk about our world. And in the many world’s interpretation, there is a part that concerns the whole universe. It is the part of the MWI where there is no collapse. There is no collapse here, no question. But there are no many worlds. Many worlds is when I perform my measurement, I split the world. In teleportation, in every world, and jump on Bob’s qubit, and they jump at the moment of the measurement. So there is no other explanation within the world.
- CAB:
- In the teleportation protocol, the records of the measurement eventually affect—and get entangled with—many other record-like systems, as well as many systems in the environment. In the Schrodinger picture, this leads to a wave function with four highly entangled terms, which, for all practical purposes, can no longer interact with one another via quantum interference: each term becomes autonomous. What is more, in each term, there are relative properties between systems, which give a consistent account of what resembles a quasi-classical single “world”. This is the quantum theory of Everett, the unitarily evolving universal wave function, with important analyses further developed by Zeh, Zurek, Gell-Mann, Hartle, Saunders, Wallace and others.
Is it also yours? It appears to me that you grant fundamental importance to notions such as “macroscopic objects” in a “definite classically described state” from which you define your “worlds” (as the totality of all such objects) [22]. The importance that you grant those words is also manifest in your attempt at explaining teleportation within those worlds as if the universal wave function was not a fundamental description but just a convenient way to stack all those worlds together. Moreover, defining worlds via intuitive appeals to classicality and macroscopicity leads you close to a collapse theory; and in both cases, one is forced to suggest that in teleportation, and jump to Bob’s qubit.
To come back to descriptors, they also admit a decomposition into a sum of relative descriptors, which, like in the Schrödinger picture, account for relative properties between systems. Yet, descriptors are foliated locally. See [30].
- Andrew Jordan:
- Let me make a critical comment. You made the claim that the bits that are transmitted between Alice and Bob by the telephone are really secretly quantum bits, and I must object to that because I think that if you claim that, then the logical consequence is that there is no such thing as classical information theory. I think you have to give up on classical information theory as a thing that exists. You say that, really, everything is quantum information theory. But there are classical bits. And we are communicating with a classical channel, and so there are classical channels. So how do you respond to that criticism?
- CAB:
- Classical information theory can still exist; however, not fundamentally. In fact, we know well how it is instantiated as a subcase of quantum information theory: a decohered state has a diagonal reduced density matrix whose numbers form a distribution, so we speak of its Shannon information. However, this misses my point. I took it as a premise that the world is quantum. A telephone is made of quantum systems. And yes, it looks like it is classical to me, but that is the program launched by Everett, namely, to understand how the quantum theory can explain the emergence of the classical.
- Simon Saunders:
- Rather similar question: I do not quite get it. The classical channel is really just telling Bob what the outcome of Alice’s Bell measurement is. There is very little information there, whereas and encode potentially vast amounts of information. So I just don’t quite get that. Can you elaborate?
- CAB:
- The channel is indeed telling Bob what the outcome of Alice’s Bell measurement is. But it is not just doing that. Wouldn’t you grant that any sort of classical channel that we can imagine is ultimately made of quantum systems? This is not an irrelevant fact when we are trying to solve the capacity problem of teleportation. The quantum systems involved in the communication line transfer and in a way that is locally inaccessible, resilient to decoherence and realizable in a chain reaction.
- Eric Curiel:
- I have a quite general question about the approach. How should I understand entanglement entropy in this picture? It plays a very fundamental role from condensed matter physics to black hole thermodynamics. How should I understand what seems to be the manifest non-locality of quantum mechanics that makes the efficacy of Von Neumann entanglement entropy possible?
- CAB:
- Since density matrices can be recovered from descriptors and the constant Heisenberg state, so can Von Neumann entropy. But one way to understand entanglement between systems that is more in line with the Heisenberg picture is that no observable of a subsystem has a definite outcome, while some observables on the joint system do. For instance, the preparation of on and yields the following descriptors (see Figure 3):
- Tim Maudlin:
- I have two comments of a different character. One is just coming back to this telephone. There is only one information theory; it is Shannon information. You can apply it to bits, which by definition have only two possible states, you can apply it to spin particles that have infinitely many possible states, given by your and . It doesn’t change information theory at all. In this protocol, all that is required to implement the protocol are two bits. That is all that is required. You may say, “Oh, but I have to send a quantum system physically because physics is quantum mechanics.” It doesn’t matter if Alice sends a note classically; of course, it has more than two states, right? She can write in cursive, or she can write this way, so what? The point is that the protocol merely demands that you resolve between four possibilities. That requires two bits of information. Period end of the story.
The other comment is: the reason they gave that Nobel prize was for tests of violation of Bell’s inequality at spacelike separation. That’s the reason they say it shows non-locality. Quantum teleportation is puzzling, but one thing it sure doesn’t do is violate Bell’s inequality at spacelike separation. So to say, even if it were true, “I have a local understanding of teleportation” would not at all have any influence on the reason they say those experiments are so important.
- CAB:
- The two comments are not of a different character: they answer one another. The primality of Shannon’s information in one’s mind makes one uncritical not only of its use in teleportation but also of the way in which the assumptions are coined in Bell’s theorem, namely, in terms of classical probability distributions. For whom the very use of classical probability distributions is not considered to be an assumption made by Bell, then indeed, the violation of Bell’s inequality at spacelike separation challenges locality. Otherwise, the violation simply dismisses the hypothesis that quantum theory can be underlain by classical probability distributions.
- David Wallace:
- I want to go back to the Deutsch–Hayden claim that once I have a local formulation of the theory, then the theory is local. The worry is that there are relatively clear cheap ways of making a theory local. I’m not claiming this is a cheap way. But there are cheap ways. For instance, I can just attach a copy of the state of the universe to every local system, I can say whatever my wildly nonlocal description is, in my new theory, the state of the system is the ordered pair of the state of the old theory and the state of the universe. It is horrendously expensive; call that a monadology move, for Leibniz’s fans. That framework is formally going to be local, but clearly, it is not telling us that the theory is interestingly local. I don’t think that the framework of descriptors has this character, although there are bits of it that sometimes worry me. But I just want to flag that a bit more needs to be done to clarify that a theory is local just because it has a local formalism. I think we have to avoid making moves of that kind.
- CAB:
- What you suggest does not fulfill Einstein’s criterion because if a state of the whole universe is included in the description of each localized system, then if Bob performs an operation on his system, it affects Alice’s description.
Funding
This work was supported by the Fonds de recherche du Québec—Nature et technologie and the Swiss National Science Foundation.
Acknowledgments
I am deeply grateful to Gilles Brassard, Xavier Coiteux-Roy, David Deutsch, Samuel Kuypers, Jordan Payette, William Schober, Stefan Wolf and an anonymous referee for stimulating discussions or comments on earlier versions of this article.
Conflicts of Interest
The author declares no conflict of interest.
Correction Statement
This article has been republished with a minor correction to the existing affiliation information. This change does not affect the scientific content of the article.
References
- Garisto, D. The universe is not locally real, and the physics Nobel Prize winners proved it. Scientific American, 6 October 2022. [Google Scholar]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Schilpp, P.A. Albert Einstein: Philosopher-Scientist, 3rd ed.; Open Court Publishing Co., Ltd.: Chicago, IL, USA, 1970; Volume 7. [Google Scholar]
- Deutsch, D.; Hayden, P. Information flow in entangled quantum systems. Proc. R. Soc. A Math. Phys. Eng. Sci. 2000, 456, 1759–1774. [Google Scholar] [CrossRef]
- Healey, R.A. Holism and nonseparability. J. Philos. 1991, 88, 393–421. [Google Scholar] [CrossRef]
- Wallace, D.; Timpson, C.G. Quantum mechanics on spacetime i: Spacetime state realism. Br. J. Philos. Sci. 2010, 61, 697–727. [Google Scholar] [CrossRef]
- Raymond-Robichaud, P. A local-realistic model for quantum theory. Proc. R. Soc. A 2021, 477, 20200897. [Google Scholar] [CrossRef]
- Raymond-Robichaud, P. The equivalence of local-realistic and no-signalling theories. arXiv 2017, arXiv:1710.01380. [Google Scholar]
- Bédard, C.A. The cost of quantum locality. Proc. R. Soc. A 2021, 477, 20200602. [Google Scholar] [CrossRef]
- Gottesman, D. The Heisenberg representation of quantum computers. arXiv 1998, arXiv:quant-ph/9807006. [Google Scholar]
- Heisenberg, W. Quantum-theoretical re-interpretation of kinematic and mechanical relations. Z. Phys. 1925, 33, 879–893. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef] [PubMed]
- Bédard, C.A. The ABC of Deutsch–Hayden descriptors. Quantum Rep. 2021, 3, 272–285. [Google Scholar] [CrossRef]
- DeWitt, B.S.; Graham, N. The Many Worlds Interpretation of Quantum Mechanics; Princeton University Press: Princeton, NJ, USA, 1973. [Google Scholar]
- Zurek, W.H. Quantum theory of the classical: Einselection, envariance, quantum Darwinism and extantons. Entropy 2022, 24, 1520. [Google Scholar] [CrossRef] [PubMed]
- Wallace, D. The Emergent Multiverse: Quantum Theory According to the Everett Interpretation; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Jozsa, R. The Geometric Universe; Huggett, S., Mason, L., Tod, K.P., Tsou, S.T., Woodhouse, N., Eds.; Oxford University Press: Oxford, UK, 1998; pp. 369–379. [Google Scholar]
- Penrose, R. Quantum computation, entanglement and state reduction. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 356, 1927–1939. [Google Scholar] [CrossRef]
- Maroney, O.; Hiley, B.J. Quantum state teleportation understood through the bohm interpretation. Found. Phys. 1999, 29, 1403–1415. [Google Scholar] [CrossRef]
- Vaidman, L. Transfer of Quantum Information in Teleportation. 2022. Available online: http://philsci-archive.pitt.edu/id/eprint/21447 (accessed on 26 May 2023).
- The Many-Worlds Interpretation of Quantum Mechanics Day 6, October 2022. Available online: https://www.mwi2022tau.com/ (accessed on 26 May 2023).
- Vaidman, L. Many-Worlds Interpretation of Quantum Mechanics. The Stanford Encyclopedia of Philosophy (Fall 2021 Edition). Available online: https://plato.stanford.edu/archives/fall2021/entries/qm-manyworlds/ (accessed on 26 May 2023).
- Braunstein, S.L. Quantum teleportation without irreversible detection. Phys. Rev. A 1996, 53, 1900. [Google Scholar] [CrossRef]
- Timpson, C.G. The grammar of teleportation. Br. J. Philos. Sci. 2006, 57, 587–621. [Google Scholar] [CrossRef]
- Timpson, C.G. Nonlocality and information flow: The approach of Deutsch and Hayden. Found. Phys. 2005, 35, 313–343. [Google Scholar] [CrossRef]
- Wallace, D.; Timpson, C.G. Non-locality and gauge freedom in Deutsch and Hayden’s formulation of quantum mechanics. Found. Phys. 2007, 37, 1069–1073. [Google Scholar] [CrossRef]
- Deutsch, D. Vindication of quantum locality. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 468, 531–544. [Google Scholar] [CrossRef]
- Marletto, C.; Vedral, V. Aharonov-Bohm phase is locally generated like all other quantum phases. Phys. Rev. Lett. 2020, 125, 040401. [Google Scholar] [CrossRef] [PubMed]
- Deutsch, D. The Beginning of Infinity: Explanations that Transform the World; Penguin: London, UK, 2011. [Google Scholar]
- Kuypers, S.; Deutsch, D. Everettian relative states in the Heisenberg picture. Proc. R. Soc. A 2021, 477, 20200783. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).