Hydrogen-like Plasmas under Endohedral Cavity
Abstract
1. Introduction
2. Theoretical Formalism
2.1. Oscillator Strength and Polarizability
2.2. Shannon Entropy
3. Result and Discussion
3.1. Critical Screening Constant in DHPWS and ECSCPWS
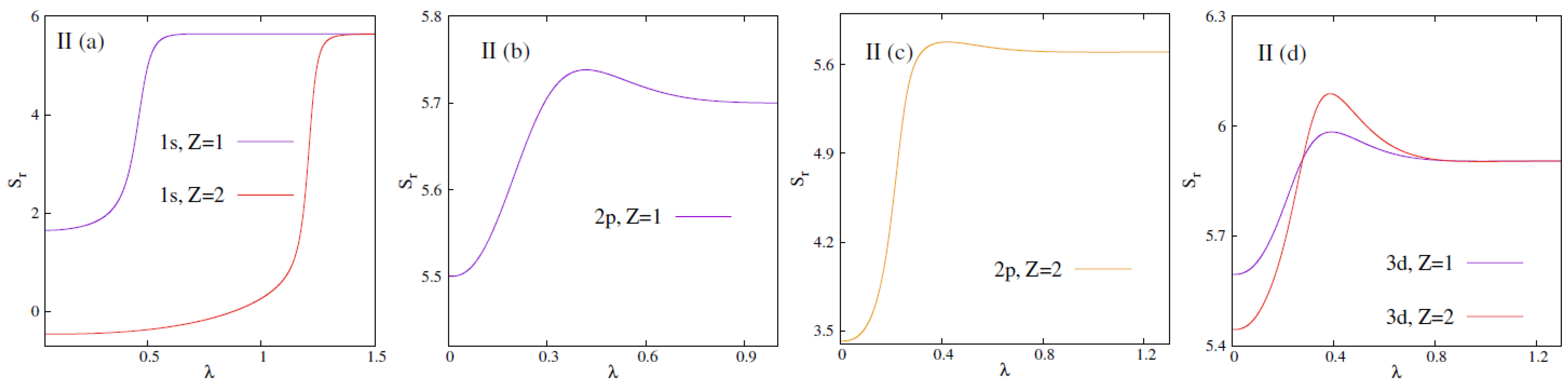
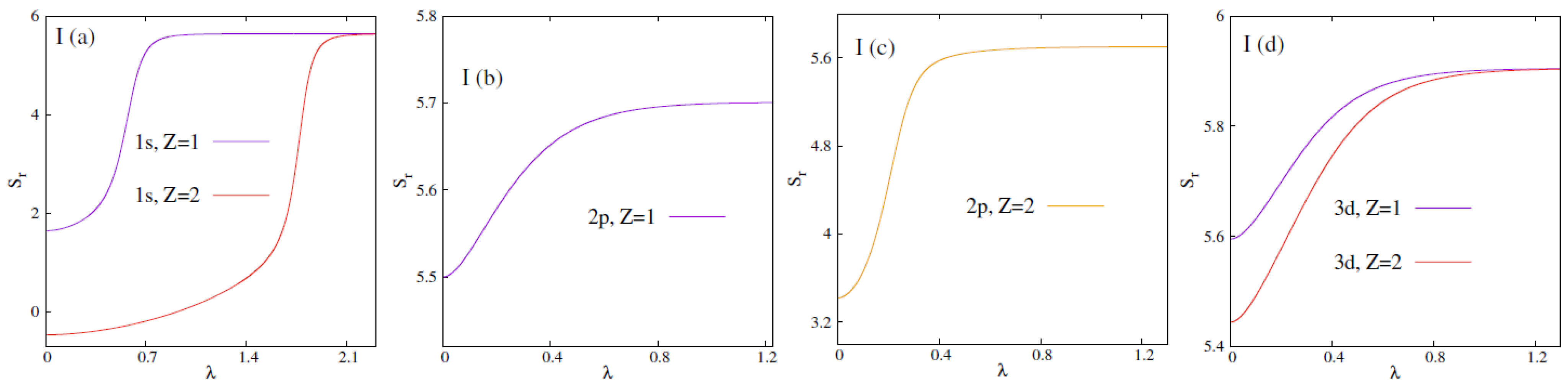
- At the onset, it should be mentioned that the qualitative behaviour of with in DHPWS and ECSCPWS are quite similar.
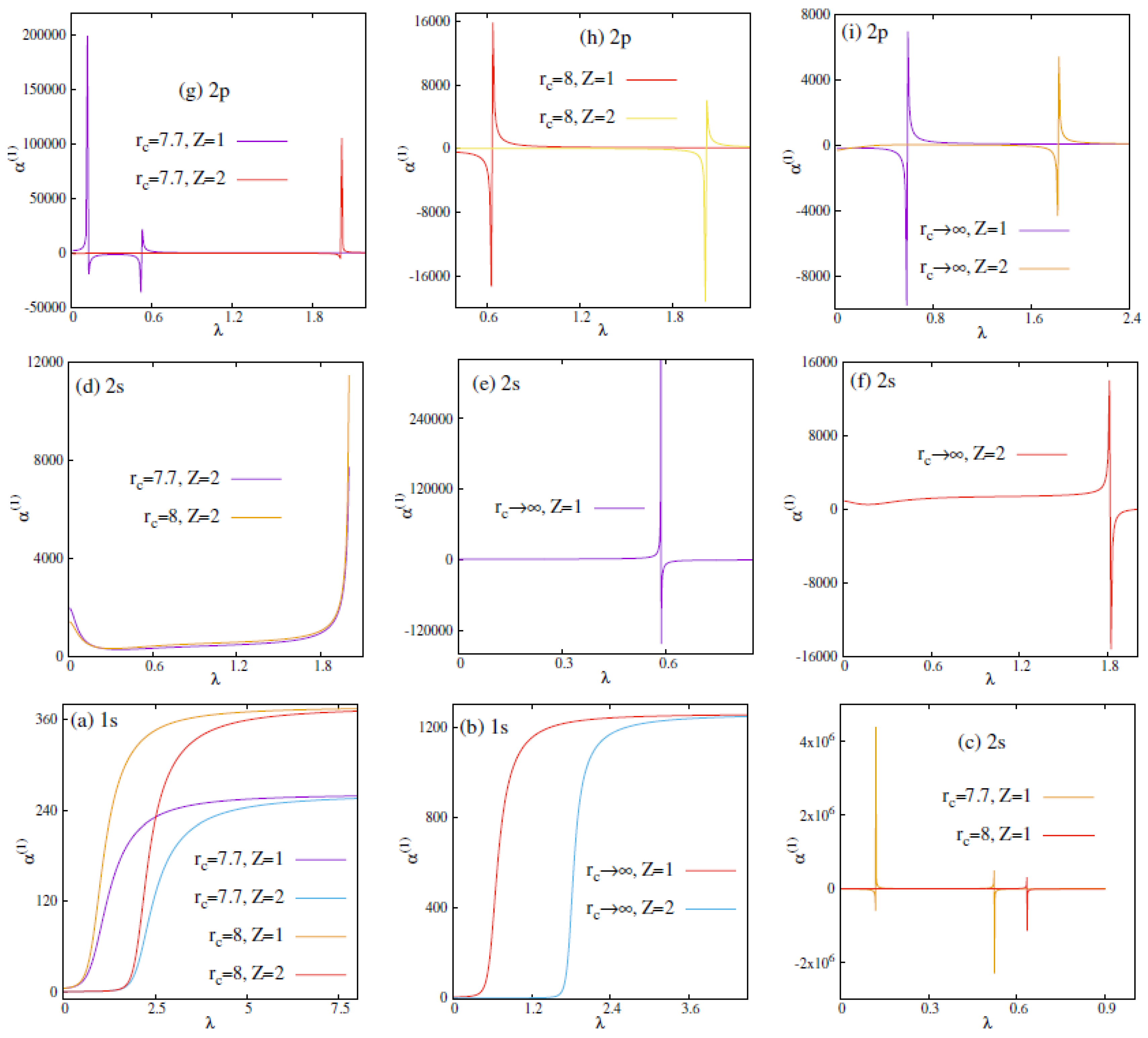
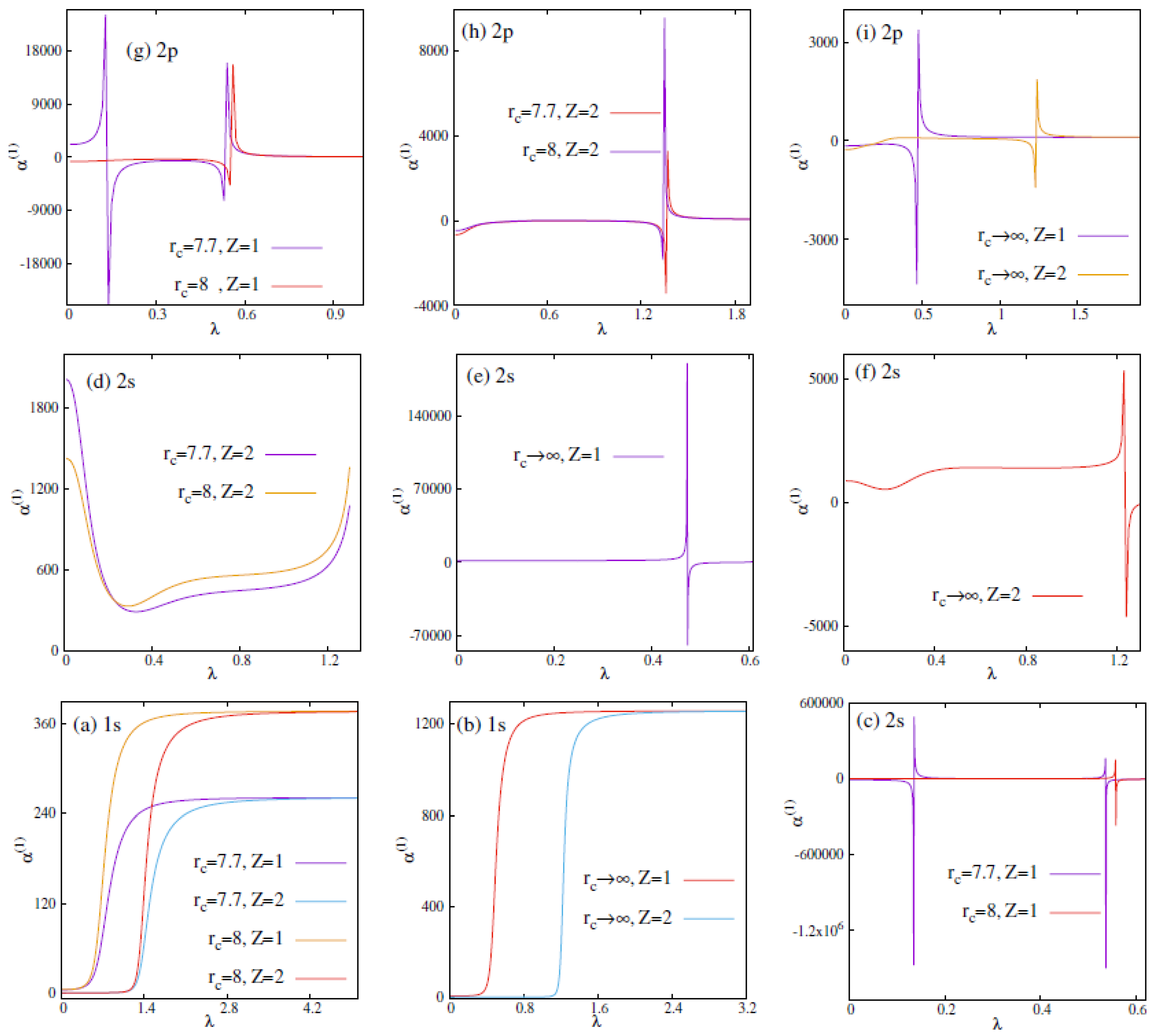
- Panels (I), (II) in Figure 1 show that there exists at least three bound states in either of the fullerene trapped plasmas. Because, in both cases, circular or node-less states with 0–2 are never going to be deleted. As a consequence, no abrupt jump in is observed. In these states increases with and finally converges to the respective limiting values.
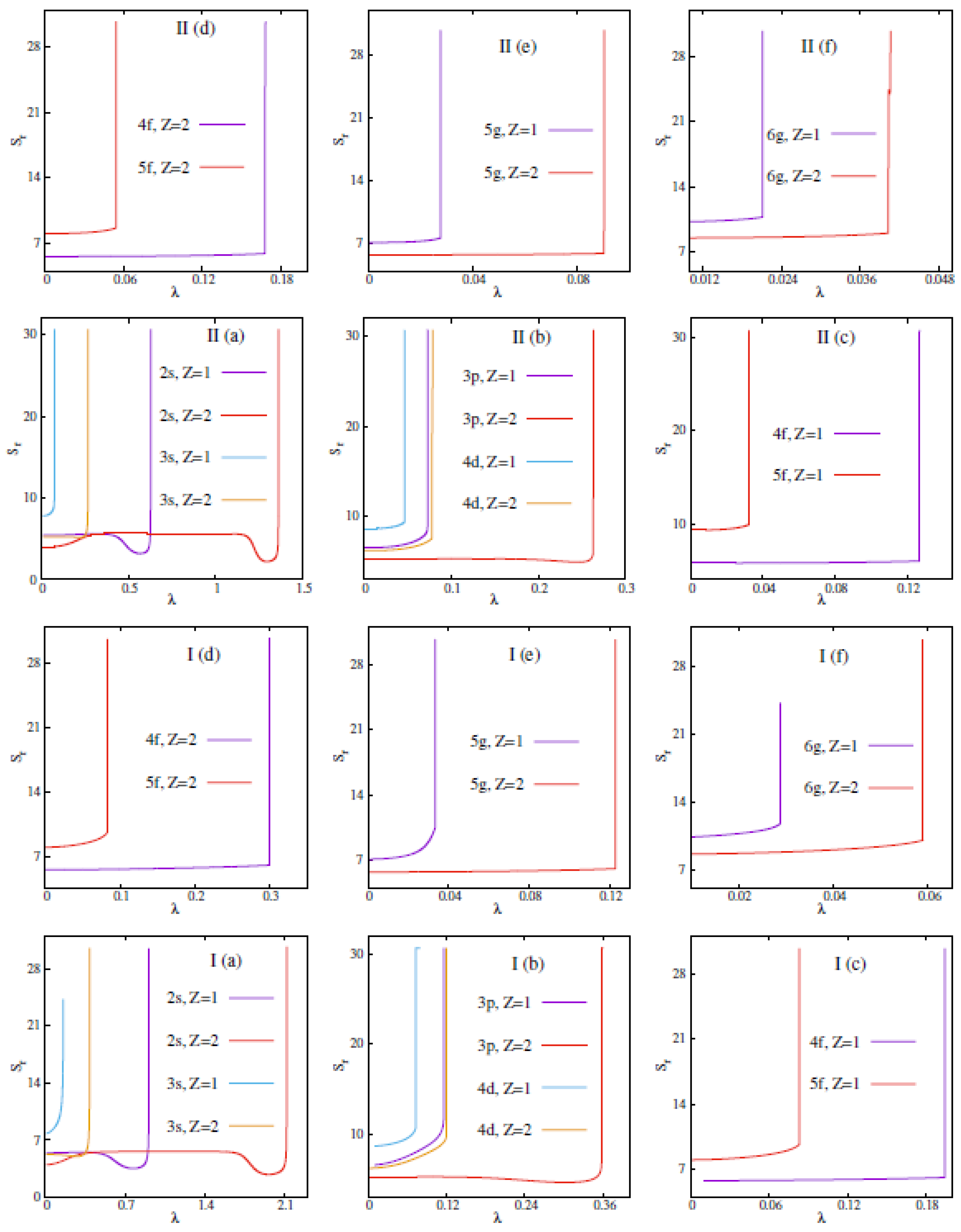
- Panels (I), (II) of Figure 2 suggest that, for a given state, there exists a characteristic at which the value jumps suddenly, signifying the phase transition. The position of these gets right shifted with a rise in Z. Here, a first order phase transition happens in both the plasmas involving states.
- These observations lead us to the conjecture that, in these two fullerene trapped plasmas, phase transition occurs for all states. However, for 0–2 states, a similar phenomenon occurs only when .
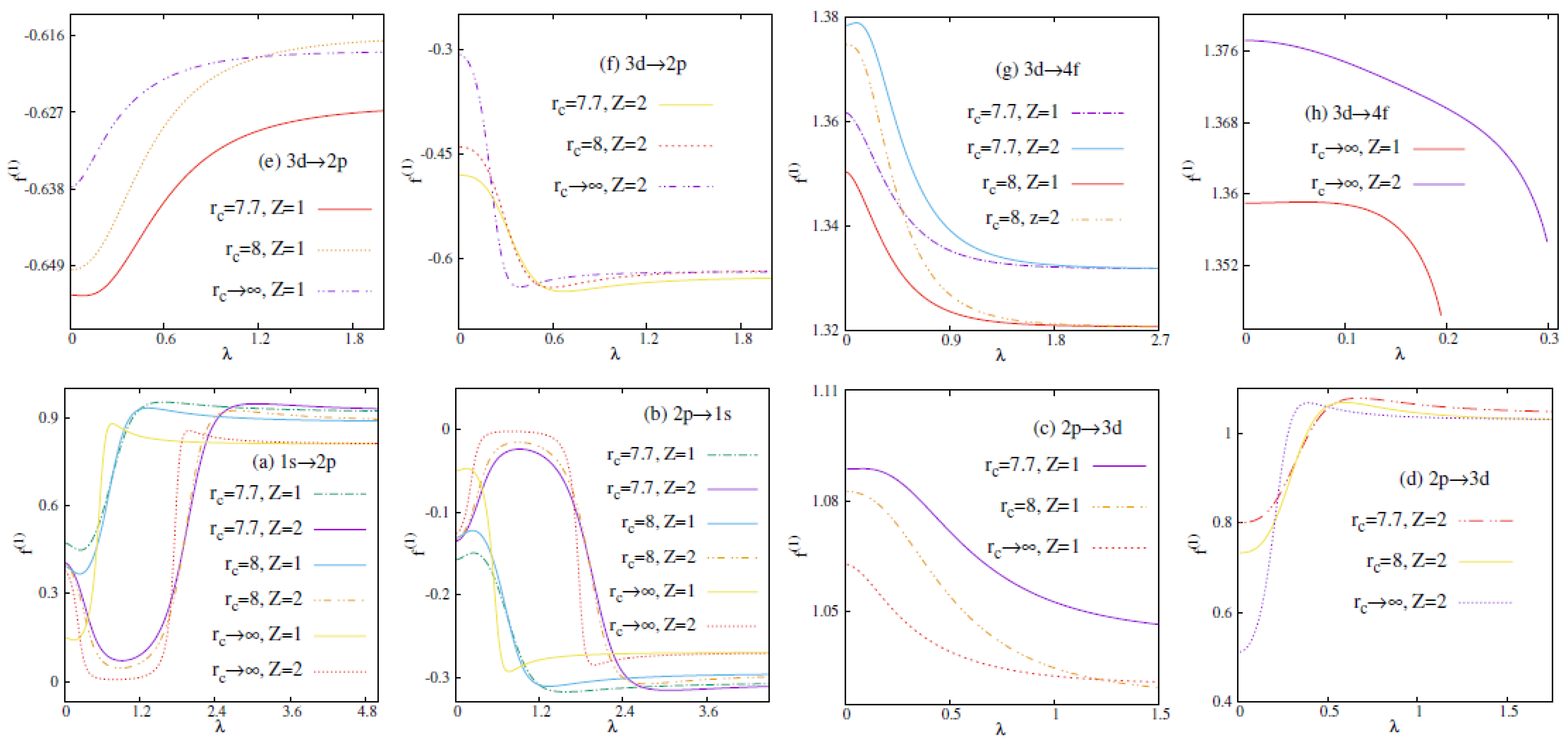
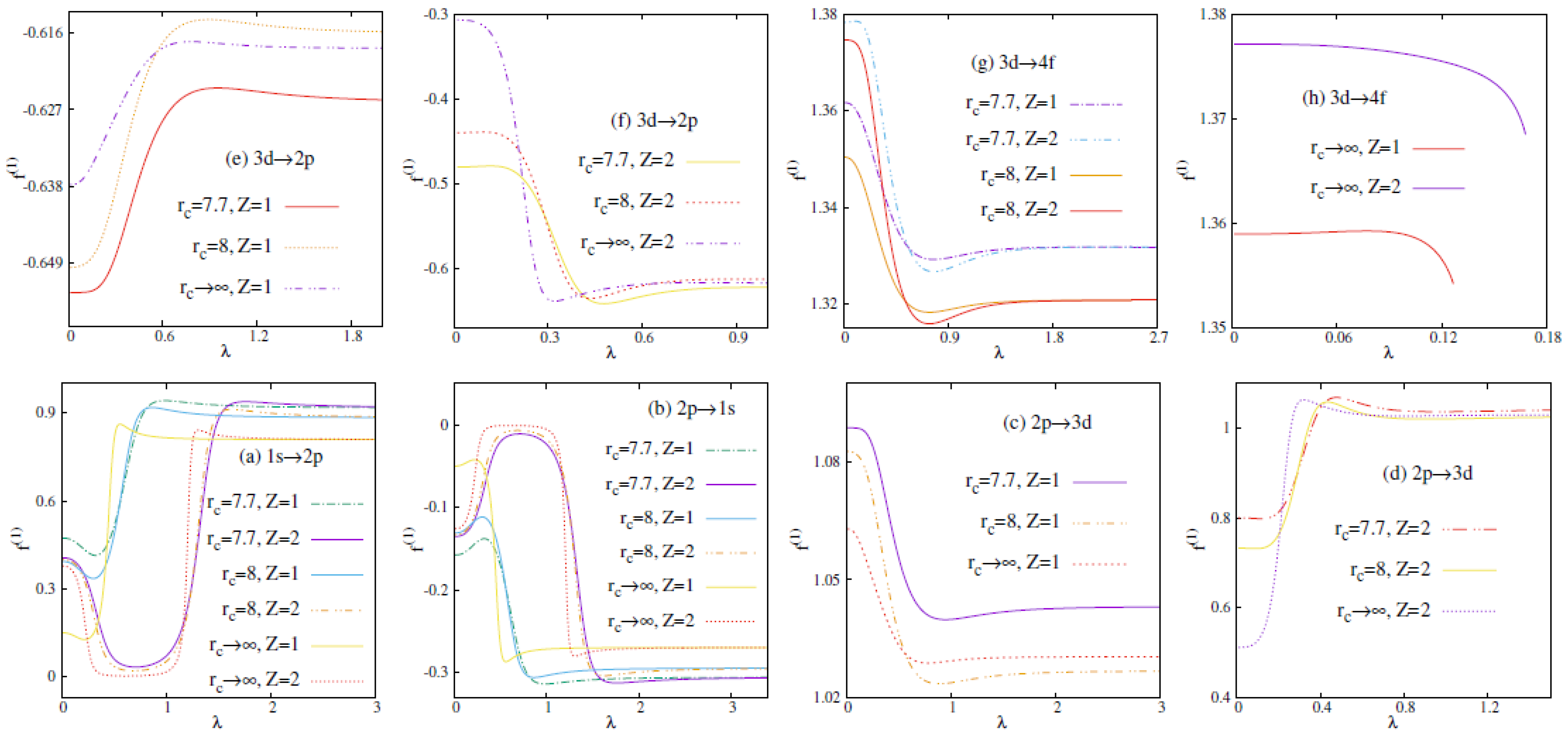
3.2. Dipole Oscillator Strength
3.3. Polarizability
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Suryanarayana, D.; Weil, J.A. On the hyperfine splitting of the hydrogen atom in a spherical box. J. Chem. Phys. 1976, 64, 510. [Google Scholar] [CrossRef]
- Ley-Koo, E.; Rubinstein, S. The hydrogen atom inside boxes with paraboloidal surfaces. J. Chem. Phys. 1980, 73, 887. [Google Scholar] [CrossRef]
- Kilcoyne, A.L.D.; Aguilar, A.; Müller, A.; Schippers, S.; Cisneros, C.; Alna’Washi, G.; Aryal, N.B.; Baral, K.K.; Esteves, D.A.; Thomas, C.M.; et al. Confinement resonances in photoionization of Xe@C60+. Phys. Rev. Lett. 2010, 105, 213001. [Google Scholar] [CrossRef][Green Version]
- Ndengué, S.A.; Motapon, O. Electric response of endohedrally confined hydrogen atoms. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 045001. [Google Scholar] [CrossRef]
- Motapon, O.; Ndengué, S.A.; Sen, K.D. Static and dynamic dipole polarizabilities and electron density at origin: Ground and excited states of hydrogen atom confined in multiwalled fullerenes. Int. J. Quantum Chem. 2011, 111, 4425. [Google Scholar] [CrossRef]
- Benjamin, S.C.; Ardavan, A.; Briggs, G.A.D.; Britz, D.A.; Gunlycke, D.; Jefferson, J.; Jones, M.A.G.; Leigh, D.F.; Lovett, B.W.; Khlobystov, A.N.; et al. Towards a fullerene-based quantum computer. J. Phys. Condens. Matt. 2006, 18, S867. [Google Scholar] [CrossRef][Green Version]
- Liu, Z.; Dong, B.W.; Meng, H.B.; Xu, M.X.; Wang, T.S.; Wang, B.W.; Wang, C.R.; Jiang, S.D.; Gao, S. Qubit crossover in the Endohedral fullerene Sc3C2@C80. Chem. Sci. 2018, 9, 457. [Google Scholar] [CrossRef][Green Version]
- Yang, W.L.; Xu, Z.Y.; Wei, H.; Feng, M.; Suter, D. Quantum-information-processing architecture with endohedral fullerenes in a carbon nanotube. Phys. Rev. A 2010, 81, 032303. [Google Scholar] [CrossRef][Green Version]
- Harneit, W. Fullerene-based electron-spin quantum computer. Phys. Rev. A 2002, 65, 032322. [Google Scholar] [CrossRef]
- Ross, R.B.; Cardona, C.M.; Guldi, D.M.; Sankaranarayanan, S.G.; Reese, M.O.; Kopidakis, N.; Peet, J.; Walker, B.; Bazan, G.C.; Van Keuren, E.; et al. Endohedral fullerenes for organic photovoltaic devices. Nat. Mater. 2009, 8, 208. [Google Scholar] [CrossRef]
- Ornes, S. Core Concept: Quantum dots. Proc. Natl. Acad. Sci. USA 2016, 113, 2796. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nishikawa, K.; Wakatani, M. Plasma Physics: Basic Theory with Fusion Applications. In Plasma Physics: Basic Theory with Fusion Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Pupysheva, O.V.; Farajian, A.A.; Yakobson, B.I. Fullerene nanocage capacity for hydrogen storage. Nano Lett. 2008, 8, 767. [Google Scholar] [CrossRef] [PubMed]
- Shinohara, H. Endohedral metallofullerenes. Rep. Prog. Phys. 2000, 63, 843. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Baltenkov, A.S.; Becker, U. Strong oscillations in the photoionization of 5s electrons in Xe@C60 endohedral atoms. Phys. Rev. A 2000, 62, 012701. [Google Scholar] [CrossRef][Green Version]
- Patil, S.H.; Sen, K.D.; Varshni, Y.P. Alkali atoms confined to a sphere and to a fullerene cage. Can. J. Phys. 2005, 83, 919. [Google Scholar] [CrossRef]
- Kurotobi, K.; Murata, Y. A single molecule of water encapsulated in fullerene C60. Science 2011, 333, 613. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Chernysheva, L.V.; Dolmatov, V.K. Confinement and correlation effects in the Xe@C60 generalized oscillator strengths. Phys. Rev. A 2011, 84, 063201. [Google Scholar] [CrossRef][Green Version]
- Connerade, J.P.; Dolmatov, V.K.; Manson, S.T. A unique situation for an endohedral metallofullerene. J. Phys. B At. Mol. Opt. Phys. 1999, 32, L395. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Amusia, M.Y.; Chernysheva, L.V. Electron elastic scattering off A@C60: The role of atomic polarization under confinement. Phys. Rev. A 2015, 92, 042709. [Google Scholar] [CrossRef][Green Version]
- Dolmatov, V.K.; Manson, S.T. Photoionization of atoms encapsulated in endohedral ions A@C60±z. Phys. Rev. A 2006, 73, 013201. [Google Scholar] [CrossRef]
- Moretto-Capelle, P.; Bordenave-Montesquieu, D.; Rentenier, A.; Bordenave-Montesquieu, A. Interaction of protons with the C60 molecule: Calculation of deposited energies and electronic stopping cross sections (v ≤ 5 au). J. Phys. B At. Mol. Opt. Phys. 2001, 34, L611. [Google Scholar] [CrossRef]
- Martínez-Flores, C. Shannon entropy and Fisher information for endohedral confined one-and two-electron atoms. Phys. Lett. A 2021, 386, 126988. [Google Scholar] [CrossRef]
- Martínez-Flores, C.; Cabrera-Trujillo, R. Derived properties from the dipole and generalized oscillator strength distributions of an endohedral confined hydrogen atom. J. Phys B At. Mol. Opt. Phys. 2018, 51, 055203. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Baltenkov, A.S.; Connerade, J.P.; Manson, S.T. Structure and photoionization of confined atoms. Radiat. Phys. Chem. 2004, 70, 417. [Google Scholar] [CrossRef]
- Nascimento, E.M.; Prudente, F.V.; Guimarães, M.N.; Maniero, A.M. A study of the electron structure of endohedrally confined atoms using a model potential. J. Phys. B At. Mol. Opt. Phys. 2010, 44, 015003. [Google Scholar] [CrossRef][Green Version]
- Lin, C.Y.; Ho, Y.K. Photoionization of atoms encapsulated by cages using the power-exponential potential. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 145001. [Google Scholar] [CrossRef]
- Bates, D.; Bederson, B. Advances in Atomic and Molecular Physics; Academic Press: Cambridge, MA, USA, 1989; Volume 25. [Google Scholar]
- Soylu, A. Plasma screening effects on the energies of hydrogen atom. Phys. Plasmas 2012, 19, 072701. [Google Scholar] [CrossRef]
- Bahar, M.K.; Soylu, A. The hydrogen atom in plasmas with an external electric field. Phys. Plasmas 2014, 21, 092703. [Google Scholar] [CrossRef]
- Paul, S.; Ho, Y.K. Hydrogen atoms in Debye plasma environments. Phys. Plasmas 2009, 16, 063302. [Google Scholar] [CrossRef]
- Bahar, M.K.; Soylu, A.; Poszwa, A. The hulthén potential model for hydrogen atoms in debye plasma. IEEE Trans. Plasma Sci. 2016, 44, 2297. [Google Scholar] [CrossRef]
- Jung, Y.D. Semiclassical transition probabilities for the electron-impact excitation of hydrogenic ions in dense plasmas. Phys. Plasmas 1995, 2, 332. [Google Scholar] [CrossRef]
- Jung, Y.D.; Yoon, J.S. Plasma-screening effects on semiclassical ionization probabilities for the electron-impact ionization of hydrogenic ions in dense plasmas. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 3549. [Google Scholar] [CrossRef]
- Saha, B.; Mukherjee, P.K. Effect of Debye plasma on the structural properties of compressed positronium atom. Phys. Lett. A 2002, 302, 105. [Google Scholar] [CrossRef]
- Qi, Y.Y.; Wang, J.G.; Janev, R.K. Bound-bound transitions in hydrogenlike ions in Debye plasmas. Phys. Rev. A 2008, 78, 062511. [Google Scholar] [CrossRef]
- Qi, Y.Y.; Wang, J.G.; Janev, R.K. Static dipole polarizability of hydrogenlike ions in Debye plasmas. Phys. Rev. A 2009, 80, 032502. [Google Scholar] [CrossRef]
- Qi, Y.Y.; Wu, Y.; Wang, J.G.; Qu, Y.Z. The generalized oscillator strengths of hydrogenlike ions in Debye plasmas. Phys. Plasmas 2009, 16, 023502. [Google Scholar] [CrossRef]
- Das, M. Transition energies and polarizabilities of hydrogen like ions in plasma. Phys. Plasmas 2012, 19, 092707. [Google Scholar] [CrossRef]
- Kang, S.; Yang, Y.C.; He, J.; Xiong, F.Q.; Xu, N. The hydrogen atom confined in both Debye screening potential and impenetrable spherical box. Cent. Eur. J. Phys. 2013, 11, 584. [Google Scholar] [CrossRef][Green Version]
- Gutierrez, F.A.; Diaz-Valdes, J. Effects of non-spherical screening for inelastic electron-ion scattering. J. Phys. B At. Mol. Opt. Phys. 1994, 27, 593. [Google Scholar] [CrossRef]
- Yoon, J.S.; Jung, Y.D. Spherical versus nonspherical plasma-screening effects on semiclassical electron–ion collisional excitations in weakly coupled plasmas. Phys. Plasmas 1996, 3, 3291. [Google Scholar] [CrossRef]
- Paul, S.; Ho, Y.K. Three-photon transitions in the hydrogen atom immersed in Debye plasmas. Phys. Rev. A 2009, 79, 032714. [Google Scholar] [CrossRef]
- Paul, S.; Ho, Y.K. Two-photon transitions in hydrogen atoms embedded in weakly coupled plasmas. Phys. Plasmas 2008, 15, 073301. [Google Scholar] [CrossRef]
- Zan, L.R.; Jiao, L.G.; Ma, J.; Ho, Y.K. Information-theoretic measures of hydrogen-like ions in weakly coupled Debye plasmas. Phys. Plasmas 2017, 24, 122101. [Google Scholar] [CrossRef]
- Bassi, M.; Baluja, K.L. Polarizability of screened Coulomb potential. Indian J. Phys. 2012, 86, 961. [Google Scholar] [CrossRef]
- Lin, C.Y.; Ho, Y.K. Effects of screened Coulomb (Yukawa) and exponential-cosine-screened Coulomb potentials on photoionization of H and He+. Eur. Phys. J. D 2010, 57, 21. [Google Scholar] [CrossRef]
- Lam, C.S.; Varshni, Y.P. Bound eigenstates of the exponential cosine screened coulomb potential. Phys. Rev. A 1972, 6, 1391. [Google Scholar] [CrossRef]
- Lai, C.S. Energies of the exponential cosine screened Coulomb potential. Phys. Rev. A 1982, 26, 2245. [Google Scholar] [CrossRef]
- Dutt, R.; Mukherji, U.; Varshni, Y.P. Energy levels and oscillator strengths for the exponential-cosine screened Coulomb potential in the shifted large-dimension expansion theory. J. Phy. B At. Mol. Phys. 1986, 19, 3411. [Google Scholar] [CrossRef]
- Bayrak, O.; Boztosun, I. Application of the asymptotic iteration method to the exponential cosine screened Coulomb potential. Int. J. Quantum Chem. 2007, 107, 1040. [Google Scholar] [CrossRef]
- Singh, D.; Varshni, Y.P. Accurate eigenvalues and oscillator strengths for the exponential-cosine screened Coulomb potential. Phys. Rev. A 1983, 28, 2606. [Google Scholar] [CrossRef]
- Paul, S.; Ho, Y.K. Solution of the generalized exponential cosine screened Coulomb potential. Comput. Phys. Commun. 2011, 182, 130. [Google Scholar] [CrossRef]
- Nasser, I.; Abdelmonem, M.S.; Abdel-Hady, A. J-Matrix approach for the exponential-cosine-screened Coulomb potential. Phys. Script. 2011, 84, 045001. [Google Scholar] [CrossRef]
- Qi, Y.Y.; Wang, J.G.; Janev, R.K. Bound-bound transitions in hydrogen-like ions in dense quantum plasmas. Phys. Plasmas 2016, 23, 073302. [Google Scholar] [CrossRef]
- Roy, A.K. Studies on some exponential-screened coulomb potentials. Int. J. Quantum Chem. 2013, 113, 1503. [Google Scholar] [CrossRef][Green Version]
- Lai, H.F.; Lin, Y.C.; Lin, C.Y.; Ho, Y.K. Bound-state energies, oscillator strengths, and multipole polarizabilities for the hydrogen atom with exponential-cosine screened coulomb potentials. Chin. J. Phys. 2013, 51, 73. [Google Scholar]
- Kuganathan, N.; Arya, A.K.; Rushton, M.J.D.; Grimes, R.W. Trapping of volatile fission products by C60. Carbon 2018, 132, 477. [Google Scholar] [CrossRef]
- Brocławik, E.; Eilmes, A. Density functional study of endohedral complexes M@C60 (M = Li, Na, K, Be, Mg, Ca, La, B, Al): Electronic properties, ionization potentials, and electron affinities. J. Chem. Phys. 1998, 108, 3498. [Google Scholar] [CrossRef]
- Kikuchi, K.; Kobayashi, K.; Sueki, K.; Suzuki, S.; Nakahara, H.; Achiba, Y.; Tomura, K.; Katada, M. Encapsulation of radioactive 159Gd and 161Tb atoms in fullerene cages. J. Am. Chem. Soc. 1994, 116, 9775. [Google Scholar] [CrossRef]
- Martínez-Flores, C.; Cabrera-Trujillo, R. Dipole and generalized oscillator strength derived electronic properties of an endohedral hydrogen atom embedded in a Debye-Hückel plasma. Matter Radiat. Extreme 2018, 3, 227. [Google Scholar] [CrossRef][Green Version]
- Mukherjee, N.; Patra, C.N.; Roy, A.K. Confined hydrogenlike ions in plasma environments. Phys. Rev. A 2021, 104, 012803. [Google Scholar] [CrossRef]
- Roy, A.K. Studies on bound-state spectra of Manning–Rosen potential. Mod. Phys. Lett. A 2014, 29, 1450042. [Google Scholar] [CrossRef][Green Version]
- Roy, A.K. Confinement in 3D polynomial oscillators through a generalized pseudospectral method. Mod. Phys. Lett. A 2014, 29, 1450104. [Google Scholar] [CrossRef][Green Version]
- Roy, A.K. Ro-vibrational spectroscopy of molecules represented by a Tietz–Hua oscillator potential. J. Math. Chem. 2014, 52, 1405. [Google Scholar] [CrossRef][Green Version]
- Mukherjee, N.; Roy, A.K. Quantum mechanical virial-like theorem for confined quantum systems. Phys. Rev. A 2019, 99, 022123. [Google Scholar] [CrossRef][Green Version]
- Mukherjee, N.; Roy, A.K. Analysis of Compton profile through information theory in H-like atoms inside impenetrable sphere. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 235002. [Google Scholar] [CrossRef]
- Zhu, L.; He, Y.Y.; Jiao, L.G.; Wang, Y.C.; Ho, Y.K. Revisiting the generalized pseudospectral method: Radial expectation values, fine structure, and hyperfine splitting of confined atom. Int. J. Quantum Chem. 2020, 120, e26245. [Google Scholar] [CrossRef]
- Ghoshal, A.; Ho, Y.K. Photodetachment of H− in dense quantum plasmas. Phys. Rev. E 2010, 81, 016403. [Google Scholar] [CrossRef]
- Xu, Y.B.; Tan, M.Q.; Becker, U. Oscillations in the photoionization cross section of C60. Phys. Rev. Lett. 1996, 76, 3538. [Google Scholar] [CrossRef][Green Version]
- Dolmatov, V.K.; King, J.L.; Oglesby, J.C. Diffuse versus square-well confining potentials in modelling A@C60 atoms. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 105102. [Google Scholar] [CrossRef][Green Version]
- Connerade, J.P.; Dolmatov, V.K.; Lakshmi, P.A.; Manson, S.T. Electron structure of endohedrally confined atoms: Atomic hydrogen in an attractive shell. J. Phys. B At. Mol. Opt. Phys. 1999, 32, L239. [Google Scholar] [CrossRef]
- Hasoğlu, M.F.; Zhou, H.L.; Manson, S.T. Correlation study of endohedrally confined alkaline-earth-metal atoms A@C60. Phys. Rev. A 2016, 93, 022512. [Google Scholar] [CrossRef][Green Version]
- Puska, M.J.; Nieminen, R.M. Photoabsorption of atoms inside C60. Phys. Rev. A 1993, 47, 1181. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Madjet, M.E.; Chakraborty, H.S.; Rost, J.M.; Manson, S.T. Photoionization of C60: A model study. J. Phys B At. Mol. Opt. Phys. 2008, 41, 105101. [Google Scholar] [CrossRef][Green Version]
- Yan, Z.C.; Babb, J.F.; Dalgarno, A.; Drake, G.W.F. Variational calculations of dispersion coefficients for interactions among H, He, and Li atoms. Phys. Rev. A 1996, 54, 2824. [Google Scholar] [CrossRef][Green Version]
- Luyckx, R.; Coulon, P.H.; Lekkerkerker, H.N.W. Dispersion interaction between helium atoms. Chem. Phys. Lett. 1977, 48, 187. [Google Scholar] [CrossRef]
- Bartolotti, L.J. Oscillator strength sum rule and the hydrodynamic analogy to quantum mechanics. Chem. Phys. Lett. 1979, 60, 507. [Google Scholar] [CrossRef]
- Mukherjee, N.; Roy, A.K. Information-entropic measures in free and confined hydrogen atom. Int. J. Quantum Chem. 2018, 118, e25596. [Google Scholar] [CrossRef]
- Estanón, C.R.; Aquino, N.; Puertas-Centeno, D.; Dehesa, J.S. Two-dimensional confined hydrogen: An entropy and complexity approach. Int. J. Quantum Chem. 2020, 120, e26192. [Google Scholar] [CrossRef]
- Jiao, L.G.; Zan, L.R.; Zhang, Y.Z.; Ho, Y.K. Benchmark values of Shannon entropy for spherically confined hydrogen atom. Int. J. Quantum Chem. 2017, 117, e25375. [Google Scholar] [CrossRef]
- Salazar, S.J.C.; Laguna, H.G.; Dahiya, B.; Prasad, V.; Sagar, R.P. Shannon information entropy sum of the confined hydrogenic atom under the influence of an electric field. Eur. Phys. J. D 2021, 75, 127. [Google Scholar] [CrossRef]
| DHPWS | ECSCPWS | ||||||
|---|---|---|---|---|---|---|---|
| State | State | ||||||
| 1 | − | − | 1 | − | − | ||
| 2 | − | − | 2 | − | − | ||
| 1 | −0.000000254 | 1 | 0.6287 | −0.000000038 | |||
| 2 | 2.1247 | −0.000000197 | 2 | 1.3618 | −0.000000165 | ||
| 1 | −0.000000439 | 1 | 0.0762 | −0.000000130 | |||
| 2 | 0.3900 | −0.000000055 | 2 | 0.2688 | −0.000000238 | ||
| 1 | − | − | 1 | − | − | ||
| 2 | − | − | 2 | − | − | ||
| 1 | −0.000000096 | 1 | 0.0730 | −0.000001331 | |||
| 2 | 0.3575 | −0.000011586 | 2 | 0.2633 | −0.000053585 | ||
| 1 | − | − | 1 | − | − | ||
| 2 | − | − | 2 | − | − | ||
| 1 | 0.0732 | −0.000000291 | 1 | 0.0466 | −0.000003059 | ||
| 2 | 0.1197 | −0.000005269 | 2 | 0.0782 | −0.000064445 | ||
| 1 | 0.1947 | −0.000000856 | 1 | 0.1267 | −0.000007139 | ||
| 2 | 0.2994 | −0.000023163 | 2 | 0.1681 | −0.000018290 | ||
| 1 | 0.0472 | −0.000016099 | 1 | 0.0323 | −0.000001631 | ||
| 2 | 0.0831 | −0.000007057 | 2 | 0.0540 | −0.000038551 | ||
| 1 | 0.0333 | −0.000000778 | 1 | 0.0278 | −0.000006697 | ||
| 2 | 0.1231 | −0.000005413 | 2 | 0.0903 | −0.000078050 | ||
| 1 | 0.0288 | −0.000005039 | 1 | 0.0210 | −0.000001928 | ||
| 2 | 0.0588 | −0.000040341 | 2 | 0.0403 | −0.000068680 | ||
| Transition | DHPWS | ECSCPWS | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1s→2p | 0.01 | 0.472909 | 0.405489 | 0.393008 | 0.399455 | 0.473031 | 0.405670 | 0.393153 | 0.399658 |
| 0.1 | 0.463893 | 0.389264 | 0.382538 | 0.380980 | 0.466412 | 0.399214 | 0.385322 | 0.392167 | |
| 0.5 | 0.506522 | 0.146559 | 0.445168 | 0.104184 | 0.506896 | 0.062774 | 0.475507 | 0.036498 | |
| 1.0 | 0.859970 | 0.072607 | 0.881023 | 0.047763 | 0.941505 | 0.069773 | 0.911234 | 0.051167 | |
| 2.5 | 0.937700 | 0.910538 | 0.902761 | 0.915478 | 0.918853 | 0.924631 | 0.884901 | 0.889980 | |
| 2p→1s | 0.01 | −0.157636 | −0.135163 | −0.131002 | −0.133151 | −0.157677 | −0.135223 | −0.131051 | −0.133219 |
| 0.1 | −0.154631 | −0.129754 | −0.127512 | −0.126993 | −0.155470 | −0.133071 | −0.128440 | −0.130722 | |
| 0.5 | −0.168840 | −0.048853 | −0.148389 | −0.034728 | −0.168965 | −0.020924 | −0.158502 | −0.012166 | |
| 1.0 | −0.286656 | −0.024202 | −0.293674 | −0.015921 | −0.313835 | −0.023257 | −0.303744 | −0.017055 | |
| 2.5 | −0.312566 | −0.303512 | −0.300920 | −0.305159 | −0.306284 | −0.308210 | −0.294967 | −0.296660 | |
| 2p→3d | 0.01 | 1.088693 | 0.800227 | 1.082666 | 0.732754 | 1.088689 | 0.800197 | 1.082677 | 0.732695 |
| 0.1 | 1.088778 | 0.806429 | 1.081425 | 0.743057 | 1.088627 | 0.798441 | 1.081926 | 0.731705 | |
| 0.5 | 1.071869 | 1.055338 | 1.054450 | 1.060247 | 1.055825 | 1.067797 | 1.036342 | 1.050053 | |
| 1.0 | 1.052710 | 1.063993 | 1.034850 | 1.045177 | 1.039857 | 1.036862 | 1.023702 | 1.020954 | |
| 2.5 | 1.043849 | 1.044600 | 1.027258 | 1.027832 | 1.042933 | 1.042720 | 1.026567 | 1.026410 | |
| 3d→2p | 0.01 | −0.653216 | −0.480136 | −0.649599 | −0.439652 | −0.653213 | −0.480118 | −0.649606 | −0.439617 |
| 0.1 | −0.653267 | −0.483857 | −0.648855 | −0.445834 | −0.653176 | −0.479064 | −0.649156 | −0.439023 | |
| 0.5 | −0.643121 | −0.633202 | −0.632670 | −0.636148 | −0.633495 | −0.640678 | −0.621805 | −0.630032 | |
| 1.0 | −0.631626 | −0.638396 | −0.620910 | −0.627106 | −0.623914 | −0.622117 | −0.614221 | −0.612572 | |
| 2.5 | −0.626309 | −0.626760 | −0.616355 | −0.616699 | −0.625760 | −0.625632 | −0.615940 | −0.615846 | |
| 3d→4f | 0.01 | 1.361677 | 1.378364 | 1.350361 | 1.374690 | 1.361703 | 1.378352 | 1.350391 | 1.374693 |
| 0.1 | 1.359552 | 1.378857 | 1.347923 | 1.373824 | 1.360468 | 1.378527 | 1.348914 | 1.374145 | |
| 0.5 | 1.342821 | 1.355667 | 1.330534 | 1.342513 | 1.333760 | 1.336163 | 1.321648 | 1.322866 | |
| 1.0 | 1.334518 | 1.337464 | 1.322958 | 1.325371 | 1.329986 | 1.328230 | 1.319261 | 1.317836 | |
| 2.5 | 1.331894 | 1.331979 | 1.320806 | 1.320868 | 1.331802 | 1.331794 | 1.320741 | 1.320736 | |
| Transition | DHPWS | ECSCPWS | ||||||
|---|---|---|---|---|---|---|---|---|
| 1s→2p | 0.01 | 0.149983 | 0.01 | 0.377669 | 0.01 | 0.150086 | 0.01 | 0.378002 |
| 0.1 | 0.143844 | 0.1 | 0.345192 | 0.1 | 0.143408 | 0.1 | 0.363852 | |
| 0.5 | 0.405345 | 0.5 | 0.014097 | 0.5 | 0.795304 | 0.5 | 0.003368 | |
| 1.0 | 0.853185 | 1.0 | 0.008094 | 1.0 | 0.815081 | 1.0 | 0.015977 | |
| 2.5 | 0.813876 | 2.5 | 0.829531 | 2.5 | 0.809188 | 2.5 | 0.810333 | |
| 2p→1s | 0.01 | −0.049994 | 0.01 | −0.125889 | 0.01 | −0.050028 | 0.01 | −0.126000 |
| 0.1 | −0.047948 | 0.1 | −0.115064 | 0.1 | −0.047802 | 0.1 | −0.121284 | |
| 0.5 | −0.135115 | 0.5 | −0.004699 | 0.5 | −0.265101 | 0.5 | −0.001122 | |
| 1.0 | −0.284395 | 1.0 | −0.002698 | 1.0 | −0.271693 | 1.0 | −0.005325 | |
| 2.5 | −0.271292 | 2.5 | −0.276510 | 2.5 | −0.269729 | 2.5 | −0.270111 | |
| 2p→3d | 0.01 | 1.062893 | 0.01 | 0.511654 | 0.01 | 1.062940 | 0.01 | 0.511243 |
| 0.1 | 1.059233 | 0.1 | 0.563033 | 0.1 | 1.061126 | 0.1 | 0.525528 | |
| 0.5 | 1.039334 | 0.5 | 1.058267 | 0.5 | 1.033436 | 0.5 | 1.037782 | |
| 1.0 | 1.032612 | 1.0 | 1.035607 | 1.0 | 1.029282 | 1.0 | 1.028293 | |
| 2.5 | 1.030470 | 2.5 | 1.030594 | 2.5 | 1.030324 | 2.5 | 1.030294 | |
| 3d→2p | 0.01 | −0.637736 | 0.01 | −0.306992 | 0.01 | −0.637764 | 0.01 | −0.306745 |
| 0.1 | −0.635539 | 0.1 | −0.337820 | 0.1 | −0.636675 | 0.1 | −0.315316 | |
| 0.5 | −0.623600 | 0.5 | −0.634960 | 0.5 | −0.620061 | 0.5 | −0.622669 | |
| 1.0 | −0.619567 | 1.0 | −0.621364 | 1.0 | −0.617569 | 1.0 | −0.616975 | |
| 2.5 | −0.618282 | 2.5 | −0.618356 | 2.5 | −0.618194 | 2.5 | −0.618176 | |
| 3d→4f | 0.01 | 1.358996 | 0.01 | 1.377113 | 0.01 | 1.358989 | 0.01 | 1.377140 |
| 0.1 | 1.358827 | 0.1 | 1.374730 | 0.1 | 1.358891 | 0.1 | 1.376182 | |
| 0.176 | 1.352618 | 0.15 | 1.372349 | 0.12602 | 1.354588 | 0.157 | 1.372370 | |
| 0.1931 | 1.347244 | 0.255 | 1.364948 | 0.12638 | 1.354413 | 0.16724 | 1.369061 | |
| 0.19462 | 1.346487 | 0.29949 | 1.354689 | 0.12671 | 1.354225 | 0.16812 | 1.368517 | |
| State | DHPWS | ECSCPWS | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Z = 1 | Z = 2 | Z = 1 | Z = 2 | Z = 1 | Z = 2 | Z = 1 | Z = 2 | ||
| 1s | 0.01 | 4.657831 | 0.28128622 | 4.746857 | 0.2812862 | 4.6554220 | 0.2812521 | 4.7442022 | 0.2812521 |
| 0.1 | 4.881931 | 0.28451405 | 4.994924 | 0.2845141 | 4.7251882 | 0.2817758 | 4.8232375 | 0.2817759 | |
| 0.5 | 12.2287 | 0.35794112 | 14.6516 | 0.3579433 | 17.04331 | 0.3321934 | 24.00875 | 0.3321963 | |
| 1.0 | 78.7749 | 0.69849914 | 140.048 | 0.6990358 | 202.0018 | 1.1380112 | 320.2554 | 1.1591198 | |
| 2.5 | 230.696 | 128.19895 | 345.626 | 226.2246 | 259.3304 | 251.0688 | 375.0790 | 367.0643 | |
| 3.0 | 240.868 | 187.73712 | 356.253 | 299.8536 | 260.2497 | 256.3160 | 375.9265 | 372.1057 | |
| 2s | 0.01 | −6323.6041 | 1974.66567 | 2449.20791 | 1407.62883 | −6259.74897 | 2014.6251 | 2455.03251 | 1427.48523 |
| 0.1 | −25,299.096 | 762.542243 | 2096.11187 | 671.915445 | −12,087.9810 | 1214.6507 | 2197.55093 | 975.180845 | |
| 0.5 | 18,546.933 | 297.184946 | 2569.87340 | 369.786944 | 4830.94856 | 368.81438 | 2570.99350 | 481.397967 | |
| 1.0 | −252.97113 | 421.447127 | −232.042760 | 527.012512 | −26.4762447 | 481.38339 | −9.29681306 | 592.581494 | |
| 2.5 | 9.5211800 | −128.377389 | 18.4890829 | −86.8752095 | 29.6816393 | 21.677927 | 36.7365367 | 29.6077279 | |
| 3.0 | 16.629850 | −29.6973425 | 24.7934626 | −13.1804006 | 30.8831256 | 27.068895 | 37.7878081 | 34.3689306 | |
| 2p | 0.01 | 2191.410 | −643.03504 | −702.8776 | −452.1602 | 2170.076 | −656.3755 | −704.8910 | −458.8075 |
| 0.1 | 8520.618 | −237.05905 | −579.3616 | −204.1988 | 4114.992 | −388.9010 | −615.7853 | −306.8603 | |
| 0.5 | −6061.053 | −24.508518 | −694.8934 | −13.59247 | −1473.332 | −1.579597 | −678.1659 | 9.116706 | |
| 1.0 | 204.2574 | −8.8332529 | 219.5863 | −0.670906 | 100.0618 | −6.121894 | 97.77017 | −1.240847 | |
| 2.5 | 79.78501 | 152.51948 | 81.67296 | 148.6793 | 67.74707 | 71.51052 | 70.12450 | 73.50398 | |
| 3.0 | 75.37053 | 102.96430 | 77.42353 | 103.0182 | 67.26899 | 69.03491 | 69.71802 | 71.31396 | |
| State | DHPWS | ECSCPWS | ||||||
|---|---|---|---|---|---|---|---|---|
| 1s | 0.01 | 5.041120 | 0.01 | 0.2812863 | 0.01 | 5.0373245 | 0.01 | 0.2812522 |
| 0.1 | 5.405572 | 0.1 | 0.2845141 | 0.1 | 5.1638458 | 0.1 | 0.2817760 | |
| 0.5 | 71.4353 | 0.5 | 0.3579454 | 0.5 | 553.3792 | 0.5 | 0.3321994 | |
| 1.0 | 1076.49 | 1.0 | 0.7000504 | 1.0 | 1241.072 | 1.0 | 1.2523499 | |
| 2.5 | 1242.28 | 2.5 | 1183.049 | 2.5 | 1257.825 | 2.5 | 1254.207 | |
| 3.0 | 1247.93 | 3.0 | 1220.684 | 3.0 | 1258.140 | 3.0 | 1256.377 | |
| 2s | 0.01 | 1480.865 | 0.01 | 871.382822 | 0.01 | 1480.571 | 0.01 | 877.9676 |
| 0.1 | 1507.894 | 0.1 | 578.058339 | 0.1 | 1497.317 | 0.05 | 845.6145 | |
| 0.3 | 1720.036 | 0.5 | 1060.98797 | 0.2 | 1587.219 | 0.09 | 738.4854 | |
| 0.5 | 2721.953 | 1.0 | 1338.07651 | 0.3 | 1771.873 | 0.3 | 940.9011 | |
| 0.7 | −326.1830 | 1.5 | 1503.41076 | 0.5 | −1276.650 | 0.7 | 1404.159 | |
| 0.9 | 23008.31 | 2.0 | −23.222516 | 0.6 | 259.9035 | 1.3 | −65.30549 | |
| 2p | 0.01 | −150.7481 | 0.01 | −262.0658419 | 0.01 | −150.9188 | 0.01 | −264.3678 |
| 0.1 | −139.2984 | 0.1 | −152.6892619 | 0.1 | −140.9449 | 0.1 | −201.3010 | |
| 0.5 | −443.5363 | 0.5 | 69.93496507 | 0.5 | 786.5248 | 0.5 | 87.43362 | |
| 1.0 | 168.1365 | 1.0 | 64.90555224 | 1.0 | 114.3632 | 1.0 | 55.87104 | |
| 2.5 | 111.5520 | 2.5 | 133.2633406 | 2.5 | 106.2537 | 2.5 | 107.5945 | |
| 3.0 | 109.6328 | 3.0 | 119.4094711 | 3.0 | 106.1153 | 3.0 | 106.7672 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chowdhury, S.; Mukherjee, N.; Roy, A.K. Hydrogen-like Plasmas under Endohedral Cavity. Quantum Rep. 2023, 5, 459-474. https://doi.org/10.3390/quantum5020030
Chowdhury S, Mukherjee N, Roy AK. Hydrogen-like Plasmas under Endohedral Cavity. Quantum Reports. 2023; 5(2):459-474. https://doi.org/10.3390/quantum5020030
Chicago/Turabian StyleChowdhury, Saptarshi, Neetik Mukherjee, and Amlan K. Roy. 2023. "Hydrogen-like Plasmas under Endohedral Cavity" Quantum Reports 5, no. 2: 459-474. https://doi.org/10.3390/quantum5020030
APA StyleChowdhury, S., Mukherjee, N., & Roy, A. K. (2023). Hydrogen-like Plasmas under Endohedral Cavity. Quantum Reports, 5(2), 459-474. https://doi.org/10.3390/quantum5020030









