Abstract
A longstanding issue in the Everettian (Many-Worlds) interpretation is to justify and make sense of the Born rule that underlies the statistical predictions of standard quantum mechanics. The paper offers a reappraisal of Everett’s original account in light of the recent literature on the concept of typicality. It argues that Everett’s derivation of the Born rule is sound and, in a certain sense, even an optimal result, and defends it against the charge of circularity. The conclusion is that Everett’s typicality argument can successfully ground post-factum explanations of Born statistics, while questions remain about the predictive power of the Many-Worlds interpretation.
1. The Probability Problem
Reproducing the probabilistic predictions of standard quantum mechanics, i.e., the Born rule, is considered to be one of the major challenges for the Everettian (Many-Worlds) interpretation. In the literature, we find a variety of different proposals for justifying the Born rule (see [1] for an overview), as well as critics expressing serious doubts that any of them are adequate (e.g., [2,3]). This paper will defend the thesis that the original account provided by Hugh Everett III (in his 1956 doctoral thesis [4] and summarized in his 1957 paper [5]) is a satisfying solution to the probability problem—or, at least, as good a solution as one can hope for in a Many-Worlds theory. It has been unjustly dismissed by modern-day Everettians, largely because of a failure to appreciate Everett’s derivation of the Born rule as a typicality argument in the spirit of Boltzmann’s statistical mechanics.
In recent years, a number of publications have elaborated on the concept of typicality, its role in Boltzmann’s statistical mechanics [6,7,8], on how it grounds objective probabilities [9,10,11], and how typicality explanations work in general [12,13,14]. In light of this growing understanding, Everett’s typicality account of the Born rule deserves a reappraisal.
Probabilities of What?
The problem with grounding quantum probabilities in Everettian quantum mechanics is not that the theory is fundamentally deterministic. Continued philosophical debates notwithstanding, there are very successful strategies for reducing classical statistical mechanics to Newtonian dynamics or even the Born rule to another deterministic quantum theory, Bohmian mechanics [15]. The first and foremost question that arises in the context of the Many-Worlds interpretation is: probabilities of what?
This question can be understood in two ways. With an emphasis on the what part, it points to the ontology problem of Everettian quantum mechanics [3], the question of what the theory is fundamentally about and—if it is about the universal wave function or an even more abstract quantum state—how exactly the theory describes localized events in space and time. Bohmian mechanics, for instance, is about the motion of point particles in three-dimensional physical space, and the Born rule, in its most basic form, yields probability distributions for particle configurations, including those composing familiar macroscopic objects. In Everettian quantum mechanics, one would look in vain for a similarly precise answer. Oddly enough, there are many different interpretations of the Many-Worlds interpretation (see, e.g., [16,17,18,19,20]) but even the best-elaborated ones remain vague about how the theory is supposed to make contact with familiar physical reality [3,21,22]. I consider this the most serious problem of Everettian quantum mechanics, but it is not the problem I want to focus on here. For the remainder of this discussion, I will thus grant that it is possible, by whatever means or procedure, to identify “worlds” with more or less familiar macro-objects like cats and physicists and measurement devices indicating measurement results in the wave function of the universe.
The other, more surface-level way of understanding the question “probabilities of what?” is with an emphasis on the probability part. In particular, what could it even mean to ask about the probability of a specific measurement outcome if, according to the Many-Worlds interpretation, all possible outcomes actually occur?
An obvious first idea is that the probability of a certain measurement outcome refers to the relative frequency of worlds in which the said outcome occurs. In the “naive” Many-Worlds interpretation, it is assumed that, say, a spin measurement on an electron in the spin state results in exactly two worlds, one in which the outcome is spin up and one in which the outcome is spin down. The problem is then that this branch counting is clearly at odds with the probabilities predicted by standard quantum mechanics. The relative frequency of each outcome would always be , which agrees with the Born probabilities and only in the special case . According to more sophisticated, decoherence-based versions of Everettian quantum mechanics (see, in particular, [17]), the number of distinct world branches is not even well-defined and naive branch counting a non-starter. Since decoherence is both ubiquitous and vague, any decomposition of the universal quantum state into (more or less) decoherent branches is, to some extent, arbitrary. (The precise notion of decoherence is largely irrelevant to this point, but it is best to think of decoherent branches as components of the wave function that have essentially no overlap in configuration space.) As Wallace (2012) explains:
[T]here is no sense in which [decoherence] phenomena lead to a naturally discrete branching process: as we have seen in studying quantum chaos, while a branching structure can be discerned in such systems, it has no natural ‘grain’. To be sure, by choosing a certain discretization of (configuration-)space and time, a discrete branching structure will emerge, but a finer or coarser choice would also give branching. And there is no ‘finest’ choice of branching structure: as we fine-grain our decoherent history space, we will eventually reach a point where interference between branches ceases to be negligible, but there is no precise point where this occurs. As such, the question ‘How many branches are there?’ does not, ultimately, make sense.([17], pp. 99–100)
Metaphysically, this view seems even more unsettling than the naive Many-Worlds picture. We must not merely accept the existence of two cats at the end of Schrödinger’s experiment but of an indefinite number of cats (and boxes, and experimenters, and, ultimately, worlds). Still, besides reflecting a more honest attempt at identifying worlds in the wave function, the sophisticated picture explains why the theory does not predict the wrong statistics that would result from branch counting (if naive branch counting made sense). Either way, the attempt to identify quantum probabilities with frequencies of worlds fails.
Finding it hard to locate interesting probabilities in the Everettian multiverse, the next obvious idea is to locate them in our minds, i.e., interpret them as subjective probabilities. For instance, after I perform a spin measurement—but before I look at the detector to see the result—I do not know if I find myself on a branch in which the detector registered “spin up” or on a branch in which the detector registered “spin down”. What should my credence be for one or the other? If someone offers me a 2:1 bet on “spin up”, should I accept? The probabilities, in this case, arise from my self-locating uncertainty [23,24,25]. I do not know what world within the multiverse my present self inhabits, and the goal of a theoretical analysis would be to show that it is rational to assign degrees of belief according to the Born rule. Other authors, most notably Deutsch [26] and Wallace [17], have taken a more decision-theoretic perspective, trying to argue that it is rational to act in accordance with standard quantum probabilities. In this vein, Wallace proposes a set of 10 axioms to justify the use of the branch amplitudes squared for calculating expected utilities in decision problems. Maudlin [27] points out that these axioms do not allow a rational agent to split a payoff among two or more of her future copies, i.e., exploit the option all of the above that we would have in a branching multiverse. “If one were mischievous, one might even put it this way: Wallace’s ‘rationality axioms’ entail that one should behave as if one believes that Everettian quantum theory is false” (p. 804).
I will not devote to any of these approaches the detailed discussion they would deserve based on their ingenuity alone. I believe that epistemic probabilities of any kind are ultimately missing the point of vindicating the empirical adequacy of Everettian quantum mechanics. First and foremost, the theory must account for the very robust statistical regularities described by the Born rule, not for physicists’ beliefs or betting behaviors. Certain credences and decisions might be rational in virtue of the theory’s physical predictions, but we first need to understand, in objective terms, what the relevant predictions are.
Everett’s account of the Born rule is based on a typicality argument—and objective probability assignments—analogous to the derivations of statistical laws in Boltzmannian statistical mechanics. His goal is to show that the Born rule describes frequencies within typical world branches, i.e., along nearly all Many-Worlds histories, in a natural sense of “nearly all”. A similar typicality argument, although with respect to possible worlds, underlies the quantum equilibrium analysis that grounds the Born rule in Bohmian mechanics (Dürr et al. [15]; see also Bell ([28], Ch. 15) who anticipates the result).
In this paper, I will not engage in a general philosophical discussion of typicality (for that, see [10,11,12,13,14]), but continue with a concrete example that provides a good classical analog for the Everettian analysis.
2. The Galton Board
Our model “universe” is the Galton board. (For other discussions of the Galton board in terms of typicality, see [29,30].) It consists of a vertical board with a top receptacle holding solid balls, interleaved rows of pins that the balls fall through (bouncing off the pins), and a series of bins at the bottom in which the balls are finally collected (Figure 1). As a large number of balls fall through the board, we find it resulting in an approximately symmetric binomial distribution of balls over the bins (which, in turn, approximates a normal distribution).
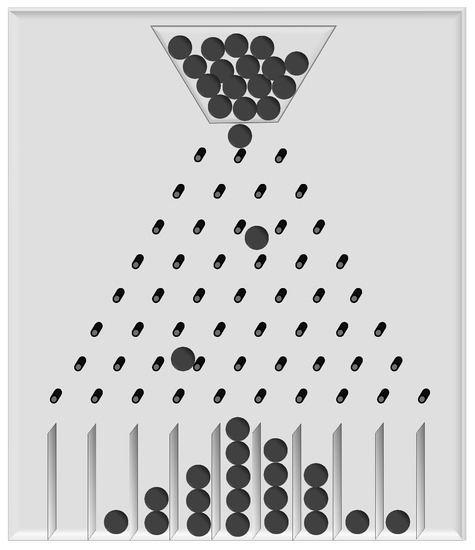
Figure 1.
Illustration of a Galton board.
Suppose our Galton board has M rows of pins and bins at the bottom (labeled ). And suppose the board starts out at as a perfectly isolated system with balls (“particles”) placed in the top receptacle. From there on, everything runs its deterministic course. The particles fall through the board and collide (nearly) elastically with the pins before coming to rest in one of the bottom bins, all following laws of classical mechanics. If denotes the fraction of particles ending up in bin , we find
This binomial distribution is, of course, exactly what we would expect if a particle has a 50:50 chance of bouncing left or right at each pin. But what exactly does this mean? And how is it supposed to explain the observed statistics? There is nothing intrinsically random about the bounces. The trajectory that each particle takes through the Galton board is completely determined by the dynamics and initial conditions of the system. That we do not know whether a given collision will deflect the particle to the left or the right (because the dynamics are quite chaotic) and have no reason to favor one possibility over the other (because of the symmetry of the setup) might be a correct observation, but it does not amount to a physical explanation of the statistical phenomenon. What do little metal balls care about our ignorance or indifference?
Let us take the (idealized) Galton board seriously as a physical system, a classical N-particle system with phase space . At time , the system starts out with an initial condition for which all particles are at the top of the board. For any , the relevant (Hamiltonian) equations of motion determine a unique evolution , where is the Hamiltonian flow. After a time T, which is sufficiently long for all the particles to have passed through the board, we consider their distribution over the bins. Mathematically, we introduce the macro-variables such that if, in the microstate , particle i is at rest in bin number k and , otherwise. The final (time T) distribution of particles, as a function of the initial microstate , is then given by
Now, a typicality explanation of the binomial distribution would be a result of the form
for sufficiently large N, where denotes the Liouville measure on . A little more precisely, for instance,
where goes quickly to zero for large N and any given . The convergence is, in fact, more mathematical abstraction than needed. What matters physically is that for the actual particle number N and reasonably small (consistent with our observation of an approximately binomial distribution).
Proving (4) for realistic micro-dynamics can, of course, be very hard and is beyond the scope of this paper. I want to focus on how such a mathematical result (if true) should be interpreted and what it accomplishes. Equation (4) should be read as saying that nearly all possible initial conditions result in an approximately binomial distribution of particles over the bins. While there exist initial conditions for which some of the bins would end up with significantly more particles—and others with significantly fewer—such initial states are very special ones, forming a set of vanishingly small measure (). A binomial distribution is, in other words, typical for the Galton board.
Compare this with Boltzmann’s explanation of the Maxwellian velocity distribution in an ideal gas:
The ensuing, most likely state, which we call that of the Maxwellian velocity distribution, since it was Maxwell who first found the mathematical expression in a special case, is not an outstanding singular state, opposite to which there are infinitely many more non-Maxwellian velocity distributions, but it is, on the contrary, distinguished by the fact that by far the largest number of possible states have the characteristic properties of the Maxwellian distribution, and that compared to this number the amount of possible velocity distributions that deviate significantly from Maxwell’s is vanishingly small. The criterion of equal possibility or equal probability of different distributions is thereby always given by Liouville’s theorem.([31], p. 252)
A general definition of the concept of typicality is as follows.
Definition 1.
Let Ω be a set (the domain or reference set of the typicality statement) and F a property that the members of Ω can possess or not. We say that F is typical within Ω if nearly all members of Ω instantiate F. The property is atypical within Ω if is typical, i.e., if nearly none of the members of Ω instantiate F.
For instance, the property of being black is typical among ravens. The property of being irrational is typical within the set of real numbers. In the context of fundamental physics and statistical mechanics, the most interesting typicality statements are those with a reference set of (possible) worlds as described by a physical theory (in which case a “property” is technically a proposition that can be true or false at each world).
For the Galton board, we note that every possible initial condition corresponds to a possible trajectory or micro-history of the N-particle system (with the boundary condition that all particles start at the top of the board). That is, if we regard the Galton board as our model universe, every X corresponds to a physically possible world. The desired typicality result thus states that the statistical “law” expressed by P—or, if we prefer, by saying that particles bounce left or right with a probability of —holds in nearly all possible worlds allowed by the microscopic laws of motion.
“Nearly all” is made precise in terms of the Liouville measure , which corresponds to the intuitive phase space volume and is distinguished as the simplest measure on that is stationary under the Hamiltonian dynamics. Stationarity is exactly the criterion Boltzmann appeals to in the above quote as he references Liouville’s theorem (although it’s good to note that typicality statements are extremely robust against variations in the measure [11,29]). As a typicality measure, the role of is not to express frequencies, or propensities, or degrees of belief, but only to characterize very large (resp. very small) sets of possible initial conditions. Stationarity ensures that large sets remain large (and small sets remain small) under time evolution, but also that can be understood as a natural measure on micro-histories [11].
It is important to appreciate that, while there are technically three measures involved in the typicality result (4), their respective meaning and status is very different. We have:
- the stationary Liouville measure as a typicality measure on phase space;
- the empirical distribution that results from the deterministic dynamics and initial conditions ;
- the theoretical probability distribution that approximates the empirical distribution for typical initial conditions.
What we can call objective probabilities are the typical relative frequencies described by P. It is neither necessary nor meaningful to interpret the phase space measure as probability distribution over “possible worlds”. Note, in particular, that we did not assume at any point that the Galton board experiment is repeated. As our model universe, it has one and only one actual history, but this history is typical with respect to the statistical distribution of particles.
The central claim is that this typicality fact provides a conclusive explanation of the observed statistics, grounded in the underlying micro-dynamics, and justifies the probabilistic hypothesis of the binomial law. We can express this as a general rationality principle underlying typicality explanations (which is related to Cournot’s principle in probability [11,32]; for a different but equally workable formulation, see [14]).
Typicality Principle (TP). Suppose we accept a theory and observe a phenomenon A. If A is typical according to , we should consider it to be conclusively explained. It is irrational to wonder further why our world is, in this particular respect, like nearly all (possible) worlds that the theory and its laws describe. (Conversely, atypical phenomena are, in general, the kind that cry out for further explanation and may ultimately compel us to revise or reject our theory.)
While I would argue that TP is an almost inevitable principle of scientific reasoning, the reader who disagrees may simply take it as a basic postulate of typicality accounts.
Finally, let me emphasize that TP is a normative principle, expressing epistemic implications of objective typicality facts. Typicality facts—e.g., the fact that nearly all possible initial conditions of the Galton board lead to an approximately binomial distribution of balls over the bins—do not depend on anyone’s ignorance or beliefs. Hence, when the phenomenon in question is a statistical regularity that can be described by a probability “law”, an objective typicality fact can explain objective probabilities.
3. Everett’s Typicality Argument
To derive the Born rule in his Many-Worlds theory, Everett provides a typicality argument that is quite analogous to the one just discussed for the Galton board and in line with the general strategy for deriving statistical laws in Boltzmannian statistical mechanics. In Everett’s account, the -measure determined by the universal wave function (that is, the branch amplitudes squared) defines a typicality measure on world branches which is used to identify statistical regularities that hold in the vast majority of them. Probabilities are once again typical relative frequencies, except that typicality is now understood relative to an actual “ensemble” of worlds (corresponding to macro- rather than micro-histories) that coexist within the Everettian multiverse. As Everett explained:
We wish to make quantitative statements about the relative frequencies of the different possible results of observation—which are recorded in the memory—for a typical observer state; but to accomplish this we must have a method for selecting a typical element from a superposition of orthogonal states. [...] The situation here is fully analogous to that of classical statistical mechanics, where one puts a measure on trajectories of systems in the phase space by placing a measure on the phase space itself, and then making assertions … which hold for “almost all” trajectories. [...] However, for us a trajectory is constantly branching (transforming from state to superposition) with each successive measurement. To have a requirement analogous to the “conservation of probability” in the classical case, we demand that the measure assigned to a trajectory at one time shall equal the sum of the measures of its separate branches at a later time. This is precisely the additivity requirement which we imposed and which leads uniquely to the choice of square-amplitude measure.([5], pp. 460–461)
Just like Boltzmann in classical statistical mechanics and Dürr, Goldstein, and Zanghì in Bohmian mechanics [15], Everett appeals to a form of stationarity to justify the choice of typicality measure. More precisely, he stipulates three requirements that distinguish the measure uniquely (see [33] for an excellent discussion):
- It should be a positive function of the complex-valued coefficients associated with the branches of the universal wave function.
- It should be a function of the amplitudes of the coefficients alone, i.e., not depend on the phases.
- It should satisfy the following additivity requirement: if a branch b is decomposed into a collection of sub-branches, the measure assigned to b should be the sum of the measures assigned to the sub-branches .
This last additivity condition can be understood diachronically as stationarity; the weight assigned to a world at any given time equals the sum of the weights assigned to its branching histories at later times. This also assures a form of locality in that the weight of a world branch is not affected by the splitting of other branches.
Understood synchronically, the additivity condition does away with the problem that the notion of a world branch is unsharp. Whether one regards some component of the wave function as corresponding to one world (in which, let us say, a particular measurement outcome occurs) or further differentiates it into two or ten or a billion distinct world branches (with the same measurement outcome, but possibly different with respect to a finer-grained description), the total measure remains the same. In other words, the amplitude-squared weight assigned to a class of worlds with a certain characteristic is well-defined, even if the number of worlds in that class is not.
As Everett ([5], p. 460) notes, “In order that this general scheme be unambiguous we must first require that the states themselves always be normalized, so that we can distinguish the coefficients from the states”. This presupposes, of course, a norm—and here, indeed, the familiar scalar product—with respect to which the branches can be normalized. It does not presuppose, however, that this scalar product has anything to do with a typicality measure. This follows from the three very plausible criteria just stated.
The measure defined by the branch amplitudes squared is not tied to ignorance, nor interpreted as a “measure of existence”, as [23] proposes. As a typicality measure, its role is to provide a natural characterization of very large (resp. very small) classes of worlds, and whether the reader will find Everett’s account of the Born rule satisfactory is bound to depend on whether she agrees that his criteria for such a measure are natural and well-justified.
To see how the typicality argument proceeds, we consider the paradigmatic example of a series of spin measurements performed on identically prepared electrons in the spin state
It is important to keep in mind that the analysis starts with such wave functions of subsystems, to which the Born rule is actually applied, and then proceeds bottom-up, from subsystems to the universe.
We now denote by and the state of the measurement device (and, in the last resort, the rest of the universe) that has registered “spin up” and “spin down”, respectively. After the first measurement, the joint (and ultimately universal) wave function will be of the form
where the index 1 indicates the first round of the experiment. The “pointer states” and are well-localized in disjoint regions of configuration space so that we have a decoherent superposition. Note, however, that this decomposition of the wave function corresponds to a very coarse-grained partition of the multiverse. In particular, no assumption is made about how many numerically distinct copies of the measurement device indicating “spin up” a term like represents, or even whether there is a well-defined number.
With the second measurement, the wave function splits anew:
The first three steps of the branching process are shown in Figure 2. We see the emergence of a structure reminiscent of the Galton board (although the discrete branching structure must be taken with a grain of salt). The conservation of the measure in each branch can be readily verified.
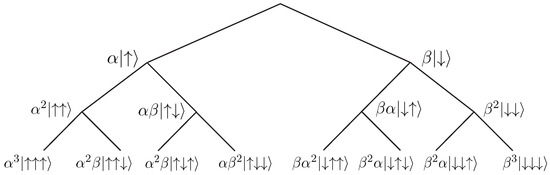
Figure 2.
Branching Many-Worlds histories after three spin measurements. Successive arrows indicate successive outcomes. Adapted from Barrett [33].
After n rounds of spin measurements, the total -weight of branches in which the outcome “spin up” was registered exactly k-times is . Writing and , we recognize this as a Bernoulli process with n independent trials and “success” probability p. A simple application of the weak law of large numbers thus allows us to conclude that, for large n, the typical relative frequency of spin up is , matching the Born statistics predicted by quantum mechanics.
The result involves again three different measures that we have to keep apart:
- the typicality measure defined in terms of branch amplitudes of the universal wave function and uniquely determined by the stationarity condition;
- empirical distributions (frequencies) that obtain within world branches, here for a sequence of spin measurements on identically prepared particles;
- the theoretical Born probabilities defined in terms of the quantum state (the wave function or perhaps density matrix) of subsystems, e.g., by . They are shown to approximate relative frequencies in typical branches.
In conclusion, the Born probabilities describe (to a good approximation) long-term frequencies along typical world branches, where “typical” is characterized in terms of the stationary typicality measure induced by the universal wave function.
4. Living and Dying in the Multiverse
What have we accomplished in regard to the probability problem? Everett’s analysis establishes that Born statistics holds across typical histories of the constantly branching multiverse. One would now like to conclude with an empirical prediction and say something like, “Hence, I should expect to experience a typical history consistent with the Born rule”. But the indexical I does not pick out an individual with a unique future history. My current branch will split repeatedly, and there will be future versions of me who experience very different statistics.
I see no way around the conclusion that the Many-Worlds theory lacks a certain predictive quality. When we ask what statistical regularity we will observe, the answer is always that any possible sequence of outcomes will be observed by some of our “descendants”. But I contend that, based on the Typicality Principle stated in Section 2, Everett’s argument successfully grounds post-factum explanations. When I lie on my deathbed and wonder why I have experienced a history consistent with standard quantum mechanics, I will die in peace knowing that this is typical, that nearly all Many-Worlds histories—in the most natural sense of “nearly all” that the theory allows—manifest phenomena consistent with Born’s statistical hypothesis.
Because of the persistent difficulty in making sense of probabilistic predictions, Everett’s account does not resolve all doubts about whether the “Many Worlds theory can recover the usual understanding of the implications of Born’s Rule” ([3], p. 189). But if one understands the probability problem as one of accounting for objective statistical regularities, a typicality result is certainly optimal in the following sense: Born statistics are the empirical regularity we need to explain, and establishing that they obtain in nearly all world branches is the best we can hope for since the Born rule will definitely be false in some.
Those who regard the justification of Born’s rule primarily as a problem of decision making should also be happy with Everett’s result. It allows us to conclude that we should follow the Born rule to maximize utility for typical future selves. This is a reasonable maxim since, for atypical branches, all bets are off anyway. We cannot make rational choices for descendants for whom the fundamental laws of nature will manifest in unpredictable and unrecognizable ways. Even from the perspective of logical parsimony, Everett’s account—with three axioms for the typicality measure and adding one rationality principle for typicality—fares better than most contemporary alternatives.
For critics who insist that “typicality” is just another word for “high probability”, Wilhelm [13] (in addition to discussing formal, conceptual, and metaphysical differences between typicality and probability) makes the interesting observation that Everett’s typicality explanation is manifestly distinct from a probabilistic explanation—at least if one agrees that probabilistic explanations presuppose only one of multiple alternatives to actually obtain.
“[I]n Everettian quantum mechanics, the various possible outcomes of any given experiment all obtain. [...] But in probabilistic explanations, that cannot happen. In probabilistic explanations, the event invoked in the explanandum is the only outcome, of the various possible mutually exclusive outcomes, that occurs”.
One might try to evade Wilhelm’s argument by falling back on self-locating probabilities: only one of the copies of D.L. existing in the multiverse is the branch-indexical I. But me being me does not seem like the right explanandum. There is no self-locating uncertainty in the deathbed scenario; I know what life I have lived and hence what branch of the multiverse I have inhabited. For better or worse, the typicality explanation ends with the fact that the Born rule holds across the vast majority of world branches. To ask further, for the probability that I find myself on any one of the branches (as if my ego had been somehow thrown at random into the multiverse) strikes me as redundant at best and meaningless at worst.
5. Is Everett’s Derivation Circular?
Finally, one must wonder why modern Everettians have almost universally dismissed Everett’s account of the Born rule that came with the birth of the Many-Worlds interpretation. The most common objection seems to be that Everett’s derivation involves a circularity. Wallace, in his authoritative book The Emergent Multiverse, expresses this charge very pointedly:
In his original paper (1957) [Everett] proved that if a measurement is repeated arbitrarily often, the combined mod-squared amplitude of all branches on which the relative frequencies are not approximately correct will tend to zero. And of course this is circular: it proves not that mod-squared amplitude equals relative frequency, but only that mod-squared amplitude equals relative frequency with high mod-squared amplitude.
Substitute ‘probability’ for ‘mod-squared amplitude’, though, and the circularity should sound familiar; indeed, Everett’s theorem (as is well known) is just the Law of Large Numbers transcribed into quantum mechanics. So the circularity in Everett’s argument is just the circularity in the simplest form of frequentism, disguised by unfamiliar language. That simplest form of frequentism may indeed be hopeless, but so far Everettian quantum mechanics has neither helped nor hindered it.([17], p. 127)
But Everett does not argue that probability equals relative frequency with high probability. He argues that relative frequencies equal mod-squared amplitudes in nearly all world branches, and there is nothing circular about that. “Probability” is not explained in terms of “probability”, nor do we enter an infinite regress of frequencies of frequencies of frequencies. In any case, Everett’s argument is not based on the simplest form of frequentism but on typicality, a concept he explicitly appeals to. For a detailed discussion of how typicality avoids the main objections against (actual and hypothetical) frequentism, I refer the reader to Hubert (2021) [10].
The circularity charge against Everett is easily fueled by the misperception that his derivation is simply “ in, out”, that something tantamount to Born’s rule is already assumed by using branch amplitudes squared as the typicality measure. To understand why this is wrong, one must appreciate the different meanings and statuses of the measures and quantum states involved. The typicality measure is defined in terms of the universal wave function and justified by Everett’s three assumptions discussed in Section 3. Its role is to provide a natural and well-defined notion of “nearly all world branches”, and its status analogous to that of the stationary Liouville measure as the natural typicality measure for classical mechanics. The Born rule is defined in terms of quantum states of subsystems, e.g., states like (5) that we prepare for particles undergoing a measurement experiment. It turns out to describe relative frequencies (in ensembles of subsystems) along typical world branches. The status of the -distribution is similar to that of the binomial distribution for particles on the Galton board, which we discussed in Section 2, or to the status of the Maxwell distribution that Boltzmann derived as the equilibrium distribution of an ideal gas. Boltzmann showed that for nearly all microstates (with respect to the stationary Liouville measure), the relative frequency of particles with velocity in is approximately . Whoever claims that this seminal result is circular, must at least admit that Everett is in good company.
In the Everettian case, we have the mathematically convenient but didactically unfortunate situation that the natural typicality measure and the derived probability law describing typical frequencies have the same mathematical form. Both are “amplitudes squared”—for world branches of the universal wave function and projections of subsystem wave functions, respectively. But this is a non-trivial feature of the quantum theory and its linear Schrödinger dynamics. It is a result, not a premise, of the statistical analysis. In particular, we could not have run the same argument with branch amplitudes to the power as typicality measure and infer that typical frequencies are described by a probability law. Such a derivation would already fail because the weights of the world branches would not be conserved under the branching process.
In conclusion, Everett’s typicality account of the Born rule is neither conceptually nor logically circular. And its mathematical simplicity should not blind us to the fact that it is quite profound.
Funding
This research received no external funding. The author is the Women’s Division Career Advancement Chair Fellow at the Technion and gratefully acknowledges support from the program.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
I thank Lev Vaidman, two anonymous referees, and participants of the 2022 workshop “The Many-Worlds Interpretation of Quantum Mechanics” in Tel Aviv for valuable comments (including the critical ones). I thank Stephen Lyle for his help with the proofreading.
Conflicts of Interest
The author declares no conflict of interest.
References
- Vaidman, L. Many-Worlds Interpretation of Quantum Mechanics. In The Stanford Encyclopedia of Philosophy, Fall 2021 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2021. [Google Scholar]
- Bricmont, J. Making Sense of Quantum Mechanics; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Maudlin, T. Philosophy of Physics: Quantum Theory; Princeton University Press: Princeton, NJ, USA, 2019. [Google Scholar]
- Everett, H. The Theory of the Universal Wave Function. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1956. [Google Scholar]
- Everett, H. “Relative State” Formulation of Quantum Mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef]
- Goldstein, S. Boltzmann’s Approach to Statistical Mechanics. In Chance in Physics: Foundations and Perspectives; Bricmont, J., Dürr, D., Galavotti, M.C., Ghirardi, G., Petruccione, F., Zanghì, N., Eds.; Springer: Berlin, Germany, 2001; pp. 39–54. [Google Scholar]
- Lazarovici, D.; Reichert, P. Typicality, Irreversibility and the Status of Macroscopic Laws. Erkenntnis 2015, 80, 689–716. [Google Scholar] [CrossRef]
- Bricmont, J. Making Sense of Statistical Mechanics; Undergraduate Lecture Notes in Physics; Springer International Publishing: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Goldstein, S. Typicality and Notions of Probability in Physics. In Probability in Physics; Ben-Menahem, Y., Hemmo, M., Eds.; The Frontiers Collection; Springer: Berlin/Heidelberg, Germany, 2012; pp. 59–71. [Google Scholar] [CrossRef]
- Hubert, M. Reviving Frequentism. Synthese 2021, 199, 5255–5284. [Google Scholar] [CrossRef]
- Lazarovici, D. Typicality versus Humean Probabilities as the Foundation of Statistical Mechanics. In The Probability Map of the Universe: Essays on David Albert’s Time and Chance; Loewer, B., Winsberg, E., Weslake, B., Eds.; Harvard University Press: Cambridge, MA, USA, 2023. [Google Scholar]
- Maudlin, T. The Grammar of Typicality. In Statistical Mechanics and Scientific Explanation: Determinism, Indeterminism and Laws of Nature; Allori, V., Ed.; World Scientific: Singapore, 2020. [Google Scholar]
- Wilhelm, I. Typical: A Theory of Typicality and Typicality Explanation. Br. J. Philos. Sci. 2019, 73, 561–581. [Google Scholar] [CrossRef]
- Wilhelm, I. The Typical Principle. Br. J. Philos. Sci. 2022; Online First. [Google Scholar] [CrossRef]
- Dürr, D.; Goldstein, S.; Zanghì, N. Quantum Equilibrium and the Origin of Absolute Uncertainty. J. Stat. Phys. 1992, 67, 843–907. [Google Scholar] [CrossRef]
- Barrett, J.A. The Quantum Mechanics of Minds and Worlds, 1st ed.; Oxford University Press: Oxford, NY, USA, 2001. [Google Scholar]
- Wallace, D. The Emergent Multiverse: Quantum Theory According to the Everett Interpretation; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Carroll, S.M.; Singh, A. Mad-Dog Everettianism: Quantum Mechanics at Its Most Minimal. arXiv 2018, arXiv:1801.08132. [Google Scholar] [CrossRef]
- Vaidman, L. Ontology of the Wave Function and the Many-Worlds Interpretation. In Quantum Worlds: Perspectives on the Ontology of Quantum Mechanics; López, C., Holik, F., Lombardi, O., Fortin, S., Eds.; Cambridge University Press: Cambridge, UK, 2019; pp. 93–106. [Google Scholar] [CrossRef]
- Ney, A. The World in the Wave Function: A Metaphysics for Quantum Physics; Oxford University Press: Oxford, NY, USA, 2021. [Google Scholar]
- Maudlin, T. Can the World Be Only Wave-Function? In Many Worlds? Everett, Quantum Theory, and Reality; Saunders, S., Barrett, J., Kent, A., Wallace, D., Eds.; Oxford University Press: Oxford, UK, 2010; pp. 121–143. [Google Scholar]
- Lazarovici, D.; Reichert, P. The Point of Primitive Ontology. Found. Phys. 2022, 52, 120. [Google Scholar] [CrossRef]
- Vaidman, L. On Schizophrenic Experiences of the Neutron or Why We Should Believe in the Many-worlds Interpretation of Quantum Theory. Int. Stud. Philos. Sci. 1998, 12, 245–261. [Google Scholar] [CrossRef]
- Sebens, C.T.; Carroll, S.M. Self-Locating Uncertainty and the Origin of Probability in Everettian Quantum Mechanics. Br. J. Philos. Sci. 2018, 69, 25–74. [Google Scholar] [CrossRef]
- McQueen, K.J.; Vaidman, L. In defence of the self-location uncertainty account of probability in the many-worlds interpretation. Stud. Hist. Philos. Sci. Part Stud. Hist. Philos. Mod. Phys. 2019, 66, 14–23. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum Theory of Probability and Decisions. Proc. R. Soc. London Ser. Math. Phys. Eng. Sci. 1999, 455, 3129–3137. [Google Scholar] [CrossRef]
- Maudlin, T. Critical Study—David Wallace, The Emergent Multiverse: Quantum Theory According to the Everett Interpretation. Noûs 2014, 48, 794–808. [Google Scholar] [CrossRef]
- Bell, J.S. Speakable and Unspeakable in Quantum Mechanics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Maudlin, T. What Could Be Objective about Probabilities? Stud. Hist. Philos. Sci. Part Stud. Hist. Philos. Mod. Phys. 2007, 38, 275–291. [Google Scholar] [CrossRef]
- Dürr, D.; Froemel, A.; Kolb, M. Einführung in Die Wahrscheinlichkeitstheorie Als Theorie Der Typizität; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Boltzmann, L. Vorlesungen über Gastheorie; J. A. Barth: Leipzig, Germany, 1896; Volume 1. [Google Scholar]
- Shafer, G.; Vovk, V. The Sources of Kolmogorov’s Grundbegriffe. Stat. Sci. 2006, 21, 70–98. [Google Scholar] [CrossRef]
- Barrett, J.A. Typicality in Pure Wave Mechanics. Fluct. Noise Lett. 2016, 15, 1640009. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).