A Study of Strong Confinement Regions Using Informational Entropy
Abstract
1. Introduction
2. Theoretical Background
2.1. System of Interest
2.2. Shannon Informational Entropy
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Connerade, J.P. Confining and compressing the atom. Eur. Phys. J. D 2020, 74, 211. [Google Scholar] [CrossRef]
- Sen, K.D. (Ed.) Electronic Structure of Quantum Confined Atoms and Molecules; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Sabin, J.R.; Brändas, E.; Cruz, S.A. (Eds.) Advances in Quantum Chemistry: Theory of Confined Quantum Systems vol 57 e 58; Academic Press: New York, NY, USA, 2009. [Google Scholar]
- García-Miranda, J.J.; Garza, J.; Ibarra, I.A.; Martínez, A.; Martínez-Sánchez, M.A.; Rivera-Almazo, M.; Vargas, R. Electronic Structure of Systems Confined by Several Spatial Restrictions. In Chemical Reactivity in Confined Systems; John Wiley Sons, Ltd.: Hoboken, NJ, USA, 2021; Chapter 4; p. 69. [Google Scholar] [CrossRef]
- LEY-KOO, E. Recent progress in confined atoms and molecules: Superintegrability and symmetry breakings. Rev. Mex. Fis. 2018, 64, 326. [Google Scholar] [CrossRef]
- El-Gammal, F.N. Confined atoms in plasma environment: Variational Monte Carlo calculations. Mol. Phys. 2021, 119, e1879302. [Google Scholar] [CrossRef]
- Maniero, A.M.; de Carvalho, C.R.; Prudente, F.V.; Jalbert, G. Oscillating properties of a two-electron quantum dot in the presence of a magnetic field. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 185001. [Google Scholar] [CrossRef]
- Saha, S.; Jose, J. Shannon entropy as a predictor of avoided crossing in confined atoms. Int. J. Quantum Chem. 2020, 120, e26374. [Google Scholar] [CrossRef]
- Cruz, E.; Aquino, N.; Prasad, V. Localization–delocalization of a particle in a quantum corral in presence of a constant magnetic field. Eur. Phys. J. D 2021, 75, 106. [Google Scholar] [CrossRef]
- Deshmukh, P.C.; Jose, J.; Varma, H.R.; Manson, S.T. Electronic structure and dynamics of confined atoms. Eur. Phys. J. D 2021, 75, 166. [Google Scholar] [CrossRef]
- Prudente, F.V.; Guimarães, M.N. Confined Quantum Systems Using the Finite Element and Discrete Variable Representation Methods. In Electronic Structure of Quantum Confined Atoms and Molecules; Sen, K.D., Ed.; Springer: Cham, Switzerland, 2014; Chapter 5; pp. 101–143. [Google Scholar]
- Zicovich-Wilson, C.; Planelles, J.H.; Jaskólski, W. Spatially Confined Simple Quantum Mechanical Systems. Int. J. Quantum Chem. 1994, 50, 429. [Google Scholar] [CrossRef]
- Costa, L.S.; Prudente, F.V.; Acioli, P.H.; Neto, J.J.S.; Vianna, J.D.M. A study of confined quantum systems using the Woods-Saxon potential. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 2461. [Google Scholar] [CrossRef]
- Connerade, J.P.; Dolmatov, V.K.; Lakshmi, P.A.; Manson, S.T. Electron structure of endohedrally confined atoms: Atomic hydrogen in an attractive shell. J. Phys. B At. Mol. Opt. Phys. 1999, 32, L239. [Google Scholar] [CrossRef]
- Baltenkov, A.S. Resonances in photoionization cross sections of inner subshells of atoms inside the fullerene cage. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 2745. [Google Scholar] [CrossRef]
- Nascimento, E.M.; Prudente, F.V.; Guimarães, M.N.; Maniero, A.M. A study of the electron structure of endohedrally confined atoms using a model potential. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 015003. [Google Scholar] [CrossRef]
- Salazar, S.J.C.; Laguna, H.G.; Prasad, V.; Sagar, R.P. Shannon-information entropy sum in the confined hydrogenic atom. Int. J. Quantum Chem. 2020, 120, e26188. [Google Scholar] [CrossRef]
- De Morais, G.d.S.T.; Custodio, R. Assessment of a numeric variational method for the solution of confined multielectron atoms. J. Mol. Model. 2021, 27, 212. [Google Scholar] [CrossRef]
- Rodriguez-Bautista, M.; Vargas, R.; Aquino, N.; Garza, J. Electron-density delocalization in many-electron atoms confined by penetrable walls: A Hartree–Fock study. Int. J. Quantum Chem. 2018, 118, e25571. [Google Scholar] [CrossRef]
- Pasteka, L.F.; Helgaker, T.; Saue, T.; Sundholm, D.; Werner, H.J.; Hasanbulli, M.; Major, J.; Schwerdtfeger, P. Atoms and molecules in soft confinement potentials. Mol. Phys. 2020, 118, e1730989. [Google Scholar] [CrossRef]
- Barbosa, T.N.; Almeida, M.M.; Prudente, F.V. A quantum monte carlo study of confined quantum systems: Application to harmonic oscillator and hydrogenic-like atoms. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 055002. [Google Scholar] [CrossRef]
- Prudente, F.V.; Costa, L.S.; Viana, J.D.M. A study of two-electron quantum dot spectrum using discrete variable representation method. J. Chem. Phys. 2005, 123, 224701. [Google Scholar] [CrossRef]
- Bielinska-Waz, D.; Karwowski, J.; Diercksen, G.H.F. Spectra of confined two-electron atoms. J. Phys. B At. Mol. Opt. Phys. 2001, 34, 1987. [Google Scholar] [CrossRef]
- Gueorguiev, V.G.; Rau, A.R.P.; Draayer, J.P. Confined one-dimensional harmonic oscillator as a two-mode system. Am. J. Phys. 2006, 74, 394. [Google Scholar] [CrossRef]
- Montgomery, H.; Aquino, N.; Flores-Riveros, A. The ground state energy of a helium atom under strong confinement. Phys. Lett. A 2010, 374, 2044. [Google Scholar] [CrossRef]
- Aquino, N.; Flores-Riveros, A.; Rivas-Silva, J. The compressed helium atom variationally treated via a correlated Hylleraas wave function. Phys. Lett. A 2003, 307, 326. [Google Scholar] [CrossRef]
- Flores-Riveros, A.; Aquino, N.; Montgomery, H. Spherically compressed helium atom described by perturbative and variational methods. Phys. Lett. A 2010, 374, 1246. [Google Scholar] [CrossRef]
- Sen, K.D. (Ed.) Statistical Complexity: Applications in Electronic Struture; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar] [CrossRef]
- Nascimento, W.S.; Prudente, F.V. Shannon entropy: A study of confined hydrogenic-like atoms. Chem. Phys. Lett. 2018, 691, 401. [Google Scholar] [CrossRef]
- Estañón, C.R.; Aquino, N.; Puertas-Centeno, D.; Dehesa, J.S. Crámer-Rao complexity of the confined two-dimensional hydrogen. Int. J. Quantum Chem. 2021, 121, e26424. [Google Scholar] [CrossRef]
- Mukherjee, N.; Roy, A.K. Information-entropic measures for non-zero l states of confined hydrogen-like ions. Eur. Phys. J. D 2018, 72, 118. [Google Scholar] [CrossRef]
- Majumdar, S.; Mukherjee, N.; Roy, A.K. Various complexity measures in confined hydrogen atom. Chem. Phys. Lett. 2017, 687, 322. [Google Scholar] [CrossRef]
- Jiao, L.; Zan, L.; Zhang, Y.; Ho, Y. Benchmark values of Shannon entropy for spherically confined hydrogen atom. Int. J. Quantum Chem. 2017, 117, e25375. [Google Scholar] [CrossRef]
- Martínez-Flores, C. Shannon entropy and Fisher information for endohedral confined one- and two-electron atoms. Phys. Lett. A 2021, 386, 126988. [Google Scholar] [CrossRef]
- Martínez-Sánchez, M.A.; Vargas, R.; Garza, J. Shannon Entropy for the Hydrogen Atom Confined by Four Different Potentials. Quantum Rep. 2019, 1, 208. [Google Scholar] [CrossRef]
- Nascimento, W.S.; de Almeida, M.M.; Prudente, F.V. Coulomb Correlation and Information Entropies in Confined Helium-Like Atoms. Eur. Phys. J. D 2021, 75, 171. [Google Scholar] [CrossRef]
- Majumdar, S.; Roy, A.K. Shannon Entropy in Confined He-Like Ions within a Density Functional Formalism. Quantum Rep. 2020, 2, 189. [Google Scholar] [CrossRef]
- Lee, M.J.; Jung, Y.D. Characteristics of Shannon’s Information Entropy of Atomic States in Strongly Coupled Plasma. Entropy 2020, 22, 881. [Google Scholar] [CrossRef]
- Zan, L.R.; Jiao, L.G.; Ma, J.; Ho, Y.K. Information-theoretic measures of hydrogen-like ions in weakly coupled Debye plasmas. Phys. Plasmas 2017, 24, 122101. [Google Scholar] [CrossRef]
- Carrillo, R.S.; Gil-Barrera, C.A.; Sun, G.H.; Solaimani, M.; Dong, S.H. Shannon entropies of asymmetric multiple quantum well systems with a constant total length. Eur. Phys. J. Plus 2021, 136, 1060. [Google Scholar] [CrossRef]
- Carrillo, R.S.; Dong, Q.; Sun, G.H.; Silva-Ortigoza, R.; Dong, S.H. Shannon entropy of asymmetric rectangular multiple well with unequal width barrier. Results Phys. 2022, 33, 105109. [Google Scholar] [CrossRef]
- Song, X.D.; Sun, G.H.; Dong, S.H. Shannon information entropy for an infinite circular well. Phys. Lett. A 2015, 379, 1402. [Google Scholar] [CrossRef]
- Gadre, S.R.; Sears, S.B.; Chakravorty, S.J.; Bendale, R.D. Some novel characteristics of atomic information entropies. Phys. Rev. A 1985, 32, 2602. [Google Scholar] [CrossRef] [PubMed]
- Site, L.D. Shannon entropy and many-electron correlations: Theoretical concepts, numerical results, and Collins conjecture. Int. J. Quantum Chem. 2014, 115, 1396. [Google Scholar] [CrossRef]
- Saha, S.; Jose, J. Shannon entropy as an indicator of correlation and relativistic effects in confined atoms. Phys. Rev. A 2020, 102, 052824. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Osawa, E. Information Entropy of Fullerenes. J. Chem. Inf. Model. 2015, 55, 1576. [Google Scholar] [CrossRef]
- Sabirov, D.S. Information entropy of mixing molecules and its application to molecular ensembles and chemical reactions. Comput. Theor. Chem. 2020, 1187, 112933. [Google Scholar] [CrossRef]
- Sabirov, D.S. Information entropy changes in chemical reactions. Comput. Theor. Chem. 2018, 1123, 169. [Google Scholar] [CrossRef]
- Park, K.; Kim, J.; Moon, S.; An, K. Maximal Shannon entropy in the vicinity of an exceptional point in an open microcavity. Sci. Rep. 2020, 10, 12551. [Google Scholar] [CrossRef] [PubMed]
- Nascimento, W.S.; Prudente, F.V. Sobre um estudo da entropia de Shannon no contexto da mecânica quântica: Uma aplicação ao oscilador harmônico livre e confinado. Quim. Nova 2016, 39, 757. [Google Scholar] [CrossRef]
- Guimarães, M.N.; Prudente, F.V. A study of the confined hydrogen atom using the finite element method. J. Phys. B At. Mol. Phys. 2005, 38, 2811. [Google Scholar] [CrossRef]
- Prudente, F.V.; Soares Neto, J.J. Optimized mesh for the finite-element method using a quantum-mechanical procedure. Chem. Phys. Lett. 1999, 302, 43. [Google Scholar] [CrossRef]
- Nascimento, W.S.; de Almeida, M.M.; Prudente, F.V. Information and quantum theories: An analysis in one-dimensional systems. Eur. J. Phys. 2020, 41, 025405. [Google Scholar] [CrossRef]
- Goldman, S.; Joslin, C. Spectroscopic properties of an isotropically compressed hydrogen atom. J. Phys. Chem. 1992, 96, 6021. [Google Scholar] [CrossRef]
- Yáñez, R.J.; Van Assche, W.; González-Férez, R.; Dehesa, J.S. Entropic integrals of hyperspherical harmonics and spatial entropy of D-dimensional central potentials. J. Math. Phys. 1999, 40, 5675. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 1975, 44, 129. [Google Scholar] [CrossRef]
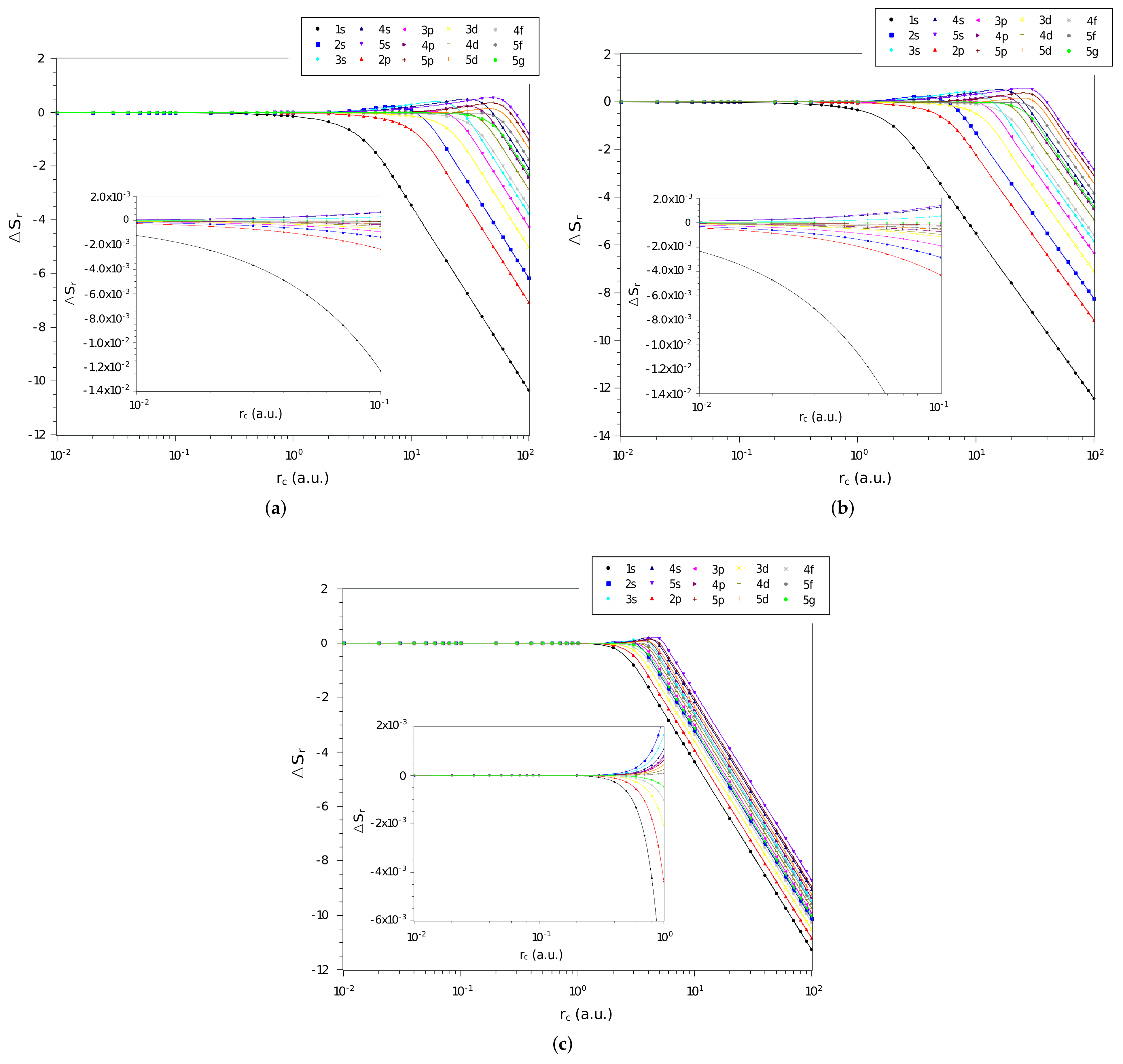
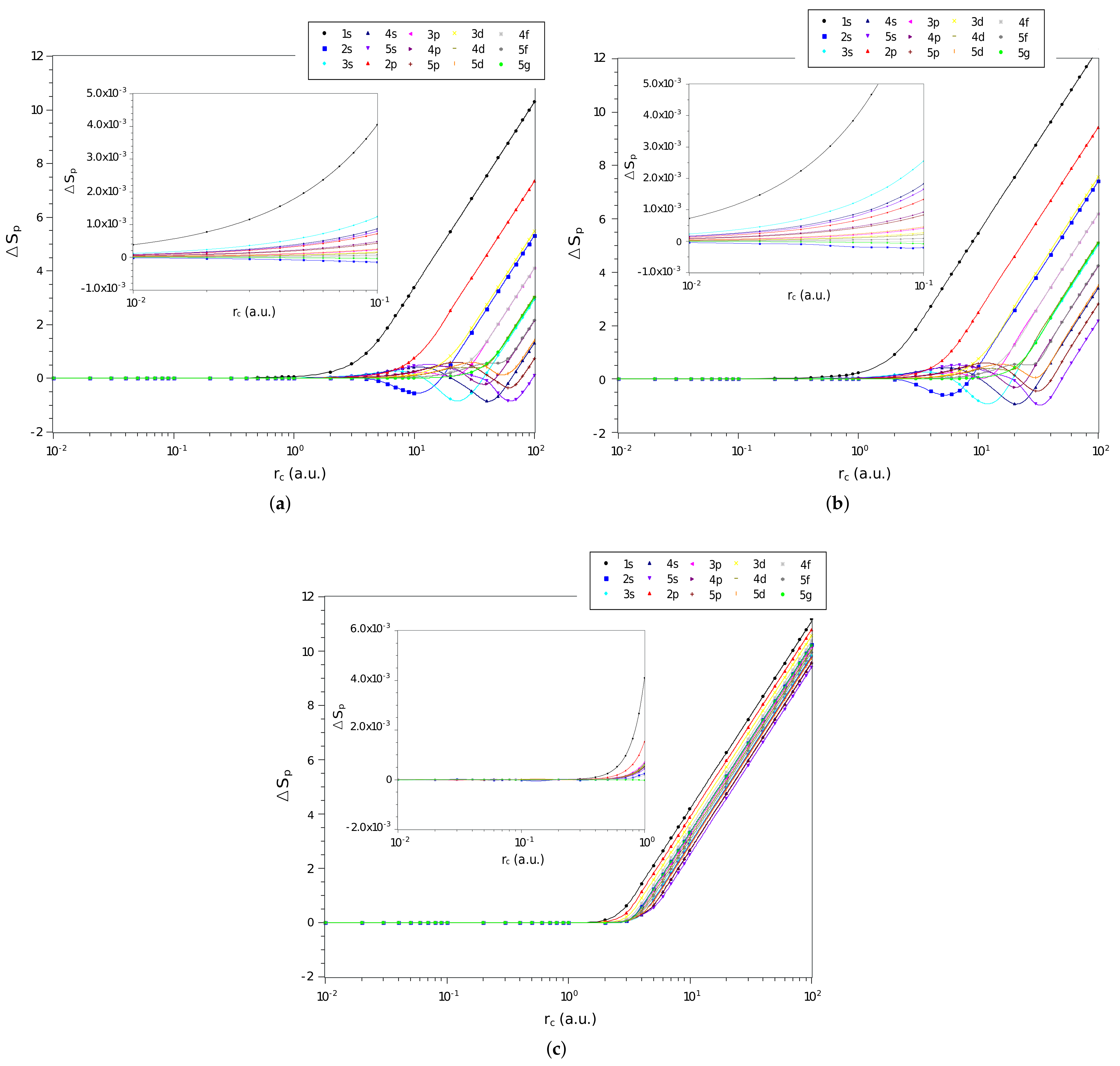
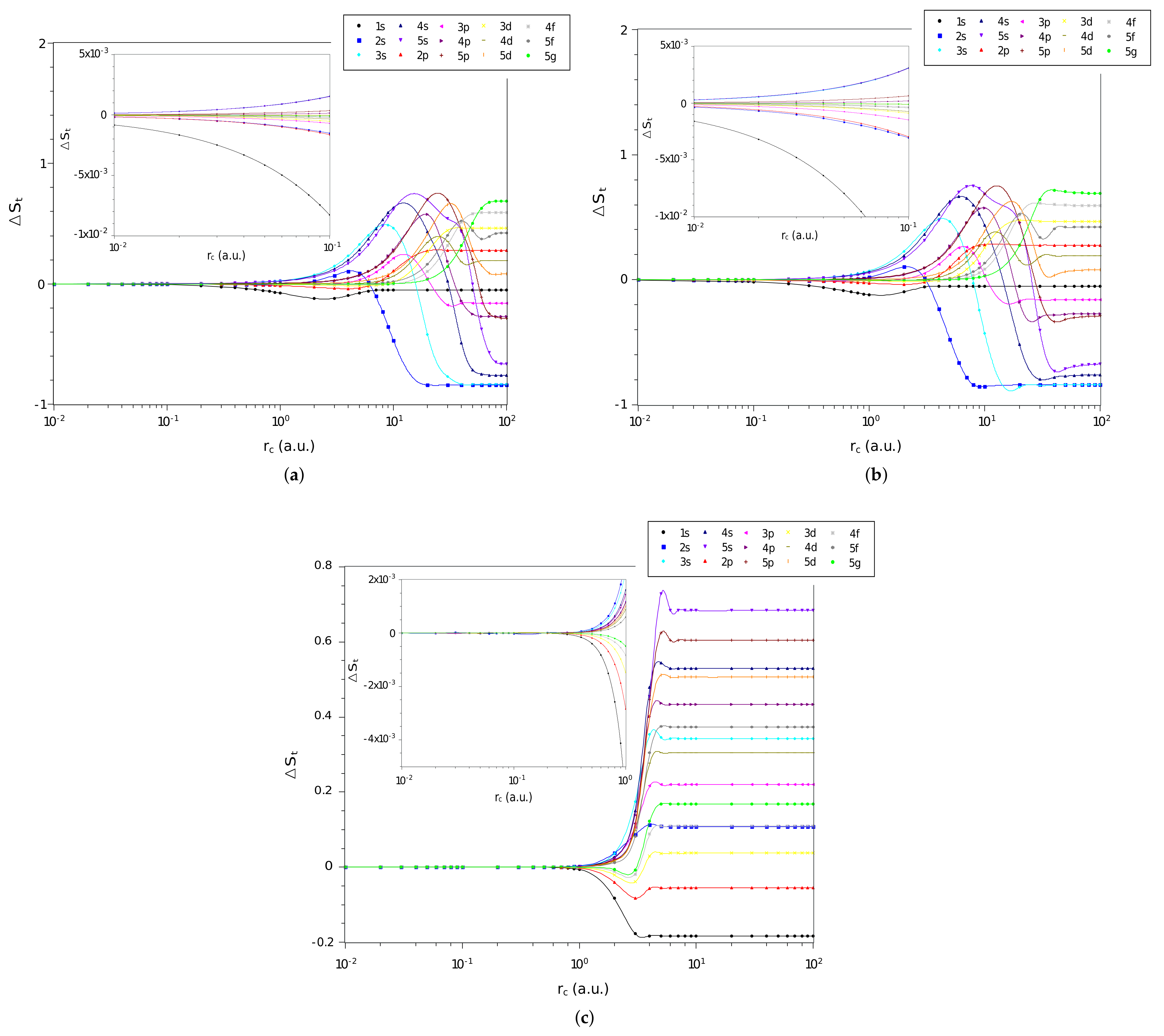


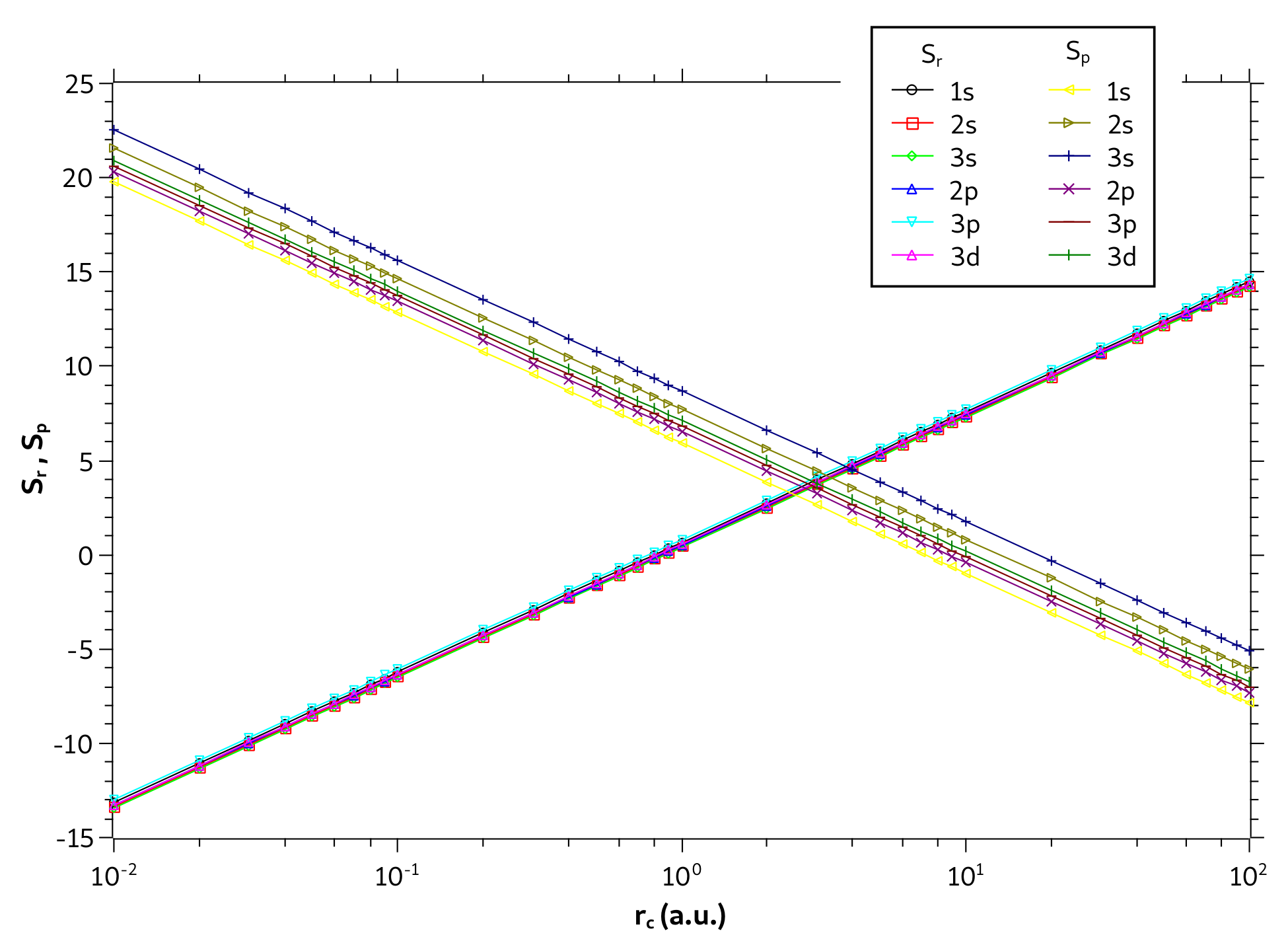

| Strong | Intermediate | Weak | ||
|---|---|---|---|---|
| HC | 0.040 | |||
| IS | 0.035 | |||
| HO | 0.000 | – | – |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, A.d.J.; Prudente, F.V.; Guimarães, M.N.; Nascimento, W.S. A Study of Strong Confinement Regions Using Informational Entropy. Quantum Rep. 2022, 4, 544-557. https://doi.org/10.3390/quantum4040039
Santos AdJ, Prudente FV, Guimarães MN, Nascimento WS. A Study of Strong Confinement Regions Using Informational Entropy. Quantum Reports. 2022; 4(4):544-557. https://doi.org/10.3390/quantum4040039
Chicago/Turabian StyleSantos, Ademir de J., Frederico V. Prudente, Marcilio N. Guimarães, and Wallas S. Nascimento. 2022. "A Study of Strong Confinement Regions Using Informational Entropy" Quantum Reports 4, no. 4: 544-557. https://doi.org/10.3390/quantum4040039
APA StyleSantos, A. d. J., Prudente, F. V., Guimarães, M. N., & Nascimento, W. S. (2022). A Study of Strong Confinement Regions Using Informational Entropy. Quantum Reports, 4(4), 544-557. https://doi.org/10.3390/quantum4040039






