Fricke Topological Qubits
Abstract
1. Introduction
2. The -Character Variety of a Manifold
A Sage Program for Computing the -Character Variety of
3. The Cubic Surface and Two-Bridge Links
3.1. The -Character Variety for a Once Punctured Torus
3.2. The Surface , the Link and Fricke Topological Qubits
Topological Qubits from
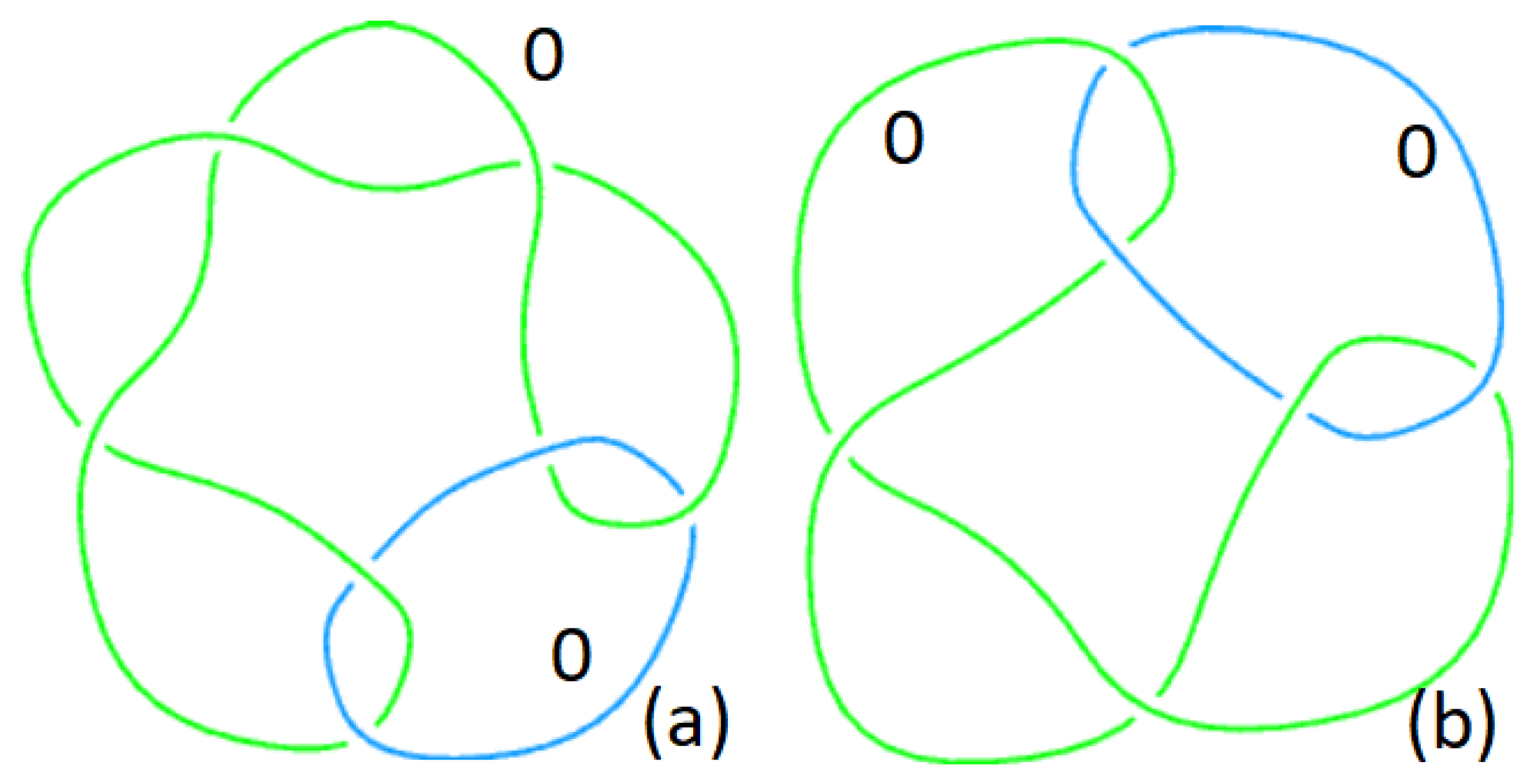
3.3. The Surface and the Link
4. The Fricke Cubic Surface and Three-Bridge Links
4.1. The -Character Variety for the Quadruply Punctured Sphere
4.2. A Compact Component of
4.3. The Character Variety for the Manifold and for Its Covering Manifolds
4.4. Painlevé VI and the Riemann-Hilbert Correspondence
5. Discussion and Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Buluta, I.; Ashhab, S.; Nori, F. Natural and artificial atoms for quantum computation. Rep. Prog. Phys. 2011, 74, 104401. [Google Scholar] [CrossRef]
- Obada, A.S.F.; Hessian, H.A.; Mohamed, A.B.A.; Homid, A.H. A proposal for the realization of universal quantum gates via superconducting qubits inside a cavity. Ann. Phys. 2013, 334, 47–57. [Google Scholar] [CrossRef]
- Top 10 Quantum Computing Experiments of 2019. Available online: https://medium.com/swlh/top-quantum-computing-experiments-of-2019-1157db177611 (accessed on 1 November 2022).
- Timeline of Quantum Computing and Communication. Available online: https://en.wikipedia.org/wiki/Timeline_of_quantum_computing_and_communication (accessed on 1 November 2022).
- Topological Quantum Computer. Available online: https://en.wikipedia.org/wiki/Topological_quantum_computer (accessed on 1 January 2021).
- Pachos, J.K. Introduction to Topological Quantum Computation; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Amaral, M.; Chester, D.; Fang, F.; Irwin, K. Exploiting anyonic behavior of quasicrystals for topological quantum computing. Symmetry 2022, 14, 1780. [Google Scholar] [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Fang, F.; Chester, D.; Irwin, K. Character varieties and algebraic surfaces for the topology of quantum computing. Symmetry 2022, 14, 915. [Google Scholar] [CrossRef]
- Asselmeyer-Maluga, T. Topological quantum computing and 3-manifolds. Quantum Rep. 2021, 3, 153–165. [Google Scholar] [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Universal quantum computing and three-manifolds. Symmetry 2018, 10, 773. [Google Scholar] [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Group geometrical axioms for magic states of quantum computing. Mathematics 2019, 7, 948. [Google Scholar] [CrossRef]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Quantum computation and measurements from an exotic space-time R4. Symmetry 2020, 12, 736. [Google Scholar] [CrossRef]
- Goldman, W.M. Trace coordinates on Fricke spaces of some simple hyperbolic surfaces. In Handbook of Teichmüller Theory; European Mathematical Society: Zürich, Switzerland, 2009; Volume 13, pp. 611–684. [Google Scholar]
- Hehl, F.W.; von der Heyde, P.; Kerlick, G.D.; Nester, J.M. General relativity with spin and torsion: Foundations and prospects. Rev. Mod. Phys. 1976, 48, 393–416. [Google Scholar] [CrossRef]
- Yang, C.N. Integral Formalism for Gauge Fields. Phys. Rev. Lett. 1974, 33, 445, Erratum in Phys. Rev. Lett. 1975, 35, 1748. [Google Scholar] [CrossRef]
- MacDowell, S.W.; Mansouri, F. Unified geometric theory of gravity and supergravity. Phys. Rev. Lett. 1977, 38, 739–742, Erratum in Phys. Rev. Lett. 1977, 38, 1376. [Google Scholar] [CrossRef]
- Trautman, A. The geometry of gauge fields. Czechoslov. J. Phys. B 1979, B29, 107–116. [Google Scholar] [CrossRef]
- Ryu, S.; Takayanagi, T. Holographic derivation of entanglement entropy from AdS/CFT. Phys. Rev. Lett. 2006, 96, 181602. [Google Scholar] [CrossRef] [PubMed]
- Van Raamsdonk, M. Building up spacetime with quantum entanglement. Gen. Relativ. Gravit. 2010, 42, 2323. [Google Scholar] [CrossRef]
- Ashley, C.; Burelle, J.P.; Lawton, S. Rank 1 character varieties of finitely presented groups. Geom. Dedicata 2018, 192, 1–19. [Google Scholar] [CrossRef]
- Python Code to Compute Character Varieties. Available online: http://math.gmu.edu/~slawton3/Main.sagews (accessed on 1 May 2021).
- Bosma, W.; Cannon, J.J.; Fieker, C.; Steel, A. (Eds.) Handbook of Magma Functions; Edition 2.23; University of Sydney: Sydney, Australia, 2017; 5914p. [Google Scholar]
- Cantat, S.; Loray, F. Holomorphic dynamics, Painlevé VI equation and character varieties. arXiv 2007, arXiv:0711.1579. [Google Scholar]
- Farb, B.; Margalit, D. A Primer on Mapping Class Groups; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Cantat, S. Bers and Hénon, Painlevé and Schrödinger. Duke Math. J. 2009, 149, 411–460. [Google Scholar] [CrossRef]
- The Thistlethwaite Link Table. Available online: http://katlas.org/wiki/The_Thistlethwaite_Link_Table (accessed on 1 September 2021).
- Benedetto, R.L.; Goldman, W.M. The topology of the relative character varieties of a quadruply-punctured sphere. Exp. Math. 1999, 8, 85–103. [Google Scholar] [CrossRef]
- Iwasaki, K. An area-preserving action of the modular group on cubic surfaces and the Painlevé VI. Commun. Math. Phys. 2003, 242, 185–219. [Google Scholar] [CrossRef]
- Inaba, M.; Iwasaki, K.; Saito, M.H. Dynamics of the sixth Painlevé equation. arXiv 2005, arXiv:math.AG/0501007. [Google Scholar]
- Scorpian, A. The Wild World of 4-Manifolds; American Mathematical Society: Providence, RI, USA, 2005. [Google Scholar]
- Planat, M.; Aschheim, R.; Amaral, M.M.; Irwin, K. Quantum computing, Seifert surfaces and singular fibers. Quantum Rep. 2019, 1, 12–22. [Google Scholar] [CrossRef]
- Wu, Y.-Q. Seifert fibered surgery on Montesinos knots. arXiv 2012, arXiv:1207.0154. [Google Scholar]
- Saito, M.H.; Terajima, H. Nodal curves and Riccati solutions of Painlevé equations. J. Math. Kyoto Univ. 2004, 44, 529–568. [Google Scholar] [CrossRef]
- Deng, D.-L.; Wang, S.-T.; Sun, K.; Duan, L.-M. Probe Knots and Hopf Insulators with Ultracold Atoms. Chin. Phys. Lett. 2018, 35, 013701. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Behavior of Floquet Topological Quantum States in Optically Driven Semiconductors. Symmetry 2019, 11, 1246. [Google Scholar] [CrossRef]
- Smalyukh, I.I. Review: Knots and other new topological effects in liquid crystals and colloids. Rep. Prog. Phys. 2020, 83, 106601. [Google Scholar] [CrossRef]
- Stalhammar, M. Knots and Transport in Topological Matter. Ph.D. Thesis, Stockholm University, Stockholm, Switzerland, 2022. [Google Scholar]
- Mason, L.J.; Woodhouse, N.M.J. Self-duality and the Painlevé transcendents. Nonlinearity 1993, 6, 569–581. [Google Scholar] [CrossRef]
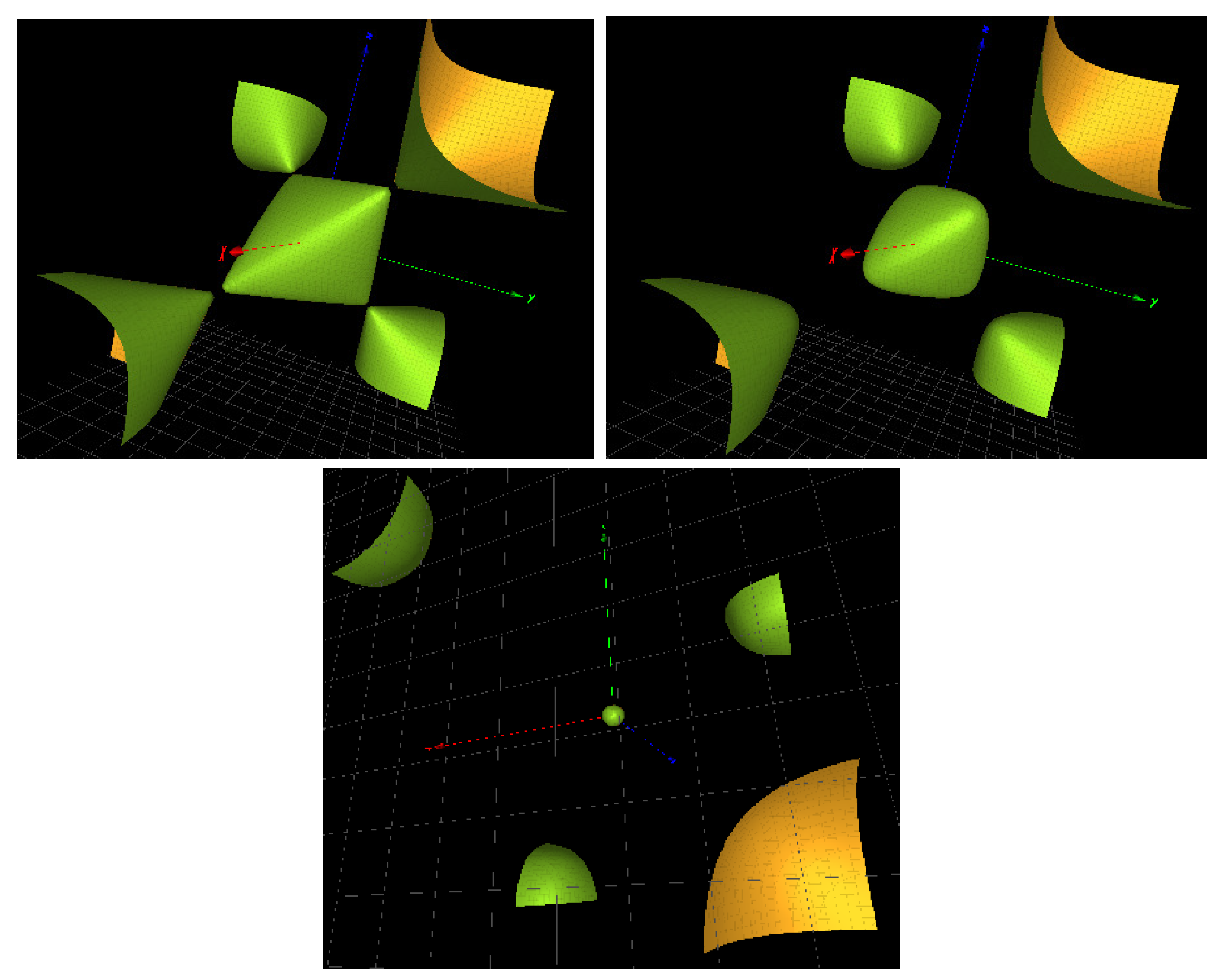
| manifold | ||||||||
| Painlevé type | ||||||||
| char var | T | T | ≈ | T | ≈ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Planat, M.; Chester, D.; Amaral, M.M.; Irwin, K. Fricke Topological Qubits. Quantum Rep. 2022, 4, 523-532. https://doi.org/10.3390/quantum4040037
Planat M, Chester D, Amaral MM, Irwin K. Fricke Topological Qubits. Quantum Reports. 2022; 4(4):523-532. https://doi.org/10.3390/quantum4040037
Chicago/Turabian StylePlanat, Michel, David Chester, Marcelo M. Amaral, and Klee Irwin. 2022. "Fricke Topological Qubits" Quantum Reports 4, no. 4: 523-532. https://doi.org/10.3390/quantum4040037
APA StylePlanat, M., Chester, D., Amaral, M. M., & Irwin, K. (2022). Fricke Topological Qubits. Quantum Reports, 4(4), 523-532. https://doi.org/10.3390/quantum4040037







