Learning Mixed Strategies in Quantum Games with Imperfect Information
Abstract
:1. Introduction
2. Classical and Quantum Games
3. Learning Model
3.1. Learning Algorithm
| Algorithm 1 Agents learning mixed strategies in quantum games |
|
3.2. Decentralized Model
4. Results
4.1. Classic vs. Quantum Performance
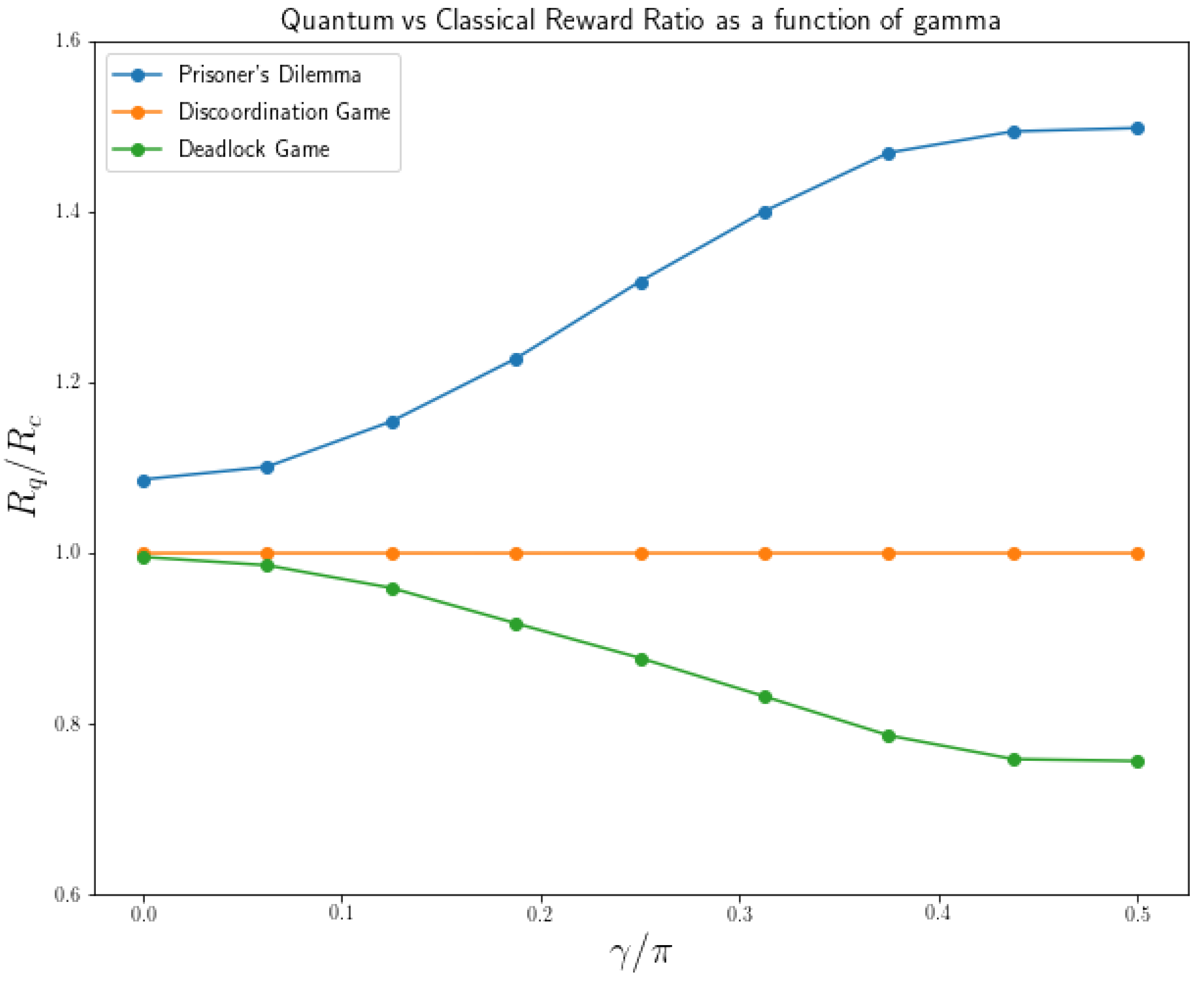
4.2. Entanglement Dependency
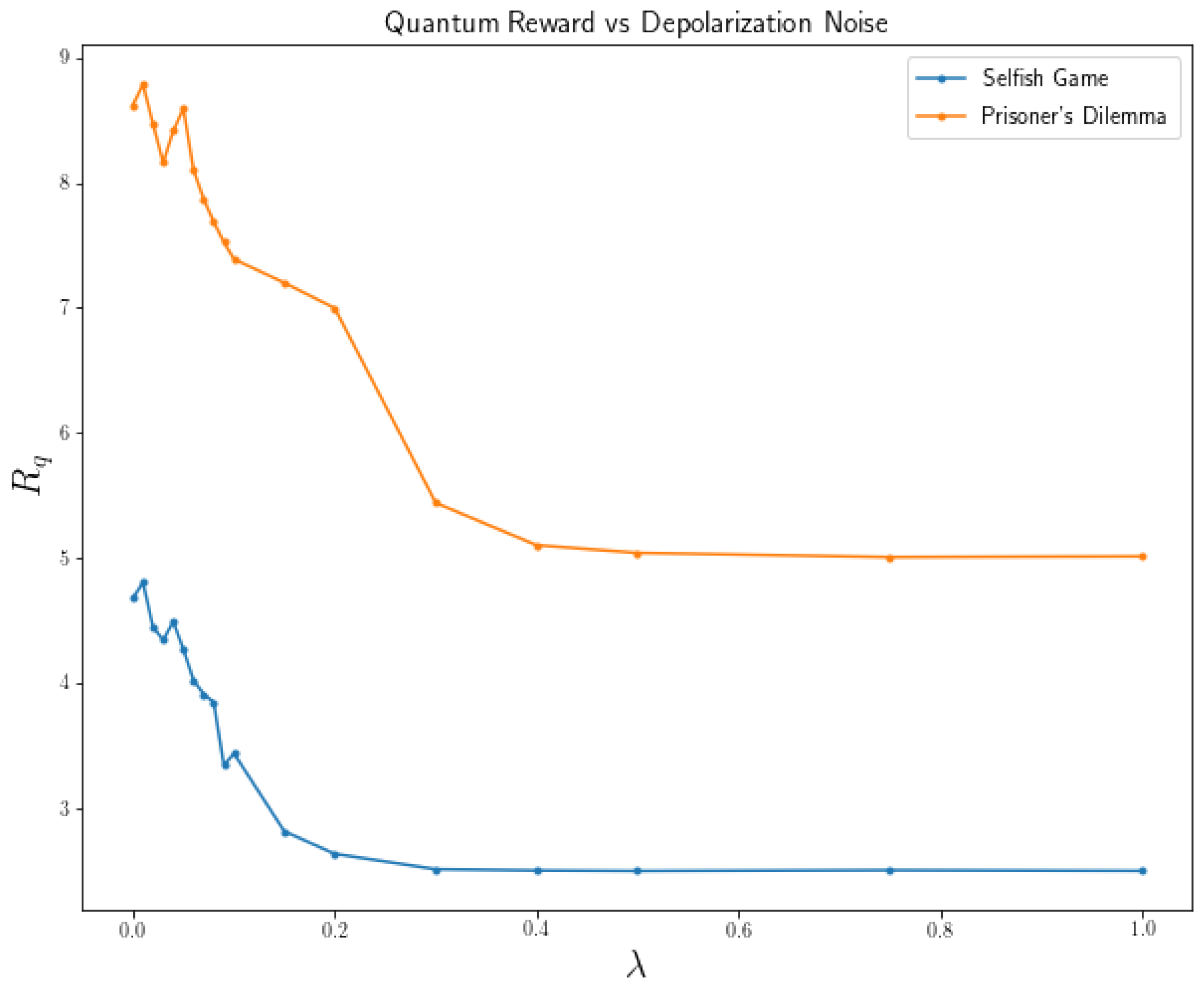
4.3. Noise Dependency
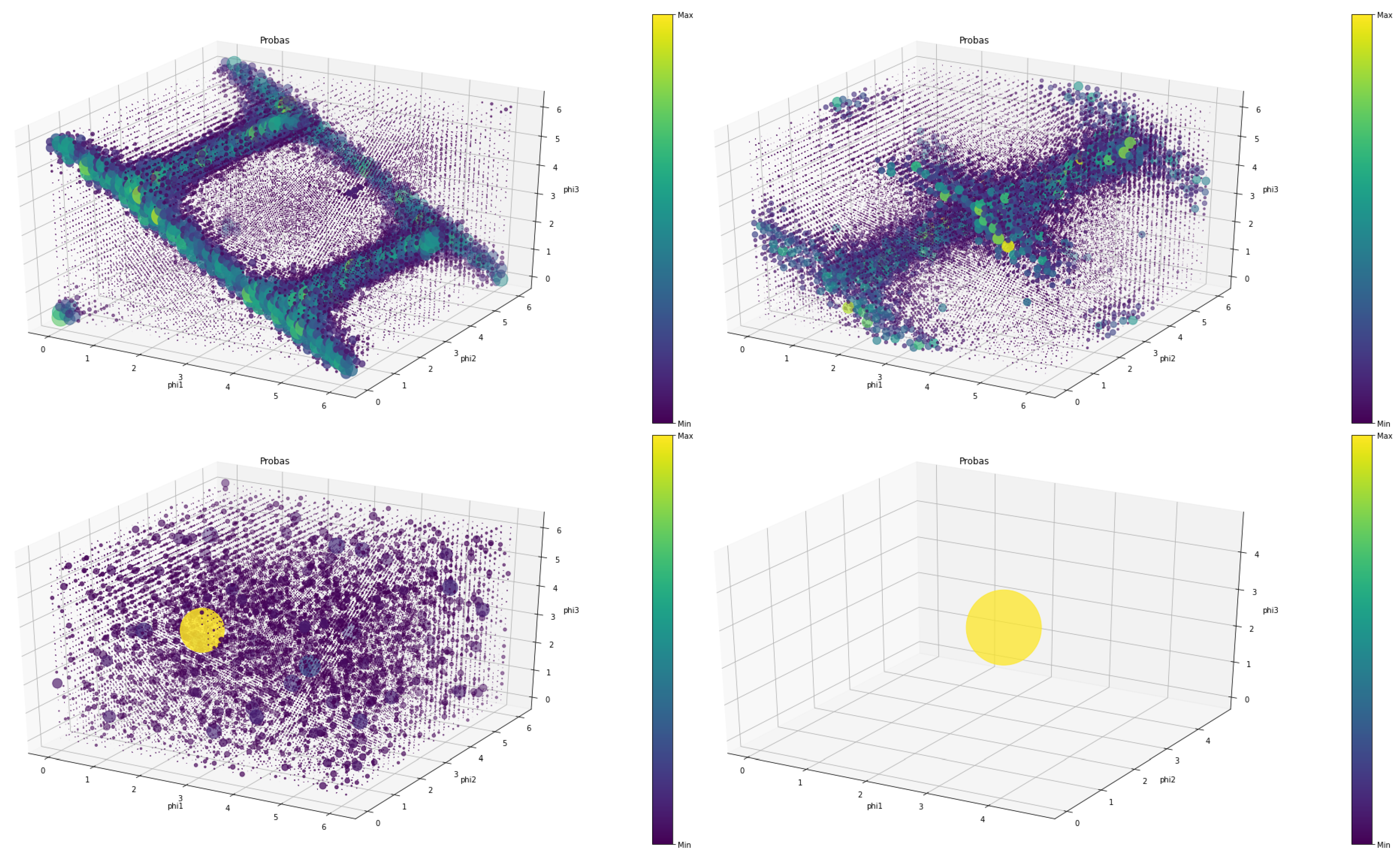
4.4. Mixed Strategies Visualization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Eisert, J.; Wilkens, M.; Lewenstein, M. Quantum games and quantum strategies. Phys. Rev. Lett. 1999, 83, 3077. [Google Scholar] [CrossRef] [Green Version]
- Khan, F.S.; Solmeyer, N.; Balu, R.; Humble, T.S. Quantum games: A review of the history, current state, and interpretation. Quantum Inf. Process. 2018, 17, 1–42. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; Zhang, J.; Koehler, G.J. A survey of quantum games. Decis. Support Syst. 2008, 46, 318–332. [Google Scholar] [CrossRef]
- Benjamin, S.C.; Hayden, P.M. Multiplayer quantum games. Phys. Rev. A 2001, 64, 030301. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Wang, Y.; Liu, J.T.; Wang, K.L. N-player quantum minority game. Phys. Lett. A 2004, 327, 98–102. [Google Scholar] [CrossRef]
- Brunner, N.; Linden, N. Connection between Bell nonlocality and Bayesian game theory. Nat. Commun. 2013, 4, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Kolokoltsov, V.N. Quantum mean-field games with the observations of counting type. Games 2021, 12, 7. [Google Scholar] [CrossRef]
- Piotrowski, E.W.; Sładkowski, J. Quantum market games. Phys. A Stat. Mech. Appl. 2002, 312, 208–216. [Google Scholar] [CrossRef] [Green Version]
- Samadi, A.H.; Montakhab, A.; Marzban, H.; Owjimehr, S. Quantum Barro–Gordon game in monetary economics. Phys. A Stat. Mech. Appl. 2018, 489, 94–101. [Google Scholar] [CrossRef] [Green Version]
- de Sousa, P.B.M.; Ramos, R.V. Multiplayer quantum games and its application as access controller in architecture of quantum computers. Quantum Inf. Process. 2008, 7, 125–135. [Google Scholar] [CrossRef]
- Zabaleta, O.G.; Barrangú, J.P.; Arizmendi, C.M. Quantum game application to spectrum scarcity problems. Phys. A Stat. Mech. Appl. 2017, 466, 455–461. [Google Scholar] [CrossRef] [Green Version]
- Solmeyer, N.; Dixon, R.; Balu, R. Quantum routing games. J. Phys. A Math. Theor. 2018, 51, 455304. [Google Scholar] [CrossRef] [Green Version]
- Silva, A.; Zabaleta, O.G.; Arizmendi, C.M. Mitigation of Routing Congestion on Data Networks: A Quantum Game Theory Approach. Quantum Rep. 2022, 4, 135–147. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, J. An overview of multi-agent reinforcement learning from game theoretical perspective. arXiv 2020, arXiv:2011.00583. [Google Scholar]
- Fudenberg, D.; Levine, D.K. Whither game theory? Towards a theory of learning in games. J. Econ. Perspect. 2016, 30, 151–70. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Wu, H.; Wang, Z.; Li, H. Finding nash equilibrium for imperfect information games via fictitious play based on local regret minimization. Int. J. Intell. Syst. 2022, 37, 6152–6167. [Google Scholar] [CrossRef]
- Cesa-Bianchi, N.; Lugosi, G. Prediction, Learning, and Games; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Mengel, F. Learning across games. Games Econ. Behav. 2012, 74, 601–619. [Google Scholar] [CrossRef]
- Ostaszewski, M.; Grant, E.; Benedetti, M. Structure optimization for parameterized quantum circuits. Quantum 2021, 5, 391. [Google Scholar] [CrossRef]
- Benedetti, M.; Lloyd, E.; Sack, S.; Fiorentini, M. Parameterized quantum circuits as machine learning models. Quantum Sci. Technol. 2019, 4, 043001. [Google Scholar] [CrossRef] [Green Version]
- Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
- Jerbi, S.; Gyurik, C.; Marshall, S.; Briegel, H.; Dunjko, V. Parametrized quantum policies for reinforcement learning. Adv. Neural Inf. Process. Syst. 2021, 34, 28362–28375. [Google Scholar]
- Iqbal, A.; Toor, A. Evolutionarily stable strategies in quantum games. Phys. Lett. A 2001, 280, 249–256. [Google Scholar] [CrossRef]
- Leung, M.L. Classical vs quantum games: Continuous-time evolutionary strategy dynamics. arXiv 2011, arXiv:1104.3953. [Google Scholar]
- Piotrowski, E.W.; Sładkowski, J.; Szczypińska, A. Reinforced learning in market games. In Econophysics and Economics of Games, Social Choices and Quantitative Techniques; Springer: Berlin/Heidelberg, Germany, 2010; pp. 17–23. [Google Scholar]
- Mammeri, Z. Reinforcement learning based routing in networks: Review and classification of approaches. IEEE Access 2019, 7, 55916–55950. [Google Scholar] [CrossRef]
- Khan, F.S.; Bao, N. Quantum Prisoner’s Dilemma and High Frequency Trading on the Quantum Cloud. Front. Artif. Intell. 2021, 4, 769392. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef] [Green Version]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Du, J.; Xu, X.; Li, H.; Zhou, X.; Han, R. Entanglement playing a dominating role in quantum games. Phys. Lett. A 2001, 289, 9–15. [Google Scholar] [CrossRef]




| \ | Player 1 | ||
| \ | C | D | |
| Player 0 | C | (a; b) | (c; d) |
| D | (e; f) | (g; h) | |
| (a) Version 1 | |||
| \ | Player 1 | ||
| \ | C | D | |
| Player 0 | C | (6.6; 6.6) | (0; 10) |
| D | (10; 0) | (3.3; 3.3) | |
| (b) Version 2 | |||
| \ | Player 1 | ||
| \ | C | D | |
| Player 0 | C | (5; 5) | (−10; 30) |
| D | (30; −10) | (−5; −5) | |
| (a) Version 1 | |||
| \ | Player 1 | ||
| \ | C | D | |
| Player 0 | C | (6.6; 6.6) | (10; 0) |
| D | (0; 10) | (3.3; 3.3) | |
| (b) Version 2 | |||
| \ | Player 1 | ||
| \ | C | D | |
| Player 0 | C | (5; 5) | (30; −10) |
| D | (−10; 30) | (−5; −5) | |
| (a) Discoordination game. | |||
| \ | Player 1 | ||
| \ | R | L | |
| Player 0 | R | (10; 0) | (0; 10) |
| L | (0; 10) | (10; 0) | |
| (b) Selfish game. | |||
| \ | Player 1 | ||
| \ | R | L | |
| Player 0 | R | (0; 0) | (0; 10) |
| L | (10; 0) | (0; 0) | |
| Games | Classical Equilibriums | Quantum Equilibriums | ||
|---|---|---|---|---|
| Nash | Obtained | Tendency | Obtained | |
| Prisoner’s Dilemma v1 | [3.3; 3.3] | [3.316; 3.316] | [5; 5] | [4.968; 4.962] |
| Prisoner’s Dilemma v2 | [−5; −5] | [−4.837; −4.857] | [10; 10] | [10.142; 9.618] |
| Deadlock game v1 | [6.6; 6.6] | [6.581; 6.585] | [5; 5] | [4.979; 4.964] |
| Deadlock game v2 | [5; 5] | [5.046; 5.055] | [10; 10] | [9.652; 9.464] |
| Disco-ordination Game | [5; 5] | [5.001; 4.999] | [5; 5] | [4.987; 5.013] |
| Selfish Game | [0; 0] | [0.148; 0.094] | [5; 5] | [4.952; 4.946] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, A.; Zabaleta, O.G.; Arizmendi, C.M. Learning Mixed Strategies in Quantum Games with Imperfect Information. Quantum Rep. 2022, 4, 462-475. https://doi.org/10.3390/quantum4040033
Silva A, Zabaleta OG, Arizmendi CM. Learning Mixed Strategies in Quantum Games with Imperfect Information. Quantum Reports. 2022; 4(4):462-475. https://doi.org/10.3390/quantum4040033
Chicago/Turabian StyleSilva, Agustin, Omar Gustavo Zabaleta, and Constancio Miguel Arizmendi. 2022. "Learning Mixed Strategies in Quantum Games with Imperfect Information" Quantum Reports 4, no. 4: 462-475. https://doi.org/10.3390/quantum4040033
APA StyleSilva, A., Zabaleta, O. G., & Arizmendi, C. M. (2022). Learning Mixed Strategies in Quantum Games with Imperfect Information. Quantum Reports, 4(4), 462-475. https://doi.org/10.3390/quantum4040033







