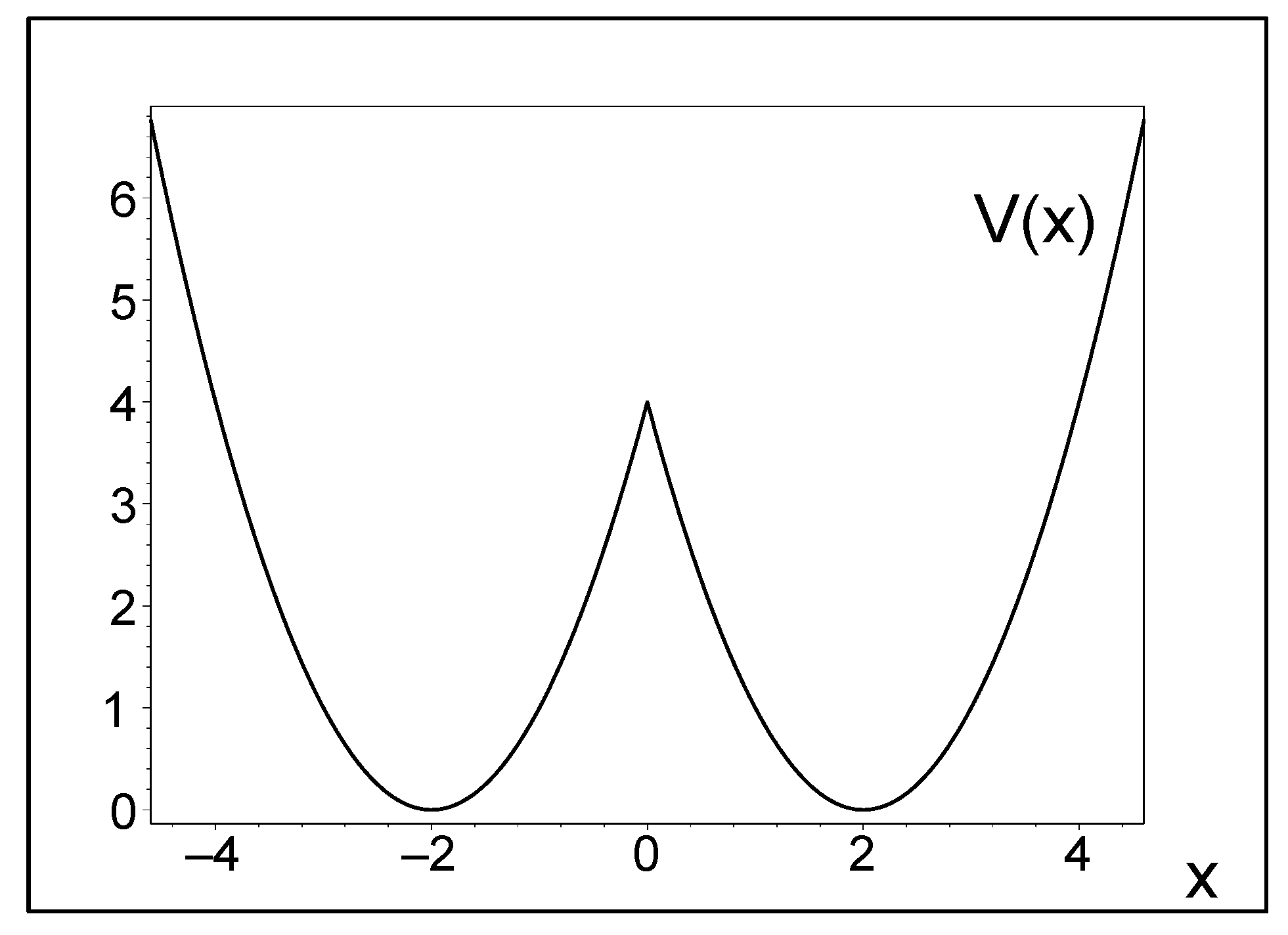
Displaced Harmonic Oscillator V ∼ min [(x + d)2, (x − d)2] as a Benchmark Double-Well Quantum Model
Abstract
1. Introduction
1.1. Motivation in Physics
1.2. Motivation in Mathematics
2. Polynomial Solvability
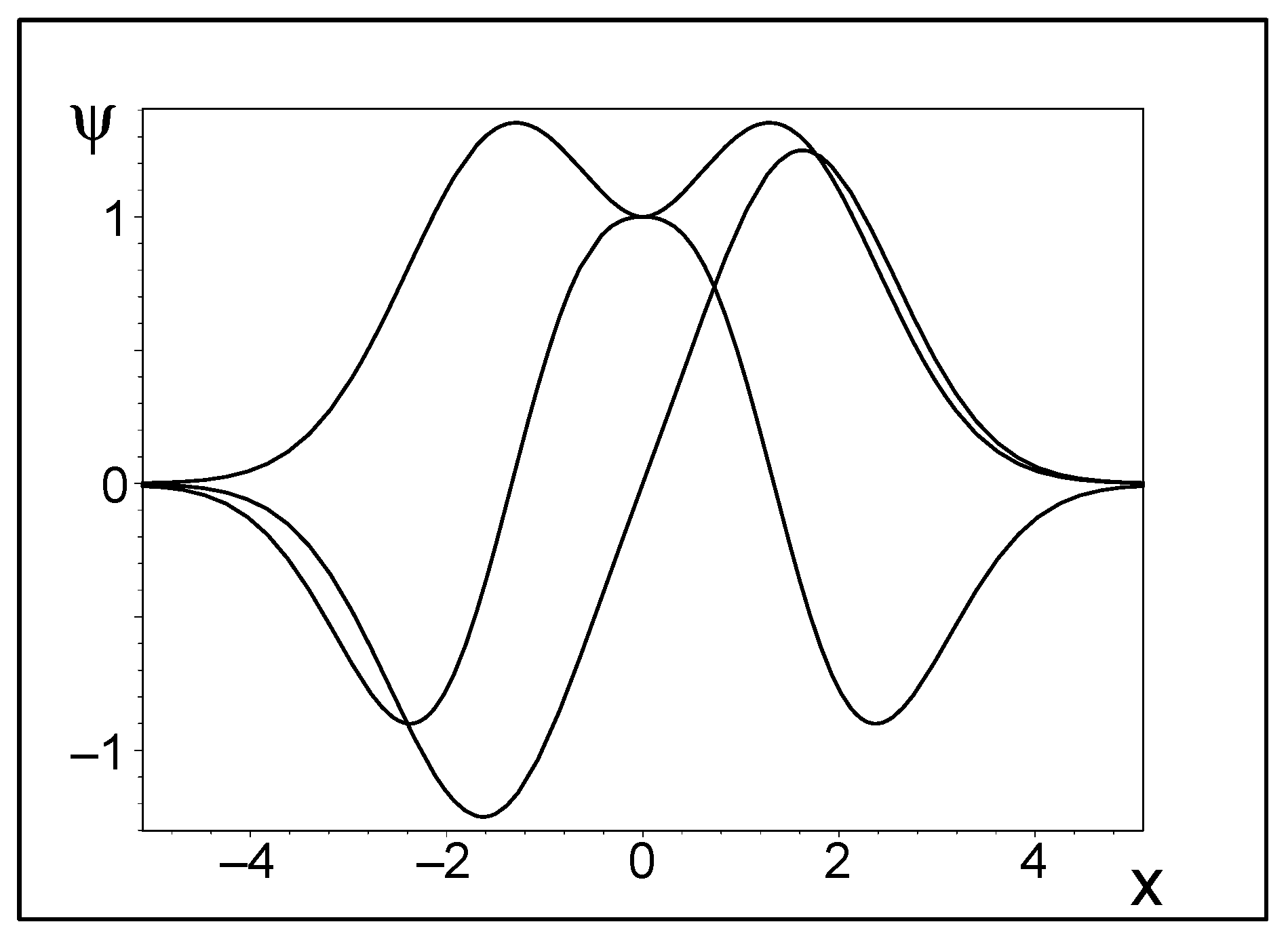
2.1. The Matching of States in the Origin
2.2. The Simplest Polynomial Solution
2.3. Systematic Approach
2.4. General Case
3. Special-Function Solvability
3.1. Single-Well Dynamical Regime with
3.2. Double-Well Dynamical Regime with
- relate the quantum number of a bound-state energy to the number of the finite nodal zeros of ;
- enable us to perturb , localize the related maximal real (and, say, positive) finite nodal zero and find the one-to-one correspondence between the exact-bound-state-energy limits of and of .
4. The Displacement-Dependence of the Spectrum
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Flügge, S. Practical Quantum Mechanics I; Springer-Verlag: Berlin, Germany, 1971. [Google Scholar]
- Cooper, F.; Khare, A.; Sukhatme, U. Supersymmetry and quantum mechanics. Phys. Rep. 1995, 251, 267. [Google Scholar] [CrossRef]
- Ushveridze, A.G. Quasi-Exactly Solvable Models in Quantum Mechanics; IOPP: Bristol, UK, 1994. [Google Scholar]
- Witten, E. Dynamical breaking of supersymmetry. Nucl. Phys. B 1981, 188, 513. [Google Scholar] [CrossRef]
- Quesne, C.; Bagchi, B.; Mallik, S.; Bila, H.; Jakubsky, V.; Znojil, M. PT-supersymmetric partner of a short-range square well. Czech. J. Phys. 2005, 55, 1161. [Google Scholar] [CrossRef]
- Znojil, M. Symmetrized quartic polynomial oscillators and their partial exact solvability. Phys. Lett. A 2016, 380, 1414–1418. [Google Scholar] [CrossRef]
- Quesne, C. Quasi-exactly solvable symmetrized quartic and sextic polynomial oscillators. Eur. Phys. J. Plus 2017, 132, 450. [Google Scholar] [CrossRef]
- Znojil, M. Symmetrized exponential oscillator. Mod. Phys. Lett. A 2016, 31, 1650195. [Google Scholar] [CrossRef]
- Sasaki, R. Confining non-analytic exponential potential V(x)=g2exp(2|x|) and its exact Bessel-function solvability. arXiv 2016, arXiv:1611.02467. [Google Scholar]
- Sasaki, R.; Znojil, M. One-dimensional Schroedinger equation with non-analytic potential V(x)=−g22exp(−|x|) and its exact Bessel-function solvability. J. Phys. A Math. Theor. 2016, 49, 445303. [Google Scholar] [CrossRef]
- Znojil, M. Morse potential, symmetric Morse potential and bracketed bound-state energies. Mod. Phys. Lett. A 2016, 31, 1650088. [Google Scholar] [CrossRef]
- Sasaki, R. Symmetric Morse potential is exactly solvable. arXiv 2016, arXiv:1611.05952. [Google Scholar]
- Messiah, A. Quantum Mechanics; North Holland: Amsterdam, The Netherlands, 1961. [Google Scholar]
- Thom, R. Structural Stability and Morphogenesis. In An Outline of a General Theory of Models; Benjamin: Reading, UK, 1975. [Google Scholar]
- O’Dell, D.H.J. Quantum Catastrophes and Ergodicity in the Dynamics of Bosonic Josephson Junctions. Phys. Rev. Lett. 2012, 109, 150406. [Google Scholar] [CrossRef] [PubMed]
- Zeeman, E.C. Cxatastrophe Theory-Selected Papers 1972–1977; Addison-Wesley: Reading, UK, 1977. [Google Scholar]
- Available online: https://en.wikipedia.org/wiki/Catastrophe_theory (accessed on 15 August 2022).
- Goldberg, A.Z.; Al-Qasimi, A.; Mumford, J.; O’Dell, D.H.J. Emergence of singularities from decoherence: Quantum catastrophes. Phys. Rev. A 2019, 100, 063628. [Google Scholar] [CrossRef]
- Znojil, M. Arnold’s potentials and quantum catastrophes. Ann. Phys. 2020, 413, 168050. [Google Scholar] [CrossRef]
- Arteca, G.A.; Fernández, F.M.; Castro, E.A. Large Order Perturbation Theory and Summation Methods in Quantum Mechanics; Lecture Notes in Chemistry; Springer: Berlin, Germany, 1990; Volume 53. [Google Scholar]
- Znojil, M.; Borisov, D.I. Arnold’s potentials and quantum catastrophes II. Ann. Phys. 2022, 442, 168896. [Google Scholar] [CrossRef]
- Singh, V.; Biswas, S.N.; Datta, K. Anharmonic oscillator and analytic theory of continued fractions. Phys. Rev. D 1978, 18, 1901. [Google Scholar] [CrossRef]
- Turbiner, A.V. Quasi-exactly solvable problems and sl(2) algebra. Commun. Math. Phys. 1988, 118, 467. [Google Scholar] [CrossRef]
- Fring, A. A new non-Hermitian E2-quasi-exactly solvable model. Phys. Lett. A 2015, 379, 873. [Google Scholar] [CrossRef]
- Fring, A. E2-quasi-exact solvability for non-Hermitian models. J. Phys. A Math. Theor. 2015, 48, 145301. [Google Scholar] [CrossRef]
- Znojil, M. Quasi-exactly solvable quartic potentials with centrifugal and Coulombic terms. J. Phys. A Math. Gen. 2000, 33, 42034211. [Google Scholar] [CrossRef][Green Version]
- Znojil, M. Harmonic oscillator well with a screened Coulombic core is quasi-exactly solvable. J. Phys. A Math. Gen. 1999, 32, 4563. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Quasi-exactly solvable quartic potential. J. Phys. A Math. Gen. 1998, 31, L273. [Google Scholar] [CrossRef]
- Available online: http://dlmf.nist.gov/13.7 (accessed on 15 August 2022).
- Arnold, V.I. Catastrophe Theory; Springer: Berlin, Germany, 1992. [Google Scholar]
- Znojil, M. Horizons of stability. J. Phys. A Math. Theor. 2008, 41, 244027. [Google Scholar] [CrossRef]
- Znojil, M. Quantum catastrophes: A case study. J. Phys. A Math. Theor. 2012, 45, 444036. [Google Scholar] [CrossRef]
- Lévai, G.; Ruzicka, F.; Znojil, M. Three solvable matrix models of a quantum catastrophe. Int. J. Theor. Phys. 2014, 53, 2875. [Google Scholar] [CrossRef]
- Bender, C.M.; Wu, T.T. Anharmonic oscillator. Phys. Rev. 1969, 184, 1231. [Google Scholar] [CrossRef]
- Turbiner, A.V.; Ushveridze, A.G. Anharmonic oscillator: Constructing the strong-coupling expansions. J. Math. Phys. 1988, 29, 2053. [Google Scholar] [CrossRef]
- Alvarez, G. Bender-Wu branch points in the cubic oscillator. J. Phys. A Math. Gen. 1995, 27, 4589. [Google Scholar] [CrossRef]
- Eremenko, A.; Gabrielov, A. Analytic continuation of eigenvalues of a quartic oscillator. Comm. Math. Phys. 2009, 287, 431. [Google Scholar] [CrossRef]
- Hille, E. Ordinary Differential Equations in the Complex Domain; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Znojil, M. Avoided level crossings in quasi-exact approach. Nucl. Phys. B 2021, 967, 115431. [Google Scholar] [CrossRef]
- Znojil, M. Relocalization switch in a triple quantum dot molecule in 2D. Mod. Phys. Lett. B 2020, 34, 2050378. [Google Scholar] [CrossRef]
- Znojil, M. Polynomial potentials and coupled quantum dots in two and three dimensions. Ann. Phys. 2020, 416, 168161. [Google Scholar] [CrossRef]
- Goldstone, J. Field theories with superconductor solutions. Il Nuovo Cimento 1961, 19, 154. [Google Scholar] [CrossRef]

| N | Polynomial | Elimination of |
|---|---|---|
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| ⋮ | … | … |
| N | Polynomial | Elimination of |
|---|---|---|
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| ⋮ | … | … |
| Shift | Energy Estimates | |
|---|---|---|
| Lower | Upper | |
| 0 | 1 | 1 |
| 0.25 | 0.768972 | 0.768974 |
| 0.50 | 0.635528 | 0.635530 |
| 0.75 | 0.590300 | 0.590301 |
| 1.00 | 0.618910 | 0.618920 |
| 1.50 | 0.801493 | 0.801494 |
| 2.00 | 0.951410 | 0.951420 |
| ∞ | 1 | 1 |
| Shift | Energy Estimates | |
|---|---|---|
| Lower | Upper | |
| 0 | 3 | 3 |
| 0.25 | 2.483910 | 2.483920 |
| 0.50 | 2.060760 | 2.060770 |
| 0.75 | 1.724710 | 1.724720 |
| 1.00 | 1.468460 | 1.468470 |
| 1.50 | 1.157479 | 1.157480 |
| 2.00 | 1.035760 | 1.035770 |
| ∞ | 1 | 1 |
| Shift | Energy Estimates | |
|---|---|---|
| Lower | Upper | |
| 0 | 5 | 5 |
| 0.25 | 4.34600 | 4.34700 |
| 0.50 | 3.79410 | 3.79420 |
| 0.75 | 3.34470 | 3.34471 |
| 1 | 3 | 3 |
| 1.50 | 2.64860 | 2.64870 |
| 2.00 | 2.73500 | 2.73510 |
| ∞ | 3 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Znojil, M. Displaced Harmonic Oscillator V ∼ min [(x + d)2, (x − d)2] as a Benchmark Double-Well Quantum Model. Quantum Rep. 2022, 4, 309-323. https://doi.org/10.3390/quantum4030022
Znojil M. Displaced Harmonic Oscillator V ∼ min [(x + d)2, (x − d)2] as a Benchmark Double-Well Quantum Model. Quantum Reports. 2022; 4(3):309-323. https://doi.org/10.3390/quantum4030022
Chicago/Turabian StyleZnojil, Miloslav. 2022. "Displaced Harmonic Oscillator V ∼ min [(x + d)2, (x − d)2] as a Benchmark Double-Well Quantum Model" Quantum Reports 4, no. 3: 309-323. https://doi.org/10.3390/quantum4030022
APA StyleZnojil, M. (2022). Displaced Harmonic Oscillator V ∼ min [(x + d)2, (x − d)2] as a Benchmark Double-Well Quantum Model. Quantum Reports, 4(3), 309-323. https://doi.org/10.3390/quantum4030022






