Schrödinger Equation with Geometric Constraints and Position-Dependent Mass: Linked Fractional Calculus Models
Abstract
:1. Introduction
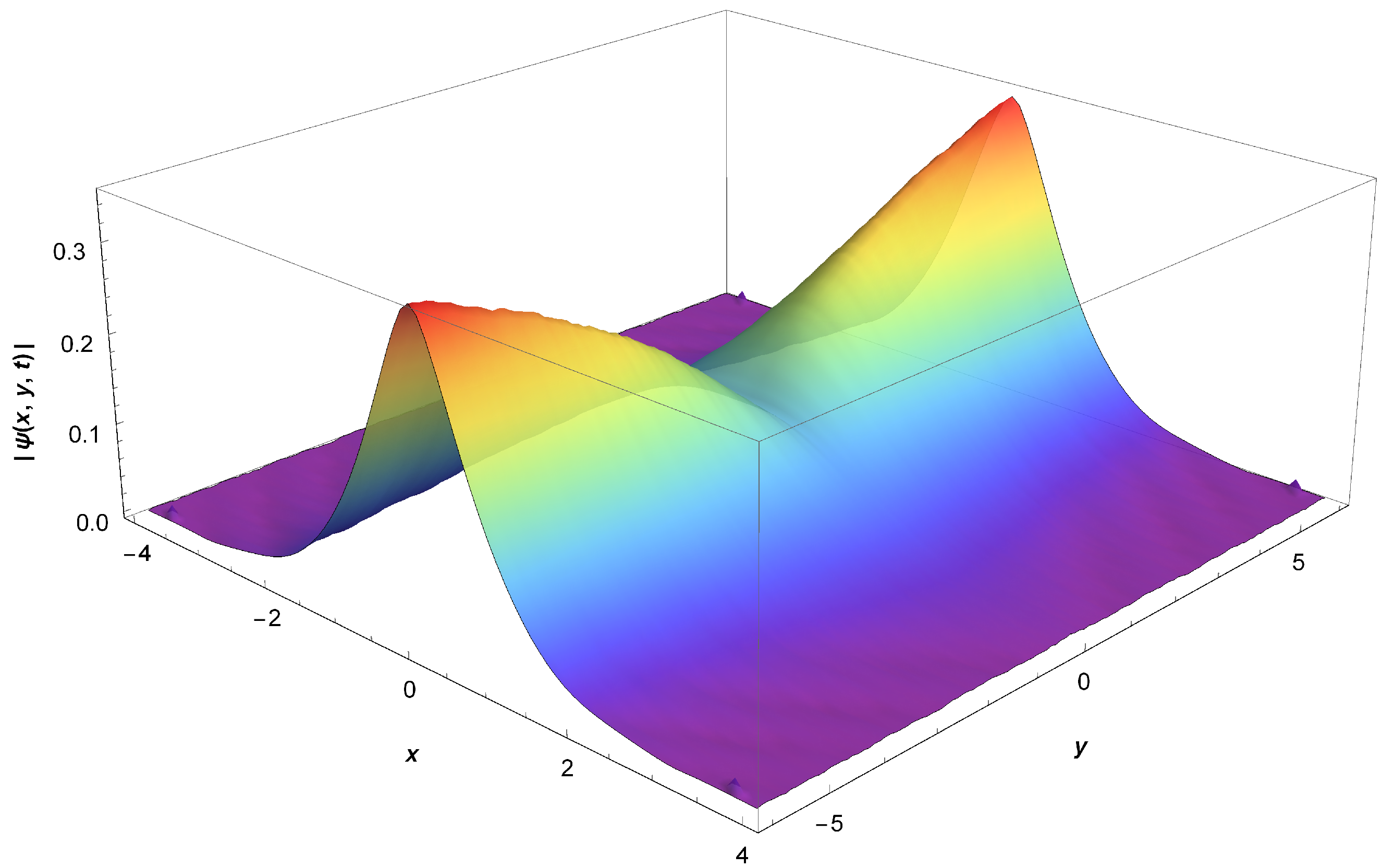
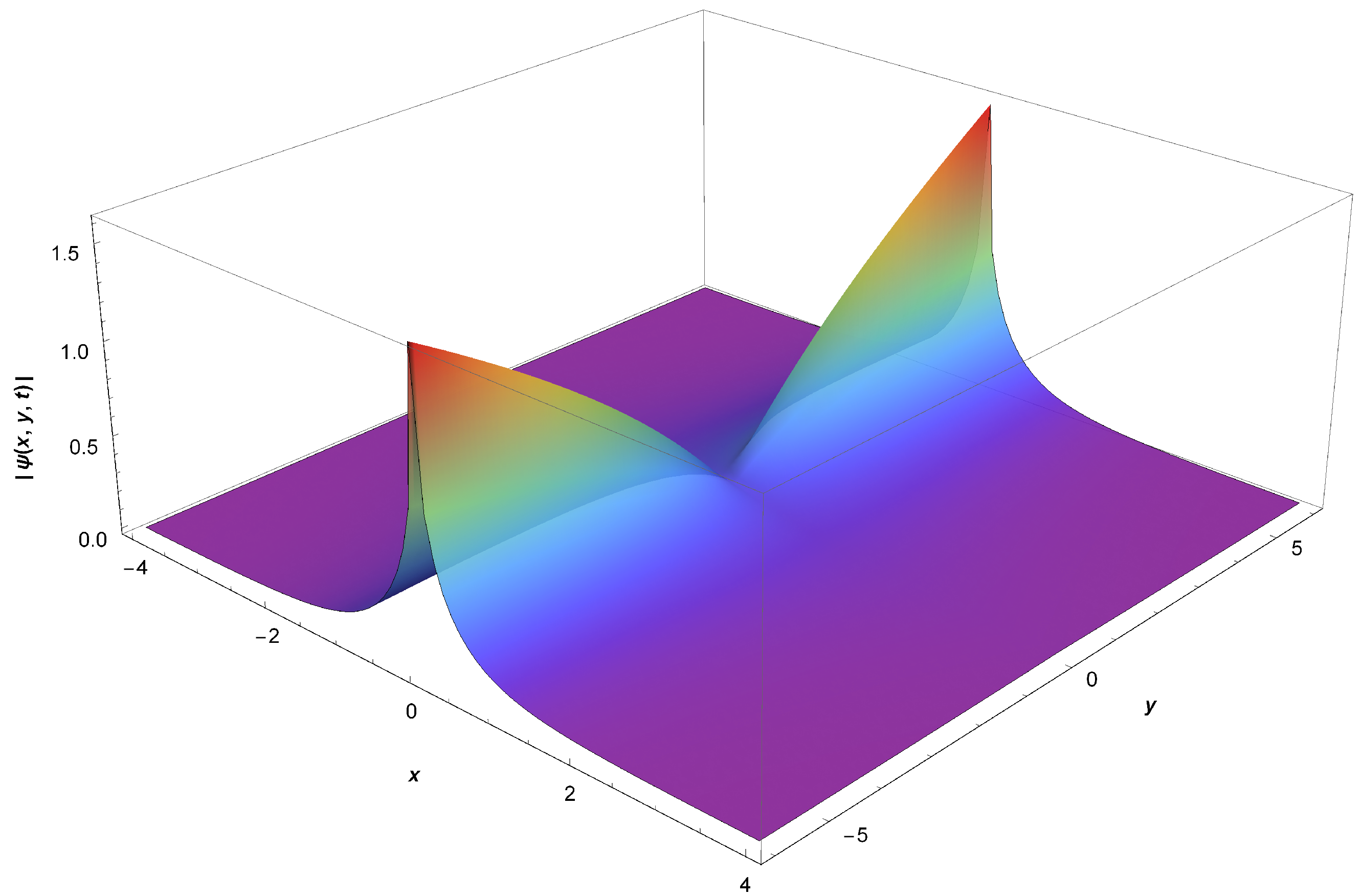
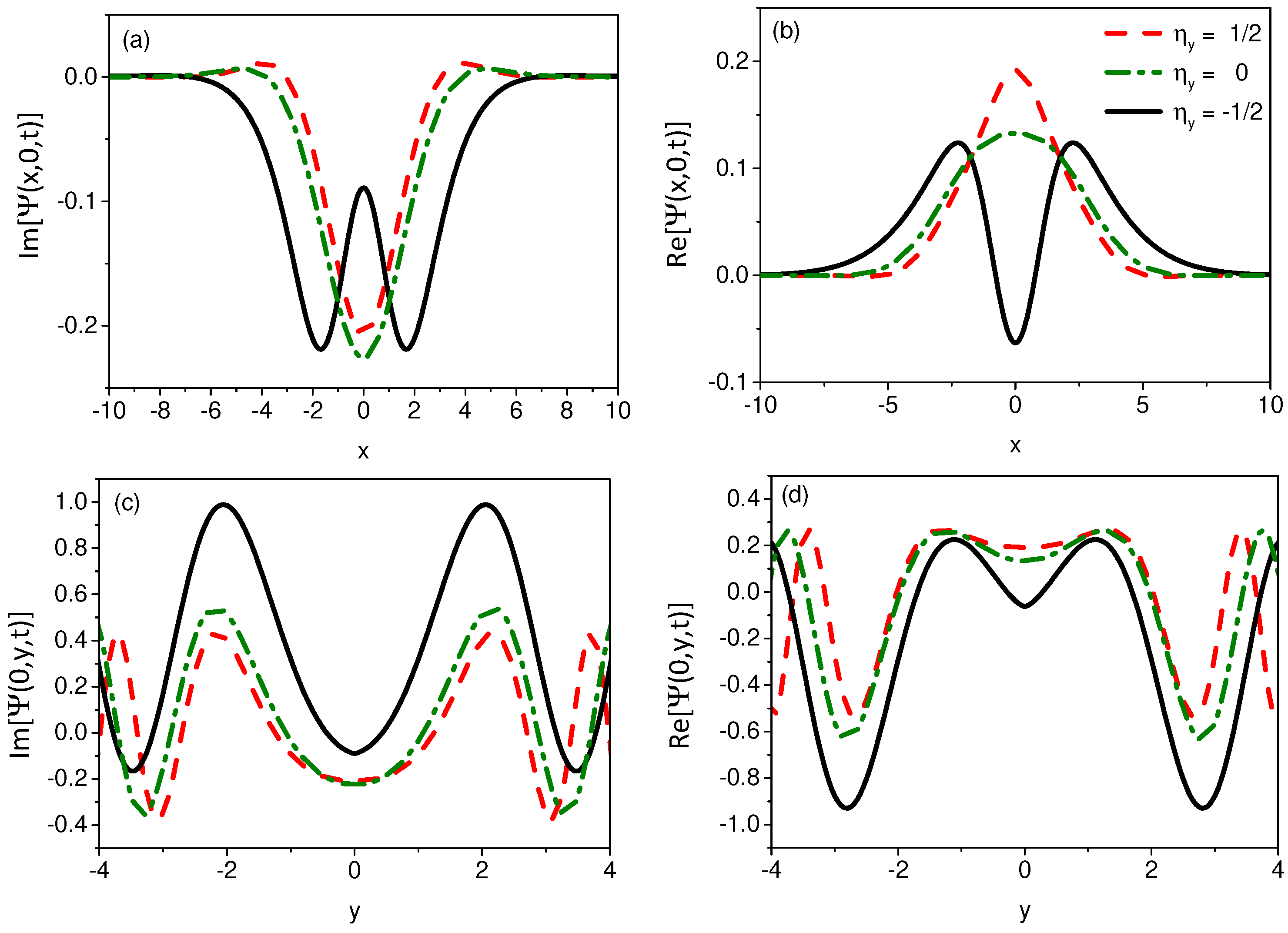
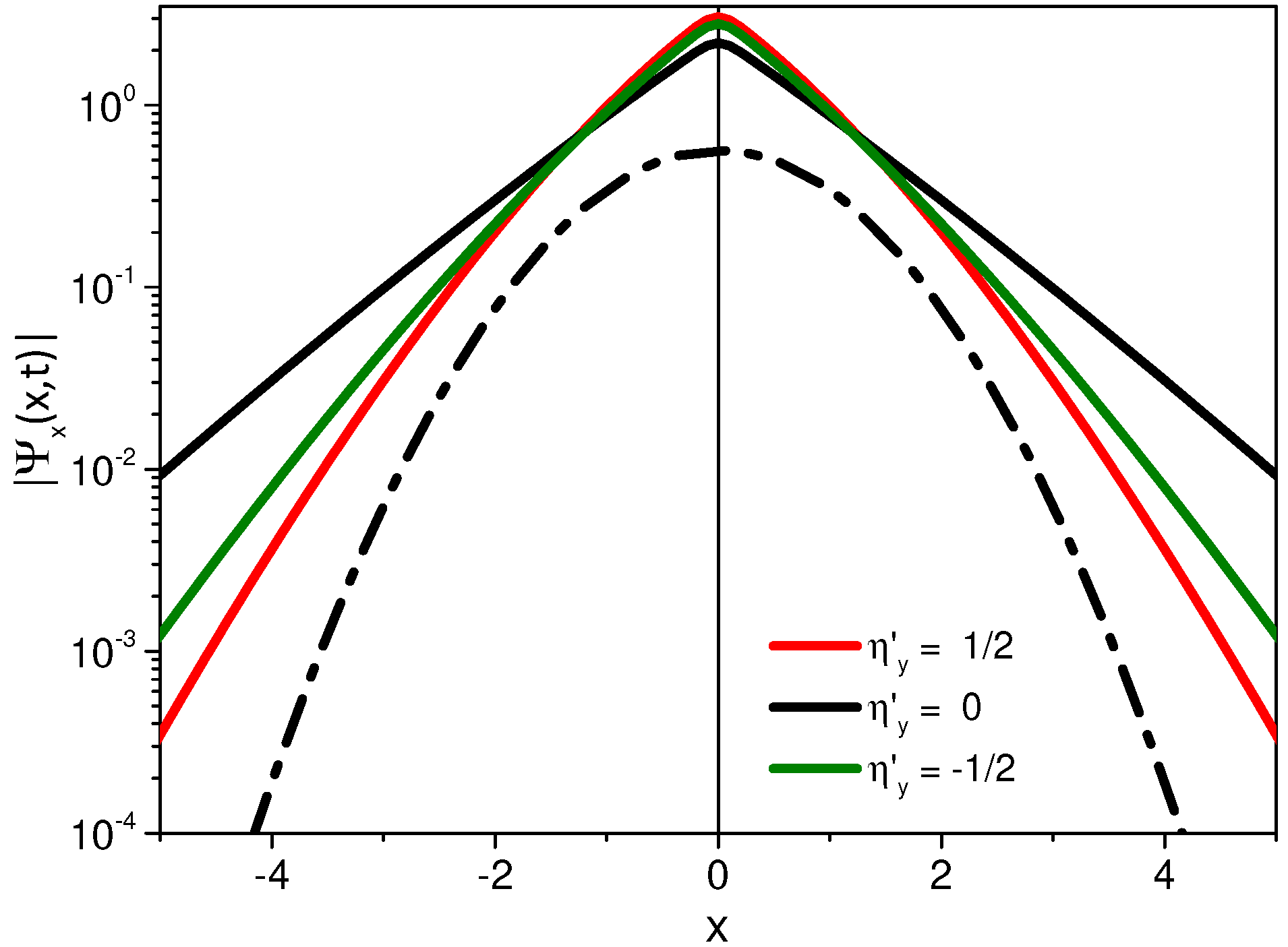
2. Schrödinger’s Equation and Geometric Constraints
2.1. and
2.2. and
2.3. and
3. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feynman, R.P.; Hibbs, A.R.; Styer, D.F. Quantum Mechanics and Path Integrals; Courier Corporation: Chelmsford, MA, USA, 2010. [Google Scholar]
- Nelson, E. Derivation of the Schrödinger equation from Newtonian mechanics. Phys. Rev. 1966, 150, 1079. [Google Scholar] [CrossRef]
- Nelson, E. Dynamical Theories of Brownian Motion; Princeton University Press: Princeton, NJ, USA, 2020; Volume 106. [Google Scholar]
- Wallstrom, T.C. On the derivation of the Schrödinger equation from stochastic mechanics. Found. Phys. Lett. 1989, 2, 113–126. [Google Scholar] [CrossRef]
- Baublitz, M., Jr. Derivation of the Schrödinger equation from a stochastic theory. Prog. Theor. Phys. 1988, 80, 232–244. [Google Scholar] [CrossRef]
- Anderson, J.B. A random-walk simulation of the Schrödinger equation: H+3. J. Chem. Phys. 1975, 63, 1499–1503. [Google Scholar] [CrossRef]
- Laskin, N. Fractional Quantum Mechanics; World Scientific Publishing Company: Singapore, 2018. [Google Scholar]
- Laskin, N. Fractals and quantum mechanics. Chaos 2000, 10, 780–790. [Google Scholar] [CrossRef]
- Laskin, N. Fractional Schrödinger equation. Phys. Rev. E 2002, 66, 056108. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018; p. 395. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Singapore, 2011. [Google Scholar]
- De Oliveira, E.C.; Costa, F.S.; Vaz, J. The fractional Schrödinger equation for potentials. J. Math. Phys. 2010, 51, 123517. [Google Scholar] [CrossRef]
- Jiang, X.; Qi, H.; Xu, M. Exact solutions of fractional Schrödinger-like equation with a nonlocal term. J. Math. Phys. 2011, 52, 042105. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Ribeiro, H.V.; dos Santos, M.A.F.; Rossato, R.; Mendes, R.S. Time dependent solutions for a fractional Schrödinger equation with delta potentials. J. Math. Phys. 2013, 54, 082107. [Google Scholar] [CrossRef]
- Dong, J.; Xu, M. Some solutions to the space fractional Schrödinger equation using momentum representation method. J. Math. Phys. 2007, 48, 072105. [Google Scholar] [CrossRef]
- Naber, M. Time fractional Schrödinger equation. J. Math. Phys. 2004, 45, 3339–3352. [Google Scholar] [CrossRef]
- Iomin, A. Fractional-time Schrödinger equation: Fractional dynamics on a comb. Chaos Solitons Fractals 2011, 44, 348–352. [Google Scholar] [CrossRef]
- Iomin, A.; Méndez, V.; Horsthemke, W. Comb model: Non-Markovian versus Markovian. Fractal Fract. 2019, 3, 54. [Google Scholar] [CrossRef]
- Petreska, I.; de Castro, A.S.; Sandev, T.; Lenzi, E.K. The time-dependent Schrödinger equation in non-integer dimensions for constrained quantum motion. Phys. Lett. A 2020, 384, 126866. [Google Scholar] [CrossRef]
- Petreska, I.; Sandev, T.; Lenzi, E.K. Comb-like geometric constraints leading to emergence of the time-fractional Schrödinger equation. Mod. Phys. Lett. A 2021, 36, 2130005. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. A new approach to the schrodinger equation with position-dependent mass and its implications in quantum dots and semiconductors. J. Phys. Chem. Solids 2020, 140, 109384. [Google Scholar] [CrossRef]
- Alhaidari, A. Solution of the Dirac equation with position-dependent mass in the Coulomb field. Phys. Lett. A 2004, 322, 72–77. [Google Scholar] [CrossRef]
- Yu, J.; Dong, S.H. Exactly solvable potentials for the Schrödinger equation with spatially dependent mass. Phys. Lett. A 2004, 325, 194–198. [Google Scholar] [CrossRef]
- Gönül, B.; Özer, O.; GönüL, B.; Üzgün, F. Exact solutions of effective-mass Schrödinger equations. Mod. Phys. Lett. A 2002, 17, 2453–2465. [Google Scholar] [CrossRef]
- Barranco, M.; Pi, M.; Gatica, S.M.; Hernández, E.S.; Navarro, J. Structure and energetics of mixed 4He-3He drops. Phys. Rev. B 1997, 56, 8997–9003. [Google Scholar] [CrossRef]
- Von Roos, O. Position-dependent effective masses in semiconductor theory. Phys. Rev. B 1983, 27, 7547–7552. [Google Scholar] [CrossRef]
- Von Roos, O.; Mavromatis, H. Position-dependent effective masses in semiconductor theory. II. Phys. Rev. B 1985, 31, 2294–2298. [Google Scholar] [CrossRef] [PubMed]
- Sakurai, J.; Napolitano, J. Modern Quantum Mechanics, 2nd ed.; Person New International Edition: London, UK, 2014. [Google Scholar]
- Ribeiro, H.V.; Tateishi, A.A.; Alves, L.G.; Zola, R.S.; Lenzi, E.K. Investigating the interplay between mechanisms of anomalous diffusion via fractional Brownian walks on a comb-like structure. New J. Phys. 2014, 16, 093050. [Google Scholar] [CrossRef]
- Arkhincheev, V.; Baskin, E. Anomalous diffusion and drift in a comb model of percolation clusters. Sov. Phys. JETP 1991, 73, 161–300. [Google Scholar]
- Wang, Z.; Lin, P.; Wang, E. Modeling multiple anomalous diffusion behaviors on comb-like structures. Chaos Solitons Fractals 2021, 148, 111009. [Google Scholar] [CrossRef]
- Liang, Y.; Wang, S.; Chen, W.; Zhou, Z.; Magin, R.L. A survey of models of ultraslow diffusion in heterogeneous materials. Appl. Mech. Rev. 2019, 71, 040802. [Google Scholar] [CrossRef]
- Bunde, A.; Havlin, S.; Stanley, H.; Trus, B.; Weiss, G. Diffusion in random structures with a topological bias. Phys. Rev. B 1986, 34, 8129. [Google Scholar] [CrossRef]
- O’Shaughnessy, B.; Procaccia, I. Diffusion on fractals. Phys. Rev. A 1985, 32, 3073–3083. [Google Scholar] [CrossRef]
- O’Shaughnessy, B.; Procaccia, I. Analytical Solutions for Diffusion on Fractal Objects. Phys. Rev. Lett. 1985, 54, 455–458. [Google Scholar] [CrossRef]
- Richardson, L.F. Atmospheric diffusion shown on a distance-neighbour graph. Proc. Math. Phys. Eng. Sci. 1926, 110, 709–737. [Google Scholar]
- Boffetta, G.; Sokolov, I.M. Relative Dispersion in Fully Developed Turbulence: The Richardson’s Law and Intermittency Corrections. Phys. Rev. Lett. 2002, 88, 094501. [Google Scholar] [CrossRef]
- Daniel ben Avraham, S.H. Diffusion and Reactions in Fractals and Disordered Systems; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Su, N.; Sander, G.; Liu, F.; Anh, V.; Barry, D. Similarity solutions for solute transport in fractal porous media using a time- and scale-dependent dispersivity. Appl. Math. Model. 2005, 29, 852–870. [Google Scholar] [CrossRef]
- Shah, K.; Jarad, F.; Abdeljawad, T. Stable numerical results to a class of time-space fractional partial differential equations via spectral method. J. Adv. Res. 2020, 25, 39–48. [Google Scholar] [CrossRef]
- Shah, K.; Naz, H.; Sarwar, M.; Abdeljawad, T. On spectral numerical method for variable-order partial differential equations. AIMS Math. 2022, 7, 10422–10438. [Google Scholar] [CrossRef]
- Khan, H.; Khan, A.; Chen, W.; Shah, K. Stability analysis and a numerical scheme for fractional Klein-Gordon equations. Math. Methods Appl. Sci. 2019, 42, 723–732. [Google Scholar] [CrossRef]
- Bushnaq, S.; Shah, K.; Tahir, S.; Ansari, K.J.; Sarwar, M.; Abdeljawad, T. Computation of numerical solutions to variable order fractional differential equations by using non-orthogonal basis. AIMS Math. 2022, 7, 10917–10938. [Google Scholar] [CrossRef]
- Shah, K.; Arfan, M.; Ullah, A.; Al-Mdallal, Q.; Ansari, K.J.; Abdeljawad, T. Computational study on the dynamics of fractional order differential equations with applications. Chaos Solitons Fractals 2022, 157, 111955. [Google Scholar] [CrossRef]
- Liang, Y.; Chen, W.; Cai, W. Hausdorff Calculus: Applications to Fractal Systems; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2019; Volume 6. [Google Scholar]
- Wyld, H.W. Mathematical Methods for Physics, 2nd ed.; Advanced Book Classics, Advanced Book Program; Perseus Books: New York, NY, USA, 1999. [Google Scholar]
- Mota-Furtado, F.; O’Mahony, P. Eigenfunctions and matrix elements for a class of eigenvalue problems with staggered ladder spectra. Phys. Rev. A 2006, 74, 044102. [Google Scholar] [CrossRef]
- Mota-Furtado, F.; O’Mahony, P. Exact propagator for generalized Ornstein-Uhlenbeck processes. Phys. Rev. E 2007, 75, 041102. [Google Scholar] [CrossRef]
- Bezuglyy, V.; Mehlig, B.; Wilkinson, M.; Nakamura, K.; Arvedson, E. Generalized ornstein-uhlenbeck processes. J. Math. Phys. 2006, 47, 073301. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lenzi, E.K.; Evangelista, L.R.; Ribeiro, H.V.; Magin, R.L. Schrödinger Equation with Geometric Constraints and Position-Dependent Mass: Linked Fractional Calculus Models. Quantum Rep. 2022, 4, 296-308. https://doi.org/10.3390/quantum4030021
Lenzi EK, Evangelista LR, Ribeiro HV, Magin RL. Schrödinger Equation with Geometric Constraints and Position-Dependent Mass: Linked Fractional Calculus Models. Quantum Reports. 2022; 4(3):296-308. https://doi.org/10.3390/quantum4030021
Chicago/Turabian StyleLenzi, Ervin K., Luiz R. Evangelista, Haroldo V. Ribeiro, and Richard L. Magin. 2022. "Schrödinger Equation with Geometric Constraints and Position-Dependent Mass: Linked Fractional Calculus Models" Quantum Reports 4, no. 3: 296-308. https://doi.org/10.3390/quantum4030021
APA StyleLenzi, E. K., Evangelista, L. R., Ribeiro, H. V., & Magin, R. L. (2022). Schrödinger Equation with Geometric Constraints and Position-Dependent Mass: Linked Fractional Calculus Models. Quantum Reports, 4(3), 296-308. https://doi.org/10.3390/quantum4030021








