Quantum Holography from Fermion Fields
Abstract
:1. Introduction
2. Why QFT for Quantum Holography? The Logical Thread of the Problem
2.1. A New Entropy Bound for QHP
2.2. Spin Networks and Black Hole Entropy
2.3. From Fermionic QFT to QHP
- (1)
- Consider a fermionic quantum field theory on .
- (2)
- Double the degrees of freedom of the fermion field in the environment E.
- (3)
- Consider the discrete geometry of LQG (spin network’s edges that puncture ). For simplicity, we will take to be the ordinary sphere .
- (4)
- Assume that at each puncture, it corresponds an excitation of the fermion field (i.e., a half-integer spin particle).
- (5)
- Because of the doubling of the degrees of freedom performed on the fermion field, at each puncture, a fermionic particle on has its double in E.
- (6)
- From (4) and (5) it follows that, through a suitable projection of the particle living in the environment E, at each puncture, it is possible to associate a spin network’s edge in E, which is “dual” to the original one in .
- (7)
- A Bogolyubov transformation on the fermionic operators allows us to interpret the “dual” spin network’s edge as the “mirror image” of the original one.
- (8)
- All the above mathematical procedure performed on the ordinary sphere is more straightforward when we consider the fuzzy sphere [26] instead of . In this case, the background space is itself quantum, and this induces a reduction of the infinite degrees of freedom of the fermion field to a finite number. What remains of the original fermion field at a point (the latter becoming a cell) is what we will call a “spike” of quantum information.
- (9)
- The geometrical quantization in terms of spin networks on the ordinary sphere discussed above reduces the infinite degrees of freedom to a finite number, but there is the need of doubling the degrees of freedom in order to achieve the QHP. Instead, the Lorentz invariant “regularization” of the fermion field on the non-commutative “lattice”, where the sites are the cells of the fuzzy sphere (corresponding to the punctures of the spin network’s edges on the ordinary sphere) leads automatically to the QHP.
3. Doubling the Fermionic Degrees of Freedom Leads to Double Punctures
3.1. Bogolyubov Transformations for Fermions
3.2. Projections of Fermions
3.3. Rotations of the Spinors
4. Fermions and the Fuzzy Sphere
4.1. The Fuzzy Sphere and the QHP
4.2. From Fermion Fields to Quantum Information “Spikes”
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hooft, G.T. Dimensional reduction in quantum gravity. arXiv 1993, arXiv:gr-qc/9310026. [Google Scholar]
- Susskind, L. The world as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef] [Green Version]
- Bekenstein, J.D. Black holes and entropy. Conserv. Revolut. 1973, D7, 2333. [Google Scholar] [CrossRef]
- Bousso, R. The holographic principle. Rev. Mod. Phys. 2002, 74, 825. [Google Scholar] [CrossRef] [Green Version]
- Maldacena, J. The large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1998, 2, 23. [Google Scholar] [CrossRef]
- Rovelli, C. Black Hole Entropy from Loop Quantum Gravity. Phys. Rev. Lett. 1996, 16, 3288. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashtekar, A.; Baez, J.; Corichi, A.; Krasnov, K. Quantum Geometry and Black Hole Entropy. Phys. Rev. Lett. 1998, 80, 904. [Google Scholar] [CrossRef] [Green Version]
- Ashtekar, A.; Baez, J.; Krasnov, K. Quantum Geometry of Isolated Horizons and Black Hole Entropy. arXiv 2000, arXiv:gr-qc/0005126. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Rovelli, C.; Smolin, L. Spin networks and quantum gravity. Phys. Rev. D 1995, 52, 5743. [Google Scholar] [CrossRef] [Green Version]
- Penrose, R. Theory of quantised directions. In Quantum Theory and Beyond; Bastin, T., Ed.; Cambridge University Press: Cambridge, UK, 1971; p. 875. [Google Scholar]
- Zizzi, P.A. Holography, Quantum Geometry and Quantum Information Theory. Entropy 2000, 2, 39. [Google Scholar] [CrossRef] [Green Version]
- Zizzi, P.A. A minimal model for quantum gravity. Mod. Phys. Lett. 2005, A20, 645. [Google Scholar] [CrossRef] [Green Version]
- Zizzi, P.A. Quantum Computation toward Quantum Gravity, Gen. Relativ. Gravit. 2001, 33, 1305. [Google Scholar] [CrossRef]
- Umezawa, H. Advanced Field Theory: Micro Macro and Thermal Concepts; American Institute of Physics: New York, NY, USA, 1993. [Google Scholar]
- Umezawa, H.; Vitiello, G. Quantum Mechanics; Bibliopolis: Napoli, Italy, 1985. [Google Scholar]
- Celeghini, E.; Rasetti, M.; Vitiello, G. Quantum Dissipation. Ann. Phys. 1992, 215, 156. [Google Scholar] [CrossRef]
- Blasone, M.; Jizba, P.; Vitiello, G. Dissipation and Quantization. Phys. Lett. A 2001, 287, 205. [Google Scholar] [CrossRef] [Green Version]
- Vitiello, G. Dynamical Rearrangement of Symmetry. Ph.D. Thesis, The University of Wisconsin, Madison, WI, USA, 1974. [Google Scholar]
- Blasone, M.; Jizba, P.; Vitiello, G. Quantum Field Theory and Its Macroscopic Manifestations: Boson Condensation, Ordered Patterns and Topological Defects; Imperial College Press: London, UK, 2011. [Google Scholar]
- Bogoliubov, N.N. On a new method in the theory of superconductivity. Riv. Nuovo Cim. 1958, 7, 794. [Google Scholar] [CrossRef]
- Takahashi, Y.; Umezawa, H. Thermo Field Dynamics. Int. J. Mod. Phys. B 1996, 10, 1755. [Google Scholar] [CrossRef]
- Martellini, M.; Sodano, P.; Vitiello, G. Vacuum structure for a quantum field theory in curved space-time. Nuovo Cim. A 1978, 48, 341. [Google Scholar] [CrossRef]
- Stone, M.H. Linear Transformations in Hilbert Space. III. Operational Methods and Group Theory. Proc. Natl. Acad. Sci. USA 1930, 16, 172. [Google Scholar] [CrossRef] [Green Version]
- Neumann, J.V. Die Eindeutigkeit der Schrödingerschen Operatoren. In Mathematische Annalen; Springer: Berlin/Heidelberg, Germany, 1931; Volume 104, p. 570. [Google Scholar]
- Madore, J. The fuzzy sphere. Class. Class. Quantum Gravity 1992, 9, 69. [Google Scholar] [CrossRef]
- Zizzi, P. Quantum Information Hidden in Quantum Fields. Quantum Rep. 2020, 2, 33. [Google Scholar] [CrossRef]
- Grosse, H.; Prešnajder, P. The Dirac operator on the fuzzy sphere. Lett. Math. Phys. 1995, 33, 171. [Google Scholar] [CrossRef] [Green Version]
- Rovelli, C.; Smolin, L. Discreteness of area and volume in quantum gravity. Nucl. Phys. B 1995, 442, 593. [Google Scholar] [CrossRef] [Green Version]
- Rovelli, C. A physical prediction from Quantum Gravity: The Quantization of the Area. In Texas/Pascos 92: Relativistic Astrophysics and Particle Cosmology; Akerlof, C.W., Srednicki, M.A., Eds.; New York Academy of Sciences: New York, NY, USA, 1993; Volume 688. [Google Scholar]
- Immirzi, G. Quantum Gravity and Regge calculus. Nucl. Phys. B Proc. Suppl. 1997, 57, 65. [Google Scholar] [CrossRef] [Green Version]
- Wheeler, J.A. It from Bit. In Sakharov Memorial Lectures on Physics; Keldysh, L., Feinberg, V., Eds.; Nova Science: New York, NY, USA, 1992; Volume 2. [Google Scholar]
- Priest, G. Paraconsistent logic. In Handbook of Philosophical Logic, 2nd ed.; Gabbay, D., Guenthner, F., Eds.; Kluwer: Dordrecht, The Netherlands, 2002; Volume 6, pp. 287–394. [Google Scholar]
- Zizzi, P.; Pessa, E. From SU(2) Gauge Theory to Qubits on the Fuzzy Sphere. Int. J. Theor. Phys. 2014, 53, 25. [Google Scholar] [CrossRef] [Green Version]
- Wilson, K.G. New Phenomena. In Subnuclear Physics; Zichichi, A., Ed.; Plenum Press: New York, NY, USA, 1977; Part A; p. 69. [Google Scholar]
- Zizzi, P. Qubits and quantum spaces. Int. J. Quantum Inf. 2005, 3, 287–291. [Google Scholar] [CrossRef] [Green Version]
- Murphy, G. C*-Algebras and Operator Theory; Academic Press: Boston, MA, USA, 1990. [Google Scholar]
- Kruszynski, P.; Woronowicz, S.L. A non-commutative Gelfand-Naimark theorem. J. Oper. Theory 1982, 8, 361. [Google Scholar]
- Iorio, A.; Lambiase, G.; Vitiello, G. Entropy of Black Holes: A Quantum Algebraic Approach. Entropy 2002, 4, 168–182. [Google Scholar] [CrossRef]
- Lloyd, S. Computational capacity of the universe. Phys. Rev. Lett. 2002, 88, 237901. [Google Scholar] [CrossRef] [Green Version]
- Lloyd, S.; Ng, Y.J. Black hole computers. Sci. Am. 2004, 291, 52. [Google Scholar] [CrossRef]
- Zizzi, P. Spacetime at the Planck scale: The Quantum Computer View. In The Foundations of Quantum Mechanics; Garola, C., Rossi, A., Sozzo, S., Eds.; World Scientific: Cesena, Italy, 2004; pp. 345–358. [Google Scholar]
- Wheeler, J.A. Geometrodynamics; Academic Press: Boston, MA, USA, 1962. [Google Scholar]
- Wheeler, J.A.; Misner, C.W.; Thorne, K.S. Gravitation; Freeman & Co.: San Francisco, CA, USA, 1973. [Google Scholar]
- Hawking, S. Particle Creation by Black Holes. Comm. Math. Phys. 1975, 43, 199. [Google Scholar] [CrossRef]
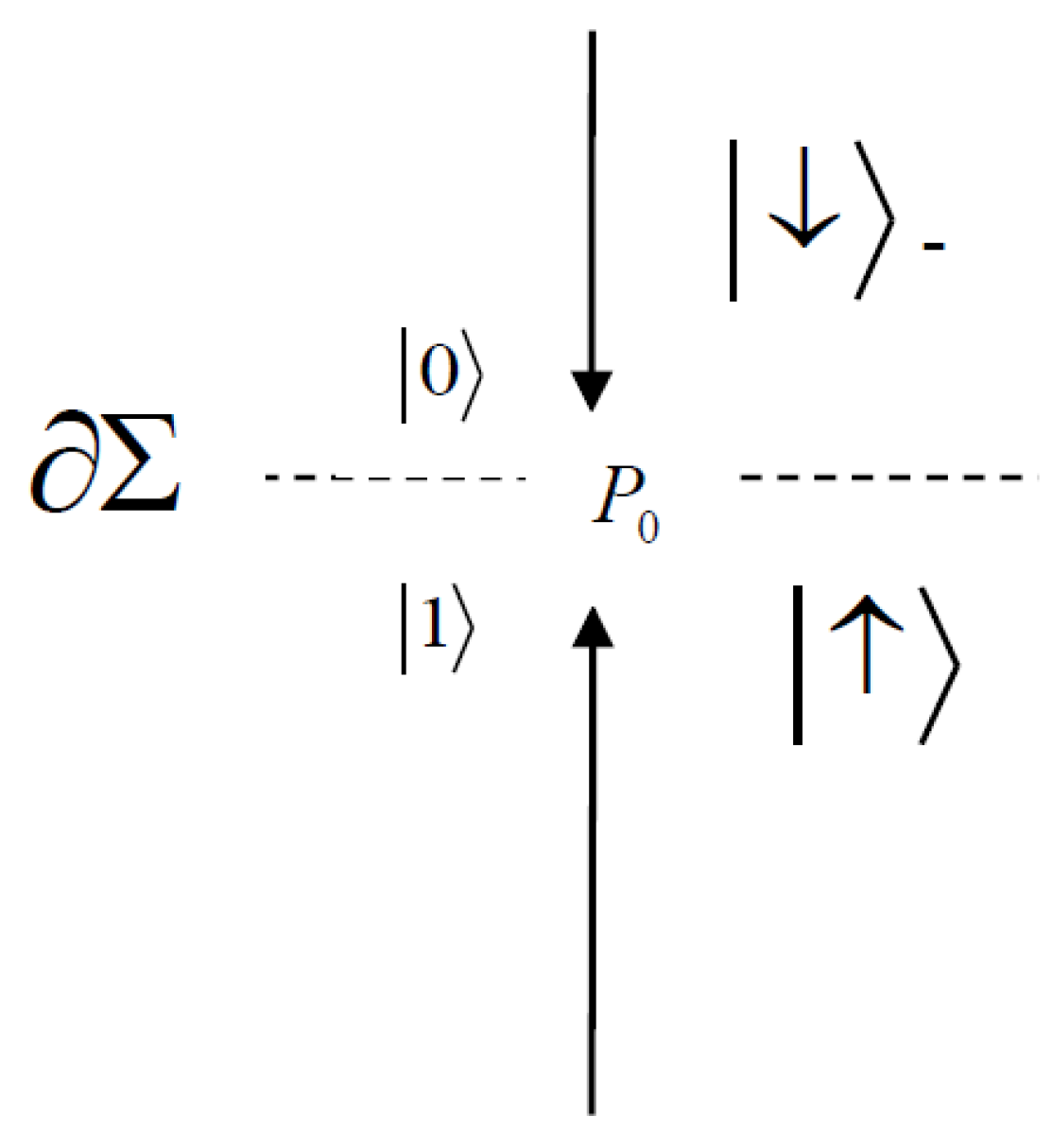
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zizzi, P. Quantum Holography from Fermion Fields. Quantum Rep. 2021, 3, 576-591. https://doi.org/10.3390/quantum3030037
Zizzi P. Quantum Holography from Fermion Fields. Quantum Reports. 2021; 3(3):576-591. https://doi.org/10.3390/quantum3030037
Chicago/Turabian StyleZizzi, Paola. 2021. "Quantum Holography from Fermion Fields" Quantum Reports 3, no. 3: 576-591. https://doi.org/10.3390/quantum3030037
APA StyleZizzi, P. (2021). Quantum Holography from Fermion Fields. Quantum Reports, 3(3), 576-591. https://doi.org/10.3390/quantum3030037



