Bose–Einstein Condensation Processes with Nontrivial Geometric Multiplicities Realized via 𝒫𝒯−Symmetric and Exactly Solvable Linear-Bose–Hubbard Building Blocks
Abstract
:1. Introduction
2. Bose-Einstein Condensation
2.1. Symmetric Bose–Hubbard Model
2.2. BEC-Formation Patterns
3. Nontrivial Geometric Multiplicities at Small
3.1. Three Bosons and
3.2. Four Bosons and
4. BEC Models of Any Dimension and Multiplicity
4.1. Canonical Representation
4.2. Transition Matrices
4.3. Geometric Multiplicities : Realization
5. Physics behind the Generalized BH Model
5.1. Change of Phase: Two Alternative Physical Interpretations
5.2. The Role of Symmetry
6. Combinatorics behind the Classification
6.1. Classification Scheme
6.2. An Alternative Notation
7. Discussion
7.1. The Specific Features of Bosons
7.2. The Problem of the Non-Uniqueness of the Model
7.3. A Remark on the Theory of Quantum Phase Transitions
8. Summary
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Christodoulides, D.; Yang, J.-K. (Eds.) Parity-Time Symmetry and Its Applications; Springer: Singapore, 2018. [Google Scholar]
- Bender, C.M. PT Symmetry in Quantum and Classical Physics; World Scientific: Singapore, 2018. [Google Scholar]
- Bagarello, F.; Gazeau, J.-P.; Szafraniec, F.; Znojil, M. (Eds.) Non-Selfadjoint Operators in Quantum Physics: Mathematical Aspects; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Semorádová, I.; Siegl, P. Diverging eigenvalues in domain truncations of Schrödinger operators with complex potentials. arXiv 2021, arXiv:2107.10557. [Google Scholar]
- Exner, P.; Tater, M. Quantum graphs: Self-adjoint, and yet exhibiting a nontrivial PT-symmetry. arXiv 2021, arXiv:2108.04708. [Google Scholar]
- Caliceti, E.; Graffi, S.; Maioli, M. Perturbation theory of odd anharmonic oscillators. Commun. Math. Phys. 1980, 75, 51. [Google Scholar] [CrossRef]
- Fernández, F.M.; Guardiola, R.; Ros, J.; Znojil, M. Strong-coupling expansions for the PTsymmetric oscillators V(r) = aix + b(ix)2 + c(ix)3. J. Phys. A Math. Gen. 1998, 31, 10105–10112. [Google Scholar] [CrossRef]
- Buslaev, V.; Grecchi, V. Equivalence of unstable anharmonic oscillators and double wells. J. Phys. A Math. Gen. 1993, 26, 5541–5549. [Google Scholar] [CrossRef]
- Andrianov, A.A.; St. Petersburg State University, St. Petersburg, Russia. Private communication, 2008.
- Bender, C.M.; Milton, K.A. Nonperturbative Calculation of Symmetry Breaking in Quantum Field Theory. Phys. Rev. D 1998, 57, 3595. [Google Scholar] [CrossRef] [Green Version]
- Bender, C.M.; Boettcher, S. Real Spectra in Non-Hermitian Hamiltonians Having PT Symmetry. Phys. Rev. Lett. 1998, 80, 5243. [Google Scholar] [CrossRef] [Green Version]
- Scholtz, F.G.; Geyer, H.B.; Hahne, F.J.W. Quasi-Hermitian Operators in Quantum Mechanics and the Variational Principle. Ann. Phys. 1992, 213, 74–101. [Google Scholar] [CrossRef]
- Bender, C.M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 2007, 70, 947. [Google Scholar] [CrossRef] [Green Version]
- Mostafazadeh, A. Pseudo-Hermitian Quantum Mechanics. Int. J. Geom. Meth. Mod. Phys. 2010, 7, 1191–1306. [Google Scholar] [CrossRef] [Green Version]
- Hiller, M.; Kottos, T.; Ossipov, A. Bifurcations in Resonance Widths of an Open Bose-Hubbard Dimer. Phys. Rev. A 2006, 73, 063625. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. Broken Hermiticity phase transition in Bose-Hubbard model. Phys. Rev. A 2018, 98, 052102. [Google Scholar] [CrossRef] [Green Version]
- Graefe, E.M.; Günther, U.; Korsch, H.J.; Niederle, A.E. A non-Hermitian PT symmetric Bose-Hubbard model: Eigenvalue rings from unfolding higherorder exceptional points. J. Phys. A Math. Theor. 2008, 41, 255206. [Google Scholar] [CrossRef]
- Kato, T. Perturbation Theory for Linear Operators; Springer: Berlin/Heidelberg, Germany, 1966. [Google Scholar]
- Znojil, M. Passage through exceptional point: Case study. Proc. Roy. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190831. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M.; Borisov, D.I. Anomalous mechanisms of the loss of observability in non-Hermitian quantum models. Nucl. Phys. B 2020, 957, 115064. [Google Scholar] [CrossRef]
- Garcia, S.R.; Putinar, M. Complex symmetric operators and applications. Trans. AMS 2005, 358, 1285. [Google Scholar] [CrossRef] [Green Version]
- Sloane, N.J.A. Number of Partitions of n That Do Not Contain 1 as a Part. Available online: http://oeis.org/A002865/ (accessed on 30 October 2020).
- Znojil, M. Admissible perturbations and false instabilities in PT-symmetric quantum systems. Phys. Rev. A 2018, 97, 032114. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. Perturbation Theory Near Degenerate Exceptional Points. Symmetry 2020, 12, 1309. [Google Scholar] [CrossRef]
- Znojil, M. Exceptional points and domains of unitarity for a class of strongly non-Hermitian real-matrix Hamiltonians. J. Math. Phys. 2021, 62, 052103. [Google Scholar] [CrossRef]
- Bloch, I.; Hänsch, T.W.; Esslinger, T. An Atom Laser with a cw Output Coupler. Phys. Rev. Lett. 1999, 82, 3008. [Google Scholar] [CrossRef] [Green Version]
- Graefe, E.-M.; Korsch, H.J.; Niederle, A.E. Quantum-classical correspondence for a non-Hermitian Bose-Hubbard dimer. Phys. Rev. A 2010, 82, 013629. [Google Scholar] [CrossRef] [Green Version]
- Teimourpour, M.H.; Zhong, Q.; Khajavikhan, M.; El-Ganainy, R. Higher Order EPs in Discrete Photonic Platforms. In Parity-Time Symmetry and Its Applications; Christodoulides, D., Yang, J.-K., Eds.; Springer: Singapore, 2018; pp. 261–276. [Google Scholar]
- Stone, M.H. On one-parameter unitary groups in Hilbert Space. Ann. Math. 1932, 33, 643. [Google Scholar] [CrossRef]
- Trefethen, L.N.; Embree, M. Spectra and Pseudospectra; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Krejčiřík, D.; Siegl, P.; Tater, M.; Viola, J. Pseudospectra in non-Hermitian quantum mechanics. J. Math. Phys. 2015, 56, 103513. [Google Scholar] [CrossRef]
- Znojil, M. Unitary unfoldings of Bose-Hubbard exceptional point with and without particle number conservation. Proc. Roy. Soc. A Math. Phys. Eng. Sci. A 2020, 476, 20200292. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, G. Bender-Wu branch points in the cubic oscillator. J. Phys. A Math. Gen. 1995, 28, 4589–4598. [Google Scholar] [CrossRef]
- Berry, M.V. Physics of Nonhermitian Degeneracies. Czechosl. J. Phys. 2004, 54, 1039–1047. [Google Scholar] [CrossRef]
- Heiss, W.D. Exceptional points—Their universal occurrence and their physical significance. Czechosl. J. Phys. 2004, 54, 1091–1100. [Google Scholar] [CrossRef]
- Borisov, D.I.; Růžička, F.; Znojil, M. Multiply Degenerate Exceptional Points and Quantum Phase Transitions. Int. J. Theor. Phys. 2015, 54, 42934305. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. Complex symmetric Hamiltonians and exceptional points of order four and five. Phys. Rev. A 2018, 98, 032109. [Google Scholar] [CrossRef] [Green Version]
- Znojil, M. The Number of Decompositions of F(n,1) into Disjoint Unions. Available online: https://oeis.org/A335631 (accessed on 4 June 2021).
- Znojil, M. The Number of Decompositions of H(n,1) into Disjoint Unions. Available online: https://oeis.org/A336739 (accessed on 4 June 2021).
- Klaiman, S.; Günther, U.; Moiseyev, N. Visualization of Branch Points in P T -Symmetric Waveguides. Phys. Rev. Lett. 2008, 101, 080402. [Google Scholar] [CrossRef] [Green Version]
- Cartarius, H.; Wunner, G. Model of a PT-symmetric Bose-Einstein condensate in a double-well potential. Phys. Rev. A 2012, 86, 013612. [Google Scholar] [CrossRef] [Green Version]
- Bose, S.N. Plancks Gesetz und Lichtquantenhypothese. Z. Phys. 1924, 26, 178–181. [Google Scholar] [CrossRef]
- Einstein, A. Quantentheorie des einatomigen idealen Gases; Königl. Preuss. Akad. d. Wissenschaften Sitzungsberichte: Berlin, Germany, 1924; pp. 261–267. [Google Scholar]
- Stone, A.D. The Indian Comet, in Einstein and the Quantum; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Avdeenkov, A.V.; Zloshchastiev, K.G. Quantum Bose liquids with logarithmic nonlinearity: Self-sustainability and emergence of spatial extent. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 195303. [Google Scholar] [CrossRef] [Green Version]
- Scott, T.C.; Zloshchastiev, K.G. Resolving the puzzle of sound propagation in liquid helium at low temperatures. Low Temp. Phys. 2019, 45, 1231. [Google Scholar] [CrossRef]
- Cai, X.-M. Boundary-dependent self-dualities, winding numbers, and asymmetrical localization in non-Hermitian aperiodic one-dimensional models. Phys. Rev. B 2021, 103, 014201. [Google Scholar] [CrossRef]
- Liu, Y.-X.; Jiang, X.-P.; Cao, J.-P.; Chen, S. Non-Hermitian mobility edges in one-dimensional quasicrystals with parity-time symmetry. Phys. Rev. B 2020, 101, 174205. [Google Scholar] [CrossRef]
- Bian, Z.; Xiao, L.; Wang, K.; Zhan, X.; Onanga, F.A.; Růžička, F.; Yi, W.; Joglekar, Y.N.; Xue, P. Conserved quantities in parity-time symmetric systems. Phys. Rev. Res. 2020, 2, 022039(R). [Google Scholar] [CrossRef]
- Znojil, M.; Růžička, F.; Zloshchastiev, K.G. Schroedinger equations with logarithmic self-interactions: From antilinear PT-symmetry to the nonlinear coupling of channels. Symmetry 2017, 9, 165. [Google Scholar] [CrossRef] [Green Version]
- Xu, T.; Chen, Y.; Li, M.; Meng, D.-X. General stationary solutions of the nonlocal nonlinear Schrodinger equation and their relevance to the PT-symmetric system. Chaos 2019, 29, 123124. [Google Scholar] [CrossRef] [Green Version]
- Ramirez, R.; Reboiro, M.; Tielas, D. Exceptional Points from the Hamiltonian of a hybrid physical system: Squeezing and anti-Squeezing. Eur. Phys. J. D 2020, 74, 193. [Google Scholar] [CrossRef]
- Moiseyev, N. Non-Hermitian Quantum Mechanics; CUP: Cambridge, UK, 2011. [Google Scholar]
- Dyson, F.J. General Theory of Spin-Wave Interactions. Phys. Rev. 1956, 102, 1217–1230. [Google Scholar] [CrossRef]
- Krejčiřík, D.; Lotoreichik, V.; Znojil, M. The minimally anisotropic metric operator in quasi-Hermitian quantum mechanics. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20180264. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Znojil, M. Solvable model of quantum phase transitions and the symbolic-manipulation-based study of its multiply degenerate exceptional points and of their unfolding. Ann. Phys. 2013, 336, 98–111. [Google Scholar] [CrossRef] [Green Version]
- Borisov, D.I. Eigenvalues collision for PT-symmetric waveguide. Acta Polytech. 2014, 54, 93. [Google Scholar] [CrossRef]
- Messiah, A. Quantum Mechanics I; Springer: Amsterdam, The Netherlands, 1961. [Google Scholar]
- Znojil, M. Theory of response to perturbations in non-hermitian systems using five-Hilbert-space reformulation of unitary quantum mechanics. Entropy 2020, 22, 80. [Google Scholar] [CrossRef] [PubMed] [Green Version]
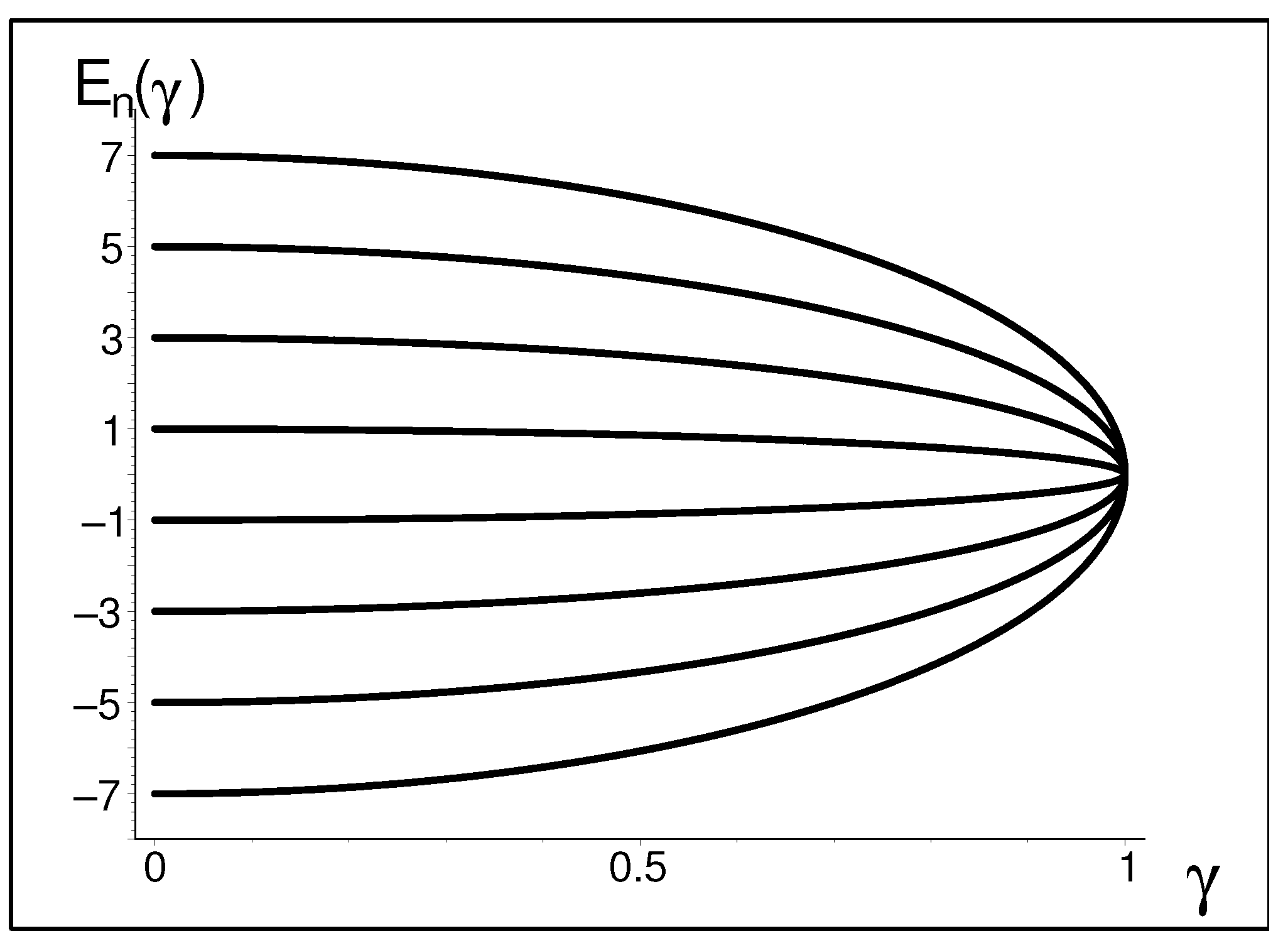
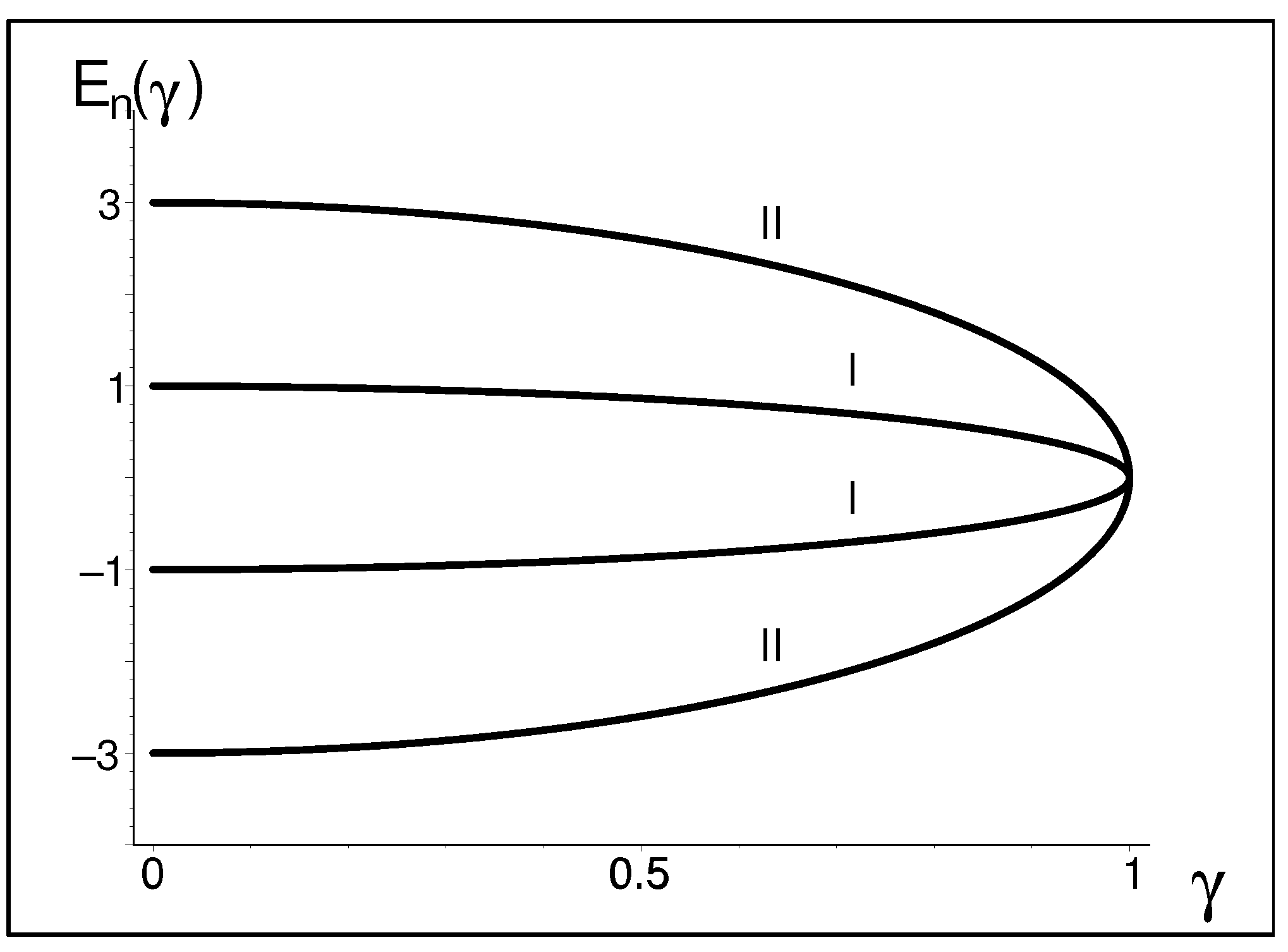

| N | |||
|---|---|---|---|
| 2 | [2] | 1 | 1 |
| 3 | [3] | 1 | 1 |
| 4 | [4], [2,2] | 2 | 2 |
| 5 | [5], [3,2] | 2 | 2 |
| 6 | [6], [4,2], [3,3], [2,2,2] | 4 | 3 |
| 7 | [7], [5,2], [4,3], [3,2,2] | 4 | 3 |
| 8 | [8], [6,2], [5,3], [4,4], | ||
| [4,2,2], [3,3,2], [2,2,2,2] | 7 | 4 |
| N | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 2 | 4 | 4 | 7 | 8 | 12 | 14 | 21 | 24 | 34 | 41 | 55 | 66 | 88 | 105 | 137 |
| N | # | K | m | Partition | Set |
|---|---|---|---|---|---|
| 2 | 1 | 1 | 0 | [2] | {1} |
| 3 | 1 | 1 | 0 | [3] | {1} |
| 4 | 1 | 1 | 0 | [4] | {1} |
| 2 | 2 | 1 | [2,2] | {1,3} | |
| 5 | 1 | 1 | 0 | [5] | {1} |
| 2 | 2 | 1 | [3,2] | {1,4} | |
| 3 | 2 | 1 | [3,2] | {2,2} | |
| 6 | 1 | 1 | 0 | [6] | {1} |
| 2 | 2 | 1 | [4,2] | {1,5} | |
| 3 | 3 | 3 | [2,2,2] | {1,3,5} | |
| 7 | 1 | 1 | 0 | [7] | {1} |
| 2 | 2 | 1 | [5,2] | {1,6} | |
| 3 | 2 | 2 | [4,3] | {2,2} | |
| 4 | 3 | 3 | [3,2,2] | {1,4,6} | |
| 5 | 3 | 3 | [3,2,2] | {2,2,6} | |
| 6 | 3 | 3 | [3,2,2] | {3,2,4} |
| N | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 3 | 6 | 4 | 11 | 6 | 17 | 7 | 32 | 8 | 47 |
| N | Partitions (18) of | # | Isospectral–Hamiltonian Indices | # |
|---|---|---|---|---|
| 2 | 2 | 1 | {1} | 1 |
| 3 | 3 | 1 | {02} | 1 |
| 4 | 4, 2 + 2 | 2 | {13}, {1}{3} | 2 |
| 5 | 5, 3 + 2 | 2 | {024}, {02}{4}, {04}{2} | 3 |
| 6 | 6, 4+2, 3+3, 2+2+2 | 4 | {135}, {13}{5}, {1}{3}{5} | 3 |
| 7 | 7, 5 + 2, 4 + 3, | 4 | {0246}, {024}{6}, {04}{26}, | 6 |
| 3+2+2 | {02}{4}{6}, {04}{2}{6}, {06}{2}{4} | |||
| 8 | 8, 6 + 2, 5 + 3, 4 + 4, 4 + 2 + 2, | 7 | {1357}, {135}{7}, {13}{5}{7}, | 4 |
| 3 + 3 + 2, 2 + 2 + 2 + 2 | {1}{3}{5}{7} |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Znojil, M. Bose–Einstein Condensation Processes with Nontrivial Geometric Multiplicities Realized via 𝒫𝒯−Symmetric and Exactly Solvable Linear-Bose–Hubbard Building Blocks. Quantum Rep. 2021, 3, 517-533. https://doi.org/10.3390/quantum3030034
Znojil M. Bose–Einstein Condensation Processes with Nontrivial Geometric Multiplicities Realized via 𝒫𝒯−Symmetric and Exactly Solvable Linear-Bose–Hubbard Building Blocks. Quantum Reports. 2021; 3(3):517-533. https://doi.org/10.3390/quantum3030034
Chicago/Turabian StyleZnojil, Miloslav. 2021. "Bose–Einstein Condensation Processes with Nontrivial Geometric Multiplicities Realized via 𝒫𝒯−Symmetric and Exactly Solvable Linear-Bose–Hubbard Building Blocks" Quantum Reports 3, no. 3: 517-533. https://doi.org/10.3390/quantum3030034
APA StyleZnojil, M. (2021). Bose–Einstein Condensation Processes with Nontrivial Geometric Multiplicities Realized via 𝒫𝒯−Symmetric and Exactly Solvable Linear-Bose–Hubbard Building Blocks. Quantum Reports, 3(3), 517-533. https://doi.org/10.3390/quantum3030034






