Shannon Entropy for the Hydrogen Atom Confined by Four Different Potentials
Abstract
:1. Introduction
2. Methodology
3. Results
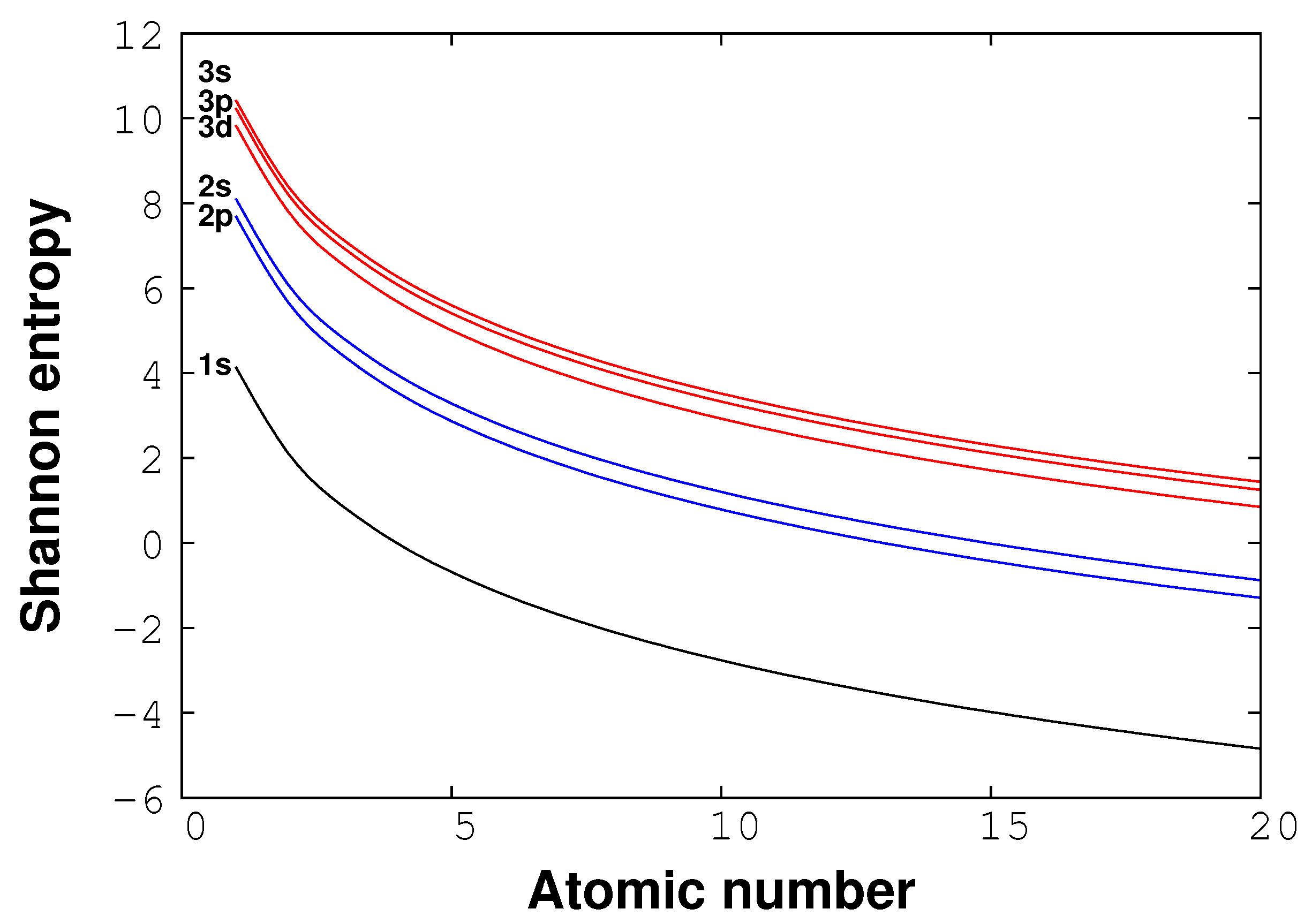
3.1. Free Hydrogen Atom
- The first integral vanishes for s orbitals ().
- The second integral does not contribute to the final result for orbitals that satisfy the relationship (no nodes in the wave-function).
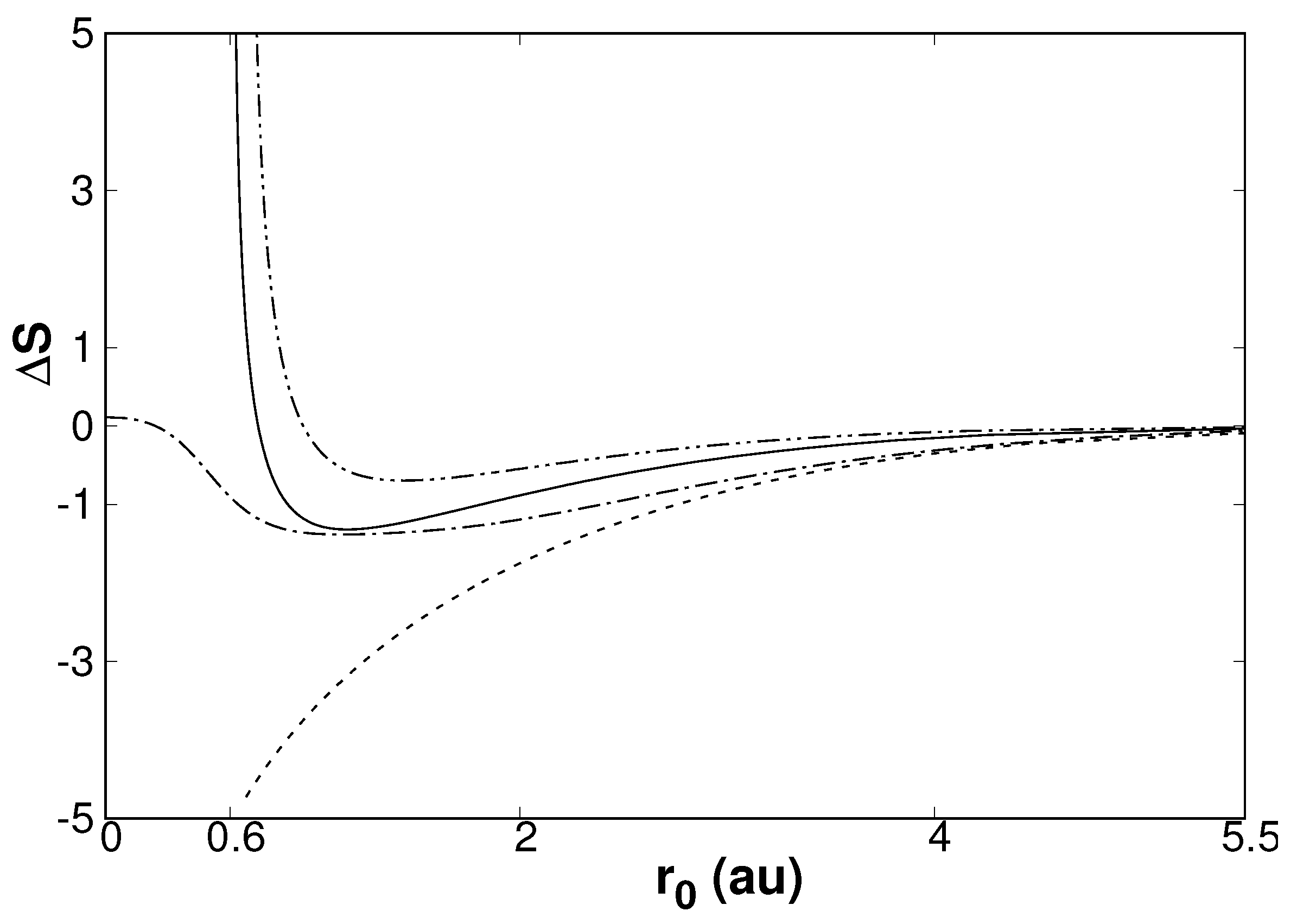
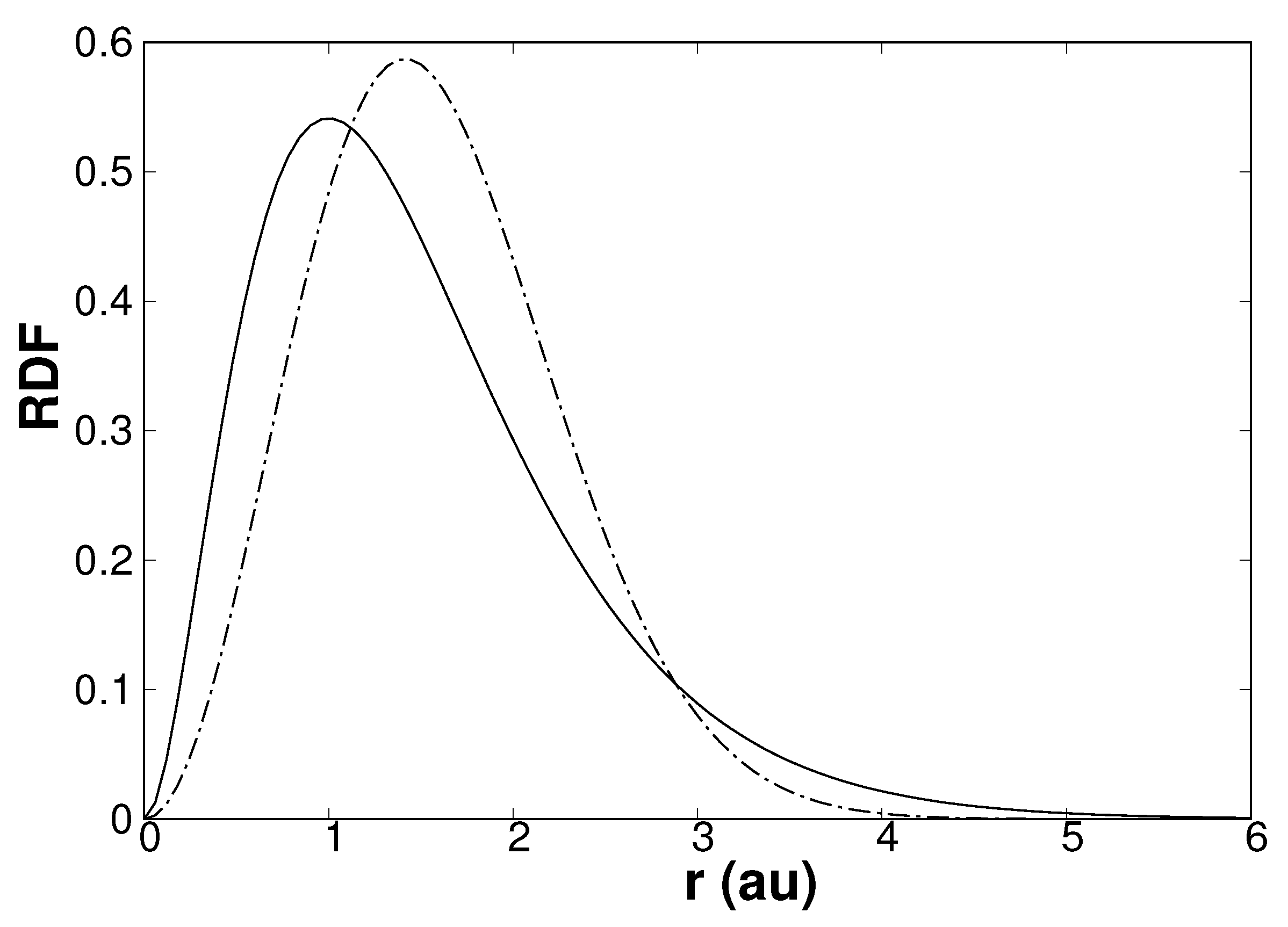
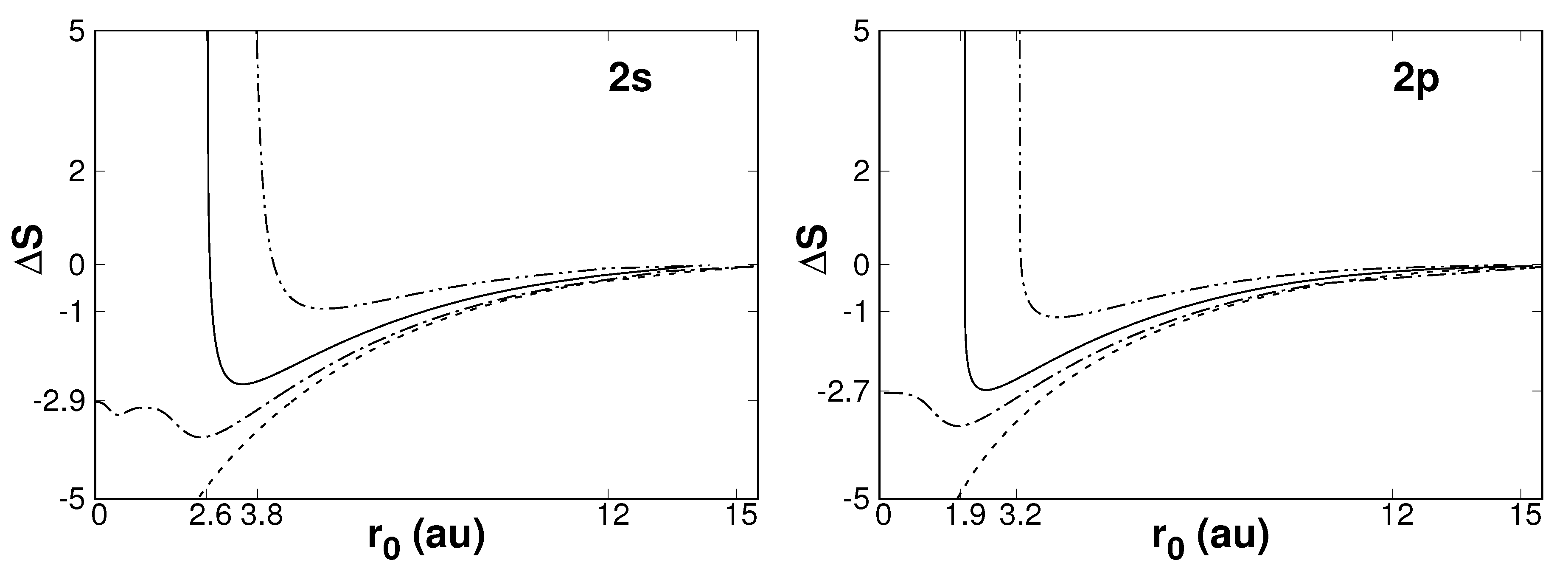
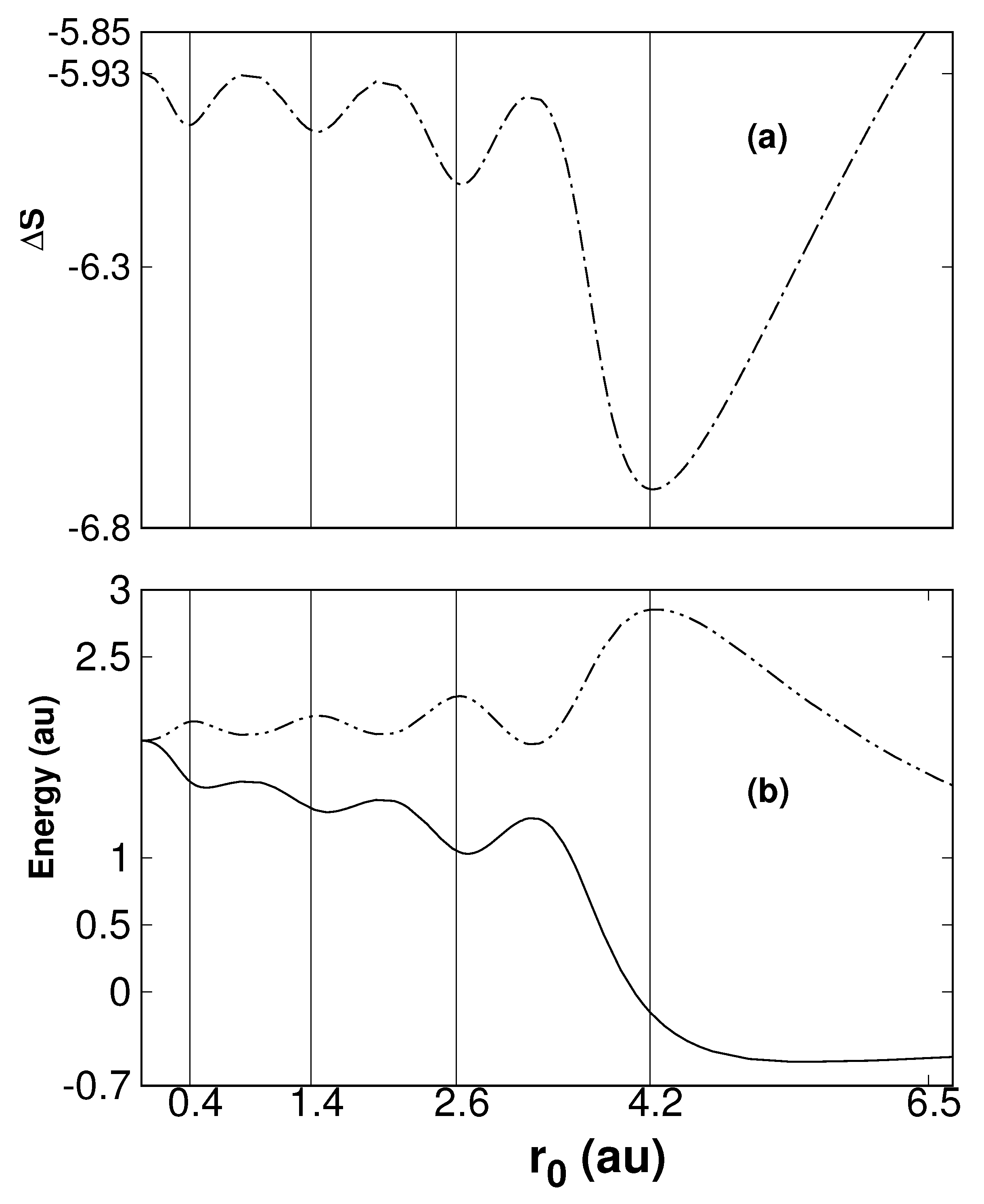
3.2. Confined Hydrogen Atom
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Michels, A.; Boer, J.D.; Bijl, A. Remarks concerning molecular interaction and their influence on the polarisability. Physica 1937, 4, 981. [Google Scholar] [CrossRef]
- Sommerfeld, A.; Welker, H. Künstliche Grenzbedingungen beim Keplerproblem. Ann. Phys. 1938, 32, 56–65. [Google Scholar] [CrossRef]
- Jortner, J.; Coulson, C.A. Environmental effects on atomic energy levels. Mol. Phys. 1961, 24, 451–464. [Google Scholar] [CrossRef]
- Gorecki, J.; Byers-Brown, W. Padded-box model for the effect of pressure on helium. J. Phys. B At. Mol. Opt. Phys. 1988, 21, 403–410. [Google Scholar] [CrossRef]
- Connerade, J.P.; Dolmatov, V.K.; Lakshmi, P.A.; Manson, S.T. Electron structure of endohedrally confined atoms: Atomic hydrogen in an attractive shell. J. Phys. B At. Mol. Opt. Phys. 1999, 32, L239–L245. [Google Scholar] [CrossRef]
- Dolmatov, V. Photoionization of Atoms Encaged in Spherical Fullerenes. Adv. Quantum Chem. 2009, 58, 13–68. [Google Scholar]
- Ivanov, S.; Burke, K.; Levy, M. Exact high-density limit of correlation potential for two-electron density. J. Chem. Phys. 1999, 110, 10262–10268. [Google Scholar] [CrossRef] [Green Version]
- Ludeña, E.V. Exact analytic total energy functional for Hooke’s atom generated by local-scaling transformations. Int. J. Quantum Chem. 2004, 99, 297–907. [Google Scholar] [CrossRef]
- Martínez-Sánchez, M.A.; Rodriguez-Bautista, M.; Vargas, R.; Garza, J. Solution of the Kohn–Sham equations for many-electron atoms confined by penetrable walls. Theor. Chem. Acc. 2016, 135, 207. [Google Scholar] [CrossRef]
- Duarte-Alcaráz, F.A.; Martínez-Sánchez, M.A.; Rivera-Almazo, M.; Vargas, R.; Rosas-Burgos, R.A.; Garza, J. Testing one-parameter hybrid exchange functionals in confined atomic systems. J. Phys. B At. Mol. Opt. Phys. 2019, 52, 135002. [Google Scholar] [CrossRef]
- Sarsa, A.; Buendía, E.; Gálvez, F.J. Multi-configurational explicitly correlated wave functions for the study of confined many electron atoms. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 145003. [Google Scholar] [CrossRef]
- Gálvez, F.J.; Buendía, E.; Sarsa, A. Confinement effects on the electronic structure of M-shell atoms: A study with explicitly correlated wave functions. Int. J. Quantum Chem. 2017, 117, e25421. [Google Scholar] [CrossRef]
- Ludeña, E.V. SCF Hartree–Fock calculations of ground state wavefunctions of compressed atoms. J. Chem. Phys. 1978, 69, 1770. [Google Scholar] [CrossRef]
- Connerade, J.P.; Dolmatov, V. Controlling orbital collapse from inside and outside a transition element. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 3557–3564. [Google Scholar] [CrossRef]
- Connerade, J.P.; Dolmatov, V.; Lakshmi, P.A. The filling of shells in compressed atoms. J. Phys. B At. Mol. Opt. Phys. 2000, 33, 251–264. [Google Scholar] [CrossRef]
- Garza, J.; Vargas, R.; Vela, A. Numerical self-consistent-field method to solve the Kohn-Sham equations in confined many-electron atoms. Phys. Rev. E 1998, 58, 3949–3954. [Google Scholar] [CrossRef]
- Sen, K.D.; Garza, J.; Vargas, R.; Vela, A. Effective pressure induced electronic transition in spherically confined alkali metal atoms. Proc. Indian Nat. Sci. Acad. 2004, 70A, 675. [Google Scholar]
- Guerra, D.; Vargas, R.; Fuentealba, P.; Garza, J. Modeling pressure effects on the electronic properties of Ca, Sr, and Ba by the confined atoms model. Adv. Quantum Chem. 2009, 58, 1. [Google Scholar]
- Rodriguez-Bautista, M.; Díaz-García, C.; Navarrete-López, A.M.; Vargas, R.; Garza, J. Roothaan’s approach to solve the Hartree-Fock equations for atoms confined by soft walls: Basis set with correct asymptotic behavior. J. Chem. Phys. 2015, 143, 034103. [Google Scholar] [CrossRef]
- Rodriguez-Bautista, M.; Vargas, R.; Aquino, N.; Garza, J. Electron-density delocalization in many-electron atoms confined by penetrable walls: A Hartree–Fock study. Int. J. Quantum Chem. 2018, 118, 2018. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Corso, H.H.; Laguna, H.G.; Sagar, R.P. Localization-delocalization phenomena in a cyclic box. J. Math. Chem. 2012, 50, 233–248. [Google Scholar] [CrossRef]
- Corso, H.H.; Castaño, E.; Laguna, H.G.; Sagar, R.P. Measuring localization-delocalization phenomena in a quantum corral. J. Math. Chem. 2013, 51, 179–193. [Google Scholar] [CrossRef]
- Sen, K.D. Characteristic features of Shannon information entropy of confined atoms. J. Chem. Phys. 2005, 123, 074110. [Google Scholar] [CrossRef]
- Mukherjee, N.; Roy, A.K. Information-entropic measures for non-zero l states of confined hydrogen-like ions. Eur. Phys. J. D 2018, 72, 118. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, N.; Roy, A.K. Information-entropic measures in free and confined hydrogen atom. Int. J. Quantum Chem. 2018, 118, e25596. [Google Scholar] [CrossRef]
- Aquino, N.; Campoy, G.; Montgomery, H.E. Highly Accurate Solutions for the Confined Hydrogen Atom. Int. J. Quantum Chem. 2007, 107, 1548–1558. [Google Scholar] [CrossRef]
- Ley-Koo, E.; Rubinstein, S. The hydrogen atom within spherical boxes with penetrable walls. J. Chem. Phys. 1979, 71, 351–357. [Google Scholar] [CrossRef]
- Martínez-Sánchez, M.A.; Aquino, N.; Vargas, R.; Garza, J. Exact solution for the hydrogen atom confined by a dielectric continuum and the correct basis set to study many-electron atoms under similar confinements. Chem. Phys. Lett. 2017, 690, 14–19. [Google Scholar] [CrossRef]
- Gadre, S.R.; Sears, S.B.; Chakravorty, S.J.; Bendale, R.D. Some novel characteristics of atomic information entropies. Phys. Rev. A 1985, 32, 2602–2606. [Google Scholar] [CrossRef]
- Jiao, L.; Zan, L.; Zhang, Y.; Ho, Y. Benchmark values of Shannon entropy for spherically confined hydrogen atom. Int. J. Quantum Chem. 2017, 117, e25375. [Google Scholar] [CrossRef]
- Yáñez, R.J.; Van Assche, W.; Dehesa, J.S. Position and momentum information entropies of the D-dimensional harmonic oscillator and hydrogen atom. Phys. Rev. A 1994, 50, 3065–3079. [Google Scholar] [CrossRef] [PubMed]
- Aquino, N.; Flores-Riveros, A.; Rivas-Silva, J. Shannon and Fisher entropies for a hydrogen atom under soft spherical confinement. Phys. Lett. A 2013, 377, 2062–2068. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Sánchez, M.-A.; Vargas, R.; Garza, J. Shannon Entropy for the Hydrogen Atom Confined by Four Different Potentials. Quantum Rep. 2019, 1, 208-218. https://doi.org/10.3390/quantum1020018
Martínez-Sánchez M-A, Vargas R, Garza J. Shannon Entropy for the Hydrogen Atom Confined by Four Different Potentials. Quantum Reports. 2019; 1(2):208-218. https://doi.org/10.3390/quantum1020018
Chicago/Turabian StyleMartínez-Sánchez, Michael-Adán, Rubicelia Vargas, and Jorge Garza. 2019. "Shannon Entropy for the Hydrogen Atom Confined by Four Different Potentials" Quantum Reports 1, no. 2: 208-218. https://doi.org/10.3390/quantum1020018
APA StyleMartínez-Sánchez, M.-A., Vargas, R., & Garza, J. (2019). Shannon Entropy for the Hydrogen Atom Confined by Four Different Potentials. Quantum Reports, 1(2), 208-218. https://doi.org/10.3390/quantum1020018







