Abstract
The basic notion of physical system states is different in classical statistical mechanics and in quantum mechanics. In classical mechanics, the particle system state is determined by its position and momentum; in the case of fluctuations, due to the motion in environment, it is determined by the probability density in the particle phase space. In quantum mechanics, the particle state is determined either by the wave function (state vector in the Hilbert space) or by the density operator. Recently, the tomographic-probability representation of quantum states was proposed, where the quantum system states were identified with fair probability distributions (tomograms). In view of the probability-distribution formalism of quantum mechanics, we formulate the superposition principle of wave functions as interference of qubit states expressed in terms of the nonlinear addition rule for the probabilities identified with the states. Additionally, we formulate the probability given by Born’s rule in terms of symplectic tomographic probability distribution determining the photon states.
1. Introduction
The superposition principle of quantum states, identified with the wave functions introduced by Schrödinger [1], is the fundamental property of quantum systems. Its formulation provides the possibility to associate with two wave functions corresponding to the two pure states of the system, the third function which is an arbitrary linear combination of the two wave functions. A property of the quantum world is that this combination also corresponds to a physical state of the system. An analogous formulation takes place for two state vectors in a Hilbert space and the linear combination of these vectors [2]. The foundation of quantum mechanics and the role of superposition principle were also discussed for quantum states [3,4], which are associated with the density matrices of density operators acting in the Hilbert space, introduced in [5,6]. The foundations of quantum optics were developed in connection with coherence properties of the electromagnetic-field states in [7,8] as well as in [9].
The aim of this paper is to demonstrate how such a phenomenon as interference of quantum states, described by the superposition principle of complex wave functions, is considered in the probability representation of quantum mechanics [10,11,12,13,14,15,16,17,18,19,20,21]. In the probability picture, the interference is described by the nonlinear addition rule of the probabilities describing the superposed states; the rule provides the probabilities describing the superposition state, and this corresponds to the nonlinear addition rule of the projectors. We demonstrate this rule on an example of the superposition of qubit states.
The superposition principle describes the interference phenomenon in quantum mechanics. Since the density operators and provide the expression for the density operator of superposition state , where vector is a linear combination of vectors and , the superposition principle can be formulated as an addition rule of the probabilities (quantum-state tomograms). We provide explicitly an example of such addition rule for a particular system, namely, for the spin-1/2 particle or the two-level atom.
The other goal of this paper is to formulate Born’s rule for probabilities given by an overlap of two state wave functions in the form of expression providing the probability as a function of probabilities determining the states given by the density operators and . The result obtained shows that such a complete quantum phenomenon as the interference of wave functions can be formulated by applying only classical tools like probabilities used in classical statistics.
This paper is organized as follows:
Section 2 is ad memoriam of Roy Glauber and George Sudarshan, where we give a short review of their fundamental results in quantum physics. In Section 3, we provide a brief review of the scientific results of our colleague Viktor Dodonov, in connection with his 70th anniversary. In Section 4, we discuss the qubit-state density matrix in the probability representation using classical-like probability distributions of dichotomic variables [22]. Section 5 is devoted to the superposition principle in the probability representation, while the quantum suprematism picture of qubit states is presented in Section 6 and Born’s rule is formulated as a nonlinear addition rule of probabilities in Section 7. We discuss quantum tomography of continuous variables and quantum tomography of coherent states in Section 8 and Section 9, respectively. Born’s rule for oscillator states are considered in Section 10. Finally, our results and prospectives are given in Section 11.
2. Ad Memoriam of Roy Glauber and George Sudarshan
Last year we suffered great losses. Professor Roy J. Glauber and Professor E.C. George Sudarshan, founders of quantum optics, passed away in 2018. We are extremely sad about this. (Ad Memoriam of Roy Glauber and George Sudarshan was also presented in the talks of Margarita A. Man’ko at the 26th Central European Workshop on Quantum Optics {CEWQO} (Paderborn University, Germany, 3–7 June 2019) [23] and the 18th International Symposium “Symmetries in Sciences” (Gasthof Hotel Lamm, Bregenz, Vorarlberg, Austria, 4–9 August 2019) [24] and will be published in the Journal of Russian Laser Research (2019) and the Journal of Physics: Conference Series (2020), respectively.)

These distinguished scientists made famous discoveries in the foundations of quantum physics that provide the possibility today to raise quantum optics and quantum mechanics to a level of understanding such that quantum technologies can now be developed. The operation of such devices as lasers is based on understanding the coherence properties of radiation and realizing how to achieve the conditions for obtaining such properties.

In 1963, the notion of the coherent state of electromagnetic-field oscillations as well as the terminology “coherent state” of an arbitrary oscillator were introduced. Roy Glauber and George Sudarshan simultaneously published the papers [7,8] where the properties of coherent states were discussed. These publications are cited in the majority of papers where quantum optics and quantum information technologies are discussed.
The general linear positive map of the density matrix to the other density matrices for finite-dimensional systems was presented in the form [25], which later on was generalized in [26] for arbitrary systems. In addition, we should point out that the new evolution equation for open quantum systems, which generalizes the Schrödinger equation for the wave function and the von Neumann equation for the density matrix considered in the case of unitary evolution to the case of nonunitary evolution, was obtained in [27,28] and called the GKSL equation.
The pioneer scientific results obtained by these distinguished researchers play an important role in developing quantum optics. Studies of the properties of quantum states, especially the coherence and squeezing phenomena, correlations, unitary evolution, and the evolution of the electromagnetic fields in the presence of dissipation are based on the original results of Glauber and Sudarshan. All applications of quantum optics discussed in connection with the development of quantum technologies, motivated by the attempts to construct quantum computers and quantum information devices, are based on the theoretical notion and foundations of quantum mechanics associated with the results obtained by Glauber and Sudarshan.
A specific phase-space quasidistribution representation of quantum states, which employs the basis of coherent states, was introduced independently by Glauber and Sudarshan—it is called the Glauber–Sudarshan P-representation. This representation plays an important role in discussing the properties of quantum systems analogously to the Wigner quasidistribution function [29] and the Husimi–Kano quasidistribution [30,31]. These famous contributions play an important role in the foundations of quantum optics and quantum information, and in developing future quantum technologies.
Substantial developments in laser physics were made at the Lebedev Physical Institute in Moscow by Nikolay G. Basov, who won the Nobel Prize in 1964 together with Aleksandr M. Prokhorov and Charles H. Townes due to their revolutionary work in the invention of masers and lasers (as well as laser physics based on quantum mechanics and quantum optics). The official formulation reads that the Nobel Prize was given “for fundamental work in the field of quantum electronics, which has led to the construction of oscillators and amplifiers based on the maser–laser principle”.
Roy J. Glauber received the Nobel Prize in 2005 “for his contribution to the quantum theory of optical coherence”, along with John L. Hall and Theodor W. Hansch who received the Nobel Prize “for their contributions to the development of laser-based precision spectroscopy, including the optical frequency comb technique”. Roy Glauber made an important contribution to the nuclear physics providing a rigorous analysis of the scattering theory. Additionally, the important results were obtained by Glauber in the theory of correlation functions in quantum optics. The correlation functions play a substantial role on the analysis of classical and quantum phenomena in radiation fields.
Professor Glauber exercised substantial influence on the development of quantum optics in European Scientific Centers—he would invite young researchers to Harvard University for collaborations, among which we can list Fritz Haake from Germany, Paolo Tombesi from Italy, Vladimir Man’ko from the Soviet Union, and Stig Stenholm from Finland.
Since the entire scientific life of M.A. Man’ko was connected with the Lebedev Physical Institute, she was a witness and participant in the collaboration of Roy Glauber with Lebedev scientists. The results of these collaborations were published in such series as the Proceedings of the Lebedev Institute [32] and Journal of Experimental and Theoretical Physics [33]. Among the four Nobel-prize papers, there was a paper by G. Schrade, V.I. Man’ko, W.P. Schleich, and R. Glauber [34], where the collaboration of Harvard University, the Lebedev Institute (Moscow), and University of Ulm was mentioned.
As for George Sudarshan, the great scientist, we are happy to recall that he was in Moscow many times due to the International Workshops on Squeezed States, Group Theoretical Colloquium, and the International Conference on Squeezed States and Uncertainty Relations. Particular mention should be made of the University Federico II of Naples and especially Professor Giuseppe Marmo who enabled many European scientists to collaborate with Professor Sudarshan in Italy.
There exist other representations, like the probability representation of quantum states [35,36,37,38,39], where states are identified with fair probability distributions. The state superposition is expressed in this representation using the addition rule for the probabilities. We are happy to let the readers of the Journal of Russian Laser Research know that famous results concerning the study of entanglement phenomenon, quantum tomography, and superposition principle in terms of density operators were published by Sudarshan with coauthors in [3,4,40,41].

The famous book—Foundations of Quantum Optics [9], written by John Klauder and George Sudarshan and translated into Russian—is an excellent textbook on the foundation of quantum theory; it is used in all universities of the world, including universities in Russia, by students and professors to obtain basic knowledge in developing new quantum technologies in the future.
The results of Glauber and Sudarshan mentioned above provided the theoretical basis in studies of the evolution of open quantum systems, theory of quantum channels, and applications of these approaches in future quantum technologies. Therefore, we are extremely pleased to be able to witness these deep international connections today, and we show below a kaleidoscope of pictures taken recently and a long time ago connected with participants of the ICSSUR series (with Professor Young Suh Kim, the Founder) and the CEWQO series (with Professor Jozsef Janszky, the Founder), as well as some other meetings.
3. Professor Viktor V. Dodonov: On the Occasion of His 70th Birthday
On 26 November 2018, Viktor V. Dodonov, a recognized Russian physicist and current professor at the National University of Brazil (Brazilia), turned 70. In addition to his University academic activity, Professor Dodonov is an Editorial board member of our Journal of Russian Laser Research published by Springer in New York, and we celebrate this date with all our friends and colleagues, see also [42].

Professor Viktor V. Dodonov—in addition to his scientific activity and obtaining many interesting results in foundations and applications of quantum theory—participated together with us during all his scientific life in organizing conferences, workshops, and publications of the Proceedings of the conferences, and is the Editorial Board member of Journal of Russian Laser Research. Together with Vladimir Man’ko, he has issued the book Invariants and the Evolution of Nonstationary Quantum Systems, published by Nauka in Moscow as volume No. 183 of the Lebedev Institute Proceedings and translated into English by Nova Science Publishers, Commack, New York in 1983 [43], where many of his results on time-dependent integrals of motion, parametric oscillators, even and odd coherent states, and general theory of uncertainty relations were presented.
Professor Dodonov is the coauthor of the paper [44] where developing the approach of Glauber and Sudarshan for describing the superposition of coherent states modeling Schrödinger cat states, and where the even and odd coherent states were introduced. He is also the coauthor of papers [45,46], where the idea of experimental checking of the nonstationary Casimir effect (later on called in the literature the dynamical Casimir effect) using the devices based on Josephson junctions was suggested. The photons created due to the dynamical Casimir effect were predicted to be in squeezed states. Experimental results demonstrating the existence of this effect were obtained in [47].
A substantial contribution of foundations of quantum mechanics was done by Professor Dodonov, who extended the approach for analyzing the uncertainty relations [48,49]. The new kinds of uncertainty relations for different physical observables including the position and momentum, spin variables, as well as entropic inequalities play an important role in discussing quantum-information devices and quantum-channel technique.
In times of the Soviet Union, Viktor Dodonov together with the Lebedev people organized several international meetings in Moscow, Moscow Region (Zvenigorod), Urmala (Latvia), Baky (Azerbaijan), Tambov (his native place), and so on. Scientific Programs of the conferences and publication of the Proceedings were always a prerogative of Dodonov—he did this job perfectly.
We are absolutely happy to have Professor Dodonov as the Editorial Board Member of Journal of Russian Laser Research, as permanent referee of Physica Scripta, and hope that he will help us to produce referee’s estimation of contributions to Quantum Reports, where we announced to publish the Proceedings of the 16th ICSSUR.
We wish Viktor V. Dodonov long scientific activity and continuation of his work with us!






4. Qubit States in the Probability Representation
The density matrix of the spin-1/2 state is 2 × 2 matrix ; for spin projections on the z axis , it reads
where are probabilities to have spin projections and on the z axis. Off-diagonal matrix elements provide the condition of hermiticity of the density matrix . The non-negativity of the eigenvalues of this matrix gives i.e., .
Recently [50,51], the probability representation of the density matrix was found to be
One can check that the number , , is the probability to have the spin projection on the z axis equal to in the state with the density matrix . This means that, in view of Born’s rule, the probability reads
The state with the density matrix is the pure state with the state vector , which is the eigenstate of the Pauli matrix determining the spin-projection operator on the z-axis.
The number is given by an analogous relation
where the density matrix with the state vector It is the eigenvector of the Pauli matrix determining the spin-projection operator on the x-axis.
One can easily check that, due to Born’s rule, the number
is the probability to have the spin projection on the y-axis equal to in the state with the density matrix , since , and the state vector is the eigenvector of the Pauli matrix determining the spin-projection operator on the y-axis.
The state of spin equal to can be determined by three probability distributions , , and , which can be considered as probabilities for three different nonideal classical coins in such a game as coin flipping, coin tossing, or heads or tails, which is the practice of throwing a coin in the air and checking which side is showing when it lands, in order to choose between two alternatives or ; .
For quantum states, there exist quantum correlations given by the condition or
This condition does not take place for classical coins.
5. Pure States of Qubits and Their Superposition
The classical condition for these probabilities, e.g., if , reads
One can check that the density matrix of the pure state , providing the density matrix
of the form (2), where
represents a pure state if and only if
The inequalities
are forbidden for “quantum” coins or for spin-1/2 projection probabilities in the state with any density matrix .
Thus, we show that the pure state of spin equal to is determined by three probabilities to have spin projection on the three directions x, y, and z, respectively. This means that all properties of spin-1/2 states, including the superposition principle, can be formulated in terms of these probabilities.
In view of gauge invariance of wave functions, we assume the first component of the Pauli spinor to be a real and non-negative number; the second component can be given as a complex number , where the phase is the function of the probabilities, i.e,
We point out that new trigonometric formulas (11) are expressed in terms of probabilities [50] describing dichotomic random variables.
Thus, for two arbitrary pure spin states and , the superposition principle means the following:
The Pauli spinors , such that and , the numbers and are expressed in terms of probabilities satisfying the equality ; they also have the form
Due to gauge invariance of quantum-state vectors, these spinors are determined up to the phase factors by the three probabilities , , and . The density matrix expressed in terms of the numbers , , and , provides the addition rule of the probabilities , , and , , , determining the nonorthogonal vectors and yielding the explicit relations
where
Equations (13)–(15) provide the addition rule for probabilities determining the pure states and in the general case where these states are not orthogonal. Here, we use the same parameters , , and defining the complex numbers and .
At , the above number . The relative phase in the superposition of states and is determined by the phase of the complex number , . The obtained rule of probability addition corresponds to the formula for superposition principle obtained in [3]—for , it reads
where is an arbitrary projector, and are the probabilities such that .
Taking the trace of Equation (16) yields
which does not hold in general, but holds if .
Thus, we see that pure and mixed states of the spin-1/2 system can be identified with three probability distributions , , and .
Assume that we have three nonideal classical coins in such a game as coin flipping, coin tossing, or heads (“UP”) or tails (“DOWN”), which is the practice of throwing a coin in the air and checking which side is showing when it lands, in order to choose between three alternatives or ; . We interpret the numbers , , and as “coin” probabilities to be in the position “UP” for each coin, and , , and , to be in the position “DOWN”.
For pure states, there is the rule of nonlinear addition of the distributions that is equivalent to the superposition of Pauli spinors. This rule can be illustrated by addition of two Triadas of Malevich’s squares determined by “coin” probabilities , , , , , , and , , , and providing the probabilities , , as a result. This rule can be illustrated by the formula for adding the probabilities
where symbol of the addition means that we use the probabilities , , and associated with complex numbers and determining the superposition of states and .
6. Illustration of the Qubit State by Triada of Malevich’s Squares
Now, we explain how to illustrate qubit states by Triada of Malevich’s squares [50,52,53,54,55,56].
Given the triangle with sides ; ,
in the above equation, the addition is modulo 3. We construct three squares with sides associated with triangle as shown in Figure 1 and called Triada of Malevich’s squares. The sum of the areas of these three squares is expressed in terms of the three probabilities as
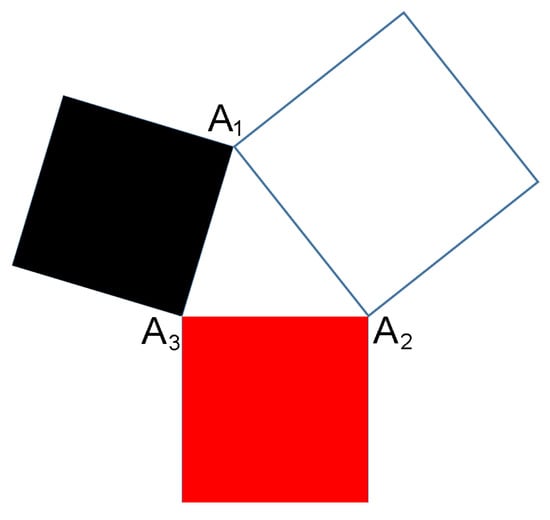
Figure 1.
Triada of Malevich’s squares corresponding to the spin-1/2 state and determined by the triangle .
The three squares constructed, using the sides of the triangle, are analogs of the Triada of Malevich’s squares in art. The properties of area S associated with the triada, given by Equation (20), are different for the classical system states and for the quantum system states, namely, for three classical coins and for qubit states.
For classical coins, the numbers , , and take any values in the domains —this means that for statistics of classical coins the area of the Triada of Malevich’s squares satisfies the inequality
For qubit states, the probabilities to have spin projections along three orthogonal directions satisfy the non-negativity condition of the density matrix—this provides the maximum value of the sum of areas of three Malevich’s squares .
The formulas obtained correspond to the addition rule for two Triadas of Malevich’s squares, illustrated by Figure 2.
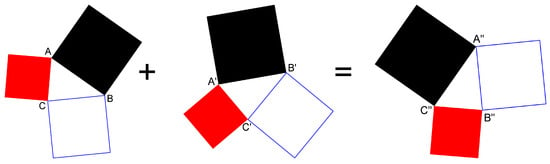
Figure 2.
The superposition principle for two pure spin-1/2 states as a result of addition of two Triadas of Malevich’s squares, which yields the Triada of Malevich’s squares associated with the addition rule.
7. Born’s Rule for Qubits as a Quadratic Form of Probabilities
Born’s rule provides the probability to obtain the properties of the state with the density matrix
if one measures these properties in the state with the density matrix
According to Born’s rule , we have the equality .
Thus, the probabilities , , ; , due to Born’s rule, provide the probability which, as the function of probabilities , , , , , and , reads
i.e., we expressed the probability given by Born’s rule in terms of probabilities determining two states of qubit. It is worth noting that the above formula provides the probability given by a quadratic form of other probabilities; such quadratic forms were not considered in the literature related to probability theory. Such expression of Born’s probability is a generic property of qubit and qudit states, which can be given by the quadratic form, we will prove this in a future publication.
8. Probability in Quantum Mechanics and Quantum Optics for States with Continuous Variables
Now, we formulate, for continuous variables, the superposition principle of quantum-state wave functions in the probability representation of quantum mechanics, where the states are identified with probability distributions.
In standard formulation of quantum mechanics, the pure states are associated with complex wave functions . The mixed states are associated with density matrices , which are Hermitian matrices with unit trace and non-negative eigenvalues.
Recently [35,37,38,57], the probability representation of quantum states for both continuous variables like quantum-oscillator states and for discrete variables, like spin states or N-level atom states, was introduced. The review and development of the tomographic-probability distribution of quantum states are given in [39,51,58,59]. On the other hand, the classical-particle states are determined either by their position and momentum (if there is no fluctuations) or by the probability-distribution functions , such that in the case of presence of fluctuations like, e.g., thermal fluctuations.
In quantum mechanics, there exist different quasiprobability distribution representations of quantum states like the Wigner function [29], which is similar to the classical probability distribution in the phase space, but it can take negative values and, due to this fact, it is not the probability distribution.
Nevertheless, there exists the bijective map of the density matrices (density operators ) onto fair probability distributions both for continuous variables [37] given by the Radon transform of the Wigner function and determined by the trace of the product of operator and Dirac delta-function of a specific operator, it is
Operators and are the position and momentum operators; is the identity operator. Here, the Dirac delta-function of operator is given by , the Fourier transform with being photon quadrature (oscillator’s position) and and , real parameters determining the reference frame in the phase space where the oscillator’s position X is considered.
For and , the probability distribution of variable X is called the optical tomogram of quantum radiation state. The inverse transform reads
Thus, the state (photon state, oscillator’s state) can be described either by the density operator or by the tomographic-probability distribution , since they contain the same information on the state.
The superposition principle of the wave functions means that, for two given wave functions and describing two different pure states and , the wave function reads and the state vector is where and are complex coefficients, also describes the physical system state.
9. Coherent State Superposition
We consider nonlinear addition of tomographic-probability distributions corresponding to the superposition of coherent states , i.e., normalized eigenstates of the oscillator annihilation operator , introduced and studied in quantum optics by Roy Glauber and George Sudarshan [7,8]. The wave function of the coherent state in the position representation reads
The tomogram of the state with the wave function is given by its fractional Fourier transform [60]
This formula provides tomogram of the coherent state in the form of Gaussian distribution
where and .
The superposition of states introduced and called even and odd coherent states in [44] provides the addition rule for tomographic-probability distributions and , it is given by the formula
Thus, the first two terms of the tomographic-probability distributions are contributions of states and , while the other two terms describe the contribution of the interference term into the tomographic-probability distribution.
In terms of state vectors and , we have the addition rule of the form
Thus, we can formulate the addition rule of the tomographic-probability distributions as follows:
where
10. Born’s Rule for Continuous Variables
In the general case, Born’s rule provides the probability to have the properties of a system state with density operator if these properties are measured in the system with the density operator , given as . If one has the operator and the operator , such that one maps an operator onto the function , and the function is mapped onto the operator , the generic formula for Born’s rule reads
where is the kernel providing the probability in the formalism of the used operators and .
As we discussed for symplectic-tomography scheme, , we have that
Thus, the kernel is given by the formula
As operator , we used the density operators and . Applying this kernel, we obtain Born’s rule for symplectic tomograms.
In fact, one has the relation for probabilities (Born’s rule) in terms of tomograms and , where
i.e.,
Thus, the tomographic-probability distributions determining the oscillator states and provide the probability to have the properties of the pure state if they are measured in the pure state .
We expressed the probability given by Born’s rule in terms of tomographic-probability distributions determining the photon states. It is worth noting that Born’s rule (34) is given by functional quadratic form of tomographic probabilities determined by the parameters and , characterizing the reference frames analogous to the qubit case.
11. Conclusions
On an example of spin - 1/2, we showed that for quantum systems considered in the probability representation of quantum mechanics, the superposition principle can be expressed as a specific nonlinear addition rule of the probabilities determining pure quantum states. From the viewpoint of simplex theory, the new nonlinear expressions obtained in the form of polynomials of several variables (probabilities), which again yield the probabilities, can be obtained using the discussed qubit-system properties.
We found an explicit expression for the probability determined by Born’s rule in terms of the probabilities determining the quantum states.
Additionally, we considered the superposition principle of quantum system states with continuous variables, like oscillator’s ones, and discussed the addition rule of the tomographic-probability distributions on the example of even and odd coherent states, which demonstrate that generic properties of addition of probabilities for arbitrary state vectors for both discrete (spin) variables and continuous variables (oscillator) can be formulated as the nonlinear addition rule of probability distributions describing the states.
Author Contributions
Conceptualization, M.A.M.; writing–original draft preparation, I.Y.D. and M.A.M.; writing–review and editing, I.Y.D. and M.A.M.; supervision, M.A.M.
Funding
This research received no external funding.
Acknowledgments
M.A.M. thanks the Organizers of the 16th International Conference on Squeezed States and Uncertainty Relations (Madrid, 17–21 June 2019) and especially Luis Sanchez-Soto and Alberto Ibort for their invitation and kind hospitality. This paper is the talk of M.A.M. at the 16th International Conference on Squeezed States and Uncertainty Relations (Universidad Complutense de Madrid, Spain, 17–21 June 2019). Section Ad Memoriam of Roy Glauber and George Sudarshan was also presented in the talks of M.A.M. at the 26th Central European Workshop on Quantum Optics (Paderborn University, Germany, 3–7 June 2019) and the 18th International Symposium “Symmetries in Sciences” (Gasthof Hotel Lamm, Bregenz, Voralberg, Austria, 4–9 August 2019) and will be published in the Journal of Russian Laser Research (2019) and the Journal of Physics: Conference Series (2020), respectively.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Schrödinger, E. Quantisierung als Eigenwertproblem (Zweite Mitteilung). Ann. Phys. 1926, 384, 361–376, 489–527. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Principles of Quantum Mechanics; Clarendon Press: Oxford, UK, 1981; ISBN 9780198520115. [Google Scholar]
- Man’ko, V.I.; Marmo, G.; Sudarshan, E.C.G.; Zaccaria, F. On the Relation between Schrödinger and von Neumann Equations. J. Russ. Laser Res. 1999, 20, 421–437. [Google Scholar] [CrossRef]
- Sudarshan, E.C.G. Search for Purity and Entanglement. J. Russ. Laser Res. 2003, 24, 195–203. [Google Scholar] [CrossRef]
- Landau, L. Das Dämpfungsproblem in der Wellenmechanik. Z. Phys. 1927, 45, 430–441. [Google Scholar] [CrossRef]
- Von Neumann, J. Wahrscheinlichkeitstheoretischer Aufbau der Quantenmechanik. Gött. Nach. 1927, 1927, 245–272. [Google Scholar]
- Glauber, R.J. Photon Correlations. Phys. Rev. Lett. 1963, 10, 84–86. [Google Scholar] [CrossRef]
- Sudarshan, E.C.G. Equivalence of Semiclassical and Quantum Mechanical Descriptions of Statistical Light Beams. Phys. Rev. Lett. 1963, 10, 277–279. [Google Scholar] [CrossRef]
- Klauder, J.R.; Sudarshan, E.C.G. Fundamentals of Quantum Optics; Benjamin: New York, NY, USA, 1968; ISBN 978-0486450087. Russian translation, Mir: Moscow, USSR, 1970. [Google Scholar]
- Man’ko, M.A. Probability Representation of Spin States and Inequalities for Unitary Matrices. Theor. Math. Phys. 2011, 168, 985–993. [Google Scholar] [CrossRef]
- Man’ko, M.A.; Man’ko, V.I. Probability Description and Entropy of Classical and Quantum Systems. Found. Phys. 2011, 41, 330–344. [Google Scholar] [CrossRef]
- Man’ko, M.A.; Man’ko, V.I. Dynamic Symmetries and Entropic Inequalities in the Probability Representation of Quantum Mechanics. AIP Conf. Proc. 2011, 1334, 217–248. [Google Scholar] [CrossRef]
- Man’ko, M.A.; Man’ko, V.I. The Probability Representation as a New Formulation of Quantum Mechanics. J. Phys. Conf. Ser. 2012, 380, 012005:1–012005:14. [Google Scholar] [CrossRef]
- Man’ko, M.A.; Man’ko, V.I. Tomographic Entropic Inequalities in the Probability Representation of Quantum Mechanics. AIP Conf. Proc. 2012, 1488, 110–121, [Beauty in Physics: Theory and Experiment: In Honor of Francesco Iachello on the Occasion of His 70th Birthday (Bijker, R., Ed.; Hacienda Cocoyoc, Mexico, 14–18 May 2012)]. [Google Scholar] [CrossRef]
- Man’ko, M.A.; Man’ko, V.I. Statistics of Observables in the Probability Representation of Quantum and Classical System States. AIP Conf. Proc. 2012, 1424, 234–245, [Quantum Theory: Reconsideration of Foundations-6 (Adenier, G., Khrennikov, A.Yu., Eds.)]. [Google Scholar] [CrossRef]
- Man’ko, M.A.; Man’ko, V.I.; Marmo, G.; Simoni, A.; Ventriglia, F. Introduction to Tomography, Classical and Quantum. Nuovo Cimento C 2013, 36, 163–182. [Google Scholar] [CrossRef]
- Man’ko, M.A. Tomographic Rényi Entropy of Multimode Gaussian States. Phys. Scr. 2013, 87, 038113:1–038113:3. [Google Scholar] [CrossRef]
- Man’ko, M.A. Joint Probability Distributions and Conditional Probabilities in the Tomographic Representation of Quantum States. Phys. Scr. 2013, T153. [Google Scholar] [CrossRef]
- Man’ko, M.A.; Man’ko, V.I. Entanglement and Other Quantum Correlations of a Single Qudit State. Int. J. Quantum Inf. 2014, 12, 156006. [Google Scholar] [CrossRef]
- Man’ko, M.A.; Man’ko, V.I. Hidden Correlations in Indivisible Qudits as a Resource for Quantum Technologies on Examples of Superconducting Circuits. J. Phys. Conf. Ser. 2016, 698. [Google Scholar] [CrossRef]
- Man’ko, M.A. Conditional Information and Hidden Correlations in Single-Qudit States. J. Russ. Laser Res. 2017, 38, 211–222. [Google Scholar] [CrossRef][Green Version]
- Man’ko, M.A.; Man’ko, V.I.; Marmo, G.; Ventriglia, F.; Vitale, P. Dichotomic Probability Representation of Quantum States. arXiv 2019, arXiv:1905.10561. [Google Scholar]
- 26th Central European Workshop on Quantum Optics. Available online: https://cewqo2019.uni-paderborn.de/ (accessed on 24 September 2019).
- The Legendary Symmetries in Science Symposia. Available online: https://itp.uni-frankfurt.de/symmetries-in-science/ (accessed on 24 September 2019).
- Sudarshan, E.C.G.; Mathews, P.M.; Rau, J. Stochastic Dynamics of Quantum-Mechanical Systems. Phys. Rev. 1961, 121, 920–924. [Google Scholar] [CrossRef]
- Kraus, K. States, Effects and Operations. Fundamental Notions of Quantum Theory; Böhm, A., Dollard, J.D., Wootters, W.H., Eds.; Springer: Berlin, Germany, 1983; ISBN 978-3-540-12732-1. [Google Scholar]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely Positive Dynamical Semigroups of N-Level Systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Lindblad, G. On the Generators of Quantum Dynamical Semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Wigner, E. On the Quantum Correction For Thermodynamic Equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Husimi, K. Some Formal Properties of the Density Matrix. Proc. Phys. Math. Soc. Jpn. 1940, 22, 264–314. [Google Scholar] [CrossRef]
- Kano, Y. A New Phase-Space Distribution Function in the Statistical Theory of the Electromagnetic Field. J. Math. Phys. 1965, 6, 1913–1915. [Google Scholar] [CrossRef]
- Glauber, R.; Man’ko, V.I. Damping and Fluctuations in the Systems of Two Entangled Quantum Oscillators. In Group Theory, Gravitation, and Physics of Elementary Particles, Proceedings of the Lebedev Physical Institute; [in Russian]; Komar, A.A., Ed.; Nauka: Moscow, Russia, 1986; Volume 167, [English translation by Nova Science: Commack, New York, 1987; Volume 167, ISBN 9780941743020]. [Google Scholar]
- Glauber, R.; Man’ko, V.I. Damping and Fluctuations in the Systems of Two Entangled Quantum Oscillators. Zh. Eksp. Teor. Fiz. 1984, 87, 790–804, [Sov. Phys. JETP 1984, 60, 450–457]. [Google Scholar]
- Schrade, V.I.; Man’ko, V.I.; Schleich, W.P.; Glauber, R. Wigner Functions in the Paul Trap. Quantum Semiclass. Opt. 1995, 7, 307–325. [Google Scholar] [CrossRef]
- Man’ko, V.I.; Man’ko, O.V. Spin State Tomography. J. Exp. Theor. Phys. 1997, 85, 430–434. [Google Scholar] [CrossRef]
- Chernega, V.N.; Man’ko, O.V.; Man’ko, V.I. Subadditivity Condition for Spin Tomograms and Density Matrices of Arbitrary Composite and Noncomposite Qudit Systems. J. Russ. Laser Res. 2014, 35, 278–290. [Google Scholar] [CrossRef][Green Version]
- Mancini, S.; Man’ko, V.I.; Tombesi, P. Symplectic Tomography as Classical Approach to Quantum Systems. Phys. Lett. A 1996, 213, 1–6. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Man’ko, V.I. Positive Distribution Description for Spin States. Phys. Lett. A 1997, 229, 335–339. [Google Scholar] [CrossRef]
- Asorey, M.; Ibort, A.; Marmo, G.; Ventriglia, F. Quantum Tomography Twenty Years Later. Phys. Scr. 2015, 90, 074031:1–074031:17. [Google Scholar] [CrossRef]
- Man’ko, V.I.; Marmo, G.; Sudarshan, E.C.G.; Zaccaria, F. Photon Distribution in Nonlinear Coherent States. J. Russ. Laser Res. 2000, 21, 305–316. [Google Scholar] [CrossRef]
- Man’ko, V.I.; Marmo, G.; Sudarshan, E.C.G.; Zaccaria, F. Entanglement Structure of the Adjoint Representation of the Unitary Group and Tomography of Quantum States. J. Russ. Laser Res. 2003, 24, 507–543. [Google Scholar] [CrossRef]
- Klimov, A.B.; Man’ko, O.V.; Man’ko, V.I. Professor Viktor V. Dodonov: On the Occasion of His 70th Birthday. J. Russ. Laser Res. 2019, 40, 105–106. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Man’ko, V.I. Invariants and the Evolution of Nonstationary Quantum Systems. In Proceedings of the Lebedev Physical Institute; Markov, M.A., Ed.; Nauka: Moscow, Russia, 1987; Volume 183, ISSN 0203-5820. [English translation by Nova Science: Commack, New York, USA, 1989, Volume 183]. [Google Scholar]
- Dodonov, V.V.; Malkin, I.A.; Man’ko, V.I. Even and Odd Coherent States and Excitations of a Singular Oscillator. Physica 1974, 72, 597–615. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Man’ko, O.V.; Man’ko, V.I. Correlated States in Quantum Electronics (Resonant Circuit). J. Sov. Laser Res. 1989, 10, 413–420. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Klimov, A.B.; Man’ko, V.I. Nonstationary Casimir Effect and Oscillator Energy Level Shift. Phys. Lett. A 1989, 142, 511–513. [Google Scholar] [CrossRef]
- Wilson, C.M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J.R.; Duty, T.; Nori, F.; Delsing, P. Observation of the Dynamical Casimir Effect in a Superconducting Circuit. Nature 2011, 479, 376–379. [Google Scholar] [CrossRef]
- Dodonov, V.V. ‘Nonclassical’ States in Quantum Optics: A ‘Squeezed’ Review of the First 75 Years. J. Opt. B Quantum Semiclass. 2002, 4, R1–R33. [Google Scholar] [CrossRef]
- Dessano, H.; Dodonov, A.V. One- and Three-Photon Dynamical Casimir Effects Using a Nonstationary Cyclic Qutrit. Phys. Rev. A 2018, 98, 022520:1–022520:7. [Google Scholar] [CrossRef]
- Chernega, V.N.; Man’ko, O.V.; Man’ko, V.I. Triangle Geometry of the Qubit State in the Probability Representation Expressed in Terms of the Triada of Malevich’s Squares. J. Russ. Laser Res. 2017, 38, 141–149. [Google Scholar] [CrossRef]
- Man’ko, V.I.; Marmo, G.; Ventriglia, F.; Vitale, P. Metric on the space of quantum states from relative entropy. Tomographic reconstruction. J. Phys. A Math. Theor. 2017, 50, 335302:1–335302:29. [Google Scholar] [CrossRef]
- Chernega, V.N.; Man’ko, O.V.; Man’ko, V.I. Quantum Suprematism Picture of Triada of Malevich’s Squares for Spin States and the Parametric Oscillator Evolution in the Probability Representation of Quantum Mechanics. J. Phys. Conf. Ser. 2018, 1071, 012008:1–012008:13. [Google Scholar] [CrossRef]
- Man’ko, M.A. Hidden Correlations in Quantum Optics and Quantum Information. J. Phys. Conf. Ser. 2018, 1071, 012015:1–012015:15. [Google Scholar] [CrossRef]
- Man’ko, M.A.; Man’ko, V.I. New Entropic Inequalities and Hidden Correlations in Quantum Suprematism Picture of Qudit States. Entropy 2018, 20, 692. [Google Scholar] [CrossRef]
- Lopez-Saldivar, J.A.; Castaños, O.; Nahmad-Achar, E.; López-Peña, R.; Man’ko, M.A.; Man’ko, V.I. Geometry and Entanglement of Two-Qubit States in the Quantum Probabilistic Representation. Entropy 2018, 20, 630. [Google Scholar] [CrossRef]
- Lopez-Saldivar, J.A.; Castaños, O.; Man’ko, M.A.; Man’ko, V.I. A New Mechanism of Open System Evolution and Its Entropy Using Unitary Transformations in Noncomposite Qudit Systems. Entropy 2019, 21, 736. [Google Scholar] [CrossRef]
- Man’ko, M.A.; Man’ko, V.I. Properties of Nonnegative Hermitian Matrices and New Entropic Inequalities for Noncomposite Quantum Systems. Entropy 2015, 17, 2876–2894. [Google Scholar] [CrossRef]
- Asorey, M.; Facchi, P.; Man’ko, V.I.; Marmo, G.; Pascazio, S.; Sudarshan, E.G.C. Radon Transform on the Cylinder and Tomography of a Particle on the Circle. Phys. Rev. A 2007, 76. [Google Scholar] [CrossRef]
- Ibort, A.; Man’ko, V.I.; Marmo, G.; Simoni, A.; Ventriglia, F. An Introduction to the Tomographic Picture of Quantum Mechanics. Phys. Scr. 2009, 79. [Google Scholar] [CrossRef]
- Man’ko, V.I.; Mendes, R.V. Non-Commutative Time-Frequency Tomography. Phys. Lett. 1999, A263, 53–61. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).