Experimentally Accessible Witnesses of Many-Body Localization
Abstract
:1. Introduction
2. Probing Disordered Optical Lattice Systems
3. Measurements Considered Feasible
4. Phenomenology of Many-Body Localization
5. Feasible Witnesses
5.1. Absence of Particle Transport
5.2. Slow Spreading of Information
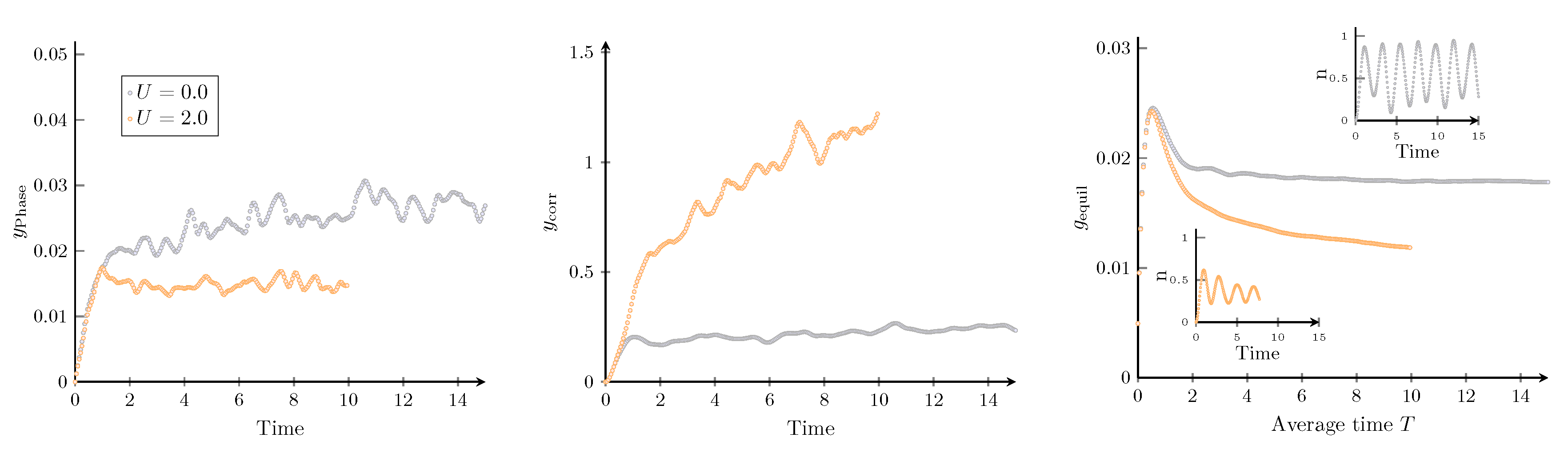
5.3. Dephasing and Equilibration
5.4. Present and Future Experimental Realizations
6. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Numerical Details

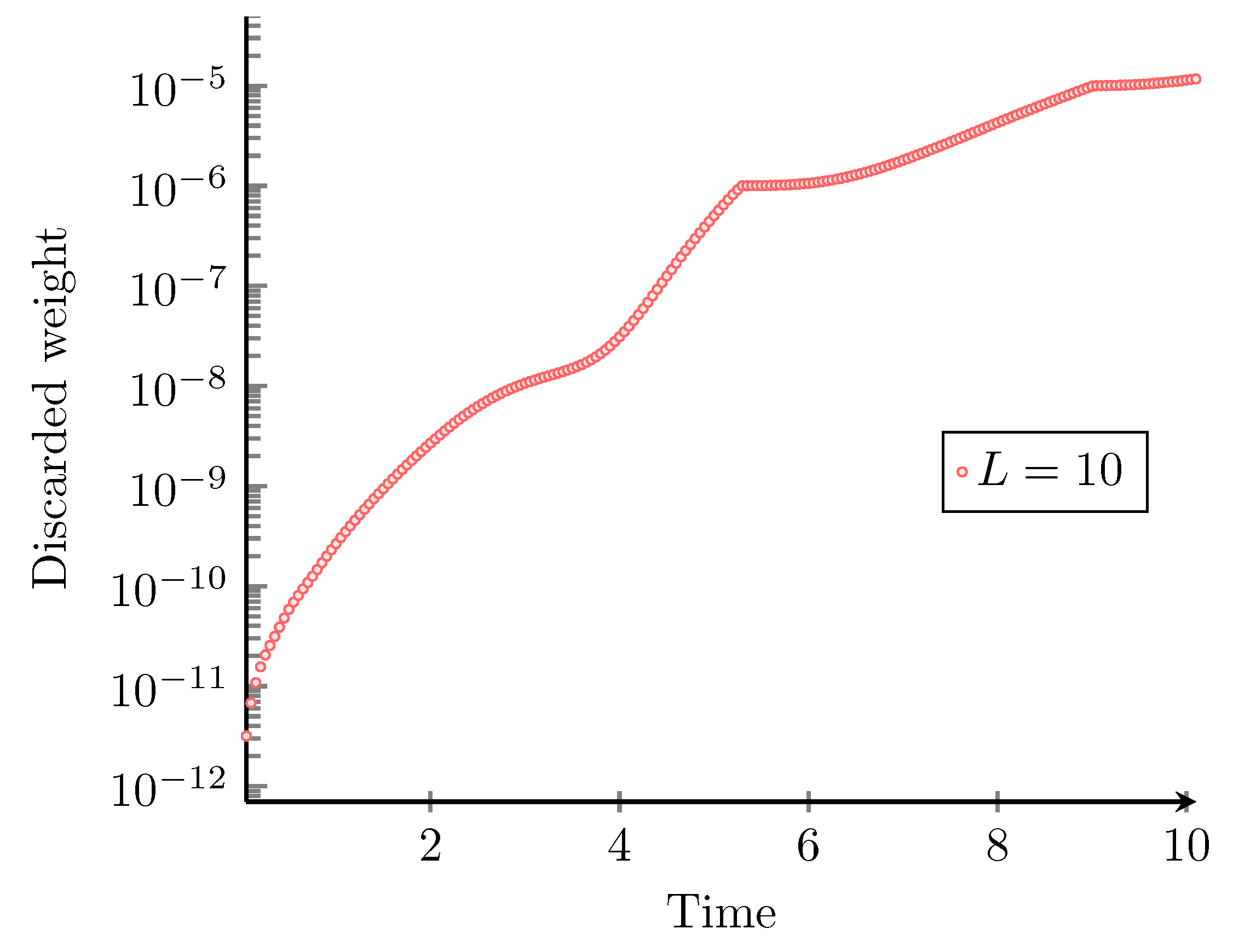
Appendix B. Bosonic Model with On-Site Interactions

References
- Basko, D.M.; Aleiner, I.L.; Altshuler, B.L. Metal-insulator transition in a weakly interacting many-electron system with localized single-particle states. Ann. Phys. 2006, 321, 1126. [Google Scholar] [CrossRef]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1958, 109, 1492. [Google Scholar] [CrossRef]
- Nandkishore, R.; Huse, D.A. Many-Body Localization and Thermalization in Quantum Statistical Mechanics. Ann. Rev. Cond. Mat. Phys. 2015, 6, 15–38. [Google Scholar] [CrossRef] [Green Version]
- Pal, A.; Huse, D.A. The many-body localization transition. Phys. Rev. B 2010, 82, 174411. [Google Scholar] [CrossRef]
- Oganesyan, V.; Huse, D.A. Localization of interacting fermions at high temperature. Phys. Rev. B 2007, 75, 155111. [Google Scholar] [CrossRef] [Green Version]
- Polkovnikov, A.; Sengupta, K.; Silva, A.; Vengalattore, M. Non-equilibrium dynamics of closed interacting quantum systems. Rev. Mod. Phys. 2011, 83, 863. [Google Scholar] [CrossRef]
- Eisert, J.; Friesdorf, M.; Gogolin, C. Quantum many-body systems out of equilibrium. Nat. Phys. 2015, 11, 124–130. [Google Scholar] [CrossRef] [Green Version]
- Gogolin, C.; Eisert, J. Equilibration, thermalisation, and the emergence of statistical mechanics in closed quantum systems. Rep. Prog. Phys. 2016, 79, 056001. [Google Scholar] [CrossRef] [Green Version]
- Znidaric, M.; Prosen, T.; Prelovsek, P. Many-body localization in the Heisenberg XXZ magnet in a random field. Phys. Rev. B 2008, 77, 064426. [Google Scholar] [CrossRef]
- Bardarson, J.H.; Pollmann, F.; Moore, J.E. Unbounded Growth of Entanglement in Models of Many-Body Localization. Phys. Rev. Lett. 2012, 109, 017202. [Google Scholar] [CrossRef] [Green Version]
- Goold, J.; Clark, S.R.; Gogolin, C.; Eisert, J.; Scardicchio, A.; Silva, A. Total correlations of the diagonal ensemble herald the many-body localisation transition. Phys. Rev. B 2015, 92, 180202(R). [Google Scholar] [CrossRef]
- Eisert, J.; Cramer, M.; Plenio, M.B. Area laws for the entanglement entropy. Rev. Mod. Phys. 2010, 82, 277. [Google Scholar] [CrossRef]
- Bauer, B.; Nayak, C. Area laws in a many-body localised state and its implications for topological order. J. Stat. Mech. 2013, 2013, P09005. [Google Scholar] [CrossRef]
- Friesdorf, M.; Werner, A.H.; Brown, W.; Scholz, V.B.; Eisert, J. Many-body localisation implies that eigenvectors are matrix-product states. Phys. Rev. Lett. 2015, 114, 170505. [Google Scholar] [CrossRef] [PubMed]
- Srednicki, M. Chaos and quantum thermalization. Phys. Rev. E 1994, 50, 888–901. [Google Scholar] [CrossRef] [Green Version]
- Kim, I.H.; Chandran, A.; Abanin, D.A. Local integrals of motion and the logarithmic light cone in many-body localised systems. Phys. Rev. B 2015, 91, 085425. [Google Scholar]
- Chandran, A.; Carrasquilla, J.; Kim, I.H.; Abanin, D.A.; Vidal, G. Spectral tensor networks for many-body localisation. Phys. Rev. B 2015, 92, 024201. [Google Scholar] [CrossRef]
- Friesdorf, M.; Werner, A.H.; Goihl, M.; Eisert, J.; Brown, W. Local constants of motion imply transport. New J. Phys. 2015, 17, 113054. [Google Scholar] [CrossRef]
- Serbyn, M.; Papić, Z.; Abanin, D.A. Local Conservation Laws and the Structure of the Many-Body Localized States. Phys. Rev. Lett. 2013, 111, 127201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huse, D.A.; Nandkishore, R.; Oganesyan, V. Phenomenology of fully many-body-localized systems. Phys. Rev. B 2014, 90, 174202. [Google Scholar] [CrossRef] [Green Version]
- Schreiber, M.; Hodgman, S.S.; Bordia, P.; Lüschen, H.P.; Fischer, M.H.; Vosk, R.; Altman, E.; Schneider, U.; Bloch, I. Observation of many-body localization of interacting fermions in a quasi-random optical lattice. Science 2015, 349, 842. [Google Scholar] [CrossRef] [PubMed]
- Bordia, P.; Lüschen, H.P.; Hodgman, S.S.; Schreiber, M.; Bloch, I.; Schneider, U. Coupling Identical one-dimensional Many-Body Localized Systems. Phys. Rev. Lett. 2016, 116, 140401. [Google Scholar] [CrossRef] [PubMed]
- Wiersma, D.S.; Bartolini, P.; Lagendijk, A.; Righini, R. Localization of light in a disordered medium. Nature 1997, 390, 671–673. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Nascimbene, S. Quantum simulations with ultracold quantum gases. Nat. Phys. 2012, 8, 267. [Google Scholar] [CrossRef]
- Eisert, J.; Brandao, F.G.; Audenaert, K.M. Quantitative entanglement witnesses. New J. Phys. 2007, 9, 46. [Google Scholar] [CrossRef]
- Audenaert, K.M.R.; Plenio, M.B. When are correlations quantum? New J. Phys. 2006, 8, 266. [Google Scholar] [CrossRef]
- Guehne, O.; Reimpell, M.; Werner, R.F. Estimating entanglement measures in experiments. Phys. Rev. Lett. 2007, 98, 110502. [Google Scholar] [CrossRef]
- Gring, M.; Kuhnert, M.; Langen, T.; Kitagawa, T.; Rauer, B.; Schreitl, M.; Mazets, I.; Smith, D.A.; Demler, E.; Schmiedmayer, J. Relaxation and Prethermalization in an Isolated Quantum System. Science 2012, 337, 1318. [Google Scholar] [CrossRef]
- Steffens, A.; Friesdorf, M.; Langen, T.; Rauer, B.; Schweigler, T.; Hübener, R.; Schmiedmayer, J.; Riofrio, C.A.; Eisert, J. Towards experimental quantum field tomography with ultracold atoms. Nat. Commun. 2015, 6, 7663. [Google Scholar] [CrossRef]
- Luitz, D.J.; Laflorencie, N.; Alet, F. Many-body localisation edge in the random-field Heisenberg chain. Phys. Rev. B 2015, 91, 081103. [Google Scholar] [CrossRef]
- Singh, R.; Bardarson, J.H.; Pollmann, F. Signatures of the many-body localization transition in the dynamics of entanglement and bipartite fluctuations. New J. Phys. 2016, 18, 023046. [Google Scholar] [CrossRef] [Green Version]
- Serbyn, M.; Papić, Z.; Abanin, D.A. Criterion for many-body localization-delocalization phase transition. Phys. Rev. X 2015, 5, 041047. [Google Scholar] [CrossRef]
- Serbyn, M.; Knap, M.; Gopalakrishnan, S.; Papic, Z.; Yao, N.Y.; Laumann, C.R.; Abanin, D.A.; Lukin, M.D.; Demler, E.A. Interferometric Probes of Many-Body Localization. Phys. Rev. Lett. 2014, 113, 147204. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Singh, R.; Moessner, R. Probing many-body localisation by spin noise spectroscopy. Phys. Rev. B 2015, 92, 180205. [Google Scholar] [CrossRef]
- Vasseur, R.; Parameswaran, S.A.; Moore, J.E. Quantum revivals and many-body localization. Phys. Rev. B 2015, 91, 140202. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.Y.; Hild, S.; Zeiher, J.; Schauß, P.; Rubio-Abadal, A.; Yefsah, T.; Khemani, V.; Huse, D.A.; Bloch, I.; Gross, C. Exploring the many-body localization transition in two dimensions. Science 2016, 352, 1547–1552. [Google Scholar] [CrossRef] [Green Version]
- Trotzky, S.; Chen, Y.A.; Flesch, A.; McCulloch, I.P.; Schollwoeck, U.; Eisert, J.; Bloch, I. Probing the relaxation towards equilibrium in an isolated strongly correlated one-dimensional Bose gas. Nat. Phys. 2012, 8, 325. [Google Scholar] [CrossRef]
- Ros, V.; Müller, M.; Scardicchio, A. Integrals of motion in the many-body localized phase. Nucl. Phys. B 2015, 891, 420–465. [Google Scholar] [CrossRef] [Green Version]
- Lieb, E.H.; Robinson, D.W. The finite group velocity of quantum spin systems. Commun. Math. Phys. 1972, 28, 251–257. [Google Scholar] [CrossRef]
- Daley, A.J.; Kollath, C.; Schollwoeck, U.; Vidal, G. Time-dependent density-matrix renormalization- group using adaptive effective Hilbert spaces. J. Stat. Mech. 2004, 2004, P04005. [Google Scholar] [CrossRef]
- Kirsch, W. An invitation to random Schroedinger operators. arXiv 2007, arXiv:0709.3707. [Google Scholar]
- Germinet, F.; Klein, A. Bootstrap multi-scale analysis and localization in random media. Commun. Math. Phys. 2001, 222, 415. [Google Scholar] [CrossRef]
- Wall, M.L.; Carr, L.D. Open Source TEBD. 2013. Available online: http://physics.mines.edu/downloads/software/tebd(2009) (accessed on 12 June 2019).
- Burrell, C.K.; Eisert, J.; Osborne, T.J. Information propagation through quantum chains with fluctuating disorder. Phys. Rev. A 2009, 80, 052319. [Google Scholar] [CrossRef] [Green Version]
- Gross, C.; Bloch, I.; (Max-Planck-Institut für Quantenoptik, Garching, Germany). Personal communication, 2018.
- Lukin, A.; Rispoli, M.; Schittko, R.; Tai, M.E.; Kaufman, A.M.; Choi, S.; Khemani, V.; Leonard, J.; Greiner, M. Probing entanglement in a many-body-localized system. arXiv 2018, arXiv:1805.09819. [Google Scholar]
- Rispoli, M.; Lukin, A.; Schittko, R.; Kim, S.; Tai, M.E.; Léonard, J.; Greiner, M. Quantum critical behavior at the many-body-localization transition. arXiv 2018, arXiv:1812.06959. [Google Scholar]
- Cramer, M.; Bernard, A.; Fabbri, N.; Fallani, L.; Fort, C.; Rosi, S.; Caruso, F.; Inguscio, M.; Plenio, M. Spatial entanglement of bosons in optical lattices. Nat. Commun. 2013, 4, 2161. [Google Scholar] [CrossRef]
- Jones, E.; Oliphant, T.; Peterson, P. SciPy: Open Source Scientific Tools for Python; ResearchGate: Berlin, Germany, 2001. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goihl, M.; Friesdorf, M.; Werner, A.H.; Brown, W.; Eisert, J. Experimentally Accessible Witnesses of Many-Body Localization. Quantum Rep. 2019, 1, 50-62. https://doi.org/10.3390/quantum1010006
Goihl M, Friesdorf M, Werner AH, Brown W, Eisert J. Experimentally Accessible Witnesses of Many-Body Localization. Quantum Reports. 2019; 1(1):50-62. https://doi.org/10.3390/quantum1010006
Chicago/Turabian StyleGoihl, Marcel, Mathis Friesdorf, Albert H. Werner, Winton Brown, and Jens Eisert. 2019. "Experimentally Accessible Witnesses of Many-Body Localization" Quantum Reports 1, no. 1: 50-62. https://doi.org/10.3390/quantum1010006
APA StyleGoihl, M., Friesdorf, M., Werner, A. H., Brown, W., & Eisert, J. (2019). Experimentally Accessible Witnesses of Many-Body Localization. Quantum Reports, 1(1), 50-62. https://doi.org/10.3390/quantum1010006




