Adjoint Optimization for Hyperloop Aerodynamics

Abstract

This work investigates how the vehicle-to-tube suspension gap governs compressible flow physics and operating margins in Hyperloop-class transport at 10 kPa. To our knowledge, this is the first study to apply adjoint aerodynamic optimization to mitigate gap-induced choking and shock formation in a full pod–tube configuration. Using a steady, pressure-based Reynolds-averaged Navier-Stokes (RANS) framework with the GEnerlaized K-Omega (GEKO) turbulence model, a simulation for the cruise conditions was performed at M = 0.5–0.7 with a mesh-verified analysis (medium grid within 0.59% of fine) to quantify gap effects on forces and wave propagation. For small gaps, the baseline pod triggers oblique shocks and a near-Kantrowitz condition with elevated drag and lift. An adjoint shape update—primarily refining the aft geometry under a thrust-equilibrium constraint—achieves 27.5% drag reduction, delays the onset of choking by ~70%, and reduces the critical gap from d/D ≈ 0.025 to ≈0.008 at M = 0.7. The optimized configuration restores a largely subcritical passage, suppressing normal-shock formation and improving gap tolerance. Because propulsive power at fixed cruise scales with drag, these aerodynamic gains directly translate into operating-power reductions while enabling smaller gaps that can relax tube-diameter and suspension mass requirements. The results provide a gap-aware optimization pathway for Hyperloop pods and a compact design rule-of-thumb to avoid choking while minimizing power.

1. Introduction

The transportation sector plays a vital role in global economic and social growth. Modern train systems, primarily wheel-rail and maglev, face distinct challenges: wheel-rail trains suffer from frictional losses, while maglev trains eliminate this issue through electromagnetic levitation. However, aerodynamic drag remains a significant barrier to reducing travel time, necessitating continued technological innovation [1,2,3]. An Evacuated Tube Transport (ETT) system combines magnetic levitation with vacuum technology, effectively reducing mechanical resistance and aerodynamic drag, which significantly boosts the vehicles’ maximum speed [4,5,6]. The vacuum tube transportation system is a highly promising technology with numerous advantages. However, it also encounters various problems and constraints, especially in the case of a crack. The pressure wave will significantly impact the flow field, leading to catastrophic disasters, as predicted by Kim [7,8].

In recent years, the term “Hyperloop” has emerged in scientific discussions, referring to a “high-speed vehicle traveling in a tube.” Musk’s alpha hyperloop proposal suggested operating at a low pressure of 0.001 atm, similar to that of the space station, which presents significant safety and operational challenges. To address these concerns, a safer operating pressure, comparable to the altitude of certified passenger airplanes, is recommended. Given that some private jets operate at altitudes up to 51,000 feet and the Concorde at 60,000 feet, this study adopts an operating pressure of 10 kPa [9,10,11,12].

Numerous studies have explored the physics of flow around the vehicle-tube system and the resulting aerodynamic forces. Most of these research works have relied on axisymmetric models, simplifying the early design process by assuming one-dimensional compressible flow. However, these models often overlook the impact of the vehicle’s proximity to the tube wall [13,14,15,16,17,18]. Few studies have addressed this issue, including the work of Bi et al. [19] and Zhou et al. [20]. Their investigations include the effect of the suspension gap on the aerodynamic characteristics of the evacuated tube maglev. They utilized numerical modeling to show that the suspension gap mainly affects the pressure and temperature distributions at the surface near the suspension gap of the maglev train. Hu et al. [21] conducted numerical simulations to study the effect of the track on aerodynamic characteristics and pressure propagations. They used Detached Eddy Simulation (DES) to capture the flow structures around the vehicle and shock wave boundary layer interactions. Their analysis showed that the track has a minor influence on pressure wave propagation.

As part of Saudi Arabia’s Vision 2030 initiatives, the King Abdulaziz University High-Speed Transportation Research Group developed a universal hyperloop model to study aero-propulsive vehicles in a low-pressure environment of 10 kPa. They employed a surrogate model and analyzed the vehicle-tube system using both Computational Fluid Dynamics (CFD) and a developed 1-D method across various Mach numbers and blockage ratios [11,12]. The real model of a train in a tube/tunnel involves many challenges. The real model would not be axisymmetric due to the tube/tunnel effect as well as the track/suspension effect, which will impact the aerodynamics and thermal loads on the vehicle and the closed environment [22]. A methodology to correct the area between the tube and the vehicle to successfully apply the axisymmetric condition has been developed by Opgenoord et al. [23,24].

Adjoint-based optimization methods have been increasingly utilized in aerodynamic design, particularly in the context of high-speed transportation systems like the Hyperloop system [25]. Galido et al. applied the adjoint aerodynamics optimization on the mixer after the air compressor to enhance the performance of the internal ducting system of the hyperloop [26]. These methods offer efficient exploration of complex design spaces by evaluating shape sensitivities with minimal computational cost, which is crucial for achieving optimal aerodynamic performance in transonic flows [27]. Furthermore, Li et al. successfully performed adjoint aerodynamics optimization on a maglev train and proposed a methodology for optimizing the train nose shape [28]. Rather than mesh deformed techniques, other researchers adopted the optimization of the train nose/tail using the surrogate models [29,30,31].

Optimizing the aerodynamic design of the vehicle’s external shape, particularly regarding the suspension gap, is crucial for minimizing drag and maintaining an optimal gap that reduces the structural weight of the tube. In the baseline vehicle design, the flow field is complex, with a significant increase in drag due to the combined effects of under-expanded jet flow, shear layers, and oblique shock waves near the suspension gap. This research investigates how adjoint-based aerodynamic shape optimization can improve the performance of a high-speed vehicle traveling in a low-pressure tube, focusing on drag reduction and mitigating the effects of small suspension gaps. This area has been largely overlooked in previous studies, making it a valuable contribution to ongoing research in Hyperloop aerodynamics [11,12,32].

This numerical work utilized the RANS and $k-\omega$ GEKO turbulence model to analyze the influence of the gap on the pressure wave propagation and the aerodynamic performance. The gap ranges from 25 to 300 mm. The critical gap distance that shows a rapid change in the drag is calculated, and the optimum gap is found to be 100 mm. Then, to enhance the system performance, an adjoint design optimization of the vehicle’s baseline model with a gap of 100 mm was performed to minimize the drag force by using 250 control points, and the thrust was a design constraint. To ensure the accuracy and robustness of the current simulations, a validation study of the computational methodology was carried out through (a) a comparison with published experimental measurements of a hemisphere model at supersonic speeds [33], and (b) the grid convergence study.

This paper makes four contributions:

• Gap-aware optimization: To our knowledge, the first adjoint optimization of a Hyperloop pod that explicitly targets gap-induced choking and wall–jet interactions in a full pod–tube model.
• Verified methodology: A mesh-verified RANS/GEKO framework (medium vs. fine deviation 0.59%) suitable for design studies at 10 kPa and M = 0.5–0.7.
• Headline results: 27.5% drag reduction, ~70% delay of choking onset, and critical gap lowered from d/D ≈ 0.025 to ≈0.008 for M = 0.7.
• Design rule-of-thumb: For transonic cruise at 10 kPa, standard pods must maintain a clearance-to-diameter ratio (d/D) above 0.025 to prevent choked flow. An optimized pod, however, remains stable down to a ratio of approximately 0.008. This lower limit is a practical design target, as it accommodates the millimeter-level gaps used in magnetic levitation systems.

The paper is organized as follows: Section 2 outlines the numerical simulation setup and the adjoint optimization method employed in this study. Section 3 presents the results of the analysis and discusses the findings, and Section 4 concludes with the overall outcomes and implications of the research.

2. Materials and Methods

All CFD simulations were performed using ANSYS Fluent 2024 R1 and ANSYS ICEM CFD (Ansys Inc., Canonsburg, PA, USA), running on the Aziz Supercomputer at King Abdulaziz University (Jeddah, Saudi Arabia).

The flow is modeled using the compressible Reynolds-Averaged Navier–Stokes equations. The equations in index form are given as:

$${\displaystyle \frac{\partial }{\partial x_i}}\left[\overline{\rho }\overline{u_i}\right]=0$$

(1)

$${\displaystyle \frac{\partial }{\partial x_j}}\left[\overline{\rho }\overline{u_i}\overline{u_j}+\overline{p}{\delta }_{ij}-\left(1+{\displaystyle \frac{{\mu }_t}{\mu }}\right)\overline{{\tau }_{ij}}\right]=0$$

(2)

$${\displaystyle \frac{\partial }{\partial x_j}}\left[\overline{\rho }\overline{u_j}\overline{E}+\overline{u_j}\overline{p}-\left(1+{\displaystyle \frac{{\mu }_t}{\mu }}\right)\overline{u_i}\overline{{\tau }_{ij}}-\left(c_p{\displaystyle \frac{\mu }{\mathrm{P}\mathrm{r}}}+c_p{\displaystyle \frac{{\mu }_t}{{\mathrm{P}\mathrm{r}}_t}}\right){\displaystyle \frac{\partial \overline{T}}{\partial x_j}}\right]=0$$

(3)

where $\overline{u_i}$, $\overline{\rho }$, $\overline{p}$, $\overline{E},\overline{T}$ are the average velocity vector, density, pressure, total energy per unit mass, and temperature, respectively. The viscous stress tensor is defined as:

$$\overline{{\tau }_{ij}}=\mu \left({\displaystyle \frac{\partial \overline{u_i}}{\partial x_j}}+{\displaystyle \frac{\partial \overline{u_j}}{\partial x_i}}-{\displaystyle \frac{2}{3}}{\displaystyle \frac{\partial \overline{u_k}}{\partial x_k}}{\delta }_{ij}\right)$$

(4)

The adjoint optimization limitations required a constant laminar viscosity coefficient (µ). For the detailed analysis of the baseline and the final optimum cases, a fine grid with a relaxed number of iterations was used, and the Sutherland law was applied. The ideal gas law was used to close the system of equations. The laminar Prandtl number (Pr) is fixed at 0.67 with $C_p=1$006.43 J/kg-K.

The k–ω GEKO turbulence model [34,35] was employed to compute the turbulent viscosity coefficient within the steady compressible RANS framework. This model was selected after evaluating conventional closures such as SST k–ω and Spalart–Allmaras, since GEKO offers a tunable coefficient set $(C_{sep},C_{jet},C_{NW},C_{mix})$ that can interpolate between the behaviours of k–ε and SST k–ω, allowing improved prediction of flow separation, wall-jet interaction, and compressibility effects. Such capabilities are critical for the present confined transonic flow inside the Hyperloop tube, where adverse pressure gradients and shear-layer detachment are expected. The built-in blending function and default parameter set were used, and the model performance was verified against the experimental results of Stine [33], confirming good agreement and demonstrating the robustness of the current numerical setup.

The RANS–GEKO approach provides an efficient and stable solution methodology for large parametric design studies, but it also involves several simplifying assumptions. The time-averaged formulation neglects transient wake oscillations, vortex-shedding, and acoustic waves that may occur in real-world conditions. Consequently, it captures the mean aerodynamic loads but not the instantaneous fluctuations that could influence comfort or dynamic stability. These limitations are acknowledged and discussed further in Section 4 (Discussion and Limitations), where the potential extension to Unsteady-RANS (URANS) or hybrid DES approaches is identified as future work.

The vehicle–tube flow system can be compared to a de Laval nozzle [36,37], where the contraction region near the nose and the expansion region toward the tail produce acceleration and pressure recovery, respectively. Because the flow velocity in the annular passage is high, local shock waves can form, reducing the mass-flow rate through the gap and leading to choking when the Kantrowitz limit is reached. Under these conditions, the mass flow no longer increases with further gap reduction, marking the onset of a critical confinement regime important for the present aerodynamic optimization [37].

$${\left({\displaystyle \frac{A_2}{A_1}}\right)}_{\mathrm{Kantrowitz}}=M_1{\left({\displaystyle \frac{\gamma +1}{2}}\right)}^{{\displaystyle \frac{\gamma +1}{2\left(\gamma -1\right)}}}{\left[\left(1+{\displaystyle \frac{\gamma -1}{2}}{M}_1^2\right)\right]}^{{\displaystyle \frac{\gamma +1}{2\left(\gamma -1\right)}}}\times {\left[{\displaystyle \frac{\left(\gamma +1\right)M_1^2}{\left(\gamma -1\right)M_1^2+2}}\right]}^{-{\displaystyle \frac{\gamma }{\gamma -1}}}{\left[{\displaystyle \frac{\gamma +1}{2\gamma M_1^2-\left(\gamma -1\right)}}\right]}^{{\displaystyle \frac{-1}{\gamma -1}}}$$

(5)

The flow continuity condition is checked using the Knudsen number ($kn$). The Knudson number is defined as the particle mean free path length over the characteristic length scale [38], and Equation (6). Flow regimes could be continuous or discrete based on the Knudsen number. If $kn$ > 0.001, the flow is no longer a continuum. Based on the operating pressure and vehicle speed, the Knudsen number is $5.4\times {10}^{-5},$ such that it satisfies the continuum assumption of the flow.

$$kn=\sqrt{{\displaystyle \frac{\gamma \pi }{2}}}{\displaystyle \frac{M}{Re}}$$

(6)

2.1. Model Description and Computational Domain

The high-speed vehicle baseline model’s major dimensions are provided in Figure 1, which also depicts the computational domain used during the setup. The domain length of 1042 m was applied during this simulation. The vehicle cruise speed is M = 0.7, and the operating pressure is 10 kPa. The gap distance varies from 25 to 300 mm. The vehicle length is 42 m, and the fan radius for the baseline model is 1.3 m, where the exit jet Mach number is unity with the radius of 1.1 m. The mass flow rate is adjusted for the cruise Mach number to maintain the thrust-drag equilibrium state. Our previous work showed the advantage of utilizing an air compressor/fan to lower the power required to push the vehicle into the low-pressure tube system at M = 0.7 [12]. The vehicle nose and tail parts are elliptical, and the following equation provides the surface shape for these parts. The blockage ratio, $\beta =A_{pod}/A_{tube}=0.36$, where the tube diameter = 5 m, and the vehicle diameter = 3 m. The term “baseline model” is the model with a suspension gap of 0.1 m based on the optimum distance observed during the investigation. The specifications of the vehicle-tube system are presented in

Table 1. Vehicle-tube system baseline design specifications.

Parameter	Symbol	Value
Operating Pressure	$p$	10,000 $\mathrm{P}\mathrm{a}$
Operating Temperature	$T$	300 K
Vehicle’s Diameter (D)	$D_p$	3.0 m
Tube Diameter	$D$	5.0 m
Vehicle’s Length	$L_p$	42.0 m
Vehicle’s Mach number	$M$	0.5–0.7
Baseline Design Blockage Ratio	$\beta$	0.36
Gap Distance	$d$	25–300 mm

. Equation (7) defines the elliptical contour of the nose and tail parameterized by a/b.

$${\displaystyle \frac{x_{n,t}^2}{L_{n,t}^2}}+{\displaystyle \frac{y_{n,t}^2}{R_{n,t}^2}}=1$$

(7)

2.2. Computational Grid

A structured hexahedral grid exhibited localized high aspect ratios near the wall due to the elongated boundary-layer cells required for accurate viscous-sub-layer resolution. The maximum aspect ratio in the near-wall region was approximately 1200, while in the core flow and wake zones, the aspect ratio remained below 50, ensuring numerical stability and smooth cell transitions. The GEKO turbulence model used in this work is specifically formulated to handle arbitrary $y^{+}$ values within the logarithmic layer, which mitigates the sensitivity to such aspect ratio variations and avoids degradation of numerical accuracy in highly stretched regions, as presented in Figure 2.

The non-dimensional wall distance was maintained between $y^{+}\approx 5-10$ for the medium and fine grids, providing wall-resolved predictions within the log-law region. The grid convergence test confirmed that the flow variables and aerodynamic coefficients were nearly independent of mesh density: the medium grid ($8.16$ Million cells) showed less than 1% variation relative to the fine grid (16.1 Million cells). The grid-refinement ratio between successive levels was about 3:1, which satisfies the conventional requirement for three-dimensional CFD validation. This refinement level, combined with consistent $y^{+}$ control and aspect ratio management, ensures that the current mesh resolution is adequate for capturing the pressure-gradient and shear-stress distributions around the pod and within the tube [34,35]. All simulations were conducted using ANSYS Fluent 2024 R1, employing the density-based steady-state solver suitable for compressible transonic flow regimes. The PISO (Pressure-Implicit with Splitting of Operators) algorithm was used for pressure–velocity coupling to enhance convergence stability and accuracy in flows with strong compressibility effects. Second-order upwind discretization was applied to the momentum, energy, and turbulence transport equations to minimize numerical diffusion and maintain high-fidelity gradient resolution. Convergence was considered achieved when all residuals dropped below ${10}^{-5}$ and aerodynamic forces reached steady values [34,39].

2.3. Boundary Conditions

Figure 1 and Figure 2 display the boundary conditions defined for the simulations and adjoint optimization. The propulsion system is an air-breathing type with a jet exit powered by an electric motor. A simplified model of jet propulsion was used to reduce computational costs while still accurately representing the key aerodynamic effects for the simulations by specifying mass flow outlet/inlet combinations for the fan entrance face and exhaust. The vehicle’s air-breathing propulsion system was modeled using a simplified fixed-mass-flow approach consistent with previous Hyperloop aero-propulsive analyses. An axial compressor with an assumed isentropic efficiency of ≈0.86 and a pressure ratio of ≈1.2 was used to represent the fan stage performance at cruise. The corresponding mass-flow rate varied between 107 kg/s and 150 kg/s for Mach 0.5–0.7, values that agree with the computational setup adopted by Gray et al. [40,41] for boundary-layer-ingestion configurations. This parametric treatment captures the essential aerodynamic effect of the compressor on the pressure field and drag–thrust balance, while avoiding the added complexity of a full performance-map model; thus, the compressor operates under a steady corrected-mass-flow condition throughout the simulation [40,41]. The tube walls were set to move relative to the flow speed while the vehicle remained stationary, with a no-slip condition applied to all walls.

Table 2. Vehicle initial inflow/outflow boundary conditions.

Mach Number	$\dot{\mathit{m}}$ (kg/s)
0.5	107
0.7	150

shows the mass flow defined at different Mach numbers. Symmetry was applied to the surface, slicing the domain along the x-y plane to reduce computational costs.

The simulations were conducted for a low-pressure environment with a far-field static pressure of 10 $\mathrm{k}\mathrm{P}\mathrm{a}$ and free-stream temperature of 300 K. The tube wall was modeled as a moving wall with a velocity equal in magnitude and opposite in direction to the vehicle cruise speed, $U_{\mathrm{wall}}=-U_{\infty }=-M_{\infty }{a}_{\infty }$, allowing the vehicle to remain stationary in the computational domain while reproducing the correct relative motion. The resulting flow conditions yield a mass-flow ratio of ${\dot{m}}_{\mathrm{actual}}/\left({\rho }_{\infty }{A}_{\mathrm{duct}}{U}_{\infty }\right)\approx 0.82$, meaning that about 18% of the theoretical flow is displaced by the confinement of the tube, an effect consistent with the piston-induced blockage reported by Bizzozero et al. [42]. This setup accurately defines the working point of the Hyperloop pod as per Table 2 in a 10 kPa environment, ensuring realistic aerodynamic loading and boundary-condition fidelity. The tube inlet/outlet faces were set to pressure far field as utilized in the work of Niu et al. and Zhou et al. [43,44,45].

The running vehicle in the current system has an air compressor that operates with an electric motor and a jet exit. These components generate the required thrust and prevent the flow choking that occurs in the confined space between the vehicle and tube at cruise conditions. The inlet of the aero-fan has a defined total temperature and pressure ratio, as shown in Equation (8).

$${\displaystyle \frac{T_{f,t}}{T_f}}=1+{\displaystyle \frac{\gamma -1}{2}}{M}_f^2,{\pi }_f={\displaystyle \frac{p_{f,t}}{p_f}}={\left(1+{\displaystyle \frac{\gamma -1}{2}}{M}_f^2\right)}^{{\displaystyle \frac{\gamma }{\gamma -1}}}$$

(8)

Now, the corrected mass flow rate at the aero-fan model is given by:

$$\dot{m}=A_v\psi \left(M_j\right){\rho }_f{c}_f{\left(T_j/T_f\right)}^{-1/2}{;M}_j=A_v\psi \left(M_j\right)\left(\gamma p_f/c_f\right){\left(T_j/T_f\right)}^{-1/2}{M}_j$$

(9)

The ratio between the jet exit and the inlet is $\psi \left(M_j\right)=A_j/A_{inlet}$. Studying and verifying the effect of the corrected mass flow on the piston pressure is important for using the aero-fan in the vehicle and reducing the drag levels [42].

2.4. Adjoint Design Optimization

Adjoint aerodynamic optimization is a powerful technique that iteratively adjusts design variables to refine the shape and performance of aerodynamic systems, with the goal of minimizing or maximizing specific objectives, such as drag reduction. In this work, the objective is to decrease operational costs by reducing the power required to operate the vehicle through drag reduction and eliminating choking phenomena. The external shape was parameterized using the multi-variable polynomial method during the optimization process [46].

Several comparative studies have explored the relative performance of global and local search methods for aerodynamic shape optimization. However, most of these studies provide qualitative results without offering a definitive conclusion on which method is superior [47,48,49,50,51,52]. There is a general consensus that local search methods tend to be more efficient at finding an optimum, though they carry the risk of converging on a local minimum. A key advantage of the adjoint method is that the cost of computing the complete sensitivity vector remains independent of the number of design variables [53]. This feature makes the adjoint solver particularly appealing for aerodynamic shape optimization aimed at minimizing drag in Hyperloop systems.

The goal of aerodynamic shape optimization is to minimize or maximize an objective function $J_{,}$ such as drag or lift, under given constraints, including thrust, flow conditions, operating conditions, and design blockage ratio, all in relation to a parameterized shape $\Gamma$. Additional constraints can be applied by selecting a set of feasible designs $F$. Drag is calculated based on the shape $\Gamma$, which is dependent on the flow state denoted by $w$. Thus, the notations $D(w,\Gamma )$ and Thrust $(w,\Gamma )$ were used, where $1\le i\le m$ represents the design iteration. For each iteration, the CFD solver updated the flow field variables $w$ according to the modified shape $\Gamma$ [54,55,56,57].

$$\left(\mathrm{P}\right)\left\{\begin{array}{c}\min Drag=D\left(\mathrm{w},{\Gamma }_{\mathrm{i}}\right)\\ Thrust=\dot{m}\left(V_j-V_{\infty }\right)=D\left(\mathrm{w},{\Gamma }_i\right)\end{array}\right.$$

(10)

Here, $\left(w,{\Gamma }_i\right)$ represents the state equation, which defines a unique flow state $w$ for a given shape $\Gamma$ across the entire domain ${\Omega }_{\Gamma }$. During the optimization process, the jet velocity is manually controlled to maintain the steady-state cruise condition. The vehicle’s external shape ${\Gamma }_i=\Gamma \left(x_i,y_i,z_i\right)$ is adjusted using control points, as depicted in Figure 3. While Lyu [58] suggested a minimum of 200 control points for a transonic wing, the flow field in this study is similarly complex. Therefore, to enhance the robustness of the adjoint optimization, the number of control points has been increased to 250, focusing on the morphing region [59,60,61].

The discrete adjoint solver process is illustrated in Figure 4. The XDSM tool from MDOLAB [62] was used to outline the adjoint aero-propulsive optimization of the vehicle. The discrete adjoint solver, embedded in ANSYS FLUENT 2024, modifies the surface coordinates in regions sensitive to the objective function. During the optimization iterations, the surface coordinates are adjusted, with the $y$ and $z$ coordinates changing symmetrically. Altering the $y$ and $z$ coordinates at the exit impacts the mass flow rate, and thrust levels must always equal the drag force during the cruise mission. In this study, thrust refers exclusively to the aerodynamic jet propulsion component generated by the air-breathing fan–nozzle system. The magnetic levitation and linear motor propulsion mechanisms that would exist in a complete Hyperloop system were not modeled here since their contributions are minor in this design, as the focus is on the aerodynamic flow physics and shape optimization. Accordingly, the thrust–drag equilibrium enforced during the simulations applies only to the aerodynamic forces acting on the vehicle body and jet exhaust, ensuring a consistent force balance for the steady cruise condition considered in the adjoint optimization.

Shape parameterization techniques are categorized into those that only optimize surface points and those that deform both the surface and the surrounding interior mesh. The former includes normal displacement of surface nodes, control points of Bézier–Bernstein or NURBS curves like Class-Shape Transformation (CST) methods [60], particularly for elliptical shapes at the nose and tail, as shown in Equation (7).

For the current problem, the drag is our cost function, $w$ is the flow field variables, $\Gamma$ is the design variable vector. To find the adjoint operator in aerodynamic shape optimization, the process begins by defining the objective function $J$, which typically represents aerodynamic performance metrics like drag or lift, dependent on flow variables $w$ (e.g., velocity, pressure) and design variables $\Gamma$ (e.g., shape parameters). The flow governing equations (RANS equations) are then defined as $R(w,\Gamma )=0$, representing the fluid behavior [54,55,60]. These equations are linearized around a steady-state solution, yielding variations in residuals with respect to changes in flow variables $\delta w$ and design variables $\delta \Gamma$ [56].

Next, a Lagrange multiplier (adjoint variable) $\lambda$ is introduced to enforce the flow equations as a constraint, leading to an augmented objective function $J_{\mathrm{a}\mathrm{u}\mathrm{g}}=J(w,\Gamma )+{\lambda }^{T}R(w,\Gamma )$. The adjoint equation is derived by varying $J_{\mathrm{a}\mathrm{u}\mathrm{g}}$ with respect to $w$, resulting in

$${\lambda }^T=-{\displaystyle \frac{\partial J}{\partial w}}{\left({\displaystyle \frac{\partial R}{\partial w}}\right)}^{-1}$$

(11)

This provides the sensitivities of the objective function to changes in flow variables. Finally, the gradient of $J$ with respect to design variables $\Gamma$ is computed as

$${\displaystyle \frac{dJ}{d\Gamma }}={\displaystyle \frac{\partial J}{\partial \Gamma }}+{\lambda }^T{\displaystyle \frac{\partial R}{\partial \Gamma }},$$

(12)

allowing the design to be updated in the optimization process [56,57], then the adjoint solver would be given by:

$$D=D(\Gamma ,w)$$

(13)

The first variation in the cost function is given by:

$$\delta D={\displaystyle \frac{\partial D^T}{\partial w}}\delta w+{\displaystyle \frac{\partial D^T}{\partial \Gamma }}\delta \Gamma$$

(14)

Here, the variation $\delta w$ of the flow field variables will depend on the design variable change $\delta \Gamma$, through the variation in the flow equation. During the adjoint optimization, the number of design iterations was specified as 30. The number of design iterations in some research was between 20 and 30 design points, and the number of solution iterations in each iteration was 600 [26,28,61]. The medium level of the grid, which contains $8.2\times {10}^6$ cells, was adopted since the grid convergence study shows a 1% error compared with the fine grid level.

The geometry sensitivity is illustrated in Equation (12), with the primary objective of adjoint aerodynamic optimization being drag minimization. The sensitivity of the shape to drag force (X-force) is depicted in Figure 5, highlighting the significant impact of the area gradient on the flow field. These gradient influences velocity, pressure, and other flow properties, making regions with substantial area changes the most sensitive part [28,32].

As defined in

Table 3. Setup for the vehicle shape optimization.

	Function or Variable	Description	Quantity
Minimize	$\mathrm{D}\mathrm{r}\mathrm{a}\mathrm{g}$	Drag force
with respect to	$y,z$	$y,z$ coordinate of FFD points	250
		Total design variables	250
subject to	$\mathrm{T}\mathrm{h}\mathrm{r}\mathrm{u}\mathrm{s}\mathrm{t}=\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{g}$	Thrust constraint	1
	${\mathrm{r}}_{\mathrm{n},\mathrm{t}}\ge {r_{n,t}}_{\mathrm{baseline}}$	Minimum-tail/nose exit jet radius constraint	2
	$L_{n,t}\ge {L_{n,t}}_{\mathrm{baseline}}$	Minimum Nose/tail part length	2
	$-0.1<\Delta y,\Delta \mathrm{z}<0.1\mathrm{m}$	Design variable bounds	1
Total constraints			256

, the optimization setup includes 250 Free Form Deformation (FFD) points distributed across 10 different longitudinal locations, as shown in Figure 3. To maintain the effectiveness of the area gradient, which is crucial for controlling the Kantrowitz limit and minimizing vehicle-tube drag and piston effects, the deformed shape must not be reduced below the baseline model.

The parameterization of the nose and tail sections is essential for reconstructing the model after adjoint optimization. The output from the adjoint solver is a Stereolithography (STL) file containing the deformed shape coordinates. An elliptical parameterization is applied to the nose and tail using the $x_{n,t}$ for the nose/tail x-coordinate, $L_{n,t}$ for the tail/nose length, and $r_{n,t}$ for the radii at the inlet and exit positions as represented in Equation (7).

The flowchart in Figure 6 outlines the aerodynamic design optimization process for a high-speed vehicle in a tube, comprising several key stages. Initially, the problem is defined, and objectives and constraints are set in the Initial Setup. This is followed by the Geometry Definition phase, where the vehicle and tube geometries are specified. The next stage is Meshing, where the computational grid is created. The solver setup phase configures the CFD solver and establishes boundary conditions. Following this, initial simulations are conducted for various suspension gap distances for selected design iterations. The Adjoint Solver performs the adjoint-based optimization, leading to the Optimization phase, where the geometry is updated to minimize drag while maintaining thrust-drag equilibrium. Finally, in post-processing, the results are analyzed and visualized, with comparisons made between the baseline and optimized designs.

2.5. Validation and Verification

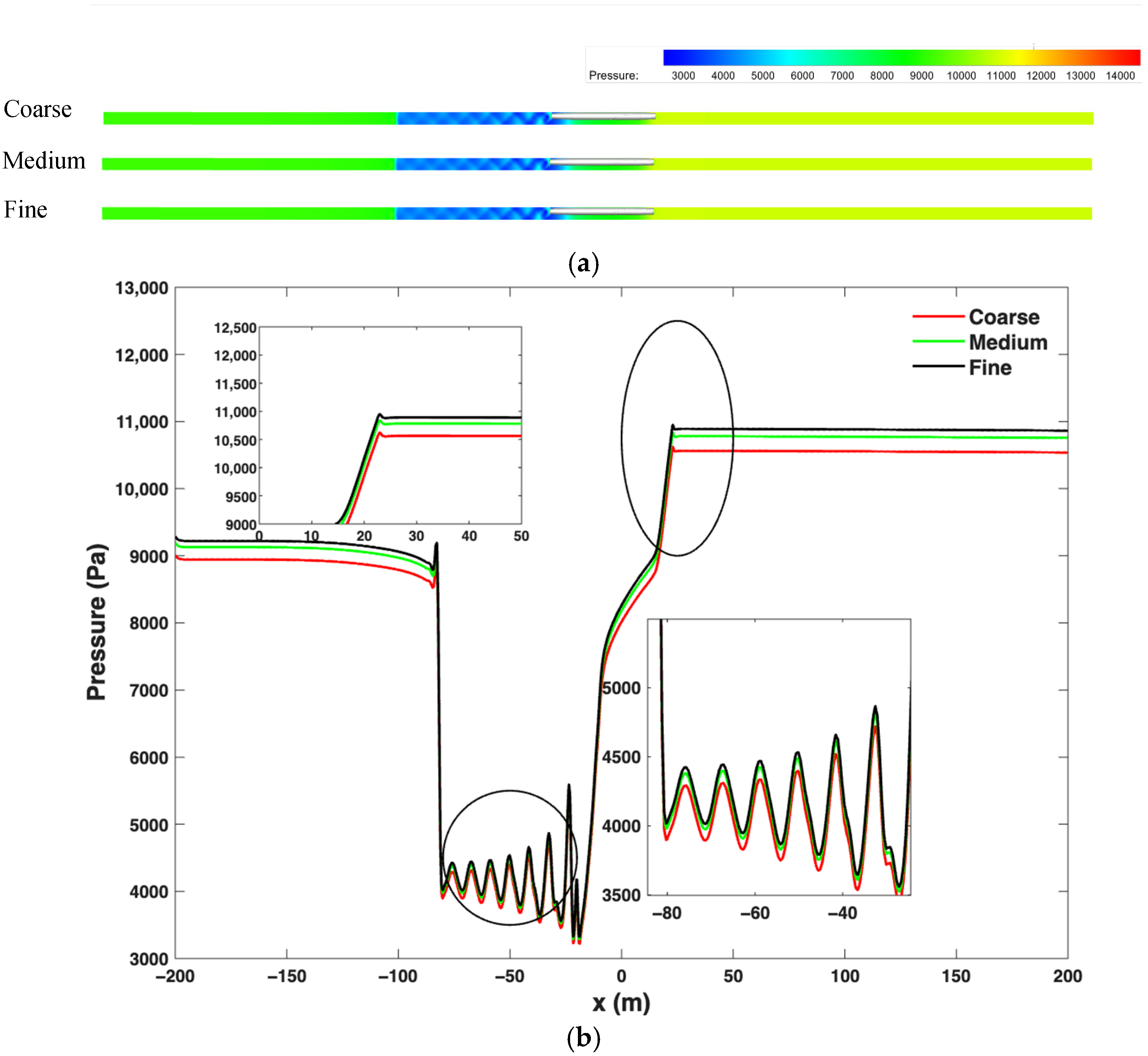
Grid Independence Study

Three levels of grid were used to check the grid independence, as presented in

Table 4. Grid levels used for independence check (d/D = 0.025 model).

Grid Level	Grid Size (Elements)	Element Size	Y+	Drag, (N)	Error, %
Coarse	2,405,210	10 mm	~10	9920	2.27%
Medium	8,159,310	7.5 mm	~5	10,210	0.59%
Fine	16,159,310	2.5 mm	~1	10,150	0.00%

. The structured hexahedral element type was utilized in this study; a 100 mm case study gap is the current case of investigating grid independence.

The cell-count refinement factors are $N_{\mathrm{med}}/N_{\mathrm{coarse}}=3.39$ and $N_{\mathrm{fine}}/N_{\mathrm{med}}=1.98$ (overall $N_{\mathrm{fine}}/N_{\mathrm{coarse}}=6.72$). In terms of an equivalent linear grid-spacing ratio, these correspond to $r_h\approx 1.50$ and $1.25$, respectively (overall $r_h\approx 1.88$). The medium grid deviates from the fine grid by 0.59% in drag, so the medium grid was used for optimization, while the fine grid served to verify grid independence, as shown in Table 4. Consequently, the analysis extensively used the medium grid to decrease the numerical budget. Also, the flow is ensured to be continuous with tiny grid levels, especially when the y+ approaches 1. The cell Knudsen number $K{n}_c$ is $1.5\times {10}^{-4}$ [56,63,64].

The pressure propagation in the tube with three grid levels is presented in Figure 7. The results show that all grid levels coincide. Hence, the medium level of the grid was used during the adjoint optimization, and the other cases for the analysis of the baseline and optimized design flow diagnosing.

2.6. Experimental Validation Model

The hemisphere model of Stine et al. [33] was used to verify the accuracy of the numerical turbulence model employed in this study and its analysis, namely $k-\omega$ GEKO. The model was simplified by an axisymmetric model, as shown in Figure 8, with its dimensions as illustrated in [42]. Although the flow regime is supersonic, this model is considered a verification model in previous literature and resembles the vehicle-tube model [42,57]. The grid was created using the ANSYS ICEM CFD 2024 meshing tool. The near-wall layer is considered to satisfy a value of y+ ≈ 0.5. A grid containing around 115,000 cells was used to simulate the flow around the hemisphere numerically. The test was conducted at a pressure of 1 atm and M = 1.97. The pressure inlet/outlet boundary conditions were applied to the inlet and outlet, respectively. As provided in Figure 8, the pressure coefficient estimated by the GEKO model agrees with the experimental results [33]. Together with the grid convergence study, this validation confirms that the numerical setup provides reliable predictions within a 2% margin of error, establishing sufficient accuracy for the subsequent optimization work.

While the validation case of Stine et al. [33] was conducted at a supersonic Mach number of 1.97, the present Hyperloop simulations operate in the transonic regime (Mach 0.7) within a low-pressure environment of 10 kPa. Despite the difference in flow regime and Reynolds number—lower by roughly an order of magnitude in the current setup—the shock structure and pressure-distribution patterns predicted by the GEKO turbulence model exhibit strong qualitative agreement with the experimental data. The SST $k-\omega$ model aligns closely with GEKO because GEKO is built on the same $k-\omega$ framework, causing both models to exhibit nearly identical near-wall behavior and thus produce matching ($C_p$) predictions. Both configurations show a bow-shock formation ahead of the hemispherical nose and comparable post-shock pressure gradients, confirming that the solver and turbulence model accurately reproduce compressible-flow physics across distinct Mach regimes. This comparison in Figure 9 supports the validity of the numerical framework and demonstrates its robustness for transonic Hyperloop applications where direct experimental data are unavailable. Together with the grid convergence study, this validation confirms that the numerical setup provides reliable predictions within a 2% margin of error, establishing sufficient accuracy for the subsequent optimization work.

3. Results

3.1. Aerodynamic Analysis of the Baseline Model with Various Suspension Gaps

This section deals with the aerodynamic analysis associated with investigating the gap effect on the baseline model. First, we show the pressure wave propagations measured in the tube center, characteristics of the aerodynamic force, and finally, the flow field diagnosis near the vehicle. The occurrence of a normal shock wave in the 100 mm gap (baseline design) configuration corresponds to the onset of the Kantrowitz limit, where the effective throat area between the vehicle and tube wall becomes sufficiently restricted for the local Mach number to reach unity. Under these conditions, the flow chokes and a normal shock forms downstream of the throat to restore subsonic conditions. For larger gaps, the flow passage area is greater and the Mach number remains below unity throughout the duct, maintaining a subcritical (unchoked) regime. This explains why the 100 mm case exhibits a distinct normal shock while cases with larger suspension gaps do not, confirming the sensitivity of the system to the local area ratio and blockage-induced choking phenomena. Figure 10 provides the pressure distribution along the tube centerline at d/D = 0.033, 0.025, and 0.0167 gaps, respectively. The results indicated that the pressure magnitude at the compression region increases with decreasing the gap distance $d$. The flow structure after the vehicle for all simulated cases shows OSW (Oblique Shock Waves) with many reflections and extended downstream to longer distances. However, for the case of d/D = 0.033, the flow expanded to shorter distances and terminated by a normal shock wave (although the number of solution iterations was similarly fixed at 10,000 iterations as presented in the pressure contour Figure 11.

The corrected mass flow rate ingested by the air compressor significantly influences the maximum pressure on the vehicle–tube interface, $p_{max}$, as illustrated in Figure 12. When the air compressor operates at low revoultion per minute (RPM), the air-breathed mass flow is reduced, leading to an increase in piston pressure at the front of the vehicle. Additionally, the corrected mass flow rate ratio, which is the ratio of the corrected mass flow to the mass flow at the fan inlet and the cruise flow Mach number, as described in Equation (9), also has a notable effect.

3.2. Gap Effects on the Aerodynamic Drag and Lift Forces

Figure 13 illustrates the variation in drag and lift coefficients ($C_D$&$C_L$), as a function of the gap ratio $d/D$ for Mach numbers $M=0.5$ and $0.7$. At larger gap ratios ($d/D>0.033$), the drag remains relatively constant for both Mach numbers, while the lift is close to zero. However, as the gap decreases below ($d/D=0.033$), both drag and lift increase sharply, especially at $M=0.7$, indicating stronger aerodynamic forces as the vehicle approaches the tube wall. This highlights the significant impact of wall proximity on aerodynamic performance, with higher Mach numbers leading to more pronounced effects on both drag and lift, particularly in the critical region where the gap is small.

3.3. Baseline Model Flow Structure

To understand the rise in drag when the gap $d/D<0.03$, further investigations were conducted. It was found that the drag rise has a strong relation to the under-expanded jet and oblique shock wave that formed at the end of the vehicle due to flow choking and interacting with the jet core and shear layer, causing the jet to bend downward to maintain pressure balance.

The interaction between an under-expanded jet and a shear layer with an oblique shock wave from tube walls creates a complex flow field pattern, as provided in Figure 14. The complex flow-field impacts the stability and performance of the system. This interaction depends on several factors such as vehicle speed, expansion jet size and shape, and oblique shock wave angle.

It is desirable to avoid under-expanded jet (UXJ) conditions in a jet-propelled Hyperloop system, as such conditions can induce performance losses, increase aerodynamic drag, and potentially generate damaging unsteady loads on internal structures. A practical solution is the use of an adjustable nozzle or exhaust system that allows the jet to undergo near-perfect expansion across varying operating conditions. As shown in Figure 15, the incoming co-flows (CF1 and CF2) that bypass the vehicle’s jet core (JC) interact strongly with the jet as it propagates downstream. Due to the asymmetry between the two co-flows, the jet becomes inclined, bending toward the lower-momentum side. The velocity of CF1 is higher than that of both the jet core and the opposite co-flow (CF2), creating a lateral compression effect. This compression of the co-flows promotes jet expansion, while the moderate under-expansion of the jet, in turn, compresses CF1 and CF2.

The resulting shock-cell structure within the jet core is characterized by a sequence of diamond-shaped shocks, with the lengths of the first three shock cells (Sx1, Sx2, and Sx3) estimated to be approximately 1b, 2b, and 3b, respectively, where b denotes the jet exit diameter. The overall inclination of the jet plume is further illustrated in Figure 14 using the Mach Disc (MD) iso-surface, highlighting the deformation of the jet axis under the influence of asymmetric co-flow conditions.

The UXJ with co-flows asymmetry and the wall gap has more complications in the jet and flow structure after the vehicle, and the Coanda effect [41] is present in this case. The jet is directed downward when the vehicle reaches the tube wall with less gap. The directed jet increases the lift force and imposes a pitching moment on the vehicle, which endangers the vehicle from hitting the tube wall. To examine how the jet flow inclination angle varies with the d/D ratio, Figure 16 shows that the inclination angle aligns with the center of the jet core, directly influencing the thrust. The vertical component of this thrust creates a pitching moment, leading to vehicle instability. The formula in Equation (15) is used to estimate the thrust vector angle $\theta$. The estimated values of ${\theta }_1=13°,{\theta }_2=20°,$ and ${\theta }_3=17°$ for the various gaps d/D of 0.033, 0.025, and 0.0167, respectively.

$$\theta ={\tan }^{-1}\left({\displaystyle \frac{Lift}{Thrust}}\right)={\tan }^{-1}\left({\displaystyle \frac{Lift}{Drag}}\right)$$

(15)

Figure 17 presents a symmetrical model without wall proximity, focusing only on the complex flow structure behind the vehicle. The figure shows that an under-expanded jet forms at the jet center, with symmetrical co-flows alongside the vehicle. The vehicle’s tube stimulates supersonic flow at the divergent (expansion) section.

The jet’s flow structure reveals a distinct X-shaped pattern, formed by shock diamonds due to the interaction of expansion and compression waves. The jet expands, creating three X-structures (SX1, SX2, SX3), and transitions from supersonic to subsonic mixing, influenced by the expansion rate. The supersonic mixing zone extends approximately 40 m, ending with a normal shockwave that initiates a subsonic mixing zone with wakes.

The observed flow dynamics have significant implications for Hyperloop systems. Shock diamonds and pressure fluctuations can increase drag and noise. Understanding factors influencing the supersonic mixing zone and shockwave location is crucial for optimizing aerodynamic efficiency and minimizing the environmental impact of Hyperloop systems. The study’s findings offer valuable insights into these complex flow phenomena, contributing to the development of sustainable high-speed transportation.

3.4. Adjoint Aerodynamic Shape Optimization of the Vehicle

An adjoint-based aerodynamic shape optimization was carried out on the baseline model with a gap distance of 0.1 m (d/D = 0.033), $M=0.7,\mathrm{a}\mathrm{n}\mathrm{d}\beta =0.36$. The aim was to minimize drag using 250 control points while maintaining thrust-drag equilibrium as a constraint.

The convergence history of the adjoint optimization (Figure 18a) demonstrates a smooth and monotonic reduction in drag, with convergence achieved after approximately 26 iterations. This trend confirms the stability of the discrete adjoint solver and indicates that the optimization process avoided shallow local minima. The final solution produced a drag reduction of nearly 27.5%, underscoring the efficiency of the adjoint approach for handling the complex aerodynamic interactions between the pod, suspension gap, and tube wall. The corresponding shape evolution during the optimization process (Figure 18b) reveals that most geometric modifications occur in the aft region of the vehicle. The baseline tail geometry, which promoted shock reflections and flow choking, was progressively elongated and streamlined, leading to smoother pressure gradients and reduced adverse jet–wall interactions. In contrast, only minor adjustments were observed at the nose, reflecting the lower sensitivity of the forward section to choking phenomena. These deformation patterns align with the sensitivity maps presented earlier, which showed that the strongest adjoint gradients were concentrated in the tail region.

The final optimized flow field (Figure 18c) highlights the aerodynamic benefits of these shape modifications. Whereas the baseline configuration exhibited strong oblique shock waves and partial choking in the throat, the optimized pod produces a largely subsonic flow passage with no evidence of choking. The pressure distribution is more uniform, and the Mach number contours resemble those of a converging–diverging nozzle operating in a fully subsonic regime. Although the optimized solution maintained thrust–drag equilibrium at cruise, it also reduced jet velocity, suggesting that additional design features, such as a center-body insert at the nozzle exit, may be necessary to support accelerated motion phases. Overall, the optimized design delayed the onset of choking by approximately 70% compared with the baseline and lowered the critical gap ratio from 0.025 to 0.008, thus enhancing both aerodynamic performance and operational robustness of the system.

Figure 19 compares the pressure flow field and Mach number contours for baseline, design iteration 15, and optimized models at d/D = 0.033, M = 0.7, and β = 0.36. Through the development of design iterations and evolutions, the flow field was significantly enhanced, and the complex flow structure turned into subsonic flow with enhanced performance, with a 27.5% reduction in drag, resulting in cost savings and a more environmentally friendly system. Furthermore, the flow choking and shock wave observed in the baseline configuration have been successfully eliminated in the optimized shape configuration. The flow through the tube-vehicle resembles a fully subsonic nozzle (i.e., where flow passage is not choked). Flow speed increases through the nose section and reaches its maximum subsonic speed at the throat (constant area section). The flow then decelerates through the tail section and exits at the rear of the vehicle as a subsonic jet with a velocity slightly more than that required to balance the drag force, which is why the center body is required in this case.

3.5. Optimized Model Performance with Various Suspension Gaps

Figure 20 illustrates the drag of the optimized and baseline models at various suspension gaps. The optimized model enhanced the suspension gap performance by reducing the critical gap to d/D < 0.01, which in turn will decrease the structural weight of the suspension system.

3.6. The Effect of the Optimization Process on the Kantrowitz Limit

The investigation into the aerodynamic performance of a high-speed vehicle within a low-pressure tube revealed critical insights into the impact of suspension gaps on aerodynamic forces, particularly drag and lift. The study explored various gap distances (d/D) at Mach numbers 0.5 and 0.7, highlighting the complexities introduced by the vehicle’s proximity to the tube wall.

One of the key findings is that smaller gap distances, particularly when d/D < 0.033, lead to significant aerodynamic challenges. At these small gaps, the flow structure becomes increasingly complex, characterized by the formation of oblique shock waves and flow choking. These phenomena result in a marked increase in both drag and lift coefficients, which not only diminishes the vehicle’s efficiency but also raises stability concerns, particularly at higher speeds. The presence of flow separation and reattachment near the vehicle’s tail further complicates the flow dynamics, contributing to increased aerodynamic drag.

To address these aerodynamic challenges, an adjoint-based aerodynamic optimization was performed on the baseline vehicle model. The optimization focused on minimizing drag while maintaining thrust as a design constraint to ensure cruise condition equilibrium. The results of the optimization were promising, with the optimized vehicle design demonstrating a significant reduction in drag—approximately 27.5%. This reduction was primarily achieved by reshaping the vehicle’s tail section, which mitigated the adverse effects of shock waves and flow choking. The optimization also led to a smoother flow transition from supersonic to subsonic speeds, enhancing overall aerodynamic efficiency.

The optimized design also altered the critical gap distance at which drag begins to rise significantly. In the baseline configuration, this critical distance was around d/D~0.033. However, after optimization, the critical gap distance was reduced to d/D~0.008, indicating that the optimized design is more tolerant of smaller gaps. Thus, it allows for greater flexibility in vehicle–tube spacing without compromising performance. This improvement not only lowers operating costs by reducing energy consumption but also offers practical advantages in the design and operation of future hyperloop systems.

The Kantrowitz limit, which defines the threshold for flow choking in the vehicle–tube system, was significantly improved through adjoint optimization. This approach delayed the onset of choking and enhanced overall aerodynamic performance, as shown in Figure 21. The optimization process gradually adjusted the area gradient between the exit and inlet ($A_2/A_1)$. Initially, the baseline design (blue circle) was entirely within the choking flow region (white area on the chart). During the adjoint optimization, the design evolved: point 10 (green circle) moved closer to the limit, point 25 reached the limit line, and the final optimized design at point 30 (black circle) fully transitioned into the no-choking area (pink area).

4. Discussion and Implications

This study deployed an adjoint aerodynamic shape optimization specifically to suspension-gap-induced choking and wall–jet interactions in a three-dimensional Hyperloop pod inside a tube with jet propulsion. Prior Hyperloop/ETT works largely rely on 1-D or axisymmetric surrogates that do not resolve confinement physics at small gaps; here, the optimizer acts directly on the external pod geometry (250 FFD control points) under a cruise thrust–drag equilibrium constraint (Section 2.4; Figure 3; Table 3). This closes a methodological gap between “what the gap does” and “how to design the pod so the gap stops doing it.

4.1. Verified Numerics Support the Design Claims

A three-level grid study (Table 4) shows medium–fine drag deviation = 0.59% with errors referenced to the fine grid, and refinement factors $N_{m\mathrm{e}\mathrm{d}}/N_{c\mathrm{o}\mathrm{a}\mathrm{r}\mathrm{s}\mathrm{e}\mathrm{e}}$ = 3.39 and $N_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{e}}/N_{\mathrm{m}\mathrm{i}\mathrm{d}}$ = 1.98 (overall 6.72×); pressure-wave comparisons across grids coincide (Figure 7). This justifies running the optimization on the medium grid while reserving the fine grid for verification (Section 2.5).

Section 3.1 shows that small gaps push the annular passage toward a Kantrowitz-like throat, forcing the local Mach number to unity and creating a downstream normal shock (baseline d = 100 mm, d/D ≈ 0.033). Pressure-centerline histories (Figure 10) and planar contours (Figure 11) document this transition; larger gaps keep the passage subcritical with no normal shock (Section 3.1). The resulting shock topology amplifies drag and lift and perturbs the jet–shear layer system behind the pod—mechanisms that the adjoint procedure targets by reshaping the aft body (Section 3.3 and Section 3.4). The optimizer primarily reduces the area-gradient-driven acceleration at the tail and reorganizes the under-expanded jet interaction with the wall-bounded shear layers (Figure 14, Figure 15, Figure 16 and Figure 19), suppressing shock-induced penalties and restoring a largely subcritical passage. The geometry-sensitivity map (Figure 5) guides these changes by concentrating updates where drag sensitivities are highest (Section 2.4).

4.2. Headline Performance with System-Level Meaning

The optimized pod attains ≈ 27.5% drag reduction, delays choking onset by ~70%, and lowers the critical gap from d/D ≈ 0.025–0.033 (baseline) to ≈0.008 at M = 0.7 (Figure 19; Section 3.4). At fixed cruise speed, propulsive power scales with drag (P = D·V), so these aerodynamic gains translate directly into operating-power reductions and a broader safe-gap envelope.

4.3. Impacts on Hyperloop Design

(i)

Power and energy: At fixed cruise speed, P = D·V; therefore, a 27.5% drag cut implies a comparable reduction in required propulsive power. For a given duty cycle, it reduces energy per km and can shrink power-electronics margins. (See Section 3.4; Figure 19, Figure 20 and Figure 21 for the drag trends that underpin this mapping.)

(ii)

Tube and suspension sizing: Lowering the critical gap from d/D ≈ 0.025–0.033 to ≈0.008 widens the safe-gap envelope (Figure 20), enabling smaller clearances without encountering choking. This can relax tube-diameter and suspension-mass requirements at the system level (Section 3.4).

(iii)

Stability margins: By mitigating shock-induced lift excursions near the wall (Figure 13, Figure 15 and Figure 16), the optimized shape improves static stability in near-critical gaps (Section 3.2 and Section 3.3), reducing risk of wall strikes and easing control-law demands.

(iv)

Manufacturability & integration: The aft-body updates are compatible with composite lay-up and ±2 mm tooling tolerances; integration with maglev suspensions and linear motors is straightforward because the optimization acts on outer mold lines, not on the levitation/propulsion hardware.

5. Conclusions

This study investigates and analyzes the aerodynamic performance of a high-speed vehicle traveling within a low-pressure tube. The gap between the vehicle and the tube wall affects both drag and lift forces, which are key factors in the vehicle’s efficiency and stability.

Our findings showed that when the gap becomes very small, particularly below a ratio (d/D) of 0.03, the aerodynamic challenges multiply. Complex flow patterns, including shock waves and flow choking, lead to a significant increase in drag and lift, which can reduce the vehicle’s efficiency and pose stability risks, especially at higher speeds.

To address these issues, we applied an adjoint-based aerodynamic shape optimization. This approach proved effective, reducing drag by about 27.5% by reshaping the vehicle’s tail, which in turn delayed the onset of choking and made the flow smoother as it transitioned from supersonic to subsonic speeds. Additionally, the optimization process improved the Kantrowitz limit, allowing the vehicle to operate more reliably even at smaller gap distances. This means that future designs could have greater flexibility in vehicle–tube spacing without sacrificing performance.

One of the key outcomes of this study was the ability to lower the critical gap distance that causes aerodynamic issues, from d/D $\approx$ 0.03 to 0.008. This not only improves aerodynamic performance but also reduces operational costs and energy use, making the system more sustainable and cost-effective. Beyond drag reduction, this work introduces a novel methodology for gap-aware aero-propulsive design of Hyperloop vehicles. Unlike prior studies that largely ignored suspension-gap effects, this research integrates adjoint optimization with propulsion boundary conditions to systematically address choking and wall–jet interactions.

The present optimization framework demonstrates that significant aerodynamic efficiency gains can be achieved through adjoint-based surface refinement; however, practical implementation in a real Hyperloop system requires consideration of manufacturing, integration, and operational constraints. The optimized geometry exhibits sharper curvature near the tail section, which may demand tighter manufacturing tolerances and more complex composite tooling. At full scale, maintaining ±2 mm fairing accuracy is feasible using automated Carbon fiber reinforced polymer (CFRP) layups, but could increase tooling costs. Moreover, integrating the optimized pod shape with magnetic-levitation suspensions and linear motors introduces structural and dynamic coupling effects not captured in the aerodynamic-only model.

The previous works on flow simulations also assume steady, axisymmetric, and perfectly rigid boundaries, while real pods experience vibration, thermal expansion, and small alignment deviations inside the tube. These factors can modify flow symmetry and slightly alter drag and pressure distributions. Future work will extend the framework to coupled fluid–structure and energy analyses, incorporating noise propagation, transient wave effects, and long-duration operational cycles. Such multidisciplinary optimization is expected to quantify lifecycle performance and validate the applicability of the present design under realistic Hyperloop operating conditions. In summary, our work demonstrates the potential of using adjoint optimization techniques to tackle the aerodynamic challenges of Hyperloop systems. The research offers practical solutions that could be applied to future designs, contributing to the development of faster, more efficient, and environmentally friendly high-speed transportation. This study lays a strong foundation for continued innovation in this technology area.