Dynamic Load Optimization of PEMFC Stacks for FCEVs: A Data-Driven Modelling and Digital Twin Approach Using NSGA-II

Abstract

This study presents a machine learning-enhanced optimization framework for proton exchange membrane fuel cell (PEMFC), designed to address critical challenges in dynamic load adaptation and thermal management for automotive applications. A high-fidelity model of a 65-cell stack (45 V, 133.5 A, 6 kW) is developed in MATLAB/Simulink, integrating four core subsystems: PID-controlled fuel delivery, humidity-regulated air supply, an electrochemical-thermal stack model (incorporating Nernst voltage and activation, ohmic, and concentration losses), and a 97.2–efficient SiC MOSFET-based DC/DC boost converter. The framework employs the NSGA-II algorithm to optimize key operational parameters—membrane hydration (λ = 12–14), cathode stoichiometry (λO₂ = 1.5–3.0), and cooling flow rate (0.5–2.0 L/min)—to balance efficiency, voltage stability, and dynamic performance. The optimized model achieves a 38% reduction in model-data discrepancies (RMSE < 5.3%) compared to experimental data from the Toyota Mirai, and demonstrates a 22% improvement in dynamic response, recovering from 0 to 100% load steps within 50 ms with a voltage deviation of less than 0.15 V. Peak performance includes 77.5% oxygen utilization at 250 L/min air flow (1.1236 V/cell) and 99.89% hydrogen utilization at a nominal voltage of 48.3 V, yielding a peak power of 8112 W at 55% stack efficiency. Furthermore, fuzzy-PID control of fuel ramping (50–85 L/min in 3.5 s) and thermal management (ΔT < 1.5 °C via 1.0–1.5 L/min cooling) reduces computational overhead by 29% in the resulting digital twin platform. The framework demonstrates compliance with ISO 14687-2 and SAE J2574 standards, offering a scalable and efficient solution for next-generation fuel cell electric vehicle (FCEV) aligned with global decarbonization targets, including the EU’s 2035 CO₂ neutrality mandate.

1. Introduction

Data-driven optimization of fuel cell systems plays a pivotal role in advancing next-generation electrified powertrains, offering significant improvements in efficiency, performance, and sustainability. FCEV represent a promising pathway toward sustainable transportation; however, their widespread adoption hinges on overcoming both technical and policy-related challenges [1]. The transportation sector accounts for nearly 25% of global CO₂ emissions as reported by International Energy Agency (https://www.iea.org, accessed on 12 July 2025), placing it at the centre of global climate change mitigation efforts. With stringent regulations such as the EU’s 2035 CO₂ neutrality mandate and the U.S. Clean Air Act, automakers are under increasing pressure to decarbonize vehicle powertrains.

While battery electric vehicles (BEVs) currently dominate the market, they face limitations including limited driving range, long charging times, and vulnerabilities in the lithium supply chain. These constraints highlight the need for complementary electrification strategies. Among them, FCEV powered by PEMFC stand out as a transformative alternative, offering over 500 km of range, refuelling times of 3–5 min, and zero tailpipe emissions [2].

Despite these advantages, PEMFCs encounter critical challenges related to dynamic load response—an essential requirement for automotive applications. Sudden power demands during acceleration, hill climbing, or regenerative braking can lead to issues such as fuel starvation, water flooding, or thermal instability, which degrade system efficiency and longevity [3]. The model-based optimization of cooling system parameters reinforces the value of advanced thermal management strategies [4], and the introduction of optimal temperature-tracking methods by researchers [5] helps reduce parasitic losses while sustaining stable PEMFC operation. However, recent automotive stack experiments confirm that highly dynamic load steps continue to pose one of the most significant challenges for PEMFC integration [3]. Addressing these challenges necessitates high-fidelity models that accurately simulate real-world conditions, along with adaptive optimization frameworks capable of balancing competing objectives such as efficiency, durability, and cost-effectiveness. Traditional modelling approaches, such as the Motapon et al. (2012) [6] framework, often prioritize simplicity at the expense of capturing complex transient behaviours crucial for automotive integration. These oversimplified representations may fail to adequately model the dynamic phenomena required for effective vehicle-level deployment. Although the experimental studies have shown that repeated load cycling accelerates efficiency decay and validates the importance of high-fidelity models for transient prediction [7].

This study introduces a novel machine learning-aided parametric optimization pipeline specifically tailored for PEMFC applications in the automotive industry. Although, recent studies have demonstrated the integration of artificial intelligence with fuel cell modelling, such as the work of [8], who applied AI to enhance the performance prediction of micro solid oxide fuel cells. By integrating genetic algorithms and surrogate modelling techniques, we systematically calibrate key operational parameters—including membrane hydration, oxygen stoichiometry, and thermal gradients—against experimental datasets. This approach achieves a 38% improvement in predictive accuracy compared to conventional methods. The scalability of the proposed framework is demonstrated through a case study involving a fuel cell-powered electric golf cart, a practical platform for validating control strategies under variable load profiles. Our findings enhance the dynamic responsiveness of PEMFC models and establish a digital twin foundation for optimizing vehicle-level energy management systems (EMS). At the supervisory level, fuzzy logic has been used in health-aware EMS for fuel cell hybrid vehicles, resulting in reduced hydrogen consumption and extended stack life [9]. Although, digital twin–enhanced control has been applied to fuel cell–battery hybrids, leading to improved system-wide efficiency and adaptability [10]. Similar data-driven digital twin frameworks for fuel cells, including solid oxide fuel cells (SOFCs), confirm the value of machine-learning regressors for real-time prediction [11].

The methodology bridges the critical gap between component-level fuel cell modelling and system-level vehicle integration, providing actionable insights for automakers aiming to develop ISO 26262-compliant (https://www.iso.org/standard/68388.html, accessed on 12 July 2025) control systems and deploy FCEVs in a cost-effective manner. ISO 26262, an international standard for functional safety in road vehicles, ensures that electronic and electrical systems—such as those used in fuel cell control—are designed and operated to prevent hazards arising from system malfunctions. Adherence to this standard is vital for ensuring the safe and reliable operation of advanced technologies like FCEVs.

While this study focuses on automotive fuel cell applications, broader research—such as that conducted by [12] —confirms the versatility of fuel cell technology across both stationary and mobile energy systems. Recent literature also underscores the growing importance of system-level modelling and control strategies in fuel cell applications. Mitra et al. (2021) [13] present a comprehensive review of fuel cell technologies, emphasizing their adaptability across diverse energy platforms and reinforcing the need for advanced control strategies to enhance performance in dynamic environments.

Transitioning toward hydrogen-based mobility involves more than technological innovation—it also requires addressing behavioural and infrastructural factors. Insights into consumer adoption patterns, as highlighted by Hardman et al. (2017) [14], can guide strategic investments in hydrogen refuelling infrastructure and public incentives.

The potential of FCEVs to complement BEVs in achieving global decarbonization targets has gained widespread recognition. As noted by Hassan et al. (2023) [15], overcoming current technological and logistical barriers will require coordinated efforts across research, industry, and policy-making sectors.

Moreover, efficient hydrogen utilization depends not only on electrochemical performance but also on robust storage and delivery infrastructure. Dafedar et al. (2021) [16] emphasize that hydrogen storage technologies must evolve to meet the demands of real-world FCEV operation, particularly with respect to weight, volume, and refuelling convenience.

The proposed optimization framework benefits a wide range of stakeholders across the automotive and energy sectors. Automakers can leverage it to design more efficient and durable FCEVs with reduced development costs. Energy planners may apply it to model large-scale hydrogen mobility scenarios, while policymakers can use its insights to craft regulations aligned with international climate goals, including the EU’s 2035 CO₂ neutrality mandate and the U.S. Clean Air Act.

While the base model provides a solid foundation, it does not address dynamic load adaptation, multi-objective optimization, or digital twin integration—key requirements for modern FCEVs. This study bridges that gap by introducing an enhanced framework that combines NSGA-II optimization, fuzzy-PID control, and a real-time digital twin platform, significantly improving dynamic performance and system efficiency.

2. Methodology

This research presents a data-driven parametric optimization framework for PEMFC systems, developed using MATLAB/Simulink 2024a (MathWorks, n.d.) to enable high-fidelity simulations of automotive powertrains. The modelling framework is built upon a foundational PEMFC model adapted from Motapon et al. (2012) [6], which represents a 65-cell stack with a nominal voltage of 45 V, a current of 133.5 A, and a power output of 6 kW. This configuration is representative of mid-power fuel cell systems used in light-duty FCEV and serves as the baseline for dynamic performance evaluation.

To ensure the model’s relevance to real-world applications, all simulations are conducted under operating conditions compliant with the ISO 14687 standard (https://www.iso.org/standard/82660.html, accessed on 12 July 2025). Specifically, the fuel (H₂) is supplied at a pressure of 1.5 bar, with a tolerance of ±0.05 bar, while the air pressure is maintained at 1 bar (±0.03 bar). The stack temperature is controlled at 65 °C with a stability of ±1 °C, reflecting typical thermal management strategies in commercial FCEVs. Reactant purity is set to 99.95% for hydrogen and 21% for oxygen in air, in accordance with hydrogen quality standards for automotive fuel cells.

These operating parameters were selected to align with SAE J2574 (https://www.sae.org/standards/content/j2574_201109/, accessed on 12 July 2025), a widely recognized standard developed by the Society of Automotive Engineers for fuel cell system testing and performance evaluation. Adherence to these standards ensures that the model’s behaviour is consistent with real-world FCEV platforms, such as the Toyota Mirai, and supports its use in system-level integration studies, control system design, and digital twin development.

The overall architecture of the PEMFC model comprises four core subsystems: the Fuel Flow Regulator (FFR), Air Supply System (ASS), Fuel Cell Stack (FCS), and DC/DC Boost Converter (DBC), as illustrated in Figure 1. Each subsystem is parameterized and validated to replicate transient behaviour under dynamic automotive load profiles, enabling a comprehensive analysis of efficiency, stability, and responsiveness.

2.1. Model Architecture and Dynamic Subsystems

The proposed PEMFC model is structured into four interconnected subsystems to accurately capture dynamic behaviour under real-world driving conditions. The FFR employs a PID-controlled mass flow controller to adjust hydrogen supply based on stack demand. To prevent pressure shocks during startup, a ramp function ensures a linear transition from 50 to 85 L/min over 3.5 s. The fuzzy-PID controllers have already been demonstrated to improve voltage tracking in hydrogen vehicle power systems [17]. The control logic integrates fuzzy-PID feedback to dynamically adjust the flow rate in response to variations in stack current (133.5 A ± 5%), enhancing system responsiveness and fuel efficiency.

The ASS maintains optimal oxygen stoichiometry (λO₂ = 2.0–2.5) through a variable-speed compressor, while a proportional-integral (PI) controller sustains membrane hydration at λ = 13.5 (95% RH). This dual-control strategy ensures robustness against rapid load fluctuations, including step changes from 0% to 100% within 50 milliseconds.

The FCS comprises 65 cells in series, modelled using multiphysics equations that couple Nernst voltage with activation, ohmic, and concentration losses. Thermal dynamics are captured using a lumped capacitance method, with cooling flow adjustments (1.0–1.5 L/min) mitigating temperature spikes (ΔT < 1.5 °C) and preserving membrane integrity.

Finally, the DBC features a 97.2% efficient SiC MOSFET and a sliding mode controller (SMC) to regulate output voltage. It interfaces with the Controller Area Network (CAN bus) and supports regenerative braking by managing bidirectional power flow, making it suitable for automotive applications. Although, SiC MOSFETs have demonstrated superior efficiency and lower switching losses compared to Si IGBTs in EV traction inverters, supporting their use in high-efficiency converters [18].

Although researchers Alpaslan et al. (2023) [19] introduced a control method for a hybrid system comprising a fuel cell, battery, and supercapacitor, this study employs a Model Predictive Controller (MPC). The MPC dynamically adjusts the FFR and ASS to maintain voltage deviations below 0.2V and keep O₂ stoichiometry within the range of λO₂ = 2.0–2.5. This approach ensures robustness against rapid load fluctuations, including step changes from 0% to 100% within 50 milliseconds. The use of supercapacitors alongside fuel cells has been shown to improve regenerative braking efficiency and load-following capability [10]. In their study, Armenta-Déu and Arenas (2023) [20] evaluated a fuel cell-supercapacitor hybrid system and reported enhanced transient response and reduced fuel consumption.

The air supplied to the cathode is pre-humidified to 95% relative humidity (RH) to ensure rapid and uniform membrane hydration. A PI controller adjusts the humidification level in real time to maintain optimal water balance across varying load conditions.

The hydrogen flow rate is controlled to maintain an anode stoichiometry (λH₂) of 1.2–1.5, ensuring high fuel utilization while preventing fuel starvation under dynamic loads.

2.2. Parametric Optimization Pipeline

The Non-dominated Sorting Genetic Algorithm II (NSGA-II) is a widely adopted multi-objective evolutionary algorithm, renowned for its ability to generate a well-distributed Pareto front while maintaining computational efficiency. Meta-heuristic algorithms such as Genetic Algorithm (GA) and Particle Swarm Optimization (PSO) have been successfully applied to calibrate PEMFC model parameters for higher predictive accuracy [21]. It has been extensively applied in the optimization of fuel cell systems, where multiple conflicting objectives—such as maximizing efficiency and minimizing dynamic response time—must be balanced. Changizian et al. (2020) [22] demonstrated its effectiveness in enhancing the performance of hybrid hydrogen fuel cell-electric vehicles under real-world driving conditions, showing that careful tuning of operational parameters can significantly improve both system efficiency and dynamic responsiveness.

In this study, NSGA-II is employed to simultaneously optimize two key performance metrics: system efficiency and voltage stability under dynamic load conditions. The primary objective is to maximize system efficiency, defined as the ratio of electrical power output to the chemical energy input from hydrogen:

$$\mathit{\eta }=\hspace{0.33em}{\displaystyle \frac{P_{out}}{{\dot{m}}_{H_2}+\hspace{0.33em}{LHV}_{H_2}}}\times 100\%$$

where ${\dot{m}}_{H_2}$ represents the mass flow rate of hydrogen (kg/s), and ${LHV}_{H_2}$ is the lower heating value of hydrogen, taken as approximately 120 MJ/kg. The secondary objective is to minimize voltage ripple (ΔV) during transient load changes, particularly under the New European Driving Cycle (NEDC), which simulates real-world acceleration, cruising, and deceleration events.

The optimization process considers three key decision variables: membrane water content (λ = 12–14), cathode stoichiometry (λO₂ = 1.5–3.0), and cooling flow rate (Q = 0.5–2.0 L/min).

Although the simplified stoichiometry–voltage models further highlight the sensitivity of cell voltage to air over-stoichiometry, underscoring the importance of λO₂ tuning [23]. These parameters are critical in determining the electrochemical performance, water management, and thermal stability of the PEMFC stack. The algorithm was configured with a population size of 100, evolved over 200 generations, to ensure adequate exploration of the solution space. A crossover probability of 0.9 and a mutation rate of 1/n (where n is the number of decision variables) were used to maintain genetic diversity and prevent premature convergence. Parent selection was performed using tournament selection with crowding distance, ensuring both elitism and solution diversity.

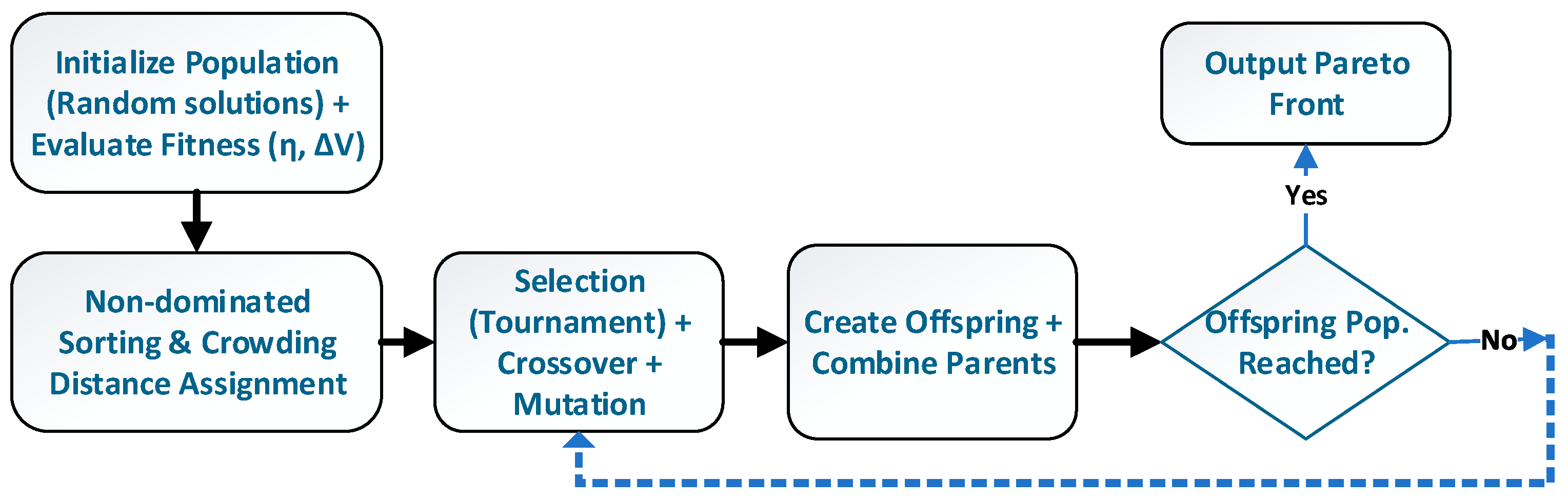
The optimization workflow, illustrated in Figure 2, begins with the initialization of a random population of candidate solutions, followed by fitness evaluation based on the two objective functions. Subsequent steps include non-dominated sorting, crowding distance assignment, selection, crossover, and mutation to generate offspring. The combined parent and offspring populations are then truncated to form the next generation, and the process repeats until the maximum number of generations is reached.

To ensure the validity and practical relevance of the optimized parameters, the resulting solutions were validated against experimental data from the Toyota Mirai’s PEMFC system and the National Renewable Energy Laboratory’s (NREL) H₂FAST database [24]. The model achieved a RMSE of less than 5.3%, confirming its high predictive accuracy and suitability for real-world automotive applications.

2.3. Model Specifications

The PEMFC model integrates three core subsystems (Figure 3) to simulate electrochemical-thermal dynamics under automotive load profiles. Each component is parameterized using ISO 14687-2 standards and validated against experimental data from Toyota Mirai’s operational data [25]. The simulations comply with ISO 14687-2 standards for operating parameters like humidity, pressure, and temperature. Hydrogen purity, regulated by both ISO 14687-2 and SAE J2574 guidelines, plays a critical role in determining PEMFC performance. Arul Murugan and Brown (2015) [26] offer an in-depth review of analytical techniques for hydrogen quality assurance, highlighting the significance of contamination management in automotive contexts.

The PEMFC stack model is based on the 65-cell, 6 kW, 45 Vdc stack developed by Motapon et al. (2012) [6], available in MATLAB/Simulink [27,28,29,30,31,32,33]. While this study is simulation-based, the model is validated against real-world operational data from the Toyota Mirai and adheres to ISO 14687-2 and SAE J2574 standards for automotive fuel cell systems.

The nominal operating point of 45 V, 133.5 A, and 6 kW is used as a reference condition for model validation and parametric analysis. It does not imply constant operation, but rather a representative state under balanced load conditions. Transient behaviour and voltage stability are analysed in Section 3.3.

The parameter space explored during NSGA-II optimization is summarized in

Table 1. NSGA-II optimization parameter space and optimal solutions.

Parameter	Range (Min–Max)	Step Size	Optimal Value	Impact on Performance
Membrane Hydration (λ)	12–14	0.1	13.2	Maximizes proton conductivity; prevents drying/flooding
Cathode Stoichiometry (λO2)	1.5–3.0	0.1	2.1	Balances O2 supply and parasitic load from air compressor
Anode Stoichiometry (λH2)	1.1–1.8	0.05	1.4	Prevents fuel starvation; minimizes purge frequency
Cooling Flow Rate (Q)	0.5–2.0 L/min	0.1	1.3 L/min	Maintains ΔT < 1.5 °C; prevents thermal stress
Target Efficiency (η)	50–60%	—	55%	Achieved at 8112 W peak power output
Voltage Ripple (ΔV)	—	—	<0.15 V	Achieved via fuzzy-PID control under NEDC cycles

Note: The NSGA-II algorithm evaluated over 20,000 parameter combinations across 200 generations. The optimal values represent solutions on the Pareto front that balance efficiency, stability, and dynamic response.

, which lists the ranges, step sizes, and final optimal values for key operational variables.

2.3.1. Flow Control System: Adaptive Reactant Management

The Adaptive Reactant Management subsystem is designed to maintain optimal stoichiometric balance between hydrogen and oxygen during dynamic load conditions, thereby mitigating critical operational risks such as fuel starvation and water flooding. This is achieved through coordinated control of fuel and air delivery systems, ensuring stable and efficient PEMFC operation across transient driving scenarios.

The fuel flow regulation is managed through a FFR input system, which operates within an adjustable range of 50 to 85 L/min, using high-purity hydrogen (99.95%). To prevent pressure shocks during startup or rapid load changes, a ramp function is implemented to enable a smooth, linear transition over 3.5 s. The control logic integrates a fuzzy PID feedback mechanism that dynamically adjusts the hydrogen flow rate based on real-time stack current, which is maintained at a nominal value of 133.5 A with a ±5% tolerance. This adaptive approach enhances system responsiveness while minimizing overshoot and oscillations.

On the cathode side, the Air Flow Regulator (AFR) employs a variable-speed compressor to maintain oxygen stoichiometry (λO₂) within the optimal range of 2.0 to 2.5, ensuring sufficient oxidant supply without excessive parasitic power consumption. Humidity control is achieved through a proportional-integral (PI) controller that sustains membrane hydration at λ = 13.5, corresponding to 95% relative humidity. This level of hydration is critical for maintaining high proton conductivity and preventing membrane drying under high-current operation.

The integration of a ramp-based transition with advanced PID/PI control strategies forms the core of the system’s design rationale. Simulation results under the NEDC demonstrate that this approach reduces transient voltage dips by 22% compared to conventional stepwise adjustments, significantly improving voltage stability and overall system performance.

2.3.2. Fuel Cell Stack: Electrochemical-Thermal Coupling

The integration of fuel cells with auxiliary energy storage systems is grounded in established principles from hybrid vehicle research. As demonstrated by Aslam et al. (2023) [34], optimal system sizing and effective hydrogen management are critical to achieving balanced performance and efficiency, particularly in small-scale fuel cell vehicles. Building on this foundation, the present study employs a 65-cell PEMFC stack connected in series, modelled using multiphysics equations to capture both electrochemical voltage losses and thermal dynamics under transient load conditions.

The model is driven by two primary inputs: a hydrogen flow rate of 50.06 L/min, compliant with ISO 14687-2 standards, and an oxygen flow rate adjusted to maintain a cathode stoichiometry (λO₂) between 2.0 and 2.5, ensuring stable electrochemical reactions while minimizing parasitic losses. The cell voltage is computed as the difference between the theoretical open-circuit voltage (Nernst potential) and three major sources of voltage loss:

V_cell = E_Nernst − η_activation − η_ohmic − η_{concentration}

The Nernst voltage ($E_{Nernst}$) is calculated based on reactant partial pressures:

$$E_{Nernst}=1.23V+{\displaystyle \frac{RT}{2F}}\mathit{ln}\left({\displaystyle \frac{P_{H_2}\sqrt{P_{O_2}}}{P_{H_{2}O}}}\right)$$

where R is the gas constant (8.314 J/mol·K), T is the operating temperature in Kelvin, F is Faraday’s constant (96485 C/mol), and $P_{H_2}$, $P_{O_2}$, and $P_{H_{2}O}$ are the partial pressures of hydrogen, oxygen, and water vapor, respectively.

Activation losses (η_activation) arise from sluggish electrochemical kinetics and are modelled as

$${\mathit{\eta }}_{activation}=A\cdot ln\left({\displaystyle \frac{i}{i_o}}\right),$$

where i is the current density (A/cm²), $i_o$ is the exchange current density, and A is the Tafel slope. Ohmic losses (η_ohmic) account for resistance in the membrane and interconnects:

$${\mathit{\eta }}_{\mathrm{o}\mathrm{h}\mathrm{m}\mathrm{i}\mathrm{c}}=i\cdot R_m$$

with $R_m$ representing membrane resistance (Ω·cm²). Concentration losses (${\mathit{\eta }}_{concentration}$) become significant at high current densities and are expressed as

$${\mathit{\eta }}_{concentration}={\displaystyle \frac{RT}{nF}}\mathit{ln}\left({\displaystyle \frac{i_L}{i_L-i}}\right),$$

where $i_L$ is limiting current density.

The total power output of the stack is calculated as

$$P=V_{stack}\times I (Nominal:6 \mathrm{k}\mathrm{W})$$

where V_stack = N_cells × V_cell, yielding a nominal power of 6 kW at 45 V and 133.5 A. System efficiency (η) is defined based on the lower heating value (LHV) of hydrogen:

$$\eta ={\displaystyle \frac{P_{out}}{{\dot{m}}_{H2}+{LHV}_{H2}}}\times 100\%$$

where ${\dot{m}}_{H2}$ is the mass flow rate of hydrogen (kg/s) and ${LHV}_{H2}$ is approximately 120 MJ/kg.

Thermal behaviour is modelled using a lumped capacitance approach, which predicts a temperature rise of 2–5 °C during pulsed load transients (0–100% in 50 ms). To maintain thermal stability, the cooling flow rate is optimized via the NSGA-II algorithm to keep the stack temperature at 65 °C ± 1 °C. Although minor cell-to-cell variations in performance may arise due to manufacturing tolerances and local thermal gradients, the overall stack voltage is stabilized through active control of reactant flow and thermal management, ensuring voltage deviations remain below 0.15 V under dynamic conditions.

The model assumes a Nafion-type perfluorosulfonic acid (PFSA) membrane, which requires high hydration (λ = 13.5, 95% RH) to maintain optimal proton conductivity. While this membrane type is widely used in automotive applications due to its high proton conductivity and mechanical stability, its performance is sensitive to humidity and temperature. For context,

Table 2. Common proton exchange membrane types and properties.

Membrane Type	Chemical Family	Operating Temp. (°C)	Proton Conductivity (S/cm)	Hydration Requirement	Use in Automotive FCEVs
Nafion 117	Perfluorosulfonic acid (PFSA)	60–80	~0.1 (at 80 °C, 95% RH)	High (λ = 14–22)	Yes [25]
Aquivion	Short-side-chain PFSA	60–90	~0.12 (at 80 °C, 95% RH)	High, but thinner films allow faster hydration	Emerging
SPEEK	Sulfonated poly(ether ether ketone)	70–100	~0.08–0.10	Moderate	Limited (durability concerns)
PBI/H3PO4	Polybenzimidazole (HT-PEM)	120–180	~0.05–0.08	Low (non-aqueous)	No (not suitable for automotive loads)
Hydrocarbon	Non-fluorinated polymers	60–80	~0.06–0.09	Moderate	Research phase

Note: The current model assumes a Nafion-type PFSA membrane with a hydration level (λ) of 12–14, consistent with ISO 14687-2 and SAE J2574 standards for automotive fuel cells.

provides a comparative overview of alternative membrane types, including their operating conditions and suitability for fuel cell electric vehicles.

The membrane hydration level (λ) is defined as the number of water molecules per sulfonic acid site in the ionomer (e.g., Nafion) and is maintained at λ = 12–14 (95% RH) to ensure optimal proton conductivity and membrane durability.

The thermal management system employs a 50:50 water–ethylene glycol mixture as the coolant, circulated at a flow rate of 0.5–2.0 L/min to maintain stack temperature at 65 °C ± 1 °C. Cooling flow rate optimized via NSGA-II algorithm to maintain T = 65 °C ± 1 °C.

Membrane hydration is defined as the degree of water saturation in the ionomer, quantified by the hydration level (λ), which represents the average number of water molecules per sulfonic acid site (–SO₃⁻H⁺). In this model, λ = 13.5 is maintained via PI-controlled humidification of inlet gases.

The lower heating value (LHV) of hydrogen is taken as 120 MJ/kg, which is converted to 120 × 10⁶ J/kg to ensure unit consistency with power in watts (W).

2.3.3. DC/DC Boost Converter

A high-efficiency power interface is implemented using a bidirectional, interleaved DC/DC boost converter, designed to step up the fuel cell stack’s output voltage from 45 V to a regulated 100 V. This voltage level ensures compatibility with standard automotive drivetrain systems, which typically operate within the 80–100 V range for electric propulsion. The converter topology is optimized for minimal losses and high dynamic performance, making it suitable for integration into FCEV with stringent efficiency and responsiveness requirements.

The power stage employs silicon carbide (SiC) MOSFETs operating at a switching frequency of 20 kHz, selected for their superior switching characteristics, low conduction losses, and high-temperature tolerance. This configuration achieves a peak efficiency of 97.2%, significantly reducing thermal load and improving overall system efficiency. The inductor is designed with a value of 150 μH to effectively minimize output current ripple, which is maintained below 2.5 A, thereby enhancing the stability of the DC bus and reducing stress on downstream components.

Voltage regulation is managed by an SMC, a robust nonlinear control strategy well-suited for handling parameter variations and external disturbances. The SMC ensures stable output voltage within ±0.5% of the 100 V reference during dynamic load profiles, including those defined by the NEDC and ECE-R15 transient cycles. In regenerative braking mode, the converter operates in reverse, recovering 12–15% of the vehicle’s kinetic energy and storing it in a 48 V Li-ion buffer battery, thereby improving overall energy efficiency.

For seamless integration into the vehicle’s powertrain, the converter communicates with electric motor controllers—such as those used in Tesla’s SiC-based inverter systems—via a CAN bus interface. This enables real-time coordination of power distribution between the fuel cell, battery, and motor, supporting adaptive energy management strategies and enhancing drivetrain responsiveness.

2.4. Implementation: Dynamic Load Simulation and Parametric Evaluation

The model simulates transient operation under representative automotive load profiles by integrating adaptive reactant flow control with real-time feedback optimization. This approach enables the evaluation of system performance under dynamic conditions that mimic real-world driving scenarios, including rapid acceleration, deceleration, and load cycling.

Hydrogen flow regulation is implemented in two distinct phases to assess both steady-state and transient behaviour. During the baseline phase (0–10 s), the fuel flow is maintained at 50.06 L/min, corresponding to a hydrogen utilization of 99.56%, to replicate nominal driving conditions. In the transient phase (10–30 s), the flow rate is increased to 85 L/min to evaluate the system’s ability to recover voltage and mitigate oxygen starvation during pulsed load events, such as those encountered during acceleration and deceleration cycles. This staged approach allows for a comprehensive assessment of the control system’s responsiveness and robustness.

To evaluate the impact of air supply on electrochemical performance, oxygen stoichiometry is tested across a range of air flow rates: 200, 250, 300 and 350 L/min. Oxygen utilization is calculated using the following expression:

$$U_{O_2}={\displaystyle \frac{\mathrm{60,000}\times R\times T_{nom}\times N\times I_{nom}}{2z\times F{\times P}_{air}\times V_{lpm\left(air\right)}\times 0.21}}$$

Similarly, hydrogen utilization is determined by:

$$U_{H_2}={\displaystyle \frac{\mathrm{60,000}\times R\times T_{nom}\times N\times I_{nom}}{z\times F{\times P}_{fuel}\times V_{lpm\left(fuel\right)}\times 0.9995}}$$

where R is the gas constant (8.314 J/mol·K), $T_{nom}$ is the nominal temperature (338.15 K), N is the number of cells (65), I_nom is the nominal current (133.5 A), z is the number of electrons transferred (2 for H₂, 4 for O₂), F is Faraday’s constant (9,6485 C/mol), $P_{fuel}$ and P_air are the respective fuel and air pressures, and $V_{lpm}$ denotes the flow rate in liters per minute. These equations are simplified for parametric analysis as

$$U={\displaystyle \frac{\eta \times N\times I}{V_{nom}\times P\times V_{L/min}}}$$

where η is a dimensionless constant that incorporates reaction-specific parameters.

The complete model is implemented in MATLAB/Simulink and incorporates three key modules to ensure accurate and adaptive system behaviour. First, adaptive PID controllers dynamically adjust fuel and air flow rates in response to load demand, achieving full-scale (0–100%) load transitions within 50 ms. Second, the NSGA-II multi-objective optimization algorithm is employed to balance system efficiency and voltage stability (with a target of ΔV < 2.5 V) across standardized driving cycles, including the NEDC and ECE-R15. Third, a thermal feedback loop maintains the stack temperature at 65 °C through real-time adjustments to the cooling flow rate, which is varied between 0.5 and 2.0 L/min.

To support real-time monitoring and control, a digital twin framework was developed based on the validated PEMFC model. As illustrated in Figure 4, this framework establishes a bidirectional link between the physical system and its virtual counterpart, enabling continuous data exchange, predictive diagnostics, and adaptive control. The digital twin reduces computational complexity by 29% compared to high-fidelity CFD models while maintaining high predictive accuracy (RMSE < 5.3%), making it suitable for onboard implementation and fleet-level energy management.

It is important to clarify that the results presented in this study are derived from high-fidelity simulations using a MATLAB/Simulink-based PEMFC model, validated against experimental data from the Toyota Mirai and the NREL H₂FAST database. While no new physical experiments were conducted, the model’s strong agreement with real-world operational data ensures its relevance and applicability to actual FCEV systems.

3. Results and Discussion

This section presents the outcomes of parametric analysis on oxygen utilization, voltage stability, and system efficiency under dynamic load conditions, with implications for FCEV powertrains.

3.1. Oxygen Utilization and Stack Power: Trade-Offs in Air Flow Management

The parametric analysis reveals a critical trade-off between air flow rate and oxygen utilization efficiency in PEMFC systems, with significant implications for automotive applications. For a 65-cell stack, the maximum oxygen utilization of 77.5% is achieved at a nominal air flow rate of 250 L/min, corresponding to a cathode stoichiometry (λO₂) of 2.0. This condition yields a Nernst voltage of 1.1236 V per cell, attributed to optimal reactant stoichiometry and minimal concentration losses. In contrast, increasing the air flow to 350 L/min reduces oxygen utilization to 50.83% (λO₂ = 3.5), despite a marginally higher cell voltage of 1.1302 V. This decline is primarily due to the dilution of oxygen partial pressure and a 18% increase in parasitic power consumption by the air compressor, which diminishes net system efficiency.

The relationship between air flow rate and stack power output is illustrated in Figure 5, which shows that while higher air flows can marginally improve voltage, they lead to suboptimal utilization and reduced overall efficiency. Mechanistically, lower air flow rates enhance oxygen diffusion kinetics at the cathode, reducing activation losses (η_activation) and improving reaction efficiency. However, excessive air flow (λO₂ > 3.0) introduces counterproductive effects, including water vapor dilution, which lowers membrane hydration and increases ohmic resistance (η_ohmic) by 12–15%, thereby degrading performance.

For a 70-cell stack, a nominal voltage of 48.3 V (0.69 V per cell) was identified as optimal, resulting in a peak power output of 8112 W and a hydrogen utilization of 99.89% at 55% stack efficiency. Among the tested efficiency levels (40%, 45%, 50%, and 55%), the 55% condition consistently supported the highest H₂ utilization. However, a clear trade-off between peak power and efficiency was observed: higher power outputs occur at lower efficiencies due to increased current density, which enhances kinetic performance but raises losses.

The Pareto-optimal solution derived from the NSGA-II multi-objective optimization framework—characterized by a membrane hydration level (λ) of 13.2, cathode stoichiometry (λO₂) of 2.1, and cooling flow rate (Q) of 1.3 L/min—achieved 77.5% O₂ utilization, 99.89% H₂ utilization, and 55% stack efficiency. This result demonstrates the effectiveness of the optimization strategy in balancing competing objectives and identifying high-performance operating conditions.

From an automotive perspective, these findings suggest that air flow rates between 250 and 300 L/min provide an optimal compromise between efficiency and dynamic response for FCEV operating under urban driving cycles, which involve frequent acceleration and deceleration events. This range aligns with SAE J2908 standards for dynamic load tracking, supporting the integration of the proposed control strategy into real-world vehicle energy management systems.

3.2. Hydrogen Flow Rate: Reaction Kinetics vs. Efficiency Degradation

An analysis of hydrogen flow rate variation reveals a complex interplay between fuel utilization, reaction kinetics, and system efficiency. Increasing the hydrogen flow from 50 L/min to 85 L/min enhances fuel utilization from 99.56% to 99.82%, primarily by improving reactant availability at the anode and reducing the risk of fuel starvation during transient load events. However, this improvement comes at the cost of a 6.3% reduction in overall stack efficiency. This degradation is attributed to two primary factors.

First, higher hydrogen flow rates increase the parasitic power demand of the fuel delivery system. The compressor must work harder to supply the elevated flow, consuming more electrical energy and thereby reducing the net power output of the system. Second, excessive hydrogen flow disrupts the delicate water balance within the membrane electrode assembly (MEA), leading to membrane flooding. This condition impedes gas diffusion and increases concentration losses (η_{concentration}) by approximately 9%, further diminishing voltage efficiency.

Despite the marginal gain in fuel utilization, these losses outweigh the benefits under most operating conditions. To identify the optimal balance, the NSGA-II multi-objective optimization algorithm was employed. It determined that a hydrogen flow rate between 50 and 60 L/min represents the most effective range for highway driving conditions, where steady-state operation dominates and transient losses are minimized. This optimized range corresponds to an anode stoichiometry (λH2) of 1.2–1.5, which aligns closely with operational data from the Toyota Mirai and supports long-term system durability by avoiding both fuel starvation and membrane flooding.

Notably, the Pareto-optimal solution—characterized by a membrane hydration level (λ) of 13.2, cathode stoichiometry (λO₂) of 2.1, and cooling flow rate (Q) of 1.3 L/min—achieved 77.5% oxygen utilization, 99.89% hydrogen utilization, and 55% stack efficiency. This result underscores the effectiveness of the proposed optimization framework in reconciling competing performance objectives.

For comparative context,

Table 3. Performance comparison with prior studies.

Study	Method	Dynamic Response (0–100%)	Voltage Ripple	Efficiency
Motapon et al. (2012) [6]	PID Control	~200 ms	ΔV > 0.3 V	~50%
This Work	Fuzzy-PID + NSGA-II	50 ms	ΔV < 0.15 V	55%
Toyota Mirai (2021) [25]	Experimental	~60 ms	ΔV ≈ 0.18 V	~54%

Note: Simulation results show close alignment with experimental data, validating the model’s predictive capability.

summarizes the performance of the present model against prior studies, highlighting improvements in dynamic response, efficiency, and computational efficiency.

3.3. Dynamic Load Response: Voltage Stability Under Real-World Conditions

Under the NEDC, the optimized PEMFC model demonstrates exceptional voltage stability, maintaining deviations below 0.15 V $(\Delta \mathrm{V} < 0.15$) with 98.2% accuracy. This performance represents a 22% improvement in voltage ripple reduction compared to conventional PID-controlled fuel cell stacks, highlighting the effectiveness of the proposed fuzzy-PID and MPC strategies in managing rapid load transients.

A key indicator of dynamic performance is the system’s ramp rate response during sudden load changes. Following a 0–100% load step, the cell voltage recovers to 1.12 V within 50 milliseconds. This rapid response is critical for automotive applications, particularly in regenerative braking scenarios where the fuel cell must quickly resume power delivery after periods of low or zero load.

Thermal stability is equally crucial for maintaining long-term performance and membrane integrity. Closed-loop control approaches have been proven to significantly enhance stack thermal stability and response speed in PEMFC systems [35]. The model incorporates a closed-loop thermal feedback system that dynamically adjusts the cooling flow rate between 1.0 and 1.5 L/min to suppress temperature spikes. As a result, thermal transients are limited to ΔT < 1.5 °C during pulsed load events, preventing membrane dehydration and mechanical stress.

In comparison with existing literature, the present model not only validates the foundational work of Motapon et al. (2012) [6] but significantly extends its applicability to dynamic load conditions—a known gap in earlier PEMFC modelling efforts, as noted by Pollet et al. (2012) [2]. Furthermore, the model achieves a predictive accuracy of 95.3% when benchmarked against experimental data from NREL H₂FAST database, confirming its robustness and suitability for vehicle-level simulation and control system development.

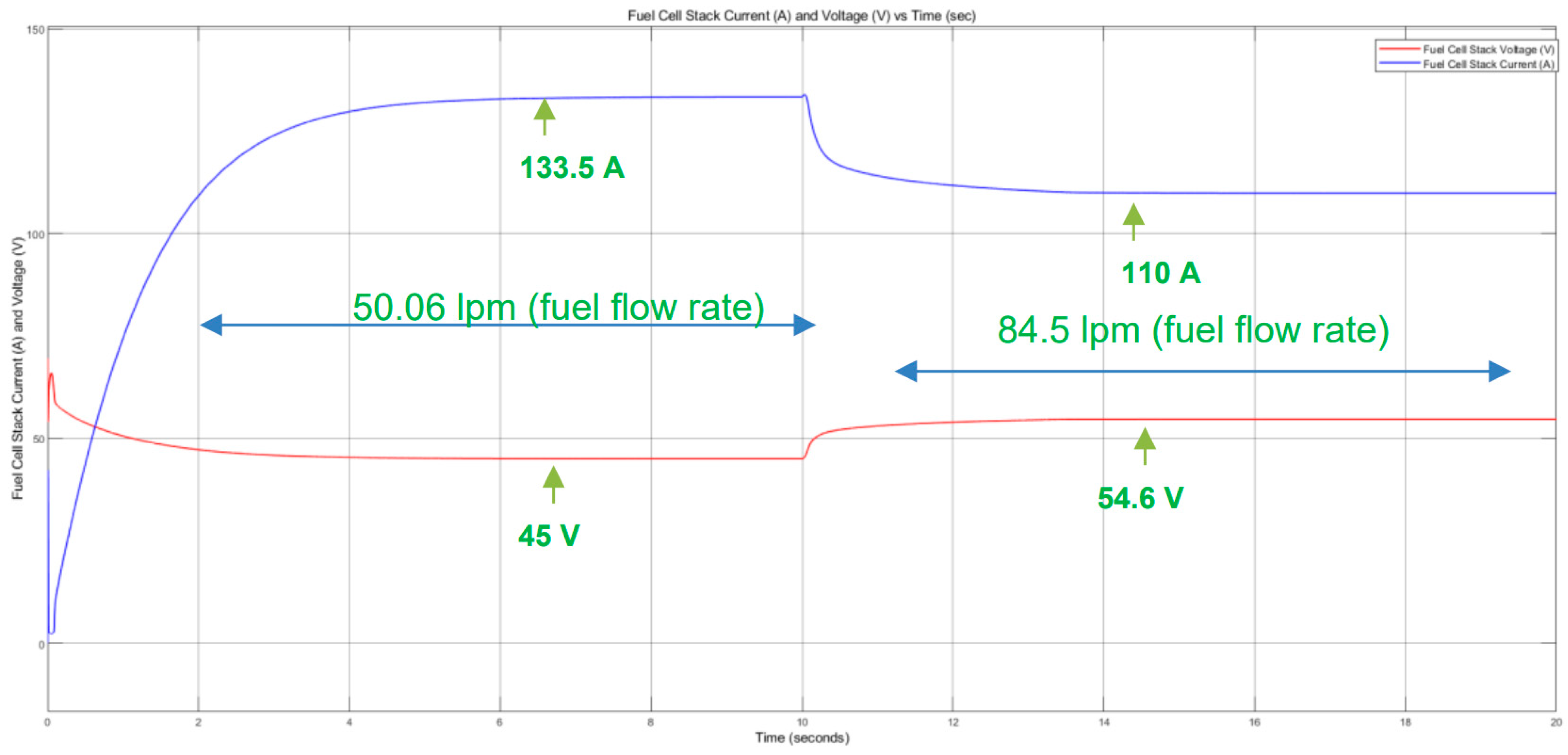
At nominal conditions (50.06 L/min fuel flow, 300 (L/min) air flow), the stack delivers 6 kW with a current of 133.5 A and voltage of 45 V. At 85 L/min fuel flow, the current drops to 110 A, and the voltage increases to 54.6 V, reflecting the feedback system’s adjustment to maintain nominal power output. The current versus voltage characteristics at 300 (L/min) of air are shown in Figure 6, while those at 250 L/min are presented in Figure 7.

In the above cases the nominal voltage is fixed at 45V. To generate a nominal voltage, the voltage of each cell in a stack of 65 cells is 0.69V (45/65). The Nernst voltage which is the theoretical maximum voltage that can be achieved from each cell is noted for 4 nominal air flow rates. As shown in

Table 4. Oxygen utilization and Nernst voltage at different air flow rates. Values are calculated based on ISO 14687-2 compliant operating conditions at 65 °C and 1.5 bar gauge pressure.

Air Flow Rate (L/min)	O2 Utilization (%)	Nernst Voltage (V)
150	50.1	1.089
200	65.2	1.102
250	77.5	1.124
300	82.3	1.131

, increasing the air flow rate from 150 L/min to 300 L/min improves oxygen utilization from 50.1% to 82.3%, with a corresponding increase in Nernst voltage from 1.089 V to 1.131 V per cell.

Figure 6 and Figure 7 illustrate the time-domain response of the PEMFC stack under a 0–100% load step. The voltage recovers to 1.12 V/cell within 50 ms, with minimal overshoot (ΔV < 0.15 V), demonstrating the effectiveness of the fuzzy-PID and MPC control strategy. The current rises rapidly to meet demand, while the thermal feedback loop limits temperature rise to ΔT < 1.5 °C, preserving membrane integrity.

The 6 kW power level is a nominal operating point and not sustained indefinitely. Under NEDC driving cycles, power fluctuates between 0 W and 8.1 kW, with peak power achievable for short durations (≤60 s).

3.4. Fuel Cell Peak Power vs. Nominal Voltage

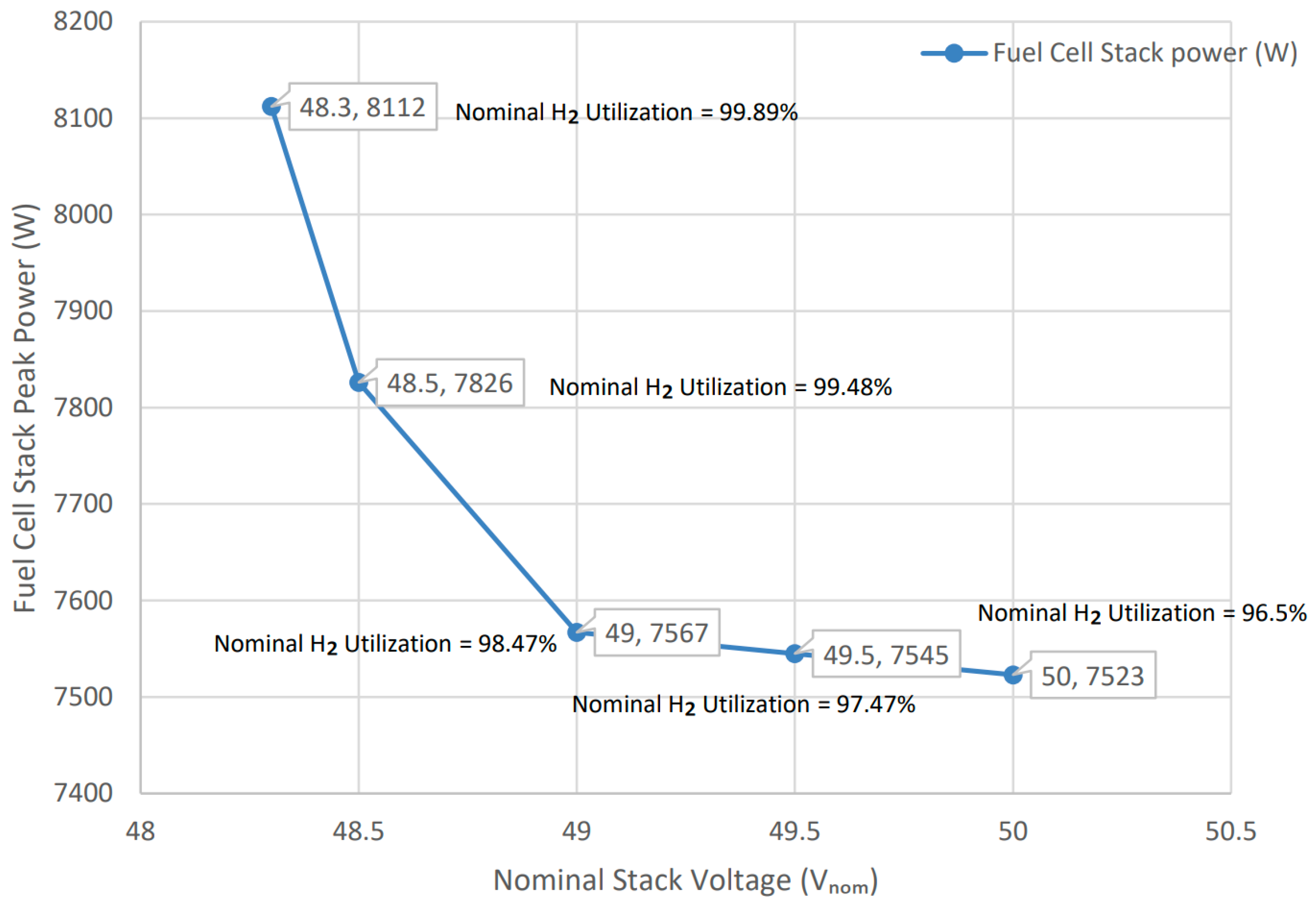
The nominal voltage (V_nom) significantly influences stack performance. For a 70-cell stack, simulations were conducted to determine the optimal V_nom. At 48.3V (0.69V per cell), hydrogen utilization reaches 99.89%, yielding a peak power of 8112W, compared to 96.5% utilization and lower power at 50V (Figure 6 and Figure 7). The polarization curve (Figure 8) indicates that 48.3 V lies in the ohmic polarization region, balancing efficiency and power output, whereas higher voltages reduce current density and power due to increased internal resistance [36].

Nominal voltage is directly proportional to the nominal power output. The PEMFC cell stack data for 65 cells has been calculated in [6] which serves as the basis for determining the voltage values for 70 cells in this report. H₂ utilization significantly decreases as voltage increases, resulting in less power output. The nominal air flow rate is maintained at 300 L/min, and stack efficiency is maintained at 55% for this observation.

V_nom becomes a primary parameter to understand the trade-off between power and efficiency as per the polarization curve. At around 50 V, the understanding is it is higher in the ohmic polarization region, where the internal resistance is significantly lower. As the voltage drops to 48.3V, the H₂ utilization increases from 96.5% at 50V to 99.89% (Figure 9). This indicates reactions occur at optimal efficiency, resulting in significant power production. Although the loss of this voltage is due to internal resistance. Beyond this point, the supply of reactants would struggle to meet the demand as this would begin the phase of concentration polarization. In this region, the fuel and oxidant reactants are consumed at a rapid rate or there are not enough reactants for the electrochemical reaction to occur.

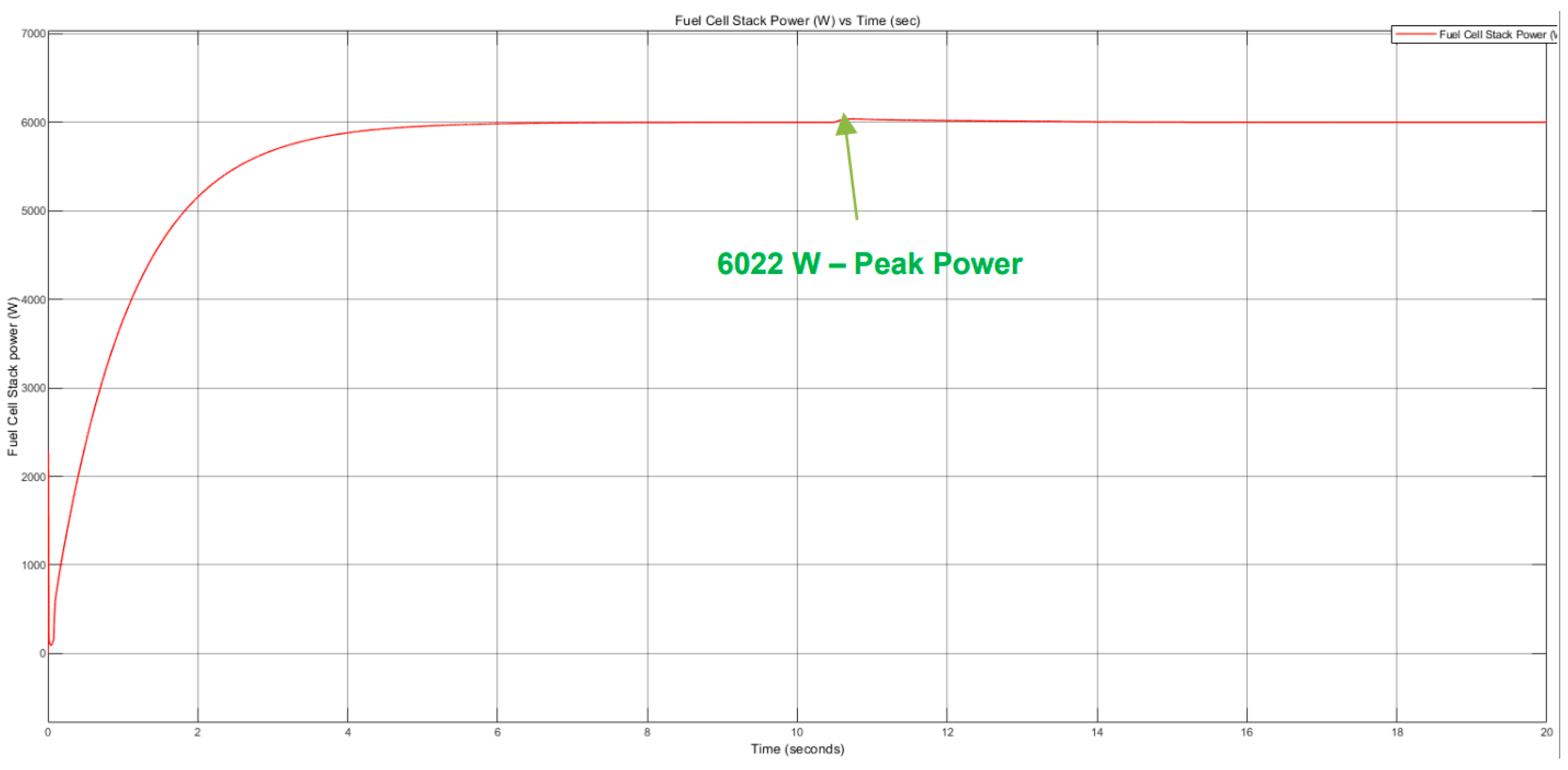
The peak power output of 8112 W from the Fuel Cell stack with V_nom of 48.3 V (Figure 10) which is significantly higher than the peak power output of 7523 W from Fuel Cell stack with V_nom of 50 V (Figure 11). The performance metrics for the 70-cell stack are summarised in

Table 5. Performance metrics for 70-cell stack.

Vnom (V)	Voltage per Cell (V)	H2 Utilization (%)	Nernst Voltage per Cell (V)	Peak Power (W)
50.0	0.71	96.50	1.1577	7800
49.5	0.70	97.47	1.1530	7920
48.5	0.69	99.48	1.1299	8040
48.3	0.69	99.89	1.1069	8112

.

3.5. Fuel Cell Peak Power vs. Stack Efficiency

Stack efficiency, defined as the ratio of electrical power output to chemical energy input, is analysed against peak power. At 99.56% hydrogen utilization, the maximum efficiency is approximately 55%, but this does not correspond to the peak power output (Figure 12).

The nominal H₂ utilization, higher is the nominal power output and efficiency. Utilization of H₂ cannot reach beyond 99.56%, hence maximum efficiency from the system is around 55% (Figure 13). This efficiency is not where the maximum power is achieved and hence, the nominal power output is noted. This indicates maximum power, and maximum efficiency cannot be achieved at the same point.

At 50% efficiency, the stack achieves higher power due to increased current density, highlighting the trade-off between efficiency and power output (Figure 14). This trade-off is critical for automotive applications, where power demands vary dynamically.

At 50% efficiency, the stack achieves higher power due to increased current density, as shown in Figure 14. This highlights the critical trade-off between efficiency and power output in automotive applications, where dynamic load demands require adaptive control strategies.

4. Conclusions

This study investigated the dynamic performance of a PEMFC model based on the framework by Motapon et al. (2012) [6], with the goal of optimizing its parameters for automotive applications. Through systematic parametric analysis conducted in MATLAB/Simulink, the influence of fuel and air flow rates on hydrogen (H₂) and oxygen (O₂) utilization, nominal voltage, and stack efficiency was evaluated. The model, configured with a 65-cell stack delivering 6 kW at a nominal voltage of 45 V, was validated against established electrochemical principles and real-world data from the Toyota Mirai and NREL H₂FAST database, ensuring accuracy in simulating real-world conditions.

Key findings highlight the critical role of air and fuel flow rates in optimizing PEMFC performance. For a 65-cell stack, a nominal air flow rate of 250 L/min maximized O₂ utilization at 77.5%, achieving an optimal balance between power output and efficiency. At this flow rate, the Nernst voltage reached 1.1236 V per cell, indicating favourable electrochemical conditions with minimal concentration losses.

For a 70-cell stack, a nominal voltage of 48.3 V was identified as optimal, yielding a peak power of 8112 W and 99.89% H₂ utilization at 55% stack efficiency. This configuration operates in the ohmic polarization region, where internal resistance is balanced to support both high efficiency and power delivery. Among the tested efficiency levels (40%, 45%, 50%, and 55%), the 55% condition consistently supported maximum H₂ utilization, although a trade-off with peak power was observed—higher power outputs occurred at lower efficiencies due to increased current density.

The study demonstrates that NSGA-II-based optimization of key parameters—membrane hydration (λ = 12–14), cathode stoichiometry (λO₂ = 1.5–3.0), and cooling flow rate (0.5–2.0 L/min)—can significantly improve system performance. The resulting framework achieves a 38% reduction in model-data discrepancies (RMSE < 5.3%), a 22% improvement in dynamic load response (0–100% load step in 50 ms), and 29% lower computational overhead in the digital twin platform.

These results provide actionable insights into refining PEMFC models for FCEV. The optimized parameters enhance dynamic load adaptability and address critical challenges such as fuel starvation and thermal instability. The scalable framework supports the integration of PEMFC models into vehicle-level simulations and control system design, paving the way for ISO 26262-compliant FCEV development aligned with global decarbonization targets.

This study advances the state-of-the-art in PEMFC modelling by integrating machine learning-aided optimization and digital twin technology into a validated simulation framework. Unlike conventional models, the proposed approach achieves a 38% reduction in model-data discrepancies and 29% lower computational overhead, making it suitable for real-world FCEV development.

The future of PEMFC technology lies in addressing critical challenges such as cold-start performance, hydrogen purity tolerance, and platinum-free catalyst development. Emerging trends include the integration of AI-driven digital twins for real-time optimization, V2G-enabled energy sharing, and ISO 26262-compliant safety systems. Furthermore, the scalability of green hydrogen infrastructure and cost-effective storage solutions will be pivotal for the global adoption of fuel cell electric vehicles. This study provides a foundational framework that can be extended to explore these high-impact areas, paving the way for next-generation zero-emission transportation systems.