Research on a Two-Stage Human-like Trajectory-Planning Method Based on a DAC-MCLA Network
Abstract
1. Introduction
- A number of field equipment manipulators was invited to control the vehicle and collect manipulation data. The data were screened based on the similarity of transverse displacement and the degree of curvature vatiation to construct a dataset representing human manipulation behaviors.
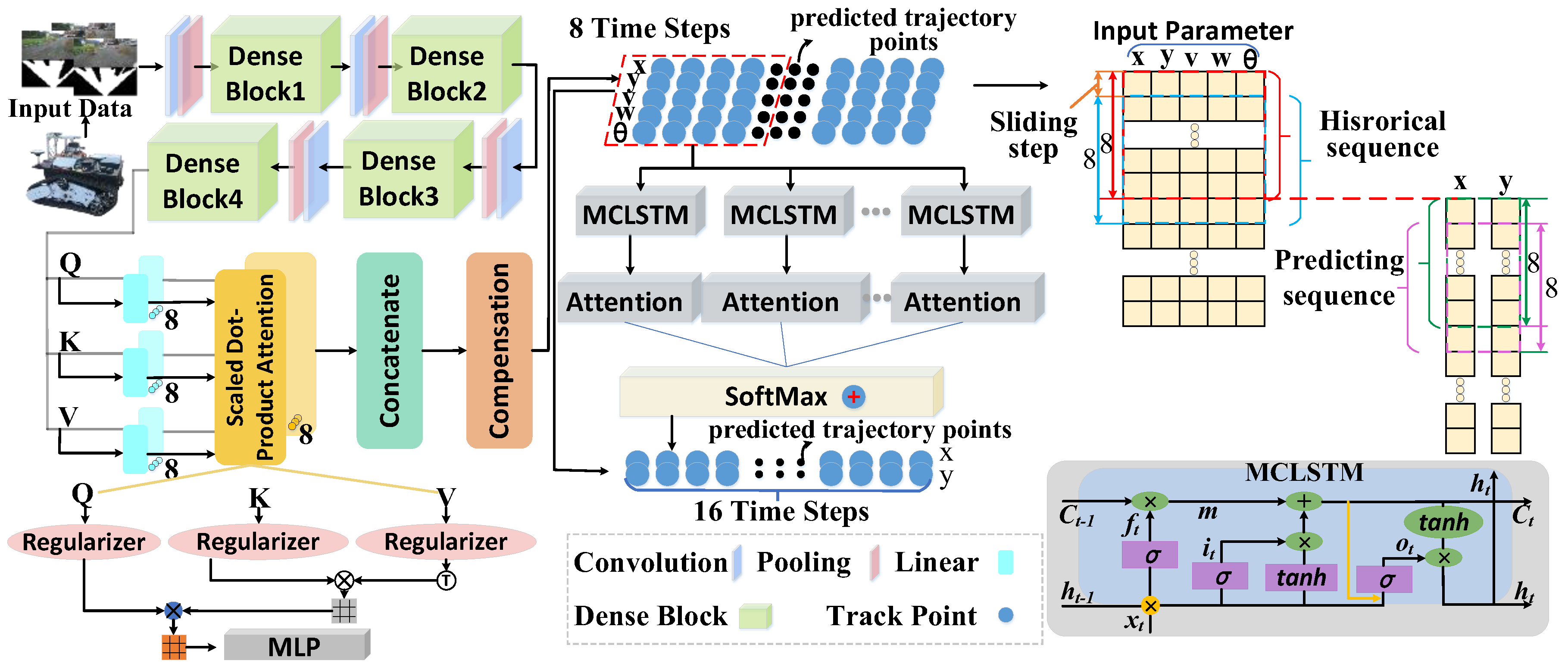
- A two-stage trajectory-planning framework is proposed. In the first stage, the DAC network predicts trajectory points (x, y, v, w, and θ) over the next eight time steps. In the second stage, the MCLA network refines the x and y trajectory points by leveraging the temporal correlations in the first-stage outputs, generating a 16-step trajectory sequence.
- A sliding multi-step prediction strategy is applied to generate long-horizon trajectory points, and vehicle dynamic parameters are incorporated as constraints to improve prediction accuracy.
2. Related Works
3. Methods
3.1. Overview of the Proposed Framework
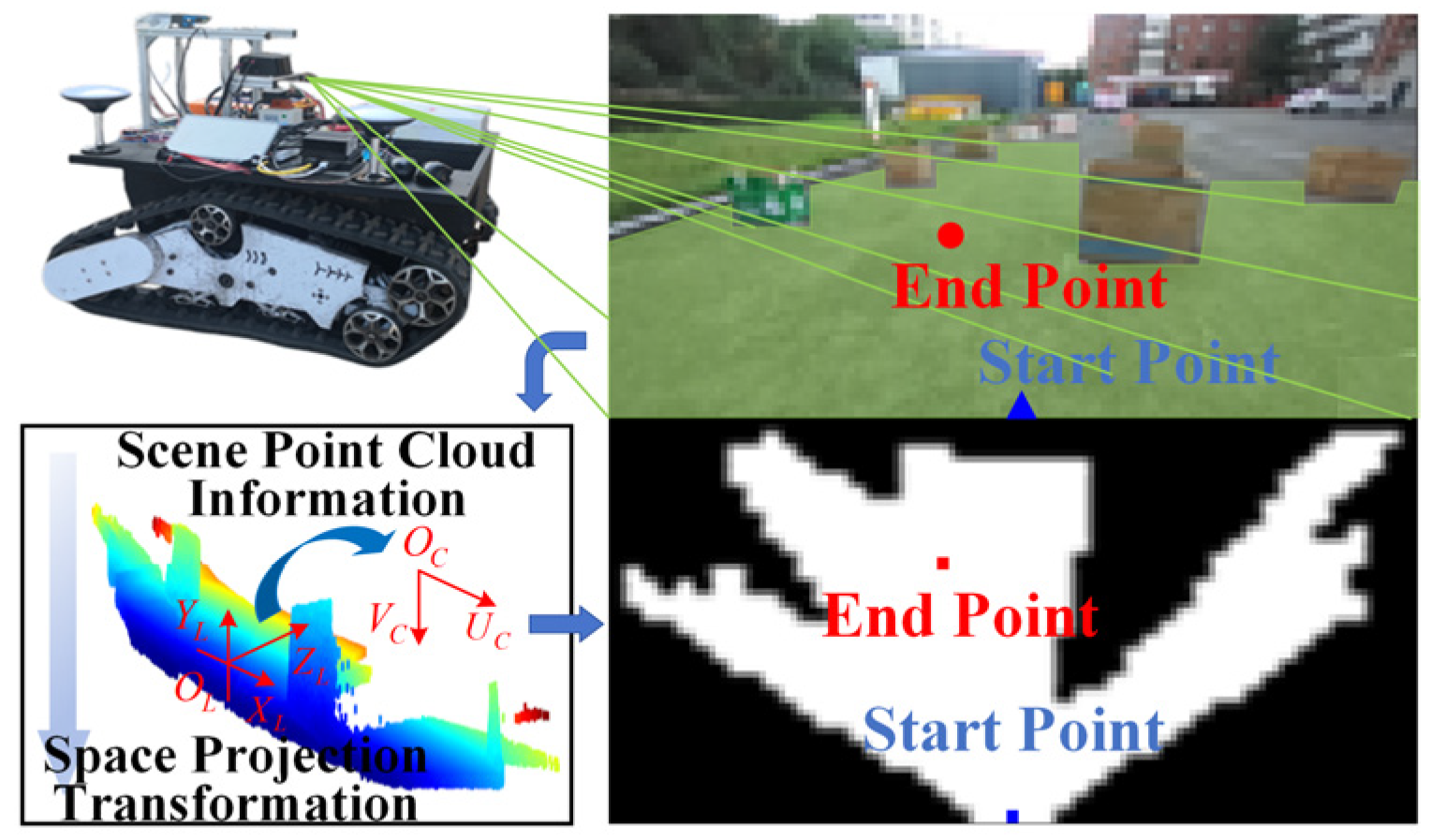
3.2. Human Manipulation Dataset Processing
- (1)
- Human manipulation trajectory analysis
- (2)
- Driving space scene processing and analysis
3.3. Design of Network Structure for Two-Stage Trajectory Planning
3.4. Model Training and Evaluation
4. Experimentation and Analysis
4.1. Ablation Experiment
4.2. Comparison Experiment
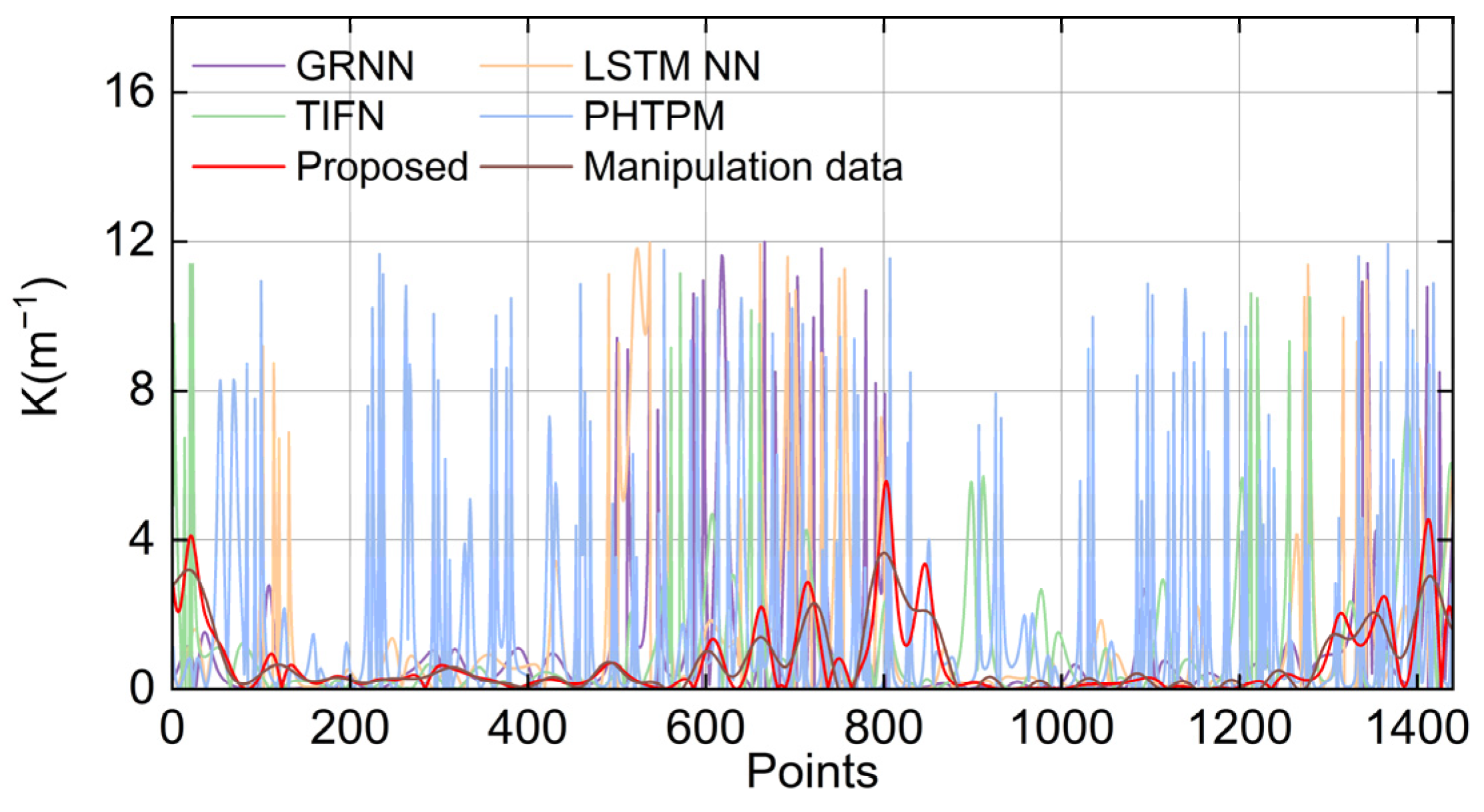
4.3. Evaluation of Trajectory Smoothness
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jo, K.; Kim, J.; Kim, D.; Jang, C. Development of autonomous car—Part I: Distributed system architecture and development process. IEEE Trans. Ind. Electron. 2014, 61, 7131–7140. [Google Scholar] [CrossRef]
- Sadat, A.; Ren, M.; Pokrovsky, A.; Lin, Y.-C. Jointly learnable behavior and trajectory planning for self-driving vehicles. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; IEEE: New York, NY, USA, 2019; pp. 3949–3956. [Google Scholar]
- Huang, Z.; Mo, X.; Lv, C. Multi-modal motion prediction with transformer-based neural network for autonomous driving. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; IEEE: New York, NY, USA, 2022; pp. 2605–2611. [Google Scholar]
- Xu, D.; Ding, Z.; He, X.; Zhao, H.; Moze, M.; Aioun, F.; Guillemard, F. Learning from naturalistic driving data for human-like autonomous highway driving. IEEE Trans. Intell. Transp. Syst. 2020, 22, 7341–7354. [Google Scholar] [CrossRef]
- Chen, S.; Chen, Y.; Zhang, S.; Zheng, N.-N. A novel integrated simulation and testing platform for self-driving cars with hardware in the loop. IEEE Trans. Intell. Veh. 2019, 4, 425–436. [Google Scholar] [CrossRef]
- Li, Y.; Wei, W.; Gao, Y.; Wang, D.; Fan, Z. PQ-RRT*: An improved path planning algorithm for mobile robots. Expert Syst. Appl. 2020, 152, 113425. [Google Scholar] [CrossRef]
- Tang, J.; Wang, Y.; Hao, W.; Liu, F.; Huang, H.; Wang, Y. A Mixed Path Size Logit-Based Taxi Customer-Search Model Considering Spatio-Temporal Factors in Route Choice. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1347–1358. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, R.; Jian, Z.; Zhan, W.; Zheng, N.; Tomizuka, M. Clothoid-Based Reference Path Reconstruction for HD Map Generation. IEEE Trans. Intell. Transp. Syst. 2023, 25, 587–601. [Google Scholar] [CrossRef]
- Noh, S. Decision-making framework for autonomous driving at road intersections: Safeguarding against collision, overly conservative behavior, and violation vehicles. IEEE Trans. Ind. Electron. 2018, 66, 3275–3286. [Google Scholar] [CrossRef]
- Schwarting, W.; Alonso-Mora, J.; Rus, D. Planning and decision-making for autonomous vehicles. Annu. Rev. Control. Robot. Auton. Syst. 2018, 1, 187–210. [Google Scholar] [CrossRef]
- Yang, W.; Zheng, L.; Li, Y.; Ren, Y.; Xiong, Z. Automated highway driving decision considering driver characteristics. IEEE Trans. Intell. Transp. Syst. 2019, 21, 2350–2359. [Google Scholar] [CrossRef]
- Xu, X.; Zuo, L.; Li, X.; Qian, L.; Ren, J.; Sun, Z. A Reinforcement Learning Approach to Autonomous Decision Making of Intelligent Vehicles on Highways. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3884–3897. [Google Scholar] [CrossRef]
- Hoel, C.-J.; Driggs-Campbell, K.; Wolff, K.; Laine, L.; Kochenderfer, M.J. Combining Planning and Deep Reinforcement Learning in Tactical Decision Making for Autonomous Driving. IEEE Trans. Intell. Veh. 2020, 5, 294–305. [Google Scholar] [CrossRef]
- Bansal, M.; Krizhevsky, A.; Ogale, A. ChauffeurNet: Learning to drive by imitating the best and synthesizing the worst. In Proceedings of the Robotics: Science and Systems 2019, Freiburg im Breisgau, Germany, 22–26 June 2019; pp. 1–10. [Google Scholar]
- Chitta, K.; Prakash, A.; Geiger, A. Neat: Neural attention fields for end-to-end autonomous driving. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 15793–15803. [Google Scholar]
- Zhu, Z.; Zhao, H. A Survey of Deep RL and IL for Autonomous Driving Policy Learning. IEEE Trans. Intell. Transp. Syst. 2022, 23, 14043–14065. [Google Scholar] [CrossRef]
- Kiran, B.R.; Sobh, I.; Talpaert, V.; Mannion, P.; Al Sallab, A.A.; Yogamani, S.; Perez, P. Deep Reinforcement Learning for Autonomous Driving: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4909–4926. [Google Scholar] [CrossRef]
- Wu, J.; Huang, Z.; Lv, C. Uncertainty-Aware Model-Based Reinforcement Learning: Methodology and Application in Autonomous Driving. IEEE Trans. Intell. Veh. 2023, 8, 194–203. [Google Scholar] [CrossRef]
- Wu, J.; Huang, Z.; Hu, Z.; Lv, C. Toward human-in-the-loop AI: Enhancing deep reinforcement learning via real-time human guidance for autonomous driving. Engineering 2023, 21, 75–91. [Google Scholar] [CrossRef]
- Wu, J.; Huang, Z.; Huang, W.; Lv, C. Prioritized experience-based reinforcement learning with human guidance for autonomous driving. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 855–869. [Google Scholar] [CrossRef] [PubMed]
- Rosbach, S.; James, V.; Großjohann, S.; Homoceanu, S.; Roth, S. Driving with Style: Inverse Reinforcement Learning in General-Purpose Planning for Automated Driving. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 2658–2665. [Google Scholar]
- Nakamura, Y.; Yamane, K.; Fujita, Y.; Suzuki, I. Somatosensory computation for man-machine interface from motion-capture data and musculoskeletal human model. IEEE Trans. Robot. 2005, 21, 58–66. [Google Scholar] [CrossRef]
- Wang, W.; Li, R.; Diekel, Z.M.; Chen, Y.; Zhang, Z.; Jia, Y. Controlling Object Hand-Over in Human–Robot Collaboration Via Natural Wearable Sensing. IEEE Trans. Hum.-Mach. Syst. 2019, 49, 59–71. [Google Scholar] [CrossRef]
- Rodriguez, M.; Orrite, C.; Medrano, C.; Makris, D. One-Shot Learning of Human Activity With an MAP Adapted GMM and Simplex-HMM. IEEE Trans. Cybern. 2017, 47, 1769–1780. [Google Scholar] [CrossRef]
- Ijspeert, A.J.; Nakanishi, J.; Hoffmann, H.; Pastor, P.; Schaal, S. Dynamical movement primitives: Learning attractor models for motor behaviors. Neural Comput. 2013, 25, 328–373. [Google Scholar] [CrossRef]
- Zhao, J.; Song, D.; Zhu, B.; Sun, Z.; Han, J.; Sun, Y. A Human-Like Trajectory Planning Method on a Curve Based on the Driver Preview Mechanism. IEEE Trans. Intell. Transp. Syst. 2023, 24, 11682–11698. [Google Scholar] [CrossRef]
- Li, G.; Yang, L.; Li, S.; Luo, X.; Qu, X.; Green, P. Human-like decision making of artificial drivers in intelligent transportation systems: An end-to-end driving behavior prediction approach. IEEE Intell. Transp. Syst. Mag. 2022, 14, 188–205. [Google Scholar] [CrossRef]
- Behera, A.; Wharton, Z.; Keidel, A.; Debnath, B. Deep CNN, Body Pose, and Body-Object Interaction Features for Drivers’ Activity Monitoring. IEEE Trans. Intell. Transp. Syst. 2022, 23, 2874–2881. [Google Scholar] [CrossRef]
- Santhosh, K.K.; Dogra, D.P.; Roy, P.P.; Mitra, A. Vehicular Trajectory Classification and Traffic Anomaly Detection in Videos Using a Hybrid CNN-VAE Architecture. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11891–11902. [Google Scholar] [CrossRef]
- Bahwini, T.; Zhong, Y.; Gu, C. Path planning in the presence of soft tissue deformation. Int. J. Interact. Des. Manuf. (IJIDeM) 2019, 13, 1603–1616. [Google Scholar] [CrossRef]
- Zhong, Y.; Shirinzadeh, B.; Yuan, X. Optimal robot path planning with cellular neural network. In Advanced Engineering and Computational Methodologies for Intelligent Mechatronics and Robotics; IGI Global: Hershey, PA, USA, 2013; pp. 19–38. [Google Scholar]
- Hills, J.; Zhong, Y. Cellular neural network-based thermal modelling for real-time robotic path planning. Int. J. Agil. Syst. Manag. 2014, 20, 261–281. [Google Scholar] [CrossRef]
- Zhou, Q.; Gao, S.; Qu, B.; Gao, X.; Zhong, Y. Crossover recombination-based global-best brain storm optimization algorithm for uav path planning. Proc. Rom. Acad. Ser. A-Math. Phys. Tech. Sci. Inf. Sci. 2022, 23, 207–216. [Google Scholar]
- You, F.; Zhang, R.; Lie, G.; Wang, H.; Wen, H.; Xu, J. Trajectory planning and tracking control for autonomous lane change maneuver based on the cooperative vehicle infrastructure system. Expert Syst. Appl. 2015, 42, 5932–5946. [Google Scholar] [CrossRef]
- Dubey, P.K.; Singh, B.; Kumar, V.; Singh, D. A Novel Approach for Comparative Analysis of Distributed Generations and Electric Vehicles in Distribution Systems. Electr. Eng. 2022, 106, 2371–2390. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, H.; Khajepour, A.; Ding, H.; Yuan, K.; Qin, Y. A Novel Local Motion Planning Framework for Autonomous Vehicles Based on Resistance Network and Model Predictive Control. IEEE Trans. Veh. Technol. 2020, 69, 55–66. [Google Scholar] [CrossRef]
- Ferguson, D.; Howard, T.M.; Likhachev, M. Motion planning in urban environments. J. Field Robot. 2008, 25, 939–960. [Google Scholar] [CrossRef]
- Wei, J.; Snider, J.M.; Gu, T.; Dolan, J.M.; Litkouhi, B. A behavioral planning framework for autonomous driving. In Proceedings of the IEEE Symposium on Intelligent Vehicle, Cluj, Romania, 2–5 June 2024; pp. 458–464. [Google Scholar]
- Li, A.; Jiang, H.; Li, Z.; Zhou, J.; Zhou, X. Human-like trajectory planning on curved road: Learning from human drivers. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3388–3397. [Google Scholar] [CrossRef]
- Li, A.; Jiang, H.; Zhou, J.; Zhou, X. Learning human-like trajectory planning on urban two-lane curved roads from experienced drivers. IEEE Access 2019, 7, 65828–65838. [Google Scholar] [CrossRef]
- Guo, C.; Liu, H.; Chen, J.; Ma, H. Temporal Information Fusion Network for Driving Behavior Prediction. IEEE Trans. Intell. Transp. Syst. 2023, 24, 9415–9424. [Google Scholar] [CrossRef]
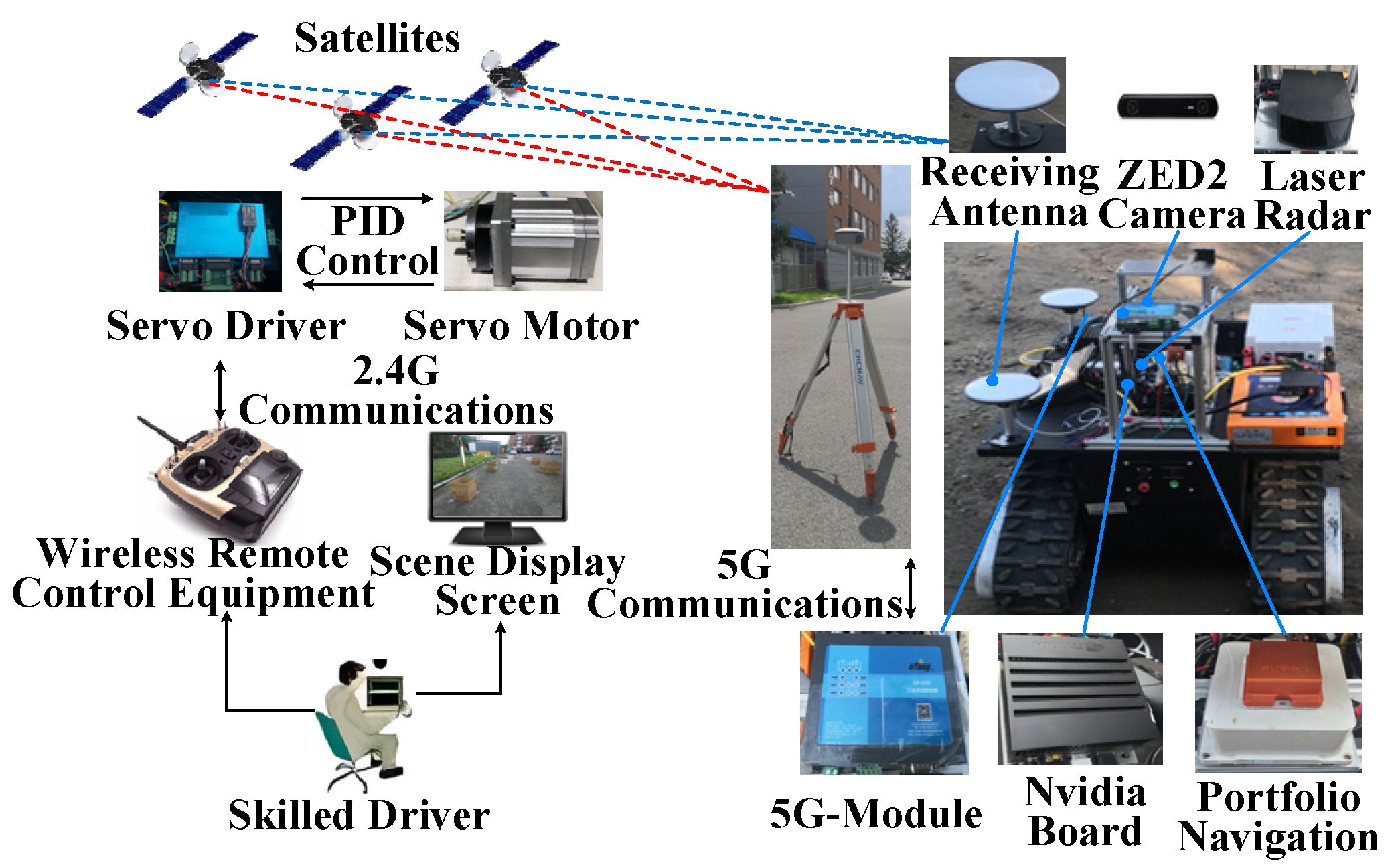
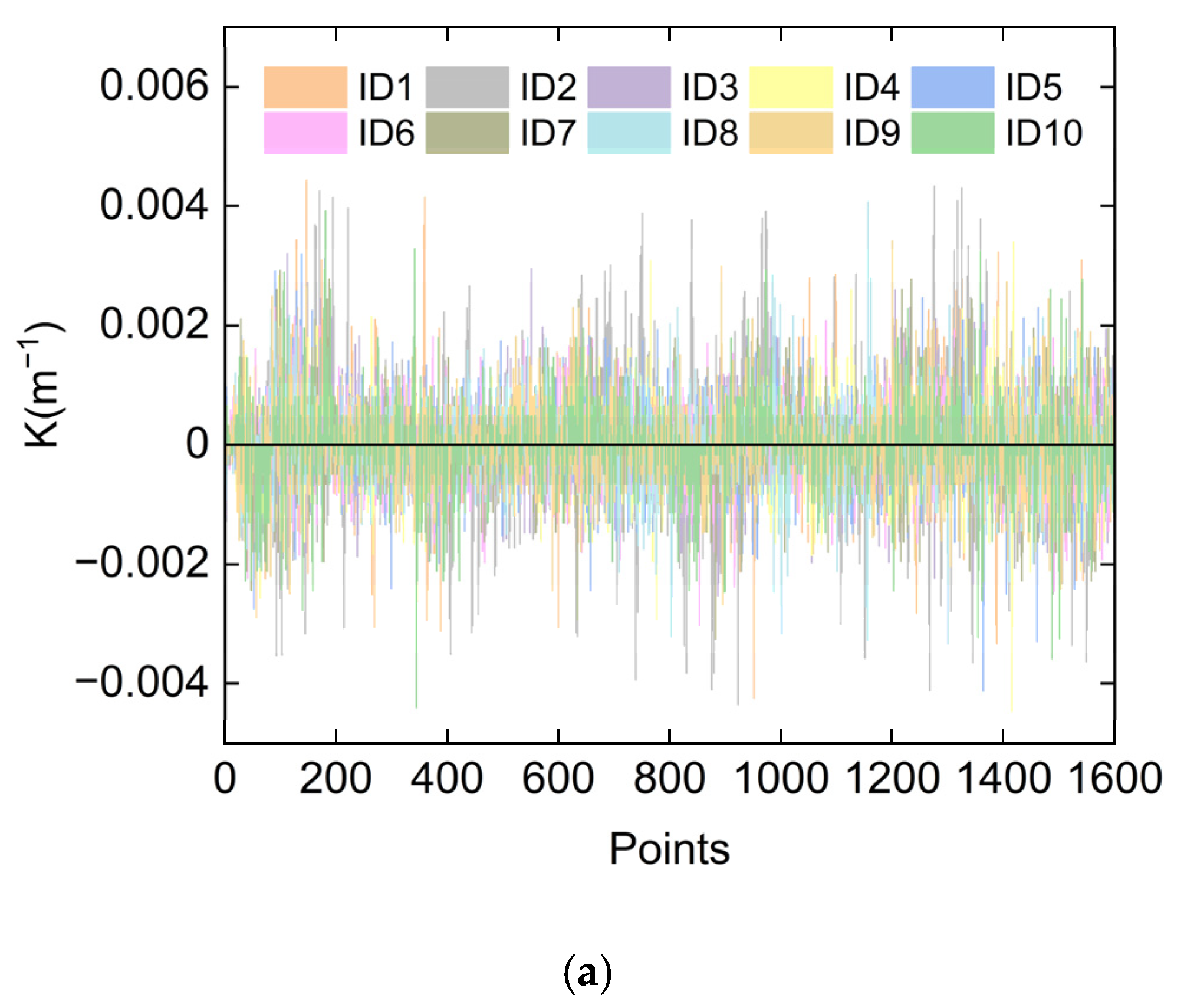
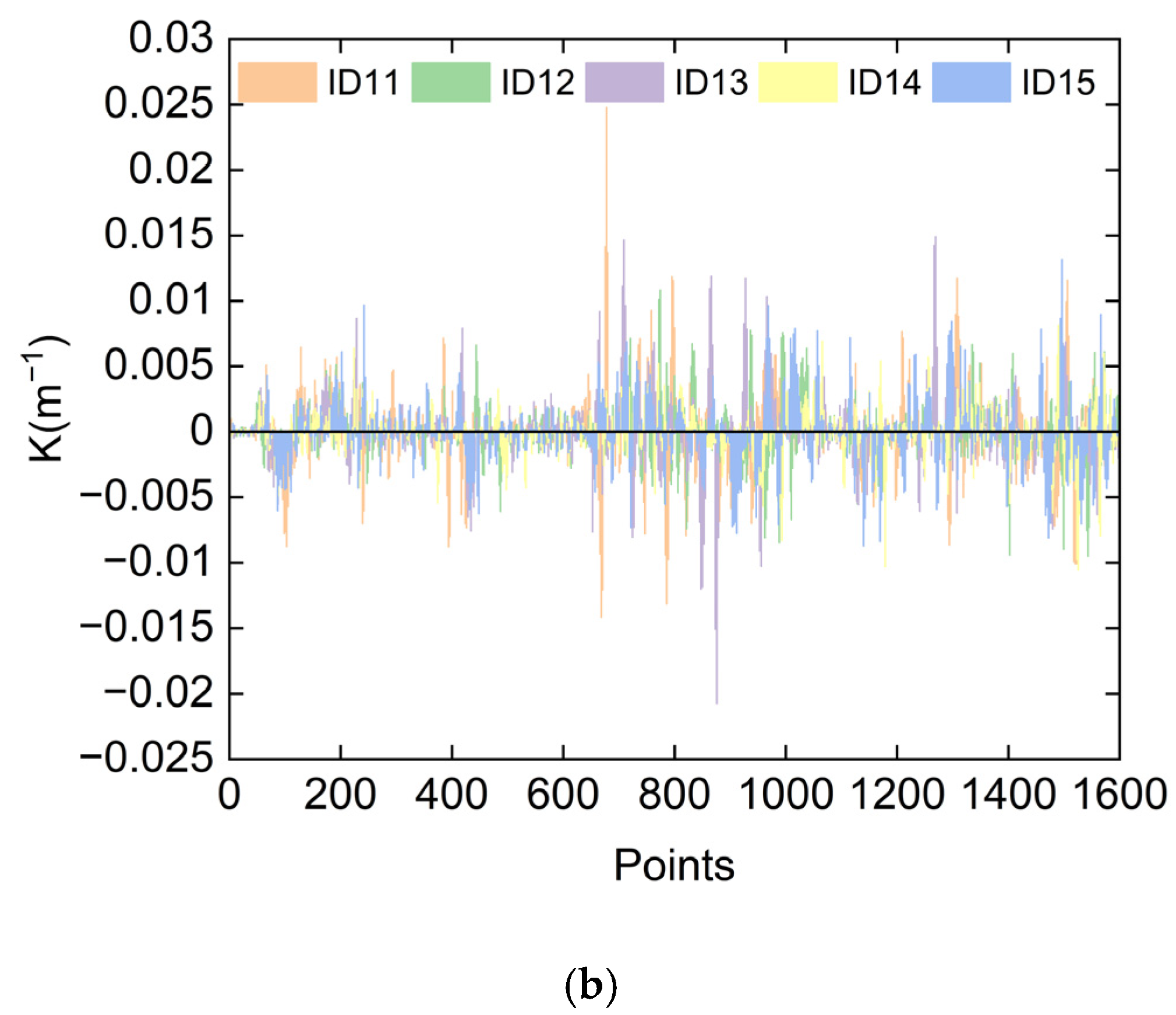
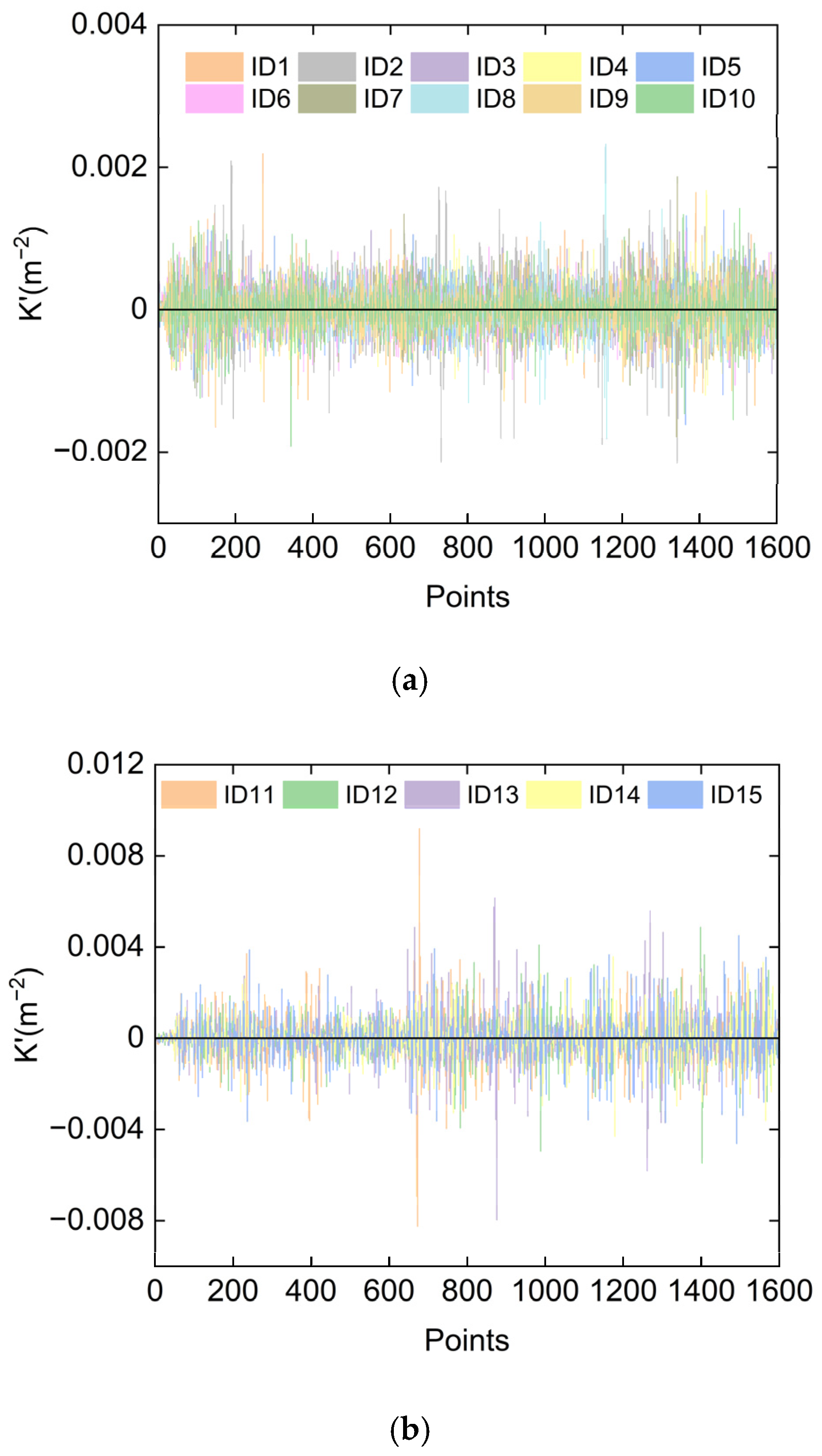
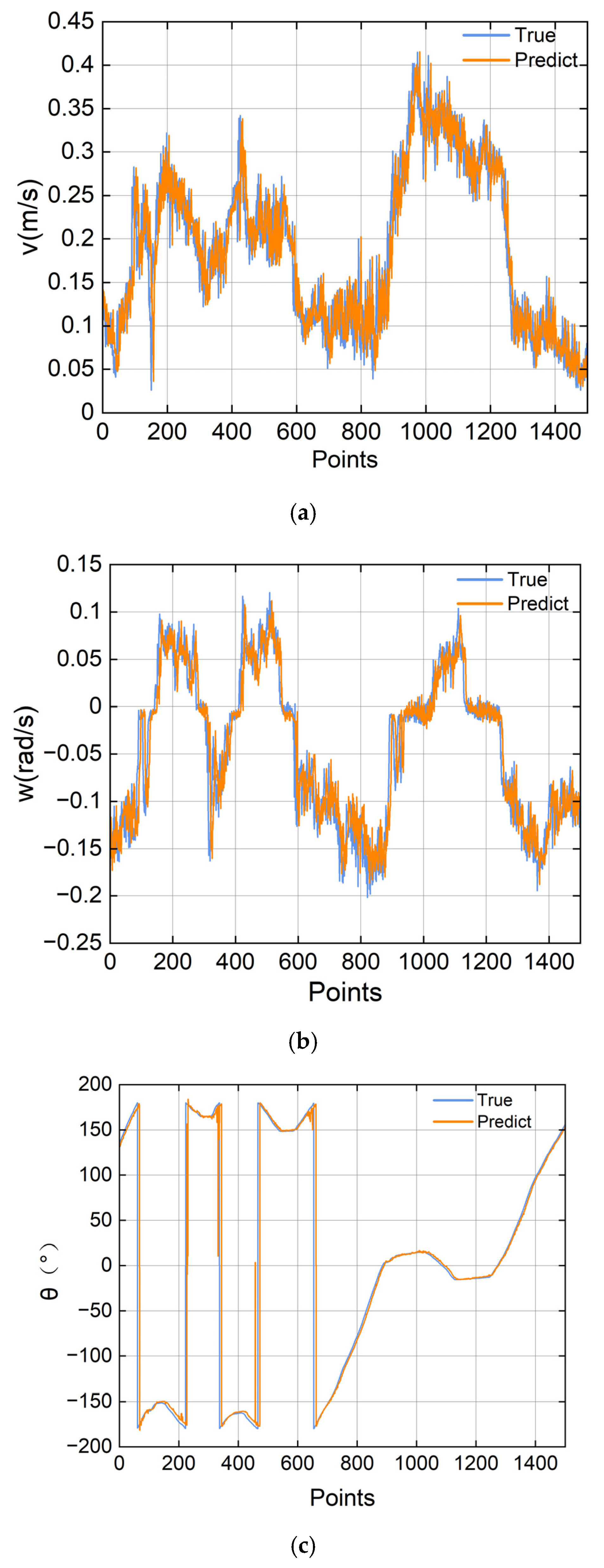
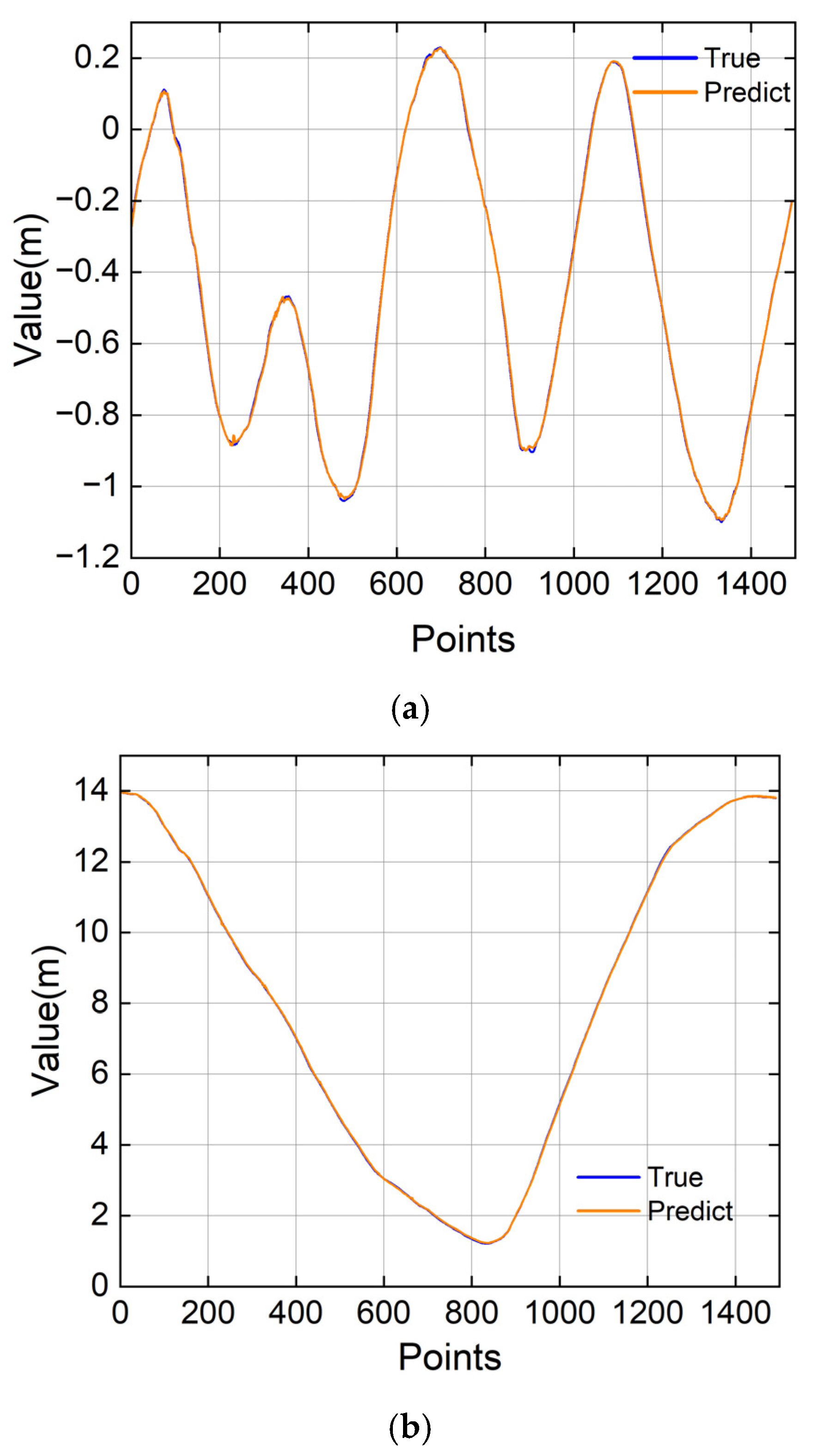
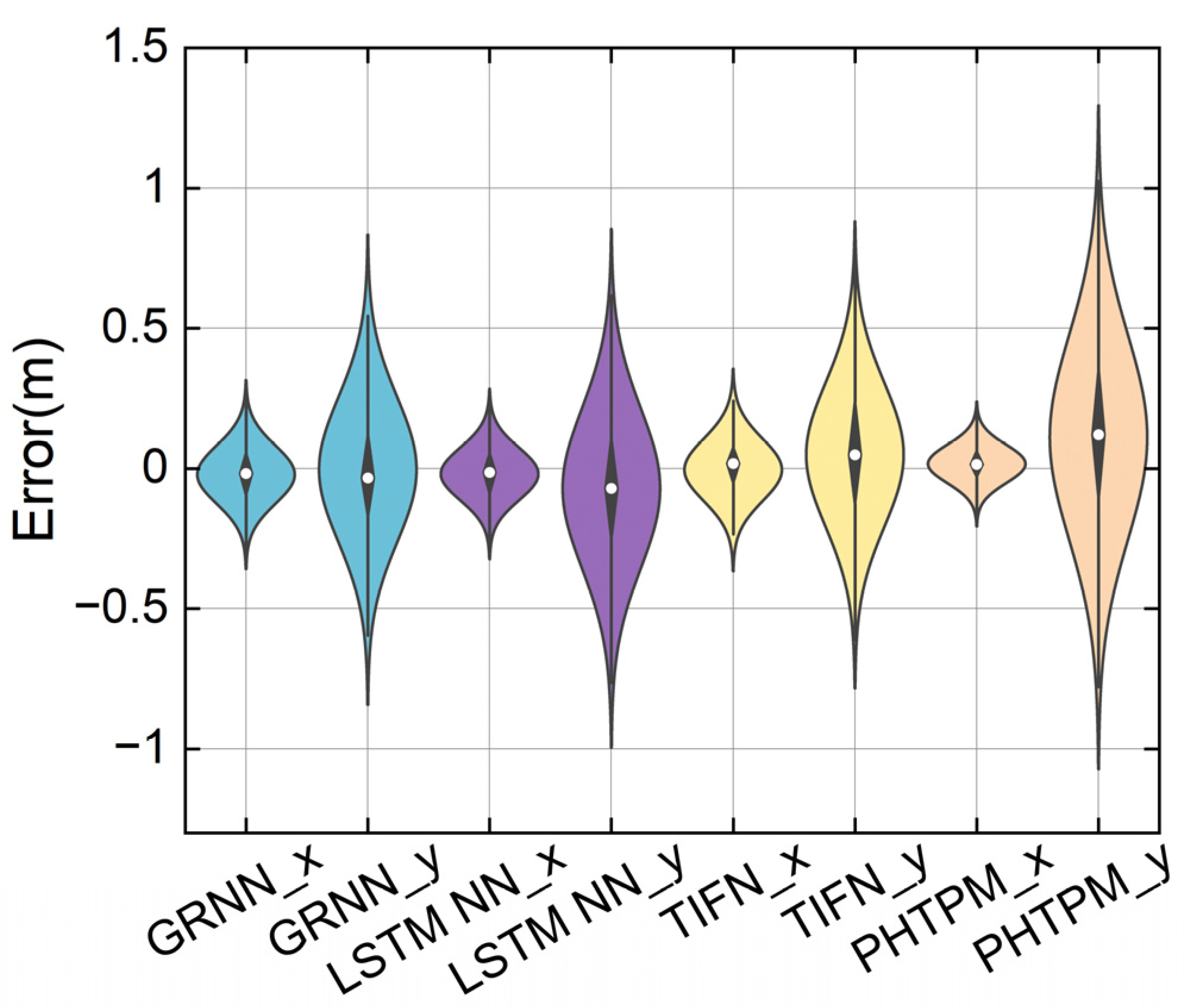
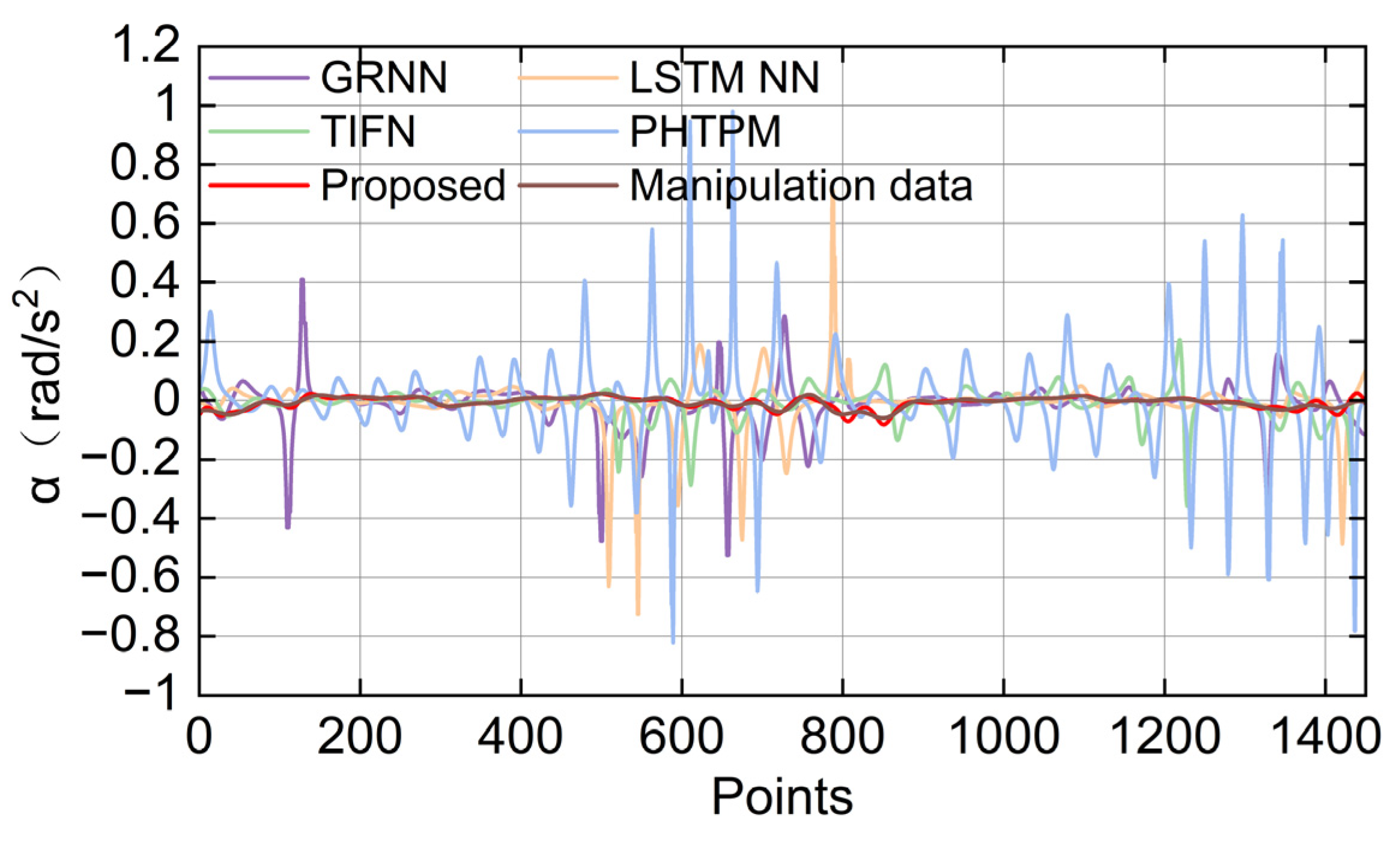
| Skilled Tester | ID2 | ID3 | ID4 | ID5 | ID6 | ID7 | ID8 | ID9 | ID10 |
| Similarity | 0.941 | 0.95 | 0.966 | 0.971 | 0.969 | 0.957 | 0.954 | 0.973 | 0.977 |
| Unskilled tester | ID11 | ID12 | ID13 | ID14 | ID15 | / | / | / | / |
| Similarity | 0.821 | 0.873 | 0.815 | 0.852 | 0.796 | / | / | / | / |
| Hyperparameter | Candidate Values | Value |
|---|---|---|
| Initial learning rate | [0.001, 0.005, 0.01, 0.02] | 0.01 |
| Learning rate drop out period | [50, 100, 150, 200] | 100 |
| Learning rate drop out factor | [0.1, 0.2, 0.5, 0.8] | 0.1 |
| Batch size | [200, 300, 400, 500] | 300 |
| Epoch number | [300, 500, 800, 1000] | 500 |
| numLayers of lstm | [1, 2, 3, 4] | 2 |
| numHiddenUnits | [128, 160, 196, 256] | 196 |
| dropoutLayer | [0.1, 0.2, 0.3, 0.5] | 0.1 |
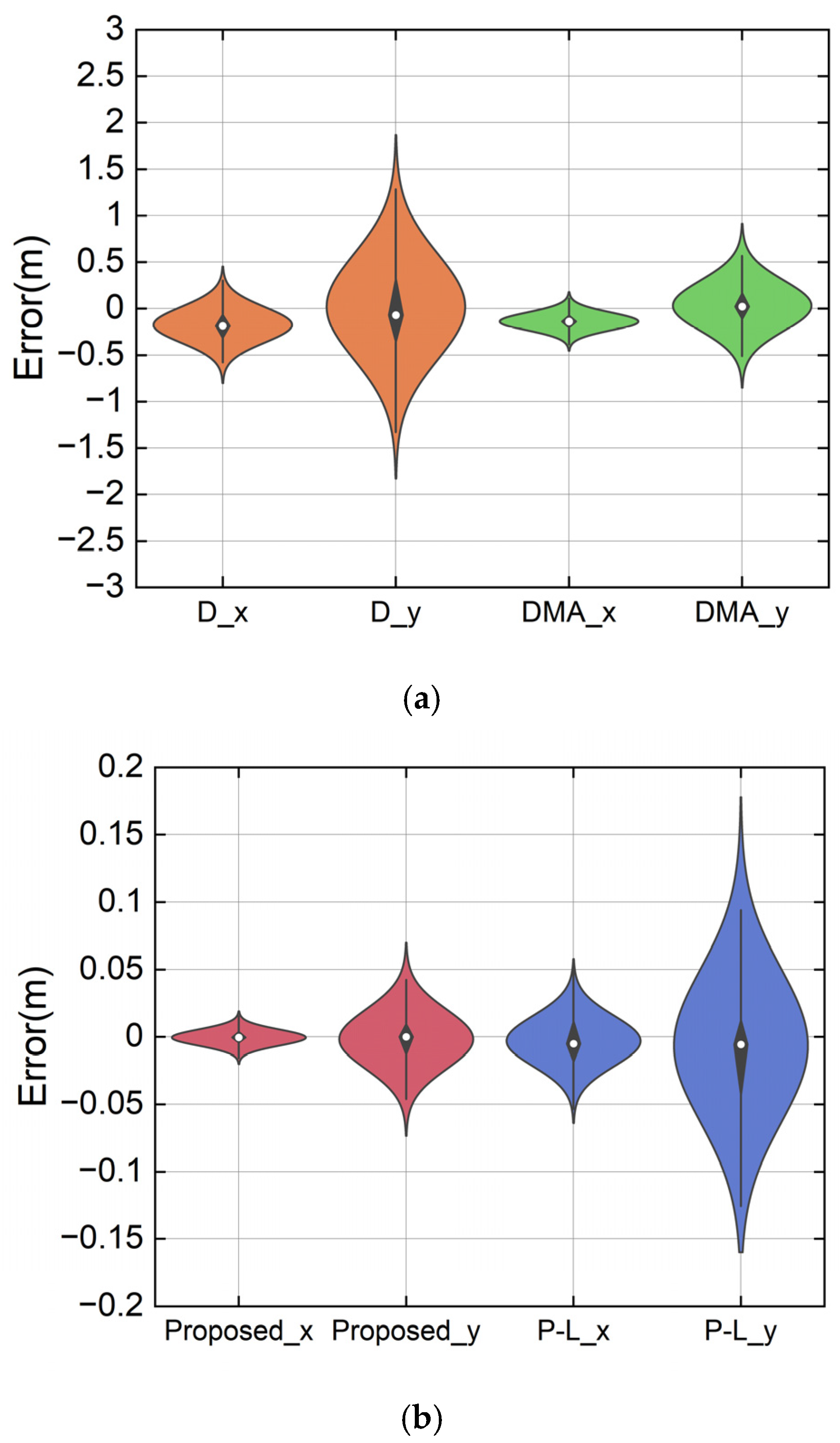
| RMSE (Proposed) | RMSE (P-L) | RMSE (D) | RMSE (DMA) | RMSE (GRNN) | RMSE (LSTM NN) | RMSE (TIFN) | RMSE (PHTPM) | |
|---|---|---|---|---|---|---|---|---|
| x | 0.006 | 0.019 | 0.259 | 0.168 | 0.105 | 0.095 | 0.11 | 0.070 |
| y | 0.022 | 0.057 | 0.568 | 0.272 | 0.257 | 0.293 | 0.259 | 0.381 |
| MAE (Proposed) | MAE (P-L) | MAE (D) | MAE (DMA) | MAE (GRNN) | MAE (LSTM NN) | MAE (TIFN) | MAE (PHTPM) | |
|---|---|---|---|---|---|---|---|---|
| x | 0.005 | 0.016 | 0.22 | 0.143 | 0.083 | 0.077 | 0.084 | 0.054 |
| y | 0.016 | 0.041 | 0.425 | 0.19 | 0.193 | 0.228 | 0.209 | 0.301 |
| Time (s) | 0.214 | 0.197 | 0.109 | 0.159 | 0.065 | 0.085 | 0.149 | 0.091 |
| SD (Proposed) | SD (GRNN) | SD (LSTM NN) | SD (TIFN) | SD (PHTPM) | SD (Manipulation Data) | |
|---|---|---|---|---|---|---|
| α (rad/s2) | 0.1248 | 0.4497 | 0.4823 | 0.296 | 0.901 | 1.116 |
| K (m−1) | 0.76 | 1.59 | 1.66 | 1.46 | 2.17 | 0.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Zhang, G.; Zhao, H. Research on a Two-Stage Human-like Trajectory-Planning Method Based on a DAC-MCLA Network. Vehicles 2025, 7, 63. https://doi.org/10.3390/vehicles7030063
Xu H, Zhang G, Zhao H. Research on a Two-Stage Human-like Trajectory-Planning Method Based on a DAC-MCLA Network. Vehicles. 2025; 7(3):63. https://doi.org/10.3390/vehicles7030063
Chicago/Turabian StyleXu, Hao, Guanyu Zhang, and Huanyu Zhao. 2025. "Research on a Two-Stage Human-like Trajectory-Planning Method Based on a DAC-MCLA Network" Vehicles 7, no. 3: 63. https://doi.org/10.3390/vehicles7030063
APA StyleXu, H., Zhang, G., & Zhao, H. (2025). Research on a Two-Stage Human-like Trajectory-Planning Method Based on a DAC-MCLA Network. Vehicles, 7(3), 63. https://doi.org/10.3390/vehicles7030063






