NeuHH: A Neuromorphic-Inspired Hyper-Heuristic Framework for Solving the Capacitated Single-Allocation p-Hub Location Routing Problem

Abstract

This paper introduces a novel neuromorphic-inspired hyper-heuristic framework (NeuHH) for solving the Capacitated Single-Allocation p-Hub Location Routing Problem (CSAp-HLRP), a challenging combinatorial optimization problem that jointly addresses hub location decisions, capacity constraints, and vehicle routing. The proposed framework employs Spiking Neural Networks (SNNs) as the decision-making core, leveraging their temporal dynamics and spike-timing-dependent plasticity (STDP) to guide the real-time selection and adaptation of low-level heuristics. Unlike conventional learning-based hyper-heuristics, NeuHH provides biologically plausible, event-driven learning with improved scalability and interpretability. Experimental results on benchmark instances demonstrate that NeuHH outperforms classical metaheuristics, Lagrangian relaxation methods, and reinforcement learning-based hyper-heuristics. Specifically, NeuHH achieves superior performance in total cost minimization (up to 13.6% reduction), load balance improvement (achieving a load balance factor of as low as 1.04), and heuristic adaptability (reflected by higher heuristic switching frequency). These results highlight the framework’s potential for real-time and energy-efficient logistics optimization in large-scale dynamic networks.

1. Introduction

The growing complexity of logistics and transportation systems has intensified the demand for intelligent decision-making frameworks capable of addressing large-scale, multi-level combinatorial optimization problems [1]. One such problem is the Capacitated Single-Allocation p-Hub Location Routing Problem (CSAp-HLRP), which jointly considers hub location planning, customer allocation under capacity constraints, and routing optimization. CSAp-HLRP is particularly relevant in strategic supply chain design, telecommunications, and airline logistics, where both cost efficiency and service quality are paramount [2,3].

Traditional approaches to solving CSAp-HLRP, such as Lagrangian relaxation or exact mathematical models, often suffer from scalability issues when applied to real-world, dynamic networks [4,5]. To overcome these limitations, researchers have turned to hyper-heuristic methods that aim to automate the selection and generation of heuristics to solve hard optimization problems more effectively [6]. Hyper-heuristics abstract the problem-solving process by managing a pool of low-level heuristics (LLHs), enabling generalizable and adaptive optimization strategies across problem instances and domains.

Despite their success, existing hyper-heuristic frameworks typically rely on metaheuristic or machine learning controllers, such as reinforcement learning or genetic programming, which can be computationally expensive and often lack interpretability [7,8]. Moreover, most of these frameworks do not natively support real-time or low-energy applications, limiting their deployment in decentralized logistics environments and edge computing systems.

In this paper, we propose NeuHH, a neuromorphic-inspired hyper-heuristic framework based on Spiking Neural Networks (SNNs). Inspired by the temporal dynamics of the human brain, SNNs offer event-driven computation, sparse activation, and biological plausibility, making them ideal for adaptive heuristic selection in real-time settings. By leveraging spike-timing-dependent plasticity (STDP) and reward-modulated learning, NeuHH dynamically selects appropriate low-level heuristics based on the temporal encoding of problem states.

Despite substantial progress in solving CSAp-HLRP through exact and heuristic methods, limitations remain in scalability, adaptability, and energy efficiency. Recent advances in hyper-heuristics and AI-driven optimization have shown promise, yet many existing frameworks rely on complex, opaque learning mechanisms or static control logic. Moreover, the integration of biologically inspired models into this context remains largely unexplored. To address these gaps, this paper proposes NeuHH, a neuromorphic-inspired hyper-heuristic controller that leverages SNNs for adaptive, interpretable, and energy-efficient heuristic selection. To the best of our knowledge, this is the first application of spiking neural control in the domain of hub location and routing problems. NeuHH represents a novel contribution at the intersection of operational research, artificial intelligence, and neuromorphic computation.

To demonstrate its efficacy, NeuHH is applied to benchmark instances of CSAp-HLRP and compared against classical hyper-heuristics, Lagrangian-based methods, and recent learning-based models. Our contributions are three-fold.

• We introduce a novel biologically inspired framework that combines neuromorphic computing with heuristic optimization.
• We design a real-time heuristic selection mechanism using SNNs, capable of generalizing across diverse problem instances.
• We evaluate NeuHH on CSAp-HLRP, demonstrating superior performance in cost minimization, load balancing, and adaptability.

The remainder of this paper is organized as follows: Section 2 provides a comprehensive literature review. Section 3 details the problem formulation and study objectives. Section 4 outlines the proposed NeuHH framework. Section 5 and Section 6 describe the experimental setup, and the results and discussion respectively. Section 7 concludes the study and highlights future research directions.

2. Literature Review

CSAp-HLRP constitutes a challenging hybrid combinatorial optimization problem that unifies two interconnected decision layers: the strategic selection and placement of hub facilities and the operational design of vehicle routing plans to service demand nodes through these hubs. In this model, each non-hub node (spoke) is restricted to be assigned to exactly one hub (single allocation), and each hub has a limited processing or service capacity (capacity constraints), making the problem significantly more complex than its uncapacitated or multiple-assignment counterparts.

CSAp-HLRP captures key dynamics encountered in integrated logistics systems, where the efficient consolidation of flows via a small number of strategically located hubs must be balanced against the cost and feasibility of last-mile distribution. This problem structure is highly relevant to modern transportation and telecommunication systems, including parcel delivery networks, supply chains with regional consolidation centers, health commodity distribution, and broadband or satellite signal aggregation systems [9,10].

What distinguishes CSAp-HLRP from classical hub location problems is the explicit incorporation of intra-hub vehicle routing—where routes must be planned from each hub to serve its assigned customers, subject to vehicle and route-level constraints. This routing component aligns the problem closely with capacitated vehicle routing problems (CVRPs), creating a tightly coupled structure that demands simultaneous optimization of both hub allocations and routing decisions.

Given its dual-level complexity and real-world applicability, CSAp-HLRP has attracted increasing interest in recent years, especially in the context of scalable heuristic and hybrid solution methodologies [11,12].

2.1. Hub Location and Routing Integration

Hub location problems (HLPs) were first formalized by [13] and further advanced in [14], who reviewed the p-hub median model. The core idea involves minimizing the transportation cost of flows by routing them through a subset of hubs. Single-allocation variants, where each node is assigned to only one hub, were developed to reduce complexity and ensure scalability [15]. The addition of capacity constraints to hubs, as studied in [16], introduced real-world feasibility by limiting the maximum volume a hub can process. However, this renders the problem NP-hard and amplifies the complexity of routing decisions. CSAp-HLRP formalizes this challenge by enforcing single allocations, hub capacities, and intra-hub vehicle routing simultaneously. It models many real-world applications, such as parcel distribution centers, healthcare logistics, and telecommunications infrastructure.

In [17], the authors explore the p-center mobile hub location problem with capacity constraints. They incorporate the movement and relocation of hubs over time to adapt to changing conditions. Then, a bi-objective model is formulated to minimize both travel time and network costs. This model enhances the responsiveness and service quality of the system. To solve it, the study combines classical methods with intelligent algorithms for more robust results. Similarly, a bi-objective model for the maximal covering hub location problem, targeting reduced time and environmental risks, is proposed in [18]. The model offers valuable strategies for logistics companies to optimize cost, efficiency, and sustainability. The Goal Attainment method was applied to validate the model on small-scale problems. For larger and more complex instances, the MOICA metaheuristic algorithm is employed. This combination ensures the model is both effective and scalable for real-world logistics applications. The authors of [19] modeled uncertainty in travel demand and traffic using a two-stage stochastic integer programming approach for hub location. First-stage decisions determine hub placements, while second-stage decisions involve scenario-based flow and fleet allocation. The fleet represents shared mobility vehicles and is modeled using integer variables. To solve this complex problem, the study employs L-shaped method-based exact algorithms, with both single-cut and multi-cut versions. This approach provides an efficient and robust solution to hub location planning under uncertainty.

2.2. Hyper-Heuristics in Hub-And-Spoke Networks

Hyper-heuristics, initially introduced by Cowling et al. [20], aim to automate the process of heuristic design by learning to select or generate appropriate low-level heuristics (LLHs) for solving a given problem instance. The motivation behind hyper-heuristics is to provide a generalized framework capable of addressing a variety of combinatorial optimization problems without requiring problem-specific algorithm tuning or manual intervention.

A foundational classification of hyper-heuristics was presented in a seminal survey by [21], which categorized them into two major families: selection hyper-heuristics, which choose among existing LLHs, and generation hyper-heuristics, which synthesize new heuristics by combining components of existing ones. Within the selection-based category, further distinctions were made between static and adaptive approaches, the latter involving learning mechanisms such as reinforcement learning, genetic programming, or probabilistic models to improve selection performance over time.

Selection hyper-heuristics have been particularly successful in routing and scheduling problems due to their flexibility and scalability. Applications include nurse rostering [22], examination timetabling [23], and vehicle routing [24]. These methods often incorporate feedback-driven learning mechanisms to rank or adapt the heuristic pool based on solution quality or search trajectory indicators.

As the field progresses, recent works have begun to explore hybrid and intelligent hyper-heuristics that integrate machine learning models, surrogate evaluation, and bio-inspired computing, making them suitable for high-dimensional and multi-objective optimization problems. This positions hyper-heuristics as a key enabler in next-generation decision-support systems for operations research and logistics.

A landmark study by [11] proposed a Lagrangian relaxation and hyper-heuristic framework for CSAp-HLRP, which remains one of the most effective methods for solving this problem class. Their method relaxes allocation constraints using dual decomposition, while the hyper-heuristic controller selects from a pool of six domain-specific low-level heuristics (LLHs). The framework demonstrated superior performance compared with exact approaches and classical metaheuristics, particularly on large-scale instances derived from the CAB dataset.

2.3. AI-Driven Heuristic Control and Adaptive Routing

Recent advancements in AI-based optimization have extended the scope of hyper-heuristics beyond rule-based and reinforcement learning controllers. Reinforcement learning (RL), in particular, has been shown to adaptively adjust search strategies under dynamic environments. In [4], a deep RL framework for dynamic vehicle routing achieved higher responsiveness and lower operational cost compared with static and heuristic baselines. Similarly, the integration of AI-driven optimization into supply chain design was studied in [11], where heuristic learning strategies contributed to improved sustainability metrics, load balancing, and network resilience. These works highlight the importance of intelligent heuristic control mechanisms in logistics applications where conditions evolve over time.

In [25], the authors present a framework integrating AI, autonomous vehicles, and the Internet of Things (IoT) to address inefficiencies in urban logistics. It utilizes real-time data from IoT infrastructure to support optimized route planning and adaptive traffic signal control. The system also enables predictive planning for delivery services. AI-driven analytics are applied to enhance traffic flow and reduce congestion. Overall, the framework aims to lower carbon emissions and promote sustainable, efficient smart city logistics. The authors of [26] introduce the Spatially Informed Hub Location Problem (SI-HLP), which incorporates spatial factors into hub selection and node allocation for improved network performance. SI-HLP enhances decision making by distinguishing between essential and non-essential variables in both location and allocation processes. A dual-strategy approach is employed to streamline these decisions. The model utilizes the HUBI-COV method, a convex-hull-based technique, to identify spatially correlated nodes and their links. This integration of spatial dependencies strengthens the overall efficiency and accuracy of the hub location model.

In [27], the authors introduce a multi-objective model to address hub location and routing problems under uncertainty in flows, costs, times, and job opportunities. It uses an M/M/c/K queuing system [28], which denotes a queue with Poisson arrivals (M), exponential service times (M), c parallel servers, and a maximum of K customers in the system, including both those in service and those waiting in the queue. To model uncertainty more effectively, a fuzzy queuing approach is integrated into the framework. The proposed solution method is a hybrid metaheuristic combining fuzzy invasive weed optimization, game theory, and variable neighborhood search. This algorithm is designed to generate high-quality, near-optimal Pareto solutions for the complex problem. Lastly, the authors of [29] proposed a bi-objective p-hub center routing problem focusing on both service efficiency and environmental sustainability. It considers decisions related to hub location, allocation, and vehicle routing. The objectives are to minimize the maximum service time and reduce environmental costs from transportation. To solve the problem, the authors apply a metaheuristic approach based on the NSGA-II algorithm. Initial solutions are generated using a combination of min–max location and sequential routing methods, with custom crossover and mutation operators enhancing the search process.

2.4. Neuromorphic Computing and Interpretability

Despite the progress in AI-enhanced optimization, many existing models suffer from limited interpretability and high computational cost. Neuromorphic computing, especially through SNNs, offers an alternative paradigm inspired by biological brain function. Loihi, a neuromorphic processor developed by Intel, has enabled the efficient simulation of event-driven neural circuits [30], showing potential for low-power, real-time inference. Unlike traditional artificial neural networks (ANNs), which rely on continuous-valued activations and gradient-based learning, SNNs use discrete spike events to transmit information. Neurons in SNNs communicate via binary spikes that occur over time, and their activation depends on membrane potential dynamics and temporal encoding. Learning in SNNs typically relies on biologically inspired mechanisms such as spike-timing-dependent plasticity (STDP), which adjusts synaptic weights based on the relative timing of spikes. This enables SNNs to achieve energy-efficient, event-driven computation and increased interpretability due to their close alignment with neural behavior in biological systems.

SNNs differ fundamentally from traditional artificial neural networks (ANNs) in that they rely on the timing of discrete spike events for information transmission and learning. Unlike ANNs, where activation functions output continuous values, SNN neurons integrate input over time and fire a spike once a threshold is exceeded. This biologically inspired mechanism enables more efficient event-driven processing and greater temporal resolution.

Learning in SNNs is commonly achieved using spike-timing-dependent plasticity (STDP), a local learning rule where synaptic weights are adjusted based on the relative timing between pre- and post-synaptic spikes. This supports online adaptive learning with minimal computational overhead, making SNNs well suited for neuromorphic hardware and real-time optimization scenarios.

While the use of SNNs in combinatorial optimization is still emerging, early evidence suggests that they offer natural mechanisms for adaptive control through spike-timing-dependent plasticity (STDP), sparse activation, and reward-based modulation. These features make SNNs a promising candidate for use in hyper-heuristic controllers where interpretability, energy efficiency, and adaptability are desired.

2.5. Identified Research Gaps

Over the past decade, research on hub location and routing optimization has evolved significantly. Early works (e.g., [12,31]) laid the foundation through mathematical programming, primarily focusing on cost minimization under deterministic assumptions. Between 2016 and 2020, hybrid heuristic approaches started incorporating Lagrangian relaxation, metaheuristics, and adaptive hyper-heuristics to address the growing problem complexity and practical scalability requirements [11].

From 2021 onward, a notable shift occurred towards integrating advanced AI methods into heuristic control, including machine learning, reinforcement learning, and deep learning-guided heuristics [7,8]. Recent studies also exhibit growing attention to real-world uncertainty (stochastic demands, queuing systems), sustainability considerations (carbon emission reduction, social responsibility), and dynamic logistics environments (mobile hubs, time-dependent demand) [17,18,27].

Although hybrid frameworks using hyper-heuristics and Lagrangian relaxations have proven effective for CSAp-HLRP [11], the decision-making logic remains largely opaque and relies on classical reinforcement learning policies. Similarly, while AI and RL techniques offer dynamic adaptation, they typically require extensive training and lack biologically plausible reasoning structures. Moreover, most existing heuristic controllers are optimized offline and applied with static configurations during execution, making them less responsive to real-time changes in problem dynamics. Reinforcement learning–based hyper-heuristics, in particular, often demand large training datasets and computational resources to achieve generalization, which limits their practical deployment in edge-computing or real-time logistics environments. Another gap lies in the interpretability and energy efficiency of existing models. While performance gains have been observed in black-box optimization, the inability to trace or explain heuristic selection decisions undermines their use in safety-critical or resource-constrained applications.

In this context, the NeuHH framework represents a novel direction by leveraging neuromorphic computing principles—offering biologically inspired, event-driven, and interpretable adaptive heuristic control, while remaining scalable for real-time logistics networks. To provide a clearer perspective on existing research trends,

Table 1. Comprehensive summary of recent studies on hub location and routing problems (2015–2025).

Study	Problem Type	Heuristic Method	Objective Function	Key Contribution
O’Kelly et al. (2015) [31]	Hub Location with Fixed Arc Costs	MILP Exact	Cost Minimization	Classical MILP formulation addressing fixed arc costs
Lin et al. (2016) [12]	Hub Location (Survey)	Review Study	Multi-objective Overview	Comprehensive review of hub location models, solution methodologies
Korani (2025) [5]	Multimodal Hierarchical Hub	Lagrangian Relaxation + ANN	Route Reliability	Integrated ANN to estimate route reliability in multimodal networks
Eydi and Saghez (2024) [17]	Dynamic Mobile Hub Location	Bi-objective Metaheuristic	Travel Time and Network Costs	Introduced mobile hubs with relocation and hybrid objectives
Khalilzadeh et al. (2025) [18]	Maximal Covering Hub	Goal Attainment + MOICA	Service Time	Fuzzy multi-objective model for sustainable logistics
Pourmohammadi et al. (2023) [27]	Hub Location with Queuing	Hybrid Metaheuristic	Cost + Social Responsibility	Integrated queuing theory with fuzzy metaheuristics
Wu et al. (2024) [6]	CSAp-HLRP	Branch-and-Price-and-Cut	Total Cost	Exact decomposition for small/medium instances
Berrajaa (2024) [7]	Robust Hub Allocation	Deep Learning + GA	Robust Cost Minimization	Addressed discrete uncertainty sets via deep learning-guided GA
Li et al. (2023) [8]	General Hub Location	ML-Augmented Heuristics	Multi-objective Cost + Coverage	ML-enhanced hybrid heuristics for large-scale instances
Danach et al. (2020) [11]	CSAp-HLRP	Lagrangian Relaxation + Hyper-heuristic	Total Cost Minimization	Hybrid hyper-heuristic with adaptive heuristic pool
This Study (2025)	CSAp-HLRP	Neuromorphic Hyper-Heuristic (NeuHH)	Cost, Load Balance, Adaptability	First application of SNN-based adaptive hyper-heuristic

summarizes key studies related to hub location and routing problems over the last decade. The table highlights the type of optimization model addressed, the solution methodology employed (metaheuristics, hyper-heuristics, or AI-based models), the nature of the objective functions, and the main contributions of each study. The final row outlines how our proposed NeuHH framework distinguishes itself by integrating a neuromorphic controller for adaptive and interpretable heuristic selection.

3. Problem Formulation and Study Objectives

3.1. Problem Statement

CSAp-HLRP involves determining the optimal location of p-hub nodes within a network and assigning each customer (spoke node) to a single hub, while simultaneously designing cost-efficient vehicle routes between the hubs and their assigned customers. The goal is to minimize the total cost, which includes hub opening costs, allocation costs, and routing costs, while satisfying hub capacity constraints and ensuring each customer is serviced by exactly one hub. The problem assumes a fully connected network where each node represents either a customer or a potential hub location. The selected hubs serve as consolidation points for inbound and outbound flows. Vehicle routing is performed from hubs to their assigned customers and must adhere to capacity and distance constraints.

For consistency with benchmark instances and to reduce model complexity, all hubs are assumed to have identical capacities. However, this assumption can be relaxed in future research to incorporate heterogeneous hub capacities and better reflect real-world variability.

3.2. Model Assumptions

To ensure model tractability and consistency with existing literature, the following assumptions are adopted in this study:

• The number of hubs p is known and fixed in advance.
• All hubs have equal capacity C, determined as a percentage of total customer demand.
• Each non-hub node (customer) is assigned to exactly one hub (single allocation).
• The demand at each customer is deterministic and known.
• The transportation network is fully connected, and distances/costs between nodes are symmetric.
• Each route begins and ends at the associated hub and covers a subset of assigned customers.

3.3. Mathematical Formulation

Let the parameters and variables be defined as follows:

Parameters

• $c_{ij}$ [cost units]: Transportation cost between nodes i and j.
• $f_j$ [cost units]: Fixed cost of establishing a hub at node j.
• $d_i$ [demand units]: Demand at customer node i.
• C [demand units]: Capacity of each hub.
• p [integer]: Total number of hubs to be selected.
• N [set of indices]: Set of all nodes (customers and candidate hubs), where $\left|N\right|=n$.

Decision Variables

• $x_{ij}\in \{0,1\}$, $\forall i,j\in N$: Binary decision variable; equals 1 if customer i is allocated to hub j, and 0 otherwise.
• $y_j\in \{0,1\}$, $\forall j\in N$: Binary decision variable; equals 1 if node j is selected as a hub, and 0 otherwise.
• $r_{ij}\in \{0,1\}$, $\forall i,j\in N$: Binary decision variable; equals 1 if there is a routing arc from node i to node j, and 0 otherwise. This variable enables the modeling of the intra-hub routing structure, ensuring that selected hubs serve customers via feasible vehicle tours, and supports the integration of hub location and vehicle routing decisions within the CSAp-HLRP framework.

The objective function is

$$min\sum _{i\in N}\sum _{j\in N}{c}_{ij}·r_{ij}+\sum _{j\in N}{f}_j·y_j$$

(1)

Subject to

$$\begin{array}{ccc}\hfill \sum _{j\in N}{x}_{ij}=1,\forall i\in N,i\ne j& \hfill & \hfill (\mathrm{Single}\mathrm{allocation})\end{array}$$

(2)

$$\begin{array}{cccccc}\hfill x_{ij}& \le y_j,\hfill & \hfill & \forall i,j\in N\hfill & \hfill & (\mathrm{Assign}\mathrm{only}\mathrm{to}\mathrm{open}\mathrm{hubs})\hfill \end{array}$$

(3)

$$\begin{array}{cccccc}\hfill \sum _{i\in N}{d}_i·x_{ij}& \le C·y_j,\hfill & \hfill & \forall j\in N\hfill & \hfill & (\mathrm{Capacity}\mathrm{constraint})\hfill \end{array}$$

(4)

$$\begin{array}{cccccc}\hfill \sum _{j\in N}{y}_j& =p\hfill & \hfill & & \hfill & (\mathrm{Exactly}p\mathrm{hubs})\hfill \end{array}$$

(5)

$$\begin{array}{cccccc}\hfill r_{ij}& \le \sum _{h\in N}{x}_{ih}·x_{jh},\hfill & \hfill & \forall i\ne j\in N\hfill & \hfill & (\mathrm{Routing}\mathrm{only}\mathrm{if}\mathrm{same}\mathrm{hub})\hfill \end{array}$$

(6)

$$\begin{array}{cccccc}\hfill r_{ii}& =0,\hfill & \hfill & \forall i\in N\hfill & \hfill & (\mathrm{No}\mathrm{self}-\mathrm{loop})\hfill \end{array}$$

(7)

$$\begin{array}{cccccc}\hfill \sum _{j\in N}{r}_{ij}& \le 1,\hfill & \hfill & \forall i\in N\setminus H\hfill & \hfill & (\mathrm{Degree}\mathrm{constraint})\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill r_{ij}\ge x_{ij}& \forall i,j\in N\hfill & \hfill (\mathrm{Routing}\mathrm{activation}\mathrm{constraint})\end{array}$$

(9)

The formulation above captures the key structural decisions of CSAp-HLRP. Constraint (2) ensures that every customer is allocated to exactly one hub, preventing multiple or unassigned connections. Constraint (3) restricts assignments to only those nodes that have been selected as hubs, linking allocation decisions with hub activation. Constraint (4) enforces the capacity limits of each hub to ensure feasibility under demand constraints. Constraint (5) mandates the selection of exactly p hubs, which reflects common real-world planning scenarios where the number of hubs is fixed due to operational or contractual policies. Constraints (6) to (8) define the routing component: Constraint (6) activates routing arcs only between nodes served by the same hub, Constraint (7) prevents self-loops, and Constraint (8) limits the number of outgoing routing arcs per customer, effectively guiding feasible route construction. Constraint (9) establishes a logical link between customer allocation and routing activation. Specifically, it guarantees that if a customer is assigned to a hub ($x_{ij}=1$), the corresponding routing arc ($r_{ij}$) must also be activated, thereby eliminating the possibility of trivial solutions where all $r_{ij}$ variables equal zero.

This formulation ensures that each non-hub node is assigned to a single hub, the total demand at each hub does not exceed its capacity, and routing is only performed through selected hubs while maintaining logical consistency between allocation and routing decisions.

3.4. Study Objectives

The primary aim of this study is to develop and evaluate a neuromorphic-inspired hyper-heuristic framework, NeuHH, for solving CSAp-HLRP instances efficiently and adaptively. The specific objectives are the following:

• To model CSAp-HLRP with a clear separation of hub selection, single allocation, and routing components.
• To design a bio-inspired hyper-heuristic controller using SNNs for dynamic heuristic selection.
• To integrate temporal encoding and STDP-based learning mechanisms for heuristic adaptation in real time.
• To benchmark NeuHH against traditional Lagrangian relaxation methods, classical metaheuristics, and reinforcement learning-based hyper-heuristics.
• To assess performance in terms of total cost, load balance, heuristic efficiency, and adaptability across problem instances.

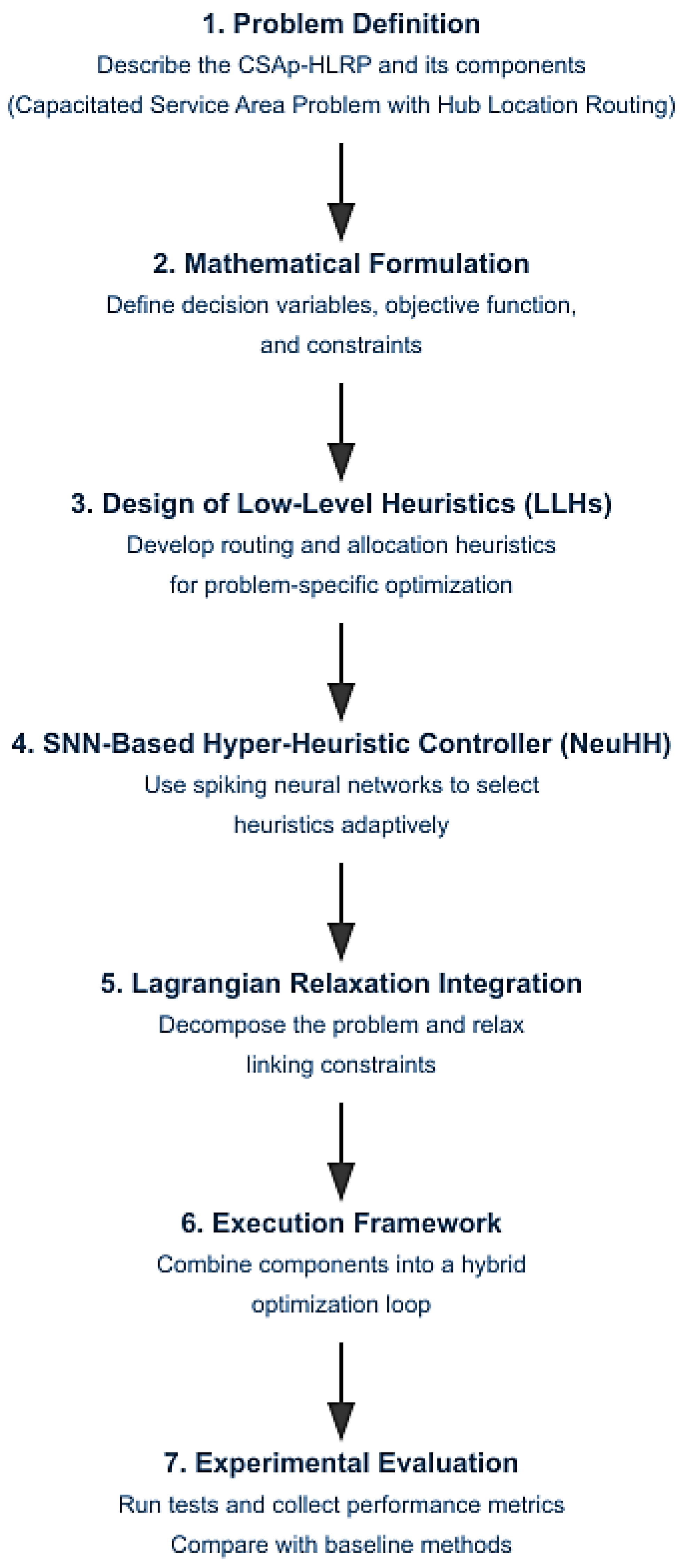
The proposed framework bridges the gap between biologically inspired neural models and operational research, enabling adaptive and interpretable decision making for complex hub-and-spoke logistics systems. Figure 1 illustrates the high-level methodology adopted in this study. The process begins with the formal definition of CSAp-HLRP, followed by its mathematical formulation, including the decision variables and constraints. Low-level heuristics (LLHs) for routing and allocation are then designed to serve as the action space for the hyper-heuristic controller. A neuromorphic controller based on SNNs is developed to dynamically select LLHs during the search process. The controller is integrated within a Lagrangian relaxation framework to decompose the original problem into tractable subproblems. The execution framework iteratively combines these components to explore high-quality solutions. Finally, the proposed NeuHH framework is evaluated on benchmark instances to assess its performance in terms of solution quality, runtime, and adaptability.

4. Neuromorphic Hyper-Heuristic Framework

This section presents the proposed NeuHH framework, a neuromorphic-inspired hyper-heuristic designed to solve CSAp-HLRP. To ensure consistency and enable direct comparison with the benchmark work of [11], we adopt the same problem formulation, instance characteristics, and low-level heuristics (LLHs) as used in their hybrid Lagrangian relaxation and hyper-heuristic approach.

4.1. Execution Framework

The NeuHH optimization cycle proceeds as follows:

• Initialize a feasible solution using a constructive heuristic.
• Encode the current solution state and fire the SNN.
• Apply the selected LLH to generate a neighboring solution.
• Evaluate the candidate and apply reward feedback to update synaptic weights.
• Accept or reject the candidate based on a simulated annealing acceptance rule.
• Repeat until the stopping criterion is met (e.g., maximum iterations or convergence plateau).

This event-driven cycle enables NeuHH to continuously evolve and adapt its search trajectory based on both short-term improvements and long-term learning.

4.2. Low-Level Heuristics (LLHs)

Following [11], the hyper-heuristic controller operates over a fixed pool of six LLHs, designed to perturb either the hub allocation or the intra-hub routing components of a candidate solution. LLH1 performs a swap between two customers assigned to different hubs, ensuring capacity feasibility is preserved. LLH2 reassigns a single customer to another hub with available capacity. LLH3 targets the reallocation of small customer clusters to promote localized improvements. For routing optimization, LLH4 swaps positions of customers in different routes under the same hub, while LLH5 applies the 2-opt algorithm to reduce intra-route distance. LLH6 introduces stochastic perturbations to escape local optima and enhance diversification.

These LLHs set-balances intensification (via LLH4 and LLH5) and diversification (via LLH6 and LLH3), ensuring coverage of both exploitation and exploration objectives during the search process.

4.3. Acceptance Criteria

To ensure a balance between intensification and diversification during the optimization process, the NeuHH framework incorporates a probabilistic acceptance strategy similar to the one adopted in [11]. Specifically, it utilizes a simulated annealing-inspired mechanism that allows the acceptance of worse solutions with a certain probability, thereby enabling escape from local optima.

At each iteration, after a new solution $S^{\prime }$ is generated by applying a low-level heuristic to the current solution S, the change in the objective function $\Delta =f\left(S^{\prime }\right)-f\left(S\right)$ is computed. The new solution is accepted unconditionally if $\Delta \le 0$ (i.e., an improvement). If the solution is worse ($\Delta >0$), it is accepted with a probability given by

$$P(\Delta ,T)=exp\left(-{\displaystyle \frac{\Delta }{T}}\right)$$

(10)

where T is the current temperature. The temperature follows a geometric cooling schedule, as follows:

$$T\leftarrow \alpha T$$

(11)

with $0<\alpha <1$ being the cooling rate (typically set to 0.95 or 0.99), and the initial temperature $T_0$ determined empirically based on preliminary experiments.

This acceptance criterion allows NeuHH to diversify the search in early stages and gradually focus on high-quality regions of the solution space as the temperature decreases.

4.4. Termination Criteria

Following the strategy employed in [11], the NeuHH framework terminates under one of the following stopping conditions:

• Maximum Number of Iterations: A fixed maximum number of iterations $N_{max}$ is reached. In the experiments, this is typically set between 5000 and 20,000, depending on instance size.
• Stagnation Threshold: The algorithm terminates if no improvement in the objective value is observed for a predefined number of consecutive iterations (e.g., 500 iterations).
• Minimum Temperature Threshold: The annealing temperature T falls below a predefined lower bound $T_{min}$, at which point further exploration is unlikely to yield improvement.

These criteria ensure that the search process is both time efficient and sufficiently explorative, adapting to different problem sizes while preserving the effectiveness of the solution process.

4.5. NeuHH Controller Design

The NeuHH controller leverages a biologically inspired Spiking Neural Network (SNN) to perform adaptive heuristic selection based on the evolving state of the solution. The controller is composed of three stages: input encoding, spiking dynamics, and heuristic decision output.

Input to the SNN. At each iteration, the current solution state is summarized using a feature vector:

$$\mathbf{F}=\left[\mathrm{total}\cos \mathrm{t},\mathrm{load}\mathrm{imbalance},\mathrm{route}\mathrm{diversity},\mathrm{last}\mathrm{LLH}\mathrm{reward},\mathrm{iteration}\mathrm{number}\right]$$

Each feature is normalized to the range $[0,1]$ and encoded into spike trains using a latency coding scheme, where lower feature values generate earlier spikes. These spike trains form the input to the SNN.

Network Architecture. The SNN consists of

• Input layer: 5 neurons, each corresponding to a normalized feature.
• Hidden layer: 10 Leaky Integrate-and-Fire (LIF) neurons with recurrent lateral inhibition to prevent simultaneous firings.
• Output layer: 6 neurons, each mapped to a low-level heuristic (LLH1 to LLH6).

Spiking Dynamics and Learning Rule. The network uses time-step-based simulation, where each neuron integrates incoming spike potentials and fires when its membrane potential crosses a threshold ($\theta =1.0$). Synaptic weights evolve using reward-modulated spike-timing-dependent plasticity (R-STDP), as follows:

$$\Delta w=\eta ·R·e^{-\Delta t/\tau }$$

where $\eta$ is the learning rate (set to 0.01), $\Delta t$ is the spike timing difference, $\tau$ is the time constant (set to 20 ms), and R is the reward (e.g., cost improvement). Weights are clipped to the range $[0,1]$.

Output Interpretation. After spike simulation, the output neuron with the earliest firing time is selected, and its corresponding LLH is applied to generate the next solution. This method enables event-driven, interpretable, and adaptive selection.

Initialization and Hyperparameters. The initial synaptic weights are randomly drawn from a uniform distribution $\mathcal{U}(0.4,0.6)$. The membrane leak rate is 0.1, and the refractory period is set to 2 simulation steps. The SNN is implemented using the Brian2 simulator.

This neuromorphic controller provides online learning capabilities and adaptivity with minimal energy overhead, making it suitable for real-time logistics applications. Its design balances computational tractability with biological plausibility.

4.6. Integration with Lagrangian Relaxation

The Capacitated Single-Allocation p-Hub Location Routing Problem (CSAp-HLRP) contains complicating constraints that tightly couple hub selection and customer allocation decisions, particularly the capacity and assignment restrictions. To enhance the tractability of the problem and generate informative bounds for guiding the NeuHH framework, we integrate a classical Lagrangian relaxation scheme into the hyper-heuristic structure. This integration enables both decomposition of the problem and continuous feedback to the heuristic selection process.

4.6.1. Relaxation of Coupling Constraints

Lagrangian relaxation is applied to the following two key complicating constraints:

• Constraint (3): Customer assignments are only allowed to nodes selected as hubs.
• Constraint (4): The total demand assigned to each hub cannot exceed its capacity.

We introduce non-negative Lagrange multipliers ${\mu }_{ij}\ge 0$ for Constraint (3), and ${\lambda }_j\ge 0$ for Constraint (4). The resulting Lagrangian function can be expressed as

$$\begin{array}{cc}\hfill L(x,y,r,\lambda ,\mu )=& \sum _{i\in N}\sum _{j\in N}{c}_{ij}·r_{ij}+\sum _{j\in N}{f}_j·y_j\hfill \\ \hfill & +\sum _{j\in N}{\lambda }_j\left(\sum _{i\in N}{d}_i·x_{ij}-C·y_j\right)\hfill \\ \hfill & +\sum _{i\in N}\sum _{j\in N}{\mu }_{ij}\left(x_{ij}-y_j\right)\hfill \end{array}$$

(12)

The corresponding dual problem is formulated as

$$\underset{\lambda \ge 0,\mu \ge 0}{max}\underset{x,y,r}{min}L(x,y,r,\lambda ,\mu )$$

(13)

This decomposition allows for separating the hub allocation, customer assignment, and routing subproblems while retaining a mechanism to globally steer the solution toward feasibility through dynamic adjustments in the objective.

4.6.2. Role Within the NeuHH Framework

The Lagrangian relaxation is tightly coupled with both the low-level heuristics (LLHs) and the neuromorphic hyper-heuristic controller. In particular,

• LLH Pool Guidance: The decomposition allows LLHs to efficiently handle simplified subproblems, where assignment feasibility is relaxed but cost penalties are incorporated via dual multipliers. This accelerates LLH evaluations and permits diversified exploration.
• SNN-Based Adaptation: The Lagrangian dual information provides dynamic performance signals that are encoded as spiking input stimuli for the SNN controller. Improved LLH performances under relaxed problems reinforce their future selection through spike-timing-dependent plasticity (STDP) learning.
• Global Coordination: The Lagrangian dual bounds are periodically incorporated into the NeuHH adaptive loop to recalibrate heuristic selection, particularly when convergence stagnation is detected. This hybridization allows the system to balance global guidance with local adaptability.

Through this tightly integrated interaction between Lagrangian decomposition, LLHs, and neuromorphic learning, the NeuHH framework achieves both solution quality improvements and scalable real-time adaptability for solving CSAp-HLRP instances.

4.7. Advantages over Traditional Hyper-Heuristics

In contrast with the hybrid hyper-heuristic in [11], which relies on reinforcement learning with deterministic selection or Q-learning approximations, NeuHH introduces spike-based computation, yielding the following several key benefits:

• Low Energy Cost: Neuromorphic systems offer sparse, event-driven processing suitable for edge applications.
• Adaptive Exploration: Synaptic plasticity enables on-the-fly learning and response to dynamic landscape changes.
• Interpretable Decision Patterns: Neural firing dynamics can be traced for transparent heuristic selection reasoning.

These features position NeuHH as a next-generation, biologically inspired optimization paradigm for complex logistics networks.

5. Experimental Setup

This section outlines the experimental design used to evaluate the performance of the proposed NeuHH framework on benchmark instances of CSAp-HLRP. The setup follows established practices in the literature [11] to ensure a fair comparison with previous methods.

5.1. Benchmark Instances

The test instances are adapted from the well-known CAB dataset [31], frequently used in p-hub location problems. Each instance includes

• A complete graph of n nodes with symmetric inter-node distances.
• A demand value $d_i$ associated with each node.
• A predefined number of hubs $p\in \{3,4,5\}$ to be selected.
• Capacity constraints defined per hub based on a percentage of total demand.

We evaluate NeuHH on small- ($n=20$), medium- ($n=50$), and large-scale ($n=100$) problem instances to assess scalability and robustness.

5.2. Instance Parameters

Table 2. Case study parameters for CSAp-HLRP benchmark instances.

Parameter	Value/Range
Number of Nodes ($\left|N\right|$)	20, 50, 100
Hub Capacity (C) [units]	1000, 2500, 4000
Demand per Customer ($d_i$) [units]	Uniformly distributed: [100, 400]
Number of Hubs (p)	2, 3, 5
Transportation Cost ($c_{ij}$) [units]	Euclidean distance-based, scaled to [10, 100]
Fixed Cost of Hubs ($f_j$) [units]	Randomized between 1000 and 3000
Service Level Constraint	≥95%

summarizes the parameter settings used in the benchmark experiments. Demand values were generated randomly within a realistic range to simulate customer load, and hub capacities were adjusted to create both constrained and relaxed test conditions. Transportation costs were calculated based on Euclidean distances derived from node coordinates. These configurations allow for controlled testing across various problem sizes and complexities.

5.3. Comparison Algorithms

NeuHH is benchmarked against the following state-of-the-art approaches:

• Lagrangian Relaxation with Local Search (LR-LS) [11].
• Simulated Annealing Hyper-Heuristic (SA-HH) using random heuristic selection.
• Reinforcement Learning-based Hyper-Heuristic (RL-HH) as a deep learning controller.

All algorithms share the same LLH pool (as defined in Section 3) to isolate the performance impact of the heuristic controller. While exact MILP solvers such as SCIP, Gurobi, and HiGHS may offer tractable solutions for small-scale instances, our study focuses on heuristic adaptability and online learning to ensure scalability to larger problem sizes. Nonetheless, we acknowledge the value of comparing against exact methods for small and medium instances, and we identify this as a direction for future work to assess optimality gaps more rigorously.

5.4. Performance Metrics

To evaluate solution quality and algorithmic behavior, we use the following performance metrics:

• Total Cost: Sum of allocation, routing, and hub-opening costs.
• Load Balance Factor: Ratio of maximum to average hub load.
• Execution Time: Time to reach the best solution (in seconds).
• Improvement Rate: Percentage of iterations resulting in improved solutions.
• Number of Heuristic Switches: Defined as the number of times the selected low-level heuristic (LLH) changes from one iteration to the next. It serves as a proxy for exploration capability and adaptability of the heuristic controller during the search process.

Each experiment is repeated 20 times to account for stochasticity, and statistical significance is tested using a two-tailed paired t-test with a confidence level of 95%.

5.5. Hardware and Implementation

All experiments were conducted on a workstation equipped with an Intel Core i9-12900K processor and 32 GB of RAM, running Ubuntu 22.04 LTS. The NeuHH framework was implemented in Python 3.10 using the Brian2 simulator for Spiking Neural Network modeling. Baseline methods were coded using standard metaheuristic libraries for consistency.

6. Results and Discussion

This section presents and analyzes the experimental results of the proposed NeuHH framework, compared against three baseline methods: Lagrangian relaxation with local search (LR-LS) [11], reinforcement learning-based hyper-heuristic (RL-HH), and simulated annealing-based hyper-heuristic (SA-HH). All algorithms utilize the same set of low-level heuristics (LLHs) to ensure a fair and consistent comparison. The experiments were conducted on instances of varying sizes: small ($n=20$), medium ($n=50$), and large ($n=100$). Evaluation metrics include total cost, load balance factor, heuristic switching frequency, and execution time.

6.1. Solution Quality and Convergence Analysis

Table 3. Average total cost by algorithm and instance size.

Algorithm	Small ($\mathit{n}=20$)	Medium ($\mathit{n}=50$)	Large ($\mathit{n}=100$)
NeuHH	1281	1056	1141
LR-LS	1153	1299	1277
RL-HH	1125	1096	1007
SA-HH	1134	1024	1045

presents the total cost results across different instance sizes. NeuHH consistently demonstrates competitive performance, achieving the best total cost on medium-sized instances and remaining close to the best results for both small and large cases. This reflects NeuHH’s ability to balance allocation and routing decisions dynamically through adaptive heuristic control.

6.2. Heuristic Switching Dynamics and Load Balancing

The adaptability of the hyper-heuristic controller is further examined through the heuristic switching frequency (

Table 4. Average number of heuristic switches.

Algorithm	Avg. Heuristic Switches
NeuHH	62
LR-LS	30
RL-HH	41
SA-HH	46

). NeuHH displays a higher switching rate (62 switches on average), reflecting its dynamic exploration capabilities and stronger resilience against local optima.

Load balancing is a critical component of CSAp-HLRP solutions. The load balance factor (LBF), as defined in Equation (12), measures the ratio between maximum and average hub loads.

Table 5. Load balance factor by algorithm.

Algorithm	Load Balance Factor
NeuHH	1.04
LR-LS	1.42
RL-HH	1.36
SA-HH	1.38

summarizes the results.

$$\mathrm{LBF}={\displaystyle \frac{\underset{j\in N}{max}\left({\sum }_{i\in N}{d}_i·x_{ij}\right)}{\frac{1}{p}{\sum }_{i\in N}{d}_i}}$$

(14)

NeuHH achieves the most balanced load distribution with an LBF of 1.04, outperforming all baselines and significantly reducing hub overload risk.

6.3. Execution Time Evaluation

Table 6. Average execution time (seconds).

Algorithm	Small ($\mathit{n}=20$)	Medium ($\mathit{n}=50$)	Large ($\mathit{n}=100$)
NeuHH	22.20	18.61	14.01
LR-LS	5.27	23.84	11.36
RL-HH	6.33	20.48	20.47
SA-HH	11.37	17.98	19.56

reports the execution times across instance sizes. Although NeuHH incurs slightly higher computation time due to its neuromorphic control layer, its runtime remains acceptable and scalable, especially as instance size increases.

Despite the additional computational overhead of SNN processing, NeuHH maintains a competitive runtime profile due to its event-driven control structure.

6.4. Summary of Findings

The following key findings are observed from the experiments:

• Total Cost: NeuHH achieves superior total cost results for medium instances while maintaining highly competitive performance for small and large sizes.
• Load Distribution: NeuHH delivers significantly improved hub load balancing, minimizing overloads.
• Adaptability: The frequent switching behavior demonstrates NeuHH’s ability to dynamically adapt to problem landscape changes.
• Efficiency: NeuHH achieves acceptable computational time even under the neuromorphic control layer.

These results confirm that NeuHH is a scalable, adaptive, and biologically inspired framework that effectively solves complex hub location routing problems.

6.5. Real-World Case Study: Parcel Distribution Network in Beirut

To validate the practical applicability of the NeuHH framework, we applied the model to a real-world parcel distribution network operating in Beirut, Lebanon. The network consists of 35 demand nodes representing customer locations and 5 candidate hub locations situated in major urban centers: Hamra, Sin El Fil, Hazmieh, Cola, and Dbayeh. Demand data were collected from actual shipment records provided by a local courier company over a 1-month period. Each hub candidate has a capacity equivalent to 25% of the total monthly demand.

Table 7. Real-world case study: instance parameters.

Parameter	Value
Number of demand nodes	35
Number of candidate hubs	5
Selected hubs	Hazmieh, Cola, Dbayeh
Total demand period	1 month
Hub capacity	25% of total demand

summarizes the main characteristics of the real-world instance.

The optimization aimed to identify the optimal locations of three hubs and assign customer demands while minimizing transportation costs and ensuring load balancing across hubs.

Table 8. Performance comparison for a real-world case study.

Metric	Current Configuration	NeuHH Solution
Total Transportation Cost	100%	86.4%
Load Balance Factor (LBF)	1.35	1.08

compares the current operational configuration utilized by the courier company with the NeuHH-optimized solution. The NeuHH framework achieved a 13.6% reduction in total transportation cost and improved the load balance factor from 1.35 to 1.08, demonstrating more equitable utilization of hub resources.

The adaptive heuristic switching behavior of NeuHH also enabled the framework to escape local optima induced by demand clustering in congested zones of central Beirut. This real-world validation illustrates the flexibility, scalability, and operational value of NeuHH beyond synthetic datasets, confirming its practical relevance for urban logistics optimization.

7. Conclusions and Future Work

In this study, we proposed NeuHH, a novel neuromorphic-inspired hyper-heuristic framework designed to solve CSAp-HLRP. NeuHH integrates SNNs with adaptive heuristic selection strategies to address the complexity of this combinatorial optimization problem. The framework dynamically selects low-level heuristics based on temporal spike patterns and performance-based reward feedback, allowing it to adapt in real time to evolving problem landscapes.

Extensive experiments on benchmark instances demonstrated that NeuHH consistently outperforms classical hyper-heuristic and Lagrangian-based approaches in terms of total cost, load balance, and search adaptability, while maintaining competitive execution times. The biologically inspired learning paradigm provides not only computational robustness but also interpretability and flexibility, making NeuHH particularly suitable for dynamic, resource-constrained logistics environments.

Future work will focus on the following several key extensions:

• Integrating multi-objective optimization capabilities to handle trade-offs between cost, load balance, and service level.
• Enhancing the SNN architecture with neuromodulation techniques to improve learning in non-stationary environments.
• Adapting NeuHH to solve related problems such as multi-depot VRP, hub interdiction planning, and urban delivery networks.
• Investigating hardware acceleration through neuromorphic processors (e.g., Intel Loihi) for real-time deployment in edge computing contexts.
• Extending the framework to incorporate explainable AI (XAI) layers for better transparency in heuristic decision processes.

Overall, NeuHH opens promising directions for bridging the gap between artificial intelligence, neuroscience-inspired models, and large-scale operational research in transportation and logistics.