Abstract
Urban transportation systems evolve toward greater diversification, scalability, and complexity. To address the escalating issue of urban traffic congestion, leveraging modern information technologies to enhance the integration of multiple transportation modes and maximize overall efficiency has emerged as a promising strategy. This study focuses on the decision making problem of urban multimodal transportation travel paths, integrating the time-varying characteristics of public transportation schedules and networks. We consider passengers’ diverse needs and systematically investigate how to optimize travel paths to minimize travel time while adhering to constraints, such as the number of interchanges and travel costs. To address this NP-hard problem, we propose and implement two optimization algorithms: a variable-length coding genetic algorithm (V-GA) and a full permutation coding genetic algorithm (F-GA). Detailed numerical analysis validates the effectiveness of both algorithms, with the V-GA demonstrating significant advantages over the F-GA in terms of solution efficiency. Our findings provide novel perspectives and methodologies for optimizing urban multimodal transportation travel paths, offering robust theoretical foundations and practical tools for enhancing urban traffic planning and travel service efficiency.
1. Introduction
In recent years, rapid economic growth, social development, and significant demographic shifts have driven substantial migration of residents to urban areas, accelerating the process of urbanization. For instance, a 2023 report by the China National Bureau of Statistics (CNBS) revealed that China’s urban population grew by 17.42% between 2013 and 2023, reaching 64.76% of the total population. While the influx of rural residents into cities injects vitality into urban economies and diversifies labor markets, it also places immense pressure on urban infrastructure—particularly transportation systems. This rapid population concentration has led to increased transportation demand, severe traffic congestion, deteriorating air quality, and parking challenges, which have become pressing issues for urban transportation planning and development [1]. To address these challenges, improving the efficiency of urban transportation systems and promoting sustainable mobility have become shared priorities among academics and practitioners. A key strategy involves prioritizing the development of public transportation and scientifically planning multimodal transportation networks. These efforts aim to alleviate road traffic congestion, shift residents toward sustainable travel modes, and enhance the overall efficiency and sustainability of urban transportation systems.
In response to the growing travel demands of urban residents, transportation systems are diversifying to include rail transit, buses, taxis, and other modes that coexist in an interdependent ecosystem. While this diversity provides users with more options, it complicates travel decision making. Traditional single-mode path planning services are no longer sufficient to meet modern urban passengers’ dynamic and varied needs, underscoring the urgency of developing multimodal travel planning services.
In real-world scenarios, passengers often experience confusion when navigating increasingly complex transportation systems. This complexity arises from modes’ diversity and inherent dynamics and uncertainties. For example, urban road congestion causes fluctuations in bus speeds, while public transportation systems like rail transit adhere to strict schedules, increasing travel time uncertainty. Moreover, passengers consider multiple factors when choosing paths, including travel time, cost, comfort, walking distance, the number of transfers, and waiting times, making path selection a multidimensional and complex problem.
In light of this context, we propose an innovative model for optimizing paths in multimodal transportation networks. The model thoroughly incorporates various factors, including public transportation schedules and the time-dependent nature of transportation systems, while introducing constraints on the number of transfers to minimize inconvenience and reduce redundancy from frequent transfers. By integrating these considerations, the model aims to enhance the travel experience, optimize route selection, and improve the practicality and effectiveness of urban travel planning. The proposed model achieves optimization of multidimensional path selection by implementing efficient algorithms, thus supporting the effective and sustainable development of urban public transportation systems. This research advances multimodal transportation planning by providing robust theoretical foundations and practical tools for enhancing urban mobility. To effectively address the urban multimodal transportation path optimization problem under time-dependent and multiple constraints, this paper introduces and compares two representative genetic algorithm encoding methods: the variable-length coding genetic algorithm (V-GA) and the full permutation coding genetic algorithm (F-GA). V-GA offers strong structural adaptability, allowing it to flexibly accommodate variations in path length and transfer nodes, making it well-suited for complex and dynamic intermodal networks. In contrast, F-GA features a stable and easy-to-implement encoding method, providing specific advantages in scenarios where the path structure is relatively fixed. The differences between the two algorithms in path representation and search strategies open diverse avenues for exploring the solution space and lay a theoretical foundation for the subsequent comparative analysis of algorithm performance.
The remainder of the paper is structured as follows. Section 2 provides a comprehensive review of existing research on urban multimodal public transportation. Section 3 introduces the problem description and the optimization model formulation for multimodal transportation networks. Section 4 describes the development and implementation of the V-GA and F-GA algorithms. Section 5 evaluates the proposed model and algorithms through experimental examples, presenting a detailed analysis and discussion of the numerical results. Finally, Section 6 concludes the paper by summarizing key findings and suggesting directions for future research.
2. Literature Review
2.1. Studies on Transportation Modes and Travel Path Selection
The travel path planning problem originates from the classical shortest path problem in multimodal transportation systems. Bellman [2] laid the groundwork for this field with a detailed study of the shortest path problem, followed by Dijkstra [3], who introduced the renowned Dijkstra’s algorithm. Building on this foundation, Witzgall and Goldman [4] extended the research by proposing the constrained shortest path problem, which incorporates one or more constraints, such as distance or cost, to limit the cumulative weights of the segments within the generated path. Nguyen [5] and Spiess [6] advanced this work by analyzing transit travel path selection as a general linear problem. Subsequent research highlighted that passengers do not always select the first available transit route; instead, they prioritize minimizing overall travel time. However, these early studies generally assumed a single transportation mode and a static network structure, failing to capture the complexity of multimodal integration and the dynamic changes in path structure in modern urban travel.
It has been recognized in the extended literature that urban public transportation path selection evolves beyond the traditional shortest path problem. The complexity arises from the need to consider multiple transportation modes and interchanges. Afrasyabi et al. [7] highlighted that passengers often combine various transportation modes within complex urban networks to reach their destinations. To address this, they proposed the crossover-based multiobjective discrete particle swarm optimization (CBMODPSO) algorithm, designed to solve route selection problems in multimodal networks incorporating metro, bus rapid transit (BRT), taxis, and walking. Lee et al. [8] developed a mixed-integer planning model for the public transportation schedule synchronization problem, which considers seamless multimodal transfers and time-dependent travel time data. Similarly, Zhu et al. [9] constructed a super network and a generalized travel cost function and proposed a nonlinear planning model with a solution algorithm based on the C-logit model to solve the co-alignment problem and the path overlap problem of multimodal transportation networks. Song et al. [10] tackled the challenge of all-day multimodal path planning, incorporating user-specific modal preferences to support mobility-as-a-service (MaaS) platform recommender systems. Meanwhile, Zhang et al. [11] explored optimal travel routes that integrate multiple transportation facilities, such as buses, subways, and shared cars, particularly for long-distance urban travel. Although the above studies have broadened the scope of path selection, most have not systematically addressed the synergistic optimization problem of scheduling constraints and path structure dynamics. Our study further develops this foundation by not only introducing multimodal combinations of buses, subways, and walking, but also by incorporating the limitation on the number of transfers as a core constraint to better align with the actual travel scenarios of travelers and enhance the model’s realistic adaptability.
2.2. Urban Multimodal Transportation Path Optimization
Research on urban multimodal transportation path optimization has extensively examined the influence of public transportation schedules on travel path selection. Kumar et al. [12] proposed a schedule-based bus assignment model for the problem of unreliable bus service, modeling passenger route choice as a Markov decision process and developing efficient solution algorithms. Wang et al. [13] conducted a pioneering systematic and empirical study of the K-shortest path problem in schedule-based public transportation systems, proposing an enhanced MS algorithm to solve the K-EAP problem using transient models. Dib et al. [14,15] proposed a heuristic method that combines the genetic algorithm (GA) and variable neighborhood search (VNS) to solve the multiobjective shortest path problem in multimodal networks, considering transportation modes like railroads, buses, trolleys, and walking. Similarly, Idri et al. [16] developed a schedule-based shortest path optimization algorithm specifically designed for multimodal networks. Dib et al. [17] further advanced the field by introducing a modal factor for computing multimodal shortest paths using a simplified version of the time dilation model. Wang et al. [18] proposed a bi-objective integer nonlinear programming (INLP) model that incorporates train schedules into flexible route planning, providing a comprehensive framework for schedule-based multimodal optimization. Additionally, Peng et al. [19,20] addressed the multimodal transportation path problem under uncertainty, developing a mathematical model to analyze the impact of schedules on transport duration. Their work underscores the critical role of transportation schedules in travel efficiency, offering valuable insights for optimizing urban multimodal transportation networks. Although previous studies have considered the impact of public transportation schedules on travel path selection, several limitations remain. First, most algorithms are based on static network assumptions, which fail to capture dynamic changes in traffic conditions. Second, the number of interchanges is often oversimplified, neglecting its significant impact on the actual travel experience of passengers. To address these issues, this paper constructs a multiobjective optimization model that simultaneously incorporates time dependence, temporal constraints, and transfer limitations, thereby enhancing the applicability and practicality of path planning in real-world urban travel environments.
2.3. Algorithms Considering a Time-Dependent Network for the Shortest Path Problem
The time-varying properties of transportation networks remain underexplored in the context of urban multimodal traffic travel path optimization. However, this aspect has attracted growing attention in related domains. Kumar et al. [21] proposed a framework for implementing the shortest path algorithm in both static and time-dependent city networks. Their study demonstrated through example analysis that the A* algorithm with landmarks and triangle inequality (ALT) performed best, offering strong scalability and ease of implementation across different networks. He et al. [22] examined the computational complexity of the time-dependent shortest path problem, focusing on the cost and time constraints associated with waiting at specific nodes. Jaballah et al. [23] introduced the concepts of the transient shortest path and vehicle routing problems, proposing a dynamic time-dependent shortest path algorithm integrated with a simulated annealing approach, and validated its effectiveness through example-based analysis. Gmira et al. [24] focused on the time-varying vehicle routing problem with time windows, highlighting how travel speed is inherently linked to the characteristics of road segments. Pugliese et al. [25] developed an optimal solution strategy using dynamic programming to address the shortest path cruising problem under time window constraints. In response to global warming and traffic congestion concerns, Liu et al. [26] investigated the green vehicle routing problem and proposed an exact method based on the branch-and-cut algorithm to solve the time-dependent green vehicle routing problem with time windows (TDGVRPTW), addressing time-dependent travel times and time window constraints. Zhou et al. [27] studied the time-dependent green location routing problem (TDGLRP), considering carbon emissions, developed an optimization model to minimize total cost, and proposed a two-stage hybrid heuristic algorithm that combines a customized greedy algorithm with an ant colony optimization algorithm. Chen et al. [28] designed a dynamic moment-matching-based A* algorithm to solve responsive shortest path problems in stochastic, time-dependent networks with spatiotemporally correlated travel times. Similarly, Cui et al. [29] proposed a vehicle routing model that considers dual customer time windows and a time-dependent road network, and they developed a memory-based algorithm combining a genetic algorithm with variable neighborhood search to solve the problem. Focusing on public transit, Guo et al. [30] introduced a method that incorporates time dependence and inter-node path flexibility, established a mixed-integer programming model, and developed a hybrid meta-heuristic algorithm for solving it. Sun [31] examined freight routing in road–rail intermodal transportation systems, incorporating soft delivery time windows, demand uncertainties, and capacity constraints. Finally, Liao et al. [32] presented a large-scale road network optimization solution, proposing the time-dependent A* with shortcuts (TDAWS) algorithm to effectively address the time-dependent shortest path problem while accounting for the dynamic nature of road networks. Existing research has primarily focused on freight systems or single-mode path optimization, offering limited applicability to complex urban passenger multimodal networks. Moreover, most algorithms rely on fixed-structure path encoding strategies, lacking the flexibility to adapt to dynamic and variable path structures. In response, we integrate time-dependent characteristics and public transportation schedule constraints into the urban intermodal path planning problem. We propose two genetic algorithms with distinctly different encoding strategies, V-GA and F-GA, designed to enhance adaptability and solution effectiveness in multimodal transportation networks to address the modeling complexity arising from diverse path structures.
In summary, existing studies on urban multimodal transportation path planning face several key limitations. First, much of the current research focuses on shortest path planning within single-mode transportation networks, overlooking the increasing diversity of transportation modes in urban environments. Second, many studies assume static network conditions, failing to adequately account for the time-varying nature of road traffic and its impact on multimodal transportation planning. Third, the scheduling constraints of public transportation systems are often underrepresented in path optimization models, limiting their practical applicability.
To bridge these gaps, this paper integrates time-varying road traffic conditions and public transportation schedules while incorporating the number of transfers as a key constraint. This approach aims to better accommodate the diverse travel needs of urban commuters. Furthermore, this study proposes two genetic algorithms with distinct encoding strategies to efficiently compute time-dependent, multi-criteria shortest paths in multimodal transportation networks with schedule constraints.
3. Problem Description and Modeling Framework
3.1. Problem Description
We present a modeling framework for urban multimodal transportation trips, with a primary focus on timetable representation. The key challenge is accurately capturing the structure of transportation schedules. To address this, we define three essential node types: station, platform, and departure event nodes. In our model, each station is assumed to have a single entrance for simplicity, even though multiple access points may exist in reality. Stations contain multiple platforms where passengers wait for transit services, and these platforms play a crucial role in facilitating transfers. To reflect the hierarchical structure of transportation hubs, we establish a relationship in which each platform belongs to a single station, while a station can contain multiple platforms. Additionally, to differentiate between transportation modes, each station is assigned a mode-specific label (e.g., bus, rail), ensuring clear identification within the multimodal network.
Because a timetable consists of discrete events (e.g., a vehicle departing from a platform), we model time using a spatio-temporal graph. In this representation, each timetable event is mapped to a vertex, where a vehicle departs from platform p at departure time dt and arrives at platform q at arrival time at. Event nodes are embedded with timestamps to track departure and arrival times, ensuring a chronological ordering in which earlier events are designated as senior nodes. Figure 1 provides a simplified schematic of a small multimodal transportation network, illustrating a structure with six stations and nine platforms.
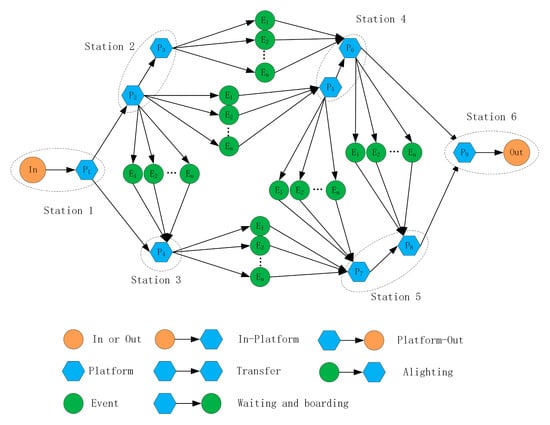
Figure 1.
Illustration of a multimodal transportation network.
The second challenge involves appropriately modeling time dependency in the urban multimodal transportation network. The time-varying nature of arcs in such networks must adhere to the first-in–first-out (FIFO) principle. To ensure computational efficiency without loss of generality, the time interval is divided into N time segments, denoted as , where , . When , it is noted as time period . The segmentation of time periods can be adjusted based on specific practical requirements. Within each time segment , the vehicle moves at a constant speed .
Assuming a vehicle departs from node at time and arrives at node after travel time , the calculation method for is described in Algorithm 1 to ensure that vehicle travel time adheres to the FIFO principle.
| Algorithm 1: Calculation method for . |
| 1: ,; 2: while do 3: 4: 5: 6: 7: end while 8: 9: end |
Considering the two challenges discussed above and for the sake of clarity in the algorithm’s description in the following section, each station is treated as a node. Consequently, Figure 1 is simplified and reformulated as a simplified network in Figure 2, where the six nodes represent the six stations.
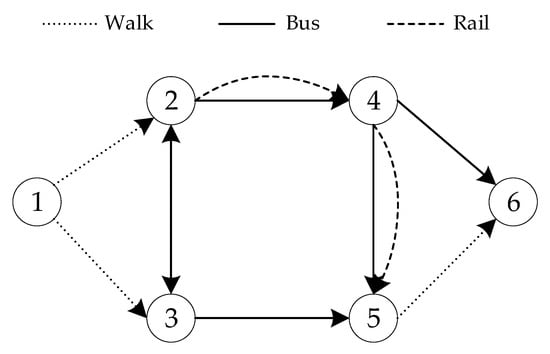
Figure 2.
A simplified network for mathematical modeling.
Let denote a multimodal directed graph with time dependency, where represents the set of nodes, is the set of arcs, and is the set of transport modes (e.g., rail, bus, walking). The travel time from node at time to node via arc . Each arc can be identified by , where and . indicate the feasibility of traveling from node to node using transport mode .
A path is multimodal if , , , , and , where a passenger’s journey starts at O at departure time and ends at D at time t, with a total travel time of . The objective is to determine the shortest multimodal path that minimizes the total travel time while adhering to the given constraints.
In our modeling framework, passengers in urban public transportation systems aim to minimize not only travel time but also other critical factors, such as cost and the number of transfers. The travel cost incurred in our study encompasses multiple components, including waiting time cost, travel time cost, and transfer time cost, providing a comprehensive measure of overall travel efficiency.
3.2. Model Framework
We formulate the following modeling framework to model urban multimodal transportation trips. Symbols and variables of the model is defined in Table 1.

Table 1.
Definitions of symbols and variables.
The moment a passenger arrives at node i to complete a transfer and reach the platform for the passenger’s next ride while adhering to the public transportation schedule is determined as follows.
Then, the departure time ai at node i is determined by
The moment a passenger arrives at node j is defined as follows.
The passenger’s waiting time at node i is given by
Therefore, the total travel time is calculated as follows.
The objective of our model is to minimize the total travel time while considering costs incurred and interchange constraints. Based on these criteria, the urban multimodal transportation travel path optimization model is formulated as follows.
Constraints:
Equation (6) defines the objective function, while Equation (7) constrains the total travel cost. Equation (8) limits the number of transfers within the travel path. Equations (9) and (10) enforce path continuity by ensuring that the journey starts at the origin O and ends at the destination D, respectively. Equation (11) maintains network equilibrium at intermediate nodes, ensuring that every passenger arriving at an intermediate node must also depart. Equation (12) restricts each transportation process to a single occurrence between any two nodes. Equation (13) limits each node to one transfer at most, while Equation (14) guarantees route continuity throughout the journey.
4. Two GA-Based Algorithms
The genetic algorithm is a computational model that simulates biological evolution. It is widely applied to various optimization problems as a global optimization search algorithm due to its simplicity, versatility, and robustness. In this study, we design a solution strategy for the proposed problem based on the genetic algorithm. The algorithm’s framework is outlined in Algorithm 2 below.
| Algorithm 2: V-GA (or F-GA). |
| Require: Parameters Pc, Pm, termination condition Nd, population size 1: Initialize the population 2: for all Nd do 3: Calculate the fitness Fit of each genetic individual in the population 4: Update the global best solution 5: Selection 6: Crossover 7: Mutation 8: end |
4.1. Coding and Decoding
Our study introduces two coding strategies for genetic algorithms: variable-length coding (V-GA) and full permutation coding (F-GA).
The V-GA chromosome encoding length varies based on the number of nodes in the route. Each chromosome consists of two segments: the first segment represents the sequence of nodes traversed, while the second segment specifies the mode of transportation between nodes. If a node is not part of the travel path, its corresponding transportation mode is denoted as 0. Consecutive identical transportation modes within the second segment are considered a continuous ride, meaning no interchange occurs. However, a direct switch between bus and rail, or a transition from bus to rail via walking, is classified as an interchange. In contrast, walking at the start or end of a journey is not considered an interchange. Figure 3 illustrates the encoding and decoding correspondences for two example travel paths within the network introduced in Figure 2. Specifically, “W”, “B” and “R” in the following figures stand for “Walk”, “Bus” and “Rail”, respectively.
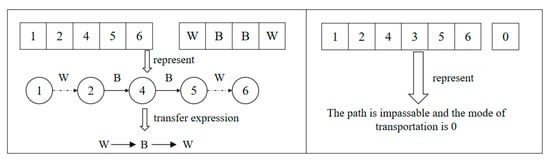
Figure 3.
Path and transportation mode diagram of V-GA.
The F-GA chromosome’s encoding is also structured into two segments. The first segment represents a full permutation of network node numbers, with the first position fixed as the departure node (node 1). The nodes appearing between node 1 and node 6 indicate the traversal path. The second segment specifies the mode of transportation between consecutive nodes. Commutations are handled in the same manner as in V-GA. Figure 4 illustrates the encoding and decoding correspondences for the F-GA chromosome of the network in Figure 2.
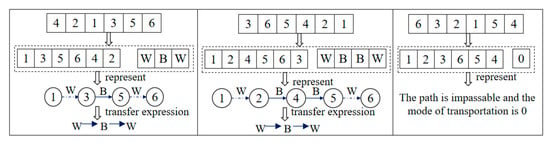
Figure 4.
Path and transportation mode diagram of F-GA.
4.2. Initial Population Generation
In genetic algorithms, the initial population may directly affect the convergence speed and the results of the algorithm. We describe the steps for generating the initial population for both V-GA and F-GA in the following section.
- (1)
- V-GA
The V-GA method leverages the characteristics of multimodal transportation by employing an adjacency matrix approach to generate the initial population. This ensures that all generated paths are valid, effectively reducing the infeasible solution space of traditional genetic algorithms. By avoiding loops and invalid paths, this approach enhances efficiency. The steps are as follows:
Step 1: Construct a connectivity adjacency matrix based on the available transportation modes in the urban multimodal transportation network. If at least one mode connects two points, they are considered connected; otherwise, they are not.
Step 2: Use the adjacency matrix to generate the first segment of an individual’s chromosome, representing the sequence of nodes. Then, randomly assign a transportation mode between nodes to form the second segment, completing the encoding of an initial individual.
Step 3: If the population size reaches the desired number, terminate the process. Otherwise, return to Step 2 and repeat.
- (2)
- F-GA
The F-GA method constructs a path from the origin to the destination by selecting network nodes, ensuring that nodes beyond the destination are excluded from the selection process. The second segment of the chromosome is generated by randomly assigning transportation modes between the selected nodes, forming a complete route representation.
4.3. Calculating Individual Fitness Values
Genetic algorithms mimic natural selection by evaluating chromosomes based on a fitness function, fostering an evolutionary process where stronger solutions prevail. Typically, a chromosome with a higher fitness value is considered superior. Because this study aims to minimize passengers’ total travel time, the fitness value is computed as the inverse of the objective function. Consequently, chromosomes representing shorter travel times yield higher fitness values, increasing their likelihood of contributing to the next generation.
4.4. Selection
The selection process aims to identify superior individuals within the current population by evaluating their fitness. Higher-fitness individuals are more likely to be chosen as parents, ensuring that advantageous traits are passed on to the next generation. The principle of selection follows the idea that well-adapted individuals have a greater probability of contributing one or more offspring to the subsequent population. Fitness can be calculated using two common approaches: the proportional fitness function and sorting-based fitness evaluation. Below, we describe several widely used selection operators.
- (1)
- Roulette selection
Roulette selection, also known as the proportional fitness selection method, is one of the most fundamental and widely used selection techniques in genetic algorithms. The core principle is that an individual’s probability of being selected is directly proportional to its fitness value. The selection process is outlined as follows: let the size of the population be n and the fitness value of its individual i be , and then the probability of i being selected is determined by Equation (15).
Clearly, the probability pi represents the proportion of individual i’s fitness relative to the total fitness sum of the population. The greater an individual’s fitness, the greater its probability of being selected, and, conversely, individuals with lower fitness have a reduced chance of selection. Once the selection probabilities for each individual are calculated, the process determines which individuals will be selected based on these probabilities.
- (2)
- Random traversal sampling
Similarly to the roulette selection operation, the probability of selection remains the same. However, individuals are selected based on random traversal sampling, which involves selecting individuals at medium distances through a stochastic process.
- (3)
- Local selection
Local selection can take two forms. The first is based on a linear neighbor set, where a defined distance creates a local area in a linear arrangement. The second form is based on a diagonal neighbor set, where individuals are selected from the two diagonals within the local area.
- (4)
- Truncated selection
The individuals in the population are ranked based on fitness, and a truncation threshold parameter (representing the percentage of individuals selected as parents) is used to define the selection boundary. Individuals positioned before the boundary are selected as the elite candidates for reproduction.
- (5)
- Tournament selection
A specified number of individuals is randomly selected from the population, with the best individual chosen as the parent. This selection process is repeated to identify additional parents for reproduction.
In this study, we primarily employ the roulette wheel strategy for the selection operation in genetic algorithms.
4.5. Crossover
- (1)
- V-GA
In the variable-length genetic algorithm, a traditional single-point crossover strategy is utilized. There are two scenarios for the chromosomes selected for crossover: first, when the two parent chromosomes share the same nodes (excluding the starting and ending nodes); and second, when the parent chromosomes have different nodes. To address these cases, a single-node crossover method is designed to perform the crossover operation on the first segment of the chromosome.
For the first case, we use the same nodes to conduct cross-operation. Assume that and are two chromosomes. Select the same node, except the starting node and the final node, as the intersection point in these two chromosomes, and switch the parts after the same node. If there are multiple identical nodes, then randomly select one sharing node as the intersection point. For example, as , then the following two new chromosomes, and , can be obtained. Obviously, these two new chromosomes are also a feasible path from starting point 1 to ending point n. Take the network shown in Figure 2 as an example. This type of crossover operation is shown in Figure 5.

Figure 5.
Diagram of the crossover operation in the V-GA algorithm with common nodes.
During crossover with identical nodes, duplicate genes may appear, resulting in a loop in the path (as shown in Figure 6), which needs to be eliminated. To resolve this, the genes between the duplicates are deleted. For instance, consider two valid parent paths, 1-2-3-5-6 and 1-3-2-4-6. If node 3 is chosen as the crossover point, the resulting offspring are 1-2-3-2-4-6 and 1-3-5-6. One of these offspring contains a loop, which is then removed by deleting the duplicated node, yielding the valid individual 1-2-4-6.
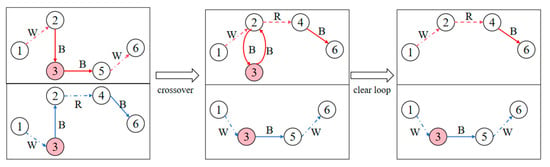
Figure 6.
Diagram of handling loop formation.
Because real-world networks are often incomplete, the second case presents a challenge where crossover operations may result in illegal individuals. These illegal individuals must be corrected to ensure the validity of the solution. For example, consider the network in Figure 2, where node 1 is the starting node and node 6 is the destination. Two valid parent paths, 1-2-4-6 and 1-3-5-6, are selected for crossover. As shown in Figure 7, a gene position {3, 2} is randomly chosen for the crossover operation. The resulting offspring path, 1-2-3-5-6, is invalid because there is no direct arc segment between node 2 and node 5. To correct this, a valid path from node 2 to node 5 is found using the method described in Section 4.1, ensuring that the child chromosome becomes a valid path.
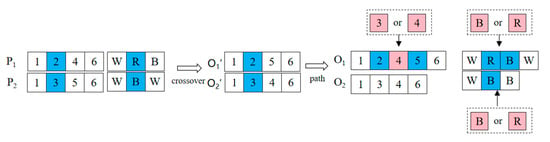
Figure 7.
Diagram of the crossover operation in the V-GA algorithm without common nodes.
After completing the crossover on the first segment of the chromosome, the transport modes for the unchanged gene segments are retained in the second segment. For the segments that have been altered, transport modes between the nodes are randomly selected to generate the corresponding second segment.
Algorithm 3 shows the pseudocode for the crossover operation of the V-GA algorithm.
| Algorithm 3: For crossover of V-GA. |
| Require: Parent solutions S1 and S2, crossover probability Pc 1: if random() <= Pc then 2: Get segments S1-1, S2-1 from S1, S2 3: Calculate the number of identical nodes n (excluding start and end points) 4: if n = 0 then 5: if min (length(S1-1), length(S2-1)) = 2 then 6: print S1 and S2 7: else then 8: Randomly choose the crossover point 9: Crossover to form O1-1, O2-1 10: if not connected at crossover points, then 11: Find connecting path 12: end if 13: end if 14: else then 15: Randomly select the identical node (excluding ends) as the crossover point 16: Crossover to form O1-1, O2-1 17: end if 18: if cycles in O1-1 or O2-1, then 19: Remove cycles 20: end if 21: Keep the original transportation mode for unchanged segments 22: Randomly select transportation mode for changed segments 23: (Optional) Further process or evaluate O1, O2 24: end if |
- (2)
- F-GA
The crossover process for full permutation encoding primarily involves exchanging the first segment of the genes. The procedure starts by randomly selecting a crossover position and then swapping the sections before the crossover point. The numbers following the crossover position are taken from the remaining numbers in the other gene and placed sequentially afterward. After completing the crossover operation for the first segment, the transportation modes between the start and end points are randomly selected to generate the corresponding second segment’s encoding. If the resulting path is not feasible, the second segment’s encoding is set to 0. The diagram for the full permutation crossover is shown in Figure 8 below.

Figure 8.
Diagram of the crossover operation in the F-GA algorithm.
4.6. Mutation
- (1)
- V-GA
A single-point mutation method is employed, which involves randomly selecting a path and choosing a mutation position, denoted as k, in the first segment of the encoding. The node at the mutation position is removed, and the Floyd algorithm is then applied to connect the path between nodes Vk−1 and Vk+1, linking the nodes before and after the mutation position. After completing the mutation on the first segment of the encoding, the transportation modes in the second segment of the encoding are retained for the gene fragments that remain unchanged. For the parts of the chromosome where the first segment has been altered, transportation modes between nodes are randomly selected to generate the corresponding second segment’s encoding. If a loop is detected, the method described in Section 4.5 is used to eliminate it. The specific mutation process is illustrated in Figure 9. When a mutation occurs at node 5, node 5 is removed, and a connected path from node 3 to node 6 is identified, forming the corresponding transportation mode and resulting in a new valid path.
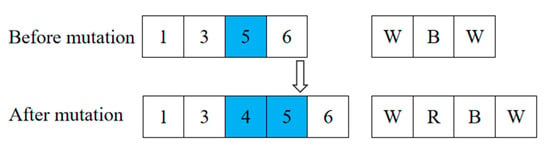
Figure 9.
Diagram of the mutation operation in the V-GA algorithm.
Algorithm 4 shows the pseudocode for the mutation operation of the V-GA algorithm.
| Algorithm 4: Mutation of V-GA. |
| Require: Parent solutions S1, mutation probability Pm
1: extract segment S1-1 from S1 with length n 2: if random() <= Pm then 3: Choose random mutation position k in S1-1 4: Remove the kth gene from S1-1 5: Find the path between (k−1)th and (k+1)th genes using Floyd’s 6: Insert this path into S1-1 to form a new segment O1-1 7 if O1-1 is unchanged then 8: keep original transportation modes 9: else then 10: Randomly select new transportation modes 11: end if 12: end if |
- (2)
- F-GA
For the mutation operation in F-GA, a two-point exchange is applied to the first segment of the chromosome’s encoding. Two genes other than the starting node (node 1) are randomly selected for exchange. Then, the transportation modes between the nodes are randomly generated to form the second segment’s encoding, resulting in the creation of a new individual in the population. The specific mutation operation is illustrated in Figure 10.
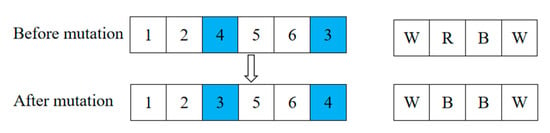
Figure 10.
Diagram of the mutation operation in the F-GA algorithm.
4.7. Elitism Strategy and Termination Condition
Both the V-GA and F-GA algorithms employ an elite retention strategy, which is designed to prevent the accidental elimination of the best individuals in the population during the iterative process. This strategy ensures that the fittest individuals are preserved and carried over to subsequent iterations, maintaining their contribution to the optimization process.
There are two common criteria for terminating a genetic algorithm. One is when the fitness function value stabilizes, showing no significant changes after several consecutive iterations. The other is to set a maximum number of iterations and stop the algorithm once this limit is reached. Given our study’s large model complexity and computational demands, waiting for the fitness function value to stabilize could lead to lengthy computation times and reduced solution efficiency. To improve efficiency, we adopted the second approach, setting a maximum of 50 generations for the algorithm and halting the operation once this number of iterations was reached.
4.8. Algorithm Complexity Analysis
In this section, we provide a detailed analysis of the computational complexity of the two genetic algorithms, V-GA and F-GA. These algorithms display considerable differences in both time and space complexity. The time complexity analysis addresses the main operational stages: population initialization, fitness evaluation, selection, crossover, and mutation.
During population initialization, V-GA constructs and traverses an adjacency matrix, resulting in a time complexity of O(n2 + m), where n is the number of nodes in the network and m is the population size. In contrast, F-GA generates individuals by randomly selecting transportation modes, with a time complexity of O(m × n). For fitness calculation, both algorithms must traverse the nodes and arcs of the paths, yielding a time complexity of O(m × k), where k is the average path length. Both algorithms employ a roulette wheel selection strategy in the selection operation, each with a time complexity of O(m). The crossover operation differs notably between the two:
- In V-GA, crossover must handle both same-node and different-node operations. Same-node crossover has an O(k) time complexity, while different-node crossover requires O(k2). Thus, the overall crossover complexity for V-GA is O(m × k2).
- In F-GA, crossover is simpler, achieved by exchanging partial gene sequences, with a time complexity of O(m × k).
Regarding the mutation operation:
- V-GA performs node deletion and reconnection, resulting in a mutation time complexity of O(k2) per individual, or O(m × k2) for the population.
- F-GA only needs to swap two randomly selected genes, with a mutation time complexity of O(1) per individual and O(m) overall.
Both V-GA and F-GA must store each chromosome and its associated fitness value for space complexity. Because each chromosome stores the path nodes and the corresponding transportation modes, the space complexity for both algorithms is O(m × k).
In summary, the total time complexity of V-GA is O(m × k2), and its space complexity is O(m × k). The total time complexity of F-GA is O(m × k), with the same space complexity as O(m × k). This analysis demonstrates that V-GA, while having higher computational overhead, provides enhanced global search capabilities and precision, making it appropriate for complex, dynamic network scenarios. In contrast, F-GA is more computationally efficient and better suited to large-scale networks with relatively stable and simple path structures.
5. Computational Experiments
When constructing numerical examples, considering that self-generated random data might lack authority and representativeness, the instances used in this paper are modified versions of the standard Solomon lxiv instances. In the Solomon instances, data are categorized into three types: clustered distribution (C class), random distribution (R class), and semi-clustered distribution (RC class). This paper selects the coordinates from point 2 to point 31 in Solomon’s C101 instance, corresponding to the nodes 1 to 30 in Figure 11, to obtain the distances between nodes. The intervals between departures of different transportation modes and the departure and arrival times are shown in Table 2. The speeds of various transportation modes are given in Table 3. Transfer time costs and waiting time costs are simplified, and detailed unit travel costs are provided in Table 4. A passenger departs from starting point 1 to destination 30 at 8:00 (480 min). How should travel be organized to minimize the time required to reach the destination under the constraints of limited travel expenses () and the number of transfers ()?
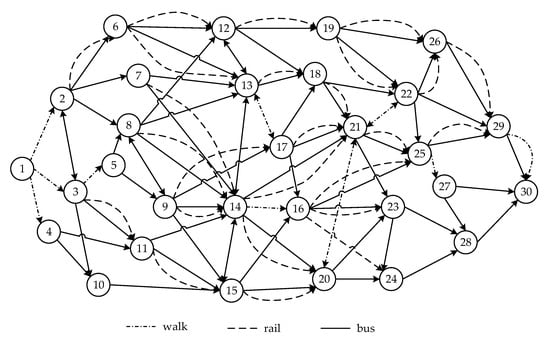
Figure 11.
An urban multimodal transportation network.

Table 2.
Time-dependent speeds and timetables of different transport modes.

Table 3.
Transfer times between different transportation modes.

Table 4.
The travel cost per unit of time.
A population size of and a maximum number of iterations () were set. The computations were conducted using MATLAB 2018b on a computer equipped with an Intel Core i5 CPU and 4.0 GB of RAM. By continuously adjusting the crossover probability (Pc) and the mutation probability (Pm), V-GA and F-GA were executed for 8 runs with varying parameters. The best fitness value (B), mean best fitness value (A), average runtime (Time), and mean number of iterations (N) required to reach the optimal value for the first time were recorded. The results are presented in Table 5.

Table 5.
Results of two algorithms under different parameters.
After running with different crossover probabilities and mutation probabilities, the best fitness value was obtained from the V-GA algorithm, and its optimal path is shown in Figure 12.
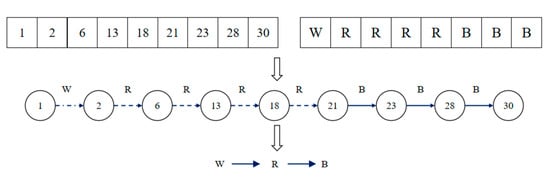
Figure 12.
The optimal travel path solution.
During the 8 runs with different parameters, in terms of the optimal value, the V-GA algorithm demonstrates good stability with minimal fluctuation in the optimal value. In contrast, the F-GA algorithm shows significant variation in each run result. From the perspective of the solution space, the V-GA algorithm’s encoding changes around valid paths during crossover and mutation. Thus, the optimization process operates within the feasible solution space. In contrast, the F-GA algorithm is more likely to generate invalid paths, leading to a population that includes infeasible solutions, expanding the solution space and resulting in more ineffective computations during the optimization process.
Detailed comparative charts of the average best fitness values, the average runtime, and the mean number of iterations until reaching the optimal value for the two algorithms under different parameters are shown in Figure 13, Figure 14 and Figure 15 respectively. It can be observed that (1) under the same parameters, the best fitness values obtained by the V-GA algorithm are lower than those of the F-GA algorithm, making the V-GA algorithm more effective than the F-GA algorithm; (2) under the same parameters, the runtime of the F-GA algorithm is shorter than that of the V-GA algorithm; and (3) in most cases, the mean number of iterations until reaching the optimal value for the first time is smaller for the F-GA algorithm compared to the V-GA algorithm.
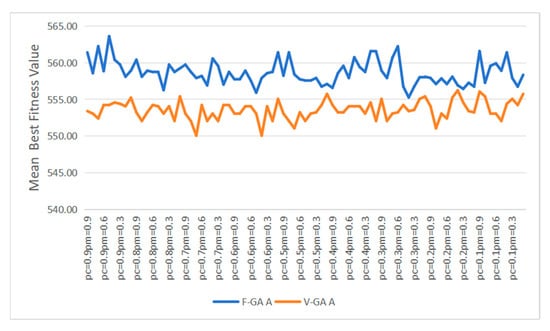
Figure 13.
The changes in the mean optimal fitness value under different parameters.
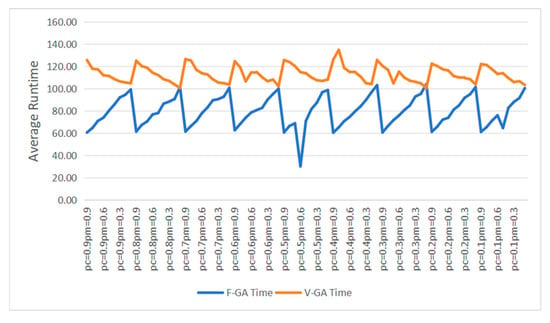
Figure 14.
The average running time under different parameters.
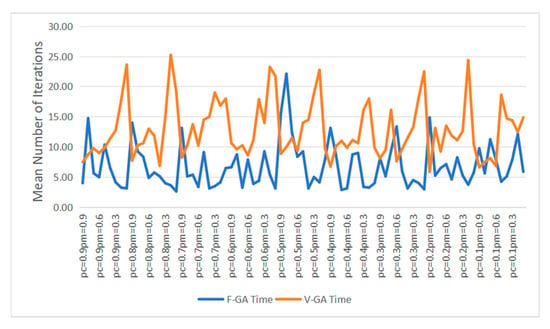
Figure 15.
The number of iterations required to reach the optimal fitness value for the first time under different parameters.
The above analysis found that the V-GA algorithm achieves the smallest mean best fitness value with two parameter combinations, crossover probability Pc = 0.7 and mutation probability Pm = 0.7, as well as Pc = 0.6 and Pm = 0.4. For the F-GA algorithm, the smallest mean best fitness value is achieved when the crossover probability Pc = 0.3 and the mutation probability Pm = 0.4. Another parameter combination closest to this value is Pc = 0.6 and Pm = 0.5. Under these parameter combinations, the impact of different population sizes on the algorithm is analyzed. Detailed data are shown in Table 6.

Table 6.
Comparison results of the two algorithms under different population sizes.
Figure 16 shows that regardless of population size, the V-GA algorithm achieves better optimal fitness values than the F-GA algorithm, which has a shorter runtime.
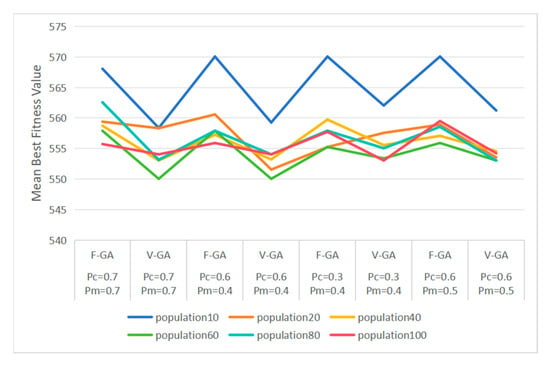
Figure 16.
Changes in the optimal fitness value under different population sizes and parameters.
To further evaluate the performance differences between V-GA and F-GA across multiple metrics, paired-sample t-tests were conducted using SPSS Statistics 26 based on the data presented in Table 5. The four metrics analyzed were best fitness value, average best fitness value, runtime, and number of iterations required to reach the optimal value for the first time. The significance test results are summarized in Table 7.

Table 7.
Statistical significance testing results between V-GA and F-GA.
The results show that V-GA significantly outperforms F-GA in terms of best fitness value (t = 7.315, p < 0.001), indicating that V-GA consistently finds better solutions across multiple runs. Similarly, for the average best fitness value, V-GA again shows a significant advantage (t = 12.570, p < 0.001), further demonstrating its stability and superiority in optimization performance. However, regarding mean runtime, V-GA exhibits a significantly longer runtime than F-GA (t = −6.785, p < 0.001). This suggests that while V-GA delivers better solution quality, it incurs higher computational overhead, which should be carefully considered in applications requiring high real-time performance. For the average number of iterations, V-GA also requires significantly more iterations than F-GA (t = −3.133, p = 0.005). This implies that V-GA performs more iterative searches to ensure higher solution accuracy, contributing further to its longer running time.
In summary, the statistical significance analysis confirms that while V-GA achieves superior solution quality compared to F-GA, it does so at the cost of increased computational time and a greater number of iterations. Therefore, V-GA is well-suited to multimodal path optimization tasks where solution quality is critical, whereas F-GA may be more appropriate for applications where computational efficiency is a priority.
6. Conclusions
We explore the optimization of urban multimodal transportation routes by integrating three primary modes: regular buses, rail transit, and walking. Our study addresses the complexities introduced by time-varying traffic conditions and public transportation schedules, optimizing for travel time, transfer frequency, and travel costs incurred. To solve this problem, we propose two optimization methods: the variable-length coding genetic algorithm (V-GA) and the full permutation coding genetic algorithm (F-GA). Numerical experiments demonstrate that V-GA outperforms F-GA, achieving more efficient optimization results with reduced computation time. Our results demonstrate the strong potential of V-GA for solving urban multimodal transportation optimization problems and lay a solid foundation for future research in this field. However, several limitations remain. First, the model is constructed on a deterministic network, which does not fully account for real-world factors, such as traffic flow fluctuations and scheduling uncertainties. Second, the current algorithm is primarily designed for predefined, structured path environments and exhibits limited responsiveness to unexpected events, particularly in boundary scenarios, such as missed connections or peak congestion. These aspects present important directions for further improvement.
To enhance the practical applicability and robustness of the proposed method, future research can be extended in the following directions:
- (1)
- Model Extension: Real-world urban multimodal networks are marked by various uncertainties. Future work could systematically include factors like traffic flow fluctuations, public transportation schedule unpredictability, and dynamic changes in user travel preferences. Developing stochastic or dynamic network models would enable more realistic and in-depth study of the path optimization problem, aligning research outcomes more closely with actual travel scenarios.
- (2)
- Introduction of Soft Time Window Constraints and Delay Penalty Mechanisms: To enhance the realism and robustness of path planning, future studies could introduce soft time window constraints and delay penalties. This would facilitate a more accurate simulation of missed or delayed trips, thereby improving the adaptability and stability of the V-GA method in complex urban transportation environments and making the planning results more practical and reliable.
- (3)
- Algorithm Improvement: Building on the findings of this study, future work could explore more advanced intelligent optimization algorithms to enhance computational efficiency and optimization performance. This would improve the overall stability and effectiveness of multimodal transportation systems, providing more efficient and higher-quality solutions for real-world applications.
- (4)
- Integration of Data-Driven and Artificial Intelligence Technologies: Future research could fully leverage historical travel and user behavior data, combined with artificial intelligence techniques, to learn from actual users’ travel patterns. This would enable dynamic optimization and adaptive model adjustment, supporting the creation of a smarter, more adaptable, and reliable multimodal transportation system that better meets diverse and personalized travel needs.
Author Contributions
Conceptualization, Y.P.; methodology, Y.P., A.M., D.Z.Y. and T.Z.; formal analysis, Y.P., A.M., D.Z.Y. and T.Z.; data curation, Y.P., A.M., T.Z. and C.X.; writing—original draft preparation, A.M. and T.Z.; writing—review and editing, D.Z.Y. and C.X.; visualization, A.M., D.Z.Y. and C.X.; supervision, D.Z.Y.; project administration, D.Z.Y.; funding acquisition, Y.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Graduate Student Tutor Team Building Program in Chongqing, No. JDDSTD2022004; the Graduate Student Research Innovation Program of Chongqing Jiaotong University, No. 2023S0060; and the Transport Science and Technology Project in Chongqing, No. CQJT-2024CZ28-3 and No. CQJT-2024CZ31-1.
Data Availability Statement
The data are available upon request.
Conflicts of Interest
All authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
References
- Sifaoui, T.; Aïder, M. Beyond green borders: An innovative model for sustainable transportation in supply chains. ARIRO-Oper. Res. 2024, 58, 2185–2237. [Google Scholar] [CrossRef]
- Bellman, R. On a routing problem. Q. Appl. Math. 1958, 16, 87–90. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Witzgall, C.; Goldman, A.J. Most profitable routing before maintenance. In Proceedings of the 27th National ORSA Meeting, Boston, MA, USA, 6–7 May 1965; Volume 13, p. B-82. [Google Scholar]
- Nguyen, S.; Pallottino, S. Equilibrium traffic assignment for large scale transit networks. Eur. J. Oper. Res. 1988, 37, 176–186. [Google Scholar] [CrossRef]
- Spiess, H. On Optimal Route Choice Strategies in Transit Networks; Université de Montréal, Centre de Recherche sur les Transports: Montreal, QC, Canada, 1983; Volume 286. [Google Scholar]
- Afrasyabi, P.; Mesgari, M.S.; Khodadai, N.; Kaveh, M. CBMODPSO: Crossover based multi-objective discrete particle swarm optimization for solving multi-modal routing problem. Res. Sq. 2022. preprint. [Google Scholar]
- Lee, K.; Jiang, Y.; Ceder, A.A.; Dauwels, J.; Su, R.; Nielsen, O.A. Path-oriented synchronized transit scheduling using time-dependent data. Transp. Res. Part C Emerg. Technol. 2022, 136, 103505. [Google Scholar] [CrossRef]
- Zhu, J.X.; Luo, Q.Y.; Guan, X.Y.; Yang, J.L.; Bing, X. A traffic assignment approach for multi-modal transportation networks considering capacity constraints and route correlations. IEEE Access 2020, 8, 158862–158874. [Google Scholar] [CrossRef]
- Song, Y.; Li, D.; Cao, Q.; Yang, M.; Ren, G. The whole day path planning problem incorporating mode chains modeling in the era of mobility as a service. Transp. Res. Part C Emerg. Technol. 2021, 132, 103360. [Google Scholar] [CrossRef]
- Zhang, T.; Hu, D.; Chen, H. Research on Urban Multi-Mode Public Transport Trip Path Based on Super Network Theory; CICTP: Xi’an, China, 2020; pp. 2502–2513. [Google Scholar]
- Kumar, P.; Khani, A. Schedule-based transit assignment with online bus arrival information. Transp. Res. Part C Emerg. Technol. 2023, 155, 104282. [Google Scholar] [CrossRef]
- Wang, S.; Yang, Y.; Hu, X.; Li, J.; Xu, B. Solving the K-shortest paths problem in timetable-based public transportation systems. J. Intell. Transp. Syst. 2016, 20, 413–427. [Google Scholar] [CrossRef]
- Dib, O.; Manier, M.A.; Moalic, L. Advanced modeling approach for computing multicriteria shortest paths in multimodal transportation networks. In Proceedings of the 2016 IEEE International Conference on Intelligent Transportation Engineering (ICITE), Singapore, 20–22 August 2016; pp. 40–44. [Google Scholar]
- Dib, O.; Moalic, L.; Manier, M.A.; Caminada, A. An advanced GA–VNS combination for multicriteria route planning in public transit networks. Expert Syst. Appl. 2017, 72, 67–82. [Google Scholar] [CrossRef]
- Idri, A.; Oukarfi, M.; Boulmakoul, A.; Zeitouni, K.; Masri, A. A new time-dependent shortest path algorithm for multimodal transportation network. Procedia Comput. Sci. 2017, 109, 692–697. [Google Scholar] [CrossRef]
- Dib, O.; Manier, M.A.; Caminada, A. Memetic algorithm for computing shortest paths in multimodal transportation networks. Transp. Res. Procedia 2015, 10, 745–755. [Google Scholar] [CrossRef]
- Wang, X.; Lv, Y.; Sun, H.; Xu, G.; Qu, Y.; Wu, J. A simulation-based metro train scheduling optimization incorporating multimodal coordination and flexible routing plans. Transp. Res. Part C Emerg. Technol. 2023, 146, 103964. [Google Scholar] [CrossRef]
- Peng, Y.; Yong, P.; Luo, Y. The route problem of multimodal transportation with timetable under uncertainty: Multi-objective robust optimization model and heuristic approach. RAIRO-Oper. Res. 2021, 55, S3035–S3050. [Google Scholar] [CrossRef]
- Peng, Y.; Luo, Y.J.; Jiang, P.; Yong, P.C. The route problem of multimodal transportation with timetable: Stochastic multi-objective optimization model and data-driven simheuristic approach. Eng. Comput. 2022, 39, 587–608. [Google Scholar] [CrossRef]
- Kumar, B.A.; Gracious, R.; Gangrade, C.; Vanajakshi, L. City-level route planning with time-dependent networks. Curr. Sci. 2020, 119, 680–690. [Google Scholar] [CrossRef]
- He, E.; Boland, N.; Nemhauser, G.; Savelsbergh, M. Time-dependent shortest path problems with penalties and limits on waiting. Inf. J. Comput. 2021, 33, 997–1014. [Google Scholar] [CrossRef]
- Jaballah, R.; Veenstra, M.; Coelho, L.C.; Renaud, J. The time-dependent shortest path and vehicle routing problem. INFOR Inf. Syst. Oper. Res. 2021, 59, 592–622. [Google Scholar] [CrossRef]
- Gmira, M.; Gendreau, M.; Lodi, A.; Potvin, J.Y. Tabu search for the time-dependent vehicle routing problem with time windows on a road network. Eur. J. Oper. Res. 2021, 288, 129–140. [Google Scholar] [CrossRef]
- Pugliese, L.D.P.; Ferone, D.; Festa, P.; Guerriero, F. Shortest path tour problem with time windows. Eur. J. Oper. Res. 2020, 282, 334–344. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Y.; Zhang, Y.; Baldacci, R.; Tang, J.; Luo, X.; Sun, W. Branch-cut-and-price for the time-dependent green vehicle routing problem with time windows. Inf. J. Comput. 2023, 35, 14–30. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, C.; Xu, Q. Time-dependent green location-routing problem under carbon cap-and-trade policy. Transp. Res. Rec. 2023, 2677, 1135–1150. [Google Scholar] [CrossRef]
- Chen, P.; Tong, R.; Yu, B.; Wang, Y. Reliable shortest path finding in stochastic time-dependent road network with spatial-temporal link correlations: A case study from Beijing. Expert Syst. Appl. 2020, 147, 113192. [Google Scholar] [CrossRef]
- Cui, S.; Sun, Q.; Zhang, Q. A time-dependent vehicle routing problem for instant delivery based on memetic algorithm. Comput. Intell. Neurosci. 2022, 2022, 5099008. [Google Scholar] [CrossRef]
- Guo, R.; Zhang, W.; Guan, W.; Ran, B. Time-dependent urban customized bus routing with path flexibility. IEEE Trans. Intell. Transp. Syst. 2020, 22, 2381–2390. [Google Scholar] [CrossRef]
- Sun, Y. Fuzzy approaches and simulation-based reliability modeling to solve a road–rail intermodal routing problem with soft delivery time windows when demand and capacity are uncertain. Int. J. Fuzzy Syst. 2020, 22, 2119–2148. [Google Scholar] [CrossRef]
- Liao, L.; Yang, S.; Lai, Y.; Zeng, W.; Yang, F.; Jiang, M. Efficient estimation of time-dependent shortest paths based on shortcuts. In Proceedings of the International Conference on Algorithms and Architectures for Parallel Processing, Copenhagen, Denmark, 10–12 October 2022; Springer International Publishing: Cham, Switzerland, 2022; pp. 18–32. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).