Abstract
This study investigates the task allocation problem for multiple mobile robots in complex real-world scenarios. To address this challenge, a distributed game-theoretic approach is proposed to enable collaborative decision-making. First, the task allocation problem for multiple mobile robots is formulated to optimize the resource utilization. The formulation also takes into account comprehensive constraints related to robot positioning and task timing. Second, a game model is established for the proposed problem, which is proved to be an exact potential game. Furthermore, we introduce a novel utility function for the tasks to maximize the resource utilization. Based on this formulation, we develop a game-theoretic coalition formation algorithm to seek the Nash equilibrium. Finally, the algorithm is evaluated via simulation experiments. Another six algorithms are used for comparative studies. When the problem scale is small, the proposed algorithm can achieve solution quality comparable to that of the benchmark algorithms. In contrast, under larger and more complex problem instances, the proposed algorithm can achieve up to a 50% performance improvement over the benchmarks. This further confirms the effectiveness and superiority of the proposed method. In addition, we evaluate the solution quality and response time of the algorithm, as well as its sensitivity to initial conditions. Finally, the proposed algorithm is applied to a post-disaster rescue scenario, where the task allocation results further demonstrate its superior performance.
1. Introduction
1.1. Motivation and Incitement
Multiple-mobile-robot systems have attracted increasing attention, owing to the improved ability and enhanced fault tolerance in complex tasks [1,2,3,4,5]. In multi-robot systems, complex tasks often require collaboration among multiple robots. These tasks may be predefined before the mission execution phase or may emerge dynamically during the mission [6]. Manual control of mobile robots is increasingly insufficient to meet the growing complexity of real-world environments. Task allocation is a critical challenge in multi-robot systems. An effective task allocation scheme can greatly enhance the efficiency of these systems. A crucial factor in task completion is ensuring that mobile robots have the necessary resources and capabilities to perform one or more tasks, as successful task execution typically requires a combination of diverse resources and capabilities. A key characteristic of multi-robot systems is their heterogeneity, with different robots possessing varying types and amounts of resources and capabilities [7,8]. As a result, tasks often require the cooperation of multiple mobile robots. In the multi-robot task allocation problem, each robot is treated as an agent. For example, in target tracking scenarios, sensor-equipped robots must coordinate to cover areas of interest. In disaster relief scenarios, rescue robots need to collaborate to complete search and rescue tasks efficiently [9]. Therefore, the task allocation process discussed in this paper can be viewed as the division of mobile robots into different coalitions to accomplish tasks, with identifying the optimal coalition structure to maximize the overall utility of the system.
In recent years, task allocation for multiple mobile robots has attracted significant attention. However, most existing studies focus on scenarios where a single robot completes the task independently [10]. These studies typically assume that a single robot can fully undertake the task, overlooking practical scenarios where the task may require multiple robots to collaborate and form a coalition for completion. Currently, research on multi-robot coalition formation for task execution remains limited. Furthermore, most existing studies on multi-robot task allocation focus on objectives such as the number of tasks, time efficiency, or total path length, with less emphasis on maximizing the resource utilization [11]. In practical applications like logistics distribution, manufacturing systems, and post-disaster rescue, the efficient utilization of resources is essential [12,13,14,15]. To address this issue, this paper proposes a resource-oriented optimization model for multi-robot task allocation. The model considers the cooperation among robots and task resource constraints. Its goal is to provide an effective solution to the task allocation problem in practical applications.
To illustrate how the proposed model operates in practical scenarios, we consider a post-disaster rescue situation where intelligent robots need to form cooperative coalitions to complete tasks. In this scenario, each disaster area is treated as a task with varying conditions and resource demands. For example, some certain areas may require basic supplies such as food, drinking water, and medicine, which necessitate the collaboration of multiple mobile robots to transport and distribute these materials. On the other hand, collapsed sites may require heavy equipment, such as autonomous excavation robots and detection robots, to clear debris and search for survivors. The robots’ capabilities are considered as a fixed resource, while the supplies they carry are seen as consumable resources. Moreover, the types and quantities of resources required in different disaster areas vary with time. Therefore, each robot selects suitable tasks based on its capabilities and the specific task requirements.
In such a scenario, due to the limited resources of each robot, a single robot cannot meet all the demands of a disaster area. Each robot may carry different types of resources and possess various capabilities, so cooperation is challenging but necessary for effective post-disaster rescue. As a result, multiple robots often collaborate to form a coalition and jointly complete rescue tasks in a given disaster area. Through this multi-robot cooperation, the rescue process can be carried out quickly and efficiently in complex post-disaster environments, improving rescue efficiency and maximizing resource utilization.
1.2. Related Work
Numerous studies have focused on the multi-robot task allocation problem, which can be classified into centralized methods, distributed methods, and learning-based approaches.
The task allocation problem for multiple robots is NP-hard, making it computationally expensive to find a globally optimal solution. Currently, centralized algorithms are widely used for their global optimization advantages, typically relying on a central control node to coordinate the task allocation among all mobile robots. However, the centralized architecture relies on a central node, and this makes the system vulnerable to failure if the node crashes. Additionally, this approach lacks robustness and reliability in case of environmental uncertainties and dynamic changes. As a result, it is challenging to meet the high reliability requirements of practical applications. Furthermore, the approach can hardly satisfy the distributed decision-making needs in such environments. In task allocation problems, distributed algorithms exhibit greater robustness compared to centralized algorithms, owing to their higher tolerance to single-point failures, better adaptability to dynamic environments, improved scalability, lower communication overhead, and enhanced information security. Since distributed methods do not rely on a single control center, the system can continue functioning even if some robots fail, thereby avoiding the single-point failure issues inherent in centralized approaches. Moreover, distributed algorithms enable robots to make autonomous decisions and adjust task allocation locally, reducing dependence on global information and enhancing adaptability to environmental changes. Additionally, as only necessary information is shared among neighboring robots, distributed methods reduce the communication bandwidth consumption and minimize the risk of data leakage. Therefore, in multi-robot task allocation scenarios, distributed algorithms are generally more robust and efficient.
1.2.1. Centralized Methods
The centralized approach includes optimization and heuristic methods. Optimization methods include exhaustive algorithms, branch-and-bound techniques, dynamic programming, mixed integer programming, and graph theory, etc. [16,17,18]. While these methods can obtain the optimal solution, the solving time increases exponentially as the problem scale grows, and the performance may deteriorate when dealing with nonlinear and complex constraints. Heuristic methods like genetic algorithms and swarm intelligence optimization make a balance between computational accuracy and time efficiency. In recent years, researchers have applied centralized approaches to address various task allocation problems. For example, with genetic algorithms, each robot is represented as a gene, and each task is represented as an index from which each gene derives its value. A chromosome consists of |A| genes, where |A| represents the number of robots. Thus, chromosomes correspond to allocation schemes. The initial population consists of multiple allocation schemes, and through genetic operations such as selection, crossover, and mutation, the algorithm evolves these initial populations toward better regions of the search space, generation by generation. Note that genetic algorithms may be influenced by various control parameters [19,20]. In [21], an improved particle swarm optimization (PSO) algorithm is proposed to maximize the number of survivors in solving the task allocation problem in multi-robot rescue scenarios. In [22], an enhanced multi-objective particle swarm optimization (MOPSO) method is introduced, which incorporates Pareto frontier refinement and a probability-based leader selection strategy to optimize and improve the PSO for collaborative multi-robot task allocation. The objective is to minimize the total travel distance of the robot team while balancing the workload among the robots. In [23], a novel multi-objective ant colony system (MOACS) approach is proposed to solve the task allocation problem in multi-robot collaboration. This approach introduces the innovative solution construction and pheromone updating rules, optimizing both the total and maximum costs of the robot team. In [24], a collaborative discrete bee colony algorithm (CDABC) is proposed for task allocation and scheduling of multiple agricultural robots in smart farms. With comprehensive experiments, the algorithm demonstrates superior performance compared to state-of-the-art algorithms by enhancing both global search and local exploitation capabilities.
1.2.2. Distributed Methods
Most distributed task allocation algorithms are based on auction algorithms, which simulate market auction mechanisms [25,26,27]. The auction algorithm consists of four components: participants, competitive items, income function, and markup strategy. It is characterized by a fast solving speed and clear, flexible operating rules. This method has been widely applied to the task allocation problem of multiple mobile robots. In recent years there have been numerous improvements and advancements to distributed auction algorithms. Based on the auction concept and consistency method, reference [28] developed two algorithms: the Consensus-Based Auction Algorithm (CBAA) for single-task allocation and the Consensus-Based Bundle Algorithm (CBBA) for multi-task allocation. It is proved that both algorithms can achieve the same solution as the greedy algorithm, and they have been applied to the multi-task allocation problem with multiple types of agents. In [29], a distributed task allocation algorithm based on sequential single-item auctions is proposed to address the task allocation problem in multi-robot systems with path constraints. However, auction-based algorithms often exhibit inefficiencies in resource utilization, as they primarily focus on task bidding and allocation rather than optimizing resource usage across robots. This limitation can lead to suboptimal exploitation of available resources, reducing the overall system efficiency. Additionally, these algorithms are typically used for individual bidding strategies over cooperative decision-making, making them less effective in forming flexible coalitions for complex tasks requiring multi-robot collaboration. Furthermore, as the number of tasks and robots increases, the computational complexity of auction mechanisms increases significantly due to the need for extensive bidding and allocation computations, which may deteriorate the real-time performance.
Another widely used distributed task allocation method is the contract net algorithm, which offers significant advantages in solving distributed problems [30]. Its principle is simple, intuitive, and easy to implement with high execution efficiency. As a result, it has been extensively applied in various fields, such as multi-robot task allocation. This distributed method shows characteristics such as parallel computation, decentralized communication, and better scalability and robustness, so it is well suited for large-scale dynamic systems. However, it is challenging to guarantee an optimal solution when this algorithm primarily relies on iterative bidding and task negotiation for allocation, which can result in high communication overhead and computational complexity in large-scale scenarios.
In addition to auction algorithms and contract network algorithms, game theory is also widely applied to distributed task allocation problems [31,32,33,34]. Game theory provides a mathematical framework for multiple robots operating in environments with both conflicting and cooperative relationships. In this framework, each robot makes decisions based on its own goals and constraints. The reward received at the end of the game, depending on the actions taken, is referred to as the payoff. A Nash equilibrium is a state in which no robot can improve its individual payoff by unilaterally changing its strategy, given that the strategies of other robots remain unchanged. Reference [35] investigates the task allocation problem for heterogeneous UAVs in collaborative strike missions, and proposes a model designed to maximize the net task reward by taking into account factors such as payload, flight path, and time coordination. Furthermore, the paper introduces a payoff-based time-variant log-linear learning algorithm. Reference [36] studies the task allocation problem in collaborative edge and cloud computing environments, transforming it into a non-cooperative game model using game theory. It also proposes optimization algorithms that quickly converge to the Nash equilibrium. Reference [37] addresses the cost allocation problem in transmission expansion planning for the power sector using cooperative game theory, where cooperation among players is aimed at maximizing their collective benefits. The paper compares various cost allocation methods and concludes that the bilateral Shapley value effectively facilitates the decentralized cost allocation. Reference [38] proposes a cooperative reconnaissance and spectrum access scheme that optimizes the task selection and bandwidth allocation through the cooperative coalition game theory. The study shows that the proposed joint optimization scheme and the new coalition order outperform traditional methods, achieving stable coalition partitioning and improved system performance. To summarize, the above studies use game theory for task allocation and multi-robot cooperation, but they pay less attention to the goals of coalition formation and resource utilization. Therefore, this paper proposes a task allocation scheme for multi-robot coalitions to maximize resource utilization efficiency.
1.2.3. Learning-Based Methods
In current multi-robot task allocation scenarios, challenges such as uncertainty, interference, and real-time implementation are increasing dramatically. Reinforcement learning methods can help robots cope with environmental uncertainty and interference, optimize decision-making, and achieve real-time task allocation through autonomous learning and experience accumulation [39,40,41]. The key advantage of reinforcement learning is to handle complexity and adapt to dynamic environments in real time, enabling robots to make effective decisions in unforeseen situations. However, a notable challenge is that large-scale systems often require substantial computational resources, and the training process is time-consuming [42].
1.3. Contributions and Paper Organization
To address the multiple-mobile-robot coalition problem with resource utilization, a distributed method based on game theory is proposed for task allocation. Since real tasks typically require multiple robots to cooperate for completion, coalition cooperation among robots becomes crucial. We use game theory to provide an effective analytical framework to model the interactions and interests among robots. This ensures efficient resource utilization and reasonable task allocation within a distributed system. By designing a well-structured game model and utility function, this paper guides robots to form stable coalitions and collaborate in task completion, thereby enhancing the system’s robustness and reliability.
The main contributions of this paper are summarized as follows:
- Existing research on multi-robot task allocation primarily focuses on task allocation and path planning, with limited attention to cooperative coalitions among robots and the optimization of resource utilization. In traditional approaches, robots are often treated as independent entities executing tasks, with task allocation based mainly on factors such as cost, distance, or completion time. However, these methods overlook the diverse resource needs of tasks and the potentiality for collaboration between robots. To address this issue, this study proposes a distributed multi-robot task allocation model which focuses on optimizing the resource utilization. Unlike previous methods, we not only consider the task allocation but also introduce the concept of robot coalitions, and this allows robots to share resources and collaboratively complete complex tasks. Specifically, we construct resource supply vectors for robots and resource demand vectors for tasks, while incorporating spatiotemporal constraints to ensure efficient task execution and fulfillment of resource requirements.
- We construct a task allocation model based on game theory and demonstrate that the game is an exact potential game. Then, we propose a coalition formation algorithm based on game theory to maximize the resource utilization. The effectiveness of the algorithm is validated via simulation experiments. This method improves overall resource utilization by using collaboration and resource sharing among mobile robots through distributed strategy updating and interactions. Unlike traditional centralized optimization methods, this algorithm allows robots to dynamically adjust the task allocation. Through the adaptive collaboration without central control, the algorithm enables more efficient resource utilization. This distributed strategy updating approach allows each robot to interact effectively with other robots. Based on its own resource status and task requirements, each robot maximizes the overall resource utilization of the system. Experimental results show that, compared to classic heuristic algorithms and the latest swarm intelligence optimization methods proposed for multiple robot task allocation, the proposed approach achieves better allocation solutions under different task scales and resource configurations, significantly improving the resource utilization and task completion efficiency.
The rest of this paper is organized as follows: Section 2 presents the task allocation problem for multiple-mobile-robot systems. Section 3 formulates a game model based on the outlined problem. In Section 4, a coalition formation algorithm based on game theory is proposed to solve for the Nash equilibrium of the game. Section 5 validates the algorithm’s performance via comparative and test experiments, and Section 6 draws the conclusion.
2. Problem Formulation of Multi-Robot Task Allocation
First, we present the relevant notations used in this study, as summarized in Table 1.

Table 1.
The notation in this paper.
In a multi-task scenario, several tasks must be completed with varying types and quantities of resource requirements. At the same time, mobile robots are equipped with different types and amounts of resources, which necessitate the collaboration among them. As a result, robots must form coalitions to effectively share resources and complete tasks. Time and space constraints often exist between robots and tasks, complicating the task allocation process. When the resources provided by a coalition of robots exceed the requirements, redundant resources will be wasted, leading to a reduction in overall resource utilization. Therefore, in the absence of a central controller, the challenge of allocating tasks efficiently while maximizing the resource utilization becomes critical. Especially under limited resources, rational task allocation can significantly improve resource efficiency and ensure the successful completion of tasks. Figure 1 presents an illustrative example of task allocation in a multi-robot system.
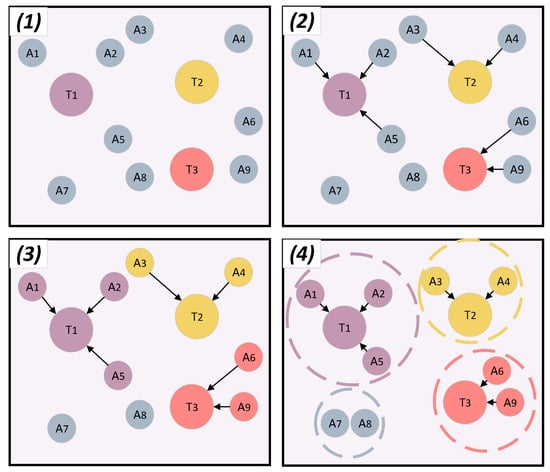
Figure 1.
Illustration of task allocation in multi-robot systems. (1) Initial task allocation state. (2) Task allocation process. (3) Task allocation results. (4) Coalition formation for task execution. Note: The arrows indicate the robots’ selection of tasks, and the circles indicate the formation of robot coalitions.
2.1. Task
A set of m heterogeneous tasks is defined as . The location of task is , where the mobile robot must reach this location in order to perform the task. The resource requirement vector of the task is represented as , where denotes the number of resource types. Additionally, represents the latest execution time of the task , which means that the task must be completed no later than this time.
2.2. Mobile Robot
A set of n heterogeneous robots is defined as . The location of robot is denoted by , and the speed of robot is . The resource supply vector of robot is represented by . Due to fuel limitations, the maximum operating time of the robot is .
2.3. Coalition
Since multiple heterogeneous robots should collaborate to complete a task, the coalition structure is denoted by . The coalition consists of a set of robots, i.e., , where represents an empty coalition. Mobile robots joining the empty coalition indicate that they are not assigned any tasks. The existence of is essential for ensuring the completeness of task allocation, as it provides robots with a clear option to stop task execution. Without , robots would be forced to join a coalition even there are no available tasks to meet their capability or resource constraints, which may lead to the suboptimal or even infeasible allocations. Moreover, in real-world scenarios, constraints such as time, resources, or collaboration requirements may prevent a robot from participating in any coalition. In such cases, serves as a necessary exit mechanism to maintain the robustness of the algorithm and prevent forced assignments that could degrade overall system performance. Allowing robots to quit the task may also help to improve the resource utilization because this may avoid inefficient allocations when a robot’s participation would not enhance coalition benefits. Furthermore, incorporating expands the solution space in optimization, enabling the algorithm to balance between executing and not executing tasks, ultimately ensuring globally optimal solutions rather than being confined to suboptimal coalition formations.
2.4. Resources
In the task allocation problem, r represents the number of resource types, and is the set of resources. The specific resources vary in different task scenarios. In the example of disaster relief, food, drinking water, and medicine are considered resources. We also consider capabilities, such as robots’ excavation and detection abilities, i.e., the resources required to accomplish tasks.
The demand for each type of resource varies across different tasks, and heterogeneous mobile robots often have different capabilities. For example, in a disaster area where the main issue is a shortage of food, but no collapse has occurred, excavation robots and detection robots are unnecessary. If a robot equipped with detection devices is assigned to deliver food and water to such an area, its detection capabilities will be wasted. In contrast, collapsed disaster areas are in greater need of detection capabilities to search for survivors. Such unreasonable task allocation can reduce the efficiency of disaster relief, leaving some areas’ needs unfulfilled, and fail to fully utilize the capabilities and resources carried by the robots.
Moreover, if a large number of robots are dispatched to the same disaster area, leading to an oversupply of food, this inefficient allocation will cause resource waste, while the food needs of other disaster-stricken areas may go unfulfilled. Therefore, when the resources supplied by a coalition exceed the resource requirements of a task, the redundant resources within the coalition are considered non-participatory in task execution and thus are not counted toward the total resource utilization.
2.5. Constraints
Due to the distance constraints between the robot and the tasks, the set of the tasks that the robot can choose to execute is a subset of the task set . A robot can perform task if and only if the following condition holds:
Formula (1) specifies that the time taken by the robot to reach the task location must not exceed the latest execution time of the task or the maximum operating time of the robot. Accordingly, the set of feasible tasks for robot is defined as follows:
From the perspective of coalition formation, the coalition that robot can join is defined as follows:
2.6. Objective Function
To evaluate the impact of different coalition structures on task allocation, resource utilization is defined as the objective function of the task allocation process. The utility of a coalition is expressed as follows:
where is the weight coefficient of resource k, reflecting its importance in task execution; is the total amount of resource k provided by coalition ; and is the amount of resource k required by task . The use of a minimization function helps prevent an excessive allocation of robots to the same task, thereby reducing the resource wastage during the task allocation process. Specifically, this utility function evaluates the extent to which the task’s resource demands are met. By incorporating a minimization function, it compares the supplied resources of the coalition with the required resources for each dimension. Any excess resources beyond the task’s requirements will not contribute to task execution. For instance, surplus food and water may not provide additional benefits to a disaster-stricken area, and autonomous excavation robots and detection robots are unnecessary for areas without structural collapse. Therefore, integrating a minimization function into the task utility function is essential, as it prevents excessive robots from being allocated to the same task, thus reducing the resource redundancy and waste. This contributes to a more efficient utilization of resources in task allocation. This approach also maximizes resource utilization under resource-constrained conditions. Notably, , which means that the empty coalition, even if it contains multiple robots, does not generate any utility.
The objective function of the entire task allocation is the total utility generated by completing all tasks, i.e.,
where C represents the coalition structure in the task allocation problem. One of the main contributions of this paper is to explore how to find the optimal or suboptimal coalition structure (set partitioning) that maximizes the objective function .
3. Game Model of the Task Allocation Problem
Given a task allocation problem with m tasks and n robots, the objective is to find a coalition structure that maximizes the system utility. However, as the number of tasks or robots increases, the size of the search space grows exponentially, so most existing methods become impractical for real-world applications. Therefore, this paper introduces a game-theoretic model to address the task allocation problem.
3.1. Introduction to the Game
Let be a game in strategic form with a finite number of players. The set of players is , the set of strategies of Player i is , and the utility function of Player i is , where is the set of strategy profiles, and R denotes the set of real numbers. For a given strategy profile , let represent the profile of strategies chosen by all players except player i, i.e., . In this notation, we sometimes refer to a strategy profile as .
3.2. Player
The robot in the task allocation problem constitutes all the players in the game. Therefore, we use the concepts of robot and player interchangeably, as this does not cause any confusion.
3.3. Strategy
The strategy set for robot is a set of coalitions that it can join, i.e.:
3.4. Utility Function
The utility of a player joining a coalition is defined as the marginal contribution. Specifically, the utility of player i joining the coalition is expressed as follows:
Equation (7) represents the marginal contribution of the robot to the task. It is defined as the difference in coalition benefits when the robot joins versus when it does not. This marginal contribution reflects the robot’s resource contribution to the coalition. By adopting marginal contribution as the utility function, each robot selects the strategy that maximizes its own utility, which corresponds to the strategy that maximizes its contribution to the coalition’s resources. This is consistent with our research objective of maximizing the resource utilization.
3.5. Potential Game
is a potential game if
where denotes the potential function of the game. A potential game requires perfect alignment between the global objective and the players’ local objective functions. That is, if a player unilaterally changed its action, the change in its objective function would be equal to the change in the potential function.
Theorem 1.
The game with Equation (7) as the utility function is an exact potential game.
Proof of Theorem 1.
In every strategy profile of the game, each robot selects a strategy, which determines the coalition it joins. Given a specific strategy profile, we can identify which robot belongs to each coalition. Conversely, if the composition of each coalition is known, then the strategies chosen by each robot can be determined, thereby specifying the overall strategy profile. Consequently, there is a one-to-one correspondence between a given strategy profile and the coalition partition of the robots. Since a Nash equilibrium is a stable strategy profile, it naturally maintains this one-to-one correspondence with the coalition structure. Since there is a one-to-one correspondence between strategy profile s and coalition structure C in the game, is used to replace . Without loss of generality, assume that player i switches from strategy j to strategy h. In this context, robot will transit from joining coalition to joining coalition . Consequently, coalition will lose robot , denoted as , while coalition will gain robot , denoted as . The strategies of all other players remain unchanged, resulting in the strategy profile of the game changing from to . That is, Consequently, this game qualifies as a potential game, with the corresponding potential function denoted as .□
3.6. Nash Equilibrium
Nash equilibrium is a fundamental concept in game theory, representing a stable state where, after a series of decisions, players achieve relatively high benefits. At this point, no player can unilaterally improve their payoff by changing their strategy. A strategy profile is called a pure strategy Nash equilibrium if and only if
Theorem 2.
In potential games, a Nash equilibrium is guaranteed to exist and can be reached through a finite sequence of strategy improvements [43].
At the Nash equilibrium, no robot can unilaterally change its strategy to improve its individual payoff, and this indicates that each robot’s strategy choice maximizes its own utility. According to the definition of potential games, at the Nash equilibrium, robots do not adjust their strategies in a way that increases the potential function, ensuring that the potential function reaches its local maximum at this point. As stated in Equation (5), the potential function in this game represents the resource utilization, meaning that the Nash equilibrium corresponds to the maximum resource utilization. Consequently, an optimal task allocation scheme can be obtained at the Nash equilibrium. Therefore, the core objective of this study is to find the Nash equilibrium solution of the game. However, not every Nash equilibrium represents an optimal coalition structure, which can be demonstrated through counterexamples. Since in a Nash equilibrium each player maximizes their utility given the strategies of the other players, the potential function remains relatively high, making this solution a high-quality suboptimal outcome.
4. The Proposed Coalition Formation Algorithm
4.1. Algorithm Introduction
A coalition formation (CF) algorithm based on game theory is proposed in this paper to address the task allocation problem in multiple-mobile-robot systems. Due to the complex task requirements and heterogeneous robots, a single robot typically cannot complete a task independently. Therefore, multiple robots must form a coalition and cooperate to accomplish the task. Most existing methods rely on a centralized architecture, which allows for global task allocation optimization but suffers from poor system robustness due to its dependence on a central node. To address this issue, this paper employs a game theory approach to develop a multiple robot coalition formation algorithm within a distributed framework, considering the complexity of multiple robot task coordination. It uses game theory to seek the optimal coalition structure and task allocation scheme, so as to achieve the Nash equilibrium and thus minimize the overall system cost.
4.2. Algorithm Innovation
The proposed algorithm has three key innovations:
First, the algorithm employs game theory to model the interaction behavior among robots. A utility function is formulated to align the Nash equilibrium with the optimal task allocation solution. The stability in distributed decision-making is thus ensured by gradually converging to the Nash equilibrium through strategy updating.
Secondly, considering the time–space constraints between tasks and robots, the algorithm can dynamically calculate the benefits of each robot’s participation in a task, so as to ensure the feasibility of the allocation scheme.
Finally, once the Nash equilibrium is reached, the algorithm incorporates a cost optimization module to reduce the operating costs of the multi-robot system and improve the resource allocation efficiency, without altering the Nash equilibrium.
4.3. Algorithm Implementation and Pseudocode
The core idea of the algorithm is to find a coalition structure by iteratively updating the robot strategies in a distributed manner, ensuring that all agent strategy profiles converge to a Nash equilibrium, reducing the system cost in the subsequent optimization phase. The algorithm process is illustrated in Figure 2, and the process can be further detailed in the following four stages:
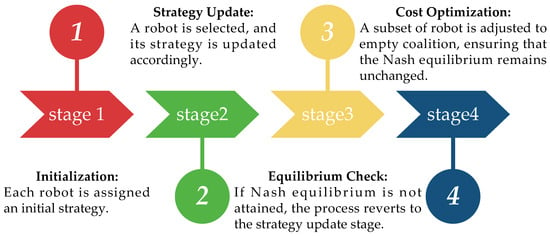
Figure 2.
Flowchart of the coalition formation algorithm.
- Stage 1. Initialization: Assign an initial strategy to each robot.
- Stage 2. Strategy Update: In each iteration, a robot is selected for strategy updating. The robot calculates the utility of each task in its strategy set. Then the task with the highest utility is selected as the new strategy.
- Stage 3. Nash Equilibrium Check: The strategy updating ends when all robot strategies are optimal given the strategies of the other robots, i.e., when the Nash equilibrium is reached. Otherwise, the strategy updating continues.
- Stage 4. Cost Optimization: Based on the Nash equilibrium, if a robot has zero utility but is not in an empty coalition, its strategy will be adjusted to join the empty coalition, thus optimizing the cost of the multi-robot system.
With the game-theory-based distributed framework, the algorithm ensures that the Nash equilibrium aligns with the optimal solution of the problem by properly designing the utility function. That is, the Nash equilibrium will be found by iteratively updating the strategies. The pseudo-code for the Algorithm 1 is as follows:
| Algorithm 1: Coalition Formation algorithm |
| Input: Output: strategy profile s 1: 2: while is_not_Nash Equilibrium do 3: choose player i from N 4: for j = 1:m do 5: if i can perform tj do |
| 6: compute 7: end if 8: end for 9: 10: end while 11: for i = 1:n do 12: if do 13: 14: end if 15: end for 16: return s |
The algorithm’s input consists of the set of mobile robots, the strategy set, and the utility function, while the output is the game’s strategy profile. The first step initializes the strategies of the robots, and the second step outlines the strategy update process. At each iteration, the algorithm selects one robot and updates its strategy to the current optimal strategy until a Nash equilibrium is reached. The function “is_not_Nash Equilibrium” in the second line of the algorithm is used to check whether the current strategy profile has reached a Nash equilibrium. If each player’s strategy in the current strategy profile is their current optimal strategy, the algorithm has reached a Nash equilibrium, and the function returns 0; otherwise, it returns 1. In lines 11–15, if a robot joins a non-empty coalition but its utility is zero, the robot’s strategy will be adjusted to join the empty coalition to reduce the system costs. Finally, the algorithm returns the strategy profile of the game.
For the task allocation problem involving n robots and m tasks, the worst-case time complexity of the algorithm is . However, in practical scenarios, the algorithm typically reaches a Nash equilibrium through a limited number of iterations, with much fewer iterations than the theoretical upper bound. Therefore, the actual runtime is much smaller than the worst-case estimate. In the simulation phase, we evaluate the time performance of the algorithm by measuring its response time. The main storage variables of the algorithm are the resource vectors of robots and tasks. Given that the resource dimension is r, the resource matrices for robots and tasks are of dimensions and , respectively. Therefore, the space complexity of the algorithm is .
5. Simulation Experiment
5.1. Benchmark Algorithms and Simulation Settings
To apply the benchmark algorithms to the task allocation problem, we model the problem as a nonlinear combinatorial optimization problem.
We select six benchmark algorithms, including classical meta-heuristic algorithms such as the Genetic Algorithm (GA) and Simulated Annealing (SA), as well as deterministic approaches like the Greedy Algorithm and Exhaustive Search. Additionally, we have incorporated the latest cultural-particle swarm optimization (CPSO) [44], and collaborative discrete bee colony algorithm (CDABC) [24], for comparison. Each of these algorithms has its own merits: the Genetic Algorithm is suitable for large-scale combinatorial optimization problems, with global search capabilities that help avoid local optima; Simulated Annealing, with its probabilistic acceptance mechanism, can effectively escape local optima, making it suitable for resource allocation problems and capable of finding good solutions in a short time; the Greedy Algorithm is fast, making it suitable for real-time decision-making scenarios and able to quickly generate feasible solutions, especially performing well in resource allocation. The CPSO is inspired by the cultural algorithm and particle swarm optimization algorithm, aiming to balance the exploration and exploitation performance while avoiding the local optima. The CDABC is an improved bee colony optimization algorithm that enhances the global search capability through a dynamic neighborhood strategy, preventing local optima while strengthening the local optimization with a critical individual neighborhood design. The exhaustive search algorithm is a method that finds the optimal solution by exploring all possible solutions. It checks each candidate solution one by one until the best solution that meets the criteria is found. Although this method guarantees finding the optimal solution, it has high computational cost and low efficiency when the problem size is large. These six algorithms are well-established and widely used for solving task allocation problems, demonstrating effective performance in various scenarios. Therefore, we selected them as baseline comparison methods to evaluate the superiorities of our proposed coalition formation algorithm.
All experiments are conducted on the MATLAB 2023a platform, with each experiment repeated independently 100 times to obtain average results, thus minimizing errors caused by randomness. We conduct both test experiments and comparative experiments. The test experiments quantitatively evaluate the solution quality by comparing the solution obtained from the coalition formation algorithm with the optimal solution of the problem. We conduct three sets of comparative experiments under different conditions. In all comparative experiments, we use the same runtime to evaluate the resource utilization efficiency of different algorithms.
First, we formulate the task allocation problem as an optimization problem, as shown in Equations (10)–(13).
Equation (10) represents the objective function of the optimization problem, which denotes the total utility of all tasks. The utility of a task is defined by its resource demand and the resource supply of the coalition, which can be derived from Equations (4) and (5). Equations (5) and (10) both represent the total resource utilization of all tasks in the task allocation problem, with the only difference being the decision variables. The decision variable of Equation (5) is the coalition structure, while the decision variable of Equation (10) is . In Equation (13), is a decision variable, where indicates that robot executes task , and indicates that robot does not execute task . Equation (11) is a constraint for the optimization problem, stating that each robot may perform no more than one task. Equation (12) represents the constraints between the tasks and the robots, where a robot can execute a task if it reaches the task location within the specified time, with the decision variable set to be 1. Equation (13) is a constraint on the decision variables, ensuring that they can only take values of 0 or 1.
All six benchmark algorithms adopt this optimization model with well-tuned parameters. We set the population size of the genetic algorithm to 50, with a crossover probability of 0.7 and a mutation probability of 0.1. The starting temperature of the simulated annealing algorithm is set to 10,000, the final temperature to 0.1, the annealing rate to 0.99, and the number of iterations at a constant temperature to 1000. The greedy algorithm selects the strategy that maximizes the objective function at each step, with no parameters. The parameter settings of the CPSO and CDABC algorithms are consistent with those in the referenced literature.
5.2. Comparative Experiments
We perform three experiments (Experiment 1, Experiment 2, and Experiment 3) to analyze how the different factors affect the algorithm performance, as follows:
- Experiment 1: We analyze the impact of resource dimension on the algorithm’s performance. The running time of all four algorithms is set to 10 s, with the number of robots being three times the number of tasks. The resource dimension r is set to 5, 10, and 15, respectively. The effect of the number of tasks on the algorithm’s objective function is shown in Figure 3.
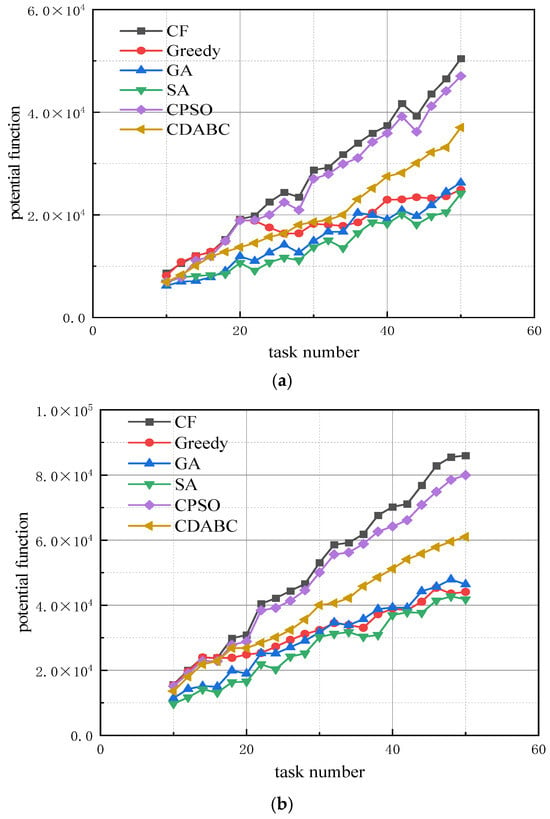
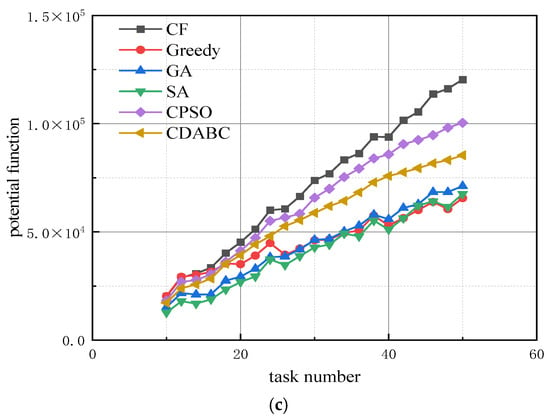 Figure 3. Effect of task quantity on algorithm performance under various resource dimensions; (a) r = 5, (b) r = 10, (c) r = 15.
Figure 3. Effect of task quantity on algorithm performance under various resource dimensions; (a) r = 5, (b) r = 10, (c) r = 15. - Experiment 2: We analyze the effect of the ratio between the number of robots and the number of tasks on the algorithm’s performance. The running time of all four algorithms is set to 10 s, with the resource dimension r fixed at 10. The number of robots is set to 3, 4, and 5 times the number of tasks, respectively. The effect of changes in the number of tasks on the algorithm’s performance is shown in Figure 4.
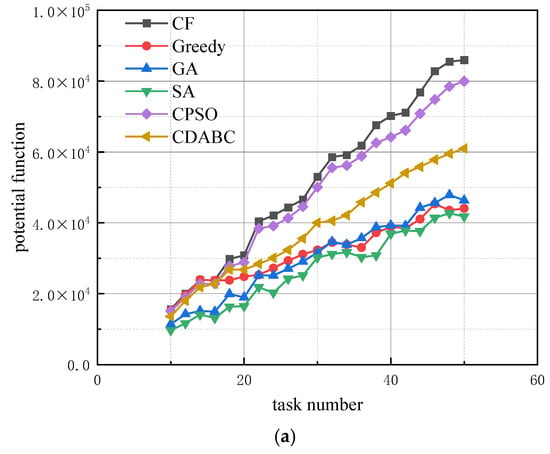
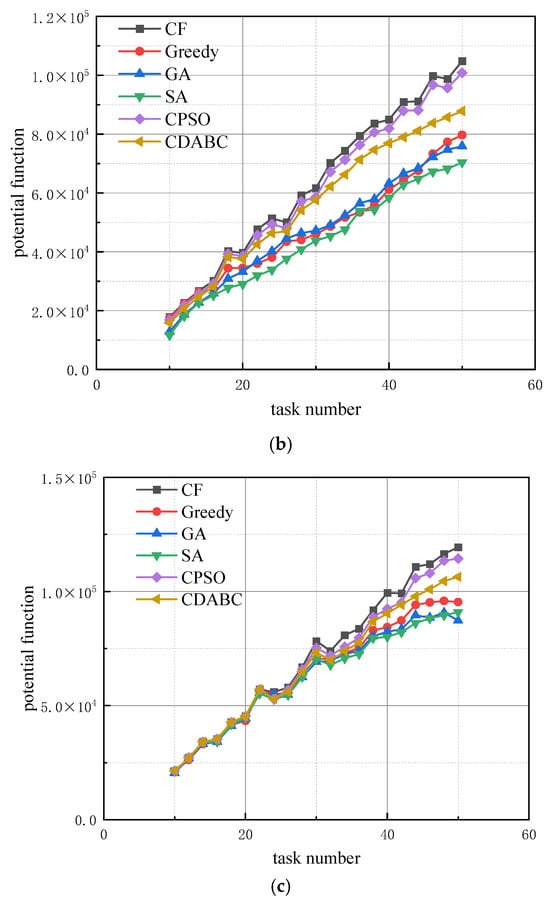 Figure 4. Effect of task quantity on algorithm performance under varying robot-to-task ratios; (a) n:m = 3, (b) n:m = 4, (c) n:m = 5.
Figure 4. Effect of task quantity on algorithm performance under varying robot-to-task ratios; (a) n:m = 3, (b) n:m = 4, (c) n:m = 5.
Experiment 3: We then analyze the effect of running time on the algorithm’s performance. The resource dimension for all four algorithms is set to 10, with the number of robots being three times the number of tasks. The running time is set to 10, 15, and 20 s, respectively. The effect of the changing number of tasks on the algorithm’s performance is shown in Figure 5.
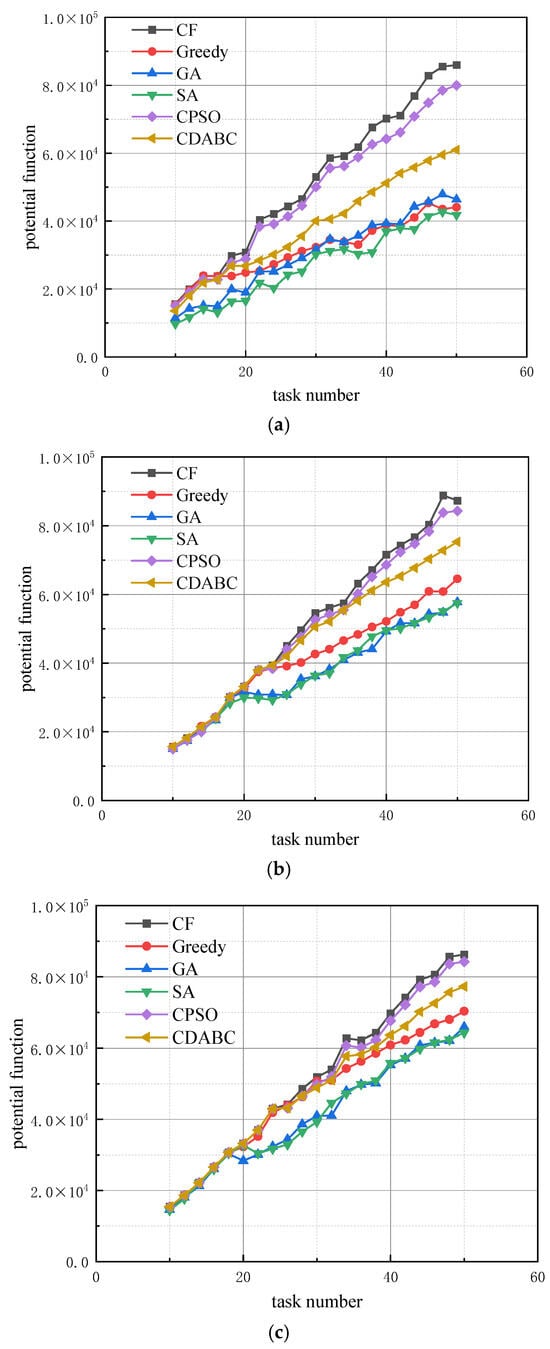
Figure 5.
Impact of task quantity on algorithm performance across different running times; (a) t = 10 s, (b) t = 15 s, (c) t = 20 s.
The experimental parameters of the three sets of experiments are shown in Table 2.

Table 2.
Experimental parameter settings.
As shown in Figure 3, under the three resource dimensions, the CF algorithm proposed in this paper consistently provides the highest quality solution. In each sub-figure, the curve of CF is significantly higher than those of the other five algorithms. When the number of tasks is small, the differences in solution quality among the six algorithms are relatively slight. However, as the number of tasks increases, this gap gradually increases, particularly in scenarios with higher resource dimensions, where the advantages of the proposed algorithm become more obvious.
The CPSO algorithm exhibits a smaller gap compared to the CF when the resource dimension is low. However, as the resource dimension increases, the gap between the two algorithms becomes more evident. When the number of tasks is small, the greedy algorithm can achieve high-quality solutions. But as the problem size grows, it tends to fall into local optima. As the resource dimension increases, the problem complexity rises significantly, leading to a decline in solution quality for other algorithms. This effect is particularly evident when the number of tasks is large. The proposed CF consistently maintains the highest solution quality, demonstrating its robustness and adaptability in complex problems.
In Figure 4, as the ratio of robots to tasks increases, the gap between the algorithms becomes smaller. This is particularly obvious when the number of tasks is large. For the same number of tasks, a higher number of robots may lead to more potential optimal solutions, making it easier for the algorithm to find the best solution. In comparison, the proposed CF algorithm in this paper demonstrates stronger performance for different task quantities.
As shown in Figure 5, the proposed CF algorithm consistently performs the best, especially when the number of tasks is large. When the running time is short, especially with a large number of tasks, the solution quality of the CF algorithm is significantly better than that of the other algorithms. This highlights the high efficiency of the CF. As the maximum running time increases, the solutions of the six algorithms converge, although a slight gap remains when the number of tasks is large. This indicates that, given sufficient running time, all six algorithms have the ability to approach the optimal solution. However, the CF algorithm can ensure higher-quality solutions in a shorter time.
As the number of tasks increases, the potential function value rises significantly, so the variance is not an inadequate measure of data fluctuations. Therefore, we use the coefficient of variation (i.e., the ratio of the standard deviation to the mean) to assess the relative variability of the data. In the aforementioned experiments, the coefficient of variation for all repeated random trials is below 2%, indicating a high level of stability in the experimental results.
When the problem scale is small, the proposed algorithm can achieve solution quality comparable to that of the benchmark algorithms. In contrast, under larger and more complex problem instances, the proposed algorithm can achieve up to a 50% performance improvement over the benchmarks.
By varying the experimental conditions, namely, the resource dimension, the ratio of robots to tasks, and the maximum running time, it is evident that the solutions obtained by the CF algorithm consistently outperform those of the other five algorithms. Additionally, the algorithm demonstrates high stability and adaptability across different scenarios.
5.3. Test Experiments
To measure the gap between the CF and the optimal solution, we compute the optimal solution using the exhaustive search algorithm. We define the Solution Quality Ratio (SQR) as the ratio of the solution obtained by our game-theoretic method to the optimal solution.
In the experiments, the number of robots is three times the number of tasks, and the resource dimensions are 3, 4, and 5, respectively. The purpose of this experiment is to evaluate the solution quality obtained by the CF algorithm. Therefore, it is not necessary to set the same runtime for both methods. The CF algorithm stops when it reaches the Nash equilibrium, while the exhaustive search algorithm stops when the optimal solution is found. We examine the effect of varying task numbers on the SQR, as shown in Figure 6.
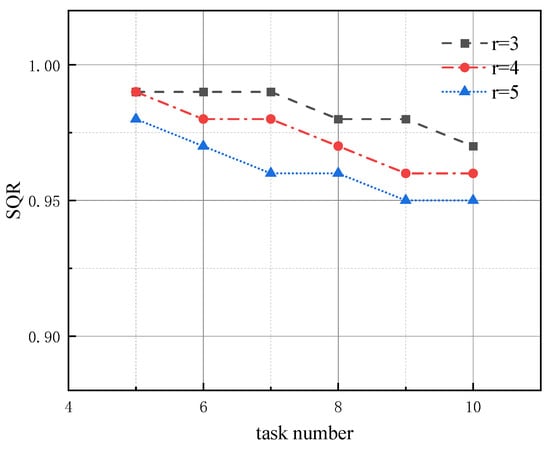
Figure 6.
Effect of the varying number of tasks on SQR.
As shown in Figure 6, with the increasing number of tasks, the SQR decreases due to the expansion of the solution space as the problem size grows. Additionally, the increasing resource dimensions also make the problem more complex, leading to a decreasing SQR. Note that SQR generally remains above 95%, indicating that the quality of the solution obtained by using the game theory method can be kept high.
The number of tasks ranges from 5 to 10, because we found during the experiment that the running time of the exhaustive search algorithm increases exponentially as the number of tasks grows. Our CF algorithm, however, does not experience a significant increase in running time as the number of tasks increases. To improve time efficiency, we traded off some algorithmic accuracy. Figure 7 shows the comparison of running time between the two algorithms when the resource dimension is 3. Generally, the proposed CF algorithm sacrifices a small amount of solution quality but significantly reduces the running time. Additionally, the algorithm ensures the robustness and scalability.
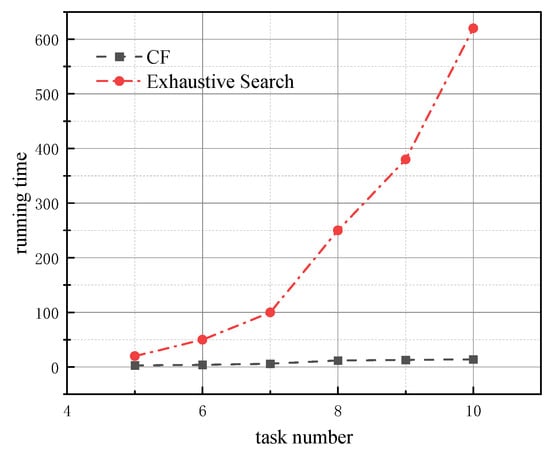
Figure 7.
Comparison of running times between CF and exhaustive search algorithm.
To further evaluate the time performance of the algorithm, we define the algorithm’s response time. The response time refers to the time required from the start of the algorithm until it reaches the Nash equilibrium, i.e., the time spent on the task allocation. The response time of the algorithm is determined by the number of iterations, so fewer iterations result in a shorter response time, i.e., a better time performance. In disaster recovery scenarios, where time is very limited, the algorithm needs to have a very short response time. Generally, there is a trade-off between the algorithm’s response time and the quality of the solution. Improving the solution quality often leads to an increase in the algorithm’s running time, which is reflected in Figure 6 and Figure 7.
To investigate the time performance of the algorithm under different scenarios, we tested the effect of varying task quantities and resource dimensions on the CF algorithm’s response time. The experimental results are shown in Figure 8.
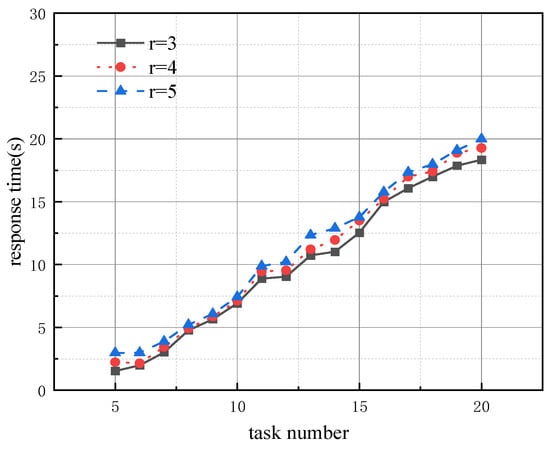
Figure 8.
Response time under different task quantities and resource dimensions.
As shown in Figure 8, the response time of the algorithm increases with the increasing number of tasks and resource dimensions, but overall remains within 20 s. Notably, as shown in Figure 7, when the number of tasks reaches 10, the exhaustive search algorithm takes over 600 s to complete. In contrast, the response time of the CF algorithm grows approximately linearly with the number of tasks, while that of the exhaustive method increases exponentially. This demonstrates the superior time efficiency of the CF algorithm.
To analyze the sensitivity of the algorithm, we study the effect of different initial strategies. For each task scenario, we randomly generate 100 initial settings, where each robot randomly selects a feasible strategy. The only difference between these settings lies in the initial strategies. We study the effect of initial strategy variations under different task quantities, as shown in Figure 9.
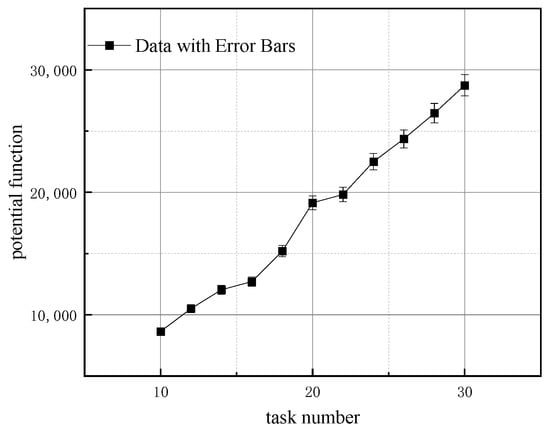
Figure 9.
Effect of initial strategies on algorithm performance with varying task number.
Figure 9 shows the curve of the average values of the potential function, with the error bars indicating the range between the maximum and minimum values. It is seen that the effect of changing the initial strategy on the algorithm is slight, with the differences between the extreme values and the mean less than 5%. This indicates that the varying initial strategy has a negligible effect on the performance of the CF algorithm.
5.4. Real-World Disaster Relief Application
In a real-world disaster relief scenario, 15 robots are assigned to 5 different disaster areas, with each disaster area treated as a separate task. The needs of each disaster area are different, including tasks such as medical assistance, material transportation, damage assessment, and debris removal. Each robot has different capabilities and resources, such as medical supplies, heavy lifting equipment, drone devices, and communication tools. The completion of these tasks relies on cooperation among multiple robots to ensure timely and effective relief in the disaster areas. With effective task allocation and resource scheduling, the needs of each disaster area are satisfied with improved resource utilization efficiency. Figure 10 illustrates the positions of the disaster areas and the mobile robots.
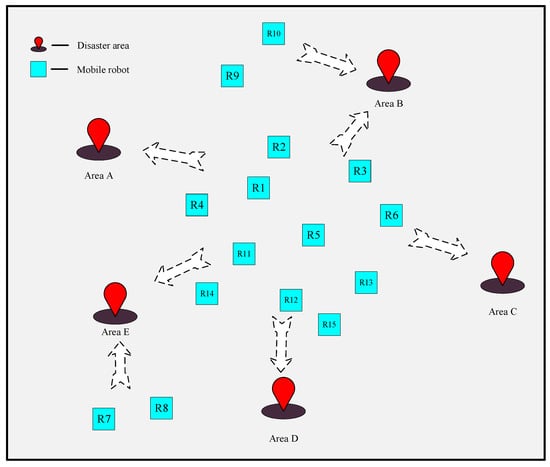
Figure 10.
Illustrative map of disaster areas and robot locations. Note: The arrows represent the robots’ choices of disaster areas for rescue.
Figure 10 illustrates a schematic map of the disaster relief scenario, where each disaster area is treated as an independent task. Robots make distributed decisions on which disaster area to assist. However, the map does not display the specific resource information of the disaster areas and robots, which is provided in Table 3 and Table 4.

Table 3.
Task requirements for disaster areas.

Table 4.
Robot capabilities.
In this scenario, we assume that the strategy set of each robot corresponds directly to the set of tasks. Therefore, the spatial locations of robots and tasks are not considered. Based on the information of robots and tasks, we apply the proposed CF algorithm to obtain the task assignment results, as shown in Table 5.

Table 5.
Task allocation result.
Table 5 presents the task allocation results based on a real-world disaster relief scenario. Each task is collaboratively completed by multiple robots with complementary capabilities, ensuring comprehensive coverage of the required resources and functionalities. The allocation results demonstrate a satisfactory match between available resources and task demands, in the meantime achieving efficient utilization of robotic resources. This verifies the effectiveness and superiorities of the proposed CF algorithm in complex real-world environments.
6. Conclusions and Future Work
This paper addresses the task allocation problem in a multi-robot system with complex spatiotemporal constraints, so as to maximize the resource utilization. A multi-robot game model is developed, where the mobile robot is considered as the player, the task subset that satisfies the spatiotemporal constraints serves as the strategy set, and the marginal contribution of the robot in performing the task is defined as the player’s utility. It is proven that the game is an exact potential game, with the potential function being the sum of the task utilities. We designed a coalition formation algorithm based on game theory to find the Nash equilibrium by iteratively improving the players’ strategies. Subsequently, we compared the proposed algorithm with the greedy algorithm, genetic algorithm, simulated annealing algorithm, CPSO, and CDABC to evaluate the performance of each algorithm under various conditions. Simulation experiments demonstrate that the solution quality obtained by the proposed coalition formation algorithm outperforms the other algorithms, especially when the number of tasks increases. Simulations are performed with varying resource dimensions, ratios of numbers of robots to tasks, and running time conditions, demonstrating that the CF method exhibits stronger robustness and adaptability to diverse task allocation scenarios. In addition, we compare the CF with the exhaustive search method to evaluate the solution quality and assess the algorithm’s response time and sensitivity to initial conditions. Finally, the proposed algorithm is applied to a post-disaster rescue scenario, where the task allocation results further demonstrate its effectiveness and superior performance.
It should be noted that in current multi-robot task allocation problems, the Euclidean distance only represents the robot’s ideal travel path. In practical applications, factors such as road networks, obstacles, and dynamic traffic conditions may affect the actual travel distance and time of robots, thus resulting in paths that are longer than the Euclidean estimate. In addition, coordination and collision avoidance among robots in multi-robot systems can further increase the actual travel time. To address this issue, a common approach is to introduce a path scaling factor, which multiplies the Euclidean distance to estimate a more realistic path cost. The choice of this scaling factor is usually based on empirical knowledge and may need to be adjusted depending on the scenario. Furthermore, task allocation and path planning can be integrated, where the robot first generates its actual path, and then feeds the resulting path cost back into the task allocation model as a constraint. However, this coupling will significantly increase the computational complexity and cost of the algorithm. Additionally, when the communication topology of robots is not a complete graph—that is, the robots can only communicate with their neighbors—a consensus mechanism is then necessary for coordination. These issues are worthy of further exploration in our upcoming studies.
Author Contributions
Conceptualization, L.L. and P.L.; methodology, L.L.; software, L.L.; validation, L.L. and P.L.; formal analysis, L.L.; investigation, L.L. and P.L.; resources, L.L.; data curation, L.L.; writing—original draft preparation, L.L. and P.L.; writing—review and editing, P.L.; visualization, L.L. and P.L.; supervision, P.L.; project administration, P.L.; funding acquisition, P.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Son, H.I.; Franchi, A.; Chuang, L.L.; Kim, J.; Bulthoff, H.H.; Giordano, P.R. Human-centered design and evaluation of haptic cueing for teleoperation of multiple mobile robots. IEEE Trans. Cybern. 2013, 43, 597–609. [Google Scholar] [PubMed]
- Peng, Y.; Zhu, W.; Yu, D.Z.; Liu, S.; Zhang, Y. Multi-Depot Electric Vehicle–Drone Collaborative-Delivery Routing Optimization with Time-Varying Vehicle Travel Time. Vehicles 2024, 6, 1812–1842. [Google Scholar] [CrossRef]
- Shan, X.; Cabani, A.; Chafouk, H. Cooperative Vehicle Localization in Multi-Sensor Multi-Vehicle Systems Based on an Interval Split Covariance Intersection Filter with Fault Detection and Exclusion. Vehicles 2024, 6, 352–373. [Google Scholar] [CrossRef]
- Mawengkang, H.; Syahputra, M.R.; Sutarman, S.; Salhi, A. A Non-Linear Optimization Model for the Multi-Depot Multi-Supplier Vehicle Routing Problem with Relaxed Time Windows. Vehicles 2024, 6, 1482–1495. [Google Scholar] [CrossRef]
- Quinton, F.; Grand, C.; Lesire, C. Market approaches to the multi-robot task allocation problem: A survey. J. Intell. Robot. Syst. 2023, 107, 29. [Google Scholar] [CrossRef]
- Seenu, N.; Kuppan Chetty, R.M.; Ramya, M.M.; Janardhanan, M.N. Review on state-of-the-art dynamic task allocation strategies for multiple-robot systems. Ind. Robot 2020, 47, 929–942. [Google Scholar]
- Luo, X.; Zavlanos, M.M. Temporal logic task allocation in heterogeneous multirobot systems. IEEE Trans. Robot. 2022, 38, 3602–3621. [Google Scholar] [CrossRef]
- Notomista, G.; Mayya, S.; Emam, Y.; Kroninger, C.; Bohannon, A.; Hutchinson, S.; Egerstedt, M. A resilient and energy-aware task allocation framework for heterogeneous multirobot systems. IEEE Trans. Robot. 2021, 38, 159–179. [Google Scholar] [CrossRef]
- Li, Q.; Li, M.; Vo, B.Q.; Kowalczyk, R. An efficient algorithm for task allocation with the budget constraint. Expert Syst. Appl. 2022, 210, 118279. [Google Scholar] [CrossRef]
- Choudhury, S.; Gupta, J.K.; Kochenderfer, M.J.; Sadigh, D.; Bohg, J. Dynamic multi-robot task allocation under uncertainty and temporal constraints. Auton. Robots 2022, 46, 231–247. [Google Scholar] [CrossRef]
- Poudel, S.; Moh, S. Task assignment algorithms for unmanned aerial vehicle networks: A comprehensive survey. Veh. Commun. 2022, 35, 100469. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, H.; Tang, D.; Zhou, T.; Gui, Y. Dynamic job shop scheduling based on deep reinforcement learning for multi-agent manufacturing systems. Robot. Comput. Integr. Manuf. 2022, 78, 102412. [Google Scholar] [CrossRef]
- Cheng, Y.; Sun, F.; Zhang, Y.; Tao, F. Task allocation in manufacturing: A review. J. Ind. Infor. Integr. 2019, 15, 207–218. [Google Scholar] [CrossRef]
- Chen, Z.; Alonso-Mora, J.; Bai, X.; Harabor, D.D.; Stuckey, P.J. Integrated task assignment and path planning for capacitated multi-agent pickup and delivery. IEEE Robot. Autom. 2021, 6, 5816–5823. [Google Scholar] [CrossRef]
- Li, P.; Duan, H. A potential game approach to multiple UAV cooperative search and surveillance. Aerosp. Sci. Technol. 2017, 68, 403–415. [Google Scholar] [CrossRef]
- Testa, A.; Notarstefano, G. Generalized assignment for multi-robot systems via distributed branch-and-price. IEEE Trans. Robot. 2021, 38, 1990–2001. [Google Scholar] [CrossRef]
- Jiang, Y. A survey of task allocation and load balancing in distributed systems. IEEE Trans. Parallel Distrib. Syst. 2015, 27, 585–599. [Google Scholar] [CrossRef]
- Martin, J.G.; Frejo, J.R.D.; García, R.A.; Camacho, E.F. Multi-robot task allocation problem with multiple nonlinear criteria using branch and bound and genetic algorithms. Intell. Serv. Robot. 2021, 14, 707–727. [Google Scholar] [CrossRef]
- Mousavi, S.; Afghah, F.; Ashdown, J.D.; Turck, K. Use of a quantum genetic algorithm for coalition formation in large-scale UAV networks. Ad Hoc Netw. 2019, 87, 26–36. [Google Scholar] [CrossRef]
- Bänziger, T.; Kunz, A.; Wegener, K. Optimizing human–robot task allocation using a simulation tool based on standardized work descriptions. J. Intell. Manuf. 2020, 31, 1635–1648. [Google Scholar] [CrossRef]
- Geng, N.; Chen, Z.; Nguyen, Q.A.; Gong, D. Particle swarm optimization algorithm for the optimization of rescue task allocation with uncertain time constraints. Complex. Intell. Syst. 2021, 7, 873–890. [Google Scholar] [CrossRef]
- Wei, C.; Ji, Z.; Cai, B. Particle swarm optimization for cooperative multi-robot task allocation: A multi-objective approach. IEEE Robot. Autom. 2020, 5, 2530–2537. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Y.; Qiu, Y.; Zhang, Q.; Huo, F.; Huangfu, Y.; Yang, C.; Zhou, J. Cooperative task allocation for multi-robot systems based on multi-objective ant colony system. IEEE Access 2022, 10, 56375–56387. [Google Scholar] [CrossRef]
- Guo, H.; Miao, Z.; Ji, J.; Pan, Q. An effective collaboration evolutionary algorithm for multi-robot task allocation and scheduling in a smart farm. Knowl. Based Syst. 2024, 289, 111474. [Google Scholar] [CrossRef]
- Wang, G.; Wang, F.; Wang, J.; Li, M.; Gai, L.; Xu, D. Collaborative target assignment problem for large-scale UAV swarm based on two-stage greedy auction algorithm. Aerosp. Sci. Technol. 2024, 149, 109146. [Google Scholar] [CrossRef]
- Bai, X.; Fielbaum, A.; Kronmüller, M.; Knoedler, L.; Alonso-Mora, J. Group-based distributed auction algorithms for multi-robot task assignment. IEEE Trans. Autom. Sci. Eng. 2022, 20, 1292–1303. [Google Scholar] [CrossRef]
- Otte, M.; Kuhlman, M.J.; Sofge, D. Auctions for multi-robot task allocation in communication limited environments. Auton. Robots 2020, 44, 547–584. [Google Scholar] [CrossRef]
- Choi, H.L.; Brunet, L.; How, J.P. Consensus-based decentralized auctions for robust task allocation. IEEE Trans. Robot. 2009, 25, 912–926. [Google Scholar] [CrossRef]
- De Ryck, M.; Pissoort, D.; Holvoet, T.; Demeester, E. Decentral task allocation for industrial AGV-systems with routing constraints. J. Manuf. Syst. 2022, 62, 135–144. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, H.; Wu, G. A Dynamic Task Scheduling Method for Multiple UAVs Based on Contract Net Protocol. Sensors 2022, 22, 4486. [Google Scholar] [CrossRef]
- Xie, B.; Gu, X.; Chen, J.; Shen, L. A multi-responsibility–oriented coalition formation framework for dynamic task allocation in mobile–distributed multi-agent systems. Int. J. Adv. Robot. Syst. 2018, 15, 1729881418813037. [Google Scholar] [CrossRef]
- Jang, I.; Shin, H.S.; Tsourdos, A. Anonymous hedonic game for task allocation in a large-scale multiple agent system. IEEE Trans. Robot. 2018, 34, 1534–1548. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Q.; Zhu, Y.; Zhang, J. Dynamics of task allocation based on game theory in multi-agent systems. IEEE Trans. Circuits Syst. Express Briefs 2018, 66, 1068–1072. [Google Scholar] [CrossRef]
- Wu, H.; Shang, H. Potential game for dynamic task allocation in multi-agent system. ISA Trans. 2020, 102, 208–220. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, J.; Xu, H.; Zhang, W.-A. Distributed dynamic task allocation for unmanned aerial vehicle swarm systems: A networked evolutionary game-theoretic approach. Chin. J. Aeronaut. 2024, 37, 182–204. [Google Scholar] [CrossRef]
- Long, S.; Long, W.; Li, Z.; Li, K.; Xia, Y.; Tang, Z. A game-based approach for cost-aware task assignment with QoS constraint in collaborative edge and cloud environments. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 1629–1640. [Google Scholar] [CrossRef]
- Shandilya, S.; Szymanski, Z.; Shandilya, S.K.; Izonin, I.; Singh, K.K. Modeling and comparative analysis of multi-agent cost allocation strategies using cooperative game theory for the modern electricity market. Energies 2022, 15, 2352. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Q.; Xu, Y.; Qi, N.; Guan, X.; Zhang, Y.; Xue, Z. Joint task assignment and spectrum allocation in heterogeneous UAV communication networks: A coalition formation game-theoretic approach. IEEE Trans. Wirel. Commun. 2020, 20, 440–452. [Google Scholar] [CrossRef]
- Zhao, X.; Zong, Q.; Tian, B.; Zhang, B.; You, M. Fast task allocation for heterogeneous unmanned aerial vehicles through reinforcement learning. Aerosp. Sci. Technol. 2019, 92, 588–594. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, J.; Cui, Y.; Fu, D.; Cong, J. Multi-USV task planning method based on improved deep reinforcement learning. IEEE Internet Things J. 2024, 11, 18549–18567. [Google Scholar] [CrossRef]
- Li, Z.; Shi, N.; Zhao, L.; Zhang, M. Deep reinforcement learning path planning and task allocation for multi-robot collaboration. Alex. Eng. J. 2024, 109, 408–423. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, N.D.; Nahavandi, S. Deep reinforcement learning for multiagent systems: A review of challenges, solutions, and applications. IEEE Trans. Cybern. 2020, 50, 3826–3839. [Google Scholar] [CrossRef] [PubMed]
- Marden, J.R.; Arslan, G.; Shamma, J.S. Cooperative control and potential games. IEEE Trans. Syst. Man. Cybern. Part B Cybern. 2009, 39, 1393–1407. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Liu, A.; Wang, J.; Kong, X. An improved fault-tolerant cultural-PSO with probability for multi-AGV path planning. Expert. Syst. Appl. 2024, 237, 121510. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).