Integrated Sensing and New Radio Communications for Air Vehicle Positioning
Abstract
1. Introduction
Literature Gaps and Contributions
- The literature on 5G NR positioning is reviewed and critically analysed.
- A methodology to model the 5G environment in an urban canyon is proposed, using advanced ray-tracing simulations, capturing signal propagation characteristics such as reflections, scattering, and diffractions caused by buildings and obstacles.
- An AI-driven RF fingerprinting technique is developed, leveraging received signal strength (RSS) and TOA data to improve positioning accuracy in multipath-rich environments.
- Machine learning algorithms for positioning are designed and implemented, specifically using Bayesian regularized artificial neural networks (BRANNs) and random forests, to enhance the precision and robustness of positioning systems.
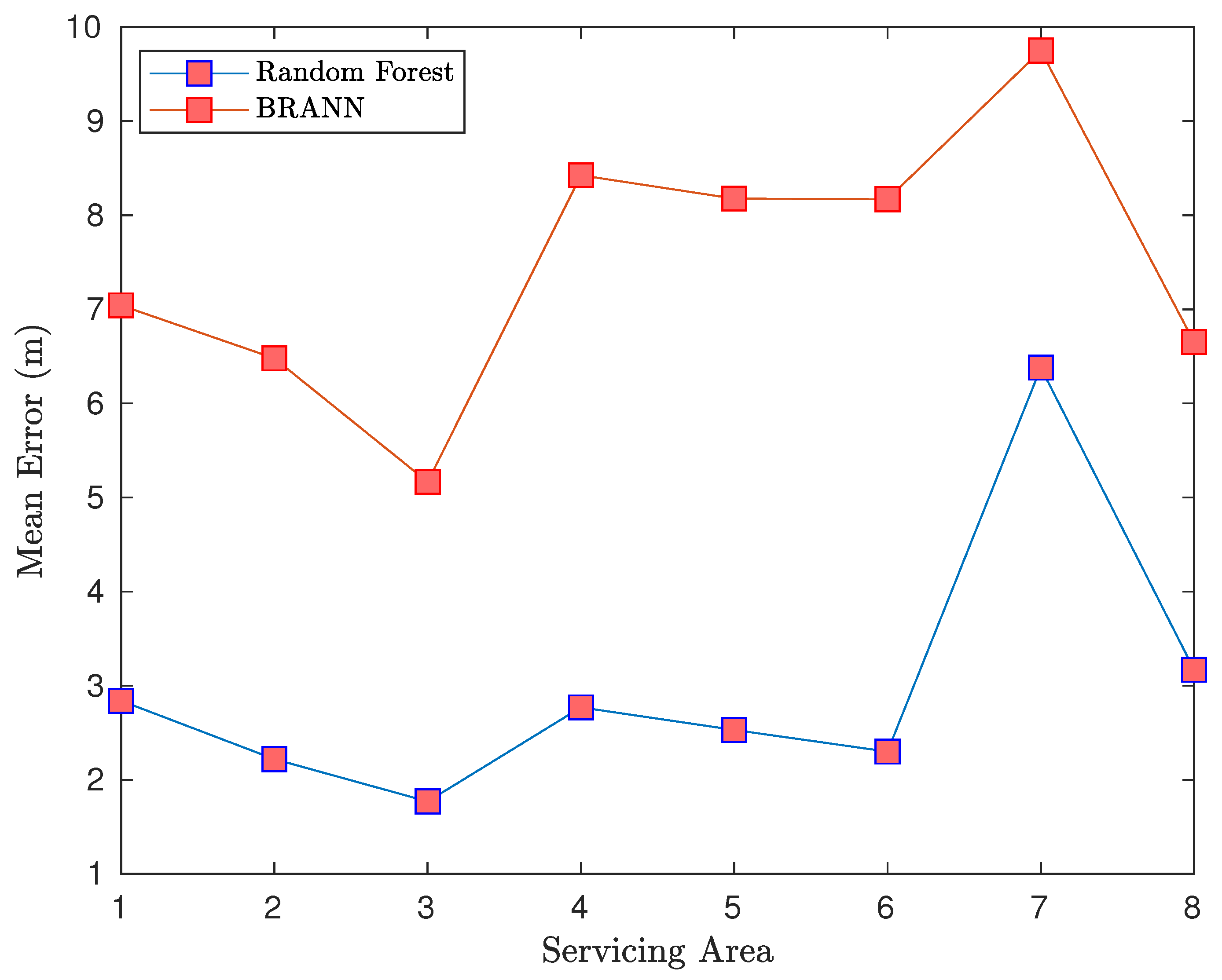
- Random forests are shown to outperform BRANN-based models.
- The proposed positioning system is extensively evaluated in a simulated urban canyon environment, demonstrating errors below 3 m in 75% of the areas studied.
2. Algorithm Development and Theory
2.1. Radio-Based Positioning
- Signal strength-based: The measurement of signal strength is related to the distance d between the receiver and transmitter through Equation (1):where is the received power at a reference distance , K corresponds to the large-scale fading fluctuations often modelled as a Gaussian random variable with zero mean and standard deviation , and is the path loss exponent with a typical value between 2 and 6 [15]. The primary benefits of signal-strength-based methods are their low cost and the elimination of the need for node-to-node network time synchronisation. Nonetheless, the positioning accuracy achieved is typically low due to the complexity of signal strength fluctuations with distance, ranging from 10 m to 50 m. Notably, multipath fading causes frequency-selective fading that is random and unpredictable, and is particularly concerning for location systems in urban areas, where LOS is frequently obstructed [16].
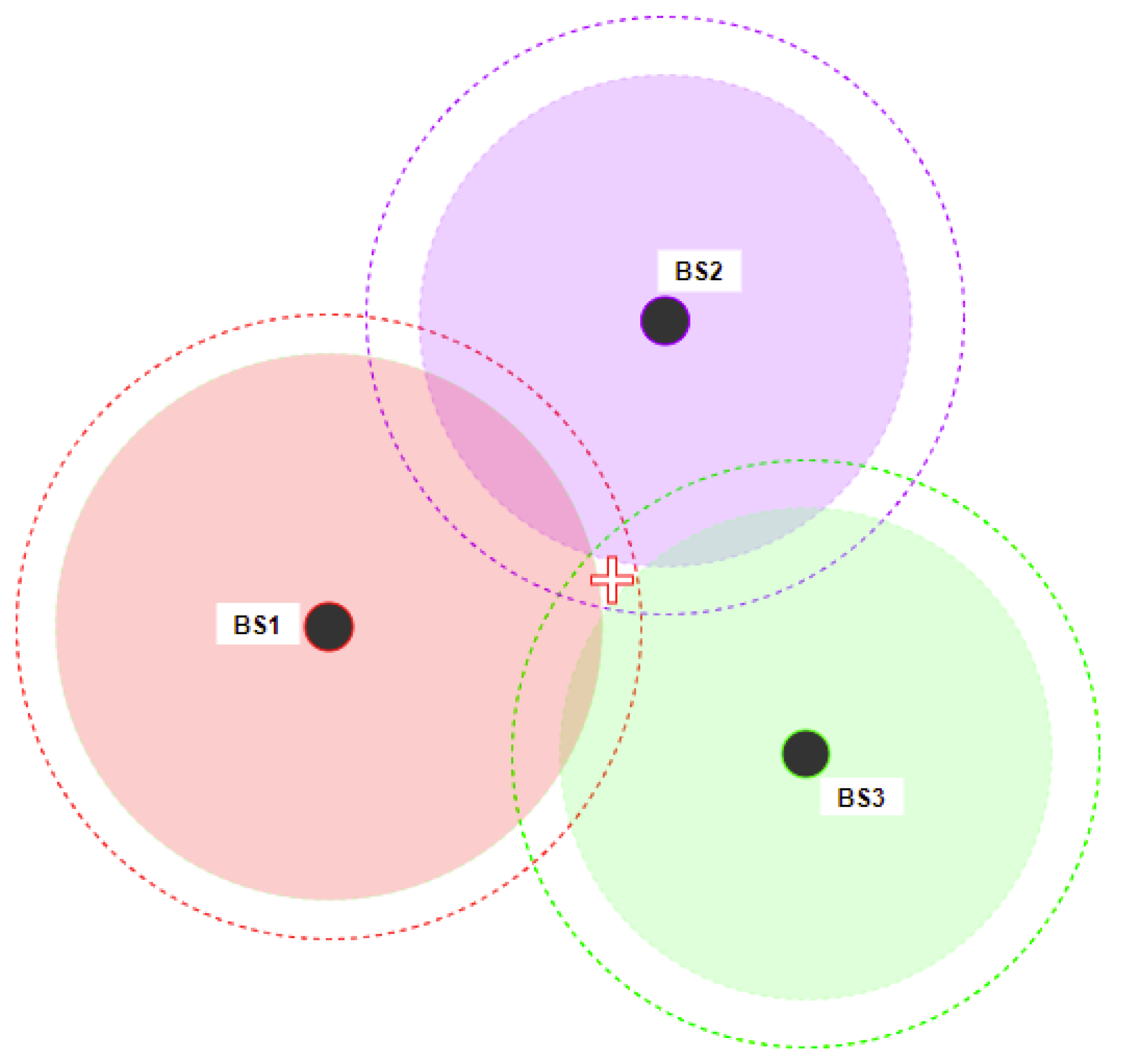
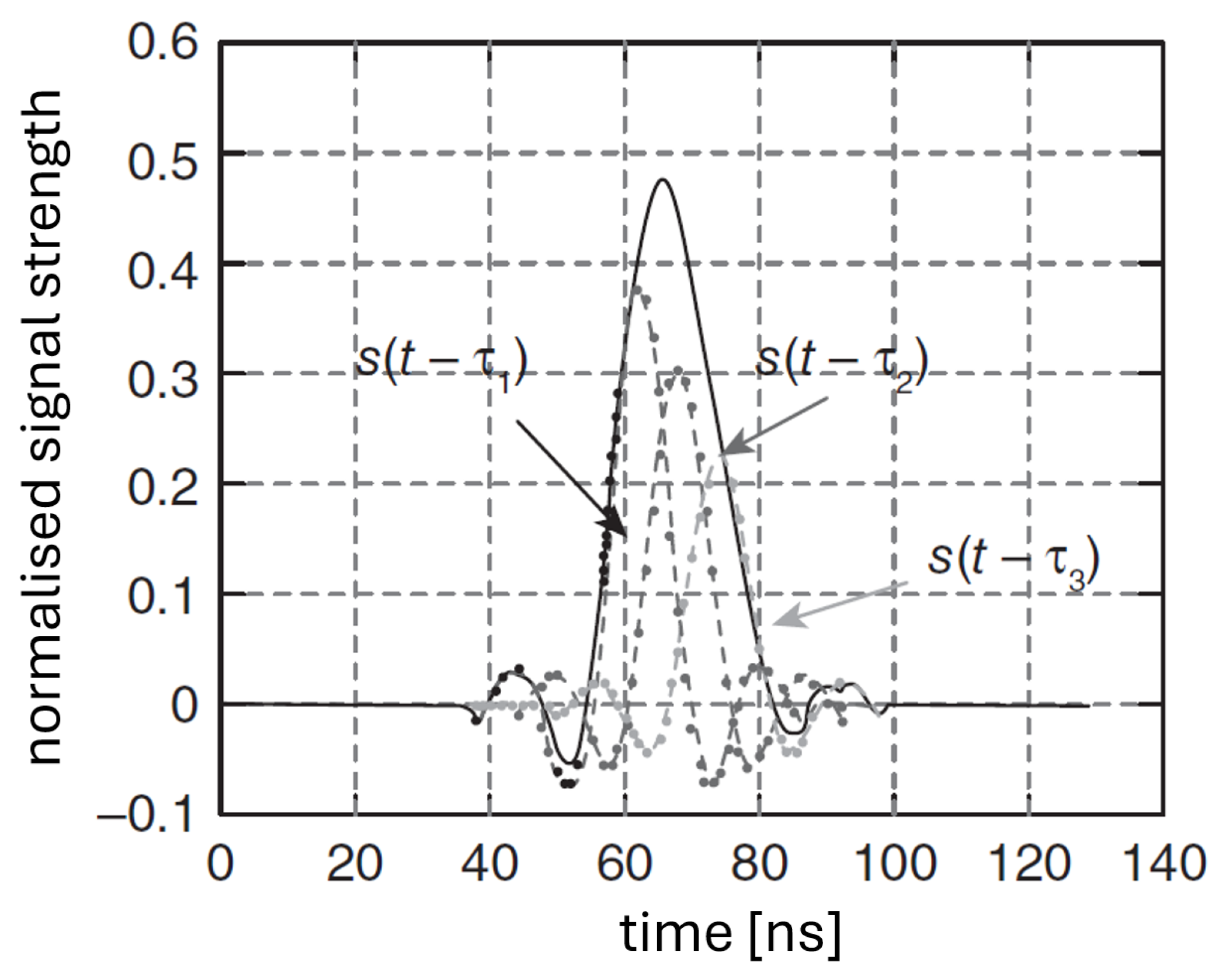
- Time-based: In time-based positioning, three approaches are typically used: one-way ranging TOA, two-way ranging round-trip time (RTT), and time difference of arrival (TDOA). When using TOA, measurements of the signal propagation delay, are used to obtain information about the separation distance between two nodes, where d is the distance between the nodes and c is the speed of the light. Using 2D geometry, a circle represents the receiver’s estimated range from each BS, and the intersections of circles represent the receiver location, as depicted in Figure 1. However, the intersection of these circles is often not an unique point due to measurement inaccuracies and multipath effects.
- Angle-based: Angle-based positioning involves measuring the angle at which signals arrive at the receiver from multiple transmitters. This method can provide high positioning accuracy. However, it often requires more complex and expensive hardware setups compared to signal-strength-based methods, and its accuracy can be significantly affected by multipath reflections and obstructions.
2.2. Multipath Interference
2.3. Noise
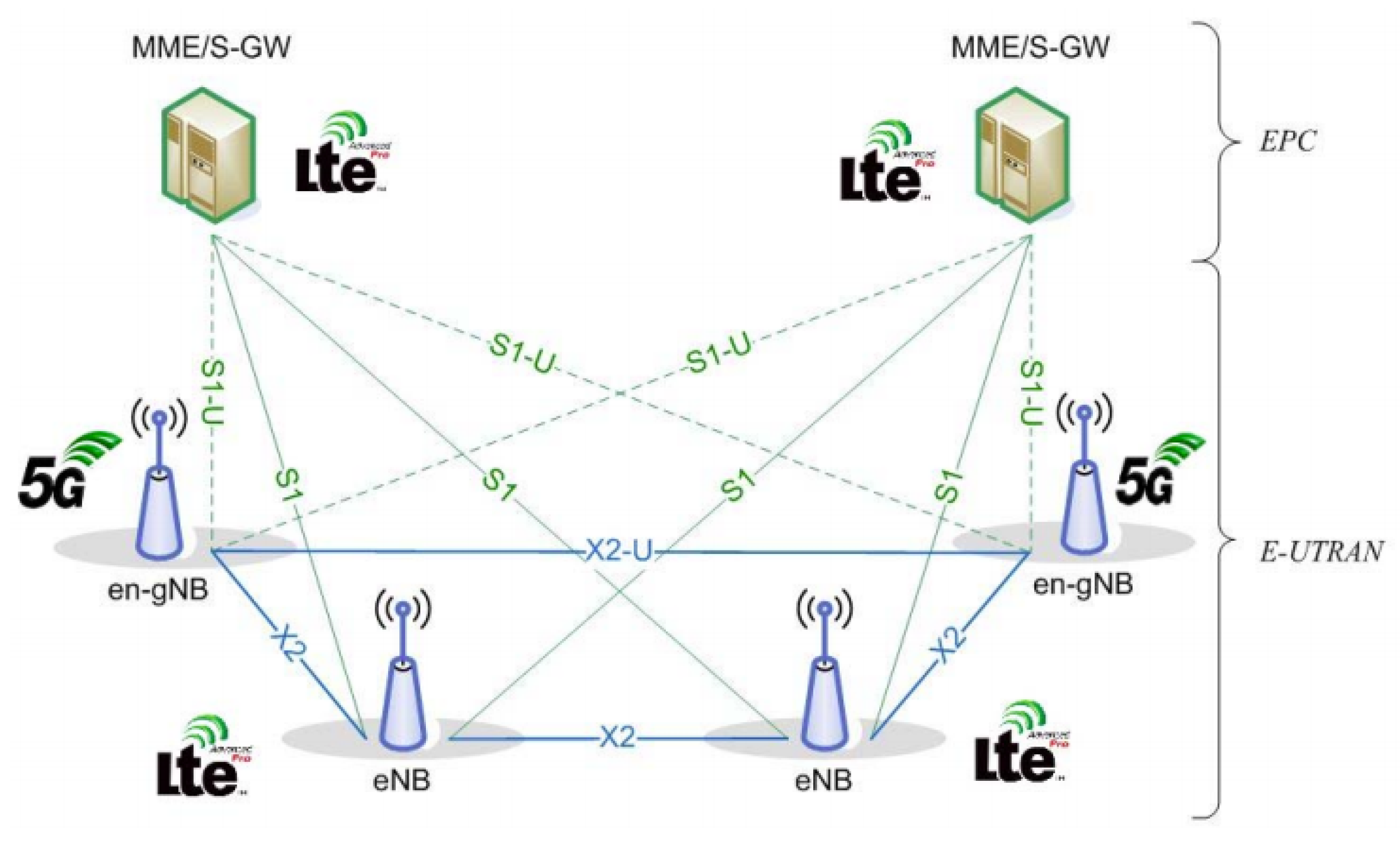
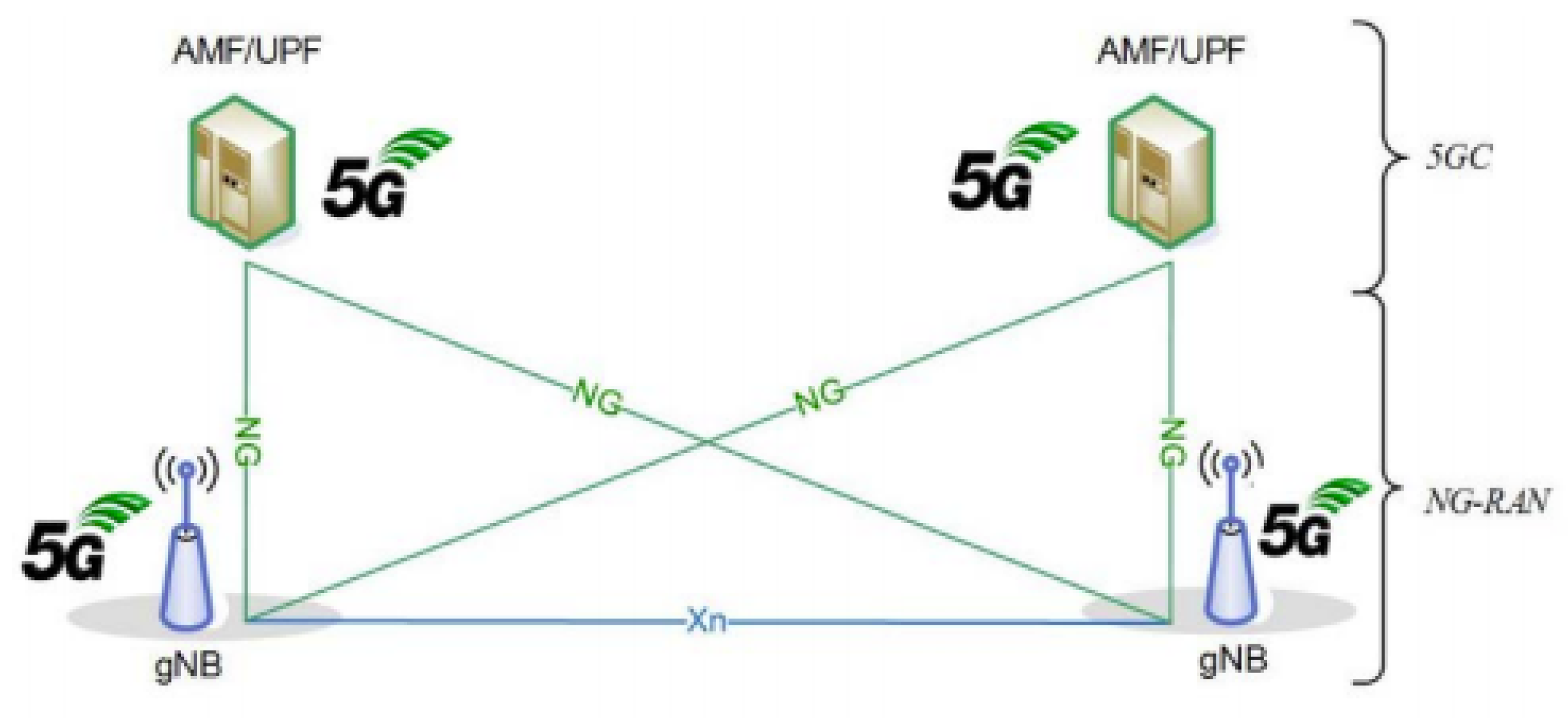
2.4. 5G Deployment
- cm-Wave 5G: Many of the frequency bands in FR1 overlap with those utilised for 4G and other mobile communication services. The FR1 band was initially designated to bands below 6 GHz, but has now been expanded to GHz in anticipation of further spectrum allocations [24].
- mm-Wave 5G: The frequency bands of FR2 range from GHz to GHz. At mm-Wave frequencies, significant attenuation losses can be compensated by using massive hybrid arrays [25]. Multipath sparsity in both the temporal and spatial domains is a crucial characteristic of mm-Wave signal propagation, which is caused by the rapidly decreasing energy of reflected mm-Wave signals, with only MPCs with few reflections being able to convey significant power.
2.5. 5G NR Positioning
- Bandwidth availability: Large bandwidth enables higher multipath resolution, translated to higher accuracy for TOA-based positioning. LTE offers a maximum bandwidth of 20 MHz, resulting in expected position errors above 63 m on 95% of the cases [27]. As shown in Table 1, the 5G network will enable bandwidths up to 100 and 400 MHz in the FR1 and FR2 bands, respectively, which can be increased up to 1 GHz using carrier aggregation techniques.
- Network density: 5G will provide better positioning accuracy by offering a range of access points for transmitting positioning pilot signals and processing user location. Rural macro cells may offer a wide coverage area because of favourable propagation conditions at sub-6 GHz frequencies in rural areas. In contrast to cm-Wave signals, mm-Wave signals are more likely to be obstructed by obstacles, and the probability of receiving NLOS signal components substantially decreases. However, mm-Wave signals suffer from significant attenuation, requiring the deployment of tiny (small, pico, and femto) cells.
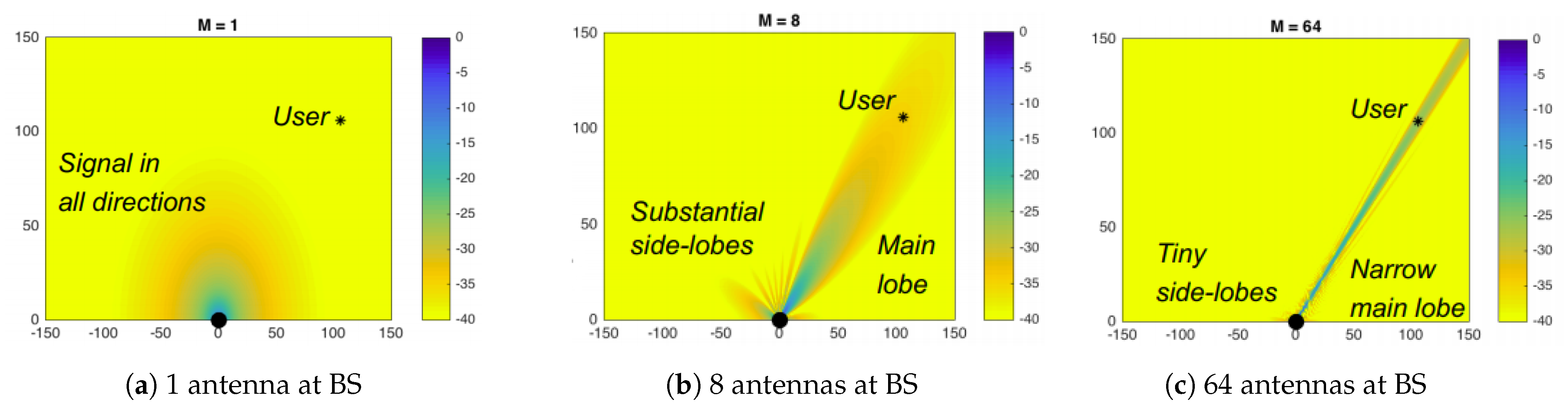
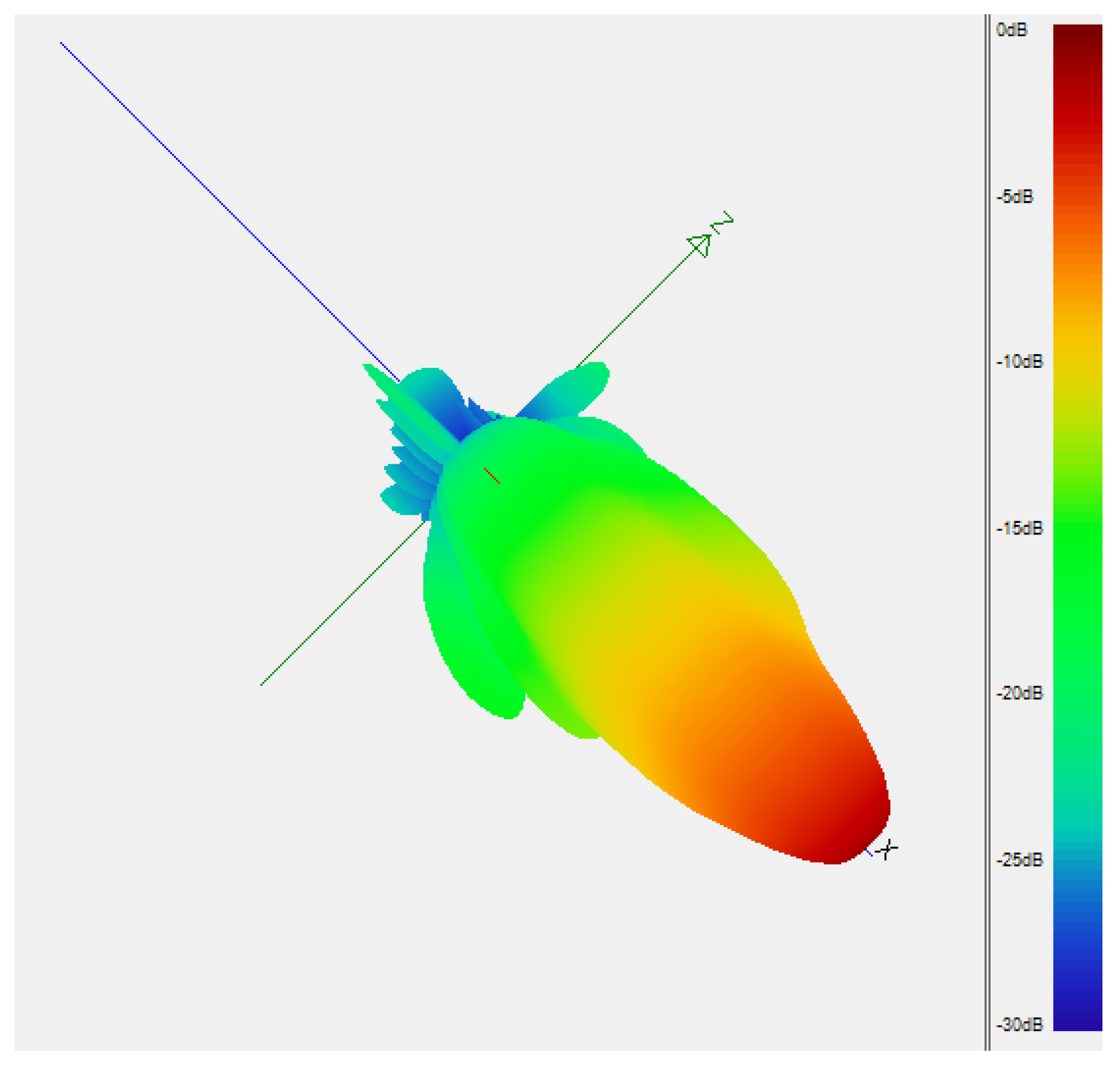
- MIMO and beamforming: MIMO antenna systems are known for achieving high spectral efficiency in wireless communication systems. This is achieved by performing parallel transmissions and increasing the number of antennas at the BS to increase the directivity of the transmitted signal. This reduces the effect of having substantial side lobes, as illustrated in Figure 5, which leads to higher spectral efficiency.
- Downlink time difference of arrival (DL-TDOA): This scheme is not fundamentally new and already existed in 4G under the name of Downlink OTDOA. It involves comparing the time difference of arrival between synchronous BSs at the receiver side. The main difference with 5G is that BSs can broadcast their own location on a broadcast channel in the 5G network, allowing the user to autonomously locate itself without the need to send measurements to the network [29].
- Multicell round-trip time: Under this method, the user must broadcast a location request to several BSs, including the serving and neighbouring BSs. The user location is then computed using the multi-RTT positioning technique. This method eliminates the need for time synchronisation, but is more susceptible to multipath positioning errors since it is a two-way communication.
- Downlink angle of departure (DL-AOD): This technique relies on DL—positioning reference signal (PRS)—reference signal received power (RSRP) measurements of downlink radio signals from numerous NR transmission/reception points (TRPs) obtained at the user, as well as knowledge of the downlink radio signals’ spatial information and TRPs’ geographical coordinates.
- Uplink angle-of-arrival (UL-AOA): The measured azimuth and zenith of arrival at numerous TRPs of uplink signals broadcasted from the user are used in the UL-AOA positioning technique. The TRPs utilise assistance data from the positioning server to measure the A-AOA and Z-AOA of the received signals, and the results are combined with other configuration information to estimate the user’s location.
2.6. RF Fingerprinting
- Offline training phase: A correlation database or “radio map” is built, containing a collection of RF signatures, using either radio propagation modelling or field measurements. Each signature is unique and associated with location data.
- Online localisation phase: During this phase, the signature of interest from the received signal is correlated with the database using a pattern-matching algorithm to estimate the geographic coordinates of the user based on the received signature.
2.7. Neural Networks and Bayesian Regularisation
2.8. Ensemble Learning
2.9. Machine Learning for Localisation
3. Methodology
3.1. Overview
3.2. Offline Training Phase
3.2.1. Modelling Software
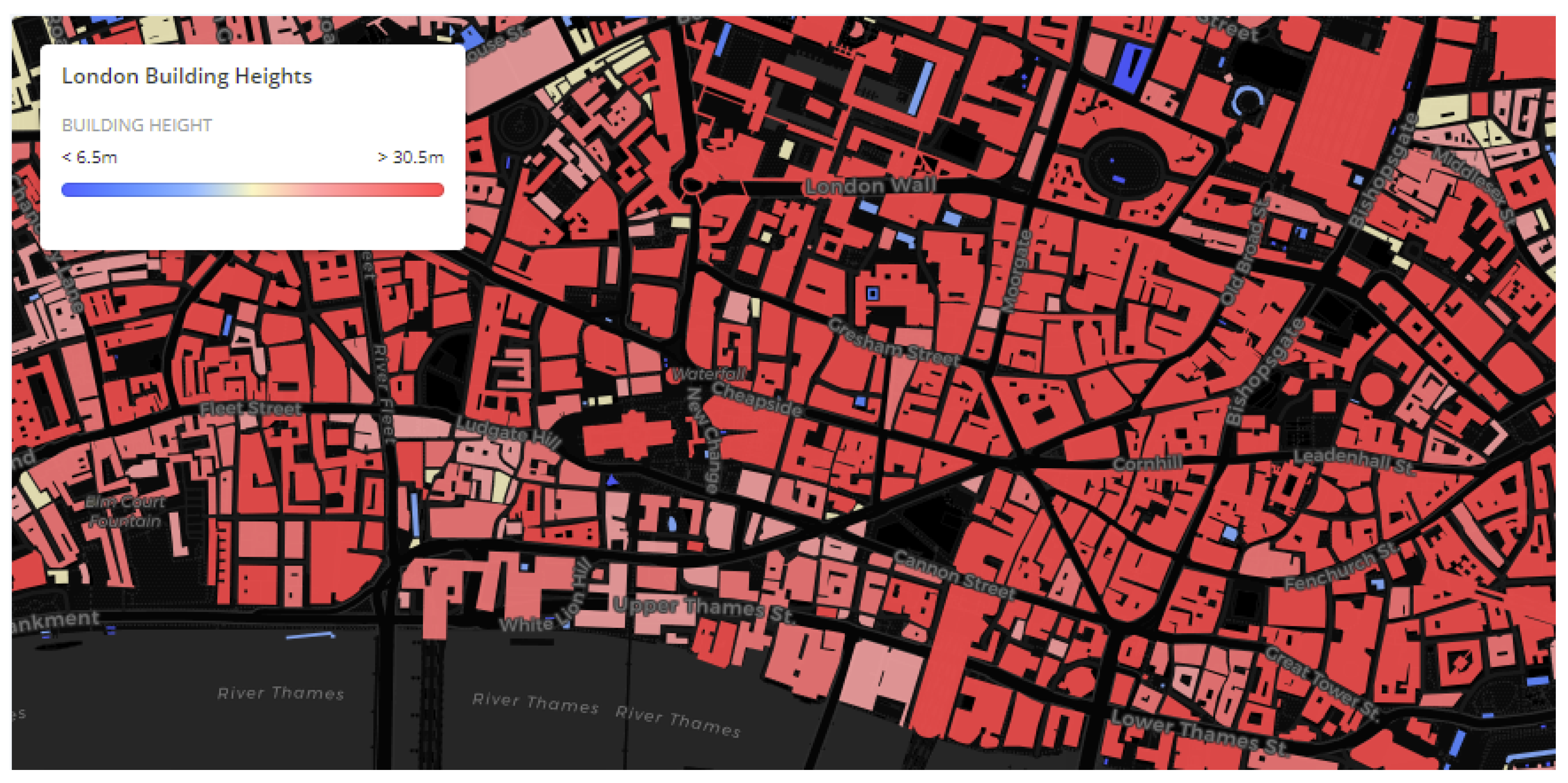
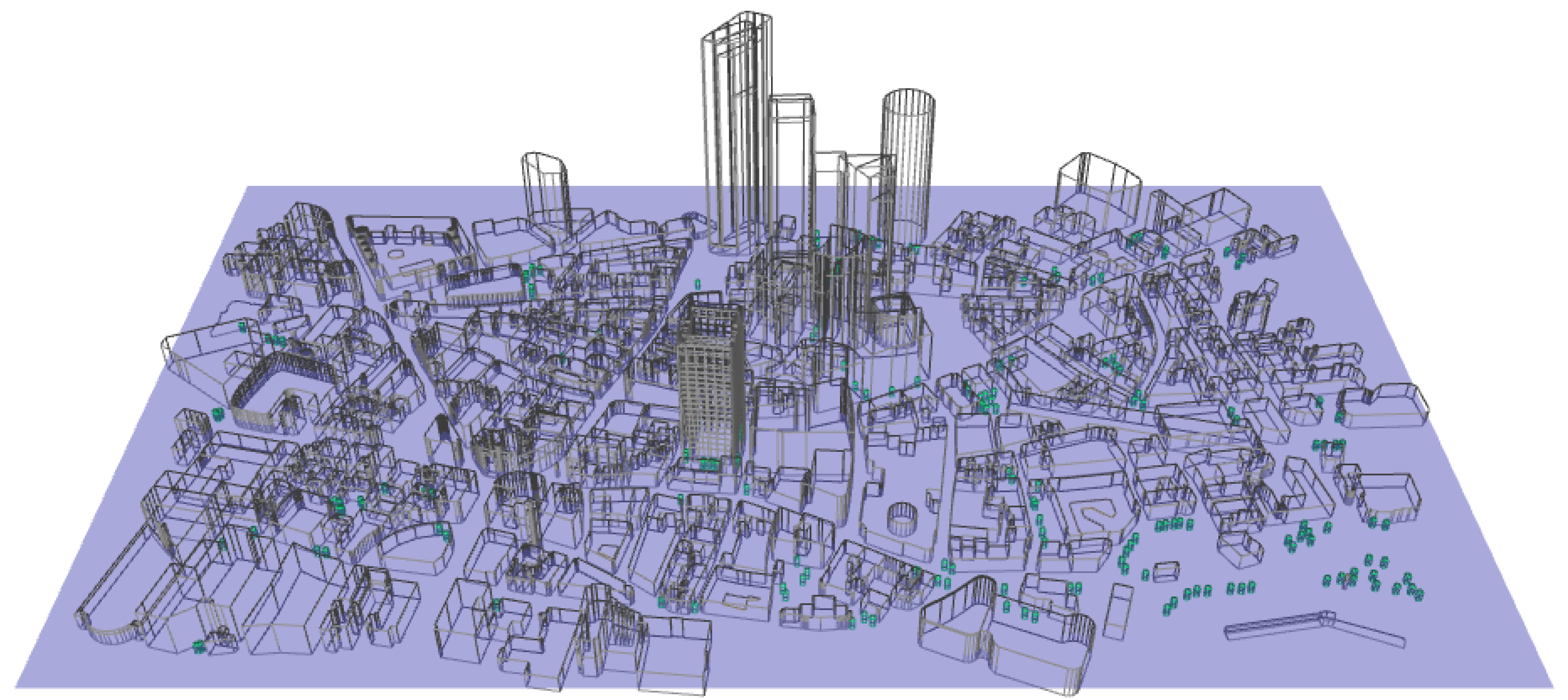
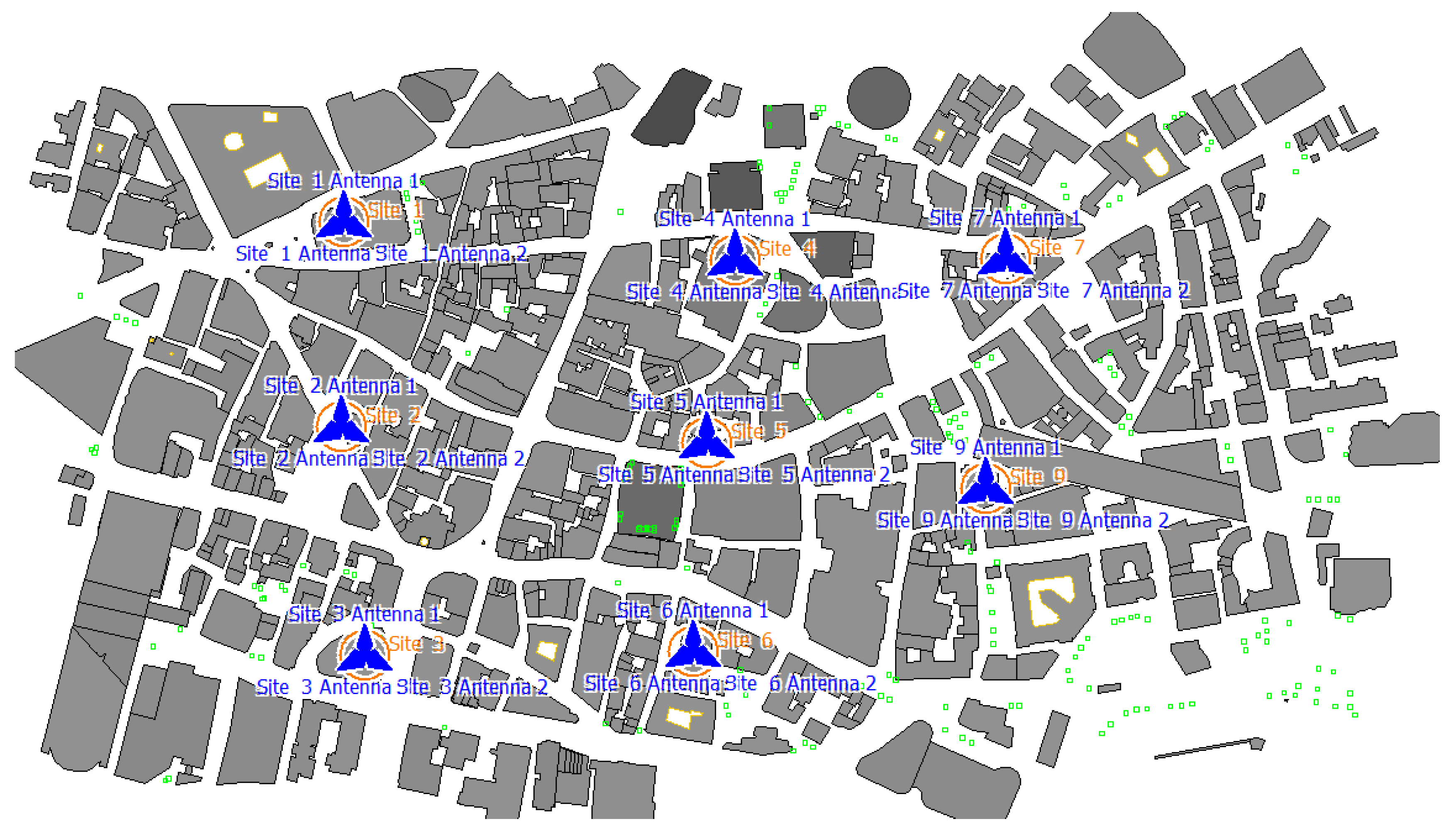
3.2.2. Urban Environment Model
3.2.3. Air Interface Model
3.2.4. Antenna Pattern
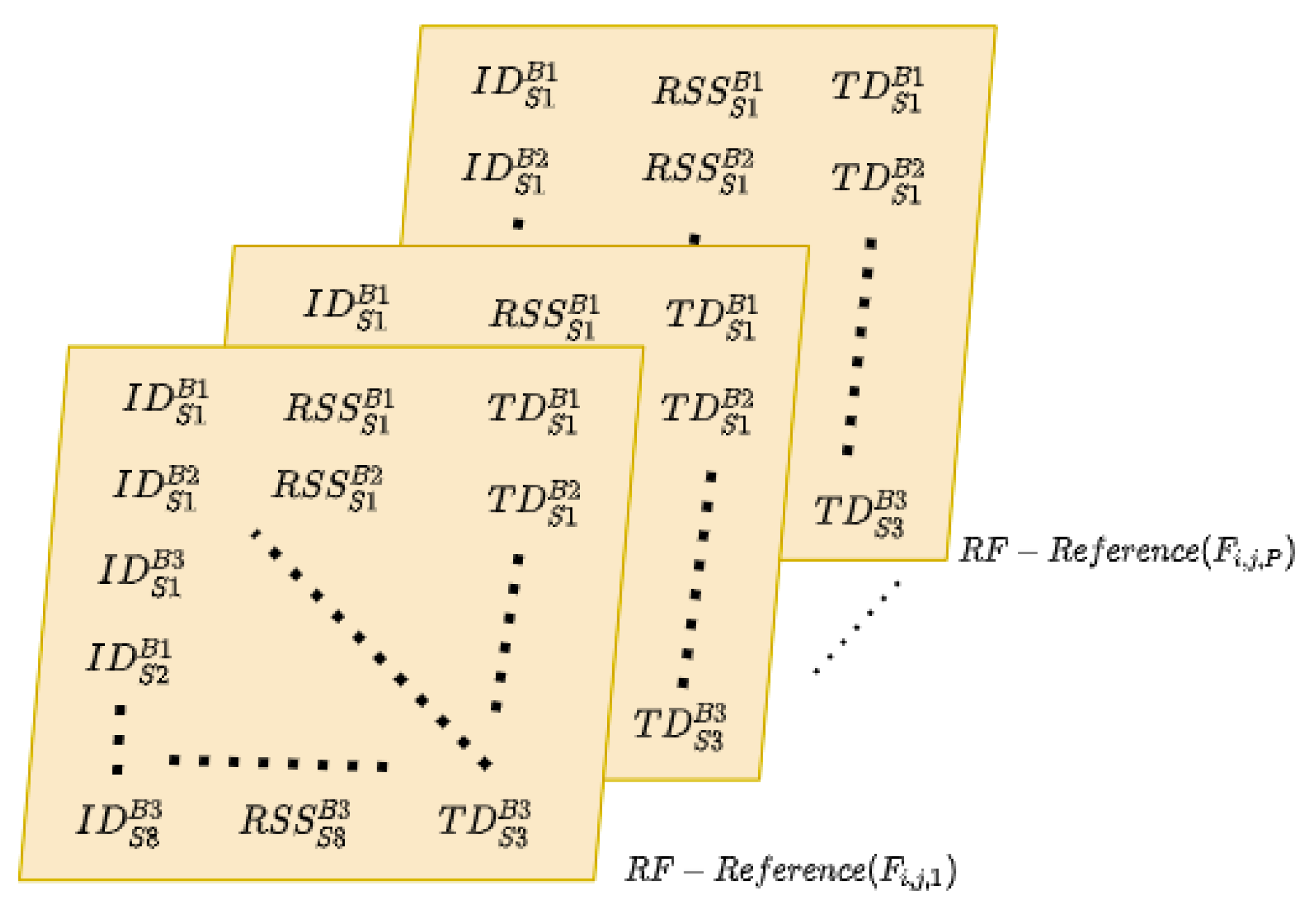
3.2.5. Correlation Database
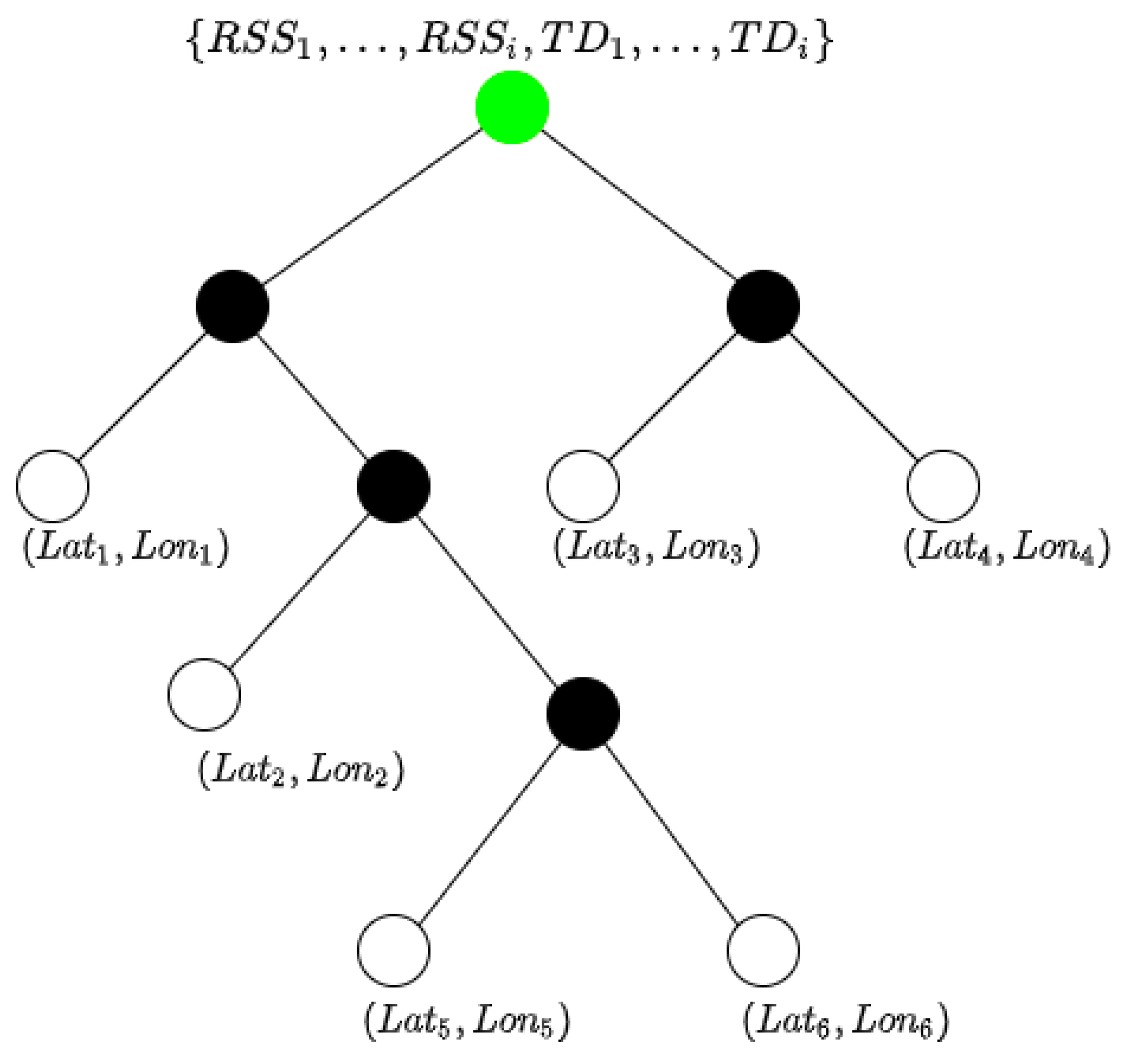
- In the first approach, a unique correlation database is built containing the full search space for RF fingerprinting, by storing the measured data in a multidimensional matrix, where each dimension corresponds to the measured RSS and the time delay of the beams from anchors in the range of the reference point, as illustrated in Figure 11. Each 2D-array corresponds to a specific geographic location, P is the number of locations processed, corresponds to the ID of each single beam per BS, and and are the strongest beam RSS and time delay from the i-th BS, respectively. Because each sector has a unique beam pattern, there is no need to filter observations from low RSS beams. When a multibeam pattern is utilised, data should be filtered to consider only those beams with a higher RSS. Information from low-RSS rays may be inaccurate, adding complexity to the algorithms while only providing minor performance improvements.
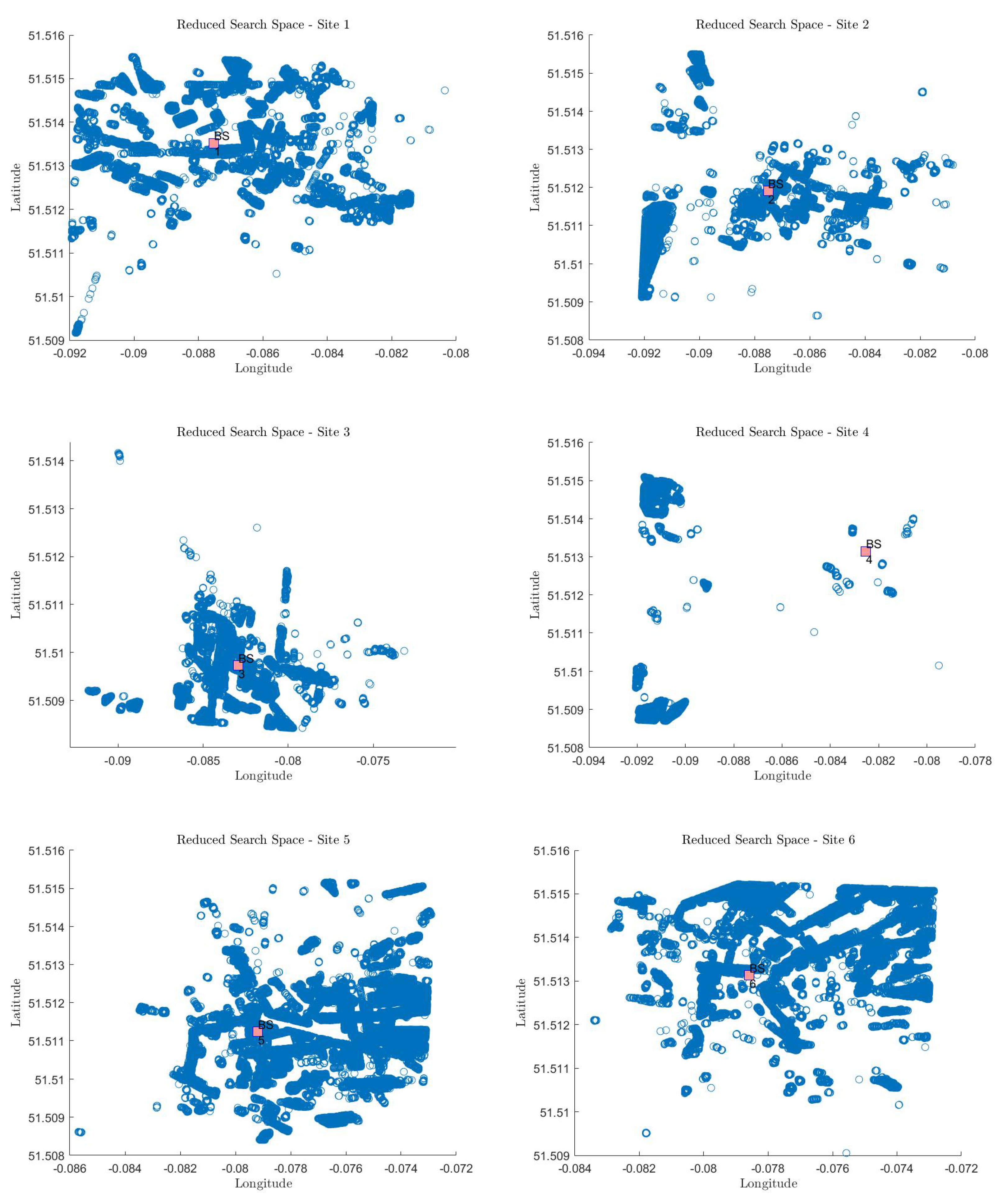
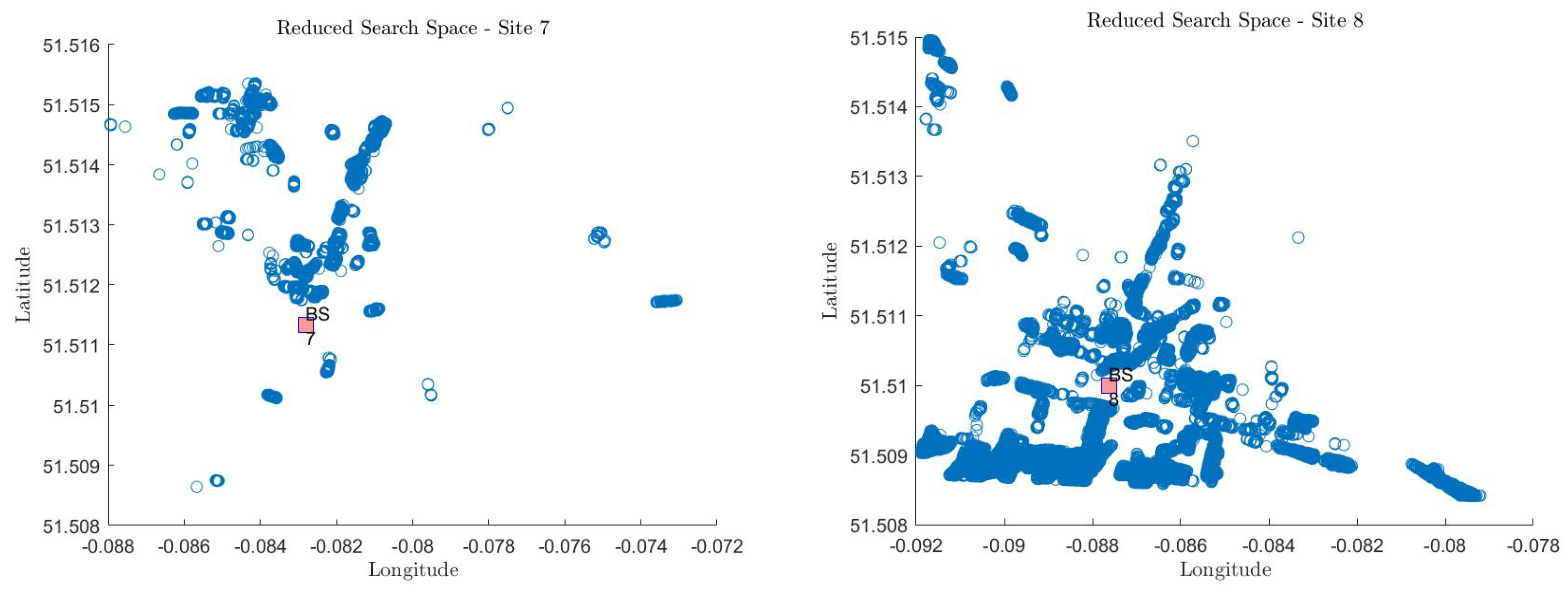
- In the second approach, a correlation database for each serving cell is developed, in which the serving BS makes the prediction. This technique takes advantage of the ability of cellular devices to determine the strongest received beam and initiate a handover procedure to partition the initial complete search space A into several smaller search spaces B, as illustrated in Figure 12, each of which corresponds to a particular service area. This produces N sub-matrices, where N is the number of BSs and each sub-matrix is associated with a specific service area, accomplished by sorting each RF-Reference in such a way that if to obtain (5):
3.3. Online Localisation Phase
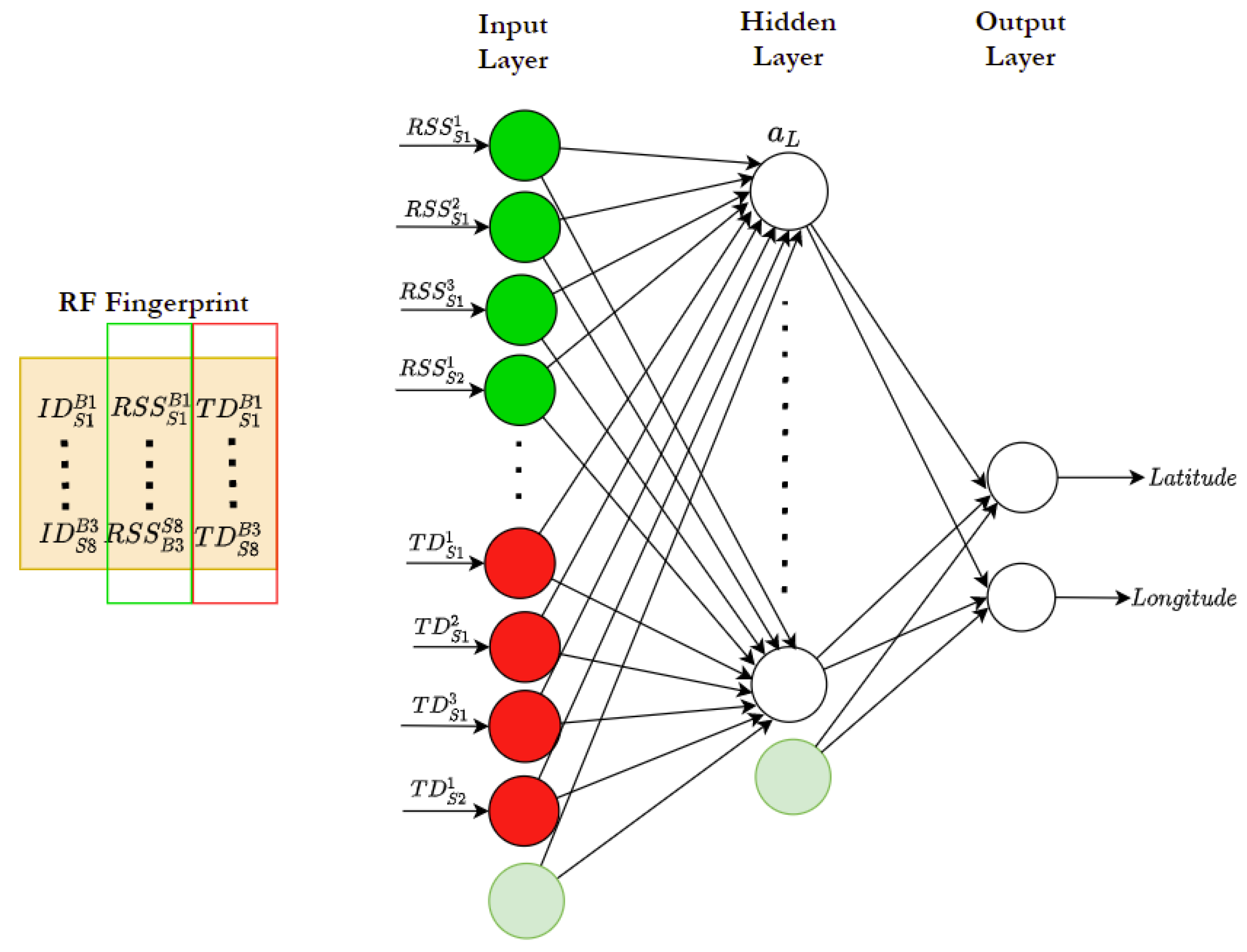
3.3.1. NN-Based Approach
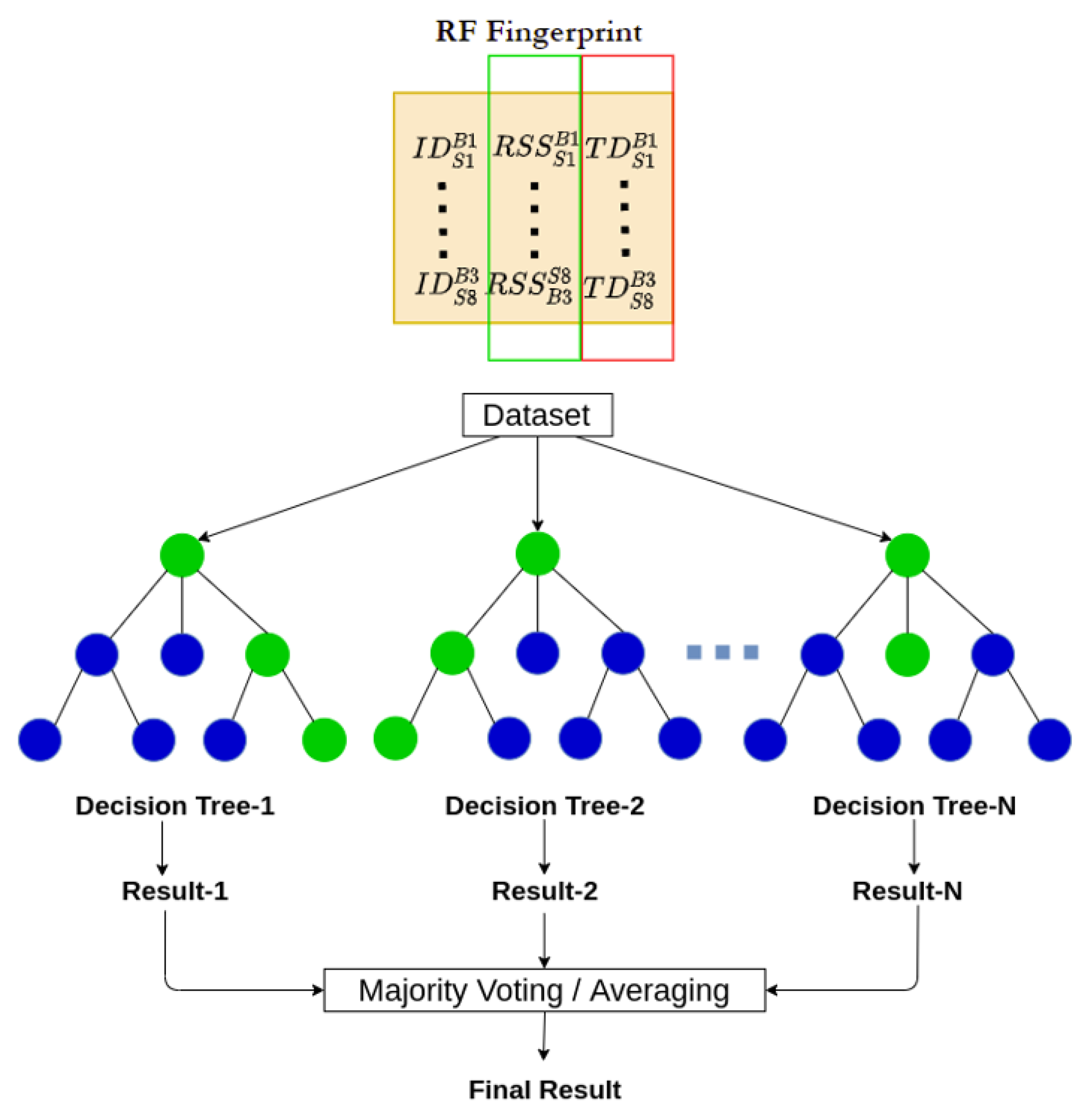
3.3.2. Random Forest
| Algorithm 1 Random forests [37] |
|
4. Testing and Evaluation
4.1. Evaluation and Analysis Metrics
4.1.1. MSE and RMSE
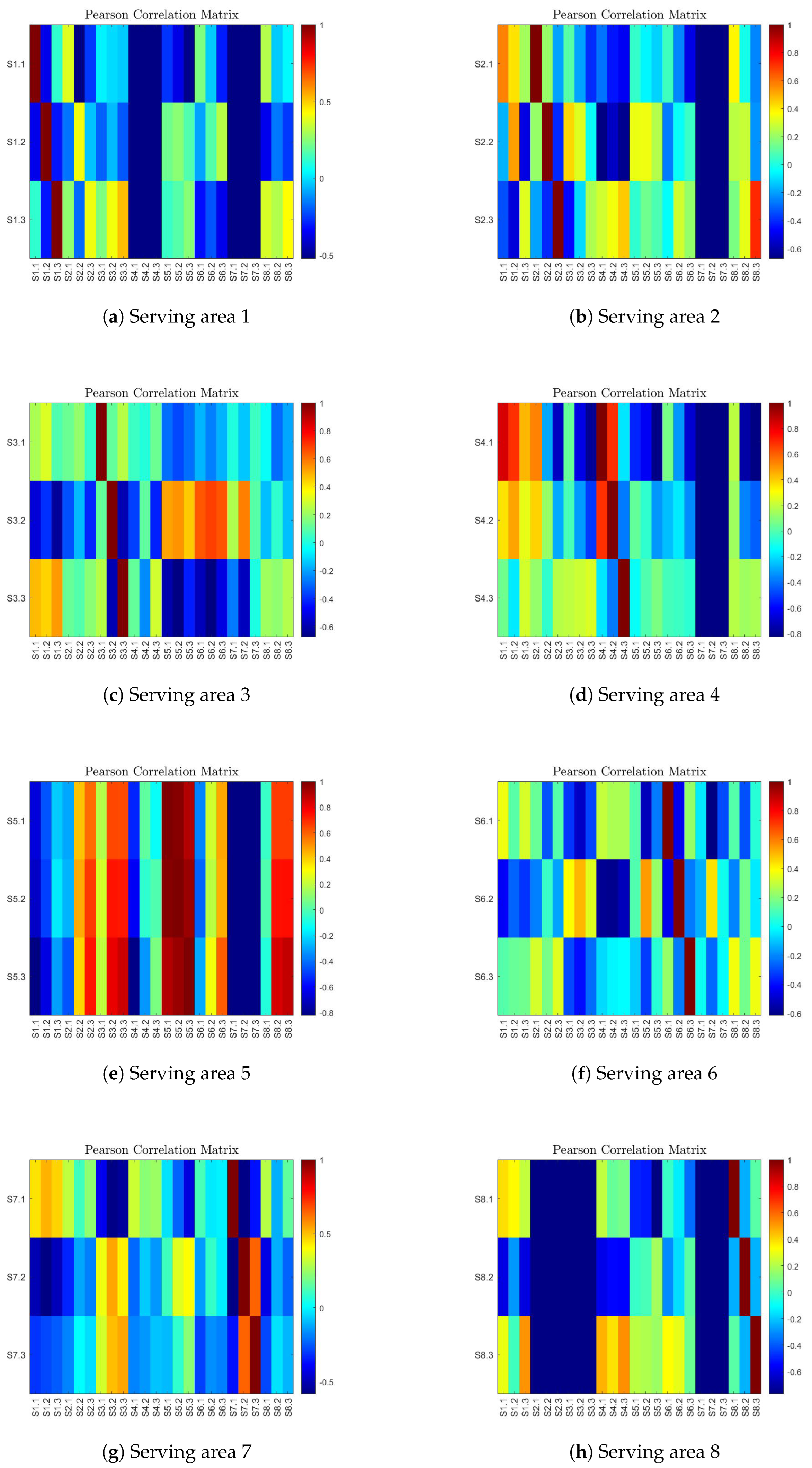
4.1.2. Pearson Correlation Coefficient
4.2. Dataset and Feature Analysis
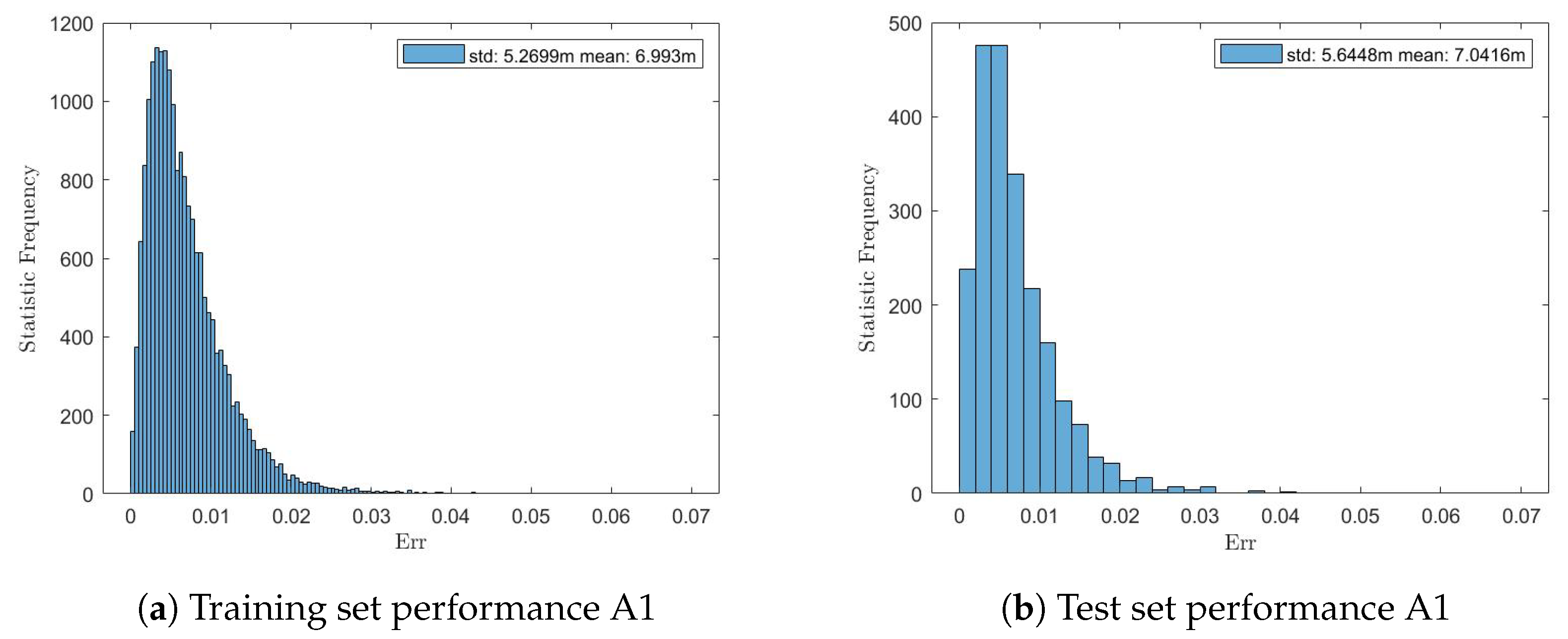
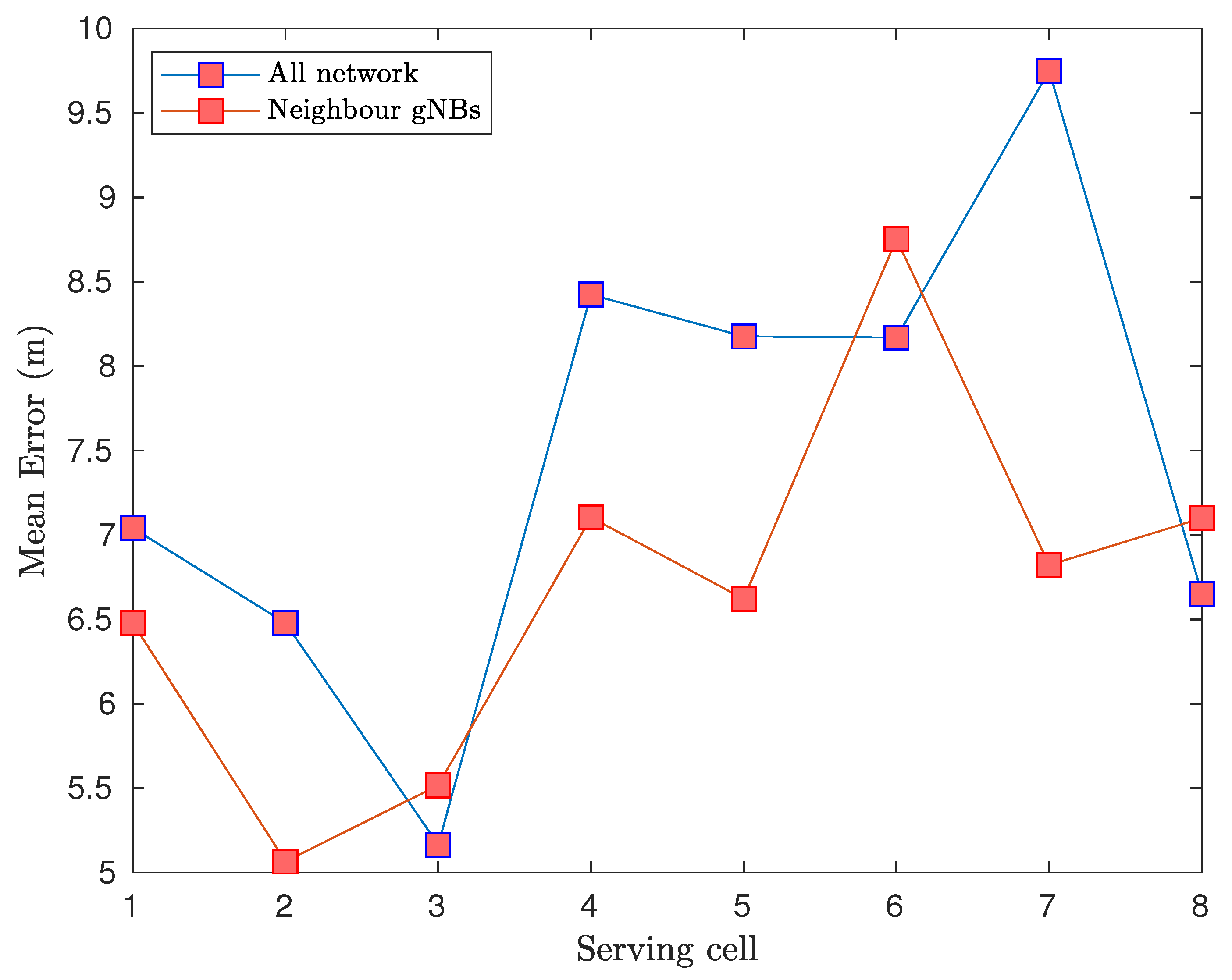
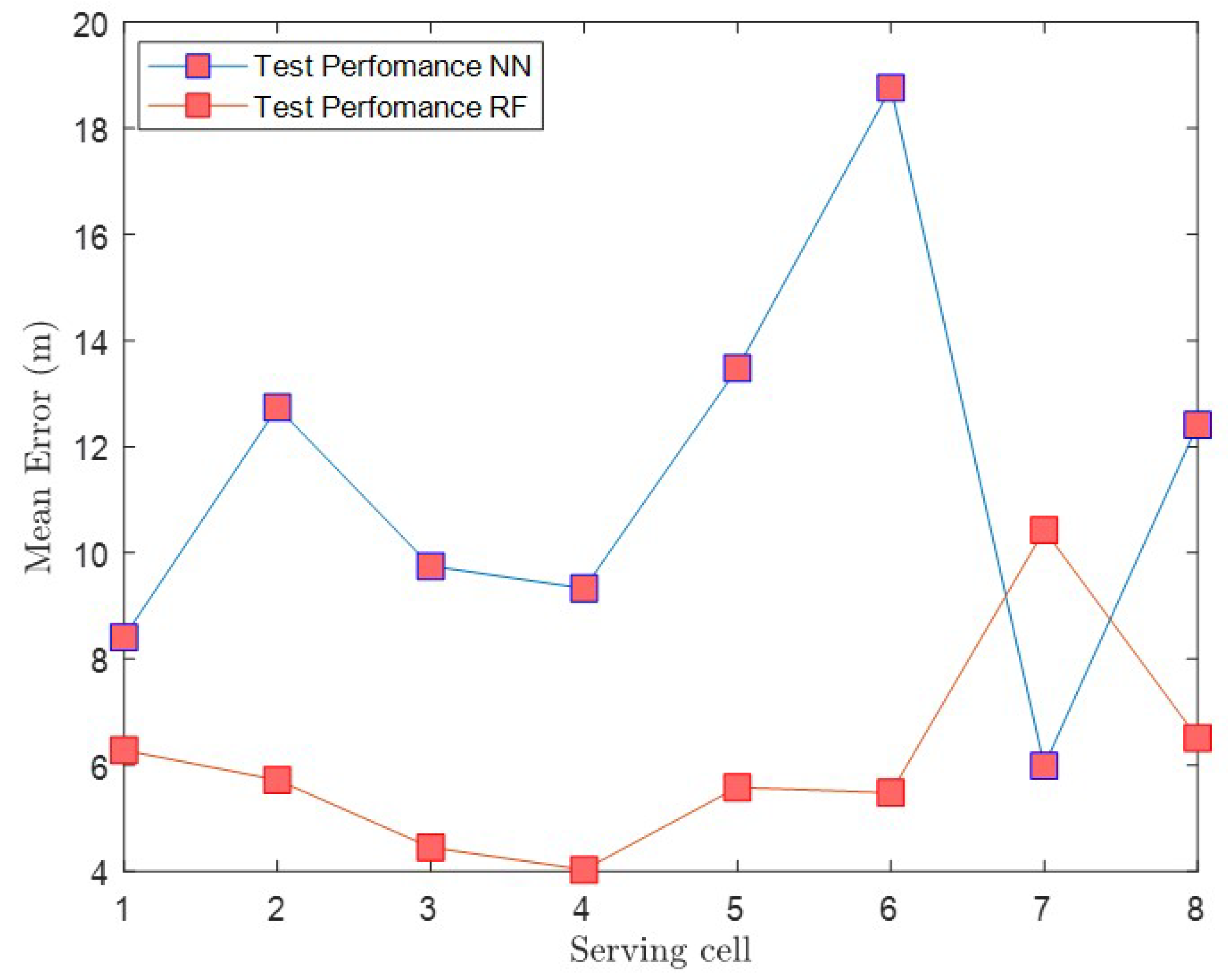
4.3. Bayesian Regularisation NN Results
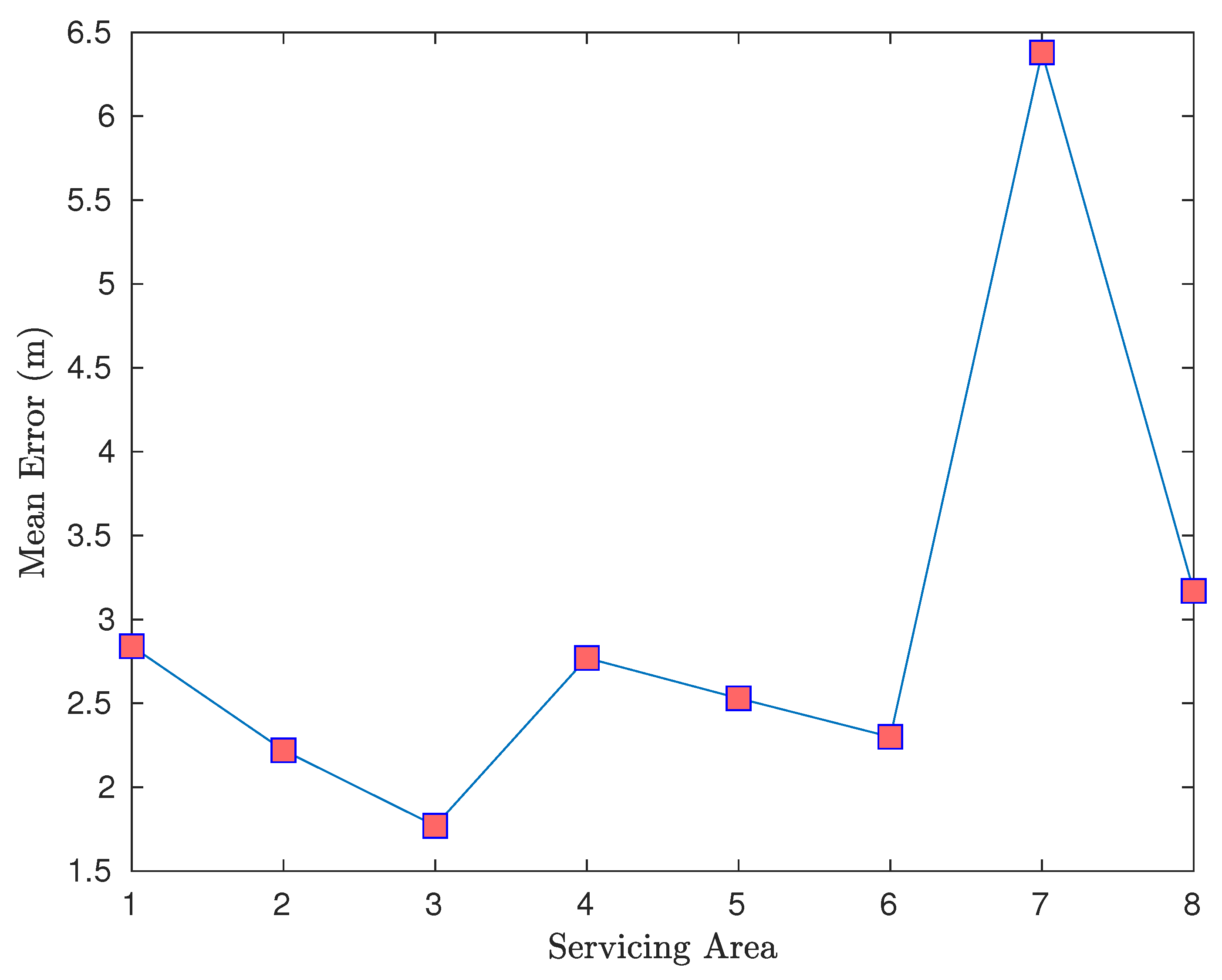
4.4. Random Forest Results
5. Conclusions
5.1. Summary
5.2. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| 4G | Fourth generation |
| 5G | Fifth generation |
| AI | Artificial intelligence |
| AOA | Angle of arrival |
| BR | Bayesian regularisation |
| BRANN | Bayesian regularised artificial neural networks |
| BS | Base station |
| CRB | Cramer–Rao low bound |
| CSI | Channel state information |
| DAA | Detect and avoid |
| DL-AOD | Downlink angle of departure |
| DL-TDOA | Downlink time difference of arrival |
| DNN | Deep neural network |
| EASA | European Union Aviation Safety Agency |
| EPC | Evolved packet core |
| FR | Frequency range |
| gNB | Next generation node |
| GNSS | Global navigation satellite systems |
| INS | Inertial navigation system |
| ITS | Intelligent transportation system |
| LM | Location management |
| LOS | Line of sight |
| LTE | Long-term evolution |
| MFML | Matched filter maximum likelihood |
| MIMO | Multiple input multiple output |
| ML | Machine learning |
| MPC | Multipath component |
| MSE | Mean squared error |
| NLOS | Non-line of sight |
| NN | Neural network |
| NR | New radio |
| NSA | Nonstandalone |
| PBN | Performance-based navigation |
| PRS | Positioning reference signal |
| RAN | Radio access network |
| RF | Radio frequency |
| ReLU | Rectified linear units |
| RMSE | Root mean squared error |
| RSRP | Reference signal received power |
| RSS | Received signal strength |
| RSSI | Received signal strength indicator |
| RTT | Round trip time |
| SA | Standalone |
| SNIR | Signal-to-noise-and-interference ratio |
| SNR | Signal-to-noise ratio |
| TDOA | Time difference of arrival |
| TOA | Time of arrival |
| TRP | Transmission/reception points |
| UAM | Urban air mobility |
| UAS | Unmanned aircraft system |
| UAV | Unmanned aerial vehicle |
| UL-AOA | Uplink angle-of-arrival |
References
- Wanniarachchi, S.T.; Turau, V. A study on the influence of 5G network planning on communication in Urban Air Mobility. In Proceedings of the 2023 IEEE 24th International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), Boston, MA, USA, 12–15 June 2023; pp. 394–399. [Google Scholar] [CrossRef]
- Warrier, A.; Aljaburi, L.; Whitworth, H.; Al-Rubaye, S.; Tsourdos, A. Future 6G communications powering vertical handover in non-terrestrial networks. IEEE Access 2024, 12, 33016–33034. [Google Scholar] [CrossRef]
- EASA. Study on the Societal Acceptance of Urban Air Mobility in Europe; European Union Aviation Safety Agency: Cologne, Germany, 2021. [Google Scholar]
- Shu, Y.; Xu, P.; Niu, X.; Chen, Q.; Qiao, L.; Liu, J. High-rate attitude determination of moving vehicles with GNSS: GPS, BDS, GLONASS, and Galileo. IEEE Trans. Instrum. Meas. 2022, 71, 5501813. [Google Scholar] [CrossRef]
- Deng, Z.; Zheng, X.; Wang, H.; Fu, X.; Yin, L.; Liu, W. A novel time delay estimation algorithm for 5G vehicle positioning in urban canyon environments. Sensors 2020, 20, 5190. [Google Scholar] [CrossRef]
- Rastorgueva-Foi, E.; Costa, M.; Koivisto, M.; Talvitie, J.; Leppäneny, K.; Valkama, M. Beam-based device positioning in mmWave 5G systems under orientation uncertainties. In Proceedings of the 2018 52nd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 28–31 October 2018; pp. 3–7. [Google Scholar] [CrossRef]
- Yuan, Z.; Guo, W.; Al-Rubaye, S. Multi-UAV wireless positioning using adaptive multidimensional scaling and extended kalman filter. In Proceedings of the 2022 IEEE Globecom Workshops (GC Wkshps), Rio de Janeiro, Brazil, 4–8 December 2022; pp. 1437–1441. [Google Scholar] [CrossRef]
- Sun, C.; Zhao, H.; Bai, L.; Cheong, J.W.; Dempster, A.G.; Feng, W. GNSS-5G hybrid positioning based on TOA/AOA measurements. In Proceedings of the China Satellite Navigation Conference, Chengdu, China, 23–25 May 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 527–537. [Google Scholar]
- Peral-Rosado, D.; José, A.; Saloranta, J.; Destino, G.; López-Salcedo, J.A.; Seco-Granados, G. Methodology for simulating 5G and GNSS high-accuracy positioning. Sensors 2018, 18, 3220. [Google Scholar] [CrossRef]
- Jagannath, A.; Jagannath, J.; Kumar, P.S.P.V. A comprehensive survey on radio frequency (RF) fingerprinting: Traditional approaches, deep learning, and open challenges. Comput. Netw. 2022, 219, 109455. [Google Scholar] [CrossRef]
- Butt, M.M.; Rao, A.; Yoon, D. RF fingerprinting and deep learning assisted UE positioning in 5G. In Proceedings of the 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 25–28 May 2020; pp. 1–7. [Google Scholar]
- Whitworth, H.; Al-Rubaye, S.; Tsourdos, A. Urban Air Mobility link budget analysis in 5G communication systems. In Proceedings of the 2023 IEEE 24th International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), Boston, MA, USA, 12–15 June 2023; pp. 400–406. [Google Scholar] [CrossRef]
- De Sousa, M.N.; Thomä, R.S. Applying random forest and multipath fingerprints to enhance TDOA localization systems. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 2316–2320. [Google Scholar] [CrossRef]
- Dong, Y.; Du, B.; Zhang, L. Target detection based on random forest metric learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1830–1838. [Google Scholar] [CrossRef]
- Rappaport, T.S. Wireless Communications: Principles and Practice; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1996; Volume 2. [Google Scholar]
- Heon Lee, J.; Michael Buehrer, R. Fundamentals of received signal strength-based position location. In Handbook of Position Location: Theory, Practice, and Advances, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018; pp. 369–404. [Google Scholar]
- Wang, Y.; Chen, X.; Liu, P. Statistical multipath model based on experimental GNSS data in static urban canyon environment. Sensors 2018, 18, 1149. [Google Scholar] [CrossRef] [PubMed]
- Michael Buehrer, R.; Venkatesh, S. Fundamentals of time-of-arrival-based position location. In Handbook of Position Location: Theory, Practice, and Advances, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018; pp. 199–236. [Google Scholar]
- Apartsin, A.; Cooper, L.N.; Intrator, N. SNR-dependent filtering for time of arrival estimation in high noise. In Proceedings of the 2010 IEEE International Workshop on Machine Learning for Signal Processing, Kittila, Finland, 29 August–1 September 2010; pp. 427–431. [Google Scholar]
- Dardari, D.; Conti, A.; Ferner, U.; Giorgetti, A.; Win, M.Z. Ranging with ultrawide bandwidth signals in multipath environments. Proc. IEEE 2009, 97, 404–426. [Google Scholar] [CrossRef]
- Release 15 Description—Summary of Rel-15 Work Items. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3389 (accessed on 15 May 2021).
- Al-Rubaye, S.; Tsourdos, A. Airport connectivity optimization for 5G ultra-dense networks. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 980–989. [Google Scholar] [CrossRef]
- 101-1 NR User Equipment (UE) Radio Transmission and Reception—Part 1: Range 1 Standalone. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3283 (accessed on 30 April 2021).
- 5G Frequency Bands, Channels for FR1 & FR2. Available online: https://www.electronics-notes.com/articles/connectivity/5g-mobile-wireless-cellular/frequency-bands-channels-fr1-fr2.php (accessed on 30 April 2021).
- Zhang, J.A.; Huang, X.; Dyadyuk, V.; Guo, Y.J. Massive hybrid antenna array for millimeter-wave cellular communications. IEEE Wirel. Commun. 2015, 22, 79–87. [Google Scholar] [CrossRef]
- Sobehy, A. Machine Learning Based localization in 5G. Ph.D. Thesis, Institut Polytechnique de Paris, Palaiseau, France, 2020. [Google Scholar]
- Medbo, J.; Siomina, I.; Kangas, A.; Furuskog, J. Propagation channel impact on LTE positioning accuracy: A study based on real measurements of observed time difference of arrival. In Proceedings of the 2009 IEEE 20th International Symposium on Personal, Indoor and Mobile Radio Communications, Tokyo, Japan, 13–16 September 2009; pp. 2213–2217. [Google Scholar]
- Mousa, M.; Al-Rubaye, S.; Inalhan, G. Unmanned Aerial Vehicle positioning using 5G New Radio technology in urban environment. In Proceedings of the 2023 IEEE/AIAA 42nd Digital Avionics Systems Conference (DASC), Barcelona, Spain, 1–5 October 2023; pp. 1–9. [Google Scholar] [CrossRef]
- 3GPP TS 38.305 version 16.1.0 Release—5G; NG Radio Access Network (NG-RAN); Stage 2 Functional Specification of User Equipment (UE) Positioning in NG-RAN. Available online: https://www.etsi.org/deliver/etsi_ts/138300_138399/138305/16.01.00_60/ts_138305v160100p.pdf (accessed on 1 March 2024).
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Okut, H. Bayesian regularized neural networks for small n big p data. In Artificial Neural Networks-Models and Applications; InTech Open: London, UK, 2016; pp. 28–48. [Google Scholar]
- Chriki, A.; Touati, H.; Snoussi, H. SVM-based indoor localization in wireless sensor networks. In Proceedings of the 2017 13th international wireless communications and mobile computing conference (IWCMC), Valencia, Spain, 26–30 June 2017; pp. 1144–1149. [Google Scholar]
- Sánchez-Rodríguez, D.; Hernández-Morera, P.; Quinteiro, J.M.; Alonso-González, I. A low complexity system based on multiple weighted decision trees for indoor localization. Sensors 2015, 15, 14809–14829. [Google Scholar] [CrossRef] [PubMed]
- Wye, K.F.P.; Zakaria, S.M.M.S.; Kamarudin, L.M.; Zakaria, A.; Ahmad, N.B.; Kamarudin, K. RSS-based fingerprinting localization with artificial neural network. J. Physics Conf. Ser. 2021, 1755, 012033. [Google Scholar]
- Pecoraro, G.; Di Domenico, S.; Cianca, E.; De Sanctis, M. CSI-based fingerprinting for indoor localization using LTE signals. EURASIP J. Adv. Signal Process. 2018, 2018, 1–18. [Google Scholar] [CrossRef]
- Open Street Map.osm File Generator. Available online: https://www.openstreetmap.org/#map=5/54.910/-3.432 (accessed on 20 March 2024).
- Manikandan, M.; Vijayakumar, P. Improving the performance of classifiers by ensemble techniques for the premature finding of unusual birth outcomes from cardiotocography. IETE J. Res. 2023, 69, 1734–1744. [Google Scholar] [CrossRef]
| Frequency Range | Frequency (MHz) | Channel Bandwidth (MHz) |
|---|---|---|
| FR1 | 410–7125 | 5, 10, 15, 20, 25, 30, 40, 50, 60, 80, 90, 100 |
| FR2 | 24,250–52,600 | 50, 100, 200, 400 |
| Parameter | Value |
|---|---|
| Nr. sectors | 3 sectors per site |
| Tx power | 40 dBm |
| Antenna gain | 15.5 dB |
| Antenna orientation (azimuth) | 0 deg |
| Antenna orientation (downlit) | 0 deg |
| Parameter | Value |
|---|---|
| Scenario | City of London |
| Sites | 8 |
| Antenna height | 35 m |
| FR1 band | n78 |
| Carrier freq. | 3550 MHz |
| Numerology | 2 |
| Planar resolution | 1 m |
| Serving Area | Hidden Neurons (RSS and Time Delay) | Hidden Neurons (RSS) |
|---|---|---|
| 1 | 55 | 40 |
| 2 | 35 | 23 |
| 3 | 51 | 62 |
| 4 | 38 | 10 |
| 5 | 51 | 51 |
| 6 | 63 | 43 |
| 7 | 51 | 60 |
| 8 | 59 | 61 |
| Network Specific | |||
|---|---|---|---|
| Site | Nr. Samples Location | Mean RSS and TD [m] | Mean RSS [m] |
| 1 | 22146 | 7.04 | 9.90 |
| 2 | 18243 | 6.48 | 9.74 |
| 3 | 21531 | 5.16 | 9.59 |
| 4 | 8790 | 8.42 | 7.46 |
| 5 | 57046 | 8.18 | 12.67 |
| 6 | 41799 | 8.17 | 16.83 |
| 7 | 2756 | 9.75 | 7.51 |
| 8 | 19177 | 6.65 | 16.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mbaye, I.; Al-Rubaye, S.; Conrad, C.; Inalhan, G. Integrated Sensing and New Radio Communications for Air Vehicle Positioning. Vehicles 2024, 6, 1665-1689. https://doi.org/10.3390/vehicles6030080
Mbaye I, Al-Rubaye S, Conrad C, Inalhan G. Integrated Sensing and New Radio Communications for Air Vehicle Positioning. Vehicles. 2024; 6(3):1665-1689. https://doi.org/10.3390/vehicles6030080
Chicago/Turabian StyleMbaye, Ibrahima, Saba Al-Rubaye, Christopher Conrad, and Gokhan Inalhan. 2024. "Integrated Sensing and New Radio Communications for Air Vehicle Positioning" Vehicles 6, no. 3: 1665-1689. https://doi.org/10.3390/vehicles6030080
APA StyleMbaye, I., Al-Rubaye, S., Conrad, C., & Inalhan, G. (2024). Integrated Sensing and New Radio Communications for Air Vehicle Positioning. Vehicles, 6(3), 1665-1689. https://doi.org/10.3390/vehicles6030080








