Motion Planning for Autonomous Vehicles Based on Sequential Optimization

Abstract

This study presents the development and analysis of a technique for planning the autonomous vehicle (AV) motion references using sequential optimization. The method determines the trajectory plan, speed and acceleration distributions, and other AV kinematic parameters. The approach combines the basics of the finite element method (FEM) and nonlinear optimization with nonlinear constraints. First, we briefly described the generalization of representing an arbitrary function by finite elements (FE) within a road segment. We chose a one-dimensional FE with two nodes and three degrees of freedom (DOF) in a node corresponding to the 5th-degree polynomial. Next, we presented a method for defining the motion trajectory. The following are considered: the formation of a restricted space for the AV’s allowable maneuvering, the motion trajectory geometry and its relation with vehicle steerability parameters, cost functions and their influences on the desirable trajectory’s nature, and the compliance of nonlinear restrictions of the node parameters with the motion area boundaries. In the second stage, we derived a technique for optimizing the AV’s speed and acceleration redistributions. The model considers possible combinations of objective functions, limiting the kinematic parameters by the tire slip critical speed, maximum speed level, maximum longitudinal acceleration, and critical lateral acceleration. In the simulation section, we compared several variants of trajectories and versions of distributing the longitudinal speed and acceleration curves. The advantages, drawbacks, and conclusions regarding the proposed technique are presented.

1. Introduction

Planning AV motion is characterized by using various techniques and methods (Claussmann et al., 2019) [1], many of which originate from tasks of modeling trajectories for robots [2,3]. The difference in planning for robots and AVs lies primarily in the fact that vehicles are high-speed, unsafe transport means experiencing the significant influence of physical characteristics at the vehicle–road interaction. In this regard, high-quality planning using optimization can be obtained based on differential equations representing the vehicle model behavior in the state space [4]. Due to the internal relations between dynamic and kinematic parameters in the equation system, it is possible to search for the distribution of vehicle model positions and velocities. However, there are also problems here, basically due to a need to numerically solve the system of differential equations at each iteration step of the nonlinear optimization. Moreover, the equation system and parameters are defined in the time domain [5,6], not in the space domain. Consequently, a small integration time step is required to maintain the stability of the equation system’s numerical solution. In addition, the vehicle model itself should not be overly complex, which is why kinematic models [7] are often used for this.

Most well-known techniques for planning the motion trajectory are based on smooth functions [8] connecting the lanes’ midpoints along the road segments. However, estimating these midpoints through computer vision may be scattered even for a straight road section. After prediction, this may lead to excessive fluctuations of the planned trajectory’s curvature because if the lane’s midpoints are fixed, its relative displacement already implies flexures within a section. This may affect the frequent change of the curvature sign, which requires excessive steering control followed by decreasing the speed and, consequently, the overall AV performance (fastest speed with satisfactory safety).

Another planning option is the search for continuous functions defined in the space domain based on the optimization process in the presence of geometric, kinematic, and physical restrictions limiting the vehicle–road interaction. The root-mean-square curvature of a path optimized within the motion boundaries can be much less than for a trajectory built by midpoints. At the same time, the technique of simultaneous trajectory and speed planning is the most desirable goal. However, with this approach, a challenge in forming a universal cost function occurs because of many variations. The latter leads to increasing the optimality search time, which can only be regulated with numerous conditions and constraints.

The solution of the issues above lies in applying sequential optimization. First, the optimal trajectory is searched, and then the kinematic parameters are distributed according to the geometric, dynamic, and physical criteria. At the same time, the question arises about the optimality criteria, their interactions, and their influence on the quality and rapidity of the optimization process. The primary characteristics of selected studies on planning the AV motion are briefly summarized in Table 1. The studies may be divided into three groups. The first group is based on the state–space vehicle modeling for using the constrained model predictive control (MPC) [4,5,9], which is often applied as a tracker of a pre-set reference curves. The second group [2,7,9,10,11] considers the trajectory and speed models separately by Lagrange polynomials or Bézier curves. At the same time, some approaches are realized in the natural (Frenet) coordinates, where all parameters are functions of the arc element. The optimal trajectory is sought from the conditions of minimizing the curvature or its derivatives under physical constraints. The third group [12,13,14] uses graph algorithms and trees of possible trajectories to be selected along the best routes for minimizing the risks of movement in the presence of static and moving interferences. In studies, a complex objective function is mostly used in which the geometric and kinematic parameters of the vehicle motion are penalized.

Table 1. Characteristics of selected studies on planning AV motion ^a.

Reference	Path Model	Speed Model	Optimization Model	Other Main Features
[2]	Seventh-order POLY curve for independent representing in the fixed local coordinates.	Robot motion with constant linear velocity.	Minimizing the maximum absolute value of the angular ACC along the planned path.	The set of possible curves: lane-change, line segment, cubic spiral, generic twirl arc, and circular arc.
[3]	State–space vehicle kinematics model, sets of clothoids, straight line segments, and circular arcs.	Constant jerk and an arc approximation over time.	Optimal path sections to ensure minimum total length with appropriate curvature transients.	Local and global path planners, car-like robot technique for low speeds, no obstacles.
[4]	Centerline of driving lane, cubic splines with multiple knots along the path.	Speed deviation as part of the total cost function.	Combine MPC tracker, minimization of the blind spot, terminal cost, and speed cost.	Continuous state–space of a bicycle model. Rectangular obstacles.
[5]	LG, LT, and heading angle positions based on a unicycle kinematic model of ego vehicle.	Vehicle speed as a variable of discrete state–space model.	Constrained MPC, objective function includes LG and LT distances to destination, minimizes jerk.	Lane selection, lane-associated potential field, collision avoidance, fail-safe strategy.
[6]	Determined by integrating over time according to the optimal LG ACC and yaw rate.	Determined based on desired ACC by integrating over time.	Potential risk fields for LT and LG control independently.	Fixed time horizon, output yaw rate and deceleration, pedestrian a moving obstacle.
[7]	Cubic POLY spiral for curvature, path is function of curvature/arc length, lattice trajectories.	Constant ACC along the trajectory and initial speed.	Cost function includes obstacle avoidance, physical limitations, rate of change of path curvature.	Bicycle model kinematics, Jacobian of the endpoint state vector, physical limitations of performance.
[8]	5th-order Bézier curves oriented on centerline reference points.	ACC profile between reference points/speed limit curve.	First and second curvature derivatives to reflect path smoothness along the curve.	Bounds for speed, LG and LT ACC, collision checking with dynamic obstacle.
[9]	3rd order POLY for LG and 2nd order for LT displacement at discrete time-step.	2nd order POLY for LG and 1st order for LT speeds at discrete time-step.	MPC based on sum of quadratic penalties for LT and LG ACC, LG jerk, LG and LT speed deviations, LT road boundaries, obstacle avoidance.	Straight 3-lane road section, road boundaries, collision avoidance, MPC, dynamic programming to produce initial guess trajectory.
[10]	5th-order polynomials for independent modeling X and Y path references.	2nd-order integrator model and MPC.	Weighted squares of LG speed, LG and LT coordinates, and obstacle parabolas.	9-DOF vehicle model, bounding parabola for obstacles, fixed horizon time.
[11]	5th order POLY for independent representing the path segment in LG and LT directions.	3rd order spline without initial ACC and with arbitrary initial ACC.	Static costs: path length, curvature and its derivative, LT offset. Dynamic costs: maximum velocity and ACC.	Static and dynamic obstacles.
[12]	Waypoints from offline map, graph for nodes, shortest path algorithm	Speed depends on the current waypoint cost and the target speed.	Waypoint costs as measured driving risk, cost equals 1 if one more obstacles are near AV.	Static obstacles as circular regions, moving obstacles as single points with speeds.
[14]	Extended rapidly exploring random tree algorithms for feasible trajectories.	Based on controller processing after path generation	Choose the best and safest trajectory, check feasibility with latest drivability map, evaluate exploration vs. optimization	Risk evaluation based on trajectory collision with obstacles or violating any rule through the drivability map.
[15]	2-layered path model, POLY local planning in Frenet coordinates.	Constant LG speed. Target configuration of LT offset, speed, and ACC.	Improved Bidirectional Rapidly-exploring Random Tree (Bi-RRT).	3-DOF vehicle model, Vector Field Histogram for choosing obstacle-free path.
[16]	Optimization-free elastic band, discrete search space, and modelling parametric path spirals.	Finding time-optimal plan under speed and ACC constraints. Linear speed profile along path.	Minimize equilibrium positions, penalizing deviations from speed profile/excessive proximity to moving objects.	Speed-based temporal planning, trajectories for static and moving objects using simulation.
[17]	Reference path as a curvature profile, local path and curvature to obtain global coordinates by the Fresnel integrals.	The minimum-time speed profile without exceeding thresholds based on tire–road adhesion limits.	Formulate a path update step as a convex optimization that minimizes the path curvature norm for distance, time-varying model for model solution.	Linearized equations of vehicle motion states, equality and inequality constraints, optimization lowers path curvature.
[18]	Possible navigation corridors, graph search for a lane-let sequence for each corridor, waypoints as ending points for candidates, path candidates using 5th-order Bézier curves, path selection by merit assessment.	Traffic-based speed profile using the inter-distance model based on a leading virtual vehicle to determine the required ACC of the ego-vehicle for keeping distance.	Merit score assigned to each candidate with weighted sum providing an intrinsic filter, criteria are based on both LG and LT average and maximum ACC and jerk, smoothness, safe chase, closeness, lane invasion, path length, average speed.	Topological relation between road elements as a graph network, borderlines, centerlines of reachable lanes, select best available corridor using lane-changing model to evaluate safety indicator.
[19]	Any method ensuring the travel feasibility.	Shortest traveling time with checking for possible collisions.	Evaluating the cost function at each node, jerk is used as input.	Safety constraints: rollover, skidding, steering rate. obstacle avoiding planning.
[20]	Path model based on integration constraints of heading angle, east and north positions as functions of curvature and curve length.	Speed profile expressed as the desired speed along the path, maximum speed is function of path curvature.	Approximates finite-horizon optimal control by a convex quadratically constrained quadratic program for time minimization.	Kinematics and dynamics constraints, motion equations in linearization form, Hessian of the objective function.
[21]	Trajectory is assumed to be given for different cases	Speed, ACC, and jerk to be presented via numeric differentiation formulas.	Cost function includes squares of absolute ACC and jerk, squared deviation from reference speed, and consistency cost.	Convex feasible set algorithm, relax nonlinear equality constraints into nondegenerate nonlinear inequality constraints.
[22]	Reference path consists of a series of way points from the route module, nonlinear optimization algorithm in the space domain to smooth the reference road.	Permissible ACC and arc length, SQP solver to calculate the optimal speed profile.	Objective function includes reference cost, obstacle cost, consistency cost, LT ACC cost, and jerk cost, LT optimized path planner: curvature, LT distance, relative angle, and control inputs.	Multilayered search to find a suitable path boundary, motion controller can provide optimal control command, kinematic error model to control LT and heading deviations for desired path.
[23]	Paths are generated by connecting sampled endpoints using cubic and quartic curvature POLY, which are functions of the arc length.	Cubic POLY functions of arc length, which include speed and ACC.	Static cost by modules of path length, curvature, LT offset, obstacle distance, dynamic cost by time duration, speed, ACC, jerk, dynamic obstacle distance.	Robust replan mechanism to react to a dynamically changing environment, partial motion planning scheme.
[24,25]	Concept of Frenet frame to assist on path planning according to a hypothetical smooth guide line.	Piecewise-jerk method	Non-linear optimization algorithm for guide line smoothing, fast quadratic programming (QP) based algorithm.	Collision-free path, minimal lateral deviation, minimal lateral movement, maximal obstacle distance.

^a POLY = polynomial, LG = longitudinal, LT = lateral, ACC = acceleration.

We note that most referred studies are highly concise and do not fully disclose the architectures of the used methods, which reduces their engineering applicability. Further, clear relations between the forecasting method, vehicle dynamics, and vehicle kinematics are not always transparent, especially for constant speeds [15] or their heuristic distribution. In addition, the transient processes of velocities and accelerations often do not differ in smoothness.

Thus, the study aims to establish a technique to find the optimal AV motion plan in a constrained space and moving obstacles and to form cost functions by evaluating their priority and mutual effects. Specifically, the study (1) develops an explicit safe motion area by optimizing the best trajectory choice in contrast to the approaches focused on conjugating the lanes’ midpoints by smooth curves; (2) elaborates a comprehensive mathematical model to implement the method of planning AV motion in a constrained space; (3) develops a mechanism to form the boundaries of permissible movement in the presence of a movable obstacle, (4) determines the criteria for finding the optimal trajectory and distribution of the kinematic parameters, considering geometric, kinematic, and physical restrictions; and (5) validates the proposed technique by carrying out a series of virtual tests for the generalized case of motion predictions.

2. Generalization of Mathematical Tools

2.1. Representing the Parameters of Planning Functions by Finite Elements

This approach represents all geometric and kinematic parameters by continuous piecewise functions based on the same basis functions of a one-dimensional finite element. Briefly consider the description of forming an arbitrary function z(x) as a superposition of basis functions weighted by the parameters’ values in the grid nodes along the x-coordinate.

Approximation. Let us suppose that the position of the vehicle mass center along the x-coordinate is represented by piecewise functions based on a set of Lagrangian polynomials with N DOF in a node determining the ordinate value z and its derivatives. Thus, each final element on the x-axis grid possesses m = 2·N DOF. Within one segment, a function z(x) may be decomposed with a set of form functions and influence coefficients that are DOF values. Introduce vectors

$${\mathit{f}}_i=\left(\begin{array}{c}{f}_1\\ ⋮\\ f_m\end{array}\right),\mathit{f}=\left(\begin{array}{c}{f}_1\\ ⋮\\ f_n\end{array}\right),{\mathit{p}}_i=\left(\begin{array}{c}{q}_1\\ ⋮\\ q_m\end{array}\right),\mathit{p}=\left(\begin{array}{c}{\mathit{p}}_1\\ ⋮\\ {\mathit{p}}_n\end{array}\right)$$

(1)

where f_k, q_k = k-th basis function and its impact coefficient (k = 1, …, m); f_i, p_i = vector of basis functions and vector of its DOF for i-th final element (i = 1, …, n).

Since the basis functions are equal to zero out of a segment considered, a function z(x) on the entire interval consisting of n segments can be expressed as follows

$$z\left(x\right)={\sum }_{i=1}^n{\sum }_{j=1}^m{f}_{ij}\left(x\right)q_{ij}={\sum }_{i=1}^n{\mathit{f}}_i^T{\mathit{p}}_i={\mathit{f}}^{\mathit{T}}\mathit{p}$$

(2)

Then, if a k-th derivative exists, it can be evaluated using Equation (2), (k = 1,…, N-1) as follows

$$\frac{d^{k}z}{d{x}^k}={\sum }_{i=1}^n{\sum }_{j=1}^m\frac{d^k}{d{x}^k}{f}_{ij}\left(x\right)p_{ij}={\sum }_{i=1}^n\frac{d^k{\mathit{f}}_i^T}{d{x}^k}{\mathit{p}}_i=\frac{d^k{\mathit{f}}^{\mathit{T}}}{d{x}^k}\mathit{p}$$

(3)

Basis functions. Let us consider an i-th final element with 3 DOF in a node along the x-coordinate based on a 5^th-order polynomial [10], the length of which equals L_i. If x = L_iξ, then dx = L_idξ, where parameter ξ $\in$ [0, 1]. The system of basis functions for an FE with L_i = 1 (Figure 1) and its three derivatives yield

$${\mathit{f}}_{\xi }=\left(\begin{array}{c}{\left(1-\xi \right)}^3\left(6{\xi }^2+3\xi +1\right)\\ \xi \left(3\xi +1\right){\left(1-\xi \right)}^3\\ {\xi }^2{\left(1-\xi \right)}^3/2\\ {\xi }^3\left(6{\xi }^2-15\xi +10\right)\\ -{\xi }^3\left(3{\xi }^2-7\xi +4\right)\\ {\xi }^3{\left(\xi -1\right)}^2/2\end{array}\right),\frac{d{\mathit{f}}_{\xi }}{d\xi }=\left(\begin{array}{c}-30{\xi }^2{\left(\xi -1\right)}^2\\ {\left(\xi -1\right)}^2\left(-15{\xi }^2+2\xi +1\right)\\ -\xi \left(5\xi -2\right){\left(\xi -1\right)}^2/2\\ 30{\xi }^2{\left(\xi -1\right)}^2\\ -{\xi }^2\left(15{\xi }^2-28\xi +12\right)\\ {\xi }^2\left(5{\xi }^2-8\xi +3\right)/2\end{array}\right)$$

(4)

$$\frac{d^2{\mathit{f}}_{\xi }}{d{\xi }^2}=\left(\begin{array}{c}-60\xi \left(2{\xi }^2-3\xi +1\right)\\ -12\xi \left(5{\xi }^2-8\xi +3\right)\\ -10{\xi }^3+18{\xi }^2-9\xi +1\\ 60\xi \left(2{\xi }^2-3\xi +1\right)\\ -12\xi \left(5{\xi }^2-7\xi +2\right)\\ \xi \left(10{\xi }^2-12\xi +3\right)\end{array}\right),\frac{d^3{\mathit{f}}_{\xi }}{d{\xi }^3}=\left(\begin{array}{c}-60\left(6{\xi }^2-6\xi +1\right)\\ -12\left(15{\xi }^2-16\xi +3\right)\\ -3\left(10{\xi }^2-12\xi +3\right)\\ 60\left(6{\xi }^2-6\xi +1\right)\\ -12\left(15{\xi }^2-14\xi +2\right)\\ 3\left(10{\xi }^2-8\xi +1\right)\end{array}\right)$$

(5)

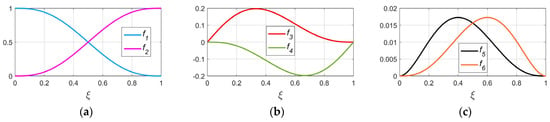
Figure 1. Basis functions of an FE with 3 DOF in a node: (a) offset, (b) rotation, and (c) rotation intensity.

Every final element may be characterized with its own length L_i. If we denote vector L_i, then

$${\mathit{L}}_i=diag\left(\begin{array}{ccc}1& L_i& \begin{array}{ccc}{L}_i^2& 1& \begin{array}{cc}{L}_i& L_i^2\end{array}\end{array}\end{array}\right)$$

(6)

Thus, functions of Equations (2) and (3) for the i-th section are expressed by universal functions of the parameter ξ, Equations (4) and (5)

$${\mathit{f}}_i={\mathit{L}}_i{\mathit{f}}_{\xi },z_i\left(x\right)=z_i\left(L_i\xi \right)={\mathit{p}}_i^T{\mathit{L}}_i{\mathit{f}}_{\xi }$$

(7)

For k-th derivative,

$$\frac{d^k{z}_i}{d{x}^k}=\frac{d}{L_{i}d\xi }\left(\frac{1}{L_i^{k-1}}{\mathit{p}}_i^T{\mathit{L}}_i\frac{d^{k-1}{\mathit{f}}_{\xi }}{d{\xi }^{k-1}}\right)={\mathit{p}}_i^T\left(\frac{{\mathit{L}}_i}{L_i^k}\right)\frac{d^k{\mathit{f}}_{\xi }}{d{\xi }^k}$$

(8)

2.2. Nonlinear Optimization

Let us assume that any function from Equations (7) and (8) can be represented through F(q), and the generalized functional is written as

$$\underset{\mathit{q}}{min}F\left(\mathit{q}\right)\mathrm{subject}\mathrm{to}\{\begin{array}{c}c\left(\mathit{q}\right)\le 0\\ c_{eq}\left(\mathit{q}\right)=0\\ \mathit{A}\mathit{q}\le \mathit{b}\\ {\mathit{A}}_{eq}\mathit{q}={\mathit{b}}_{eq}\\ {\mathit{q}}_L\le \mathit{q}\le {\mathit{q}}_U\end{array},\mathit{q}=\left(\begin{array}{c}{\mathit{q}}_1\\ ⋮\\ {\mathit{q}}_{n+1}\end{array}\right),{\mathit{q}}_i=\left(\begin{array}{c}{q}_{3\left(i-1\right)+1}\\ q_{3\left(i-1\right)+2}\\ q_{3\left(i-1\right)+3}\end{array}\right)$$

(9)

where q = set of unknown nodal parameters; c(q), c_eq(q) = vector functions of inequality and equality nonlinear constraints, respectively; A, A_eq, b, b_eq = matrices and vectors of inequality and equality linear constraints, respectively; q_L, q_U = lower and upper bounds; i $\in$ [1, n] = section number.

As a basic optimization algorithm, the sequential quadratic programming (SQP) method is used, based on the fmincon nonlinear optimization function [26]. The SQP algorithm is based on a quadratic approximation of the Lagrangian function. It is characterized by unique properties such as strict feasibility regarding founds, robustness to non-double results, and refactored linear algebra routines (more efficient in memory usage and speed).

3. Trajectory Search

3.1. Problem Generalization

This section considers the conditions under which determining an optimal trajectory can be reduced to finding a function of one variable y(x) depending on the vector q_y of parameters in the nodes. According to the generalized model in Equations (1)–(3), the lateral deviation and its two derivatives are specified in each trajectory node. Then, the optimization goal is to define the vector q_y of dimension 3(n + 1), which unambiguously determines the trajectory function in the interval [0, D] (Figure 2).

$${\mathit{q}}_{y\left(i\right)}=\left(\begin{array}{c}{y}_i\\ \frac{d{y}_i}{dx}\\ \frac{d^2{y}_i}{d{x}^2}\end{array}\right),{\mathit{q}}_y=\left(\begin{array}{c}{\mathit{q}}_{y\left(1\right)}\\ ⋮\\ {\mathit{q}}_{y\left(n+1\right)}\end{array}\right)$$

(10)

where i $\in$ [1, n + 1] = node number.

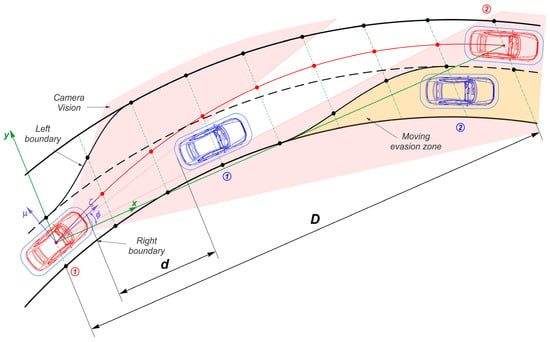
Figure 2. Scheme of the generalized task of planning the AV’s maneuver.

At the same time, within each i-th segment, the set of parameters corresponds to two adjacent nodes, that is

$${\mathit{p}}_{y\left(i\right)}=\left(\begin{array}{c}{\mathit{q}}_{y\left(i\right)}\\ {\mathit{q}}_{y\left(i+1\right)}\end{array}\right)\mathrm{and}{\mathit{p}}_y=\left(\begin{array}{c}{\mathit{p}}_{y1}\\ ⋮\\ {\mathit{p}}_{yn}\end{array}\right)$$

(11)

where i $\in$ [1, n + 1] = node number.

In this case, the trajectory function inside a segment, considering Equation (7) is

$$y_i\left(x\right)=y_i\left(L_i\xi \right)={\mathit{p}}_{yi}^T{\mathit{L}}_i{\mathit{f}}_{\xi }$$

(12)

Its k-th derivative, considering Equation (8) is

$$\frac{d^k{y}_i}{d{x}^k}={\mathit{p}}_{yi}^T\left(\frac{{\mathit{L}}_i}{L_i^k}\right)\frac{d^k{\mathit{f}}_{\xi }}{d{\xi }^k}$$

(13)

We note that the desirable vector q_y contains a unique set of nodal DOFs. The vector p_y with duplicated DOF of internal nodes is easily obtained to represent the interpolation function with the complete set of nodal parameters for each section.

3.2. Description of Trajectory Planning Objective

Figure 2 shows the generalized motion case of an AV guided by computer vision within the roadway boundaries and detecting moving obstacles. Let us assume that a road is represented by a curved section and has at least two lanes in one direction, which allows maneuvering between the lanes, including avoiding obstacles. The initial layout of vehicles corresponds to Position 1, where a need for planning the AV displacement to Position 2 emerges. Considering the section curvature, this position can be determined if sufficient visibility is ensured. We also assume that an invisible part within the outer roadway boundaries in front of the impeding vehicle is homogeneous (monotonic curvature) and can be virtually rebuilt based on satisfactory information before and behind a visibility break. Let the current position of the AV be characterized by the direction of the axis ζ of the moving coordinate system ζμ tangentially to the midline of the initial traffic lane. Then, the destination point corresponding to Position 2 is defined under the angle -ϕ to the ζ axis. The current instantaneous position can be taken as the initial relative to the new global coordinate system xy. Both the lane boundaries and the movement of an impeding vehicle are redefined. Thus, the AV must realize a displacement D within the safety boundaries, avoiding the moving obstacle from an initial distance d between the vehicles.

Under the conditions that boundary marking lines along the x-axis are unambiguous, all functions can be defined in the xy coordinate system. Consequently, the desirable trajectory and distribution of kinematic parameters are functions of one variable x. The interval [0, D] may be divided into several (n) finite elements to improve the quality of dependencies to be found. The FE grid step can be fixed or variable depending on the curvature change within the considered area and the presence of interferences and obstacles.

Thus, the outer boundaries can be redefined by the DOF values in the FE grid nodes using the same basis functions for the parameters to be found. In addition to the external boundaries, the restrictive internal conditions are imposed to limit undesirable vehicle maneuvers and to exclude interaction with the obstructions. In turn, the movable obstacle continues to follow its lane, keeping a moving safety zone behind it. Thus, the AV must move considering the evasion zone and maintain a safe space between approaching vehicles.

3.3. Determining the Maneuver Boundaries

External and Internal Boundaries. Let us assume that the marking lines are recognized by the camera vision and are processed in such a way to generate the virtual boundaries by smooth functions (Medina-Lee et al., 2021), ensuring the continuity up to the 2nd derivative in the nodes. In the case of the physical absence of internal marking lines, they can be rebuilt virtually by estimating the required lane width within defined external boundaries. In contrast, the nodal parameters of such boundaries can be obtained by averaging the corresponding parameters of the upper and lower bounds. The limitation of maneuver variations can be organized by narrowing the AV admissible motion area, correcting external boundaries with internal conditions. This situation can be formed by a superposition of the conditions for delimiting motion zones of other traffic participants and the requirement to maintain safety margins between closely moving vehicles. Consider such a procedure in Figure 3.

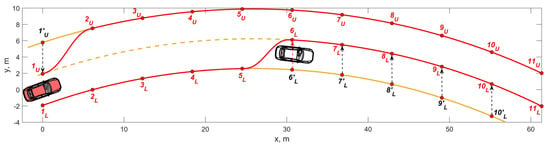
Figure 3. Forming the boundaries of the allowable area before planning a maneuver.

Initial Position. At the initial time, the AV’s mass center position corresponds to the coordinates (0, 0) in the xy system, and the yaw angle differs little from the average slope of the tangents in the nodes of closest marking lines along the vehicle sides. To increase vehicle behavior stability and limit maneuver variations near the initial position, it is necessary to lock the outer boundaries’ initial nodes on the nodes of adjacent marking lines, contributing to forming an entry corridor, as shown in Figure 3 regarding node 1. In this case, the three interpolation parameters in the node 1’_U of the outer border are replaced by the corresponding DOF of the node 1_U of the dividing marking line. As seen, this also ensures a smooth transition of the boundary between the 1_U and 2_U nodes. In this case, the lower boundary node 1_L has already been defined; however, in the case, for example, of driving in the second lane of a three-lane road, the same procedure would be applied to this node as well.

Final Position. For this case, the conditions may be either strict, specifying three restrictions at the final point (positions x_f, y_f of the vehicle mass center and the trajectory’s tangent slope estimated by a close yaw angle ϕ_f), or relaxed, omitting the ordinate value or the tangent direction, or both options together. In this case, the omitted final parameters will be determined during optimization based on the conditions of nonlinear constraints. Thus, the ordinate y_f can be smaller or larger than that under severe conditions but sufficient to ensure safety margins to the boundaries.

Bypassing Moving Obstacles. Unlike a fixed obstruction, when a safety area can be easily formed, in the case of a moving obstacle, the safety boundaries depend on a larger number of factors. The approach intensity in critical situations such as emergency braking of the impeding vehicle is the most influential. The situation is complicated since the maneuver prediction is based not on a finite time interval but on a combination of many criteria. That is, the position of an impeding vehicle at the maneuver’s end can only be estimated approximately and indirectly. Considering the AV initial position in Figure 2, it is evident that fixing the restriction zone immediately behind the impeding vehicle is extremely inexpedient since this significantly reduces the maneuver space. On the other hand, the bypass must be organized before a specific position of the impeding vehicle to reduce the likelihood of the vehicles’ critical approach. If both vehicles are in the same lane, two cases are possible: speeding up the AV and emergency braking of the impeding vehicle. Suppose the AV accelerates behind the impeding vehicle in the same lane. In this case, the distance gap between vehicles is reduced slower, requiring more lane space compared with the moving obstacle’s emergency braking. That is, the moment limiting the same lane use is related to the initial speeds and distance d in such a way to exclude the unsafe gap between these vehicles during emergency braking. Two variants are possible here. The first one is based on maintaining such a safe distance d (Figure 2) so that in the case of emergency braking after the complete stopping in the same lane a minimum safe clearance between the vehicles remains. The vehicles’ stopping distances will approximately differ by the value of the initial distance d between the vehicles. Another approach proceeds from the fact that the need for maneuvering and bypassing may appear at any time regardless the gap d and the initial speeds of the approaching vehicles. In this case, a critically short distance may occur even during the braking of both vehicles. Therefore, the AV’s bypass must ensure a collision-avoidance zone, especially in the cases of full use of the longitudinal vehicle–road adhesion φ_ζ, and decrease the steerability potential. In the first option, the level of safety is higher, but the required space is larger due to the longer initial d. In the second option, the control aggressiveness is higher, but the compactness of using the lane’s space is much better. It is also possible to use other algorithms, depending on the vehicles’ speeds and curvature within the road section. Thus, with intensive traffic and lower speeds, the second option may be more preferable and vice versa.

Estimating the stopping distances s_b in such a situation can be performed according to the following expression [27] for each set of vector components

$$s_b=v_0\left(t_{dr}+t_{re}+t_{in}/2\right)+v_0^2/\left(2{\phi }_{x}g\right)$$

(14)

where v₀ = (V_iv, V_av) = (50, 60)/3.6 = initial speeds of the impeding vehicle and AV (km/h), respectively; t_dr = (0.75, 0.5) = reaction time (s), respectively; t_in = (0.05, 0.05) = time (s) of pressure increase in the hydraulic brake circuits; t_re = (0.05, 0.05) = hydraulic actuator response time (s); φ_x = 0.85 = tire adhesion coefficient for the dry tarmac; and g = gravity acceleration (9.81 m/s²).

Determining the difference in stopping distances after substituting the value sets in Equation (14), we obtain the minimum allowable initial distance between the vehicles, considering the guaranteed safe clearance of 1.5 m: Δs_b = 12.5 m. Thus, neglecting the curvature, the initial position of the impeding vehicle’s mass center relative to the initial position of the AV can be estimated as 15 m along the lane. According to the calculations, the AV needs 30.4 m of stopping distance, and an impeding vehicle needs 19.6 m. Then, the final position of the impeding vehicle corresponds to the coordinate x ≈ 32 m. Consequently, the restriction of allowable space relative to the moving obstacle on the lane is limited (Figure 3) by transiting the lower node 6’_L of the outer boundary to the node 6_L of the lane’s inner boundary. Since the final position of the AV is set in advance and corresponds to using the second lane, the admissible space is constricted by switching nodes 7’_L–11’_L to nodes 7_L–11_L, respectively. In the final position, the assessment of the affordable area is repeated.

We note that the upper and lower boundaries of the AV’s permissible motion zone are set by the same basis functions (Figure 1) as the desirable trajectory functions but through predefined sets of nodal parameters q_U, q_L

$${\mathit{q}}_{U\left(i\right)}=\left(\begin{array}{c}{y}_{Ui}\\ \frac{d{y}_{Ui}}{dx}\\ \frac{d^2{y}_{Ui}}{d{x}^2}\end{array}\right),{\mathit{q}}_U=\left(\begin{array}{c}{\mathit{q}}_{U\left(1\right)}\\ ⋮\\ {\mathit{q}}_{U\left(n+1\right)}\end{array}\right),{\mathit{q}}_{L\left(i\right)}=\left(\begin{array}{c}{y}_{Li}\\ \frac{d{y}_{Li}}{dx}\\ \frac{d^2{y}_{Li}}{d{x}^2}\end{array}\right),{\mathit{q}}_L=\left(\begin{array}{c}{\mathit{q}}_{L\left(1\right)}\\ ⋮\\ {\mathit{q}}_{L\left(n+1\right)}\end{array}\right)$$

(15)

where i $\in$ [1, n + 1] = node number.

3.4. Trajectory Geometry

Unlike the planning trajectory for a robot, the overall dimensions and the vehicle turn feature significantly influence the trajectory form because of geometric and kinematic relations and their restrictions. Consider the process of forming a trajectory for the mass center based on the vehicle kinematic model in Figure 4.

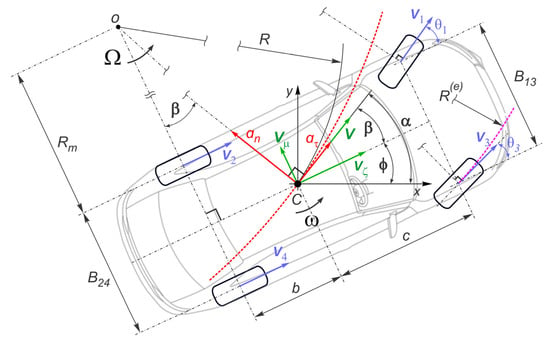
Figure 4. Relations between the mass center’s trajectory and the vehicle kinematics.

The AV moves in the xy coordinate system, as shown in Figure 2. At the same time, a moving coordinate system ζμ is fixed on the AV’s mass center C (Figure 4). In the general case, the vehicle moves along the x and y axes and rotates on the yaw angle ϕ. Proceeding from the concept of vehicle kinematics close to ideal, point C rotates around the instantaneous velocity center O with an instantaneous angular velocity Ω. The trajectory curvature, in this case, is determined by the instantaneous radius R. The absolute velocity V is directed tangentially at the angle α to the trajectory in the point C of the vehicle mass center and is decomposed into the longitudinal V_ζ and lateral V_μ components in the moving vehicle coordinate system, respectively. The absolute speed V and its longitudinal component V_ζ are mutually located at the angle β, which is also formed between the instantaneous radius R and the axis passing through the centers of the rear wheels distanced on the value b from the mass center.

Let us consider the essential geometric characteristics and their derivatives given that the function y(x) and its derivatives are defined in terms of Equations (7) and (8).

Arc Element. The elementary arc length in the case of an explicitly given function y(x) is calculated as follows

$$ds=\sqrt{d{x}^2+d{y}^2}=\sqrt{1+{\left(dy/dx\right)}^2}dx$$

(16)

Then, the change of arc length along the x coordinate is

$$s_x=\frac{ds}{dx}=\sqrt{1+{\left(dy/dx\right)}^2}\mathrm{and}ds=s_{x}dx$$

(17)

Its first derivative concerning the x-coordinate is

$$\frac{d{s}_x}{dx}=\frac{1}{2\sqrt{1+{\left(dy/dx\right)}^2}}\frac{d}{dx}{\left(\frac{dy}{dx}\right)}^2=\frac{1}{s_x}\frac{dy}{dx}\frac{d^{2}y}{d{x}^2}$$

(18)

The second derivative concerning the x-coordinate is

$$\begin{gathered} \frac{d^2{s}_x}{d{x}^2}=\frac{d}{dx}\left(\frac{1}{s_x}\frac{dy}{dx}\frac{d^{2}y}{d{x}^2}\right)=\frac{d}{dx}\left(\frac{1}{s_x}\right)\frac{dy}{dx}\frac{d^{2}y}{d{x}^2}+\frac{1}{s_x}\frac{d}{dx}\left(\frac{dy}{dx}\frac{d^{2}y}{d{x}^2}\right) \\ =\frac{1}{s_x}\left({\left(\frac{d^{2}y}{d{x}^2}\right)}^2+\frac{dy}{dx}\frac{d^{3}y}{d{x}^3}\right)-\frac{1}{s_x^2}\frac{d{s}_x}{dx}\frac{dy}{dx}\frac{d^{2}y}{d{x}^2}=\frac{1}{s_x}\left({\left(\frac{d^{2}y}{d{x}^2}\right)}^2+\frac{dy}{dx}\frac{d^{3}y}{d{x}^3}-{\left(\frac{d{s}_x}{dx}\right)}^2\right) \end{gathered}$$

(19)

Tangent Angle. The derivative at any trajectory point is the tangent of the slope angle

$$dy/dx=tan\left(\alpha \left(x\right)\right)$$

(20)

The expressions of Equations (16) and (17) may be rewritten as follows:

$$s_x=\sqrt{1+{tan}^2\left(\alpha \left(x\right)\right)}=sec\left(\alpha \left(x\right)\right)=1/cos\left(\alpha \left(x\right)\right)$$

(21)

The slope angle of the tangent at any trajectory point is

$$\alpha \left(x\right)=arctan\left(dy/dx\right)$$

(22)

The change of the tangent slope angle along an arc s is

$$\frac{d\alpha }{ds}=\frac{d\alpha }{dx}\frac{dx}{ds}=\frac{d\alpha }{dx}/\frac{ds}{dx}=\frac{1}{s_x}\frac{d\alpha }{dx}$$

(23)

In turn, the first derivative is

$$\frac{d\alpha }{dx}=\frac{d}{dx}arctan\left(\frac{dy}{dx}\right)=\frac{1}{1+{\left(dy/dx\right)}^2}\frac{d^{2}y}{d{x}^2}=\frac{1}{s_x^2}\frac{d^{2}y}{d{x}^2}$$

(24)

The second derivative, considering K to be the curvature is

$$\begin{gathered} \frac{d^2\alpha }{d{x}^2}=\frac{d}{dx}\left(\frac{1}{s_x^2}\frac{d^{2}y}{d{x}^2}\right)=\frac{d}{dx}\left(\frac{1}{s_x^2}\right)\frac{d^{2}y}{d{x}^2}+\frac{1}{s_x^2}\frac{d}{dx}\left(\frac{d^{2}y}{d{x}^2}\right) \\ =\frac{1}{s_x^2}\frac{d^{3}y}{d{x}^3}-\frac{2}{s_x^3}\frac{d{s}_x}{dx}\frac{d^{2}y}{d{x}^2}=\frac{1}{s_x^2}\frac{d^{3}y}{d{x}^3}-2K\frac{d{s}_x}{dx} \end{gathered}$$

(25)

Curvature. Curvature is defined as the rate change of the arc angle rotation along the arc itself, i.e.,

$$K\left(s\right)=d\alpha /ds$$

(26)

With an explicitly given function y(x) and considering the change of bend direction, it is given as

$$K\left(x\right)=\frac{1}{s_x}\frac{d\alpha }{dx}=\frac{1}{s_x^3}\frac{d^{2}y}{d{x}^2}=\frac{d^{2}y/d{x}^2}{{\left(\sqrt{1+{\left(dy/dx\right)}^2}\right)}^3}$$

(27)

The change of curvature along an arc s is

$$\frac{d}{ds}K\left(s\right)=\frac{d}{ds}\frac{d\alpha }{ds}=\frac{d}{dx}\left(\frac{1}{s_x}\frac{d\alpha }{dx}\right)/\frac{ds}{dx}=\frac{1}{s_x}\frac{dK\left(x\right)}{dx}$$

(28)

In turn, the change of curvature along the x-coordinate is

$$\begin{gathered} \frac{dK}{dx}=\frac{d}{dx}\left(\frac{1}{s_x^3}\frac{d^{2}y}{d{x}^2}\right)=\frac{d}{dx}\left(\frac{1}{s_x^3}\right)\frac{d^{2}y}{d{x}^2}+\frac{1}{s_x^3}\frac{d^{3}y}{d{x}^3} \\ =\frac{1}{s_x^3}\frac{d^{3}y}{d{x}^3}-\frac{3}{s_x}\frac{d{s}_x}{dx}\frac{1}{s_x^3}\frac{d^{2}y}{d{x}^2}=\frac{1}{s_x}\left(\frac{1}{s_x^2}\frac{d^{3}y}{d{x}^3}-3K\frac{d{s}_x}{dx}\right) \end{gathered}$$

(29)

The second derivative concerning the x-coordinate is

$$\begin{gathered} \frac{d^{2}K}{d{x}^2}=\frac{d}{dx}\left(\frac{1}{s_x}\left(\frac{1}{s_x^2}\frac{d^{3}y}{d{x}^3}-3K\frac{d{s}_x}{dx}\right)\right)=\frac{d}{dx}\left(\frac{1}{s_x}\right)\left(\frac{1}{s_x^2}\frac{d^{3}y}{d{x}^3}-3K\frac{d{s}_x}{dx}\right)+\frac{1}{s_x}\frac{d}{dx}\left(\frac{1}{s_x^2}\frac{d^{3}y}{d{x}^3}-3K\frac{d{s}_x}{dx}\right) \\ =-\frac{1}{s_x^2}\frac{d{s}_x}{dx}\left(\frac{1}{s_x^2}\frac{d^{3}y}{d{x}^3}-3K\frac{d{s}_x}{dx}\right)+\frac{1}{s_x}\left(\frac{d}{dx}\left(\frac{1}{s_x^2}\right)\frac{d^{3}y}{d{x}^3}+\frac{1}{s_x^2}\frac{d^{4}y}{d{x}^4}-3\left(\frac{dK}{dx}\frac{d{s}_x}{dx}+K\frac{d^2{s}_x}{d{x}^2}\right)\right) \\ =\frac{1}{s_x}\left(\frac{1}{s_x^2}\frac{d^{4}y}{d{x}^4}-\left(\frac{2}{s_x^3}\frac{d^{3}y}{d{x}^3}+4\frac{dK}{dx}\right)\frac{d{s}_x}{dx}-3K\frac{d^2{s}_x}{d{x}^2}\right) \end{gathered}$$

(30)

Immediate Radius. The instantaneous radius is defined as the reciprocal of the curvature. In this case, the radius sign determined by the curvature sign shows the direction of the immediate radius rotation and, consequently, the direction of the angular velocity Ω.

$$R\left(s\right)=1/K\left(s\right)\mathrm{or}R\left(x\right)=1/K\left(x\right)$$

(31)

Central Slip Angle. The angle β characterizes the deviation of the lateral component of the mass center velocity from the longitudinal one and can be evaluated geometrically (Figure 4)

$$\beta \left(s\right)=arcsin\left(b/R\left(s\right)\right)=arcsin\left(bK\left(s\right)\right)\mathrm{or}\beta \left(x\right)=arcsin\left(bK\left(x\right)\right)$$

(32)

Changing the angle β along an arc s of the trajectory is given by

$$\frac{d\beta }{ds}=\frac{d\beta }{dx}/\frac{ds}{dx}=\frac{1}{s_x}\frac{d\beta }{dx}$$

(33)

In turn, the component

$$\frac{d\beta }{dx}=\frac{d}{dx}\left(arcsin\left(bK\right)\right)=\frac{b}{\sqrt{1-{\left(bK\right)}^2}}\frac{dK}{dx}=k_{\beta }\frac{dK}{dx}$$

(34)

The coefficient

$$k_{\beta }=\frac{b}{\sqrt{1-{\left(bK\right)}^2}}$$

(35)

Its derivative along the coordinate x is given by

$$\frac{d{k}_{\beta }}{dx}=\frac{d}{dx}\left(\frac{b}{\sqrt{1-{\left(bK\right)}^2}}\right)=\frac{b}{2}\frac{2b^{2}K}{{\left(\sqrt{1-{\left(bK\right)}^2}\right)}^3}\frac{dK}{dx}={\left(\frac{b}{\sqrt{1-{\left(bK\right)}^2}}\right)}^{3}K\frac{dK}{dx}=k_{\beta }^{3}K\frac{dK}{dx}$$

(36)

Then, the second derivative of β concerning x is

$$\begin{gathered} \frac{d^2\beta }{d{x}^2}=\frac{d}{dx}\left(k_{\beta }\frac{dK}{dx}\right)=\frac{d{k}_{\beta }}{dx}\frac{dK}{dx}+k_{\beta }\frac{d}{dx}\left(\frac{dK}{dx}\right)=k_{\beta }^{3}K\frac{dK}{dx}\frac{dK}{dx}+k_{\beta }\left(\frac{d^{2}K}{d{x}^2}\right) \\ =k_{\beta }K{\left(k_{\beta }\frac{dK}{dx}\right)}^2+k_{\beta }\frac{d^{2}K}{d{x}^2}=k_{\beta }\left(K{\left(\frac{d\beta }{dx}\right)}^2+\frac{d^{2}K}{d{x}^2}\right) \end{gathered}$$

(37)

Yaw Angle. As a result, in contrast to the vehicle dynamic models, the vehicle yaw angle ϕ can be obtained through the angle of the tangent slope and the central slip angle (Figure 4) as follows:

$$\varphi =\alpha -\beta$$

(38)

Both the first and second (or curvature) derivatives of the considered point influence the yaw angle ϕ.

3.5. Cost Functions

This section explores the appropriate objective functions for composing an optimization basis that provides acceptable performance, has good convergence, and gives qualitative prediction models of the motion trajectory. The criteria may be represented in quadratic and normalized forms [23].

Path. The first natural criterion is the travelling distance, which, ideally, should be minimum [11]. It can be written for the desirable trajectory s as

$$I_s={\int }_0^{\mathit{s}}ds$$

(39)

Using Equation (17), for the variable x, which varies within [0, D], split the integration interval into finite elements with boundaries [x_i, x_i+1] and piecewise functions s_xi. Then,

$$I_s={\int }_0^{\mathit{D}}{s}_x\left(x\right)dx={\sum }_{i=1}^n\left({\int }_{x_i}^{x_{i+1}}{s}_{xi}\left({\mathit{p}}_{yi},x\right)dx\right)$$

(40)

The function s_xi(x) can now be represented in terms of the parameter ξ using Equation (7):

$$I_s={\sum }_{i=1}^n{L}_i{\int }_0^1{s}_{xi}\left({\mathit{p}}_{yi},L_i\xi \right)d\xi$$

(41)

The derivative function dy/dx is already included in s_x(x). Thus, the integral minimization of Equation (41) also helps decrease the tangent slope and straighten the trajectory curve. Since a quadratic form is absent in this criterion, its influence may be excessive in terms of the sensitivity of the entire functional, and the criterion itself can be reduced as

$$I_s={\sum }_{i=1}^n{L}_i{\int }_0^1{s}_{xi}\left({\mathit{p}}_{yi},L_i\xi \right)d\xi /\mathit{D}$$

(42)

Central Slip Angle. From the point of view of the vehicle kinematics and primarily such a phenomenon as the lateral slip, it is expedient to ensure a trajectory minimizing the deviation β of the absolute velocity vector V from the longitudinal vehicle axis. This requirement indicates the need for moving with the largest instantaneous radius or the smallest curvature. One can require that the quadratic deviation of β on the trajectory s be minimum.

$$I_{\beta }={\int }_0^{\mathit{s}}{\beta }^2\left(s\right)ds={\int }_0^{\mathit{D}}{\beta }^2\left(x\right)s_x\left(x\right)dx$$

(43)

Following the sequence of Equations (39)–(42), the approach for integration in finite elements gives

$$I_{\beta }={\sum }_{i=1}^n{L}_i{\int }_0^1{\beta }_i^2\left({\mathit{p}}_{yi},L_i\xi \right)s_x\left({\mathit{p}}_{yi},L_i\xi \right)d\xi$$

(44)

From the perspective of the minimum average curvature, the trajectory should as much as possible resemble a constant curvature arc. This also helps reduce the intensity of vehicle steering use by equalizing the curvature along the trajectory. An alternative to the Equation (43) integral can be found using the curvature

$$I_K={\sum }_{i=1}^n{L}_i{\int }_0^1{K}_i^2\left({\mathit{p}}_{yi},L_i\xi \right)s_x\left({\mathit{p}}_{yi},L_i\xi \right)d\xi$$

(45)

Rate of Curvature. From the point of view of maximum smoothness of transitions between the adjacent sections, the trajectory should correspond to the minimum average intensity of the curvature rate. Thus, using Equations (28) and (29),

$$I_{dK}={\int }_0^{\mathit{s}}{\left(\frac{dK\left(s\right)}{ds}\right)}^{2}ds={\int }_0^{\mathit{D}}{\left(\frac{1}{s_x\left(x\right)}\frac{dK\left(x\right)}{dx}\right)}^2{s}_x\left(x\right)dx={\int }_0^{\mathit{D}}{\left(\frac{dK\left(x\right)}{dx}\right)}^2\frac{dx}{s_x\left(x\right)}$$

(46)

Passing according to the scheme above to the parameter ξ and considering Equations (8) and (46), we obtain

$$I_{dK}={\int }_0^{\mathit{D}}{\left(\frac{dK\left(x\right)}{dx}\right)}^2\frac{dx}{s_x\left(x\right)}={\sum }_{i=1}^n{L}_i{\int }_0^1{\left(\frac{d{K}_i\left({\mathit{p}}_{yi},L_i\xi \right)}{dx}\right)}^2\frac{d\xi }{s_x\left({\mathit{p}}_{yi},L_i\xi \right)}$$

(47)

Minimization. The function W_y to be minimized can be represented in the matrix form as a linear combination of the criteria considered above:

$$W_y\left({\mathit{q}}_y\right)={\mathit{w}}_y^T{I}_y\left({\mathit{q}}_y\right)\to min$$

(48)

where q_y = vector of unknown nodal parameters, Equation (10); I_y = vector of criteria functions, w_y = vector of weighting factors.

$${\mathit{w}}_y=\left(\begin{array}{c}{w}_s\\ w_{\beta }\\ w_{dK}\end{array}\right),{\mathit{I}}_y\left({\mathit{q}}_y\right)=\left(\begin{array}{c}{I}_s\left({\mathit{q}}_y\right)\\ I_{\beta }\left({\mathit{q}}_y\right)\\ I_{dK}\left({\mathit{q}}_y\right)\end{array}\right)$$

(49)

where w_s, w_β, w_dK = weighting coefficients for the path, slip angle (curvature), and curvature rate, respectively.

3.6. Constraints

The constraints help narrow the optimum search area and reduce the required number of iterations, affecting the calculation speed.

3.6.1. Dimensional Constraints

When planning the trajectory and its derivatives, combining the vehicle safety zone with the allowable motion area’s boundaries is necessary. Figure 5 depicts the possible cases limiting the safe movement near the borders, expecting that their curvature provides the same sign within the overall vehicle length.

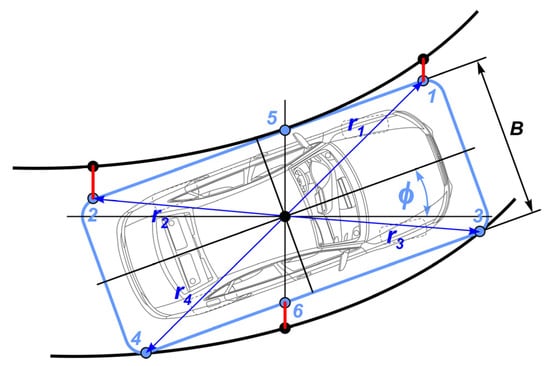
Figure 5. Scheme of the critical interactions with the motion boundaries.

Four fixed points (1–4) and two points floating (5–6) may be accepted as controlling. The fixed points are characterized by radius vectors r₁, r₂, r₃, r₄ defining the configuration of the vehicle safety contour. The floating points change positions depending on the yaw angle ϕ. There are two options for interacting with the vehicle side and a movement zone border. In the first case, the border is convex relative to the vehicle side (left points 1, 2, 5). The largest displacement of the mass center and the smallest lateral distance to the border are set by point 5, which corresponds to the vehicle location parallel to the border’s tangent at this point. In contrast, points 1 and 2 are guaranteed to keep gaps from the border. In the second variant, the boundary is concave relative to the vehicle side (right points 3, 4, 6). Therefore, if its curvature is unambiguous within the vehicle length, point 6 will be kept out of the critical zone. Thus, the upper and lower boundaries of the mass center displacement in the grid nodes are mutually related to the boundaries of the yaw angle ϕ. The conditions for non-violation of the upper bounds by points 1, 2, and 5 can be expressed as

$$y_k-y_{Uk}\left(x_k\right)\le 0$$

(50)

where y_k = critical point ordinate, y_Uk = value of the upper bound in the point x_k, (k = 1, 2, 5).

The conditions for non-violation of the lower bounds by points 3, 4, and 6 are written as

$$y_{Lk}\left(x_k\right)-y_k\le 0$$

(51)

where y_Lk = value of the lower bound in the point x_k, (k = 3, 4, 6)

At the same time, for any point k = 1, 2, 3, 4,

$$y_k=y+r_{k}sin\left({\varphi }_k+\varphi \right)\mathrm{and}{x}_k=x+r_{k}cos\left({\varphi }_k+\varphi \right)$$

(52)

where x, y, ϕ = current values of the mass center position and the vehicle yaw angle in the grid nodes; r_k, ϕ_k = radius module and angle of the critical point k location in the vehicle coordinate system.

For the floating points k = 5, 6:

$$y_k=y+r_{\mu k}/cos\left(\varphi \right)\mathrm{and}{x}_k=x$$

(53)

where r_μk = transversal coordinate of point k in the vehicle coordinate system.

We note that the modules and angles for the critical points’ vectors can be determined by passing to the polar coordinate system based on the data vectors of longitudinal r_ζk and transversal r_μk coordinates of these points.

3.6.2. Other Constraints

The model involves three other constraints related to curvature and linear equality. For the curvature constraints, the limiting value of the trajectory curvature is associated with the vehicle maneuverability limitation, which is usually set by the minimum radius R^(e)_min of the outer steered wheel. It can be recalculated to the limit R_min of the immediate radius of the mass center trajectory in the grid nodes using the vehicle geometry (Figure 4) and then converted to the curvature bound value.

$$\left|R_{min}\right|=\sqrt{{\left(\sqrt{{\left(R_{min}^{\left(e\right)}\right)}^2-{\left(c+b\right)}^2}-\frac{B_{24}}{2}\right)}^2+b^2}$$

(54)

Then, the maximum allowed curvature can be found:

$$K_{max}=1/\left|R_{min}\right|\mathrm{and}\left|K\right|\le K_{max}$$

(55)

This condition also overlaps another one, following from Equation (35) that

$$\left|K\right|\le 1/b$$

(56)

For linear equality constraints, it is necessary to form the matrix A_eq and the vector b_eq according to Equation (9) since some parameters of the first and last grid nodes are initially determined. The nodes’ positions on the x-axis and the derivatives at these nodes are given by the required boundary conditions. Thus, even after optimization this should be provided:

$${\mathit{b}}_{eq}=\left(\begin{array}{c}{y_1|}_0\\ {\frac{d{y}_1}{dx}|}_0\\ \begin{array}{c}{y_{n+1}|}_f\\ {\frac{d{y}_{n+1}}{dx}|}_f\end{array}\end{array}\right)=\left(\begin{array}{c}{q}_{y\left(1\right)}\\ q_{y\left(2\right)}\\ \begin{array}{c}{q}_{y\left(3n+1\right)}\\ q_{y\left(3n+2\right)}\end{array}\end{array}\right)$$

(57)

The matrix A_eq is rectangular with dimension 4 × 3(n + 1), where all elements are equal to 0, except for

$${\mathit{A}}_{eq\left(1,1\right)}={\mathit{A}}_{eq\left(2,2\right)}={\mathit{A}}_{eq\left(3,3n+1\right)}={\mathit{A}}_{eq\left(4,3n+2\right)}=1$$

(58)

We note that the initial vector q_y0 corresponds to the zero iteration of the optimization process. To speed up the process, the initial trajectory shape as the first approximation was specified with a half-sum of the parameters of the upper and lower boundaries. Thus,

$${\mathit{q}}_{y0}=\left({\mathit{q}}_U+{\mathit{q}}_L\right)/2$$

(59)

4. Searching Distributions of Kinematic Parameters

4.1. Problem Generalization

By analogy with Section 3, this section considers the conditions under which determining the optimal distribution of the vehicle longitudinal velocity V_ζ [28] can be reduced to the search for a one-variable function V_ζ(x) depending on the set of parameters q_vi in the grid nodes. The optimization objective is to find a vector q_v of dimension 3(n + 1), which defines the law of changing the AV longitudinal speed and acceleration along the trajectory on the interval [0, D] of the x-axis, using the already predetermined parameters q_y. Desirable vector

$${\mathit{q}}_{v\left(i\right)}=\left(\begin{array}{c}{V}_{\zeta i}\\ \frac{d{V}_{\zeta i}}{dx}\\ \frac{d^2{V}_{\zeta i}}{d{x}^2}\end{array}\right),{\mathit{q}}_v=\left(\begin{array}{c}{\mathit{q}}_{v\left(1\right)}\\ ⋮\\ {\mathit{q}}_{v\left(n+1\right)}\end{array}\right)$$

(60)

where i $\in$ [1, n + 1] = node number.

Herewith, within each i-th segment, the set of FE parameters corresponds to two adjacent nodes, i.e.,

$${\mathit{p}}_{v\left(i\right)}=\left(\begin{array}{c}{\mathit{q}}_{v\left(i\right)}\\ {\mathit{q}}_{v\left(i+1\right)}\end{array}\right)\mathrm{and}{\mathit{p}}_v=\left(\begin{array}{c}{\mathit{p}}_{v1}\\ ⋮\\ {\mathit{p}}_{vn}\end{array}\right)$$

(61)

where i $\in$ [1, n] = section number.

In this case, the speed function within a segment, considering Equation (7)

$$V_{\zeta i}\left(x\right)=V_{\zeta i}\left(L_i\xi \right)={\mathit{p}}_{vi}^T{\mathit{L}}_i{\mathit{f}}_{\xi }$$

(62)

Its k-th derivative, considering Equation (8) is

$$\frac{d^k{V}_{\zeta i}}{d{x}^k}={\mathit{p}}_{vi}^T\left(\frac{{\mathit{L}}_i}{L_i^k}\right)\frac{d^k{\mathit{f}}_{\xi }}{d{\xi }^k}$$

(63)

We note that the vector q_v to be found contains a unique nodal DOF. It is easy to obtain a vector p_v with duplicated DOFs of internal nodes to represent the interpolation function with a complete set of parameters for each section.

4.2. Kinematic Parameters and Their Derivatives

Velocity Vector of Mass Center. This velocity can be represented as the derivative of the radius-vector concerning time, as a vector sum of the longitudinal and transversal components in the vehicle coordinate system, and by decomposition in the fixed xy coordinate system (Figure 2).

$$\overrightarrow{V}=\frac{d\overrightarrow{r}}{dt}=\frac{d\overrightarrow{r}}{ds}\frac{ds}{dt}=V\overrightarrow{\tau },\overrightarrow{V}=V_{\zeta }{\overrightarrow{u}}_{\zeta }+V_{\mu }{\overrightarrow{u}}_{\mu },\overrightarrow{V}=V_x{\overrightarrow{u}}_x+V_y{\overrightarrow{u}}_y$$

(64)

Or in the matrix form

$$\overrightarrow{V}={\left(\begin{array}{c}V\\ 0\end{array}\right)}^T\left(\begin{array}{c}\overrightarrow{\tau }\\ \overrightarrow{\nu }\end{array}\right),\overrightarrow{V}={\left(\begin{array}{c}{V}_{\zeta }\\ V_{\mu }\end{array}\right)}^T\left(\begin{array}{c}{\overrightarrow{u}}_{\zeta }\\ {\overrightarrow{u}}_{\mu }\end{array}\right),\overrightarrow{V}={\left(\begin{array}{c}{V}_x\\ V_y\end{array}\right)}^T\left(\begin{array}{c}{\overrightarrow{u}}_x\\ {\overrightarrow{u}}_y\end{array}\right)$$

(65)

where $\overrightarrow{\tau }$, $\overrightarrow{\nu }$ = basis vectors of the natural coordinate system; ${\overrightarrow{u}}_{\zeta }$, ${\overrightarrow{u}}_{\mu }$ = unit vectors of the vehicle coordinate system; ${\overrightarrow{u}}_x$, ${\overrightarrow{u}}_y$ = unit vectors of the fixed coordinate system xy.

Let us introduce a matrix M of plane rotation. Then, the relations between the coordinate systems can be expressed by transitions

$$M(·)=\left(\begin{array}{cc}cos(·)& sin(·)\\ -sin(·)& cos(·)\end{array}\right),\left(\begin{array}{c}\overrightarrow{\tau }\\ \overrightarrow{\nu }\end{array}\right)=M\left(\beta \right)\left(\begin{array}{c}{\overrightarrow{u}}_{\zeta }\\ {\overrightarrow{u}}_{\mu }\end{array}\right),\left(\begin{array}{c}{\overrightarrow{u}}_{\zeta }\\ {\overrightarrow{u}}_{\mu }\end{array}\right)=M\left(\varphi \right)\left(\begin{array}{c}{\overrightarrow{u}}_x\\ {\overrightarrow{u}}_y\end{array}\right)$$

(66)

Correspondingly, for velocities

$${\left(\begin{array}{c}{V}_{\zeta }\\ V_{\mu }\end{array}\right)}^T\left(\begin{array}{c}{\overrightarrow{u}}_{\zeta }\\ {\overrightarrow{u}}_{\mu }\end{array}\right)={\left(\begin{array}{c}{V}_x\\ V_y\end{array}\right)}^T\left(\begin{array}{c}{\overrightarrow{u}}_x\\ {\overrightarrow{u}}_y\end{array}\right)\mathrm{and}\left(\begin{array}{c}{V}_x\\ V_y\end{array}\right)=M^T\left(\varphi \right)\left(\begin{array}{c}{V}_{\zeta }\\ V_{\mu }\end{array}\right)$$

(67)

Absolute Speed Module. This is defined as the change of the arc length over time and is directed tangentially to the trajectory of the vehicle mass center

$$V=\frac{ds}{dt}=\frac{ds}{dx}\frac{dx}{dt}=s_x{V}_x=\frac{V_x}{cos\left(\alpha \right)}=\frac{V_{\zeta }}{cos\left(\beta \right)}$$

(68)

where V_x = projection of absolute speed on the x-axis.

Projection of Absolute Speed. This parameter inevitably appears in all kinematic characteristics as the differential of the x-coordinate concerning time t. The linear velocity V_ζ is related to the projection V_x by the dependence

$$V_x=V_{\zeta }\frac{cos\left(\alpha \right)}{cos\left(\beta \right)}$$

(69)

Consider its derivative concerning the x-coordinate:

$$\begin{gathered} \frac{d{V}_x}{dx}=\frac{d}{dx}\left(V_{\zeta }\frac{cos\left(\alpha \right)}{cos\left(\beta \right)}\right)=\frac{d{V}_{\zeta }}{dx}\frac{cos\left(\alpha \right)}{cos\left(\beta \right)}+V_{\zeta }\frac{d}{dx}\left(\frac{cos\left(\alpha \right)}{cos\left(\beta \right)}\right) \\ =\left(\frac{d{V}_{\zeta }}{dx}+V_{\zeta }\left(\frac{d\beta }{dx}tan\left(\beta \right)-\frac{d\alpha }{dx}tan\left(\alpha \right)\right)\right)\frac{cos\left(\alpha \right)}{cos\left(\beta \right)} \end{gathered}$$

(70)

Longitudinal Speed Derivatives. The speed V_ζ is expressed by the desirable parameters q_v, which are also involved in the derivatives of V_ζ to be used for accelerations and jerks. The first and second derivatives concerning time are given by

$$\frac{d{V}_{\zeta }}{dt}=\frac{d{V}_{\zeta }}{dx}\frac{dx}{dt}=\frac{d{V}_{\zeta }}{dx}{V}_x=\frac{d{V}_{\zeta }}{dx}{V}_{\zeta }\frac{cos\left(\alpha \right)}{cos\left(\beta \right)}$$

(71)

$$\frac{d^2{V}_{\zeta }}{d{t}^2}=\frac{d}{dx}\left(\frac{d{V}_{\zeta }}{dx}\right)\frac{dx}{dt}{V}_x+\frac{d{V}_{\zeta }}{dx}\frac{d{V}_x}{dx}\frac{dx}{dt}=\frac{d^2{V}_{\zeta }}{d{x}^2}{V}_x^2+\frac{d{V}_{\zeta }}{dx}\frac{d{V}_x}{dx}{V}_x$$

(72)

where d^kV_ζ/dx^k for each i-th section is defined by Equation (63).

Lateral Speed. Since the kinematics model shown in Figure 4 assumes an ideal turn, the vehicle’s lateral speed can be expressed over the longitudinal one

$$V_{\mu }=V_{\zeta }tan\left(\beta \right)$$

(73)

The derivative concerning time is given by

$$\frac{d{V}_{\mu }}{dt}=\frac{d{V}_{\mu }}{dx}\frac{dx}{dt}=\frac{d{V}_{\mu }}{dx}{V}_x$$

(74)

which, concerning x, becomes

$$\frac{d{V}_{\mu }}{dx}=\frac{d\left(V_{\zeta }tan\left(\beta \right)\right)}{dx}=\frac{d{V}_{\zeta }}{dx}tan\left(\beta \right)+V_{\zeta }\frac{d}{dx}tan\left(\beta \right)=\frac{d{V}_{\zeta }}{dx}tan\left(\beta \right)+\frac{V_{\zeta }}{{cos}^2\left(\beta \right)}\frac{d\beta }{dx}$$

(75)

Yaw Rate. First, distinguish the instantaneous angular velocity Ω of the mass center and the actual vehicle yaw rate ω (Figure 4). Then, the first one depends only on the speed V_ζ and curvature K at the trajectory point, while the second one is characterized by the changes in the curvature and tangent slope angle. That is,

$$\Omega =\frac{V}{R}=VK=\frac{V_{\zeta }K}{cos\left(\beta \right)}$$

(76)

Using a purely mathematical approach to the expression of Equation (38), we obtain

$$\omega =\frac{d\varphi }{dt}=\frac{d\left(\alpha -\beta \right)}{dt}=\frac{d}{dt}\left(\alpha -\beta \right)=\frac{d\alpha }{dx}\frac{dx}{dt}-\frac{d\beta }{dx}\frac{dx}{dt}=\left(\frac{d\alpha }{dx}-\frac{d\beta }{dx}\right)V_x$$

(77)

Determine the derivative with respect to the x-coordinate

$$\begin{gathered} \frac{d\omega }{dx}=\frac{d}{dx}\left(\frac{d\alpha }{dx}-\frac{d\beta }{dx}\right)V_x+\frac{d{V}_x}{dx}\left(\frac{d\alpha }{dx}-\frac{d\beta }{dx}\right) \\ =\left(\frac{d^2\alpha }{d{x}^2}-\frac{d^2\beta }{d{x}^2}\right)V_x+\frac{d{V}_x}{dx}\left(\frac{d\alpha }{dx}-\frac{d\beta }{dx}\right) \end{gathered}$$

(78)

Angular acceleration. ε is represented by the derivative of the yaw rate ω concerning time:

$$\begin{gathered} \epsilon =\frac{d\omega }{dt}=\frac{d\omega }{ds}\frac{ds}{dt}=\frac{d\omega }{dx}/\frac{ds}{dx}V=\frac{1}{s_x}\frac{d\omega }{dx}\frac{V_x}{cos\left(\alpha \right)}=\frac{d\omega }{dx}{V}_x \\ =\left(\frac{d^2\alpha }{d{x}^2}-\frac{d^2\beta }{d{x}^2}\right)V_x^2+\frac{d{V}_x}{dx}\left(\frac{d\alpha }{dx}-\frac{d\beta }{dx}\right)V_x=\left(\frac{d^2\alpha }{d{x}^2}-\frac{d^2\beta }{d{x}^2}\right)V_x^2+\frac{d{V}_x}{dx}\omega \end{gathered}$$

(79)

Longitudinal and Lateral Accelerations. The accelerations in the vehicle coordinate system ζμ are derived by first differentiating Equation (67):

$$\overrightarrow{a}=\frac{d}{dt}{\left(\begin{array}{c}{V}_{\zeta }\\ V_{\mu }\end{array}\right)}^T\left(\begin{array}{c}{\overrightarrow{u}}_{\zeta }\\ {\overrightarrow{u}}_{\mu }\end{array}\right)+{\left(\begin{array}{c}{V}_{\zeta }\\ V_{\mu }\end{array}\right)}^T\frac{d}{dt}\left(\begin{array}{c}{\overrightarrow{u}}_{\zeta }\\ {\overrightarrow{u}}_{\mu }\end{array}\right)={\left(\begin{array}{c}\frac{d{V}_{\zeta }}{dt}-V_{\mu }\omega \\ \frac{d{V}_{\mu }}{dt}+V_{\zeta }\omega \end{array}\right)}^T\left(\begin{array}{c}{\overrightarrow{u}}_{\zeta }\\ {\overrightarrow{u}}_{\mu }\end{array}\right)$$

(80)

Considering Equation (73), the decomposition components along the axes are given by

$$\left(\begin{array}{c}{a}_{\zeta }\\ a_{\mu }\end{array}\right)=\left(\begin{array}{c}\frac{d{V}_{\zeta }}{dt}-V_{\mu }\omega \\ \frac{d{V}_{\mu }}{dt}+V_{\zeta }\omega \end{array}\right)=\left(\begin{array}{c}\frac{d{V}_{\zeta }}{dx}{V}_x-\omega V_{\zeta }tan\left(\beta \right)\\ \frac{d{V}_{\mu }}{dx}{V}_x+\omega V_{\zeta }\end{array}\right)$$

(81)

Jerk. The jerk characterizes the dynamic balance’s transient processes, which results in the intensity of the acceleration change. This indicator can be used to evaluate the smoothness of non-stationary motion.

$$\begin{gathered} \overrightarrow{j}=\frac{d\overrightarrow{a}}{dt}=\frac{d}{dt}{\left(\begin{array}{c}\frac{d{V}_{\zeta }}{dt}-V_{\mu }\omega \\ \frac{d{V}_{\mu }}{dt}+V_{\zeta }\omega \end{array}\right)}^T\left(\begin{array}{c}{\overrightarrow{u}}_{\zeta }\\ {\overrightarrow{u}}_{\mu }\end{array}\right)+{\left(\begin{array}{c}\frac{d{V}_{\zeta }}{dt}-V_{\mu }\omega \\ \frac{d{V}_{\mu }}{dt}+V_{\zeta }\omega \end{array}\right)}^T\frac{d}{dt}\left(\begin{array}{c}{\overrightarrow{u}}_{\zeta }\\ {\overrightarrow{u}}_{\mu }\end{array}\right) \\ ={\left(\begin{array}{c}\frac{d^2{V}_{\zeta }}{d{t}^2}-2\frac{d{V}_{\mu }}{dt}\omega -\frac{d\omega }{dt}{V}_{\mu }-V_{\zeta }{\omega }^2\\ \frac{d^2{V}_{\mu }}{d{t}^2}+2\frac{d{V}_{\zeta }}{dt}\omega +\frac{d\omega }{dt}{V}_{\zeta }-V_{\mu }{\omega }^2\end{array}\right)}^T\left(\begin{array}{c}{\overrightarrow{u}}_{\zeta }\\ {\overrightarrow{u}}_{\mu }\end{array}\right)={\left(\begin{array}{c}{j}_{\zeta }\\ j_{\mu }\end{array}\right)}^T\left(\begin{array}{c}{\overrightarrow{u}}_{\zeta }\\ {\overrightarrow{u}}_{\mu }\end{array}\right) \end{gathered}$$

(82)

Substituting predefined expressions in Equations (69)–(79) into the longitudinal component of Equation (82), we obtain

$$j_{\zeta }=\left(\frac{d^2{V}_{\zeta }}{d{x}^2}{V}_x+\frac{d{V}_{\zeta }}{dx}\frac{d{V}_x}{dx}-2\frac{d{V}_{\mu }}{dx}\omega \right)V_x-V_{\zeta }\left({\omega }^2+\epsilon tan\left(\beta \right)\right)$$

(83)

4.3. Objective Functions

Let us consider the appropriate objective functions for composing the optimization basis for distributing the speed. They must provide the best performance and give feasible predictions of the vehicle’s behavior. We note that the set of nodal parameters q_y that determine the trajectory geometry is already determined and used in the cost functions and kinematic parameters.

Travelling Time. One of the basic requirements for fastest moving to the final position is the minimum time t_min [19]. It can be represented as an integral

$$\begin{gathered} I_t={\int }_0^{\mathit{T}}dt={\int }_0^{\mathit{s}}\frac{ds}{V\left(s\right)}={\int }_0^{\mathit{D}}\frac{dx}{V\left(x\right)cos\left(\alpha \left(x\right)\right)}={\int }_0^{\mathit{D}}\frac{dx}{V_x\left(x\right)} \\ ={\sum }_{i=1}^n\left({\int }_{x_i}^{x_{i+1}}\frac{dx}{V_{xi}\left(x\right)}\right)={\sum }_{i=1}^n{L}_i{\int }_0^1\frac{d\xi }{V_{xi}\left({\mathit{p}}_{yi},{\mathit{p}}_{vi},L_i\xi \right)} \end{gathered}$$

(84)

It is seen that the higher speed values, the smaller the integral. In addition, this integral can be used to form a matrix of time intervals and a time scale vector for subsequent use in estimating motion parameters over time during the tracking.

Longitudinal Speed. An alternative to Equation (84) for forming the speed distribution is to apply the integral of the squared deviations of the actual velocities relative to preset upper-level V_ζmax as

$$\begin{gathered} I_v={\int }_0^{\mathit{s}}{\left(V_{\zeta max}-V_{\zeta }\right)}^{2}ds={\int }_0^{\mathit{D}}{\left(V_{\zeta max}-V_{\zeta }\right)}^2{s}_{x}dx \\ ={\sum }_{i=1}^n\left({\int }_{x_i}^{x_{i+1}}{\left(V_{\zeta max}-V_{\zeta i}\left(x\right)\right)}^2{s}_{xi}\left(x\right)dx\right) \\ ={\sum }_{i=1}^n{L}_i{\int }_0^1{\left(V_{\zeta max}-V_{\zeta i}\left({\mathit{p}}_{vi},L_i\xi \right)\right)}^2{s}_{xi}\left({\mathit{p}}_{yi},L_i\xi \right)d\xi \end{gathered}$$

(85)

Yaw Rate. Further, the lowest intensity of the yaw rate ω can be determined as

$$\begin{gathered} I_{\omega }={\int }_0^{\mathit{s}}{\omega }^{2}ds={\int }_0^{\mathit{D}}{\left(\omega \left(x\right)\right)}^2{s}_x\left(x\right)dx= \\ {\sum }_{i=1}^n{L}_i{\int }_0^1{\left({\omega }_{xi}\left({\mathit{p}}_{yi},{\mathit{p}}_{vi},L_i\xi \right)\right)}^2{s}_{xi}\left({\mathit{p}}_{yi},L_i\xi \right)d\xi \end{gathered}$$

(86)

Angular Acceleration. Similarly, for ε the integral criterion I_ε

$$\begin{gathered} I_{\epsilon }={\int }_0^{\mathit{s}}{\epsilon }^{2}ds={\int }_0^{\mathit{D}}{\left(\epsilon \left(x\right)\right)}^2{s}_x\left(x\right)dx \\ ={\sum }_{i=1}^n{L}_i{\int }_0^1{\left({\epsilon }_{xi}\left({\mathit{p}}_{yi},{\mathit{p}}_{vi},L_i\xi \right)\right)}^2{s}_{xi}\left({\mathit{p}}_{yi},L_i\xi \right)d\xi \end{gathered}$$

(87)

Longitudinal Acceleration. When changing the vehicle speed, it is essential to ensure a smooth increase in the speed and minimize acceleration [9], which affects the overall power balance of the vehicle’s engine. Then,

$$\begin{gathered} I_{a\zeta }={\int }_0^{\mathit{s}}{a}_{\zeta }^{2}ds={\int }_0^{\mathit{D}}{\left(a_{\zeta }\left(x\right)\right)}^2{s}_x\left(x\right)dx \\ ={\sum }_{i=1}^n{L}_i{\int }_0^1{\left(a_{\zeta i}\left({\mathit{p}}_{yi},{\mathit{p}}_{vi},L_i\xi \right)\right)}^2{s}_{xi}\left({\mathit{p}}_{yi},L_i\xi \right)d\xi \end{gathered}$$

(88)

Lateral Acceleration is one of the most substantial criteria for motion safety. The lateral acceleration characterizes the transversal reactions, the slip phenomenon, and the stability of steerability.

$$\begin{gathered} I_{a\mu }={\int }_0^{\mathit{s}}{a}_{\mu }^{2}ds={\int }_0^{\mathit{D}}{\left(a_{\mu }\left(x\right)\right)}^2{s}_x\left(x\right)dx \\ ={\sum }_{i=1}^n{L}_i{\int }_0^1{\left(a_{\mu i}\left({\mathit{p}}_{yi},{\mathit{p}}_{vi},L_i\xi \right)\right)}^2{s}_{xi}\left({\mathit{p}}_{yi},L_i\xi \right)d\xi \end{gathered}$$

(89)

Longitudinal Jerk characterizes the intensity of acceleration change in the longitudinal direction and combines almost all of the kinematic parameters. The minimization provides a smooth acceleration transient [21], ensuring a propulsion system’s stable, realizable, and predictable operation. Thus, the jerk criterion is written as follows:

$$\begin{gathered} I_{j\zeta }={\int }_0^{\mathit{s}}{j}_{\zeta }^{2}ds={\int }_0^{\mathit{D}}{\left(j_{\zeta }\left(x\right)\right)}^2{s}_x\left(x\right)dx \\ ={\sum }_{i=1}^n{L}_i{\int }_0^1{\left(j_{\zeta i}\left({\mathit{p}}_{yi},{\mathit{p}}_{vi},L_i\xi \right)\right)}^2{s}_{xi}\left({\mathit{p}}_{yi},L_i\xi \right)d\xi \end{gathered}$$

(90)

Minimization. The function W_v to be minimized can be represented in the matrix form as a linear combination of criteria considered above:

$$W_v\left({\mathit{q}}_v\right)={\mathit{w}}_v^T{\mathit{I}}_v\left({\mathit{q}}_y,{\mathit{q}}_v\right)\to min$$

(91)

where q_v = vector of unknown node parameters, Equation (60), I_v = vector of criteria functions, w_v = vector of weighting factors.

$${\mathit{w}}_v=\left(\begin{array}{c}{w}_v\\ w_{\omega }\\ w_{a\zeta }\\ w_{a\mu }\\ w_{\epsilon }\\ w_{j\zeta }\end{array}\right),{\mathit{I}}_v\left({\mathit{q}}_y,{\mathit{q}}_v\right)=\left(\begin{array}{c}{I}_v\left({\mathit{q}}_y,{\mathit{q}}_v\right)\\ I_{\omega }\left({\mathit{q}}_y,{\mathit{q}}_v\right)\\ I_{a\zeta }\left({\mathit{q}}_y,{\mathit{q}}_v\right)\\ I_{a\mu }\left({\mathit{q}}_y,{\mathit{q}}_v\right)\\ I_{\epsilon }\left({\mathit{q}}_y,{\mathit{q}}_v\right)\\ I_{j\zeta }\left({\mathit{q}}_y,{\mathit{q}}_v\right)\end{array}\right)$$

(92)

where w_v, w_ω, w_aζ, w_aμ, w_ε, w_jζ = weighting coefficients for the speed, yaw rate, longitudinal and later accelerations, and longitudinal jerk, respectively.

We note that, in the general case, the vector function I_v is determined by the set q_y of trajectory nodal parameters and q_v of velocities. However, due to the constant values of q_y, the cost function W_v depends only on the required q_v.

4.4. Optimal Kinematics Restrictions

4.4.1. Slip Critical Speed

Consider the equilibrium of the adhesion forces in the lateral vehicle direction and the transverse component of the centrifugal force that caused them:

$$m\frac{V^2}{R}cos\left(\beta \right)=mg{\phi }_{\mu }$$

(93)

where m = vehicle mass; g = gravity acceleration; φ_μ = adhesion coefficient corresponding to the vehicle’s lateral direction.

If we express the speed V via V_ζ of Equation (68), then the longitudinal critical speed V_sl by the adhesion condition [16,27] is

$$V_{sl}^2=V_{\zeta }^2,V_{sl}=\sqrt{g{\phi }_{\mu }Rcos\left(\beta \right)}$$

(94)

where

$${\phi }_{\mu }={\phi }_{max}\sqrt{1-{\left({\phi }_{\zeta }/{\phi }_{max}\right)}^2}$$

(95)

where φ_max, φ_ζ = maximum and lateral tire-road adhesion coefficients.

Considering the planned acceleration and speeds, φ_ζ may be estimated as follows:

$${\phi }_{\zeta }=a_{\zeta }/g+f_a+f_r$$

(96)

where f_r = total rolling resistance coefficient; f_a = specific drag force.

$$f_a=F_a/\left(mg\right)={\rho }_a{C}_x{A}_f/\left(2mg\right)$$

(97)

where F_a = drag force; ρ_a = air density under the normal conditions; C_x = aerodynamic drag coefficient, and A_f = frontal (projective) vehicle square.

Assuming that the turning angles of steered wheels differ little from the angle β, f_r can be estimated as

$$f_r\approx \left(\left(F_{r1}+F_{r3}\right)cos\left(\beta \right)+F_{r2}+F_{r4}\right)/\left(mg\right)$$

(98)

where F_r1, F_r2, F_r3, F_r4 = forces of wheels’ rolling resistance.

In turn,

$$F_{rk}=R_{zk}{f}_{rk}$$

(99)

where R_zk = vertical wheel load (may be accepted as mg/4); f_rk = wheel rolling resistance coefficient.

Each wheel moves at its speed; then,

$$f_{rk}=q_{sy1}+q_{sy3}\left|V_{\zeta k}\right|+q_{sy4}{\left(V_{\zeta k}/V_m\right)}^4$$

(100)

V_ζk = longitudinal speed in the k-th wheel coordinate system, V_m = speed at which the empirical measurements were made; q_sy1, q_sy3, q_sy4 = coefficients [29].

4.4.2. Linear Inequality Constraints

Maximum Speed. This corresponds to the range of preferred speeds in a given planning area. That is, the conditions in each node must be satisfied:

$$V_{\zeta i}-V_{\zeta max}\le 0$$

(101)

where i $\in$ [1, n + 1] = node number.

Then, according to Equation (9), to optimize the kinematics,

$$\mathit{b}=V_{\zeta max}\left(\begin{array}{c}1\\ 1\\ \begin{array}{c}⋮\\ 1\end{array}\end{array}\right)\le \left(\begin{array}{c}{q}_{v1}\\ q_{v4}\\ \begin{array}{c}⋮\\ q_{v\left(3n+1\right)}\end{array}\end{array}\right)$$

(102)

Matrix A in this case is rectangular with dimension (n + 1) × 3(n + 1) with non-zero elements corresponding to positions $A_{i,3i-2}=1$, i $\in$ [1, n + 1]. We note that additional checkpoints within the intervals ξ $\in$ [0,1] can improve reliability. However, these conditions must be added to the nonlinear constraints.

4.4.3. Linear Equality Constraints

In this problem, no restrictions are imposed on the values of kinematic parameters in the final node of the distribution function. For the starting point, it is essential to comply with the conditions of the current longitudinal speed and its derivative, which is included in the expression for longitudinal acceleration. Then, according to Equation (9),

$${\mathit{b}}_{eq}=\left(\begin{array}{c}{V_{\zeta 1}|}_0\\ {\frac{d{V}_{\zeta 1}}{dx}|}_0\end{array}\right)=\left(\begin{array}{c}{q}_{v1}\\ q_{v2}\end{array}\right)$$

(103)

The matrix A_eq is a rectangular matrix of dimension 2 × 3(n + 1), where all elements are equal to 0, except for $A_{eq\left(1,1\right)}=A_{eq\left(2,2\right)}=1$.

4.4.4. Vehicle Maximum Performance

One of the limiting factors is the vehicle’s maximum possible longitudinal acceleration, which can be estimated by the empirical or theoretical acceleration characteristic corresponding to the full power use. Figure 6 shows the acceleration characteristic of an Audi A4 3.2 Quattro depending on the speed of the rectilinear motion. As seen, despite the automatic transmission, the throttle response potential changes stepwise and non-linearly in general.

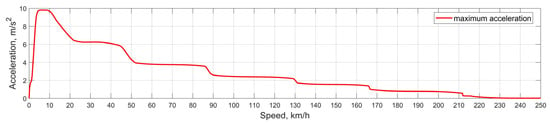
Figure 6. Audi A4 Quattro acceleration with full throttle use.

These restrictions should be included in the nonlinear optimization constraints, which allows proceeding from the vehicle’s physical capabilities depending on the peed mode. The characteristic can be represented by interpolation for the current calculations. Thus, in the checkpoints within the intervals and in each node, the conditions must be satisfied:

$$a_{\zeta k}-a_{\zeta max}\le 0$$

(104)

where k = number of the checkpoints.

4.5. Initial Conditions

We note that in the general case of curvilinear motion, the acceleration a_ζ0 at the initial point cannot directly characterize the derivative of the longitudinal speed, being related to the dependence of Equation (81). This means that the required initial parameter can be obtained from the condition

$$a_{\zeta 0}={\frac{d{V}_{\zeta }}{dx}|}_0{V}_{x0}-{\omega }_0{V}_{\zeta 0}tan\left({\beta }_0\right)\mathrm{and}{\frac{d{V}_{\zeta }}{dx}|}_0=\frac{a_{\zeta 0}+{\omega }_0{V}_{\zeta 0}tan\left({\beta }_0\right)}{V_{x0}}$$

(105)

With the virtual simulation, the required values can be obtained as the final ones of a previous cycle, and with real-world planning—by evaluation using the vehicle sensory system.

Vector of Initial Solution. In general, only the current speed value can be set in Equation (103), assuming the node’s derivatives values are zero. In the zero iteration, the following distribution of the initial speed values can be taken for the vector q_v0 such that ${\mathit{q}}_{v\left(i,3i-2\right)}=V_{\zeta 1}\left(0\right)$, i $\in$ [1, n + 1].

5. Simulation Example

The MATLAB code using the basic nonlinear optimization function fmincon was composed to test the proposed approach. Thus, several planning trajectories and speeds were performed. Table 2 shows the primary necessary physical, kinematic, and geometric data (Figure 4) of the vehicle Audi A4 Quattro [30].

Table 2. Data for simulating the AV motion prediction.

Parameter	Value	Parameter	Value	Parameter	Value
c, [m]	1.43	m, [kg]	1960	ρa, [kg/m3]	1.225
b, [m]	1.37	φmax	0.85	Cx	0.24
B24, [m]	1.551	Vζmax, [km/h]	100	Af, [m2]	2.04
|rζk|, [m]	2.5	Vζ1(0), [km/h]	60	D, [m]	61.32
|rμk|, [m]	1.2	n	10	d, [m]	12.5

5.1. Trajectory Search

Using the criteria and technique of Section 3, let us consider the possible trajectories shown in Figure 7a and the curves of the vehicle yaw angle in Figure 7b. Each curve corresponds to a different combination of weights w_y Equation (49): w_y1—trajectory 1, w_y2—trajectory 2, w_y3—trajectory 3.

$${\mathit{w}}_{y1}=\left(\begin{array}{c}2\\ 1\\ 0\end{array}\right),{\mathit{w}}_{y2}=\left(\begin{array}{c}0\\ 0\\ 3\end{array}\right),{\mathit{w}}_{y3}=\left(\begin{array}{c}0.25\\ 1\\ 2\end{array}\right)$$

(106)

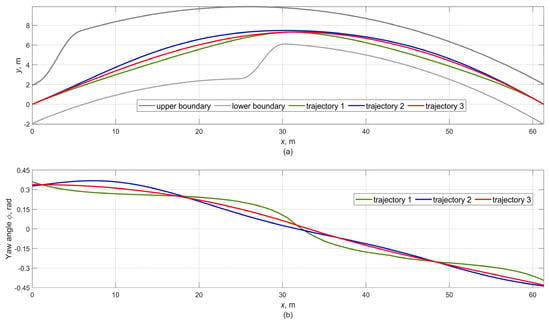
Figure 7. Variants of vehicle motion geometry depending on the priority criteria: (a) mass center trajectories and (b) yaw angles.

The sets of weighting coefficients in Equation (106) were chosen to reflect the fundamental trends ensuring, at the same time, the feasibility within the boundaries considered in Figure 3. We note that the influence of the coefficient w_S in Equation (49) is quite weighty, and the curve under its effect tends to straighten out, which sharply increases the curvature at the inflection point (approximately corresponds to x = 30 m, Figure 7a). Therefore, trajectory 1 (green) situation is softened by adding the influence of the distributed curvature factor in the vector w_y1. Trajectory 2 was formed only based on the curvature intensity criterion Equation (44), excluding the influence of the minimum path and the curvature alignment on the vector w_y2. The third option is represented by a combination w_y3 of all factors to create a compact and smooth trajectory 3.

5.2. Speed Search

For optimizing the speed distribution with the SQP algorithm [22], trajectories 2 and 3 were used to provide a compromise between smoothness and average curvature, which is essential to forecast stability. Thus, it is possible to form four variants of speed planning by two for each of the found trajectories 2 and 3. Variants v₁, v₂ are based on trajectory 2, and v₃, v₄—on trajectory 3, respectively (Figure 8). For these options, the following combinations of weighting coefficients w_v of Equation (92) are proposed:

$${\mathit{w}}_{v1}=\left(\begin{array}{c}5\\ 0\\ 3\\ 0\\ 0\\ 1\end{array}\right),{\mathit{w}}_{v2}=\left(\begin{array}{c}5\\ 0\\ 3\\ 0\\ 3\\ 3\end{array}\right),{\mathit{w}}_{v3}=\left(\begin{array}{c}5\\ 0\\ 3\\ 0\\ 0\\ 1\end{array}\right),{\mathit{w}}_{v4}=\left(\begin{array}{c}5\\ 0\\ 3\\ 0\\ 3\\ 3\end{array}\right)$$

(107)

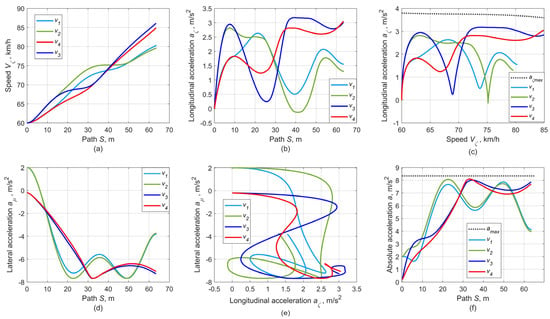
Figure 8. Results of the optimal plans for redistributing the kinematic parameters: (a) longitudinal speed along the trajectory, (b) longitudinal acceleration along the trajectory, (c) longitudinal acceleration along the longitudinal speed, (d) lateral acceleration along the trajectory, (e) relation between longitudinal and lateral accelerations, and (f) absolute acceleration along the trajectory.

Figure 8 shows the variants of distributing the main kinematic parameters such as longitudinal speed and longitudinal and lateral accelerations—to reflect their connection with the physical limitations and to demonstrate their relations with the distributions of motion trajectory. Figure 8a,b reflects the longitudinal speed V_ζ and acceleration a_ζ changes along the motion path determined by the integral of Equation (91). Figure 8c depicts the longitudinal acceleration a_ζ in the speed domain V_ζ to compare the declared accelerations with the ones provided by the vehicle physical limits (Figure 6), considering the road adhesion conditions limited by the coefficient φ_max. Figure 8d reflects the distributions of lateral accelerations along the path, simultaneously characterizing the curvature and the values of lateral reactions needed to maintain the vehicle on the trajectory. Figure 8e presents a phase portrait of the accelerations a_ζ and a_μ, reflecting their mutual influence and the limitation of adjacent physical characteristics φ_ζ and φ_μ by the adhesion ellipse [29]. Figure 8f shows the distribution of the absolute value of the vehicle mass center acceleration along the trajectory concerning the maximum possible acceleration a_max = gφ_max.

5.3. Results

5.3.1. Trajectories

As seen in Figure 7a, trajectory 1 (green) provides the shortest path but leads to significant curvature in the inflection point (x = 30 m), which requires a substantial change in direction within a relatively short path segment. In addition, some smoothing of the inflection zone results in frequent fluctuations of the vehicle yaw angle (Figure 7b), which may negatively affect the vehicle’s control. It can be assumed that for the vehicle’s high-speed mode such a trajectory will be dangerous and acceptable only when maneuvering at low speeds. Trajectory 2 (blue, Figure 7a) is formed only by the curvature intensity criterion dK/ds of Equation (28) and has the largest length S₂ = 64.95 m. An increase in the trajectory length significantly compensates for the curvature in the inflection point region, which favorably distinguishes this trajectory variant from others. On the other hand, in the second phase, the trajectory deviates more towards the upper limit, which is undesirable even with a satisfactory safety clearance, given the tire lateral elasticity and sideslip in actual conditions. Trajectory 3 (red, Figure 7a) includes all criteria where the average curvature plays a key role. The trajectory length is S₃ = 64.75 m. It differs from the most straightened yaw angle curve, moderate curvature at the inflection point, and trajectory’s layout close to the conditional lane’s midline in the second phase of the maneuver. We note that other variations of the weighting coefficients do not provide a unique trajectory nature, which characterizes the optimization process as stable and unambiguous. Thus, any combinations that exclude the excessive influence of w_S lead to variants of curves close to trajectories 2 and 3.

5.3.2. Speed and Accelerations

Trajectory 2 (variants v₁, v₂). A distinctive feature of the speed and acceleration distributions in these cases (Figure 8a–c) is a more intensive phase preceding the inflection point and a less intense phase after the trajectory inflection point (approximately x = 30 m). As noted, the influential decrease of the curvature in the trajectory’s inflection area allows increasing the speed before the inflection point, keeping it in the entry zone of the second lane corridor, and increasing it but with lesser intensity in the final phase. Since the angular acceleration a_μ (Figure 8d) reaches a close to critical value even before the inflection point; to ensure stability when entering a turn, the acceleration intensity a_ζ decreases to 0 at the beginning of the second path phase. The subsequent intensity of the a_ζ increase is moderate because of the simultaneous increase in a_μ, largely determined by the nature of the trajectory curvature.

The time needed to overcome the path t_v1 = 3.32 s, t_v2 = 3.33 s, and the speed varies from 60 to about 85 km/h. The relation between speed and time is entirely consistent with the characteristics of the vehicle Audi A4 maximum performance [30], which regulates the acceleration time: 0–60 km/h—3.1 s, 0–80 km/h—4.6 s. Therefore, maximum performance acceleration will take about 1.5 s from 60 to 80 km/h, which is much less than t_v1 and t_v2. The curvilinear motion nature is the most limiting factor in the vehicle’s performance.

Trajectory 3 (options v₃, v₄). In these variants, a more intense phase of increasing the speed and accelerations is realized after the inflection point, which is also caused by the greater local curvature reflected in the lateral acceleration a_μ. Therefore, the initial intense acceleration a_ζ stipulates increasing the speeds up to values at which a smooth passage of the a_μ peak value is ensured, after which the vehicle enters the second lane corridor with an increased intensity of acceleration a_ζ owing to the reduced curvature and, consequently, of component a_μ as well. This contributes to a stable speed increase to values higher than those for v₁, v₂.

The time for completing the path is t_v3 = 3.26 s, t_v4 = 3.32 s, and the speed varies from 60 to the maximum of about 87 km/h. As in the previous cases, the ratios of the speeds and time are consistent with the performance limits. The acceleration from 0 to 90 km/h takes 5.4 s. Therefore, for accelerating with maximum performance from 60 even up to 90 km/h, about 2.3 s is needed, which is also less than t_v3 and t_v4.

5.3.3. Satisfaction of Physical Constraints

Figure 8c,f shows the physical limitations caused by the vehicle’s internal potential and external factors of interaction with the road surface. We note that the optimal solution is well coordinated with the imposed restrictions, and the results do not violate the pre-established limitations. It is evident that such an approach expands the capabilities of finding stable optimal motion modes for any combination of external conditions.

5.3.4. Weighting Coefficients and Their Influence

A separate issue is the search for the best linear combination of the cost functions defined by the weighting vectors. In this regard, a sufficient number of virtual experiments have also been carried out, which allows the following conclusions concerning trajectories and kinematics.

Trajectories. Each combination of weighting factors reflecting the uniqueness of a trajectory variant provides both advantages and drawbacks. Obviously, in the general case, the best trajectory is determined by a compromise between the curvature, its intensity, and straightness (path length). The coefficients may vary depending on a task, where the quality of trajectory curvature distribution plays a decisive role. It can be concluded that it is desirable to distribute the weight of the coefficients in such a way as to defocus the curvature at the points of trajectory inflections (change of the yaw angle sign). At the same time, it is desirable to avoid an excessive number of inflections, which contributes to minimizing the fluctuation of acceleration a_ζ.

Kinematics. We note, first of all, that in Equation (107), weighting coefficients w_ω, w_ε corresponding to the impact of the yaw rate and angular acceleration are assumed to be zero. It is explained by the fact that their influences in the qualitative trajectory prediction are practically indistinguishable because of the path smoothness and its curvature alignment. The role of these criteria may be more essential when maneuvering under conditions of frequently changed curvature of the motion area boundaries. The first weighting coefficient w_v is responsible for the rapid increase in speed, and therefore, its value is the largest. At the same time, it is desirable to redistribute the longitudinal speed that the intensity of its change was as even as possible. The coefficient w_aζ = 3 is responsible for reducing speed fluctuations and ensuring the evenness of its change. The next factor w_aμ (0 or 3) reflects the same aspects of lateral acceleration but its influence is situational. Its non-zero value is more suitable when the sign of trajectory curvature changes often. One of the most obligatory and vital factors is the coefficient w_jζ, which reduces the intensity of transient processes in longitudinal dynamics and ensures the overall smoothness of resulting acceleration forecasts. Its weight must be balanced with the coefficient w_aζ in such a way to prevent an excessively abrupt increase in longitudinal acceleration with a simultaneous decrease in fluctuations of the longitudinal acceleration itself.

Thus, in the general case, the basic parameters for optimizing the kinematics distribution are the quadratic deviations of the longitudinal speed, acceleration, and jerk if the minimum curvature and its intensity of a trajectory model are ensured.

6. Conclusions

This paper has presented the development and analysis of a sequential optimization method for planning the AV motion reference parameters. The method determines the trajectory plan, speed and acceleration distributions, and other AV kinematic parameters. Based on this study, the following comments are offered:

Comparison with Other Approaches and the Uniqueness of the Method

• the approach combines the advantages of representing solutions by FEs and nonlinear optimization;
• the technique for limiting allowable space was considered;
• the complete mathematical apparatus was developed providing clear connections between geometric and kinematic parameters in the spatial domain, which abolishes the need for setting a time of prediction horizon;
• geometric restrictions are clearly defined in the form of nonlinear constraints, which guarantees the vehicle location within the boundaries;
• the kinematic parameters are strictly interconnected, which is shown in the formulas for acceleration and sharpness unlike other works;
• the distribution of speed and accelerations is performed directly along the trajectory without reference to time and provides natural smooth curves in contrast to the speed representation as a time function based on 2nd- or 3rd-degree polynomials proposed in many works. In this case, the acceleration and jerk are considered only along the longitudinal coordinate and are often assigned as either linear or constant, which does not reflect the real nature of the propulsion system operation;
• all the necessary procedures (unlike other works) for implementing the method in the computer simulation environment are reflected.

General validation of the approach. From the point of view of reducing the necessary procedures in motion planning, the simultaneous optimization of the trajectory and kinematic parameters would be preferable. However, with such an approach, it is not easy to satisfy all criteria, which often contradict each other, and the final objective function requires detailed study. In contrast, the proposed technique offers a two-stage prediction of the AV motion, demonstrating its mathematical logicality, clarity, workability, and efficiency in a generalized example of curvilinear movement under conditions of external boundaries and a moving obstacle. The first stage is based on ensuring movement safety in the zone of admissible limits and stability of control due to the optimal smoothness of the predicted trajectory, considering the geometric and kinematic characteristics of the AV model. The second stage ensures the distribution of kinematic parameters along the trajectory length, of which the main ones are the longitudinal speed and acceleration, based on minimizing the complex criteria determined by the internal vehicle potential and the physics of tire–road interactions. The geometric, kinematic, and physical nonlinear constraints used in the optimization steps contribute to the realism and feasibility of the proposed planning technique.

Contributions. A distinctive feature of the proposed technique is an explicit restriction of the safe motion area by optimizing the best trajectory choice in contrast to the approaches focused on conjugating the lanes’ midpoints by smooth curves. The middle line approach, especially when planning over long distances, is qualitatively worse than the optimization within the boundaries. The latter reduces the path, the average curvature, and the task of vehicle control owing to the optimally smoothed curve and satisfaction of nonlinear constraints. The complex mathematical apparatus has been developed to implement the procedure for planning the AV motion in a constrained space. The mechanism of forming the boundaries of permissible movement in the presence of a movable obstacle is stipulated. Criteria for finding optimal trajectory plans and distribution of kinematic parameters are determined and analyzed, considering geometric, kinematic and physical restrictions, including the vehicle performance potential. Many virtual tests have been carried out for the generalized example of searching for motion predictions, demonstrating the consistency of the proposed technique and the quality of the resulting plans.

Advantages. The fundamental advantage of the proposed approach consists of obtaining a significant number of reference curves mathematically related to each other, which contributes to improving the quality of AV control in tracking. The forecasting stability is ensured by the smoothness of the higher derivative functions of the desired trajectory and speed distributions. Furthermore, the vehicle has a sensory system (MEMS gyroscopes and accelerometers, wheels’ angular speed sensors) capable of evaluating in real-time the longitudinal speed, longitudinal and lateral accelerations, yaw rate, and other parameters directly. Thus, in organizing the tracking of references, the control accuracy is higher than when controlling only the speed and lateral position. The optimization settings can be tuned concerning the type of vehicle drivetrain and the presence of intelligent traction control systems. As shown in Figure 8b, entering the second lane’s corridor is possible with acceleration and deceleration. The first technique is more typical for vehicles with front-wheel drive, while the second fits rear-wheel drive. With Torque Vectoring or Sport Differential technology, the nature of the control plans can be more intense towards higher speeds and accelerations. We note that forming a complete set of parameters in the final node is unnecessary in this method, which is compensated by nonlinear constraints.

Disadvantages. The proposed model has some limitations. The search for the optimum within the permissible boundaries requires more computational procedures but provides better quality than other approaches. Furthermore, the method requires the trajectory to be strictly unambiguous along the longitudinal coordinate x, and the module of rotation angles in the nodes of boundaries must be less than 90°. On the other hand, this method corresponds to the physical and technical capabilities of computer vision technology for recognizing road marking lines. Thus, the approach’s applicability is limited by one direction movement along the boundaries with moderate curvature. To apply this technique for autonomous parking problem, for example, a modification is required.

Recommendations. Based on a series of virtual experiments, suggestions can be formed regarding the staged planning of the priority criteria and their weights in the cost function. Thus, when planning a trajectory, the preference should be given to a balance of the distributed curvature and its intensity criteria with a slight influence of the path length criterion. Furthermore, the weighting coefficients must be chosen to simultaneously meet the requirements of the trajectory curve compactness, reduce the local curvature value about the average one, and minimize fluctuations of the vehicle yaw angle—that is, to ensure the maximum trajectory unambiguity. For planning the kinematic parameters, it is recommended to focus on the criteria that ensure using a speed close to the desired level in a quadratic sense and a compromise between the intensities of longitudinal speeds and accelerations. The latter provides both smoothness of speed and acceleration (Figure 8a,b). At the same time, it is desirable to choose the weighting coefficients’ balance in such a way to preserve the physical capability of reproducing such control laws for an actual vehicle. This might occur when the transient delay problem arises due to the features of the vehicle propulsion system. If the acceleration prediction requires only non-negative values, the minimum acceleration value in the constraints must be set to a negative value close to 0. First, this will narrow the range of scattering and search for accelerations. Second, it will exclude the variants with more significant negative acceleration values, which would mean the need for using the braking system. Thus, the weighting coefficients must correspond to the task of maintaining a speed mode.

Connections with future projects. This study was aimed at confirming the effectiveness of the proposed approach for AV motion planning in general. However, many issues arise and need to be considered in future studies. First, the work used a regular FE grid, and the section length was tied to the overall vehicle dimension. However, due to the three DOFs in a node, it is possible to simulate the trajectory curvature change within a finite element in a wide range. Therefore, with a monotonically changing curvature, the length of sections may be redistributed, and the grid density can be increased in areas of obstacles localization, unsafe maneuvers, and significant curvature. The number of trajectory variations will decrease in this case. However, the grid irregularity and the reduction of the node number will positively improve the optimization procedure performance. Second, the problem of returning an AV to its initial motion lane in the presence of a moving obstacle should be addressed. In this case, it is not enough to solve only in the space domain, as considered, but a comparison of two vehicles’ motion modes in the time domain will also be required. To potentiate traffic safety and increase the productivity of computational procedures, it is necessary to increase the number of restrictions that reflect the vehicle–road interaction physics and to work out their integral descriptions for use in the equality constraints according to Equation (9).