Abstract
A crucial challenge in Bayesian modeling using Markov chain Monte Carlo (MCMC) estimation is to diagnose the convergence of the chains so that the draws can be expected to closely approximate the posterior distribution on which inference is based. A close approximation guarantees that the MCMC error exhibits only a negligible impact on model estimates and inferences. However, determining whether convergence has been achieved can often be challenging and cumbersome when relying solely on inspecting the trace plots of the chain(s) or manually checking the stopping criteria. In this article, we present a SAS macro called %automcmc that is based on PROC MCMC and that automatically continues to add draws until a user-specified stopping criterion (i.e., a certain potential scale reduction and/or a certain effective sample size) is reached for the chain(s).
1. Introduction
The Bayesian modeling framework has become more and more popular in psychology and related sciences [1]. This is because Bayesian modeling offers greater flexibility in modeling, fewer estimation problems, and more accurate estimates (e.g., [2,3,4]). Typically, Markov chain Monte Carlo (MCMC) techniques are used, which draw from the distribution of the parameters given the prior beliefs and the observed data—the so-called posterior distribution. These draws constitute one or more MCMC chains per parameter. As the chain starts from a specific initial value (also called starting value), it undergoes some iterations before it potentially reaches convergence and settles into a stable pattern. Thus, researchers need to determine whether and when estimation has converged, including whether the model estimates are approximated well by summary statistics, such as the mean, from the MCMC chain(s). Importantly, to ensure a close approximation, the MCMC error needs to be small (e.g., [5,6]). However, visually monitoring convergence by inspecting the trace plots of the chain(s) or manually checking stopping criteria can be challenging and requires expertise, which researchers, especially those new to MCMC, may lack. Fortunately, there are software options available, like the Bayes module in Mplus [7], that offer automatic convergence monitoring. These tools assess convergence by checking if a specified value for the chosen stopping criterion has been achieved [8]. However, to the best of our knowledge, such an automated tool is not yet available in SAS for PROC MCMC [9], which is another powerful tool for conducting statistical analyses based on MCMC techniques. The advantages of PROC MCMC compared with different R packages for MCMC analyses are, for example, that it shows fewer memory limitations and—due to multithreading (which is, however, not available in the online version of SAS OnDemand for Academics freely accessible for academic researchers)—is computationally more efficient [10]. Moreover, the syntax of SAS PROC MCMC is not only intuitive for beginners but also highly flexible for advanced users. By default, SAS PROC MCMC utilizes a random walk Metropolis sampler. Additionally, it provides a range of 28 standard prior distributions that can be readily applied. However, the flexibility of the procedure extends further as users can also define their own samplers and prior distributions according to their specific requirements [9]. In recent years, many articles utilizing PROC MCMC have been published in various fields. These applications cover a wide range of model classes, including multilevel modeling [11,12], mediation analyses [13,14], item response theory (IRT) modeling [10,15,16,17], and growth curve modeling [18,19].
We developed a SAS macro called %automcmc (see Supplementary Materials) that is based on PROC MCMC and that automatically continues to add iterations of the sampler until a user-specified stopping criterion (i.e., a certain potential scale reduction and/or a certain effective sample size) is reached for the chain(s). In this article, we present this macro and illustrate its use with the help of simulated data.
2. Automatic Monitoring of Stopping Criteria in Markov Chain Monte Carlo Estimation
In this section, we give a brief overview of convergence and the selection of stopping criteria in MCMC estimation, and we explain and show how the %automcmc macro can be used to apply automatic monitoring of user-specified stopping criteria for arbitrary models.
2.1. Convergence and Stopping Criteria in Markov Chain Monte Carlo
Several statistics have been proposed as stopping criteria, with the potential scale reduction (PSR) being one of the most notable [20]. For an estimate of a parameter θ based on m chain sequences of length n, the PSR is defined as proposed by Asparouhov and Muthén [21] and implemented in Mplus [7] as follows:
where W denotes the pooled variance within the chain and B is the variance between the sequences. The rationale behind this statistic is that for a chain to be considered converged, it is necessary for the ratio of the variance of the draws to the average of the variances within sequences of the chain to approach 1. This indicates minimal between-sequence variance, signifying convergence. Rather than inspecting convergence by using a single chain [5], multiple chains may be used, which is also recommended by Gelman and Rubin [20]. In this case, the PSR compares the overall variance of the draws to the average within-chain variance. Here again, when the PSR is close to 1, this is an indication of convergence. If multiple chains are run with our macro based on PROC MCMC, a two-step check is performed by first checking each chain separately and then checking whether the whole sampling process (consisting of multiple chains) has converged. However, it has been argued that besides a PSR that is close to 1, another condition should ideally be met before model estimates are computed from the chain(s): the number of independent draws from the posterior (i.e., the effective sample size; ESS) should be large [6,8,22]. Based on their simulations, Zitzmann and Hecht [6] suggested an ESS of at least 400 and ideally 1000 independent draws. Thus, in addition to the PSR—or as an alternative to it—the ESS may be selected as the stopping criterion in the macro. It is worth noting that there is a relationship between the two criteria, as demonstrated by Equation (10) in Zitzmann and Hecht [6]. This relationship allows for an approximate transformation of a specific value of the PSR into an ESS value, and vice versa, unless the autocorrelation for the samples is not large. In the case of large autocorrelations, the formula in [23] yields a better estimate of the ESS—which is why this formula is used in our macro. On the other hand, the ESS may not be very sensitive to differences between chain sequences and, therefore, provides an exact measure of the “true” effective sample size only if the burn-in phase is long enough. Thus, a combination of the PSR and the ESS criteria might be the best strategy.
2.2. The %automcmc Macro
In the following subsection, we provide a detailed description of the macro’s functionality, specifically focusing on the parameters that can be used with either default values or user-specified values. These parameters pertain to model estimation and customization of the output. Lastly, we demonstrate the application of the %automcmc macro through a series of examples.
2.2.1. Macro Parameters for Model Estimation
Two different stopping criteria may be applied that are related to one another, as noted in Section 2.1. The %automcmc macro uses the SAS %ESS autocall macro for postprocessing [9] with default settings to estimate the effective sample size for a given parameter estimate, taking into account the autocorrelation as proposed in [23]. The default stopping criterion is set to ESSconv = 1E3 meaning the effective sample size must be at least 1000 for each estimated parameter (for this recommendation, see [6]). The second stopping criterion, which uses the PSR with a default setting of PSRconv = 1.01, as suggested by Vehtari et al. [24], is satisfied when the PSR value for each estimated parameter is below the specified threshold. Either one of the stopping criteria, or both, can be ignored by setting the corresponding macro parameter to zero. If both stopping criteria are specified, which is the default setting, all the estimated parameters must satisfy both criteria. In many cases, users may need to modify only these two macro parameters.
For a single chain, the default setting applies the stopping criteria to two sequences of the chain. The first sequence, referred to as the burn-in iterations, is discarded to remove any potential influence from the initial starting values. The length of the burn-in sequence is determined by the biratio parameter, which is set to a default value of 0.50. To illustrate, consider a total chain length of 10,000 iterations. With the default biratio of 0.50, the first 5000 iterations are discarded as burn-in. The remaining iterations, from 5001 to 7500 and from 7501 to 10,000, are then used for assessing convergence using the PSR criterion. For estimating the ESS, the 5000 iterations from 5001 to 10,000 are used. Regarding the PSR, this procedure is identical to that applied in Mplus [7,8] for a single chain.
If any of the specified stopping criteria are not met for at least one parameter estimate, and the number of remaining iterations (after thinning, if specified in PROC MCMC) does not exceed the specified maximum (e.g., maxnmc = 1E4, defaulting to 10,000 iterations), PROC MCMC will be restarted. A new seed value is used, incremented by 1 from the previous PROC MCMC run’s seed value (if no seed is specified, SEED = 1 is used for the first start). Additionally, the starting values for all parameters are set based on the last iteration of the preceding PROC MCMC run. When burn-in iterations are defined in the PROC MCMC code using the NBI option, the respective number of iterations are discarded in the first PROC MCMC run (as those iterations are not included in the dataset generated by the PROC MCMC option OUTPOST). If the stopping criterion or criteria are not met and the procedure is restarted, the NBI option will automatically be set to zero. This means that no additional burn-in iterations will be employed in the subsequent PROC MCMC runs.
When multiple chains are specified (e.g., chains = 2, with the default being chains = 1), the chains are sequentially generated because PROC MCMC does not include the option for multiple chains. In this case, the specified stopping criteria are applied for each single chain. Finally, the ESS criterion (in case ESSconv is not set to 0) is applied to a combined chain consisting of all remaining chain sequences after discarding the initial burn-in iterations. Note that these chain sequences might be of different length, as the stopping criterion might be reached after different numbers of iterations in each chain. The PSR, when specified as a stopping criterion, is calculated based on these chain sequences from the different chains. In contrast to the processing of one or more single chains, however, no additional iterations will be added to the chains if the stopping criterion/criteria is/are not met. Vehtari et al. [24] suggested that at least four chains should be run by default, because “[m]ultiple chains are more to likely to reveal multimodality and poor adaptation or mixing” (p. 671).
In the case of multiple chains, starting values (also called initial values) are automatically generated using the PROC MCMC option INIT = RANDOM, except for the first chain where potentially user-specified starting values in the PROC MCMC code are used. It may happen that the generated starting values will lead to error messages of PROC MCMC and estimation will be stopped. In situations where the initial attempts to find acceptable starting values for the chains are unsuccessful, the procedure is restarted with a new seed in an attempt to generate usable starting values. However, there may be cases where even after multiple attempts with different seeds, suitable starting values cannot be found. In such situations, the process of sampling starting values is stopped after a user-specified number of procedure starts. The parameter maxsvloops (defaulting to 100) determines the maximum number of attempts allowed to find applicable starting values for all chains. When the maximum number of procedure starts is reached without finding usable starting values for all chains, the process of sampling starting values is terminated. One possible solution for addressing this issue could involve increasing the number of potential procedure starts by adjusting the parameter maxsvloops to a higher value (e.g., maxsvloops = 250). Another option is a two-step approach (see Section 3.3. for an example): in the first step, a modified model with more informative priors is used, which may help to avoid extreme starting values. The starting values generated for that model are automatically stored in datasets (_para1, _para2, … for chains 2, 3, ...; _para for chain 1) that can be used to provide starting values for the target model with the original priors in a second step by specifying svdat = yes (default: svdat = no). It should be noted that it is not possible to generate starting values with PROC MCMC if the GENERAL or DGENERAL function is used as a prior distribution.
2.2.2. Output Customization
Output customization in the context of applying the %automcmc macro refers to the ability to control what information is displayed in the SAS output window, SAS log, or stored as SAS datasets. The output that would be directly produced by the PROC MCMC command(s) is suppressed with the default setting output = no (but can be enabled by output = yes), because the focus is on the final results after the convergence criterion/criteria have been reached based on the specified chain sequence instead of only on the interim results. If the PROC MCMC code contains an ODS SELECT statement, this specific output will not be suppressed for the first start of PROC MCMC but in all following procedure starts. The final results are shown as default (results = yes) in the SAS output window and stored as a temporary SAS dataset named results in the work library as default (resultsdat = results) that includes all estimated parameters (including random effects and parameters for missing data) under the default setting outpostvar = _all_. It is also possible to restrict the estimated parameters in the specified output dataset to monitored parameters (including secondary parameters) as specified within the PROC MCMC code (e.g., by the MONITOR option in the PROC MCMC statement) by the option outpostvar = _parms_. The results are based on the chain sequence or—in the case of multiple chains—combined chain sequences (discarding burn-in iterations as specified by the biratio option), applying the SAS %SUMINT [9] autocall macro for postprocessing that calculates number of posterior draws (N), mean and standard deviation (M, SD), and highest posterior density (HPD) intervals for the specified alpha value (alpha = 0.05 as default).
It is also possible to request the PROC MCMC code that is generated by the %automcmc macro in the SAS log by the option PROCLOG = on (off as default). In this case, the starting values for the model parameters that are taken from the last iteration of the preceding PROC MCMC run are given in the lines between a BEGINCNST command and an ENDCNST command. A problematic issue can arise when the ARRAY option of PROC MCMC is used: sometimes, PROC MCMC stops with an error message (“ERROR: The value of a parameter in an array is modified. This is not allowed”.) when the ARRAY option is used in conjunction with BEGINCNST and ENDCNST to specify starting values. In such cases, the arrays must be replaced by the respective code that would be generated by PROC MCMC (for an example, see Section 3.4), or the analysis must be run on a single thread (NTHREADS = 1 in the PROC MCMC statement; SAS Technical Support, personal communication, 13 October 2022).
Another very important note refers to the use of double quotes in the PROC MCMC code that is not allowed when using the %automcmc macro. For instance, when the READ_ARRAY function is used in PROC MCMC and the column names are enclosed in double quotes, these must be replaced by single quotes.
3. Examples: Applying the %Automcmc Macro
In the following, we provide examples of item response theory (IRT) analysis using the %automcmc macro with SAS PROC MCMC [9]. The analyses were conducted on simulated data (IRTdat, see Appendix A) consisting of N = 250 observations and k = 10 items. The population model used was a one-parameter logistic (1PL) IRT model with the item discrimination parameter a set to 1. The item difficulties bj ranged from −0.9 to 0.9 with an interval of 0.2 between consecutive items. A second simulated dataset (IRT3pldat, see Appendix A) consisting of N = 250 observations was based on a three-parameter logistic (3PL) population model with aj and bj ranging from 0.80 to 1.25 and −0.9 to 0.9, respectively. The guessing parameters (cj) were all equal to 0.20. The analyses were performed using SAS 9.4 TS Level 1M6 on a Windows Version 1.0.19041 X64_10PRO platform.
We demonstrate the estimation of both the 1PL (Examples 1 to 3) and the 3PL (Example 4) model using PROC MCMC with a parameterization proposed by Stone and Zhu [16]. In this parameterization, item intercepts (dj) are used instead of item difficulties, and informative priors are specified for the item intercepts as dj~N(0, 1) and for the item discrimination parameter as a~logN(0, 1) in the 1PL model and aj~logN(0, 1) in the 3PL model. Example 1 showcases the estimation using a single chain, whereas Example 2 demonstrates the estimation using three chains.
Further, we show how starting values for multiple chains can be generated based on a model with more informative priors when the starting value generation with a target model with uninformative priors—item intercepts dj~N(0, 10,000), item discrimination a~logN(0, 6)—failed to lead to acceptable starting values (Example 3). In Example 4 we demonstrate the advantage of using the %automcmc macro in the case of a 3PL model. Finally, we show solutions to estimate a model when the ARRAY command of PROC MCMC led to an error message (Example 5).
The following section provides a step-by-step description of the five examples. We begin by presenting the target model coded in PROC MCMC. Then, we demonstrate how this code can be incorporated into the %automcmc macro to facilitate estimation with user-specified stopping criteria for the potential scale reduction (PSR) and/or effective sample size (ESS).
3.1. Example 1: 1PL Model with Informative Priors (Single Chain)
We begin with the target model as specified with PROC MCMC (Listing 1) with 5000 burn-in iterations (NBI option) and 25,000 iterations afterwards (NMC option), which are stored in the dataset ex1_2_out (OUTPOST option). The random number seed is set to 1000 (SEED option), and the number of hyperthreaded cores on the system is specified as the number of available threads (NTHREADS = −1). Regarding the output, the a and all bj parameters (b is specified as a vector by the ARRAY option) are requested by the MONITOR option.
| Listing 1: PROC MCMC Code for Example 1. |
| PROC MCMC DATA=IRTdat NBI=5000 NMC=25000 OUTPOST=ex1_2_out SEED=1000 NTHREADS=-1 MONITOR=(a b); ARRAY b [10]; ARRAY d [10]; ARRAY p [10]; PARMS a 1; PARMS d:0; PRIOR a:~LOGNORMAL(0, VAR=1); PRIOR d:~NORMAL(0, VAR=1); RANDOM theta~NORMAL(0, VAR=1) SUBJECT=person; DO j=1 TO 10; p[j]=LOGISTIC(a*theta-d[j]); b[j]=d[j]/a; END; MODEL item01~BINARY(p1); MODEL item02~BINARY(p2); MODEL item03~BINARY(p3); MODEL item04~BINARY(p4); MODEL item05~BINARY(p5); MODEL item06~BINARY(p6); MODEL item07~BINARY(p7); MODEL item08~BINARY(p8); MODEL item09~BINARY(p9); MODEL item10~BINARY(p10); RUN; |
To estimate this model with the %automcmc macro, the complete code (note that the “RUN;” statement at the end must not be included!) is simply inserted in a macro called proc_mcmc, as shown in Listing 2, followed by the execution of the %automcmc macro that runs the code. If the specified stopping criteria (ESSconv = 1000, PSRconv = 1.01) are not fulfilled, the procedure will be started again—as long as the total number of iterations is smaller than 106 (as specified by maxnmc = 1E6).
| Listing 2: Execution of PROC MCMC Code (Example 1) with the %automcmc Macro. |
| %MACRO proc_mcmc; PROC MCMC DATA=IRTdat NBI=5000 NMC=25000 OUTPOST=ex1_2_out SEED=1000 NTHREADS=-1 MONITOR=(a b); ARRAY b [10]; ARRAY d [10]; ARRAY p [10]; PARMS a 1; PARMS d:0; PRIOR a:~LOGNORMAL(0, VAR=1); PRIOR d:~NORMAL(0, VAR=1); RANDOM theta~NORMAL(0, VAR=1) SUBJECT=person; DO j=1 TO 10; p[j]=LOGISTIC(a*theta-d[j]); b[j]=d[j]/a; END; MODEL item01~BINARY(p1); MODEL item02~BINARY(p2); MODEL item03~BINARY(p3); MODEL item04~BINARY(p4); MODEL item05~BINARY(p5); MODEL item06~BINARY(p6); MODEL item07~BINARY(p7); MODEL item08~BINARY(p8); MODEL item09~BINARY(p9); MODEL item10~BINARY(p10); %MEND; %automcmc(ESSconv=1000, PSRconv=1.01, maxnmc=1E6, output=no, PROCLOG=on); |
After satisfying the stopping criteria, which took seven restarts in this example, the final results for the combined chain sequences are presented in the output window. The output includes the ESS results shown in Figure 1, the PSR results displayed in Figure 2, and the posterior summaries, which include the highest posterior density (HPD) intervals, shown in Figure 3. As can be seen in Figure 3, the final results are based on 87,500 iterations, namely the second half (biratio = 0.50 as default) of the total number of iterations, which is given by 25,000 (NMC option) × 7 (procedure restarts) = 175,000 that are stored in the specified data set ex1_2_out. As the PROCLOG option was set to “on”, the PROC MCMC code that was executed—and that is slightly modified at each step (e.g., starting values, burn-in iterations set to zero from step two on, seed incremented by one)—was listed in the SAS log.
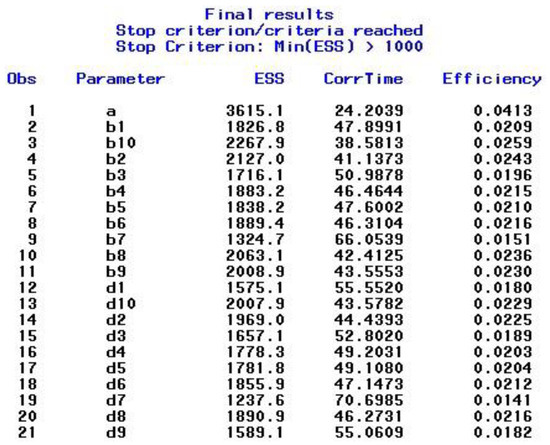
Figure 1.
Example 1—ESS for the Model Parameters.
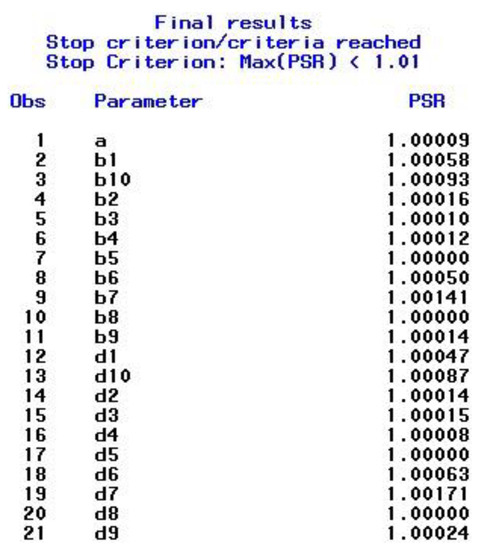
Figure 2.
Example 1—Output for Specified Parameter Estimates (PSR).
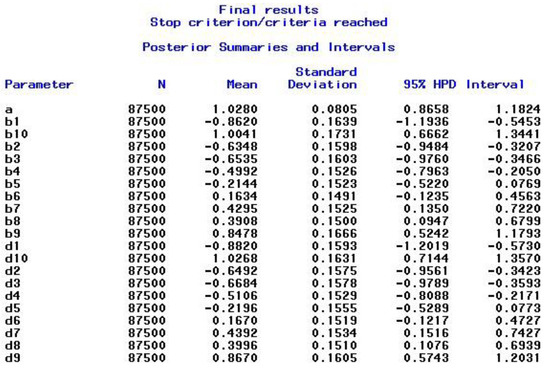
Figure 3.
Example 1—Output for Posterior Summaries and Intervals.
In many typical applications, the estimation process using the %automcmc macro will be straightforward and simple, as demonstrated in the previous example. However, there are cases where the estimation process can become more complex and require additional attention from the user. This can occur when multiple chains are used or when the PROC MCMC code includes ARRAY statements.
3.2. Example 2: 1PL Model with Informative Priors (Multiple Chains)
In Example 1, we estimated the model using a single chain. In this new scenario, Example 2, we re-estimate the model using three chains instead of just one (Listing 3). The first chain in Example 2 produces identical results to those obtained in Example 1. This outcome is expected because the same starting values (specified within PROC MCMC in the PARMS statements), the random number seed, and other settings were used. The results of the second and third chains differed because they were initiated with different sets of automatically generated starting values. For the second chain, the stopping criteria were reached after five restarts (25,000 × 5 = 125,000 iterations in total after burn-in) and for the third chain the stopping criteria were fulfilled after six restarts (25,000 × 6 = 150,000 iterations). For each chain, the results are shown in the output window (e.g., results of the third chain in Figure 4), and all iterations are stored in the specified dataset (here, OUTPOST=Ex1_2_out), followed by an underscore and the number of the chain (e.g., Ex1_2_out_1 for chain 1). The final results of the combined chain sequences (second half of each chain: 87,500, 62,500, and 75,000 for chains 1, 2, and 3) also reached the stopping criteria, and the posterior output was based on 225,000 iterations.
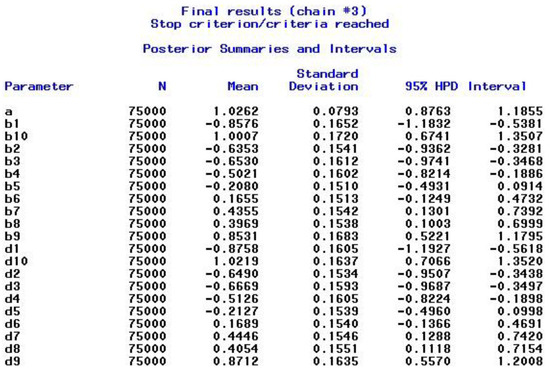
Figure 4.
Example 2—Output for Posterior Summaries and Intervals.
| Listing 3: Estimation of PROC MCMC Code (Example 2) with the %automcmc Macro. |
| %automcmc(ESSconv=1000, PSRconv=1.01, maxnmc=1E6, output=no, chains=3); |
3.3. Example 3: 1PL Model with Uninformative Priors (Multiple Chains)
In Example 3, we aimed at estimating the identical model as in Example 1 except that the priors differed by larger variances–PRIOR a:~LOGNORMAL (0, VAR = 5); PRIOR d:~NORMAL (0, VAR = 10000). In this case, even 100 attempts to find sets of starting values (with default setting maxsvloops = 100) did not lead to acceptable sets for chains 2 and 3 (with respective error messages in the SAS log). One way to handle this problem is to increase the maxsvloops macro parameter to, say, 1000. But often, a more promising approach is to estimate the starting value sets based on a model with (slightly) more informative priors (Listing 4)—here, PRIOR a:~LOGNORMAL (0, VAR = 2); PRIOR d:~NORMAL (0, VAR = 100)—and set the number of burn-in iterations to zero (NBI = 0) and the number of iterations to 1 (NMC = 1). The resulting starting values are stored in the datasets _para1 (chain 2) and _para2 (chain 3) and can be used in a subsequent analysis with the macro parameter svdat = yes after respecifying the %proc_mcmc macro to refer to the PROC MCMC code of the target model (Listing 5).
| Listing 4: Generating Starting Values (Example 3) with the %automcmc Macro. |
| %MACRO proc_mcmc; PROC MCMC DATA=IRTdat NBI=0 NMC=1 OUTPOST=ex3_out SEED=1000 NTHREADS=-1 MONITOR=(a b); ARRAY b [10]; ARRAY d [10]; ARRAY p [10]; PARMS a 1; PARMS d:0; PRIOR a:~LOGNORMAL(0, VAR=2); PRIOR d:~NORMAL(0, VAR=100); RANDOM theta~NORMAL(0, VAR=1) SUBJECT=person; DO j=1 TO 10; p[j]=LOGISTIC(a*theta-d[j]); b[j]=d[j]/a; END; MODEL item01~BINARY(p1); MODEL item02~BINARY(p2); MODEL item03~BINARY(p3); MODEL item04~BINARY(p4); MODEL item05~BINARY(p5); MODEL item06~BINARY(p6); MODEL item07~BINARY(p7); MODEL item08~BINARY(p8); MODEL item09~BINARY(p9); MODEL item10~BINARY(p10); %MEND; %automcmc(ESSconv=0, PSRconv=0, maxnmc=1E6, biratio=0, output=no, results=no, chains=3); |
| Listing 5: Estimation of PROC MCMC Code (Example 3) with the %automcmc Macro and Given Starting Values. |
| %MACRO proc_mcmc; PROC MCMC DATA=IRTdat NBI=5000 NMC=25000 OUTPOST=ex3_out SEED=1000 NTHREADS=-1 MONITOR=(a b); ARRAY b [10]; ARRAY d [10]; ARRAY p [10]; PARMS a 1; PARMS d:0; PRIOR a:~LOGNORMAL(0, VAR=5); PRIOR d:~NORMAL(0, VAR=10000); RANDOM theta~NORMAL(0, VAR=1) SUBJECT=person; DO j=1 TO 10; p[j]=LOGISTIC(a*theta-d[j]); b[j]=d[j]/a; END; MODEL item01~BINARY(p1); MODEL item02~BINARY(p2); MODEL item03~BINARY(p3); MODEL item04~BINARY(p4); MODEL item05~BINARY(p5); MODEL item06~BINARY(p6); MODEL item07~BINARY(p7); MODEL item08~BINARY(p8); MODEL item09~BINARY(p9); MODEL item10~BINARY(p10); %MEND; %automcmc(ESSconv=1000, PSRconv=1.01, maxnmc=1E6, output=no, chains=3, svdat=yes); |
3.4. Example 4: 3PL Model with Informative Priors (Single Chain)
In Example 4, we estimated a 3PL model, a type of model that is known to be especially prone to convergence issues [25]. In the first step, we estimated the model as shown in Listing 6—which we here refer to as the “standard” estimation—with 5000 burn-in iterations followed by 25,000 iterations used for parameter estimation. We then estimated the same model using our %automcmc macro with standard settings (ESSconv = 1000, PSRconv = 1.01, maxnmc = 1E6). Finally, we applied a “reference” estimation, which was identical to the “standard” estimation (Listing 6) except for the number of burn-in iterations (NBI = 50,000) and the number of iterations after burn-in (NMC = 500,000). Due to the large number of iterations, the Monte Carlo error should play no significant role. Therefore, the estimates from this approach were taken as a reference for the “standard” and the %automcmc approach. The largest absolute differences between both approaches compared with the reference approach were found for parameter estimate a6. Their posterior means were 0.07 (“standard” approach) and 0.05 (%automcmc approach) larger than in the reference approach. Even more pronounced were the differences in the posterior standard deviations (1.50, 1.25, and 1.23 for the “standard”, the %automcmc, and the reference approach, respectively) as well as in the 95% HPD credible interval limits with maximum absolute deviations from the estimates of the reference model ranging from 0.11 (%automcmc approach, upper limit) to 0.52 (“standard” approach, upper limit). A closer look at the results revealed that the a6 estimate had the lowest ESS in all approaches (204, 1058, and 4913 for the “standard”, the %automcmc, and the reference approach, respectively). It might be concluded that even a rather large number of iterations as used in the “standard” approach (25,000 iterations) may not guarantee a precise approximation in specific cases, indicating that more iterations may be needed (e.g., the %automcmc macro with default settings used 87,500 iterations).
| Listing 6: PROC MCMC Code for Example 4. |
| PROC MCMC DATA=IRT3pldat NBI=5000 NMC=25000 OUTPOST=ex4_out SEED=1000 NTHREADS=-1 MONITOR=(a b c); ARRAY a [10]; ARRAY b [10]; ARRAY c [10]; ARRAY d [10]; ARRAY p [10]; PARMS a1 1 c1 0.2 d1 0; PARMS a2 1 c2 0.2 d2 0; PARMS a3 1 c3 0.2 d3 0; PARMS a4 1 c4 0.2 d4 0; PARMS a5 1 c5 0.2 d5 0; PARMS a6 1 c6 0.2 d6 0; PARMS a7 1 c7 0.2 d7 0; PARMS a8 1 c8 0.2 d8 0; PARMS a9 1 c9 0.2 d9 0; PARMS a10 1 c10 0.2 d10 0; PRIOR a:~LOGNORMAL(0, VAR=1); PRIOR c:~BETA(5, 20); PRIOR d:~NORMAL(0, VAR=1); RANDOM theta~NORMAL(0, VAR=1) SUBJECT=person; DO j=1 TO 10; p[j]=c[j]+(1-c[j])*LOGISTIC(a[j]*theta-d[j]); b[j]=d[j]/a[j]; END; MODEL item01~BINARY(p1); MODEL item02~BINARY(p2); MODEL item03~BINARY(p3); MODEL item04~BINARY(p4); MODEL item05~BINARY(p5); MODEL item06~BINARY(p6); MODEL item07~BINARY(p7); MODEL item08~BINARY(p8); MODEL item09~BINARY(p9); MODEL item10~BINARY(p10); RUN; |
3.5. Example 5: 1PL Model with Hierarchical Priors Using Arrays
As mentioned above, in some cases, PROC MCMC does not work when ARRAY statements are applied in conjunction with BEGINCNST and ENDCNST to specify starting values together with multithreading (e.g., the number of hyperthreaded cores on the system: NTHREADS = −1). In Listing 7, we give an example analog to the model proposed in [16] of a 1PL model with a hierarchical prior for the hyperparameters of the prior distribution of the bj parameters, namely mub and varb for the mean and the variance of the normal priors, but—in contrast to [16]—applying multithreading and assigning starting values with BEGINCNST and ENDCNST. At least on our SAS for Windows system, this model could not be estimated and led to an error message (“ERROR: The value of a parameter in an array is modified. This is not allowed”.). One option to estimate this model with the %automcmc macro would be to simply run it on a single thread by deleting NTHREADS = −1 or, equivalently, specifying NTHREADS = 1 (which is the default in PROC MCMC). However, this might, in general, be less time-efficient (see, e.g., [26,27], who made the case for more efficient computations in Bayesian modeling). Therefore, an alternative model specification where the framed lines of code referring to arrays in Listing 7 is resolved to “array-free” code, as in Listing 8.
| Listing 7: PROC MCMC Code for Example 5. |
| PROC MCMC DATA=IRTdat NBI=5000 NMC=25000 OUTPOST=ex4_out SEED=1000 NTHREADS=-1; ARRAYb[10];ARRAYp[10]; PARMS a; PARMS b:; PARMS mub varb; PRIORb:~NORMAL(mub, VAR=varb); PRIOR mub~UNIFORM(-6, 6); PRIOR varb~IGAMMA(.01, SCALE=.01); PRIOR a~LOGNORMAL(0, VAR=1); RANDOM theta~NORMAL(0, VAR=1) SUBJECT=person; DOj=1TO10; p[j]=LOGISTIC(a*theta-b[j]);END; MODEL item01~BINARY(p1); MODEL item02~BINARY(p2); MODEL item03~BINARY(p3); MODEL item04~BINARY(p4); MODEL item05~BINARY(p5); MODEL item06~BINARY(p6); MODEL item07~BINARY(p7); MODEL item08~BINARY(p8); MODEL item09~BINARY(p9); MODEL item10~BINARY(p10); BEGINCNST; mub=0; varb=1; a=1; b1=0; b2=0; b3=0; b4=0; b5=0; b6=0; b7=0; b8=0; b9=0; b10=0; ENDCNST; RUN; |
| Listing 8: PROC MCMC Code for Example 5 Without ARRAY Statements. |
| PROC MCMC DATA=IRTdat NBI=5000 NMC=25000 OUTPOST=ex4_out SEED=1000 NTHREADS=-1; PARMS a; PARMS b1-b10; PARMS mub varb; PRIORb1~NORMAL(mub, VAR=varb); PRIORb2~NORMAL(mub, VAR=varb); PRIORb3~NORMAL(mub, VAR=varb); PRIORb4~NORMAL(mub, VAR=varb); PRIORb5~NORMAL(mub, VAR=varb); PRIORb6~NORMAL(mub, VAR=varb); PRIORb7~NORMAL(mub, VAR=varb); PRIORb8~NORMAL(mub, VAR=varb); PRIORb9~NORMAL(mub, VAR=varb); PRIORb10~NORMAL(mub, VAR=varb); PRIOR mub~UNIFORM(-6, 6); PRIOR varb~IGAMMA(.01, SCALE=.01); PRIOR a~LOGNORMAL(0, VAR=1); RANDOM theta~NORMAL(0, VAR=1) SUBJECT=person; p1=LOGISTIC(a*theta-b1); p2=LOGISTIC(a*theta-b2); p3=LOGISTIC(a*theta-b3); p4=LOGISTIC(a*theta-b4); p5=LOGISTIC(a*theta-b5); p6=LOGISTIC(a*theta-b6); p7=LOGISTIC(a*theta-b7); p8=LOGISTIC(a*theta-b8); p9=LOGISTIC(a*theta-b9); p10=LOGISTIc(a*theta-b10); MODEL item01~BINARY(p1); MODEL item02~BINARY(p2); MODEL item03~BINARY(p3); MODEL item04~BINARY(p4); MODEL item05~BINARY(p5); MODEL item06~BINARY(p6); MODEL item07~BINARY(p7); MODEL item08~BINARY(p8); MODEL item09~BINARY(p9); MODEL item10~BINARY(p10); BEGINCNST; mub=0; varb=1; a=1; b1=0; b2=0; b3=0; b4=0; b5=0; b6=0; b7=0; b8=0; b9=0; b10=0; ENDCNST; RUN; |
4. Automated Stopping in Related Software
Other software, too, provide the possibility to automate convergence. For example, Mplus [7] offers it as the default. Mplus assesses convergence by routinely checking if a specified value for the PSR has been achieved [8]. This value may be specified by the user. In a nutshell, the Mplus algorithm can be stated as follows: (1) iteratively sample from each parameter; (2) after every 100th iteration, discard the first half (i.e., burn-in); (3) compute the PSR for each parameter from the remaining iterations. If all PSR values fall below the prespecified maximum value, stop sampling. Otherwise, continue with MCMC.
Whereas the PSR criterion can be specified, a value for the ESS cannot be specified directly, which led Zitzmann and Hecht [6,8] to propose a workaround that takes advantage of the relationship between the ESS and the PSR, which becomes apparent when the PSR and the ESS are both computed by analysis of variance (ANOVA) estimates. This means that not only the PSR but also the ESS can be used as stopping criteria in Mplus.
Hecht et al. [28] equipped JAGS [29] with a very similar procedure in order to allow for automated stopping. The algorithm is detailed as a flow chart in their Figure 2, but it has not been published in the form of a user-friendly function. However, interested readers can find the program code in the Supplementary Materials and may use it in their own analyses with JAGS.
To the best of our knowledge, automated routines are not yet available in BUGS or Stan. As these software programs are also general-purpose samplers and thus similar to JAGS, Hecht et al.’s [28] automated routine might be easily adapted to them. As Stan in particular is being further developed in rapid steps, there is a real chance that this software will offer such a routine in the nearer future.
5. Discussion
In Bayesian modeling with Markov chain Monte Carlo (MCMC), determining chain convergence through the manual inspection of trace plots or stopping criteria can be challenging. Existing Bayesian software often lacks user-friendly automated routines for applying stopping criteria. Therefore, we introduced the %automcmc macro, built upon PROC MCMC in SAS. This macro simplifies the sampling process by automatically continuing sampling until a user-defined stopping criterion is met for the chain(s).
The macro determines when to stop by using two statistics as stopping criteria: the PSR and the ESS, which are implemented in a specific way. However, different versions of these statistics exist, and alternative statistics have been proposed in the literature. For example, Vehtari, Gelman, Carpenter, and Bürkner [24] proposed a refined PSR, which is not yet available in the macro and which might outperform the implemented one. It is interesting to note that Zitzmann, Weirich, and Hecht [8] found that different statistics tended to yield different results, a finding that certainly deserves more attention in future research. Based on the empirical findings regarding the relative performance of these statistics, the macro could be modified by refining the implemented ones or replacing them with better performing statistics. But, as noted in Section 4, the options to specify stopping criteria seem to be more restricted (if available at all) in related software compared with those in our macro.
It should be noted that a comparison of different Bayesian general-purpose software packages was beyond the scope of this article. It would nevertheless be interesting to provide an overview about the pros and cons of available packages with regard to flexibility of modeling, computational efficiency, and user-friendliness for different classes of Bayesian models, which is a topic of future research. With a focus on Bayesian multilevel modeling, such an overview—including general-purpose as well as more specialized Bayesian software for multilevel modeling—can be found in Mai and Zhang [11] (see also [30]).
By offering automated support for Bayesian analyses, our %automcmc macro serves the purpose of facilitating the application of SAS and PROC MCMC in Bayesian modeling. We hope that this macro will contribute to a widespread use of PROC MCMC, thereby promoting the growth of Bayesian methodology in various fields.
Supplementary Materials
The %automcmc macro can be downloaded at: https://doi.org/10.17605/OSF.IO/6YRJF, accessed on 6 July 2023.
Author Contributions
Conceptualization, W.W. and S.Z.; software, W.W.; validation, W.W.; investigation, W.W.; writing—original draft preparation, W.W.; writing—review and editing, W.W., M.H., and S.Z.; visualization, W.W.; supervision, S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The examples including the respective data sets are available in the Appendix A.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The examples in Section 3 for illustrating the use of the %automcmc macro and the simulated data were based on the following SAS job:
- Listing A1: SAS Code for IRT Examples.* Population model: 1 PL (a = 1, b_j = -0.9, -0.7, ... 0.9);DATA IRTdat;ARRAY item(10) item01-item10;DO person=1 TO 250;theta=NORMAL(12345);DO j=1 TO 10;item(j)=(LOGISTIC(1*(theta-(-0.9+(j-1)/5)))>RANUNI(12345));END;OUTPUT;END;DROP theta j;RUN;* Population model: 1 PL (a_j = 0.80, 0.85, ... 1.25, b_j = -0.9, -0.7, ... 0.9);* guessing: c_j = .20;DATA IRT3pldat;ARRAY item(10) item01-item10;DO person=1 TO 250;theta=NORMAL(12345);DO j=1 TO 10;item(j)=(.20+.80*LOGISTIC((0.75+0.05*j)*(theta-(-0.9+(j-1)/5)))>RANUNI(12345));END;OUTPUT;END;DROP theta j;RUN;**********************;* Examples 1 + 2 *;* informative priors *;**********************;* Model parameterizing with intercepts d_j (instead of difficulties b_j) to improve mixing (see Stone & Zhu, 2015);%MACRO proc_mcmc;PROC MCMC DATA=IRTdat NBI=5000 NMC=25000 OUTPOST=ex1_2_out SEED=1000 NTHREADS=-1 MONITOR=(a b);ARRAY b[10]; ARRAY d[10]; ARRAY p[10];PARMS a 1; PARMS d:0;PRIOR a:~LOGNORMAL(0, VAR=1); PRIOR d:~NORMAL(0, VAR=1);RANDOM theta~NORMAL(0, VAR=1) SUBJECT=person;DO j=1 TO 10; p[j]=LOGISTIC(a*theta-d[j]); b[j]=d[j]/a; END;MODEL item01~BINARY(p1);MODEL item02~BINARY(p2);MODEL item03~BINARY(p3);MODEL item04~BINARY(p4);MODEL item05~BINARY(p5);MODEL item06~BINARY(p6);MODEL item07~BINARY(p7);MODEL item08~BINARY(p8);MODEL item09~BINARY(p9);MODEL item10~BINARY(p10);%MEND;* Example 1: informative priors, single chain;%automcmc(ESSconv=1000, PSRconv=1.01, maxnmc=1E6, output=no, PROCLOG=on);* Example 2: informative priors, 3 chains;%automcmc(ESSconv=1000, PSRconv=1.01, maxnmc=1E6, output=no, chains=3);************************;* Example 3 *;* uninformative priors *;************************;* Generating starting values based on model with more informative priors (only 1 iteration necessary);%MACRO proc_mcmc;PROC MCMC DATA=IRTdat NBI=0 NMC=1 OUTPOST=ex3_out SEED=1000 NTHREADS=-1 MONITOR=(a b);ARRAY b[10]; ARRAY d[10]; ARRAY p[10];PARMS a 1; PARMS d:0;PRIOR a:~LOGNORMAL(0, VAR=2); PRIOR d:~NORMAL(0, VAR=100);RANDOM theta~NORMAL(0, VAR=1) SUBJECT=person;DO j=1 TO 10; p[j]=LOGISTIC(a*theta-d[j]); b[j]=d[j]/a; END;MODEL item01~BINARY(p1);MODEL item02~BINARY(p2);MODEL item03~BINARY(p3);MODEL item04~BINARY(p4);MODEL item05~BINARY(p5);MODEL item06~BINARY(p6);MODEL item07~BINARY(p7);MODEL item08~BINARY(p8);MODEL item09~BINARY(p9);MODEL item10~BINARY(p10);%MEND;* Example 3: generating starting values, 3 chains (no convergence criteria applied);%automcmc(ESSconv=0, PSRconv=0, maxnmc=1E6, biratio=0, output=no, results=no, chains=3);* apply original target model with uninformative priors (based on generated starting values);%MACRO proc_mcmc;PROC MCMC DATA=IRTdat NBI=5000 NMC=25000 OUTPOST=ex3_out SEED=1000 NTHREADS=-1 MONITOR=(a b);ARRAY b[10]; ARRAY d[10]; ARRAY p[10];PARMS a 1; PARMS d:0;PRIOR a:~LOGNORMAL(0, VAR=5); PRIOR d:~NORMAL(0, VAR=10000);RANDOM theta~NORMAL(0, VAR=1) SUBJECT=person;DO j=1 TO 10; p[j]=LOGISTIC(a*theta-d[j]); b[j]=d[j]/a; END;MODEL item01~BINARY(p1);MODEL item02~BINARY(p2);MODEL item03~BINARY(p3);MODEL item04~BINARY(p4);MODEL item05~BINARY(p5);MODEL item06~BINARY(p6);MODEL item07~BINARY(p7);MODEL item08~BINARY(p8);MODEL item09~BINARY(p9);MODEL item10~BINARY(p10);%MEND;* 3 chains;%automcmc(ESSconv=1000, PSRconv=1.01, maxnmc=1E6, output=no, chains=3, svdat=yes);
References
- van de Schoot, R.; Winter, S.D.; Ryan, O.; Zondervan-Zwijnenburg, M.; Depaoli, S. A systematic review of Bayesian articles in psychology: The last 25 years. Psychol. Methods 2017, 22, 217–239. [Google Scholar] [CrossRef]
- Muthén, B.; Asparouhov, T. Bayesian structural equation modeling: A more flexible representation of substantive theory. Psychol. Methods 2012, 17, 313–335. [Google Scholar] [CrossRef]
- Depaoli, S.; Clifton, J.P. A Bayesian approach to multilevel structural equation modeling with continuous and dichotomous outcomes. Struct. Equ. Model. A Multidiscip. J. 2015, 22, 327–351. [Google Scholar] [CrossRef]
- Zitzmann, S.; Lüdtke, O.; Robitzsch, A.; Hecht, M. On the performance of Bayesian approaches in small samples: A comment on Smid, McNeish, Miocevic, and van de Schoot (2020). Struct. Equ. Model. A Multidiscip. J. 2021, 28, 40–50. [Google Scholar] [CrossRef]
- Geyer, C.J. Practical Markov chain Monte Carlo. Stat. Sci. 1992, 7, 473–483. [Google Scholar] [CrossRef]
- Zitzmann, S.; Hecht, M. Going beyond convergence in Bayesian estimation: Why precision matters too and how to assess it. Struct. Equ. Model. 2019, 26, 646–661. [Google Scholar] [CrossRef]
- Muthén, L.K.; Muthén, B.O. Mplus User’s Guide, 8th ed.; Muthén & Muthén: Los Angeles, CA, USA, 1998–2017. [Google Scholar]
- Zitzmann, S.; Weirich, S.; Hecht, M. Using the effective sample size as the stopping criterion in Markov chain Monte Carlo with the Bayes module in Mplus. Psych 2021, 3, 336–347. [Google Scholar] [CrossRef]
- SAS Institute Inc. SAS/STAT® 15.1 User’s Guide; SAS Institute Inc.: Cary, NC, USA, 2018. [Google Scholar]
- Ames, A.J.; Samonte, K. Using SAS PROC MCMC for item response theory models. Educ. Psychol. Meas. 2015, 75, 585–609. [Google Scholar] [CrossRef]
- Mai, Y.; Zhang, Z. Software packages for Bayesian multilevel modeling. Struct. Equ. Model. A Multidiscip. J. 2018, 25, 650–658. [Google Scholar] [CrossRef]
- Moeyaert, M.; Rindskopf, D.; Onghena, P.; Van den Noortgate, W. Multilevel modeling of single-case data: A comparison of maximum likelihood and Bayesian estimation. Psychol. Methods 2017, 22, 760–778. [Google Scholar] [CrossRef] [PubMed]
- Miočević, M.; Gonzalez, O.; Valente, M.J.; MacKinnon, D.P. A tutorial in Bayesian potential outcomes mediation analysis. Struct. Equ. Model. A Multidiscip. J. 2018, 25, 121–136. [Google Scholar] [CrossRef] [PubMed]
- Wurpts, I.C.; Miočević, M.; MacKinnon, D.P. Sequential Bayesian data synthesis for mediation and regression analysis. Prev. Sci. 2022, 23, 378–389. [Google Scholar] [CrossRef] [PubMed]
- Leventhal, B.C.; Stone, C.A. Bayesian analysis of multidimensional item response theory models: A discussion and illustration of three response style models. Meas. Interdiscip. Res. Perspect. 2018, 16, 114–128. [Google Scholar] [CrossRef]
- Stone, C.A.; Zhu, X. Bayesian Analysis of Item Response Theory Models Using SAS; SAS Institute Inc.: Cary, NC, USA, 2015. [Google Scholar]
- Austin, P.C.; Lee, D.S.; Leckie, G. Comparing a multivariate response Bayesian random effects logistic regression model with a latent variable item response theory model for provider profiling on multiple binary indicators simultaneously. Stat. Med. 2020, 39, 1390–1406. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z. Modeling error distributions of growth curve models through Bayesian methods. Behav. Res. 2016, 48, 427–444. [Google Scholar] [CrossRef]
- McNeish, D. Fitting residual error structures for growth models in SAS PROC MCMC. Educ. Psychol. Meas. 2017, 77, 587–612. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Asparouhov, T.; Muthén, B. Bayesian analysis using Mplus: Technical implementation (Version 4). 2023. Available online: http://www.statmodel.com/download/Bayes2.pdf (accessed on 25 August 2023).
- Link, W.A.; Eaton, M.J. On thinning of chains in MCMC. Methods Ecol. Evol. 2012, 3, 112–115. [Google Scholar] [CrossRef]
- Kass, R.E.; Carlin, B.P.; Gelman, A.; Neal, R.M. Markov Chain Monte Carlo in practice: A roundtable discussion. Am. Stat. 1998, 52, 93–100. [Google Scholar] [CrossRef]
- Vehtari, A.; Gelman, A.; Simpson, D.; Carpenter, B.; Bürkner, P.-C. Rank-normalization, folding, and localization: An improved R for assessing convergence of MCMC (with discussion). Bayesian Anal. 2021, 16, 667–718. [Google Scholar] [CrossRef]
- de Ayala, R.J. The Theory and Practice of Item Response Theory; The Guilford Press: New York, NY, USA, 2009. [Google Scholar]
- Zitzmann, S. A computationally more efficient and more accurate stepwise approach for correcting for sampling error and measurement error. Multivar. Behav. Res. 2018, 53, 612–632. [Google Scholar] [CrossRef] [PubMed]
- Hecht, M.; Zitzmann, S. A computationally more efficient Bayesian approach for estimating continuous-time models. Struct. Equ. Model. A Multidiscip. J. 2020, 27, 829–840. [Google Scholar] [CrossRef]
- Hecht, M.; Gische, C.; Vogel, D.; Zitzmann, S. Integrating out nuisance parameters for computationally more efficient Bayesian estimation—An illustration and tutorial. Struct. Equ. Model. A Multidiscip. J. 2020, 27, 483–493. [Google Scholar] [CrossRef]
- Plummer, M. JAGS: Just another Gibbs SAMPLER (Version 4.3.1). Available online: https://sourceforge.net/projects/mcmc-jags/ (accessed on 16 May 2023).
- Hecht, M.; Weirich, S.; Zitzmann, S. Comparing the MCMC efficiency of JAGS and Stan for the multi-level intercept-only model in the covariance- and mean-based and classic parametrization. Psych 2021, 3, 751–779. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).