Evaluating the Effect of Planned Missing Designs in Structural Equation Model Fit Measures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Planned Missing Design
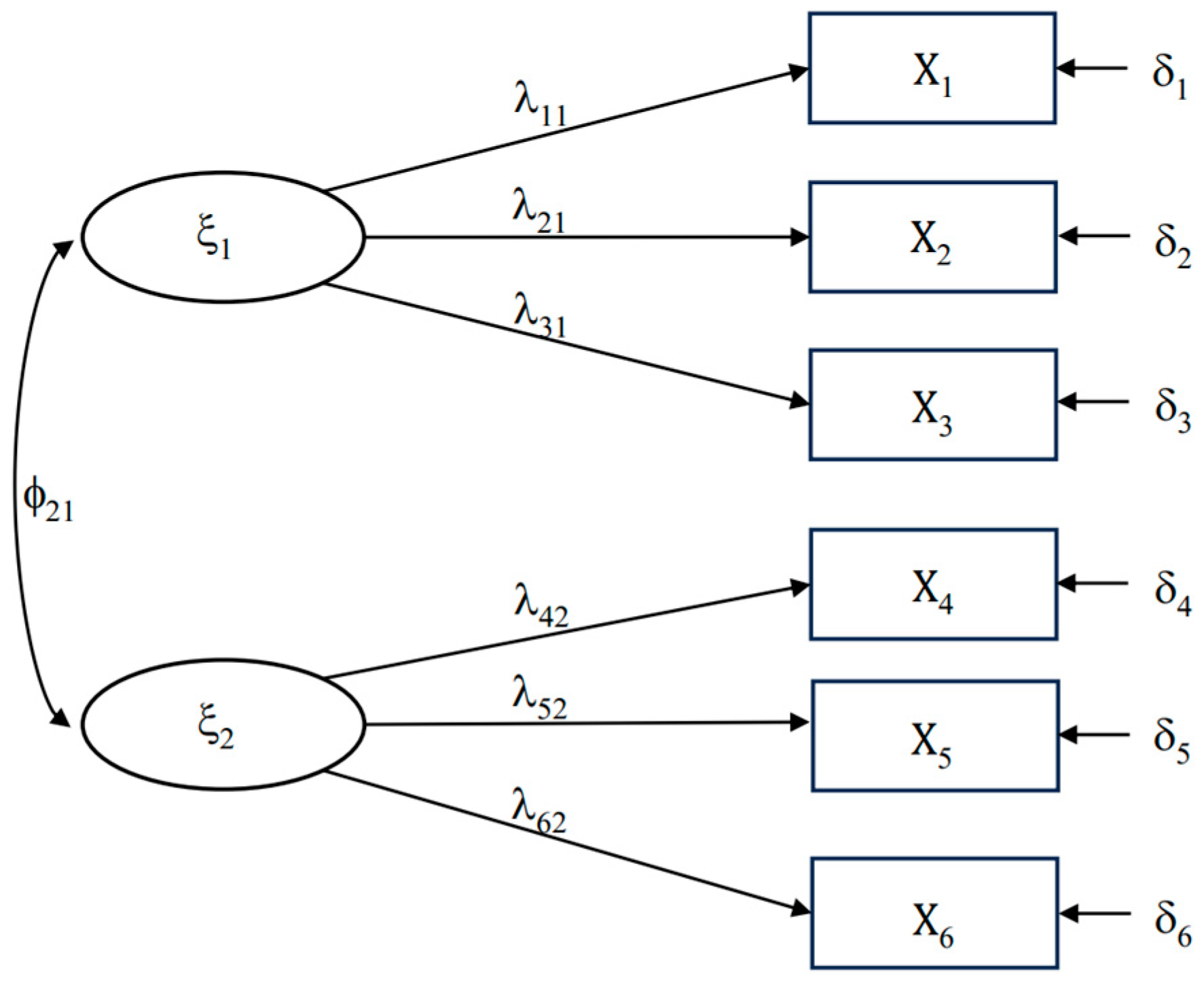
2.2. Structural Equation Model
2.3. Fit Measures
2.4. Simulation Conditions
3. Results
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Graham, J.; Taylor, B.; Olchowski, A.; Cumsville, P. Planned missing data designs in psychological research. Psychol. Methods 2006, 11, 323–343. [Google Scholar] [CrossRef]
- Graham, J.; Hofer, S.; Mackinnon, D. Maximizing the usefulness of data obtained with planned missing value patterns: An application of maximum likelihood procedures. Multivar. Behav. Res. 1996, 31, 197–218. [Google Scholar] [CrossRef] [PubMed]
- McArdle, J.J. Structural factor analysis experiments with incomplete data. Multivar. Behav. Res. 1994, 29, 409–454. [Google Scholar] [CrossRef] [PubMed]
- Raghunathan, T.; Grizzle, J. A Split Questionnaire Survey Design. J. Am. Stat. Assoc. 1995, 90, 54–63. [Google Scholar] [CrossRef]
- Enders, C.K. Applied Missing Data; The Guilford Press: New York, NY, USA, 2010; pp. 21–36. [Google Scholar]
- Jia, F.; Moore, E.W.G.; Kinai, R.; Crowe, K.S.; Schoemann, A.M.; Little, T. Planned missing data designs with small sample sizes: How small is too small? Int. J. Behav. Dev. 2014, 38, 435–452. [Google Scholar] [CrossRef]
- Moore, E.W.G.; Lang, K.M.; Grandfield, E.M. Maximizing data quality and shortening survey time: Three-form planned missing data survey design. Psychol. Sport Exerc. 2020, 51, 1–12. [Google Scholar] [CrossRef]
- Bandalous, D.L.; Finney, S.J. Factor analysis: Exploratory and confirmatory. In The Reviewer’s Guide to Quantitative Methods in the Social Sciences; Hancock, G.R., Mueller, R.O., Eds.; Routledge: New York, NY, USA, 2010; pp. 109–130. [Google Scholar] [CrossRef]
- Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E.; Tatham, R.L. Multivariate Data Analysis, 6th ed.; Pearson: Columbus, OH, USA, 2006; pp. 426–461. [Google Scholar]
- Nye, C.D. Reviewer Resources: Confirmatory Factor Analysis. Organ. Res. Methods 2022. online publishing. [Google Scholar] [CrossRef]
- Schumacker, R.E.; Lomax, R.G. A Beginner’s Guide to Structural Equation Modelling, 3rd ed.; Routledge/Taylor & Francis Group: New York, NY, USA, 2010. [Google Scholar]
- Iacobucci, D. Structural equation modelling: Fit indices, sample size, and advanced topics. J. Consum. Psychol. 2010, 20, 90–98. [Google Scholar] [CrossRef]
- Kenny, D.A.; McCoach, D.B. Effect of the number of variables on measures of fit in structural equation modelling. Struct. Equ. Model. 2003, 10, 333–351. [Google Scholar] [CrossRef]
- Shi, D.; Lee, T.; Maydeu-Olivares, A. Understanding the Model Size Effect on SEM Fit Indices. Educ. Psychol. Meas. 2019, 79, 310–334. [Google Scholar] [CrossRef]
- Cangur, S.; Ercan, I. Comparison of model Fit Indices Used in Structural Equation Modeling Under Multivariate Normality. J. Mod. Appl. Stat. Methods 2015, 14, 152–167. [Google Scholar] [CrossRef]
- Fitzgerald, C.A.; Estabrook, R.; Martin, D.P.; Brandmaier, A.M.; von Oertzen, T. Correcting the Bias of the Root Mean Squared Error of Approximation under Missing Data. Methodology 2021, 17, 189–204. [Google Scholar] [CrossRef]
- Maydeu-Olivares, A. Assessing the size of model misfit in structural equation models. Psychometrika 2017, 82, 533–558. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Savalei, V. New computations for RMSEA and CFI following FIML and TS estimation with missing data. Psychol. Methods 2023, 28, 263–283. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Sriutaisuk, S. Evaluation of Model Fit in Structural Equation Models with Ordinal Missing Data: An examination of the D 2 Method. Struct. Equ. Model. Multidiscip. J. 2020, 27, 561–583. [Google Scholar] [CrossRef]
- Liu, Y.; Sriutaisuk, S.; Chung, S. Evaluation of model fit in structural equation models with ordinal missing data: A comparison of the D 2 and MI2S methods. Struct. Equ. Model. Multidiscip. J. 2021, 28, 740–762. [Google Scholar] [CrossRef]
- Lai, K. Correct estimation methods for RMSEA under missing data. Struct. Equ. Model. Multidiscip. J. 2021, 28, 207–218. [Google Scholar] [CrossRef]
- Schoemann, A.M.; Miller, P.; Pornprasertmanit, S.; Wu, W. Using Monte Carlo simulations to determine power and sample size for planned missing designs. Int. J. Behav. Dev. 2014, 38, 471–479. [Google Scholar] [CrossRef]
- Pornprasertmanit, S.; Miller, P.; Schoemann, A.; Jorgensen, T.D. Simsem: SIMulated Structural Equation Modeling (Version 0.5-16) [R Package]. 2021. Available online: http://simsem.org/ (accessed on 1 July 2022).
- Azar, B. Finding a solution for missing data. Monit. Psychol. 2002, 33, 70. [Google Scholar]
- Peugh, J.L.; Enders, K. Missing data in educational research: A review of reporting practices and suggestions for improvement. Rev. Educ. Res. 2004, 74, 525–556. [Google Scholar] [CrossRef]
- Albaum, G.; Roster, C.A.; Wiley, J.; Rossiter, J.; Smith, S.M. Designing web surveys in marketing research: Does use of forced answering affect completion rates? J. Mark. Theory Pract. 2010, 18, 285–294. [Google Scholar] [CrossRef]
- Roster, C.A.; Albaum, G.; Smith, S.M. Topic sensitivity and Internet survey design: A cross-cultural/national study. J. Mark. Theory Pract. 2014, 22, 91–102. [Google Scholar] [CrossRef]
- De Leeuw, E.D.; Hox, J.J.; Boevé, A. Handling Do-Not-Know Answers: Exploring New Approaches in Online and Mixed-Mode Surveys. Soc. Sci. Comput. Rev. 2016, 34, 116–132. [Google Scholar] [CrossRef]
- Décieux, J.P.; Mergener, A.; Neufang, K.M.; Sischka, P. Implementation of the forced answering option within online surveys: Do higher item response rates come at the expense of participation and answer quality? Psihologija 2015, 48, 311–326. [Google Scholar] [CrossRef]
- Steijer, S.; Reips, U.-D.; Voracek, M. Forced-response in online surveys: Bias from reactance and an increase in sex-specific dropout. J. Am. Soc. Inf. Sci. Technol. 2007, 58, 1653–1660. [Google Scholar] [CrossRef]
- Sischka, P.; Décieux, J.P.; Mergener, A.; Neufang, K.M.; Schmidt, A.F. The Impact of Forced Answering and Reactance on Answering Behavior in Online Surveys. Soc. Sci. Comput. Rev. 2020, 40, 405–425. [Google Scholar] [CrossRef]
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data, 2nd ed.; Wiley: Hoboken, NJ, USA, 2002. [Google Scholar] [CrossRef]
- Graham, J.; Hofer, S.; Piccinin, A.M. Analysis with missing data in drug prevention research. In Advances in Data Analysis for Prevention Intervention Research; National Institute on Drug Abuse Research Monograph Series; Collins, L.M., Seitz, L., Eds.; National Institute on Drug Abuse: Washington, DC, USA, 1994; Volume 142, pp. 13–63. [Google Scholar] [CrossRef]
- Bollen, K. Structural Equations with Latent Variables; Wiley: New York, NY, USA, 1989; pp. 80–116, 179–223. [Google Scholar]
- Arbuckle, J.L. Full information estimation in the presence of incomplete data. In Advanced Structural Equation Modelling; Marcoulides, G.A., Schumacker, R.E., Eds.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1996; pp. 243–277. [Google Scholar]
- Golaszewski, N.M.; Bartholomew, J.B. The development of the Physical Activity and Social Support Scale. J. Sport Exerc. Psychol. 2019, 41, 215–229. [Google Scholar] [CrossRef]
- Meng, M.; He, J.; Guan, Y.; Zhao, H.; Yi, J.; Yae, S.; Li, L. Factorial Invariance of the 10-item Connor-Davidson Resilience Scale Across Gender Among Chinese Elders. Front. Psychol. 2019, 10. [Google Scholar] [CrossRef]
- In’nami, Y.; Koizumi, R. Factor Structure of the revised TOEIC® test: A multi-sample analysis. Lang. Test. 2021, 29, 131–152. [Google Scholar] [CrossRef]
- Yuan, K.-H. Fit indices versus test statistics. Multivar. Behav. Res. 2005, 40, 115–148. [Google Scholar] [CrossRef]
- Kenny, D.A.; Kanishan, B.; McCoach, D.B. The performance of RMSEA in models with small degrees of freedom. Sociol. Methods Res. 2015, 44, 486–507. [Google Scholar] [CrossRef]
- Maydeu-Olivares, A. Maximum likelihood estimation of structural equation models for continuous data: Standard errors and goodness of fit. Struct. Equ. Model. 2017, 24, 383–394. [Google Scholar] [CrossRef]
- Maydeu-Olivares, A.; Shi, D.; Rosseel, Y. Assessing fit in structural equation models: A Monte-Carlo evaluation of RMSEA versus SRMR confidence intervals and tests of close fit. Struct. Equ. Model. 2018, 25, 389–402. [Google Scholar] [CrossRef]
- Savalei, V. The relationship between root mean square error of approximation and model misspecification in confirmatory factor analysis models. Educ. Psychol. Meas. 2012, 72, 910–932. [Google Scholar] [CrossRef]
- Steiger, J.H. Structural model evaluation and modification: An interval estimation approach. Multivar. Behav. Res. 1990, 25, 173–180. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Bentler, P.M. Cutoff criteria for fit indices in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Model. 1999, 6, 1–55. [Google Scholar] [CrossRef]
- Kaplan, D. Structural Equation Modeling—Foundations and Extensions; Sage Publications: Madison, WI, USA, 2009; pp. 112–120. [Google Scholar] [CrossRef]
- Jöreskog, K.G.; Sörbom, D. LISREL VI: Analysis of Linear Structural Relationship by Maximum Likelihood and Least Squares Methods; National Educational Resources: Chicago, IL, USA, 1981; Available online: https://ssicentral.com/ (accessed on 1 July 2022).
- Kline, R.B. Principles and Practice of Structural Equation Modeling, 5th ed.; Guilford Press: New York, NY, USA, 2023; Chapter 10; pp. 156–180. [Google Scholar]
- Bentler, P.M. Comparative Fit Indices in Structural Equation Models. Psychol. Bull. 1990, 107, 238–246. [Google Scholar] [CrossRef]
- Tucker, L.R.; Lewis, C. The reliability coefficient for maximum likelihood factor analysis. Psychometrika 1973, 38, 1–10. [Google Scholar] [CrossRef]
- Jackson, D.L.; Gillaspy, J.A.; Purc-Stephenson, R. Reporting practices in confirmatory factor analysis: An overview and some recommendations. Psychol. Methods 2009, 14, 6–23. [Google Scholar] [CrossRef]
- Muthén, L.K.; Muthén, B.O. How to use a Monte Carlo Study to decide on sampled Size and Determine Power. Struct. Equ. Model. Multidiscip. J. 2002, 9, 599–620. [Google Scholar] [CrossRef]
- Madson, M.B.; Mohn, R.S.; Schumacher, J.A.; Landry, A.S. Measuring client experiences of motivational interviewing during a lifestyle intervention. Meas. Eval. Couns. Dev. 2015, 48, 140–151. [Google Scholar] [CrossRef] [PubMed]
- Derby, D.C.; Smith, T.J. Exploring the factorial structure for behavioural consequences of college student drinking. Meas. Eval. Couns. Dev. 2008, 41, 32–41. [Google Scholar] [CrossRef]
- McNeish, D.; An, J.; Hancock, G.R. The Thorny Relation Between Measurement Quality and Fit Index Cutoffs in Latent Variable Models. J. Person. Assess. 2018, 100, 43–52. [Google Scholar] [CrossRef] [PubMed]
- Robitzch, A. Modeling Model Misspecification in Structural Equation Models. Stats 2023, 6, 689–705. [Google Scholar] [CrossRef]
- Davey, A. Issues in evaluating model fit with missing data. Struct. Equ. Model. Multidiscip. J. 2005, 12, 578–597. [Google Scholar] [CrossRef]
- Hoyle, R.H. Handbook of Structural Equation Modelling; Guilford Press: New York, NY, USA, 2012. [Google Scholar]
- Zhang, X.; Savalei, V. Examining the effect of missing data on RMSEA and CFI under normal theory full-information maximum likelihood. Struct. Equ. Model. Multidiscip. J. 2020, 27, 219–239. [Google Scholar] [CrossRef]
- Moshagen, M. The model size effect in SEM: Inflated goodness-of-fit statistics are due to the size of the covariance matrix. Struct. Equ. Model. Multidiscip. J. 2012, 19, 86–98. [Google Scholar] [CrossRef]
- Hancock, G.R.; Mueller, R.O. The reliability paradox in assessing structural relations within covariance structure models. Educ. Psychol. Meas. 2011, 71, 306–324. [Google Scholar] [CrossRef]
- Themessl-Huber, M. Evaluation of the χ2-statistic and different fit-indices under misspecified number of factors in confirmatory factor analysis. Psychol. Test Assess. Model. 2014, 56, 219–236. [Google Scholar]
- Peterson, R.A. A meta-analysis of variance accounted for and factor loadings in exploratory factor analysis. Mark. Lett. 2000, 11, 261–275. [Google Scholar] [CrossRef]
- Fan, X.; Thompson, B.; Wang, L. Effects of sample size, estimation methods, and model specification on structural equation modeling fit indexes. Struct. Equ. Model. Multidiscip. J. 1999, 6, 56–83. [Google Scholar] [CrossRef]
| Question Set | ||||
|---|---|---|---|---|
| Form | X | A | B | C |
| 1 | O | O | O | NA |
| 2 | O | O | NA | O |
| 3 | O | NA | O | O |
| Number of Indicators in the Model | Questions in Each Set | |||
|---|---|---|---|---|
| X | A | B | C | |
| 18 | 1, 2, 3, 4, 6, 8, 10, 11, 12, 14, 16, 18 | 5, 13 | 7, 15 | 9, 17 |
| 36 | 1, 2, 3, 4, 7, 8, 9, 10, 13, 14, 15, 16, 19, 20, 23, 24, 25, 26, 29, 30, 31, 32, 35, 36 | 5, 6, 21, 22 | 11, 12, 27, 28 | 17, 18, 33, 34 |
| Number of Indicators | CFI | |||||||
|---|---|---|---|---|---|---|---|---|
| 18 | 36 | |||||||
| Correlation | Factor Loading | Sample Size | Complete | 3-Form | 3-Form+ Misspec | Complete | 3-Form | 3-Form+ Misspec |
| 0.1 | 0.4 | 200 | 0.964 | 0.944 | 0.942 | 0.933 | 0.878 | 0.872 |
| 500 | 0.986 | 0.982 | 0.980 | 0.986 | 0.978 | 0.977 | ||
| 1000 | 0.994 | 0.992 | 0.990 | 0.995 | 0.993 | 0.991 | ||
| 0.8 | 200 | 0.996 | 0.995 | 0.994 | 0.992 | 0.984 | 0.984 | |
| 500 | 0.999 | 0.998 | 0.998 | 0.998 | 0.998 | 0.997 | ||
| 1000 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | 0.999 | ||
| 0.9 | 0.4 | 200 | 0.971 | 0.958 | 0.706 | 0.942 | 0.895 | 0.733 |
| 500 | 0.990 | 0.987 | 0.724 | 0.988 | 0.982 | 0.806 | ||
| 1000 | 0.995 | 0.994 | 0.726 | 0.996 | 0.994 | 0.816 | ||
| 0.8 | 200 | 0.997 | 0.995 | 0.894 | 0.992 | 0.995 | 0.934 | |
| 500 | 0.999 | 0.999 | 0.897 | 0.998 | 0.999 | 0.946 | ||
| 1000 | 0.999 | 0.999 | 0.897 | 0.999 | 0.999 | 0.947 | ||
| Number of Indicators | TLI | |||||||
|---|---|---|---|---|---|---|---|---|
| 18 | 36 | |||||||
| Correlation | Factor Loading | Sample Size | Complete | 3-Form | 3-Form+ Misspec | Complete | 3-Form | 3-Form+ Misspec |
| 0.1 | 0.4 | 200 | 0.983 | 0.959 | 0.955 | 0.932 | 0.871 | 0.864 |
| 500 | 0.996 | 0.993 | 0.988 | 0.989 | 0.980 | 0.978 | ||
| 1000 | 0.999 | 0.998 | 0.994 | 0.998 | 0.996 | 1.000 | ||
| 0.8 | 200 | 0.998 | 0.996 | 0.995 | 0.992 | 0.983 | 0.984 | |
| 500 | 1.000 | 0.999 | 0.998 | 0.999 | 0.998 | 0.997 | ||
| 1000 | 1.000 | 1.000 | 0.999 | 1.000 | 1.000 | 1.000 | ||
| 0.9 | 0.4 | 200 | 0.986 | 0.969 | 0.666 | 0.942 | 0.889 | 0.717 |
| 500 | 0.998 | 0.995 | 0.687 | 0.991 | 0.984 | 0.794 | ||
| 1000 | 0.999 | 0.999 | 0.690 | 0.998 | 0.997 | 0.804 | ||
| 0.8 | 200 | 0.998 | 0.996 | 0.880 | 0.992 | 0.985 | 0.930 | |
| 500 | 1.000 | 0.999 | 0.883 | 0.999 | 0.998 | 0.942 | ||
| 1000 | 1.000 | 1.000 | 0.884 | 1.000 | 1.000 | 0.944 | ||
| Number of Indicators | SRMR | |||||||
|---|---|---|---|---|---|---|---|---|
| 18 | 36 | |||||||
| Correlation | Factor Loading | Sample Size | Complete | 3-Form | 3-Form+ Misspec | Complete | 3-Form | 3-Form+ Misspec |
| 0.1 | 0.4 | 200 | 0.055 | 0.067 | 0.069 | 0.060 | 0.075 | 0.077 |
| 500 | 0.035 | 0.042 | 0.044 | 0.038 | 0.045 | 0.047 | ||
| 1000 | 0.024 | 0.029 | 0.032 | 0.027 | 0.032 | 0.033 | ||
| 0.8 | 200 | 0.036 | 0.043 | 0.065 | 0.039 | 0.048 | 0.070 | |
| 500 | 0.023 | 0.026 | 0.052 | 0.025 | 0.029 | 0.055 | ||
| 1000 | 0.016 | 0.019 | 0.047 | 0.018 | 0.020 | 0.029 | ||
| 0.9 | 0.4 | 200 | 0.050 | 0.063 | 0.115 | 0.055 | 0.071 | 0.122 |
| 500 | 0.032 | 0.039 | 0.103 | 0.035 | 0.043 | 0.108 | ||
| 1000 | 0.023 | 0.027 | 0.099 | 0.025 | 0.030 | 0.103 | ||
| 0.8 | 200 | 0.024 | 0.031 | 0.378 | 0.027 | 0.036 | 0.392 | |
| 500 | 0.015 | 0.019 | 0.378 | 0.017 | 0.021 | 0.392 | ||
| 1000 | 0.011 | 0.013 | 0.370 | 0.012 | 0.014 | 0.392 | ||
| Number of Indicators | RMSEA | |||||||
|---|---|---|---|---|---|---|---|---|
| 18 | 36 | |||||||
| Correlation | Factor Loading | Sample Size | Complete | 3-Form | 3-Form+ Misspec | Complete | 3-Form | 3-Form+ Misspec |
| 0.1 | 0.4 | 200 | 0.013 | 0.016 | 0.016 | 0.018 | 0.025 | 0.026 |
| 500 | 0.007 | 0.008 | 0.009 | 0.007 | 0.008 | 0.009 | ||
| 1000 | 0.005 | 0.005 | 0.006 | 0.004 | 0.004 | 0.003 | ||
| 0.8 | 200 | 0.013 | 0.016 | 0.018 | 0.019 | 0.025 | 0.025 | |
| 500 | 0.007 | 0.008 | 0.010 | 0.007 | 0.008 | 0.009 | ||
| 1000 | 0.005 | 0.005 | 0.008 | 0.004 | 0.005 | 0.003 | ||
| 0.9 | 0.4 | 200 | 0.013 | 0.016 | 0.054 | 0.018 | 0.025 | 0.041 |
| 500 | 0.007 | 0.008 | 0.051 | 0.007 | 0.008 | 0.034 | ||
| 1000 | 0.005 | 0.005 | 0.051 | 0.004 | 0.004 | 0.033 | ||
| 0.8 | 200 | 0.014 | 0.016 | 0.097 | 0.018 | 0.025 | 0.056 | |
| 500 | 0.007 | 0.008 | 0.096 | 0.007 | 0.008 | 0.050 | ||
| 1000 | 0.005 | 0.005 | 0.096 | 0.004 | 0.004 | 0.049 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vicente, P.C.R. Evaluating the Effect of Planned Missing Designs in Structural Equation Model Fit Measures. Psych 2023, 5, 983-995. https://doi.org/10.3390/psych5030064
Vicente PCR. Evaluating the Effect of Planned Missing Designs in Structural Equation Model Fit Measures. Psych. 2023; 5(3):983-995. https://doi.org/10.3390/psych5030064
Chicago/Turabian StyleVicente, Paula C. R. 2023. "Evaluating the Effect of Planned Missing Designs in Structural Equation Model Fit Measures" Psych 5, no. 3: 983-995. https://doi.org/10.3390/psych5030064
APA StyleVicente, P. C. R. (2023). Evaluating the Effect of Planned Missing Designs in Structural Equation Model Fit Measures. Psych, 5(3), 983-995. https://doi.org/10.3390/psych5030064






