An Evaluation of DIF Tests in Multistage Tests for Continuous Covariates

Abstract

Multistage tests are a widely used and efficient type of test presentation that aims to provide accurate ability estimates while keeping the test relatively short. Multistage tests typically rely on the psychometric framework of item response theory. Violations of item response models and other assumptions underlying a multistage test, such as differential item functioning, can lead to inaccurate ability estimates and unfair measurements. There is a practical need for methods to detect problematic model violations to avoid these issues. This study compares and evaluates three methods for the detection of differential item functioning with regard to continuous person covariates in data from multistage tests: a linear logistic regression test and two adaptations of a recently proposed score-based DIF test. While all tests show a satisfactory Type I error rate, the score-based tests show greater power against three types of DIF effects.

1. Introduction

Psychological and educational assessments typically use models of item response theory (IRT) to statistically describe respondent-test item interactions. From a practical perspective, the IRT framework allows the application of sophisticated statistical techniques to verify important characteristics of these tests, such as aspects of the reliability and validity of the test scores [1,2,3,4]. The IRT framework further allows the application of advanced methods of test presentation, such as computerized adaptive testing (CAT) and multistage testing (MST). The principal aim of CAT and MST is to provide an economical assessment of the abilities of the individual respondents by making the presented items dependent on the respondent’s performance on previous test items. They are widely used in educational and psychological testing, for instance, in the Programme for International Student Assessment [5]. Although we will explain the key concepts underlying MST and its relation to CAT below, see [6,7,8] for more technical introductions.

The practical usefulness of the IRT framework depends on whether the chosen IRT model provides a sufficiently accurate description of the interaction of the respondents and the test items. Serious model misfit can lead to severe practical consequences, for instance, the systematic over- or underestimation of the abilities of respondents. There are multiple violations for IRT models that can be relevant in practical applications, and many of them can be interpreted as a misspecification of the IRT model used. Examples include the presence of local dependence between specific items or the over- or underestimation of the test’s dimensionality. For a discussion of these model violations in the context of MST, see, for instance, [6,9]. In this paper, we focus on differential item functioning (DIF) [10], which is related to the fairness of a test [11]. In the context of ability assessments, a test is defined to show this type of model violation when respondents of equal ability that differ with regard to a specific person covariate do not show the same probability of giving a correct response on a given item, e.g., [12]. The absence of DIF is typically regarded as a desirable characteristic of psychological and educational tests, cf. [13]. DIF implies that the probability of giving a correct response not only depends on item characteristics and the latent ability of the respondent, but also on some characteristic of the respondent (i.e., a person covariate) that can be categorical (e.g., gender), ordinal (e.g., educational level) or continuous (e.g., age). Traditionally two mutually exclusive types of DIF are discerned that can be related to these three types of covariates: Ackerman [14] defines a DIF effect to be uniform if ICCs for different values of the covariate are parallel and thus only differ by a horizontal translation. Alternatively, non-uniform DIF implies that the ICCs are not parallel, and that the change in ICCs depends on the ability. In practical assessments, the presence of such effects usually leads to unfair disadvantages for specific respondents. It is therefore necessary to check for DIF effects in practical assessments, which also include multistage tests that are based on an IRT framework. Therefore, there is a need for statistical tests that allow the detection of DIF effects in multistage tests.

We will review some of the tests proposed for this purpose in this paper. As will be shown, most of these tests focus only on the detection of DIF effects that are related to categorical covariates, that is, effects that advantage specific groups of respondents. Although some tests for the detection of DIF effects with regard to continuous covariates have been proposed in the literature for multistage tests, they have thus far not been systematically evaluated or compared.

In this paper, we aim to fill this gap in the literature by providing a systematic comparison and evaluation of several statistical procedures that were proposed for detecting this model violation by means of several simulation studies. This article expands on previous overviews of methods for DIF detection in the context of MST and CAT, for instance, [15,16]. In contrast to these earlier studies, we also discuss the topic of anchor selection in this context and point to an implementation of these methods in the R framework for statistical computing [17].

The remainder of this paper is structured as follows: In the next section, we provide an overview of MST. In the third section, we review statistical tests that were proposed for the detection of DIF in multistage tests. We then evaluate three tests for the detection of DIF effects regarding continuous covariates in a simulation study, which focuses on the detection of uniform DIF effects. We conclude our paper with a discussion of the principal findings of our study.

2. An Overview of Multistage Testing

This section introduces the principal ideas behind MST. For alternative overviews on this topic, see, e.g., [6,8,9,16,18].

The items in multistage tests are grouped in modules or testlets [8], which are presented to respondents working on the test. This presentation of modules is the main difference between multistage tests and computerized adaptive tests, where individual items are selected for presentation. The items of a module can be based on similar content [19] and are typically of similar difficulty [9]. After respondents completed a module, their performance is assessed, and the multistage test either ends or a suitable next module is selected and administered.

The rationale used for selecting modules during MST is also referred to as routing [8]. In addition to the information contained in the responses, routing can also use performance-related prior information [19] and consider content balancing and item exposure [6]. Various approaches have been proposed for routing, including assessing the test performance based on the number of correctly solved items [20] and the application of machine learning algorithms such as regression trees [21,22].

Another common approach for routing is the assessment of a respondent’s performance using an IRT model, such as the Rasch model [23] or the two-parametric logistic (2PL) model [24] and the corresponding item response function, which allows a prediction of the response behavior [6,20]. As an example, the response function of the 2PL model will be provided in the Materials and Methods section of this paper; extensive introductions to IRT are provided in the literature, e.g., [1,2,3,4,25].

In the item response function, the psychometric characteristics of test items, such as their difficulty, correspond to item parameters, whereas the ability levels of the respondents correspond to person parameters. The application of MST within an IRT framework assumes that the item parameters are sufficiently well known, for instance, based on an earlier calibration study, and that the item response function describes the interaction of the respondents and the items accurately.

After the presentation of the first module, which is also named the routing module [8,19], a multistage test based on the IRT framework typically obtains a provisional estimation of the person parameter, and the next module is selected for presentation using predefined rules. These rules can aim at optimizing the accuracy of the person parameter estimation but can also be related to controlling the exposure of individual items or item content. This procedure of obtaining provisional ability estimates and selecting the next modules is repeated until the end of the test, where a final ability estimate is returned. For a overview on possible estimation methods for the person parameter, see [6], chapter 2.3.2. These methods include, for instance, maximum likelihood (ML) estimation [26], weighted maximum likelihood (WL) estimation [27], or Bayesian point estimates [24,28].

In this paper, we consider a scenario in which the assumed item parameters that are used for item selection and ability estimation deviate from the true item parameters. It follows from the previous outline that a misspecification of the item parameters can affect the validity of the outcome of the test. In the next section, we provide an outline of methods for detecting this model violation.

3. Methods for Detecting Differential Item Functioning

It is important to consider that the items investigated for DIF can be presented in various scenarios (cf. [15]): First, one could test items that were already used as part of an operational multistage test. Here, estimates for the item parameters are readily available, and it is tested whether these estimates are stable for all respondents. This is the scenario that we focus on in this paper. Second, one could evaluate items that are not yet used for person ability estimation and are either presented scattered throughout a multistage test or in a separate section before or after a multistage test. We do not focus on this scenario here but will briefly review such a scenario at the end of this section.

Most of the methods proposed for the first scenario were designed for a setting in which the item parameters are assumed to deviate between two (or more) predefined groups of respondents. First, we will briefly describe these methods that can only be applied for DIF detection with respect to categorical covariates. Thereafter, we discuss DIF detection methods that can (also) be applied to continuous covariates. Finally, we briefly address the scenario where there are no item parameter estimates for the investigated items, and the problem of anchoring in the context of DIF detection in MST.

What all methods that are discussed below have in common is that they test the null hypothesis that the item parameters of a specific item are invariant across all respondents. As such, they can be expected to be sensitive to both uniform and non-uniform DIF effects. Although some of the methods can also be applied to polytomous items, we assume that the items of the test are dichotomous to describe the methods, that is, we assume that two responses (1 and 0) are possible for each item.

3.1. Methods for Categorical Covariates

Zwick [15] provides an overview of the methods for DIF detection in computerized adaptive tests with a focus on detecting parameter differences between a focal and a reference group. This topic was also briefly addressed by Zwick and Bridgeman [29] for multistage tests. Since the methods of test presentation in MST and CAT are comparable, these methods can also be applied for DIF detection in multistage tests, although they have, to the knowledge of the authors, not yet been implemented in openly available software packages.

3.1.1. Mantel–Haenszel Test

The Mantel–Haenszel test was originally proposed by Holland and Thayer [30] for testing DIF in individual items in linear tests, that is, tests where all respondents work on the same item set. Here, all respondents are assigned to one of K ability levels and one of two groups, which are named the focal and reference groups; in linear tests, the ability levels are usually defined based on the raw sum score (i.e., number correct scoring). If we can observe a correct or incorrect response to the evaluated item, we can observe two possible responses for each respondent, who in turn fall into one of $2\times K$ possible groups (focal or reference group combined with one of K ability levels). Therefore, each response to this item is assigned to one of $2\times 2\times K$ cells in a contingency table. The Mantel–Haenszel test now tests the null hypothesis that the ratio of correct and incorrect responses on each ability level is the same for the focal and reference groups using a test statistic that is based on a conditional odds-ratio statistic. For technical details, see [15].

Zwick [15] also describes the related standardization procedure of Dorans and Kulick [31], which is also based on the contingency table that underlies the Mantel–Haenszel test. To calculate this statistic, first, a weighted difference of the probabilities for a correct response in the focal and reference groups is calculated for each ability level. As a second step, these differences are summed to obtain a summary statistic. According to Zwick [15], this summary statistic is used as a descriptive measure for the size of a DIF effect and typically not as a formal test statistic.

Several publications addressed the application of the ideas underlying the Mantel–Haenszel test to CAT [32,33,34,35,36]. Here, the basic idea is to define the ability levels that are used for comparing the focal and reference groups not on the raw score but on the estimated person parameters. For technical details, we refer to these publications; additionally, we point out that these methods can conceptually also be applied to MST.

3.1.2. MSTSIB

This test was proposed by Gierl, Lai, and Li [37] for detecting DIF in MST and is technically based on the SIBTEST procedure of Shealy and Stout [38]. A related test named CATSIB, which was designed for application in CAT, was proposed by Nandakumar and Roussos [39]. MSTSIB aims to detect DIF effects between a focal group and a reference group. The reasoning of the test is the following: If there is no DIF between the focal and reference groups, the expected response to a given item should be identical for both groups and only depend on the estimated ability $\widehat{\theta }$ of the respondent. MSTSIB assumes that the final ability estimate provides an accurate point estimate of each respondent’s ability. Let $E{S}_R\left(\widehat{\theta }\right)$ be the probability of a correct response of a member of the reference group with an estimated ability of $\widehat{\theta }$ and $E{S}_F\left(\widehat{\theta }\right)$ be the corresponding probability for a member of the focal group. MSTSIB now defines a series of intervals in which the ability parameter estimates in the sample can fall. For each interval, the difference between $E{S}_R\left(\widehat{\theta }\right)$ and $E{S}_F\left(\widehat{\theta }\right)$ is estimated, and a weighted mean of the overall difference is calculated. The weights consider the number of respondents from the focal and reference groups in each interval. Under the null hypothesis of no DIF, this difference should be normally distributed with a mean of zero, which is used for a statistical test. For technical details on this procedure, see [37].

3.1.3. Likelihood Ratio Test

Lei, Chen, and Yu [40] proposed and evaluated a method for DIF testing in CAT that is based on a likelihood ratio test. As was the case for the previous tests, this test assumes that all respondents are assigned to either a focal or a reference group. Conceptually, this test consists of the following steps. First, the missing data resulting from the adaptive test presentation are replaced by imputed data using the assumed IRT model. Second, a likelihood ratio test was carried out that compares the likelihood of two models. In the first of these models, the item parameters of the focal and reference groups are assumed to be identical, whereas they are allowed to differ in the second model.

Conceptually, this test can also be applied with multistage tests. For a critical discussion of this approach, see [15], Section 17.3.

3.2. Methods for Continuous Covariates

In this outline, we provide a nontechnical introduction to three methods that were proposed to detect DIF with respect to a continuous covariate in multistage tests. Using the estimated ability parameters, they aim to detect differences in the response behavior between respondents that differ with regard to a continuous covariate. The three methods that we describe are (a) logistic regression and (b) two types of score-based tests. Note that there are also methods proposed for assessing parameter invariance that can be used to detect DIF with respect to a continuous covariate. An example is moderated nonlinear factor analysis (e.g., [41]). This method formulates DIF as person covariates moderating the parameters of the measurement model. Like in the linear logistic regression approach, an assumption needs to be made about the shape of the moderating effect. Typically linear effects are assumed.

3.2.1. Linear Logistic Regression

This test was proposed by Swaminathan and Rogers [42] for DIF detection in linear tests. As its name suggests, this method uses a linear logistic regression model to describe the responses of the respondents to the individual items. The dependent variable of this regression model is the observed response (0 or 1) in a given item, whereas the independent variables are the estimated ability parameters, an observed person covariate and the interaction of these two predictors. Under the null hypothesis of parameter invariance, the person covariates and the interaction should not provide any additional information on the prediction of the response in addition to the ability parameters, and therefore, their regression coefficients should be zero. The logistic regression test for a given item is now based on a likelihood ratio test that checks whether the regression coefficients of the person covariate and the interaction are zero. In this study, an item was flagged by the linear logistic regression test if the p-value of this likelihood ratio test was below 0.05.

The person covariate in this regression model can be a categorical covariate but, in principle, also a continuous covariate such as age. In the case of continuous covariates, this testing approach explicitly assumes that there is a linear relationship between the covariate tested for DIF and the logit of the predicted probability for a correct response [40]. It should also be noted that this test assumes that the ability estimation in the multistage test is sufficiently accurate. Another assumption of the statistical test used for comparing the logistic regression models is that the underlying sample is sufficiently large. For evaluations of this test in the context of CAT and linear tests, see, for instance, [40,42,43].

3.2.2. Score-Based Tests

These tests build on the tradition of score-based invariance tests that were proposed in the field of psychometrics, e.g., [44,45,46,47]. Conceptually, these tests are based on the following idea: for each item and each respondent, so-called individual score contributions can be computed. Note that the score here refers to the first derivative (i.e., gradient) of the log likelihood. Hence, the score contributions can be calculated as part of the item parameter estimation and depend on the item and person parameters, as well as the observed responses and can be interpreted as measures of model fit for each respondent-item pair. If the chosen IRT model, together with the assumed item and estimated person parameters accurately describes the responses of the respondents to a given item, these individual score contributions typically fluctuate randomly around zero. If we sum these individual score contributions over groups of test takers, the corresponding cumulative sums should also fluctuate around zero; however, if the model is not accurate, the cumulative sums can deviate strongly from zero. For a more detailed but slightly more technical introduction, see [48].

This leads to the following general procedure for score-based tests for a given item in an MST administration. First, remove all respondents who did not respond to this item. Using the remaining respondents, calculate the individual score contributions given the assumed item parameters, the observed responses to this item and the person parameter estimates. Second, order the respondents and correspondingly the individual score contributions with regard to a person covariate of interest. Third, calculate cumulative sums of the individual score contributions with regard to the order from step 2. Fourth, measure the overall deviation from the value of zero, which is expected under the null hypothesis, by a suitable test statistic. In the study at hand, we used the maximum deviation of the cumulative sums from zero calculated over all respondents and item parameter as the test statistic, which is also named the double maximum statistic [46].

In general, the exact distribution of individual score contributions that are based on person parameter estimates is unknown even though the null hypothesis is correct; a technical discussion of the asymptotic distribution is provided by Zeileis and Hornik [49]. Therefore, it is generally not possible to calculate analytical p-values for this test. This is particularly the case in small samples, as they can occur in multistage tests, which we will also show later in this study. Instead, two computational workarounds were proposed.

The idea of the first procedure is that a fit statistic based on the order of the individual score contributions (e.g., the double maximum statistic that is based on the cumulative sums of the individual score contributions) should not change significantly if the score contributions are ordered according to a person covariate that does not affect the item parameters (i.e., under the null hypothesis). The procedure consists of the following steps. First, one could permute the observed individual score contributions many times (e.g., 500) and calculate a suitable test statistic (e.g., the double maximum statistic of the cumulative sums) for the original sequence of score-based contributions, that is, ordered with regard to the person covariate, and for all permutations of this sequence. The values of this statistic that are obtained from the permutations can now serve as a reference distribution, and a comparison of the test statistic observed for the original sequence with this reference distribution allows the calculation of p-values. In the following, we name this variation the score-based permutation test.

Second, one could use the estimated person parameters as approximations for the true person parameters. Under this assumption, one could generate many (e.g., 500) artificial datasets based on the estimated person parameters and the assumed item parameters. Using these artificial datasets, one can obtain a reference distribution for an arbitrary test statistic (e.g., the double maximum statistic) under the null hypothesis that no DIF effects are present, that is, the item parameters are stable. By comparing the observed test statistic against this reference distribution, one can obtain p-values for testing this null hypothesis. In the following, we name this variation the score-based bootstrap test.

Before we evaluate these tests, it seems useful to summarize their underlying assumptions. Both tests use a person parameter estimate as a substitute for the true person parameter and, thus, require a sufficiently accurate parameter estimation. The score-based permutation test further assumes that the individual score contributions can be considered interchangeable if no DIF is present. Since the distribution of the individual score contributions also depends on the distribution of the ability parameters, this assumption could be violated when the covariate tested for DIF is related to ability differences. We will investigate this point in the simulation study reported later.

3.2.3. Detecting DIF for Nonoperational Items

When no item parameter estimates are available for items that should be investigated for DIF, it is still possible to apply DIF tests that do not require such estimates. Of the tests outlined above, this applies to the MSTSIB, the Mantel–Haenszel test, and the linear logistic regression test.

An alternative testing strategy consists of first estimating the item parameters using the observed responses. As a second step, it is possible to apply DIF tests that assess the stability of these estimates over covariates of interest. This strategy can be applied with score-based tests. We do not provide details for conciseness, but details on how score-based tests can be applied to item parameter estimates can be found in the literature, e.g., [48] or [50].

A variation of the second strategy was also applied in the presented likelihood test approach in the context of DIF tests in adaptive testing [40]. Here, the estimated item parameters were used to impute the missing data that resulted from the adaptive test presentation.

3.2.4. The Problem of Anchoring in DIF Detection in Multistage Tests

If the item parameters are treated as unknown, itemwise DIF tests for linear tests usually require the definition of a set of anchor items. For these items, it is assumed that their item parameters are invariant for the respondent population, and changes in the estimated parameters of items investigated for DIF are related to the set of anchor items.

For linear tests, it has been found that the size of the set of anchor items affects the power of DIF tests. If the set of anchor items contains items affected by DIF, this can lead to an increased rate of false-positive results in DIF tests. The set of anchor items should therefore be selected carefully, which can be either done by experts based on the item content or based on statistical algorithms. For overviews of this research see, for instance, [51,52,53].

As outlined in the previous subsection, DIF tests for multistage tests often do not require the estimation of item parameters. If the item parameters are assumed to be known, the problem of selecting a set of anchor items does not directly apply, although the model leading to these item parameter estimates may have made assumptions that are similar to the definition of anchor items. However, these DIF tests typically require the estimation of ability parameters based on the responses to items with known item parameters. If a set of items has been defined whose item parameters are assumed to be stable, this set could be used to provide an estimate of the person ability that is independent of items that are investigated for DIF. The definition of such an item set is conceptually comparable to the definition of a set of anchor items. A possible disadvantage of this procedure is that the use of a smaller item set usually leads to less precise person parameter estimates, as will also be shown later in this paper. On the other hand, if the ability estimation is based on items that possibly include items affected by DIF effects, this might lead to estimation bias. We will also investigate this effect in this study.

3.3. Aim of This Study

As outlined in the previous subsections, several methods have been proposed for the detection of DIF in MST. While some methods have been proposed for the detection of DIF with respect to a continuous covariate, they have not been systematically compared thus far. The study at hand aims to fill this gap in the literature by systemically investigating the Type I rate and power of the proposed DIF tests in a simulation study, which will be described below, for a wide range of conditions.

4. Materials and Methods

Our simulation study was based on the commonly used two-parametric logistic test model [24], which is based on the following item response function:

$$P(X_{ij}=1|{\theta }_i,{\alpha }_j,{\beta }_j)=\frac{exp\left({\alpha }_j({\theta }_i-{\beta }_j)\right)}{1+exp\left({\alpha }_j({\theta }_i-{\beta }_j)\right)}$$

Here, the item parameters ${\alpha }_j$ and ${\beta }_j$ correspond to item discrimination and item difficulty parameters, respectively, whereas ${\theta }_i$ corresponds to a person ability parameter.

In the simulation study, the sample worked on a $1\times 3\times 3$ multistage test. In this test, all respondents first worked on the same routing module, which contained tasks of medium difficulty. Based on their performance, they were afterward assigned to one of three possible modules, which corresponded to easy tasks, tasks of medium difficulty and difficult tasks. After working on this second module, they were presented with one of three additional possible modules of different difficulty levels, after which the test was ended. Figure 1 presents an overview of the possible paths through the modules of this test.

In the modules containing easy, medium and difficult tasks, the item difficulty parameters ${\beta }_j$ were drawn from normal distributions $\mathcal{N}(-0.5,1)$, $\mathcal{N}(0,1)$ and $\mathcal{N}(0.5,1)$, respectively. The item discrimination parameters ${\alpha }_j$ were drawn from a normal distribution $\mathcal{N}(1,0.01)$ for all modules.

The person parameters ${\theta }_i$ were drawn from a normal distribution, with the exact distribution depending on the simulation condition. Each person was further assigned a continuous covariate $C_i$, which was drawn from a uniform distribution $\mathcal{U}(20,80)$. This covariate can be seen as a simulation of an age covariate, which was further used for DIF testing and for the simulation of ability differences within the simulated conditions, as will be described below. It was further used for the simulation of DIF effects.

The simulation conditions varied with regard to the following characteristics:

• The length of the modules: The length of the individual modules was either 9 or 18 items, leading to an overall test length of 27 or 54 items.
• The presence of impact effects: Based on the value of $C_i$, respondents were assigned to one of two groups of comparable size, to which we will refer to as Group 1 ($C_i\le 50$) and Group 2 ($C_i>50$). These groups were used for the simulation of ability differences, that is, impact effects between the respondents. If impact was absent, the person parameters of both Group 1 and Group 2 were sampled from a standard normal distribution $\mathcal{N}(0,1)$. If impact effects were simulated, the person parameters of Group 1 were sampled from a normal distribution $\mathcal{N}(-0.5,1)$, whereas the person parameters of Group 2 were sampled from a normal distribution $\mathcal{N}(0.5,1)$.
• The presence and direction of DIF effects: We simulated conditions with and without uniform DIF effects. In the conditions without DIF effects, the item parameters underlying the observed responses were identical to the assumed item parameters, that is, those used for the estimation of the person parameters and the routing during the multistage test. In the conditions with DIF effects, this was not the case, but the assumed item difficulty parameters of the first 1, 2 or 4 items in each module (depending on the overall length of the modules and the rate of DIF items) differed from the item parameters underlying the observed item parameters depending on the value of $C_i$. The conditions with DIF effects varied with regard to the following characteristics:

  -

  The rate of DIF items: The number of items with DIF effects in a each module was either one out of nine, or two out of nine items. The DIF items were always the first presented in each module.

  -

  Direction of DIF effects: In conditions with unbalanced DIF effects, the item difficulty parameters of DIF items were all changed in the same way, depending on the type of simulated DIF effect (see below). In conditions with balanced DIF effects, the item difficulty parameters of DIF items in stages 1 and 3 of the test changed in the same way as in the condition with unbalanced DIF effects. For DIF items in stage 2, the direction of the change was reversed.

  -

  Relationship between covariate and change of item parameters (Form of the DIF effect): Depending on the value of $C_i$, the affected item difficulty parameters changed by one of three functions: If the relationship could be described by a step function, ${\beta }_i$ increased by 0.6 for all respondents with $C_i>50$ under the unbalanced DIF condition. If the relationship between the DIF effect and $C_i$ was linear, the change of ${\beta }_i$ was $0.6·\frac{C_i-20}{60}$ under the unbalanced DIF condition; therefore, it was 0 for respondents with $C_i=20$ but 0.6 for respondents with $C_i=80$. If the relationship was finally described by a U-turn function, ${\beta }_i$ was increased by 0.6 for all respondents with $C_i<35$ or $C_i>65$ under the unbalanced DIF condition. In the following, we refer to these conditions as linear, stepwise and U-turn DIF effects.

• The number of respondents: The test was completed by 200, 500 or 1000 respondents. The overall sample size limited the sizes of the samples that were available for evaluating the individual items.
• The person parameter estimation method: The person parameters were either estimated by an ML (i.e., a maximum likelihood) estimator or by a WL (i.e., a weighted maximum likelihood) estimator [27]. In case of respondents who gave only correct or only incorrect responses, the ML estimator did not lead to finite parameter estimates and the WL estimator was used instead.

For each combination of conditions, 500 datasets were simulated. All simulated datasets were analyzed with the linear logistic regression test as well as the score-based bootstrap test and the score-based permutation test, with both score-based tests using 500 bootstrap samples for calculating p-values. Each test was applied with two possible person parameter estimates. In the first variation, all items were used for estimating the person parameters. In the second variation, only items that were not affected by DIF in conditions with DIF effects were used for estimating the person ability parameters (i.e., depending on the simulation condition, the responses to the first one, two or four items of each module were not considered when estimating the person ability parameters). We will refer to this second variation as the variation in which only items suspected to be free of DIF were used for person parameter estimation.

While the score-based tests were applied using R code from the mstDIF R package [54], the linear logistic regression test was applied using R code specifically written for this study. Because modules are adaptively selected in the MST design, it is possible that some modules in stage two and stage three are administered to only a small proportion of the test takers. Consequently, there are items with only a small number of responses. Yet, in general, to reliably fit statistical models, estimate parameters, or detect effects, a minimal amount of information is required. This also applies to DIF detection. Therefore, in the simulation study, we chose to set the minimal number of responses to 100, for an item to be eligible for a DIF detection analysis. Thus, the evaluation and comparison of the DIF detection tests was limited to the items in the modules that were administered to at least 100 respondents. In Section 5.1, we will evaluate the rate of respondents above this threshold in the various conditions of our simulation study.

5. Results

Before presenting the results on the evaluation of the three tests under each condition, we will investigate (a) how often the individual modules were worked on and (b) the accuracy of the person parameter estimates under the various conditions. We will then discuss the Type I error rate and the power of the three tests under the various conditions.

5.1. Selection Rates of Individual Modules

We investigated how often individual modules were answered by 100 respondents or more under the various conditions of the simulation study, since this threshold determined whether items in this modules were investigated for DIF or not. Due to the adaptive selection of modules in the MST design, not all modules in stages two and three could be expected to be selected equally often. As follows from Figure 1, all respondents were administered the routing module in stage one. Yet in stage two and three the respondents were distributed across the three modules in each stage. Particularly in conditions with 200 respondents, often less than 100 respondents worked on the items contained in the modules in stages two and three. As an illustration, we report the response frequency in the first iteration of the condition with 200 respondents and 63 items without DIF or impact effects, where the WL estimator was used for the person parameter estimation. Here, 200 respondents worked on the module in stage one, 33, 61 and 106 respondents worked on the three modules in stage two, and 3, 77 and 120 respondents worked in the modules in stage three.

In conditions with 500 or 1000 respondents, the relative response rates to the individual modules were similar, but due to the higher sample size, more modules were worked on by 100 respondents or more. Figure 2 gives the response frequencies to the six modules in stages two and three across all 500 replications in the condition with 1000 respondents and 63 items, without DIF or impact effects, where the WL estimator was used for person parameter estimation. The figure illustrates that under these simulation conditions, especially the module in stage two that contained items of medium difficulty was less frequently selected. In the other conditions of the simulation study, similar distributions were found.

As a result of the adaptive selection in the MST design, across replications, approximately 33% of the modules were administered to 100 respondents or more in conditions with 200 respondents. As a consequence, only items from these modules were considered for the itemwise DIF tests analysis. In the conditions with 500 or 1000 respondents, this was the case for 77% and 86% of the modules, respectively.

5.2. Accuracy of the Person Parameter Estimates

As a second step, we investigated the precision of the person parameter estimates. For all datasets in all conditions, we evaluated the root mean squared error (RMSE) for the final person parameter estimate, depending on whether all items or only the items that were suspected to be free of DIF were used for the final ability estimation. As a summary statistic, we calculated the median RMSE for all datasets generated under each condition. The RMSE is calculated as the square root of the mean of the squared differences between the true person parameter and the person parameter estimate. Values close to zero correspond to an accurate estimation.

We found that the RMSE was mainly influenced by the test length and, to a lesser degree, by the estimator used. The number of respondents and the presence of impact had no obvious influence on the median RMSE. As expected, the inclusion of additional items increased the precision of the person parameter estimates, and the WL estimator led to more precise estimates than the ML estimator. A similar result was reported by Warm [27]. Furthermore, we found no strong influence of DIF effects on this measure of the precision of the ability estimates under the conditions of this simulation study.

Table 1. The range of median RMSEs for the person parameter estimation for all conditions without DIF effects.

Test Length	Estimator	RMSE Using All Items	RMSE without Possible DIF Items
27 items	ML	0.46–0.47	0.49–0.50
54 items	ML	0.32–0.33	0.34–0.35
27 items	WL	0.44–0.45	0.47–0.48
54 items	WL	0.31–0.32	0.33–0.34

presents the range of the medians of the RMSE for the various conditions of test length and the ability estimator used for conditions without DIF effects. In each row, the range was calculated over the conditions with and without impact and the different conditions of sample size and estimation method.

For conditions with DIF effects, very similar results were found. In conditions with one out of nine items showing DIF, the range of RMSEs was comparable to those found for the analogous conditions without DIF effects. In conditions with two out of nine items showing DIF, the RMSEs were slightly increased by values between 0.01 and 0.02.

5.3. Type I Error Rate

We start with considering the Type I error rate, that is, the rate of positive DIF detection in items which are not affected by DIF effects. Under all conditions without DIF effects, the Type I error rates of the bootstrap and permutation score-based tests as well as the linear logistic regression test were within a range of 0.045–0.066 and thus close to the nominal Type I error rate of 0.05.

When only items that were suspected of being DIF-free were used for the person parameter estimation, this was also the case for conditions with DIF effects when items without DIF effects were tested for DIF. In the case where all items were used for person parameter estimation, the Type I error rates of both score-based tests were in the range of 0.044–0.082 under conditions with DIF effects when one out of nine items was affected by DIF. For the linear logistic regression test, the corresponding Type I error rates were in a range of 0.051–0.062. If two out of nine items were affected by DIF, the Type I error rate of the score-based tests was in a range of 0.042–0.123, whereas the Type I error rate of the logistic regression test was in a range of 0.051–0.081. For the score-based tests, Type I error rates over 0.1 were only observed in two conditions, where an unbalanced stepwise DIF effect was simulated in a large sample size of 1000 respondents, the modules consisted of nine items and impact was present.

5.4. Power

As a first step, we estimated the influence of the various factors of the simulation study on the power of the DIF tests by applying an ANOVA. In this analysis, the power was the dependent variable, whereas the conditions of the simulation study (Number of respondents, number of items, direction of the DIF effect, rate of DIF items, relationship between covariate and DIF effect, estimation method for the person parameter) and their two-way interactions were the independent variables. After carrying out the ANOVA, we estimated the ${\eta }^2$ of each independent variable.

Table 2. All simulation conditions and two-way interactions of simulation conditions with an effect corresponding to an ${\eta }^2$ larger than or equal to 0.01 on the power of the DIF tests.

Independent Variable	${\mathit{\eta }}^2$
Form of DIF effect	0.474
Sample size	0.274
Type of DIF test	0.039
Direction of the DIF effect	0.014
Form of DIF effect × Sample size	0.066
Form of DIF effect × Presence of impact	0.030
Form of DIF effect × Type of DIF test	0.026
Sample size × Type of DIF test	0.010

shows all independent variables with a ${\eta }^2$ larger than or equal to 0.01.

All other factors not listed in Table 2 showed an ${\eta }^2$ smaller than 0.01. These included the use of DIF items for person parameter estimation, the rate of DIF items, the length of the modules, and the method used for estimating the person parameters.

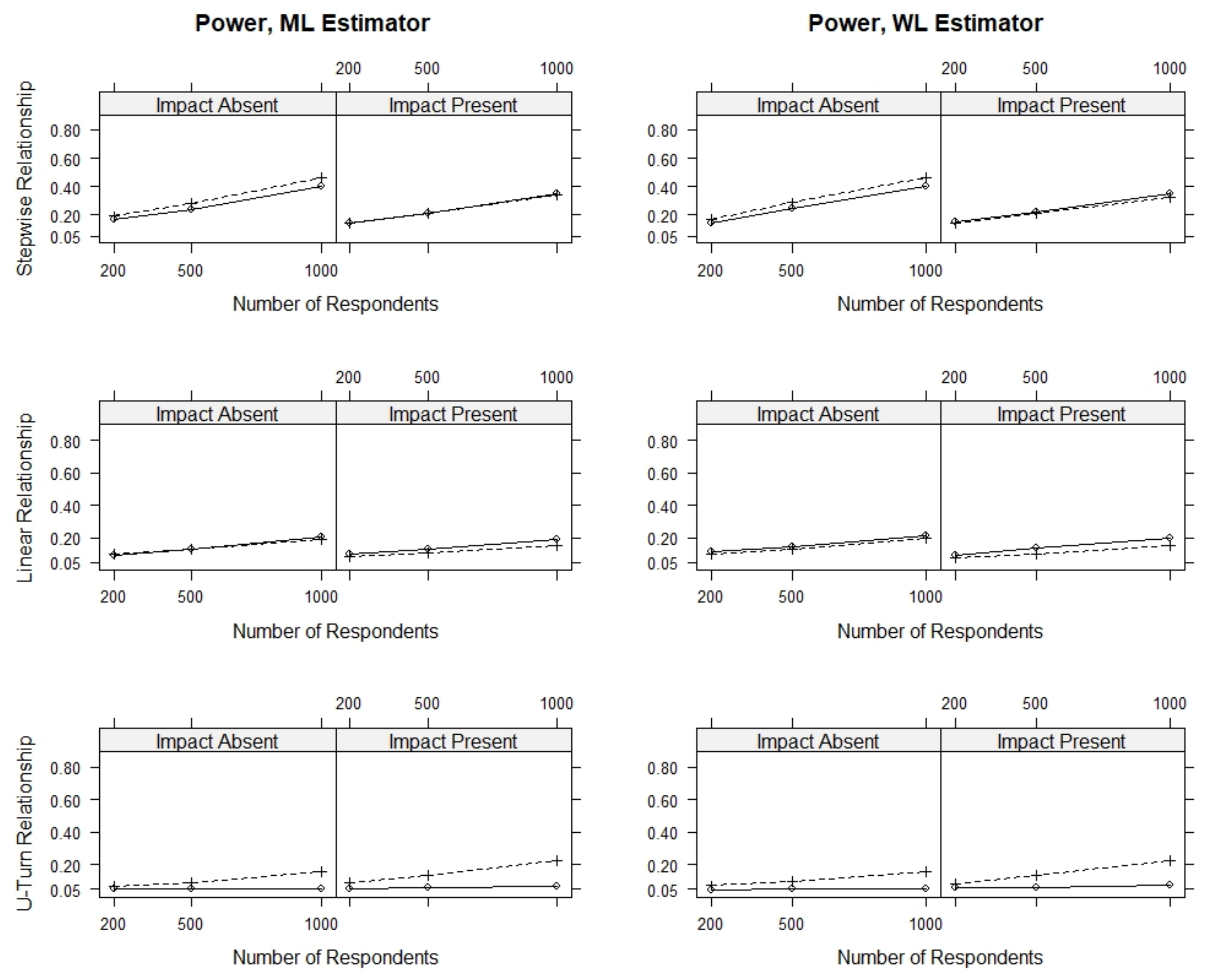
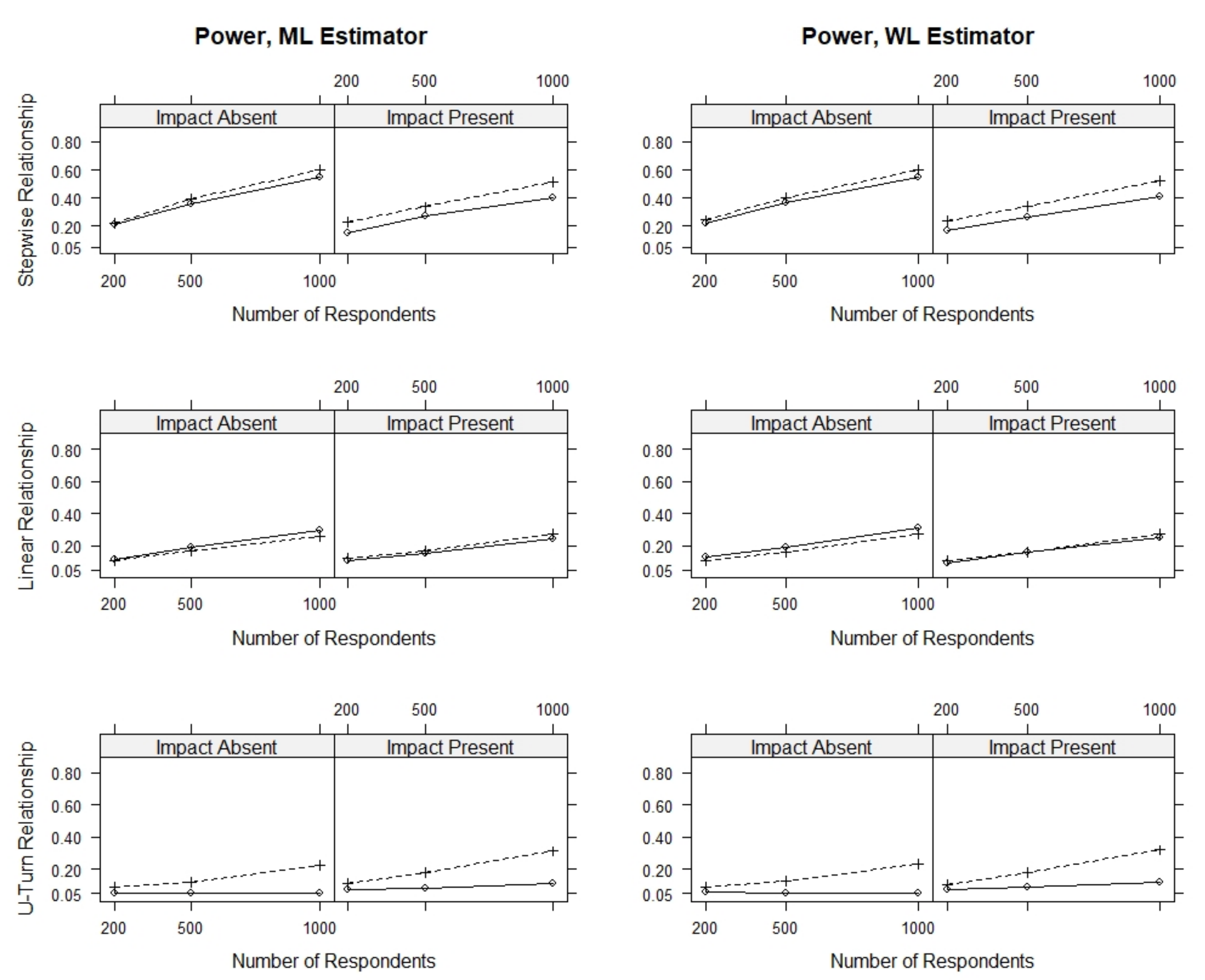
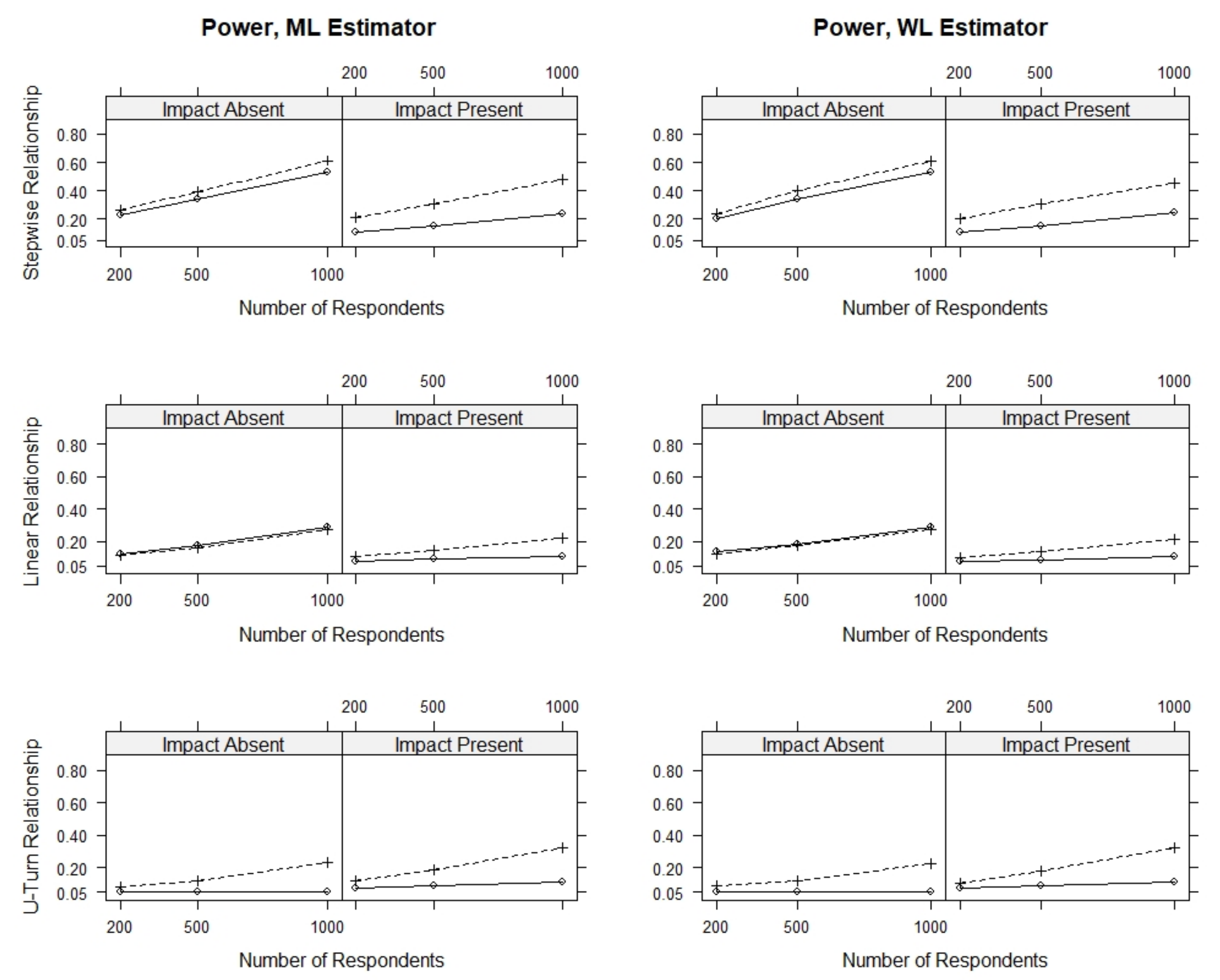
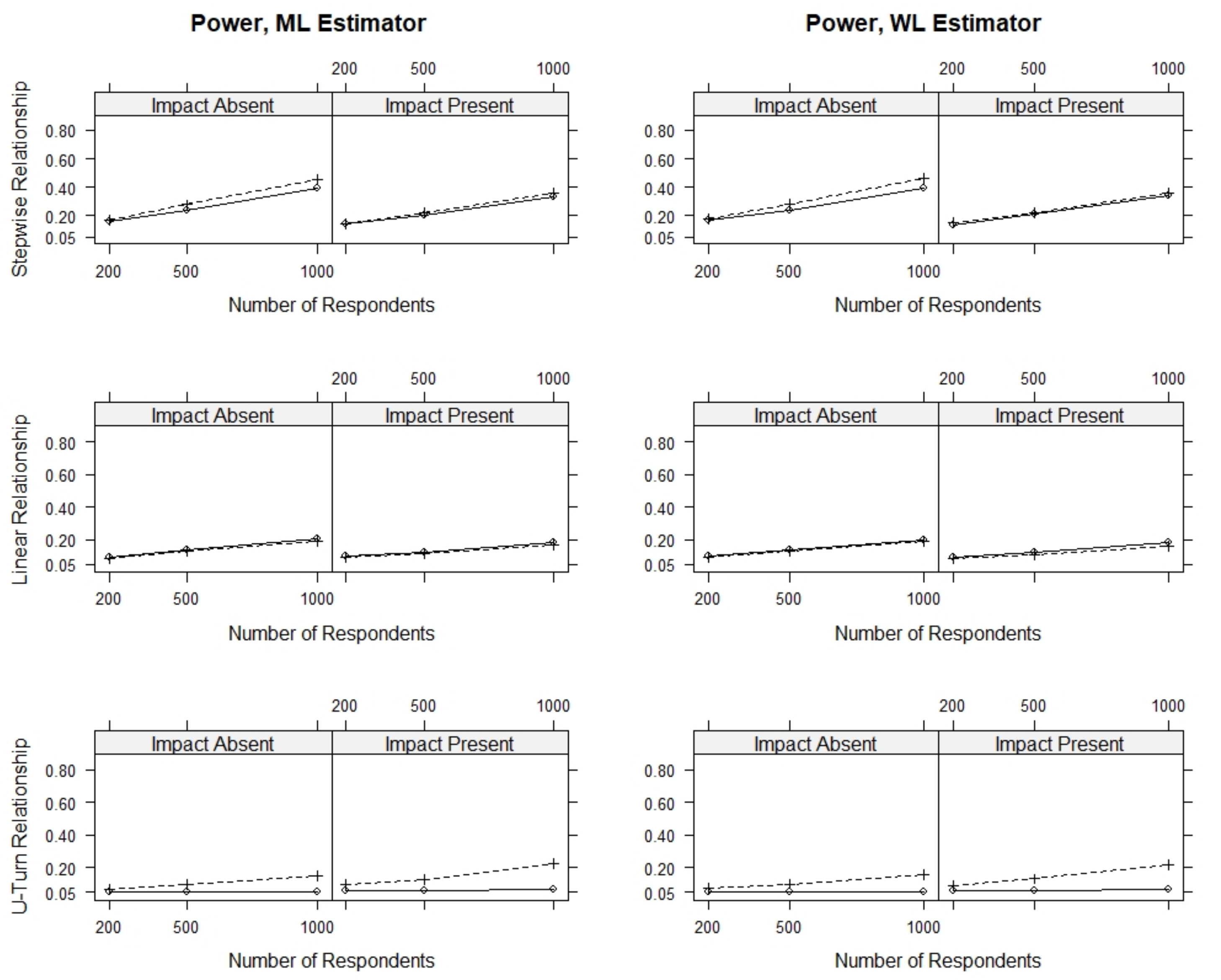
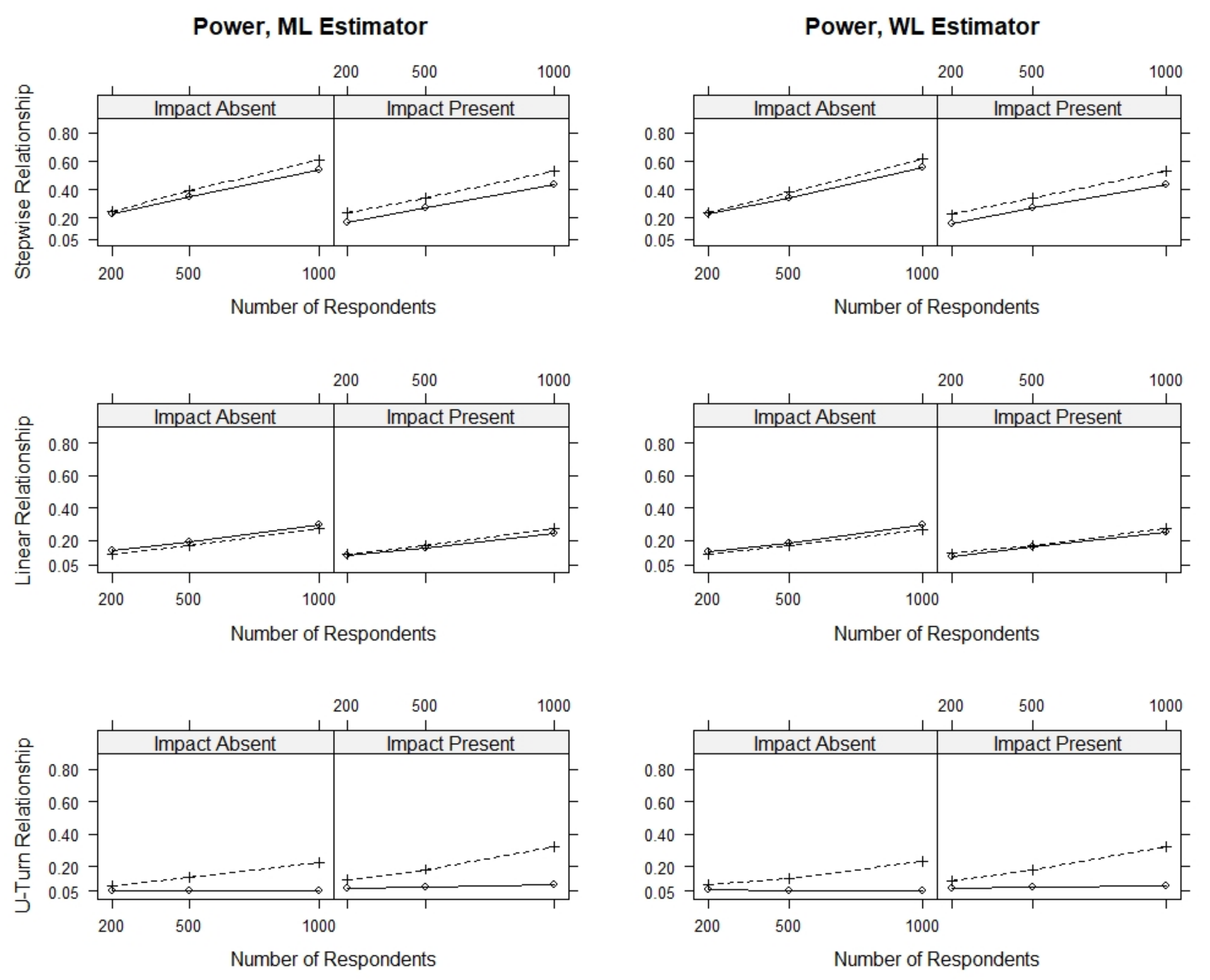
We now present the power of the various tests against the simulated DIF effects, that is, the rate of positive DIF detection when DIF is present. Since the power of the score-based bootstrap test and the score-based permutation test were almost identical under all conditions, we only present results for the bootstrap test and the linear logistic regression test. Given the results presented in Table 2, this section only presents results for conditions with modules containing nine items and one DIF item, where the person parameters were estimated using the WL estimator and where all items were used for ability estimation. We further present detailed results for all conditions where two out of nine items showed DIF in the Appendix A. 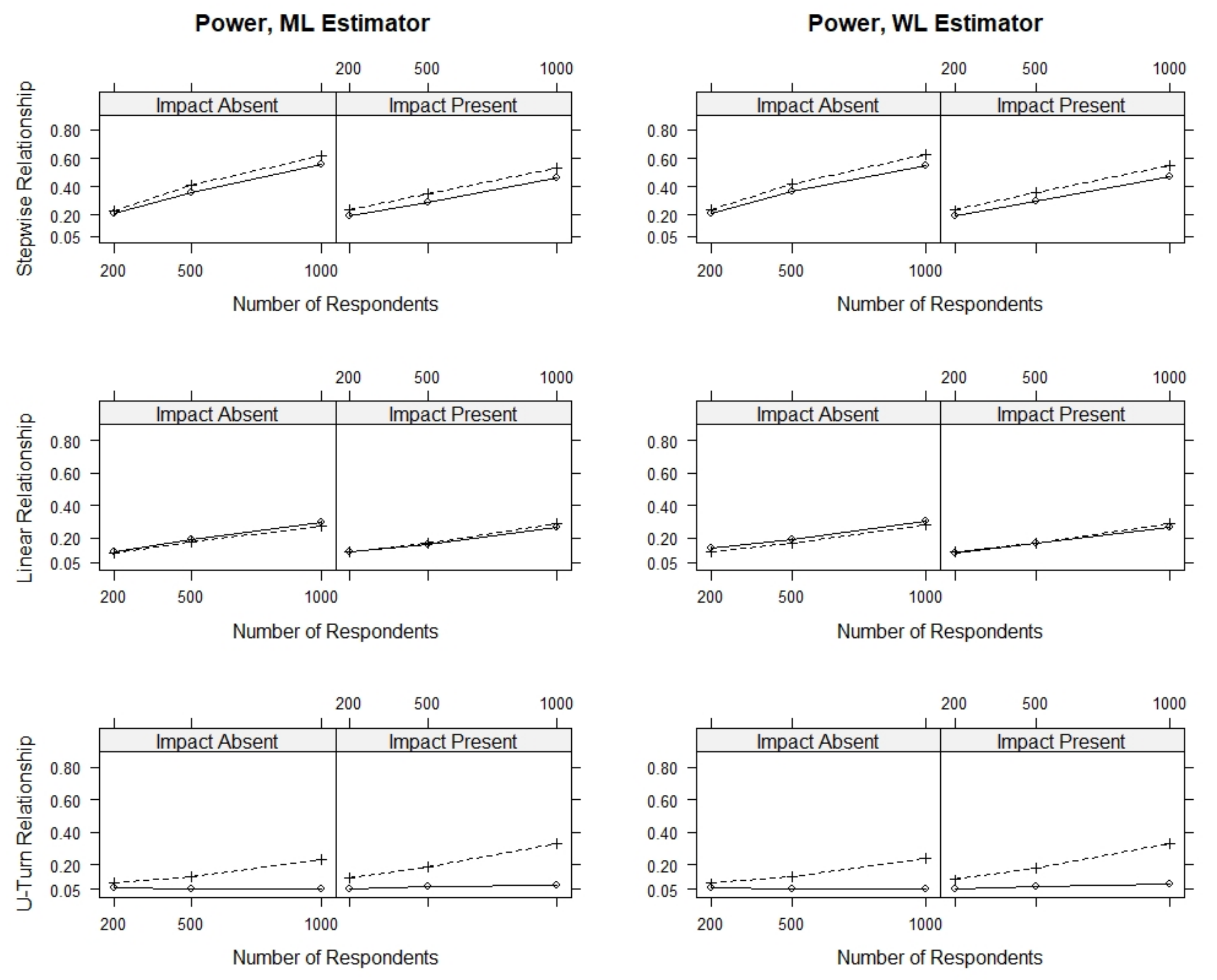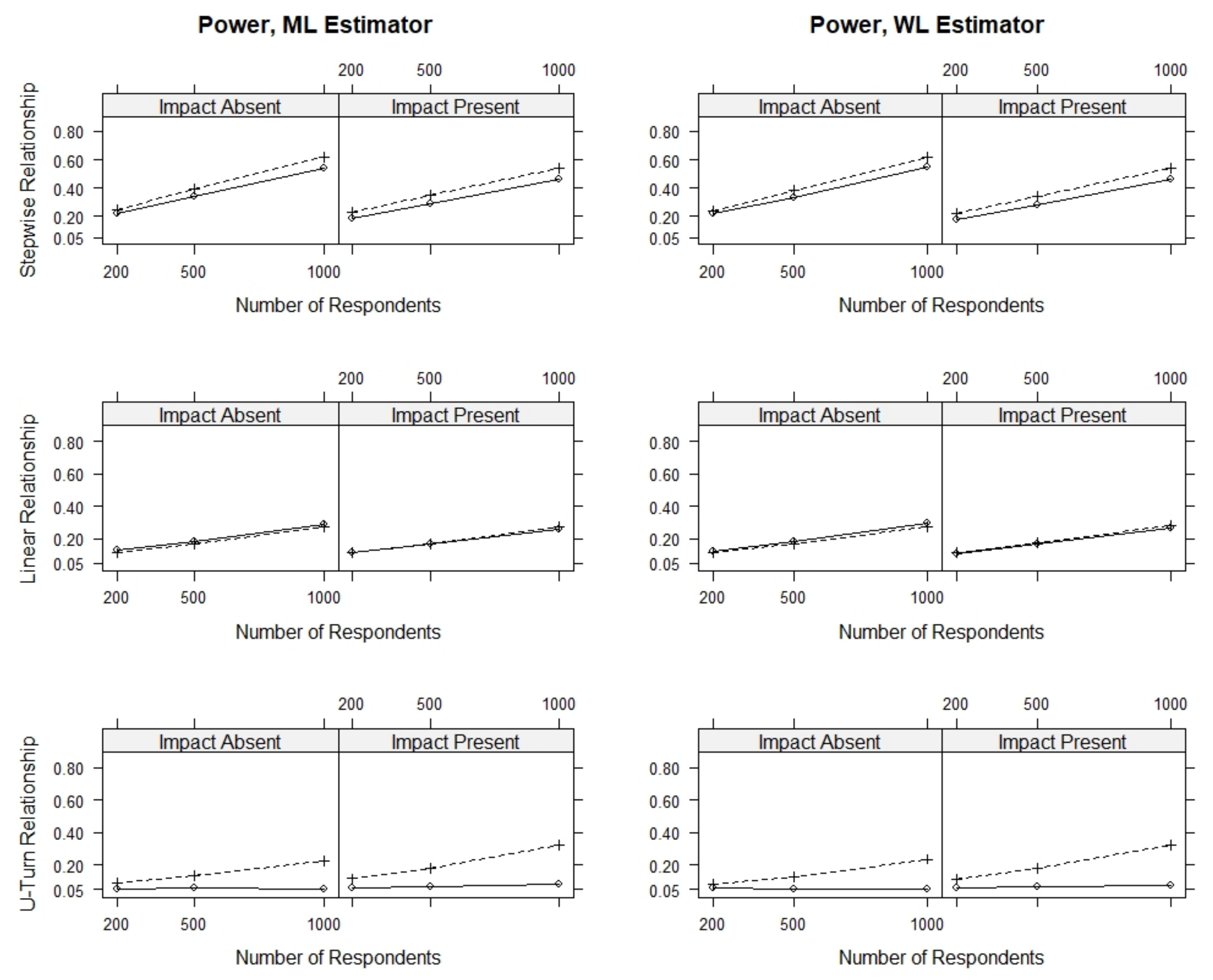Figure 3 presents the rate of significant results for various conditions of sample size, presence of impact, direction of the DIF effect and type of relationship with the person covariate. All power rates were below 0.7, and the highest power rates were observed for the largest sample size, as could be expected.

Overall, we find that the score-based tests have power against all simulated model violations, whereas the linear logistic regression test had power against the stepwise and linear DIF effects but no power against the U-turn DIF effect. The power of all three tests to detect DIF was highest under conditions with a stepwise DIF effect when compared to conditions with a linear or a U-turn DIF effect.

For all three tests, we found that the power was overall comparable for corresponding conditions with and with without ability differences, that is, conditions with and without impact. When comparing the power of the score-based tests and the linear logistic regression test, we found that the score-based tests had slightly higher power against the stepwise DIF effect, comparable power against the linear DIF effect and much higher power against the U-turn DIF effect.

6. Discussion

This study presented an evaluation of several tests for the detection of DIF effects with regard to a continuous covariate. A first practically significant finding is that, at least under the conditions of the simulation study presented here, the number of respondents working on the individual modules differs strongly for the same test, with the exception of the routing module. It follows for similar situations in practical multistage tests that there might be too few responses to individual items or modules to evaluate the presence of DIF in specific modules or to detect other model violations such as local dependence. A similar problem was observed by Zwick and Bridgeman [29]. This is particularly important for the application of DIF tests that are based on asymptotic results, such as the linear logistic regression test. In the study at hand, only items that were worked on by 100 or more respondents were used to evaluate the power and Type I error rate, but this threshold might be too low or too high depending on the item pool used and the population of respondents. Using this threshold, we found that the score-based tests and the linear logistic regression test have a Type I error rate close to the nominal alpha level. The power of all tests can be expected to increase with the underlying sample size, as is also suggested by Figure 3.

In our simulation study, we also found datasets where specific modules were rarely or never presented, obviously because the corresponding items would only be informative for a small part of the population of respondents. This can be regarded as a limitation of our study; in a similar situation in practical assessments, one could consider reassigning the items of such modules to other modules.

Although the DIF effects simulated in this study were large enough to be detected by the various DIF tests, they only had an overall small effect on the precision of the person parameter estimates, as was illustrated by the results reported in Section 5.2. We further found that the power of the various tests was only slightly increased when only DIF-free items were used for the person parameter estimation and that the use of items showing DIF effects for the person parameter estimation and subsequent DIF tests did only lead to a slight increase in false positive results in the score-based tests when there are only few DIF items in the test. In summary, these results give the impression that the person parameter estimates of multistage tests are rather robust under the conditions of this simulation study in that they still provide accurate person parameter estimates that can also be used for DIF tests. However, it should be emphasized that only one or two out of nine items were affected by DIF in our simulations; furthermore, the DIF effects were balanced in some conditions, which may also reduce the bias in the parameter estimation. Since this study strongly focused on a scenario where the item parameters were already sufficiently well known based on previous calibration studies, this rather small percentage of DIF items might be plausible here. However, the results reported in Section 5.2 suggest that the estimation of person parameters becomes increasingly biased when the rate of items affected by DIF and the size of the DIF effects themselves increase. The further investigation of the robustness of the person parameters under a variety of DIF effects is left as a topic for future studies.

A related topic concerns the questions of how to obtain an item set that can be considered as DIF-free. In our study, we have assumed that such an item set is already known, but this will often not be the case in empirical analyses. In linear tests, several strategies were suggested to obtain a set of anchor items [52,53]. The adaptation of such strategies to multistage tests could be another interesting topic for future research.

For stepwise and linear DIF effects, the linear logistic regression test demonstrated power levels that were similar to the power levels of the score-based tests. In these DIF effects, there was a monotone relation between the DIF covariate and the change in the item parameters. However, the linear logistic regression tests did not demonstrate power to detect a U-turn DIF effect, where the change of the item parameter did not correlate with the covariate. This finding is not unexpected since this test assumes a linear relationship between the covariate and the change in the probability of a correct response. While we found no condition where this test had much higher power than the score-based tests, this test was also less affected by the use of DIF items for the person parameter estimation, as we have already outlined.

When comparing the score-based permutation and bootstrap tests, it was found that both tests have very similar power and Type I error rates, at least under the conditions investigated under this study. As outlined in the introduction, the bootstrap test is based on slightly weaker assumptions; that is, it does not assume that the score contributions of all respondents are interchangeable if DIF is absent. It can therefore be recommended for practical applications so far, and future studies might compare these tests under more extensive sets of conditions. However, it might also be important to note that both tests assume that the underlying IRT model describes the observed data well. These tests might therefore be sensitive against various other model violations in addition to DIF.

7. Computational Details

The simulation studies reported in this study were carried out with the R framework for statistical computing, version 4.1.1, using the following R packages (in alphabetical order): mstDIF [54], version 0.1-6, mstR [55], version 1.2, and SimDesign [56], version 2.6.