The Theoretical and Statistical Ising Model: A Practical Guide in R
Abstract
1. Introduction
2. The Theoretical Ising Model
2.1. A Conceptual Introduction
2.2. A Model of Alignment
3. Simulating Ising Dynamics
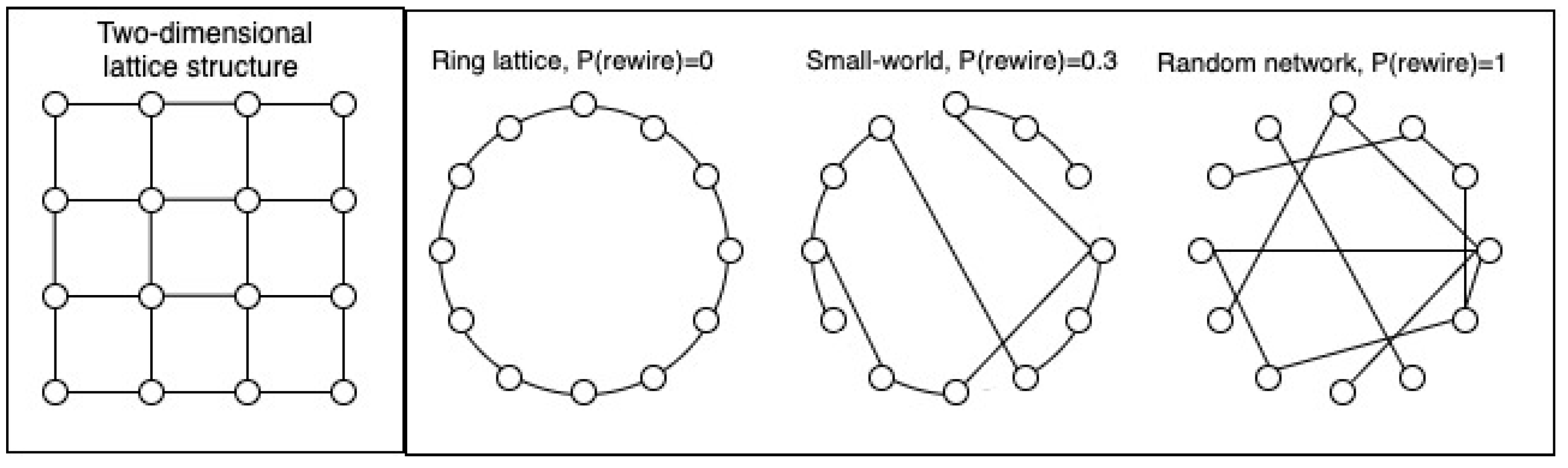
3.1. Network Structures

3.2. Equilibrium Configurations

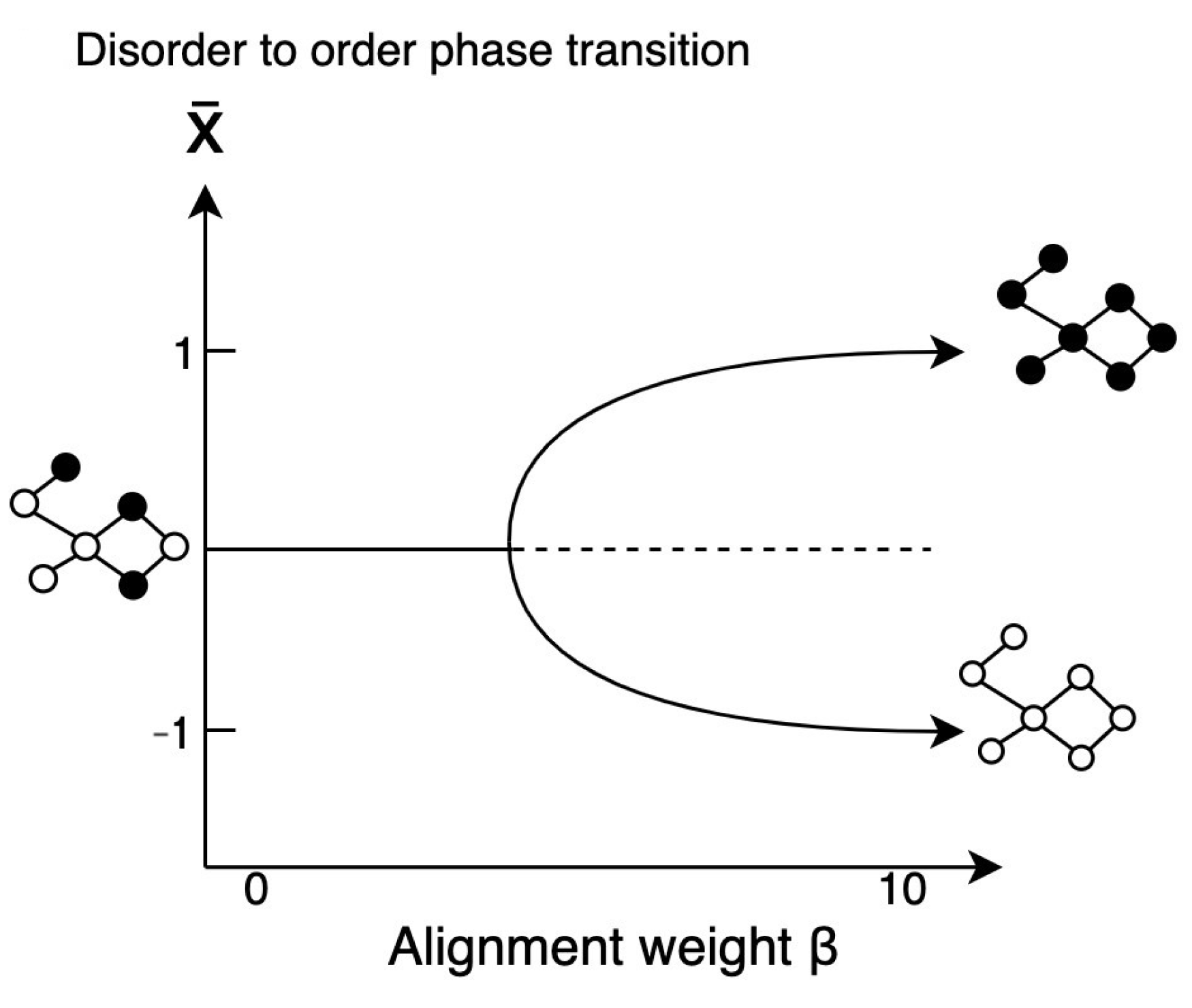
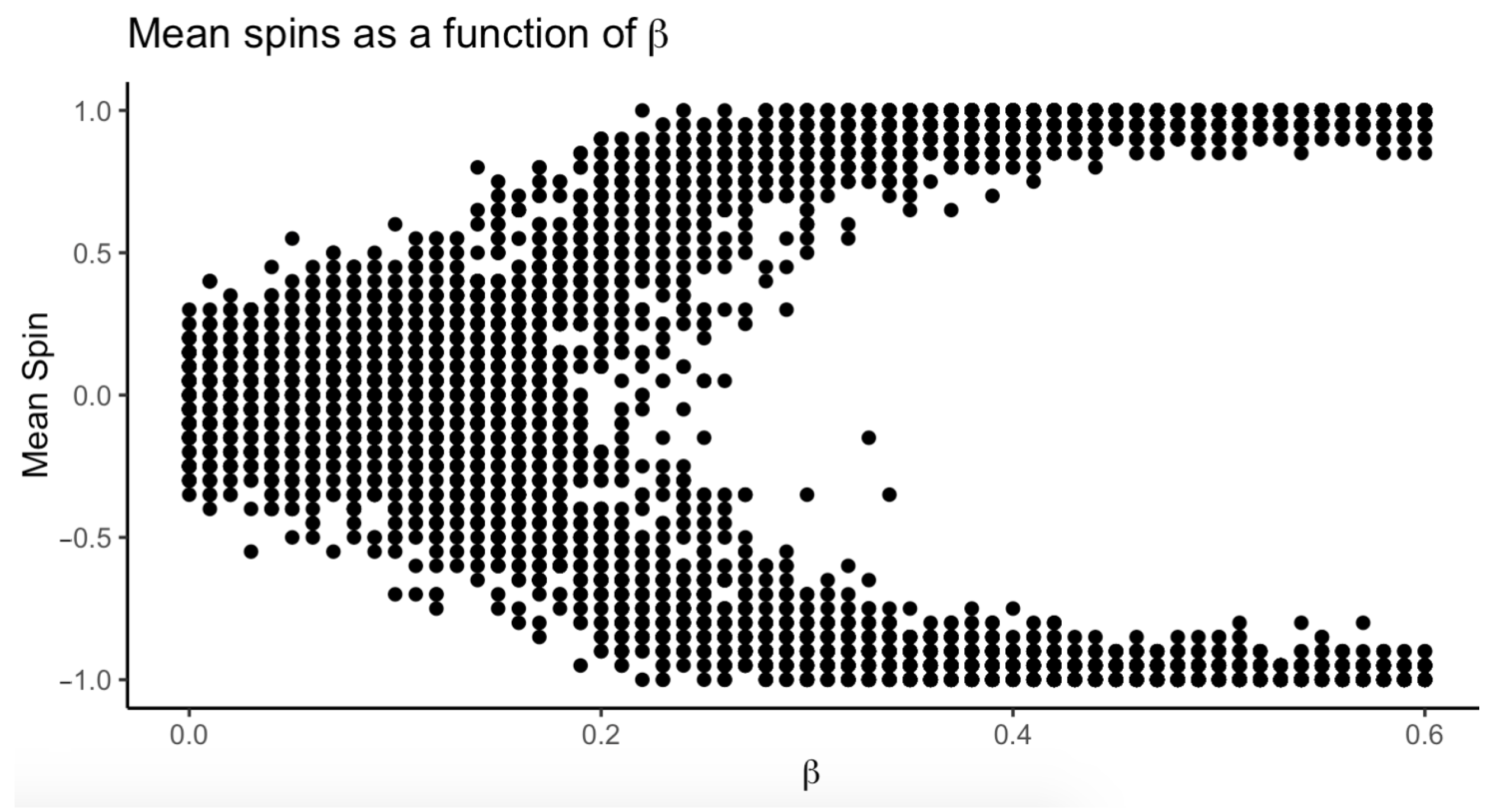
3.3. Dynamics of : A Pitchfork Bifurcation
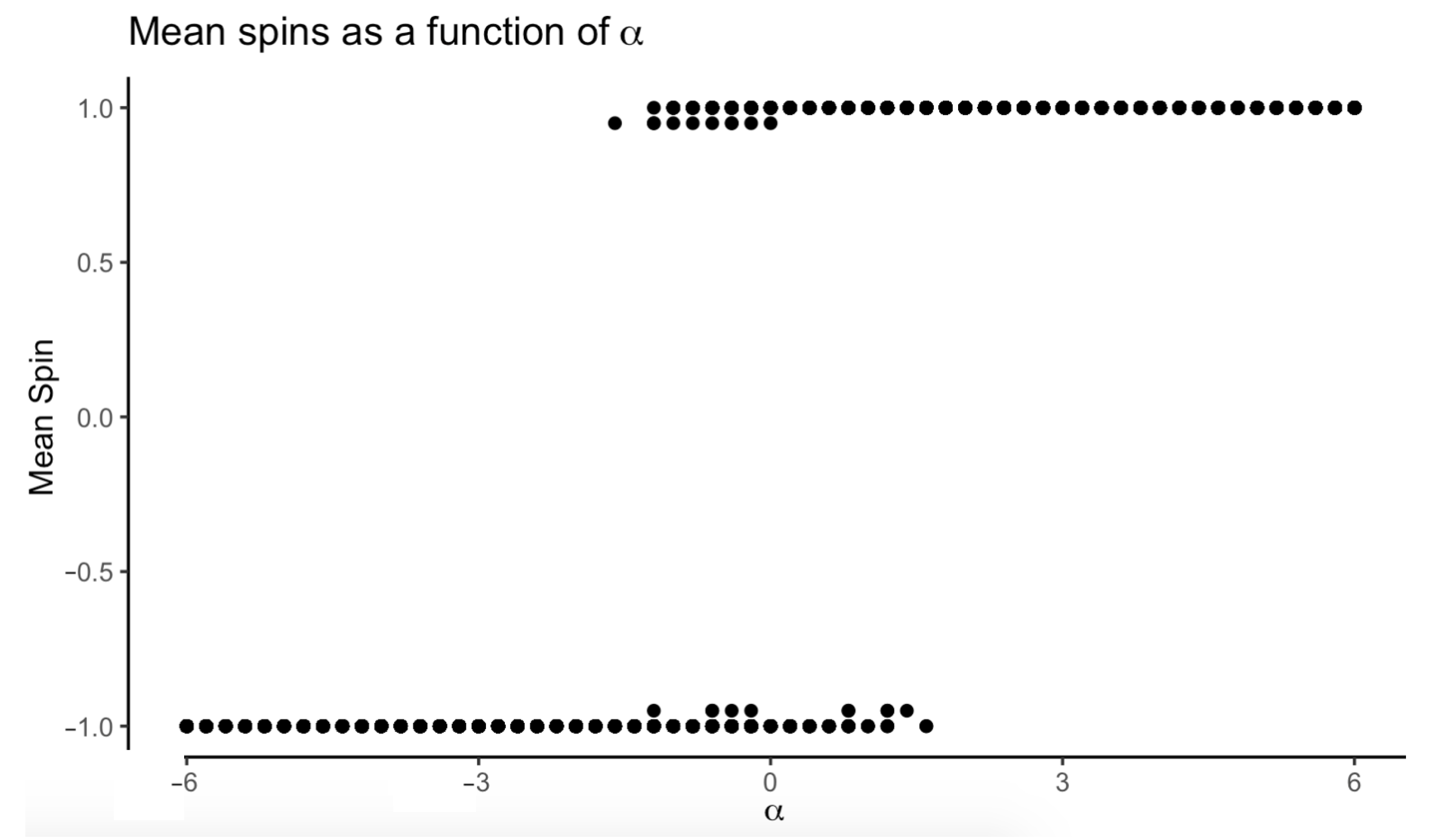
3.4. Dynamics of : Hysteresis
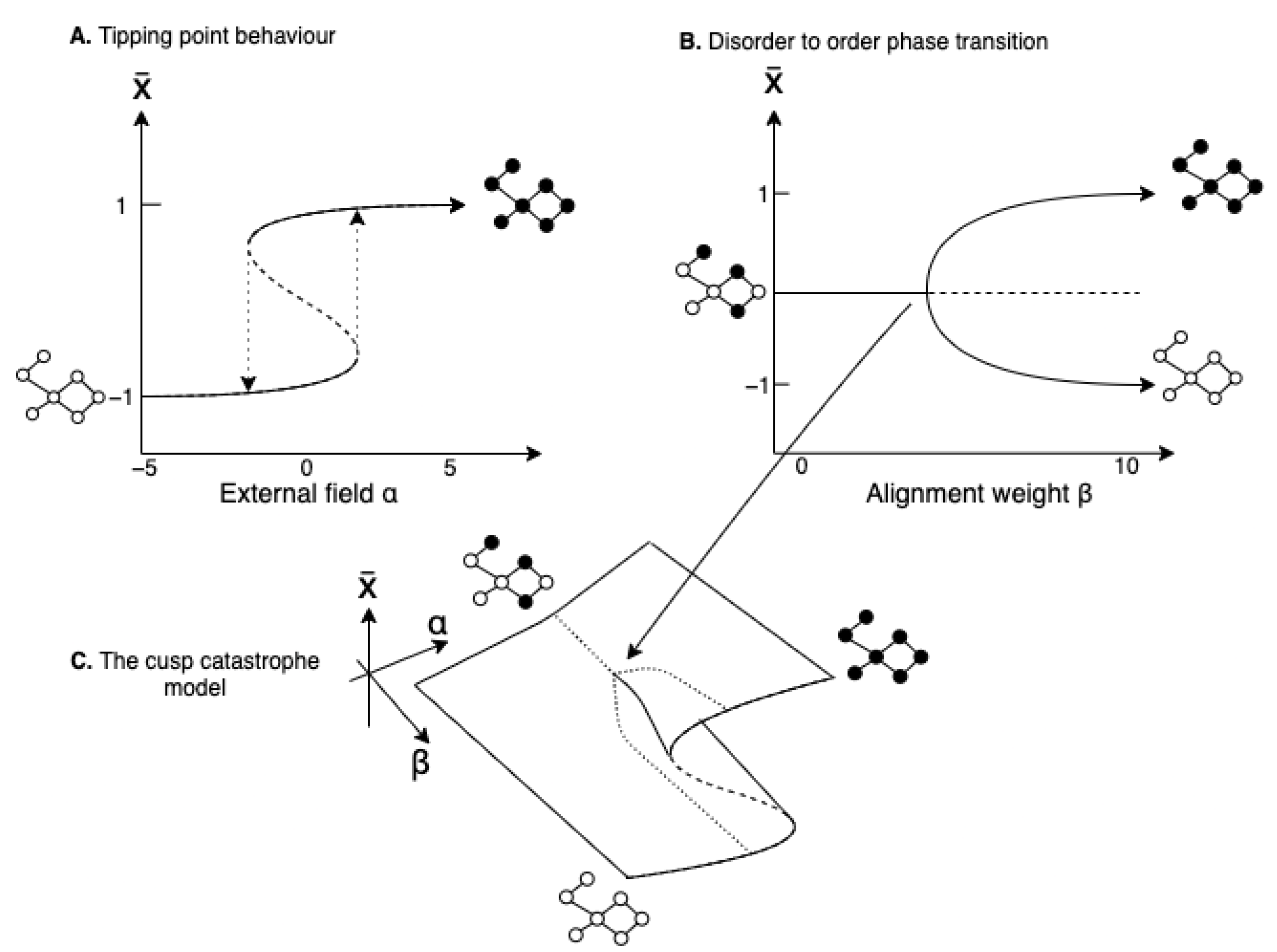
3.5. Summarising the Dynamics as a Cusp
3.6. Variable Encoding
3.7. Theoretical Applications
4. The Statistical Ising Model
4.1. A Decade of Statistical Ising Models
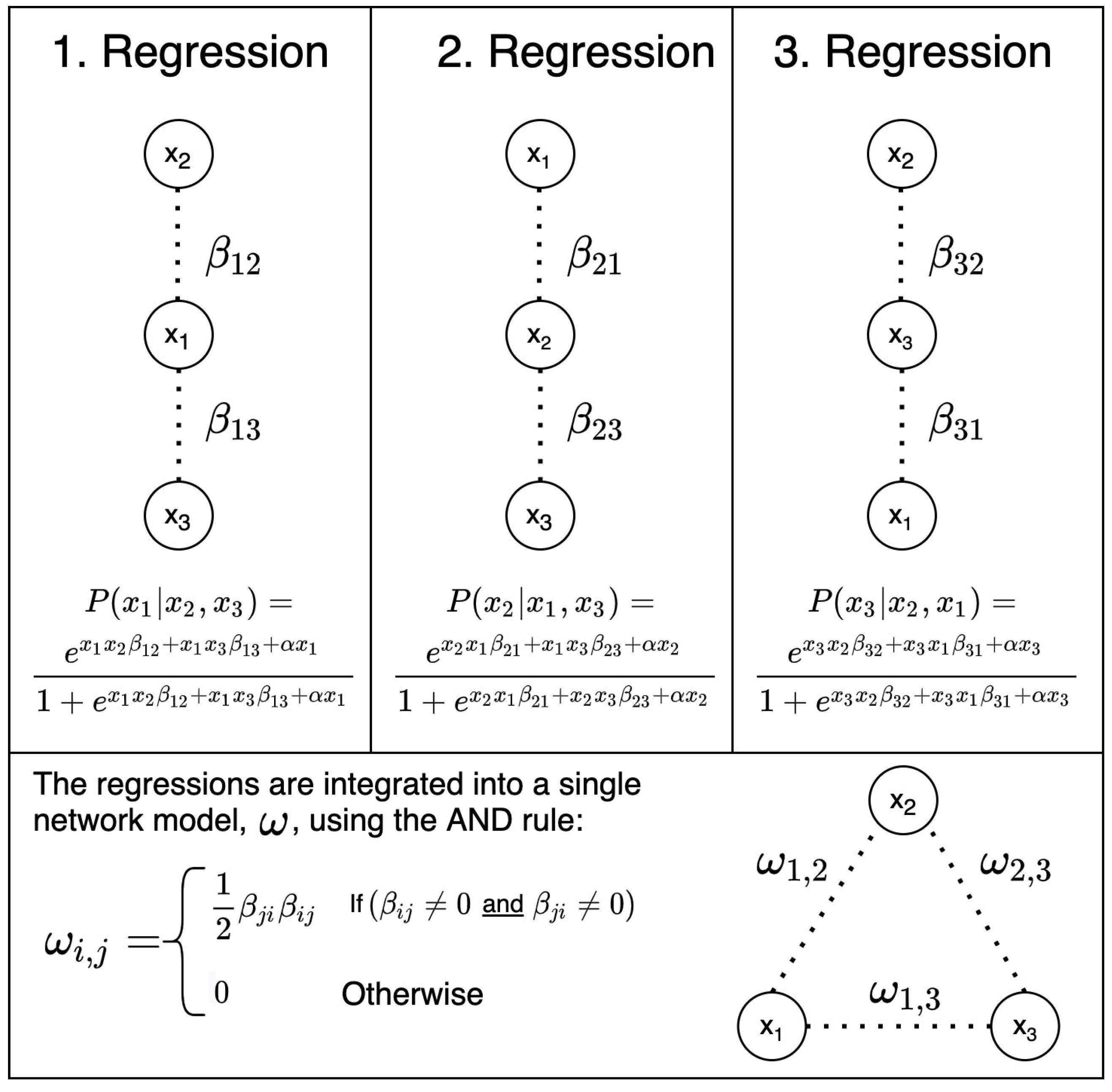
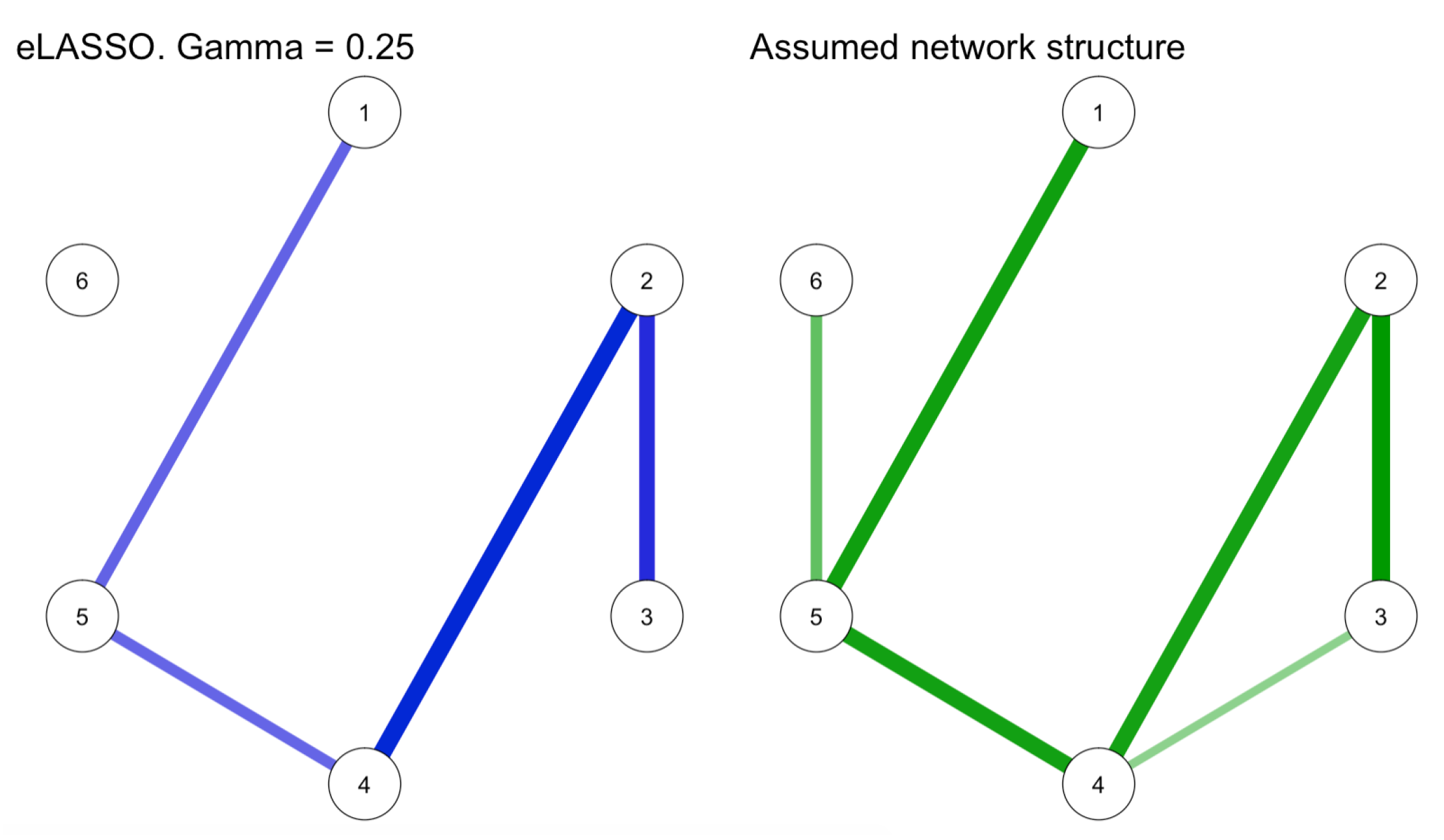
4.2. eLASSO Estimation

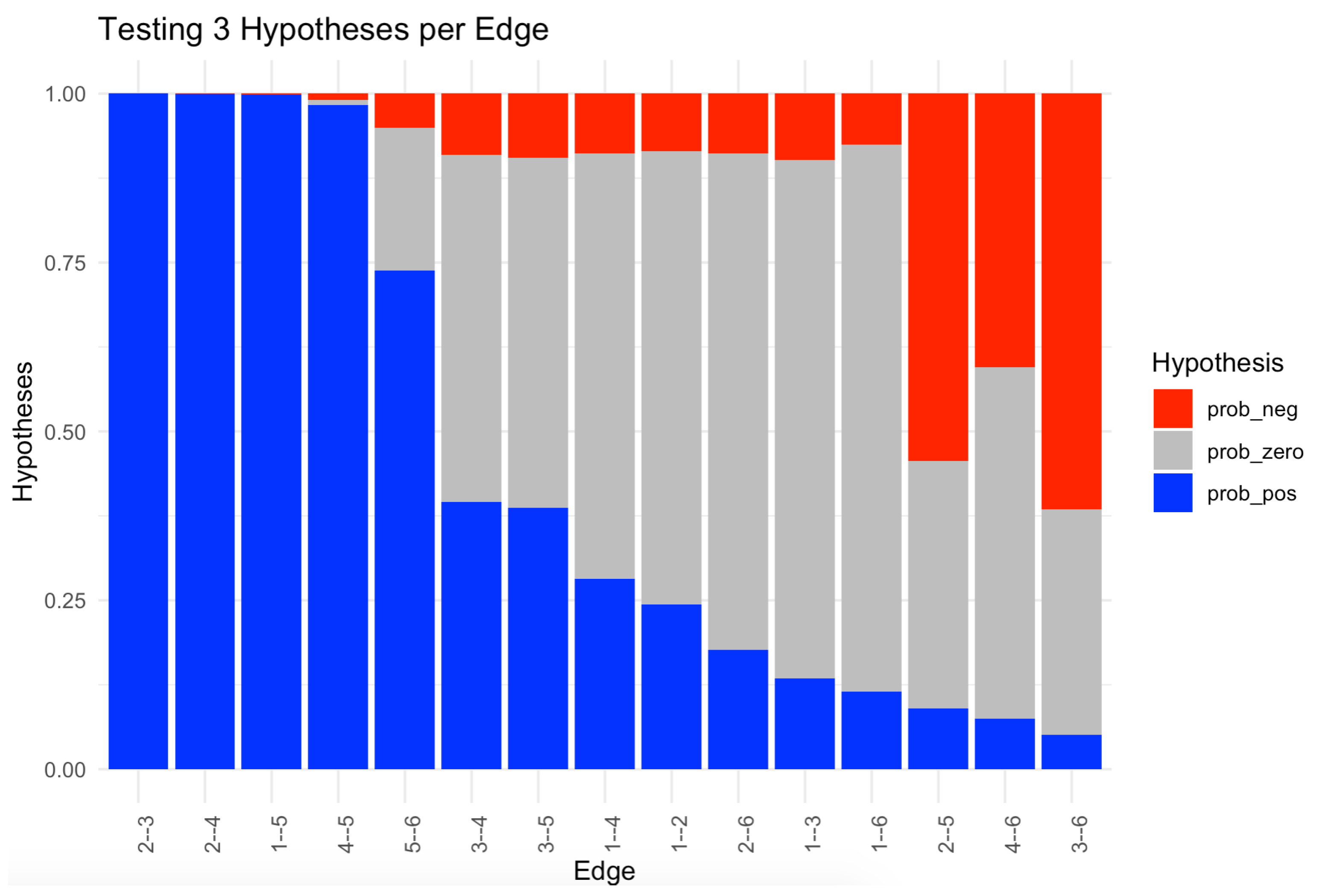
4.3. Bayesian Estimation

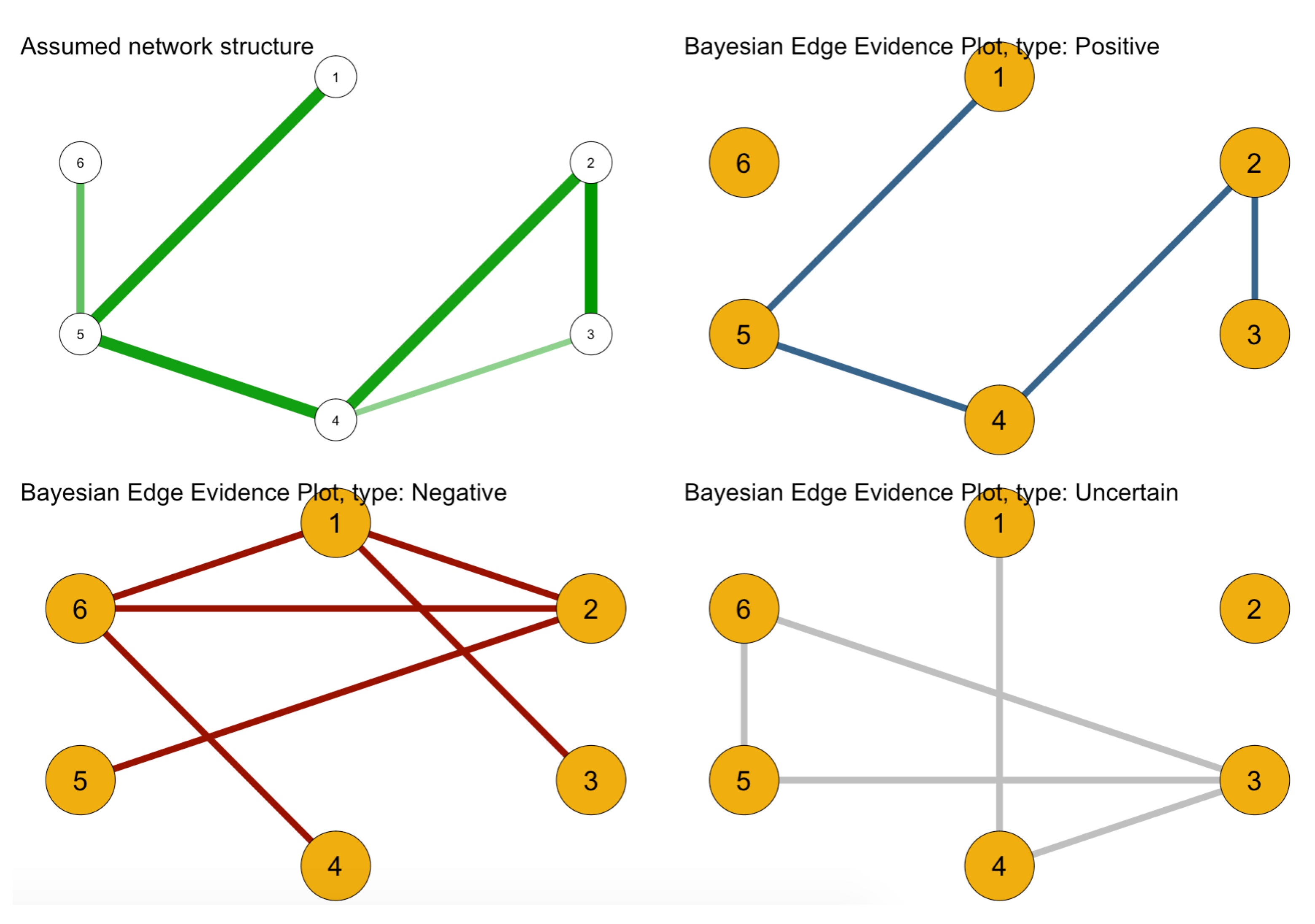

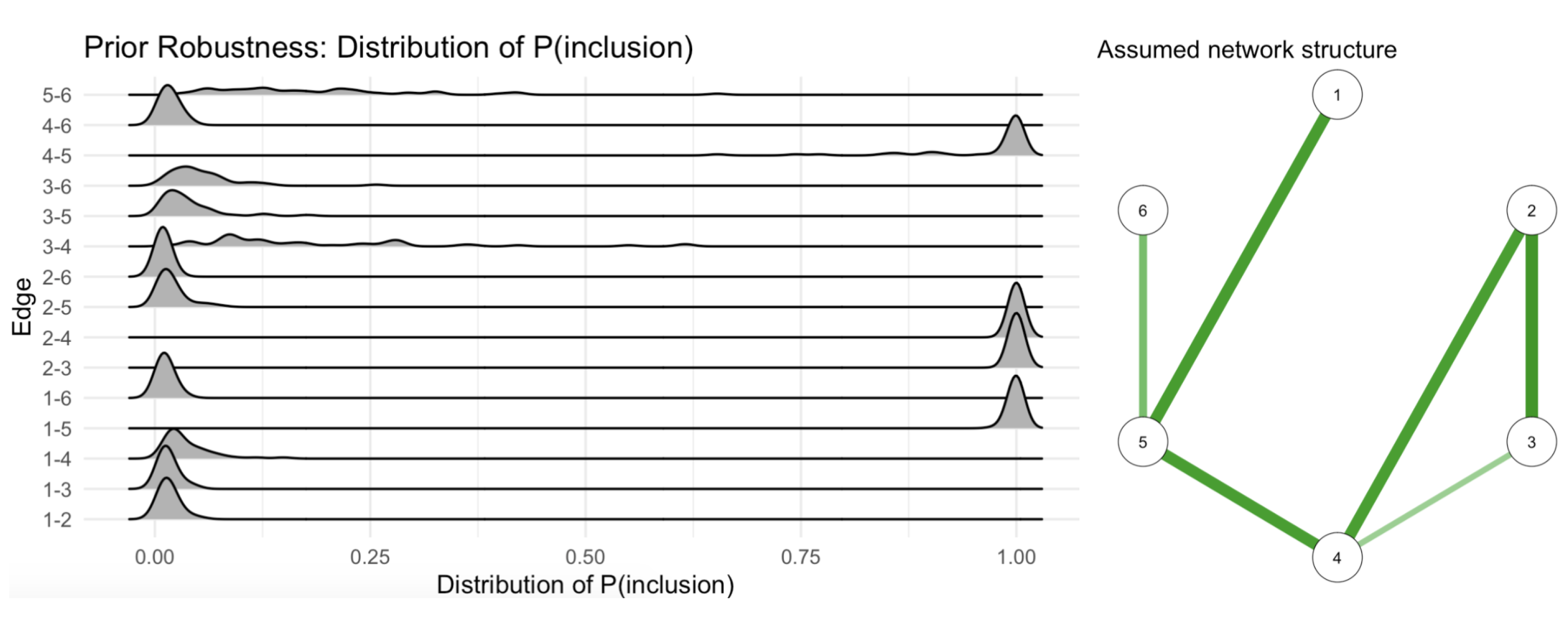

4.4. Maximum Likelihood Estimation
4.5. Summary of Recommendation

| Model | DF | BIC | AIC |
|---|---|---|---|
| Model 1: saturated | 0 | 4965 | 4862 |
| Model 2: Pruned | 11 | 4909 | 4858 |
5. The Practical Gap between Statistical and Theoretical Ising Use
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MFA | Mean-field approximation |
| MLE | Maximum likelihood estimation |
Appendix A

References
- Brush, S.G. History of the Lenz-Ising model. Rev. Mod. Phys. 1967, 39, 883. [Google Scholar] [CrossRef]
- Ernest, I. Ising: Beitrag zur theorie des ferromagnetismus. Z. Für Phys. 1926, 31, 253–258. [Google Scholar]
- Onsager, L. Crystal Statistics. I. A Two-Dimensional Model with an Order-Disorder Transition. Phys. Rev. 1944, 65, 117–149. [Google Scholar] [CrossRef]
- Bhattacharjee, S.M.; Khare, A. Fifty years of the exact solution of the two-dimensional Ising model by Onsager. Curr. Sci. 1995, 69, 816–821. [Google Scholar]
- Sole, R.V. Phase Transitions; Primers in Complex Systems; OCLC: Ocn757257299; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Galam, S. Sociophysics: A review of Galam models. Int. J. Mod. Phys. C 2008, 19, 409–440. [Google Scholar] [CrossRef]
- Kruis, J.; Maris, G. Three representations of the Ising model. Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef] [PubMed]
- van der Maas, H.L.J.; Dalege, J.; Waldorp, L. The polarization within and across individuals: The hierarchical Ising opinion model. J. Complex Netw. 2020, 8, cnaa010. [Google Scholar] [CrossRef]
- Duke, T.A.J.; Bray, D. Heightened sensitivity of a lattice of membrane receptors. Proc. Natl. Acad. Sci. USA 1999, 96, 10104–10108. [Google Scholar] [CrossRef]
- Bornholdt, S.; Wagner, F. Stability of money: Phase transitions in an Ising economy. Phys. A Stat. Mech. Appl. 2002, 316, 453–468. [Google Scholar] [CrossRef]
- Stauffer, D. Social applications of two-dimensional Ising models. Am. J. Phys. 2008, 76, 470–473. [Google Scholar] [CrossRef]
- Roudi, Y. Statistical physics of pairwise probability models. Front. Comput. Neurosci. 2009, 3, 22. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Jaynes, E.T. On the rationale of maximum-entropy methods. Proc. IEEE 1982, 70, 939–952. [Google Scholar] [CrossRef]
- Borsboom, D.; Cramer, A.O. Network analysis: An integrative approach to the structure of psychopathology. Annu. Rev. Clin. Psychol. 2013, 9, 91–121. [Google Scholar] [CrossRef]
- Robinaugh, D.J.; Hoekstra, R.H.A.; Toner, E.R.; Borsboom, D. The network approach to psychopathology: A review of the literature 2008–2018 and an agenda for future research. Psychol. Med. 2020, 50, 353–366. [Google Scholar] [CrossRef] [PubMed]
- Brandt, M.J.; Sleegers, W.W. Evaluating belief system networks as a theory of political belief system dynamics. Personal. Soc. Psychol. Rev. 2021, 25, 159–185. [Google Scholar] [CrossRef]
- Cramer, A.O.J.; van Borkulo, C.D.; Giltay, E.J.; van der Maas, H.L.J.; Kendler, K.S.; Scheffer, M.; Borsboom, D. Major Depression as a Complex Dynamic System. PLoS ONE 2016, 11, e0167490. [Google Scholar] [CrossRef]
- Dalege, J.; Borsboom, D.; Harreveld, F.V.; Lunansky, G.; Maas, H.L.J.v.d. The Attitudinal Entropy (AE) Framework: Clarifications, Extensions, and Future Directions. Psychol. Inq. 2018, 29, 218–228. [Google Scholar] [CrossRef]
- Epskamp, S.; Maris, G.K.J.; Waldorp, L.J.; Borsboom, D. The Wiley Handbook of Psychometric Testing: A Multidisciplinary Reference on Survey, Scale and Test Development; Wiley: Hoboken, NJ, USA, 2016; pp. 953–986. [Google Scholar]
- Fried, E.I.; Bockting, C.; Arjadi, R.; Borsboom, D.; Amshoff, M.; Cramer, A.O.; Epskamp, S.; Tuerlinckx, F.; Carr, D.; Stroebe, M. From loss to loneliness: The relationship between bereavement and depressive symptoms. J. Abnorm. Psychol. 2015, 124, 256. [Google Scholar] [CrossRef] [PubMed]
- Boschloo, L.; Borkulo, C.D.v.; Borsboom, D.; Schoevers, R.A. A Prospective Study on How Symptoms in a Network Predict the Onset of Depression. Psychother. Psychosom. 2016, 85, 183–184. [Google Scholar] [CrossRef] [PubMed]
- Epskamp, S.; Borsboom, D.; Fried, E.I. Estimating psychological networks and their accuracy: A tutorial paper. Behav. Res. Methods 2018, 50, 195–212. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Newman, M.; Watts, D. Renormalization group analysis of the small-world network model. Phys. Lett. A 1999, 263, 341–346. [Google Scholar] [CrossRef]
- Broido, A.D.; Clauset, A. Scale-free networks are rare. Nat. Commun. 2019, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Dalege, J.; Borsboom, D.; Van Harreveld, F.; Van den Berg, H.; Conner, M.; Van der Maas, H.L. Toward a formalized account of attitudes: The Causal Attitude Network (CAN) model. Psychol. Rev. 2016, 123, 2. [Google Scholar] [CrossRef]
- Borsboom, D.; Cramer, A.O.; Schmittmann, V.D.; Epskamp, S.; Waldorp, L.J. The small world of psychopathology. PLoS ONE 2011, 6, e27407. [Google Scholar] [CrossRef]
- Csardi, G.; Nepusz, T. The igraph software package for complex network research. InterJournal 2006, 1695, 1–9. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos; Taylor & Francis Inc.: Abingdon, UK, 2014. [Google Scholar]
- Guastello, S.J.; Koopmans, M.; Pincus, D. Chaos and Complexity in Psychology; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Epskamp, S. parSim: Parallel Simulation Studies. Available online: cran.r-project.org/web/packages/parSim/parSim.pdf (accessed on 29 September 2021).
- Dalege, J.; van der Maas, H.L.J. Accurate by Being Noisy: A Formal Network Model of Implicit Measures of Attitudes. Soc. Cogn. 2020, 38, s26–s41. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.; Foley, J.A.; Folke, C.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [CrossRef]
- Galam, S.; Gefen (Feigenblat), Y.; Shapir, Y. Sociophysics: A new approach of sociological collective behaviour. I. mean-behaviour description of a strike. J. Math. Sociol. 1982, 9, 1–13. [Google Scholar] [CrossRef]
- Ditzinger, T.; Haken, H. Oscillations in the perception of ambiguous patterns a model based on synergetics. Biol. Cybern. 1989, 61, 279–287. [Google Scholar] [CrossRef]
- Bianconi, G. Mean field solution of the Ising model on a Barabási–Albert network. Phys. Lett. A 2002, 303, 166–168. [Google Scholar] [CrossRef]
- Waldorp, L.; Kossakowski, J. Mean field dynamics of stochastic cellular automata for random and small-world graphs. J. Math. Psychol. 2020, 97, 102380. [Google Scholar] [CrossRef]
- van der Maas, H.L.J.; Kolstein, R.; van der Pligt, J. Sudden Transitions in Attitudes. Sociol. Methods Res. 2003, 32, 125–152. [Google Scholar] [CrossRef]
- Siegenfeld, A.F.; Bar-Yam, Y. An Introduction to Complex Systems Science and its Applications. arXiv 2019, arXiv:1912.05088. [Google Scholar]
- Haslbeck, J.M.; Epskamp, S.; Marsman, M.; Waldorp, L.J. Interpreting the Ising model: The input matters. Multivar. Behav. Res. 2020, 56, 303–313. [Google Scholar] [CrossRef] [PubMed]
- Kruis, J. Transformations of mixed spin-class Ising systems. arXiv 2020, arXiv:2006.13581. [Google Scholar]
- Meadows, D.H.; Meadows, D.L.; Randers, J.; Behrens, W.W. The Limits to Growth; Yale University Press: New Haven, CT, USA, 1972. [Google Scholar]
- Oberauer, K.; Lewandowsky, S. Addressing the theory crisis in psychology. Psychon. Bull. Rev. 2019, 26, 1596–1618. [Google Scholar] [CrossRef]
- Fried, E.I. Lack of theory building and testing impedes progress in the factor and network literature. PsyArXiv 2020. [Google Scholar] [CrossRef]
- Mischel, W. The Toothbrush Problem; Association for Psychological Science: Washington, DC, USA, 2008; Volume 21. [Google Scholar]
- Borsboom, D.; van der Maas, H.; Dalege, J.; Kievit, R.; Haig, B. Theory Construction Methodology: A practical framework for theory formation in psychology. PsyArXiv 2020. [Google Scholar] [CrossRef]
- Robinaugh, D.; Haslbeck, J.M.B.; Waldorp, L.; Kossakowski, J.J.; Fried, E.I.; Millner, A.; McNally, R.J.; van Nes, E.H.; Scheffer, M.; Kendler, K.S.; et al. Advancing the Network Theory of Mental Disorders: A Computational Model of Panic Disorder. PsyArXiv 2019. [Google Scholar] [CrossRef]
- Muthukrishna, M.; Henrich, J. A problem in theory. Nat. Hum. Behav. 2019, 3, 221–229. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.X.; Sornette, D. Self-organizing Ising model of financial markets. Eur. Phys. J. B 2007, 55, 175–181. [Google Scholar] [CrossRef]
- Hosseiny, A.; Bahrami, M.; Palestrini, A.; Gallegati, M. Metastable Features of Economic Networks and Responses to Exogenous Shocks. PLoS ONE 2016, 11, e0160363. [Google Scholar] [CrossRef]
- Weber, M.; Buceta, J. The cellular Ising model: A framework for phase transitions in multicellular environments. J. R. Soc. Interface 2016, 13, 20151092. [Google Scholar] [CrossRef]
- Matsuda, H. The Ising model for population biology. Prog. Theor. Phys. 1981, 66, 1078–1080. [Google Scholar] [CrossRef][Green Version]
- Nareddy, V.R.; Machta, J.; Abbott, K.C.; Esmaeili, S.; Hastings, A. Dynamical Ising model of spatially coupled ecological oscillators. J. R. Soc. Interface 2020, 17, 20200571. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Badea, T.; Nathans, J. Order from disorder: Self-organization in mammalian hair patterning. Proc. Natl. Acad. Sci. USA 2006, 103, 19800–19805. [Google Scholar] [CrossRef] [PubMed]
- Bialek, W.; Cavagna, A.; Giardina, I.; Mora, T.; Silvestri, E.; Viale, M.; Walczak, A.M. Statistical mechanics for natural flocks of birds. Proc. Natl. Acad. Sci. USA 2012, 109, 4786–4791. [Google Scholar] [CrossRef]
- Maas, H.L.J.V.D.; Dolan, C.V.; Grasman, R.P.P.P.; Wicherts, J.M.; Huizenga, H.M.; Raijmakers, M.E.J. A dynamical model of general intelligence: The positive manifold of intelligence by mutualism. Psychol. Rev. 2006, 113, 842–861. [Google Scholar] [CrossRef]
- Dalege, J.; Borsboom, D.; van Harreveld, F.; van der Maas, H.L. The Attitudinal Entropy (AE) Framework as a general theory of individual attitudes. Psychol. Inq. 2018, 29, 175–193. [Google Scholar] [CrossRef]
- Milkoreit, M.; Hodbod, J.; Baggio, J.; Benessaiah, K.; Calderón-Contreras, R.; Donges, J.F.; Mathias, J.D.; Rocha, J.C.; Schoon, M.; Werners, S.E. Defining tipping points for social-ecological systems scholarship—an interdisciplinary literature review. Environ. Res. Lett. 2018, 13, 033005. [Google Scholar] [CrossRef]
- Scheffer, M.; Bascompte, J.; Brock, W.A.; Brovkin, V.; Carpenter, S.R.; Dakos, V.; Held, H.; van Nes, E.H.; Rietkerk, M.; Sugihara, G. Early-warning signals for critical transitions. Nature 2009, 461, 53–59. [Google Scholar] [CrossRef] [PubMed]
- Lenton, T.M.; Rockström, J.; Gaffney, O.; Rahmstorf, S.; Richardson, K.; Steffen, W.; Schellnhuber, H.J. Climate tipping points—Too risky to bet against. Nature 2019, 575, 592–595. [Google Scholar] [CrossRef]
- Lenton, T.M. Early warning of climate tipping points. Nat. Clim. Chang. 2011, 1, 201–209. [Google Scholar] [CrossRef]
- Otto, I.M.; Donges, J.F.; Cremades, R.; Bhowmik, A.; Hewitt, R.J.; Lucht, W.; Rockström, J.; Allerberger, F.; McCaffrey, M.; Doe, S.S. Social tipping dynamics for stabilizing Earth’s climate by 2050. Proc. Natl. Acad. Sci. USA 2020, 117, 2354–2365. [Google Scholar] [CrossRef] [PubMed]
- Bentley, R.A.; Maddison, E.J.; Ranner, P.H.; Bissell, J.; Caiado, C.; Bhatanacharoen, P.; Clark, T.; Botha, M.; Akinbami, F.; Hollow, M. Social tipping points and Earth systems dynamics. Front. Environ. Sci. 2014, 2, 35. [Google Scholar] [CrossRef]
- Galesic, M.; Olsson, H.; Dalege, J.; van der Does, T.; Stein, D.L. Integrating social and cognitive aspects of belief dynamics: Towards a unifying framework. J. R. Soc. Interface 2021, 18, 20200857. [Google Scholar] [CrossRef]
- Page, S.E. The Model Thinker: What You Need to Know to Make Data Work for You, 1st ed.; OCLC: on1028523969; Basic Books: New York, NY, USA, 2018. [Google Scholar]
- Borsboom, D. A network theory of mental disorders. World Psychiatry 2017, 16, 5–13. [Google Scholar] [CrossRef]
- Van Borkulo, C.D.; Borsboom, D.; Epskamp, S.; Blanken, T.F.; Boschloo, L.; Schoevers, R.A.; Waldorp, L.J. A new method for constructing networks from binary data. Sci. Rep. 2014, 4, 1–10. [Google Scholar] [CrossRef]
- Fried, E.I. Theories and Models: What They Are, What They Are for, and What They Are About. Psychol. Inq. 2020, 31, 336–344. [Google Scholar] [CrossRef]
- Kindermann, R.; Snell, J.L. Markov Random Fields and Their Applications; OCLC: 1030357447; American Mathematical Society: Providence, RI, USA, 2012. [Google Scholar]
- Cox, D.R.; Wermuth, N. Linear dependencies represented by chain graphs. Stat. Sci. 1993, 8, 204–218. [Google Scholar] [CrossRef]
- Anderson, C.J.; Vermunt, J.K. Log-Multiplicative Association Models as Latent Variable Models for Nominal and/or Ordinal Data. Sociol. Methodol. 2000, 30, 81–121. [Google Scholar] [CrossRef]
- Wickens, T.D. Multiway Contingency Tables Analysis for the Social Sciences; Psychology Press: East Sussex, UK, 2014. [Google Scholar]
- Marsman, M.; Borsboom, D.; Kruis, J.; Epskamp, S.; van Bork, R.; Waldorp, L.J.; Maas, H.L.J.v.d.; Maris, G. An Introduction to Network Psychometrics: Relating Ising Network Models to Item Response Theory Models. Multivar. Behav. Res. 2018, 53, 15–35. [Google Scholar] [CrossRef]
- Ravikumar, P.; Wainwright, M.J.; Lafferty, J.D. High-dimensional Ising model selection using ι1-regularized logistic regression. Ann. Stat. 2010, 38, 1287–1319. [Google Scholar] [CrossRef]
- Haslbeck, J.M.B.; Waldorp, L.J. mgm: Estimating Time-Varying Mixed Graphical Models in High-Dimensional Data. arXiv 2020, arXiv:1510.06871. [Google Scholar] [CrossRef]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 398. [Google Scholar]
- Epskamp, S.; Kruis, J.; Marsman, M. Estimating psychopathological networks: Be careful what you wish for. PLoS ONE 2017, 12, e0179891. [Google Scholar] [CrossRef]
- Meehl, P.E. Why Summaries of Research on Psychological Theories are Often Uninterpretable. Psychol. Rep. 1990, 66, 195–244. [Google Scholar] [CrossRef]
- Williams, D.R.; Briganti, G.; Linkowski, P.; Mulder, J. On Accepting the Null Hypothesis of Conditional Independence in Partial Correlation Networks: A Bayesian Analysis. PsyArXiv 2021. Available online: psyarxiv.com/7uhx8 (accessed on 27 July 2021).
- Marsman, M.; Huth, K.; Waldorp, L.; Ntzoufras, I. Objective Bayesian Edge Screening and Structure Selection for Networks of Binary Variables. PsyArXiv 2020, 26. Available online: psyarxiv.com/dg8yx/ (accessed on 15 July 2021).
- Huth, K.; Luigjes, J.; Goudriaan, A.; van Holst, R. Modeling Alcohol Use Disorder as a Set of Interconnected Symptoms-Assessing Differences between Clinical and Population Samples and Across External Factors. PsyArXiv 2021. Available online: psyarxiv.com/93t2f/ (accessed on 25 June 2021).
- Williams, D.R.; Mulder, J. Bayesian hypothesis testing for Gaussian graphical models: Conditional independence and order constraints. J. Math. Psychol. 2020, 99, 102441. [Google Scholar] [CrossRef]
- Epskamp, S.; Isvoranu, A.M.; Cheung, M. Meta-analytic Gaussian Network Aggregation. PsyArXiv 2020. [Google Scholar] [CrossRef]

| Package::Function() | Description |
|---|---|
| IsingSampler::Isingsampler() | Flexible Ising state sampler |
| bayess:isinghm() | Metropolis–Hastings Sampler |
| igraph::make_lattice() | N dimensional lattice structures |
| igraph::sample_small_world() | Watts–Strogatz model |
| parSim::parSim() | Easy simulations and multi-core |
| ggplot2::ggplot() | Visualisation |
| set.seed() | Reproduces random numbers |
| Package::Function() | Description | Pros | Cons | Encoding |
|---|---|---|---|---|
| IsingFit::IsingFit() | eLASSO estimation | Small–medium samples detecting present edges Applicable to >20 variables | Large samples Interpreting absent edges | (1, 0) |
| psychometrics::Ising() | Full maximum likelihood | Large samples Extensive further analysis options | Small samples Max of 20 variables | Any |
| mgm::mgm() | eLASSO | For mixtures of binary, continuous, and ordinal variables | Large samples Interpreting absent edges | (1, 0) |
| rIsing::Ising() | eLASSO | Small–medium samples Detecting present edges Applicable to >20 variables | Large samples Interpreting absent edges | (1, 0) |
| rbinnet::select_structure() | Bayesian estimation Slap and spike prior | Evidence of absent edges Model uncertainty Prior information use | Work in progress Prior information dependent | (1, 0) |
| BGGM::explore(type = “binary”) | Bayesian estimation F-matrix prior | Evidence of absent edges Model uncertainty Prior information use | Prior information dependent | (1, 0) |
| BDgraph::bdgraph() | Bayesian model selection G-wishart Prior | Model uncertainty Prior information use | Prior information dependent | (1, 0) |
| IsingFit::LinTransform() | Transforms between (1, 0) and (1, −1) encodings | Works with unregularised models (psychometrics) | Any | |
| NetworkComparisonTest::NCT() | Group comparison test | Works with eLASSO models |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Finnemann, A.; Borsboom, D.; Epskamp, S.; van der Maas, H.L.J. The Theoretical and Statistical Ising Model: A Practical Guide in R. Psych 2021, 3, 593-617. https://doi.org/10.3390/psych3040039
Finnemann A, Borsboom D, Epskamp S, van der Maas HLJ. The Theoretical and Statistical Ising Model: A Practical Guide in R. Psych. 2021; 3(4):593-617. https://doi.org/10.3390/psych3040039
Chicago/Turabian StyleFinnemann, Adam, Denny Borsboom, Sacha Epskamp, and Han L. J. van der Maas. 2021. "The Theoretical and Statistical Ising Model: A Practical Guide in R" Psych 3, no. 4: 593-617. https://doi.org/10.3390/psych3040039
APA StyleFinnemann, A., Borsboom, D., Epskamp, S., & van der Maas, H. L. J. (2021). The Theoretical and Statistical Ising Model: A Practical Guide in R. Psych, 3(4), 593-617. https://doi.org/10.3390/psych3040039






