Bivariate Distributions Underlying Responses to Ordinal Variables
Abstract
:1. Introduction
The Present Study
2. The Polychoric Correlation Assuming Different Underlying Distributions
2.1. The Bivariate Normal Distribution
2.2. The Skew-Normal Distribution
2.3. Mixture of Normal Distributions
2.4. Testing Underlying Distributions
3. Illustrative Example
Example: Type D Personality Data
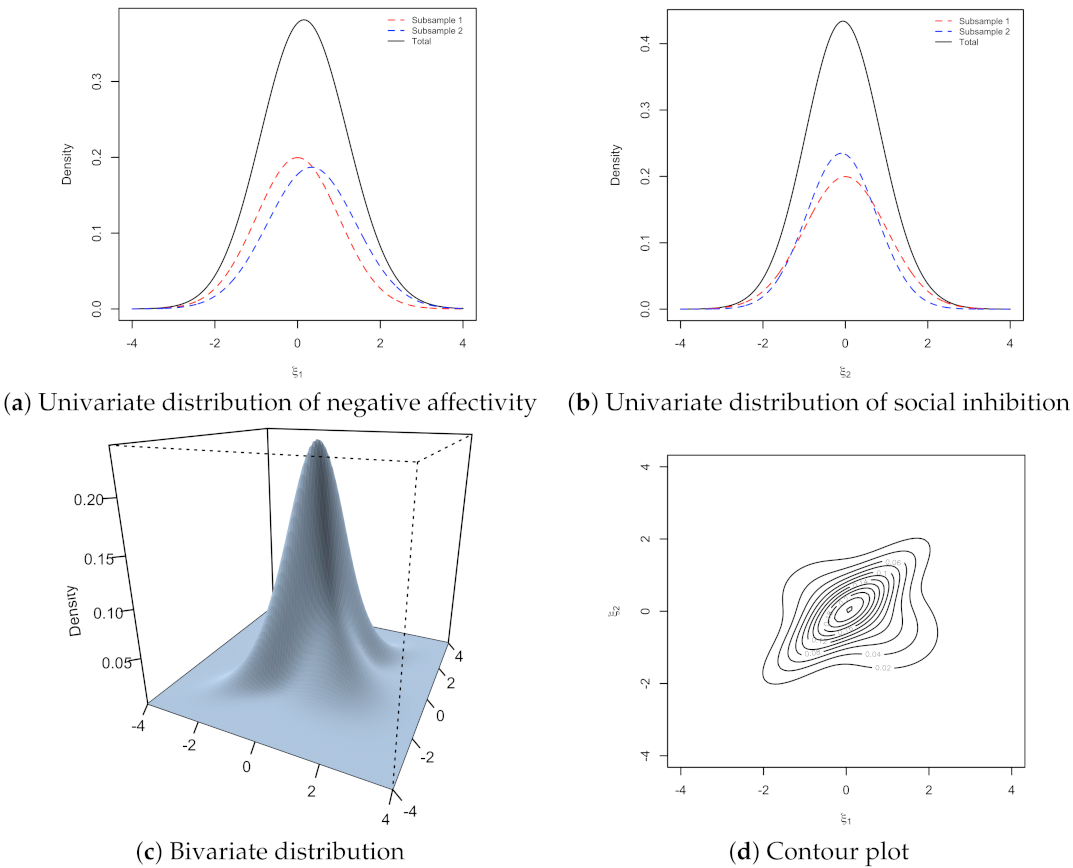
4. Empirical Study on the Fit of Different Distributions
4.1. Empirical Data
4.1.1. Type D Personality Data
4.1.2. Health Status Data
4.2. Fitted Distributions
4.3. Analysis
4.4. Results
4.4.1. Rejections of the Distributions
4.4.2. Absolute Difference in
5. Discussion
5.1. Future Research and Limitations
5.2. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- ## Script: Functions for the bivariate (skew-)normal distribution
- # Fit function
- LR_skew <- function(params) {
- nthresholds1 = length(params[1:nthresholds1])
- nthresholds2 = length(params[(nthresholds1+1):(nthresholds1+nthresholds2)])
- upperlimit1 = 10 + params[nthresholds1]
- upperlimit2 = 10 + params[nthresholds1+nthresholds2]
- limits1 = c(params[1:nthresholds1], upperlimit1)
- limits2 = c(params[(nthresholds1+1):(nthresholds1+nthresholds2)], upperlimit2)
- if(is.na(params["alpha1"])){alpha1 = 0} else {alpha1 = params["alpha1"]}
- if(is.na(params["alpha2"])){alpha2 = 0} else {alpha2 = params["alpha2"]}
- cumul = matrix(0, ncats1, ncats2)
- expp = matrix(0, ncats1, ncats2)
- for (i in 1:ncats1) {
- for (j in 1:ncats2) {
- cumul[i,j] = sn::pmsn(c(limits1[i], limits2[j]), c(0,0),
- matrix(c(1, params["corr"], params["corr"], 1),2,2),
- c(alpha1, alpha2))
- }
- }
- expp[1,1] = cumul[1,1]
- for (i in 2:ncats1) { expp[i,1] = cumul[i,1] - cumul[i-1,1] }
- for (j in 2:ncats2) { expp[1,j] = cumul[1,j] - cumul[1,j-1] }
- for (i in 2:ncats1) {
- for (j in 2:ncats2) {
- expp[i,j] = cumul[i,j] - cumul[i-1,j] - cumul[i,j-1] + cumul[i-1,j-1]
- }
- }
- pi = ifelse(expp > 0, expp, 0.0000000001)
- p = ifelse (obsp > 0, obsp, 0.0000000001)
- return(2*ntot*sum(obsp*log(p/pi)))
- }
- # Optimization
- fit_skewnorm <- function(parameters){
- results_skew = nlminb(parameters, LR_skew, control = list(rel.tol = 1e-3))
- out = data.frame(matrix(NA, 1, 1))
- colnames(out) = c("chisq")
- out$chisq = results_skew$objective
- out$df = ncats1 * ncats2 - 1 - length(results_skew$par)
- out$p = 1 - pchisq(results_skew$objective, out$df)
- out$corr = results_skew$par["corr"]
- if(!is.na(results_skew$par["alpha1"])) {
- out$alpha1 = results_skew$par["alpha1"]
- }
- if(!is.na(results_skew$par["alpha2"])) {
- out$alpha2 = results_skew$par["alpha2"]
- }
- options(scipen=999)
- return(list("results" = results_skew, "output" = out))
- }
Appendix B
- ## Script: Functions for the mixture of bivariate distributions
- # Bivariate normal distribution
- biv <- function(thresholds1, thresholds2, muvar, covma) {
- nthresholds1 = length(thresholds1)
- nthresholds2 = length(thresholds2)
- ncats1 = nthresholds1 + 1
- ncats2 = nthresholds2 + 1
- upperlimit1 = 10 + thresholds1[nthresholds1]
- upperlimit2 = 10 + thresholds2[nthresholds2]
- limits1 = c(thresholds1, upperlimit1)
- limits2 = c(thresholds2, upperlimit2)
- cumul = matrix(0, ncats1, ncats2)
- expp = matrix(0, ncats1, ncats2)
- for (i in 1:ncats1) {
- for (j in 1:ncats2) {
- cumul[i,j] = mnormt::pmnorm(c(limits1[i], limits2[j]), muvar, covma)
- }
- }
- expp[1,1] = cumul[1,1]
- for (i in 2:ncats1) { expp[i,1] = cumul[i,1] - cumul[i-1,1] }
- for (j in 2:ncats2) { expp[1,j] = cumul[1,j] - cumul[1,j-1] }
- for (i in 2:ncats1) {
- for (j in 2:ncats2) {
- expp[i,j] = cumul[i,j] - cumul[i-1,j] - cumul[i,j-1] + cumul[i-1,j-1]
- }
- }
- return(expp)
- }
- # Fit function
- LR_mixed <- function(params) {
- thresholds1 = params[1:nthresholds1]
- thresholds2 = params[(nthresholds1+1):(nthresholds1+nthresholds2)]
- nthresholds1 = length(params[1:nthresholds1])
- nthresholds2 = length(params[(nthresholds1+1):(nthresholds1+nthresholds2)])
- if(is.na(params["sigmastar1"])){sigmastar1 = 1} else {sigmastar1 = params["sigmastar1"]}
- if(is.na(params["sigmastar2"])){sigmastar2 = 1} else {sigmastar2 = params["sigmastar2"]}
- if(is.na(params["mustar1"])){mustar1 = 0} else {mustar1 = params["mustar1"]}
- if(is.na(params["mustar2"])){mustar2 = 0} else {mustar2 = params["mustar2"]}
- if(is.na(params["corrstar"])){corrstar = params["corr"]}
- else {corrstar = params["corrstar"]}
- covstar = corrstar*sqrt(sigmastar1*sigmastar2)
- expp = biv(thresholds1, thresholds2, c(0,0), matrix(c(1, params["corr"],
- params["corr"], 1),2,2))
- if (params["prop"] > 0) {
- exppstar = biv(thresholds1, thresholds2, c(mustar1, mustar2),
- matrix(c(sigmastar1, covstar, covstar, sigmastar2),2,2))
- expp = (params["prop"]*expp) + ((1-params["prop"])*exppstar)
- }
- pi = ifelse(expp > 0, expp, 0.0000000001)
- p = ifelse (obsp > 0, obsp, 0.0000000001)
- return(2*ntot*sum(obsp*log(p/pi)))
- }
- # Optimization
- fit_mix <- function(parameters, ll, uu){
- if (missing(ll)) ll = -100
- if (missing(uu)) uu = 100
- results_mixed = nlminb(parameters, LR_mixed, lower = ll, upper = uu)
- out = data.frame(matrix(NA, 1, 1))
- colnames(out) = c("chisq")
- out$chisq = results_mixed$objective
- out$df = ncats1 * ncats2 - 1 - length(results_mixed$par)
- out$p = round(1 - pchisq(results_mixed$objective, out$df), 3)
- out$corr = results_mixed$par["corr"]
- if(!is.na(results_mixed$par["mustar1"])) {
- out$mustar1 = results_mixed$par["mustar1"]
- }
- if(!is.na(results_mixed$par["mustar2"])) {
- out$mustar2 = results_mixed$par["mustar2"]
- }
- out$prop = results_mixed$par["prop"]
- if(!is.na(results_mixed$par["sigmastar1"])) {
- out$sigstar1 = results_mixed$par["sigmastar1"]
- }
- if(!is.na(results_mixed$par["sigmastar2"])) {
- out$sigstar2 = results_mixed$par["sigmastar2"]
- }
- if(!is.na(results_mixed$par["corrstar"])) {
- out$corrstar = results_mixed$par["corrstar"]
- }
- options(scipen=999)
- return(list("results" = results_mixed, "output" = out))
- }
Appendix C
- ## Script: Fitting distributions to Type D personality data
- # Required packages
- library(polycor) # we used version 3.0.6
- library(sn) # we used version 2.0.0
- library(mnormt) # we used version 0.7-10
- library(mokken) # we used version 2.0.2
- ########################
- #### Initialization ####
- ########################
- data("DS14")
- obsn = table(DS14[,"Na2"], DS14[,"Si6"])
- ncats1 = nrow(obsn)
- ncats2 = ncol(obsn)
- ntot = sum(obsn)
- obsp = obsn/ntot
- proportions2 = matrix(colSums(obsp), 1, ncats2)
- proportions1 = matrix(rowSums(obsp), ncats1, 1)
- premultiplier = matrix(0, ncats1, ncats1)
- for (i in 1:ncats1) for (j in 1:i) premultiplier[i, j] = 1
- postmultiplier = matrix(0, ncats2, ncats2)
- for (i in 1:ncats2) for (j in i:ncats2) postmultiplier[i, j] = 1
- cumulprops2 = proportions2 %*% postmultiplier
- cumulprops1 = premultiplier %*% proportions1
- nthresholds1 = ncats1 - 1
- nthresholds2 = ncats2 - 1
- thresholds1 = matrix(0, 1, nthresholds1)
- for (i in 1:nthresholds1) thresholds1[i] = qnorm(cumulprops1[i])
- thresholds2 = matrix (0, 1, nthresholds2)
- for (i in 1:nthresholds2) thresholds2[i] = qnorm(cumulprops2[i])
- corr = polycor::polychor(obsn)
- ###########################
- #### Fit distributions ####
- ###########################
- # Fit bivariate normal distribution
- results_norm = fit_skewnorm(c("th1" = thresholds1, "th2" = thresholds2,
- "corr" = corr))
- results_norm
- # Fit skew-normal distribution
- results_skew = fit_skewnorm(c("th1" = thresholds1, "th2" = thresholds2,
- "corr" = corr, "alpha" = c(2,2)))
- results_skew
- # Calculate polychoric correlation assuming a skew-normal
- dp = list(xi = c(0,0), Omega = matrix(c(1, results_skew$output$corr,
- results_skew$output$corr, 1),2,2), alpha = c(results_skew$output$alpha1,
- results_skew$output$alpha2))
- sn1 = sn::makeSECdistr(dp, family = "SN")
- summary(sn1)
- polcorr = (results_skew$output$corr-2*pi^(-1)*0.3816442*0.8618373) /
- (((1-2*pi^(-1)*0.3816442^2)*(1-2*pi^(-1)*0.8618373^2))^0.5)
- # Fit mixture distribution
- param = c("th1" = thresholds1, "th2" = thresholds2, "corr" = corr, "prop" = 0.7,
- "corrstar" = corr, "sigmastar1" = 1, "sigmastar2" = 1, "mustar1" = 0,
- "mustar2" = 0)
- results_mix = fit_mix(param, c(rep(-10, nthresholds1+nthresholds2), -1, 0, -1,
- 0.001, 0.001, -10, -10), c(rep(10, nthresholds1+nthresholds2),
- 1, 1, 1, 10, 10, 10, 10))
- results_mix
Appendix D
| Distributions | Type D Personality | Health Status | ||||
|---|---|---|---|---|---|---|
| 1e-10 | 1e-5 | 1e-3 | 1e-10 | 1e-5 | 1e-3 | |
| Normal | 0.00 | 0.00 | 0.00 | 0.82 | 0.00 | 0.00 |
| Skew-normal | 81.32 | 36.26 | 5.49 | 62.15 | 7.79 | 7.79 |
| Mixture () | 24.18 | 23.08 | 17.58 | 14.13 | 6.09 | 6.09 |
| Mixture () | 20.88 | 1.10 | 0.00 | 54.85 | 0.55 | 0.55 |
| Mixture ( free) | 42.86 | 25.27 | 7.69 | 41.55 | 4.16 | 4.16 |
References
- Pearson, K. Mathematical Contributions to the Theory of Evolution. VII. On the Correlation of Characters not Quantitatively Measurable. Philos. Trans. R. Soc. London. Ser. A Contain. Pap. Math. Phys. Character 1900, 195, 1–47. [Google Scholar] [CrossRef] [Green Version]
- Jöreskog, K.G.; Sörbom, D. PRELIS 2 User’s Reference Guide; Scientific Software International: Chicago, IL, USA, 1996. [Google Scholar]
- Babakus, E.; Ferguson, C.E. On choosing the appropriate measure of association when analyzing rating scale data. J. Acad. Mark. Sci. 1988, 16, 95–102. [Google Scholar] [CrossRef]
- Yule, G.U. On the methods of measuring association between two attributes. J. R. Stat. Soc. 1912, 75, 579–652. [Google Scholar] [CrossRef] [Green Version]
- Robitzsch, A. Why ordinal variables can (almost) always be treated as continuous variables: Clarifying assumptions of robust continuous and ordinal factor analysis estimation methods. Front. Educ. 2020, 5, 177. [Google Scholar] [CrossRef]
- Ekström, J. A Generalized Definition of the Polychoric Correlation Coefficient; Department of Statistics, UCLA: Los Angeles, CA, USA, 2011; Available online: https://escholarship.org/uc/item/583610fv (accessed on 1 September 2021).
- Jöreskog, K.G. Structural Equation Modeling with Ordinal Variables Using LISREL; Scientific Software International: Chicago, IL, USA, 2005. [Google Scholar]
- Muthén, B.; Hofacker, C. Testing the assumptions underlying tetrachoric correlations. Psychometrika 1988, 53, 563–577. [Google Scholar] [CrossRef] [Green Version]
- Şimşek, G.G.; Noyan, F. Structural equation modeling with ordinal variables: A large sample case study. Qual. Quant. 2012, 46, 1571–1581. [Google Scholar] [CrossRef]
- Timofeeva, A.Y.; Khailenko, E.A. Generalizations of the polychoric correlation approach for analyzing survey data. In Proceedings of the 2016 11th International Forum on Strategic Technology (IFOST), Novosibirsk, Russia, 1–3 June 2016; pp. 254–258. [Google Scholar] [CrossRef]
- Yamamoto, K.; Murakami, H. Model based on skew normal distribution for square contingency tables with ordinal categories. Comput. Stat. Data Anal. 2014, 78, 135–140. [Google Scholar] [CrossRef]
- Flora, D.B.; Curran, P.J. An empirical evaluation of alternative methods of estimation for confirmatory factor analysis with ordinal data. Psychol. Methods 2004, 9, 466. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.Y.; Lam, M.L. Estimation of polychoric correlation with elliptical latent variables. J. Stat. Comput. Simul. 1988, 30, 173–188. [Google Scholar] [CrossRef]
- Quiroga, A.M. Studies of the Polychoric Correlation and other Correlation Measures for Ordinal Variables. Ph.D. Thesis, Acta Universitatis Upsaliensis, Univsersity of Uppsala, Uppsala, Sweden, 1992. [Google Scholar]
- Grønneberg, S.; Foldnes, N. A Problem with discretizing Vale–Maurelli in simulation studies. Psychometrika 2019, 84, 554–561. [Google Scholar] [CrossRef]
- Foldnes, N.; Grønneberg, S. The sensitivity of structural equation modeling with ordinal data to underlying non-normality and observed distributional forms. Psychol. Methods 2021. [Google Scholar] [CrossRef]
- Foldnes, N.; Grønneberg, S. Pernicious polychorics: The impact and detection of underlying non-normality. Struct. Equ. Model. Multidiscip. J. 2020, 27, 525–543. [Google Scholar] [CrossRef]
- Foldnes, N.; Grønneberg, S. On identification and non-normal simulation in ordinal covariance and item response models. Psychometrika 2019, 84, 1000–1017. [Google Scholar] [CrossRef]
- Jin, S.; Yang-Wallentin, F. Asymptotic robustness study of the polychoric correlation estimation. Psychometrika 2017, 82, 67–85. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Azzalini, A.; Dalla Valle, A. The multivariate skew-normal distribution. Biometrika 1996, 83, 715–726. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t-distribution. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2003, 65, 367–389. [Google Scholar] [CrossRef]
- Mardia, K.V. Multivariate pareto distributions. Ann. Math. Stat. 1962, 33, 1008–1015. [Google Scholar] [CrossRef]
- Roscino, A.; Pollice, A. A generalization of the polychoric correlation coefficient. In Data Analysis, Classification and the Forward Search; Springer: Berlin/Heidelberg, Germany, 2006; pp. 135–142. [Google Scholar] [CrossRef]
- Uebersax, J.S. Latent Correlation with Skewed Latent Distributions: A Generalization of the Polychoric Correlation Coefficient and a Computer Program for Estimation. Available online: https://www.john-uebersax.com/stat/skewed.htm (accessed on 17 September 2021).
- Uebersax, J.S.; Grove, W.M. A latent trait finite mixture model for the analysis of rating agreement. Biometrics 1993, 49, 823–835. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grønneberg, S.; Moss, J.; Foldnes, N. Partial Identification of Latent Correlations with Binary Data. Psychometrika 2020, 85, 1028–1051. [Google Scholar] [CrossRef] [PubMed]
- Pearson, K. Contributions to the mathematical theory of evolution. Philos. Trans. R. Soc. Lond. A 1894, 185, 71–110. [Google Scholar] [CrossRef] [Green Version]
- Olsson, U. Maximum likelihood estimation of the polychoric correlation coefficient. Psychometrika 1979, 44, 443–460. [Google Scholar] [CrossRef]
- Azzalini, A. A class of distributions which includes the normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Agresti, A. Categorical Data Analysis; Wiley-Interscience: New York, NY, USA, 2002; Volume 482. [Google Scholar]
- Denollet, J.; Pedersen, S.S.; Vrints, C.J.; Conraads, V.M. Predictive value of social inhibition and negative affectivity for cardiovascular events and mortality in patients with coronary artery disease: The type D personality construct. Psychosom. Med. 2013, 75, 873–881. [Google Scholar] [CrossRef] [PubMed]
- Denollet, J. DS14: Standard assessment of negative affectivity, social inhibition, and Type D personality. Psychosom. Med. 2005, 67, 89–97. [Google Scholar] [CrossRef] [PubMed]
- Aaronson, N.K.; Muller, M.; Cohen, P.D.; Essink-Bot, M.L.; Fekkes, M.; Sanderman, R.; Sprangers, M.A.; Te Velde, A.; Verrips, E. Translation, validation, and norming of the Dutch language version of the SF-36 Health Survey in community and chronic disease populations. J. Clin. Epidemiol. 1998, 51, 1055–1068. [Google Scholar] [CrossRef]
- Ware, J.E.; Snow, K.K.; Kosinski, M.; Gandek, B. SF-36 Health Survey: Manual and Interpretation Guide; The Health Institute, New England Medical Center: Boston, MA, USA, 1993. [Google Scholar]
- Raykov, T.; Marcoulides, G.A. On examining the underlying normal variable assumption in latent variable models with categorical indicators. Struct. Equ. Model. Multidiscip. J. 2015, 22, 581–587. [Google Scholar] [CrossRef]
- Gay, D.M. Usage summary for selected optimization routines. Comput. Sci. Tech. Rep. 1990, 153, 1–21. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Monroe, S. Contributions to Estimation of Polychoric Correlations. Multivar. Behav. Res. 2018, 53, 247–266. [Google Scholar] [CrossRef]
- Maydeu-Olivares, A. Limited information estimation and testing of discretized multivariate normal structural models. Psychometrika 2006, 71, 57–77. [Google Scholar] [CrossRef]
- Karian, Z.A.; Dudewicz, E.J. Fitting the generalized lambda distribution to data: A method based on percentiles. Commun.-Stat.-Simul. Comput. 1999, 28, 793–819. [Google Scholar] [CrossRef]
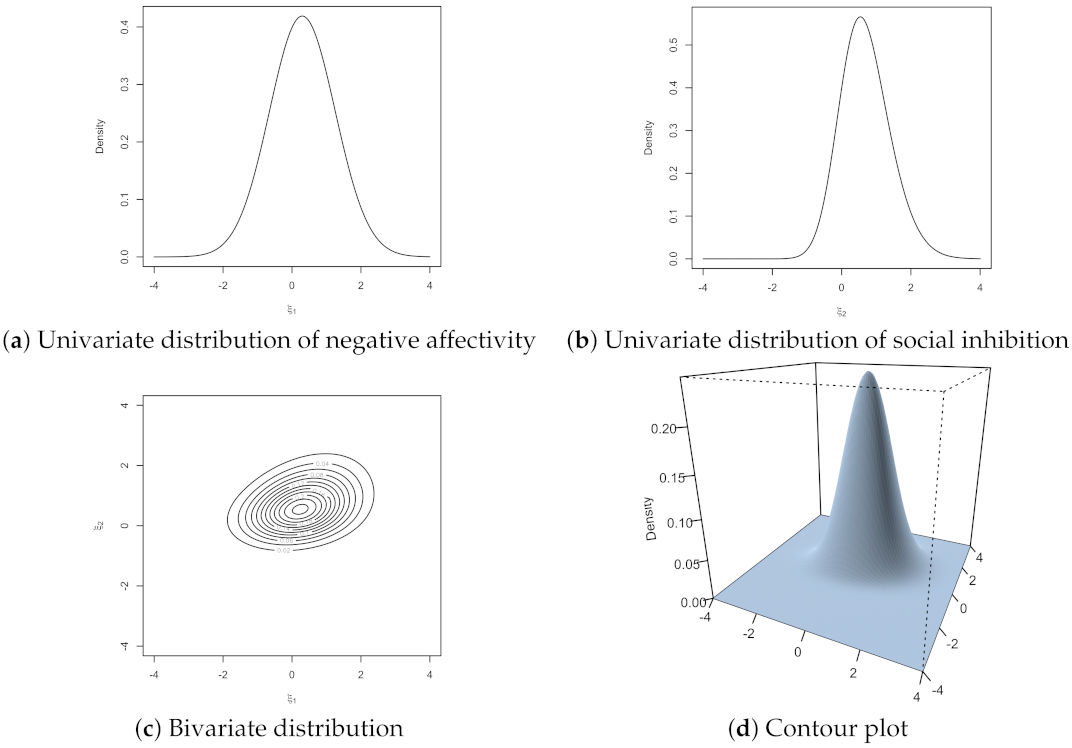
| Negative Affectivity | Social Inhibition | ||||
|---|---|---|---|---|---|
| False | Rather False | Neutral | Rather True | True | |
| False | 67 | 15 | 16 | 8 | 3 |
| Rather false | 41 | 28 | 30 | 4 | 2 |
| Neutral | 34 | 48 | 39 | 11 | 1 |
| Rather true | 35 | 22 | 34 | 28 | 5 |
| True | 24 | 10 | 11 | 11 | 9 |
| Distributions | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Normal | 1 | 3 | 3 | 4 | 7 | 9 | 17 | 19 | 24 | 700 |
| Skew-normal | −1 | 1 | 1 | 2 | 5 | 7 | 15 | 17 | 22 | 630 |
| Mixture ( fixed) | −4 | −2 | −2 | −1 | 2 | 4 | 12 | 14 | 19 | 452 |
| Mixture ( free) | −5 | −3 | −3 | −2 | 1 | 3 | 11 | 13 | 18 | 452 |
| Distributions | Type D Personality | Health Status | ||
|---|---|---|---|---|
| Unadjusted | Bonferroni Adjusted | Unadjusted | Bonferroni Adjusted | |
| Normal | 83.52 | 42.86 | 71.43 | 35.96 |
| Skew-normal | 79.55 | 44.09 | 63.09 | 20.88 |
| Mixture () | 14.94 | 0.00 | 20.78 | 4.99 |
| Mixture () | 34.07 | 6.53 | 34.63 | 12.74 |
| Mixture ( free) | 18.68 | 3.30 | 20.22 | 3.60 |
| Distributions | Type D Personality | Health Status |
|---|---|---|
| Skew-normal | 0.03 | 0.04 |
| Mixture () | 0.26 | 0.30 |
| Mixture () | 0.03 | 0.04 |
| Mixture ( free) | 0.26 | 0.31 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolbe, L.; Oort, F.; Jak, S. Bivariate Distributions Underlying Responses to Ordinal Variables. Psych 2021, 3, 562-578. https://doi.org/10.3390/psych3040037
Kolbe L, Oort F, Jak S. Bivariate Distributions Underlying Responses to Ordinal Variables. Psych. 2021; 3(4):562-578. https://doi.org/10.3390/psych3040037
Chicago/Turabian StyleKolbe, Laura, Frans Oort, and Suzanne Jak. 2021. "Bivariate Distributions Underlying Responses to Ordinal Variables" Psych 3, no. 4: 562-578. https://doi.org/10.3390/psych3040037
APA StyleKolbe, L., Oort, F., & Jak, S. (2021). Bivariate Distributions Underlying Responses to Ordinal Variables. Psych, 3(4), 562-578. https://doi.org/10.3390/psych3040037






