Abstract
The person-centered approach in categorical data analysis is introduced as a complementary approach to the variable-centered approach. The former uses persons, animals, or objects on the basis of their combination of characteristics which can be displayed in multiway contingency tables. Configural Frequency Analysis (CFA) and log-linear modeling (LLM) are the two most prominent (and related) statistical methods. Both compare observed frequencies () with expected frequencies (). While LLM uses primarily a model-fitting approach, CFA analyzes residuals of non-fitting models. Residuals with significantly more observed than expected frequencies () are called types, while residuals with significantly less observed than expected frequencies () are called antitypes. The R package confreq is presented and its use is demonstrated with several data examples. Results of contingency table analyses can be displayed in tables but also in graphics representing the size and type of residual. The expected frequencies represent the null hypothesis and different null hypotheses result in different expected frequencies. Different kinds of CFAs are presented: the first-order CFA based on the null hypothesis of independence, CFA with covariates, and the two-sample CFA. The calculation of the expected frequencies can be controlled through the design matrix which can be easily handled in confreq.
1. Introduction
Data that include categorical variables are often seen in the social sciences and psychological research. The term categorical variables typically refers to variables that, according to Steven’s [1] influential taxonomy of scale levels, have at least a nominal or ordinal scale level. Although Steven’s taxonomy was already criticized almost at the same time of its introduction, see, e.g., in [2], but see also in [3], and can also be regarded as the initial spark for a (still ongoing) controversy about scale levels and measurement of social science variables as such, e.g., in [3,4,5,6,7], it can at least provide a useful heuristic for the practice of data analysis. From such a practice perspective, the term categorical variables can be used to characterize variables that comprise few distinct trait expressions or attributes that result from the classification of any type of observation into “one of a set of mutually exclusive and collectively exhaustive categories” [8] p. 4. Based on such a broad definition that relies on the pure classification of observations, the concept of categorical variables can be extended even to so called metric variables that have only a few expressions, such as sum scores (e.g., ) of a short psychometric scale comprising of only three dichotomous items.
The person-centered approach analyzes persons or objects on the basis of combinations of characteristics, trait expressions, or attributes observed on them. A combination of such different characteristics or attributes for a person or an object is referred to as a pattern or configuration. Specifically, statistical methods can be applied to the data that, based on a null hypothesis, model the significance of occurrence of the individual pattern from a set of categorical attributes in a multivariate fashion, see, e.g., in [9]. One such multivariate non parametric procedure cf. [9] is configuration frequency analysis (CFA). CFA was developed by Gustav A. Lienert (1920–2001) and analyzes multidimensional contingency tables, see, e.g., in [10,11]. The analysis of contingency tables with the CFA follows the principle of a residual analysis. The observed frequencies of individual cells of feature combinations , conceived as multidimensional contingency tables, are compared with expected frequencies . Lienert referred to feature combinations or configurations that have significant high frequencies ( ) as types and configurations that have significant low frequencies ( ) as antitypes [11]. The expected frequencies are modeled according to a specific null hypothesis, with the most common null hypothesis being the assumption of independence of the variables under study sharing a joint multinomial distribution.
The present tutorial describes the use of the confreq R package [12] for the R language and environment for statistical computing [13]. The R package confreq allows the computation of different model formulations and null hypotheses of the Configural Frequency Analysis (CFA), and provides a link to the R package vcd [14,15] for the visualization of cross-tabulated categorical data.
2. A Person-Centered Perspective on Data
The CFA belongs to the person-centered analysis methods for categorical data structured in multidimensional contingency tables, cf. [9]. This particular person-centered perspective, in contrast to the widespread variable-centered analysis perspective, can be explained by comparing the different goals as well as the specific forms, or rather arrangements, of the data to be analyzed.
Within variable-centered approaches, correlation, regression, and factor analyses are typically used in the social sciences, see, e.g., in [16]. Here, the goal is to analyze relationships between variables based on means, variances, and covariances of scale values. For example, regression models are used to predict a criterion using multiple predictors, or structural equation models are used to analyze the relationship between independent and dependent (latent) variables and to discover hidden structures between these variables. Furthermore, principal component or principal axis analyses can be applied to the data, for example, to explore measurement models for latent variables by multiple manifest indicators. In summary, the issues investigated within this variable-centered approach essentially relate to the formation of psychological theories about linear relationships between different psychological constructs and latent variables, cf. [17].
However, there is a lot more than linear associations and correlation to explore in psychology and social sciences. Already 1911, the pioneering founding father of differential psychology William Stern [18] identified four basic disciplines in individual differences research which are summarized in Table 1. Based on Stern’s taxonomy, as shown in Table 1, the person-centered perspective on data analyses can be assigned to the two research disciplines of psychography and comparative research, depending on whether the data collected relate to an individual case, at possibly several measurement points, or to the comparative classification of several persons, or rather units of analysis. Contrary to variable-centered research, in person-centered research the analyzed differences in patterns within a sample to be analyzed (for a population) can imply any type of dependencies between the assessed characteristics. Some central propositions of the person-centered research approach to data analysis are formulated by von Eye and Bogat [19]. While the variable-centered empirical research is based on the proposition that populations are homogeneous with regard to linear relationships between variables, the person-centered research approach is based on the propositions that first, distinct subgroups may exist in a population and second, if they exist, aggregate-level parameters may contradict parameters estimated for groups or individuals cf. [19].

Table 1.
Different perspectives on data analysis according to William Stern [18].
The special person-centered perspective, in comparison to the widespread variable-centered analysis perspective, can also be illustrated by the specific form or arrangement of the data to be analyzed. Regarding this form or arrangement, typical variable-centered analysis methods start from data that are in the so-called wide form. In the wide form, the data have one column for each variable and each case has one row in the data matrix (see leftmost column in Table 2). The wide form is what most users typically already know and have in software such as SPSS®, etc. Next to the wide form of data, there is also the so-called long form of data. In long form data, every row in the data matrix represents the single observation of an interaction belonging to a particular variable and case. In this form, the data matrix essentially comprises three columns whereby the fist column holds a case identifier (person-ID), the second column holds a variable identifier (the variable names) and finally the last, third column holds the respective measure, resulting from the observed interaction between the person (first column) and the measurement instrument or unit (item), as identified in the second column (see middle column in Table 2). The long form of data is what is typically known and (at least internally) used in software computing log linear models.

Table 2.
Different forms of data representation.
Within the R package confreq [12] a third form of data representation is used, which we will name tabulated data (see rightmost column in Table 2).
Comparing the three different representations of data as depicted in Table 2, tabulated data may, on the one hand, be regarded as a “compressed representation” of the wide form of data, whereby (initially) only categorical variables are contained. The compressed representation is achieved by mapping all combinations of the categorical variables and their respective frequencies in the specific sample. As tabulated data always comprises all possible patterns resulting from all combinations of the variables involved and their respective categories, the size of the tabulated data matrix does not change with different samples. Different samples in terms of their size and quality of composition are only reflected (with an otherwise constant number of variables and categories) in the changing observed frequencies of the pattern in tabulated data. This implies that in some cases the observed frequencies also might be zero for pattern which are not observed in the empirical data.
On the other hand, tabulated data may also be considered as a special form of long form data, whereby the respective combination of the single variables—the pattern—is regarded as a “linked categorical variable”. The measured value, which is the target of the analyses, is reflected in the observed pattern frequencies for the respective sample. This perspective is taken if the model parameters (e.g., the expected frequencies) are obtained in the CFA model using the log-linear modeling (LLM) approach, as implemented in confreq [12]. In this sense, a common core in the person-centered analysis and the application of different CFA models always consists in the calculation of the expected frequencies of all possible pattern from a given number of attributes (variables).
3. Introduction to the confreq Framework in R
If not already installed on your computer, please visit the web site of the comprehensive R archive network at https://cran.r-project.org/ (accessed on 2 September 2021) first and install a current R version for your operating system. Although after installing R you already have everything you need to start working, we recommend the additional installation of an convenient R editing and development environment such as RStudio from https://www.rstudio.com/ (accessed on 2 September 2021). RStudio offers some convenient tools for managing R packages, multiple R workspaces and R-code scripts. Just like R, RStudio is available for the three most popular operating systems: Linux, Mac OS, and Windows. In order to explore the structure of confreq, and later on run the example R-code snippets, you have to install the latest version of confreq from the CRAN repositories. This is done either via the menu control in RStudio (packages –> install –> search term: ’confreq’) or by simply entering the following R command into the console.
install.packages("confreq",dependencies = TRUE)
In the following, we assume that all of these necessary preparatory steps have been completed successfully and that you have an active R workspace at the start.
The basic structure of confreq is divided into five (function) areas which are subsumed in the index in the pdf references manual (the pdf references manual is available at https://CRAN.R-project.org/package=confreq/confreq.pdf (accessed on 2 September 2021) under the key-words datasets, mainfunction, methods, misc, and finally utilities. As the name suggests, the datasets section contains a total of 5 data sets to document the functionality of confreq using various examples. Four data sets (‘lazar’, ‘Lienert1978’, ‘LienertLSD’, and ‘newborns’) are in tabulated form (cf. Table 2) and therefore carry the confreq specific R class label c(“data.frame” “Pfreq”), but the fifth one (‘suicide’) is in the (classic) wide form and thus is of class “data.frame”. Under the keyword mainfunction only two functions are listed which represent the core feature of confreq. These two functions are what most users will probably apply most often within confreq. The function CFA() calculates different variants of the CFA which can all be derived from the basic principle of residual analysis when searching for types and antitypes. The function S2CFA() deals with a variant of CFA with which significantly discriminatory configurations can be found between two (sub) samples. The feature section methods includes two generic S3 plot() and summary() methods, respectively, for both main functions in confreq. Another area with miscellaneous items lists different functions under the keyword misc. The functions listed here are typically called internally by the two main functions, but are nevertheless exported in confreq and are thus optionally available to the user to directly process specific analysis questions. Finally, there is a section named utilities under which various functions for data preparation and reorganization are subsumed. The functions dat2fre() converts categorical data from the classic wide format to tabulated data, which can then be used with the functions CFA() and S2CFA(); the function fre2dat() does the opposite. The function dat2cov() also converts data from the classic wide format into tabulated data, but here also continuous variables can be considered which are aggregated (e.g., mean aggregation) for each configuration from the categorical variables in the data set. Finally, an important function is fre2tab() which converts the tabulated data format to the typical R ’table’ format (R class “table” ). With this functionality, the connection of confreq to other packages in R or to the basic functionality for categorical data in R is given.
4. Working with confreq
In the subsequent sections, we will refer to some R-code snippets and data examples to introduce the practical use of the R package confreq for CFA. The selected data examples are either already contained in the confreq package as R data, or are generated via the corresponding R code. Therefore, nothing else than the installation of a current R version and the package confreq is needed to follow this tutorial.
4.1. A First Look on a Classical Data Example
To introduce to the principle of analyzing associations and contingency with categorical variables and the need for doing so in a multivariate fashion, we will refer to a classical data example by Lienert [11]. Based on the findings by Leuner [20] on the psychotoxic basic syndrome [Das psychotoxische Basis-Syndrom] after the intake of lysergic acid diethylamide (LSD) which is associated with symptoms such as clouding of consciousness, thought disturbance, and negative influence on affectivity, Lienert [11] analyzed the experimental data from student volunteers who had taken LSD. Three symptoms were recorded while the volunteers had taken LSD:
- Clouding of consciousness [Bewußtseinstrübungen] (C)
- Thought disturbance [Denkstörung] (T)
- Affective disturbance [Affektivitätsbeeinflussung] (A)
The observed symptoms were clinically rated according to their severeness in a dichotomous fashion in the way that ‘+’ indicates cases above the average and ‘−’ indicates cases below the average. From these variables, possible patterns or configurations result from volunteers who had participated in the LSD experiment (see Table 3). The data are included in the package confreq and the subsequent R-code snippet ‘R_snippet_001’ loads the package and makes them available in R.
| Listing 1. R_snippet_001.R. |
 |

Table 3.
Data from the Lienert LSD trial, see Lienert [11], p. 103, ‘Tabelle 1’.
With confreq the tabulated data depicted in Table 3 can be visualized in different types of ‘heat maps’ using the link capability of confreq to the graphic framework of the vcd R package [14,15] an the the grid graphics package [13]. Running the code in the snippet ‘R_snippet_002.R’, will result in two different forms of visualizing the cross tabulated data as shown in the two graphical panels in Figure 1.
| Listing 2. R_snippet_002.R. |
 |
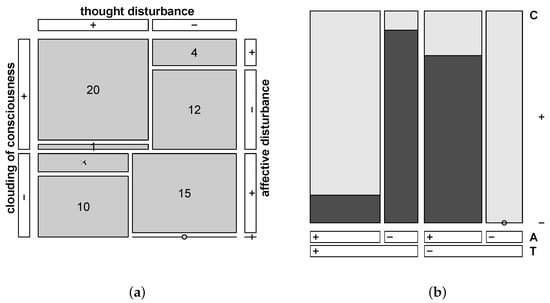
Figure 1.
Different types of graphical displays for the data from the Lienert LSD trial, see in [11] p. 103, ‘Tabelle 1’; left panel (a): ‘strucplot’ with labeling and cell frequencies added; right panel (b) ‘doubledecker’ plot to visualize the influence of explanatory variables on one dependent variable.
While in the left panel (a) all three variables are considered in a symmetrical way in the graphical representation, in the right pannel (b) the variable ‘C’ is used as dependent variable to define two (sub-)groups in order to visualize the differences between the two groups regarding the other two variables ‘T’ and ‘A’ (see Figure 1).
In a first analysis, Lienert [11] used thought disturbance (T) and affective disturbance (A) as predictor symptoms for clouding of consciousness (C) as criterion or predictive symptom [11] p. 103 and found the following relationships for both groups and the total sample respectively, as depicted in Table 4. Note that these results refer to the visualization in the right panel (b) in Figure 1.

Table 4.
Results for bivariate analysis for data from the Lienert LSD trial, see in Lienert [11], p. 103.
We can see from the results in Table 4 that for both sub groups ( and ) there is a significant relationship between affective disturbance (A) and thought disturbance (T), respectively, while for the total sample, these significant relationships seem to vanish (see Table 4). Moreover, the other bivariate relationships between clouding of consciousness (C) and thought disturbance (T) as well as clouding of consciousness (C) and affective disturbance (A) suggest for the total sample that all three variables are unrelated (, ).
The results presented here can be replicated using the Lienert-LSD-data in confreq by ruining the subsequent R-code from snippet ‘R_snippet_003.R’.
| Listing 3. R_snippet_003.R. |
 |
From these findings Lienert [11] generally concluded, that there can be connections between three characteristics, which are not reflected in bivariate relationships between two of the three characteristics each. Specifically, when using the categorical variable ‘C’ as to split the sample into two groups, different associations between the remaining two variable might emerge in the groups as compared to the total sample. Such nonlinear effects are well known as Meehl Paradox [21] or Simpson Paradox [22] see also Yule [23]. Therefore, when multivariate hypotheses are tested in the form of single bivariate hypotheses, decisive information can be lost, see, e.g., in [24] p. 516.
4.2. The CFA Main Effect Model of Independency
In order to avoid such inconsistencies and paradoxes in the analysis of multidimensional contingency tables, the multivariate analysis by means of the CFA is a useful alternative. To introduce the CFA with the package confreq, we go on with analyzing the Lienert-LSD-data by applying the CFA main effect model. This model is also named model of independency, as the null hypothesis to be tested assumes the independency of each variable forming the configurations in the data. In the framework of log-linear modeling that means that only main effects (for each variable) are considered when calculating the expected cell (pattern) frequencies. For the Lienert-LSD-data the log linear model formulation as implemented in confreq to compute the expected frequencies is given in Equation (1) as
where are the log expected frequencies of the configurations from the observed variables C, T, and A, and are their coefficients. A comprehensive introduction into the principle of log-linear model formulation of the CFA is given in [9]. Applications of the CFA as a LLM using confreq with empirical data on current research questions can be found, for example, in Sälzer and Heine [25], Stemmler and Heine [26], Börnert-Ringleb and Wilbert [27], Lazarides et al. [28], Heine and Stemmler [29].
To run the CFA main effect model with the Lienert-LSD-data the second code line in the subsequent R-snippet ‘R_snippet_004’ is used.
| Listing 4. R_snippet_004.R. |
 |
Note that for didactic purposes here the argument ‘form’ is explicitly defined using the R like representation of the equation given in (1). However, if the argument ‘form’ is not further specified, the CFA main effect model is automatically assumed in confreq.
Executing the last line in ‘R_snippet_004’ will return the summarized results, which are basically divided into three sections. The first section recapitulates the function call, the second section contains the results of the global model testing and the third part refers to the local tests for identifying types and antitypes (see console output below).
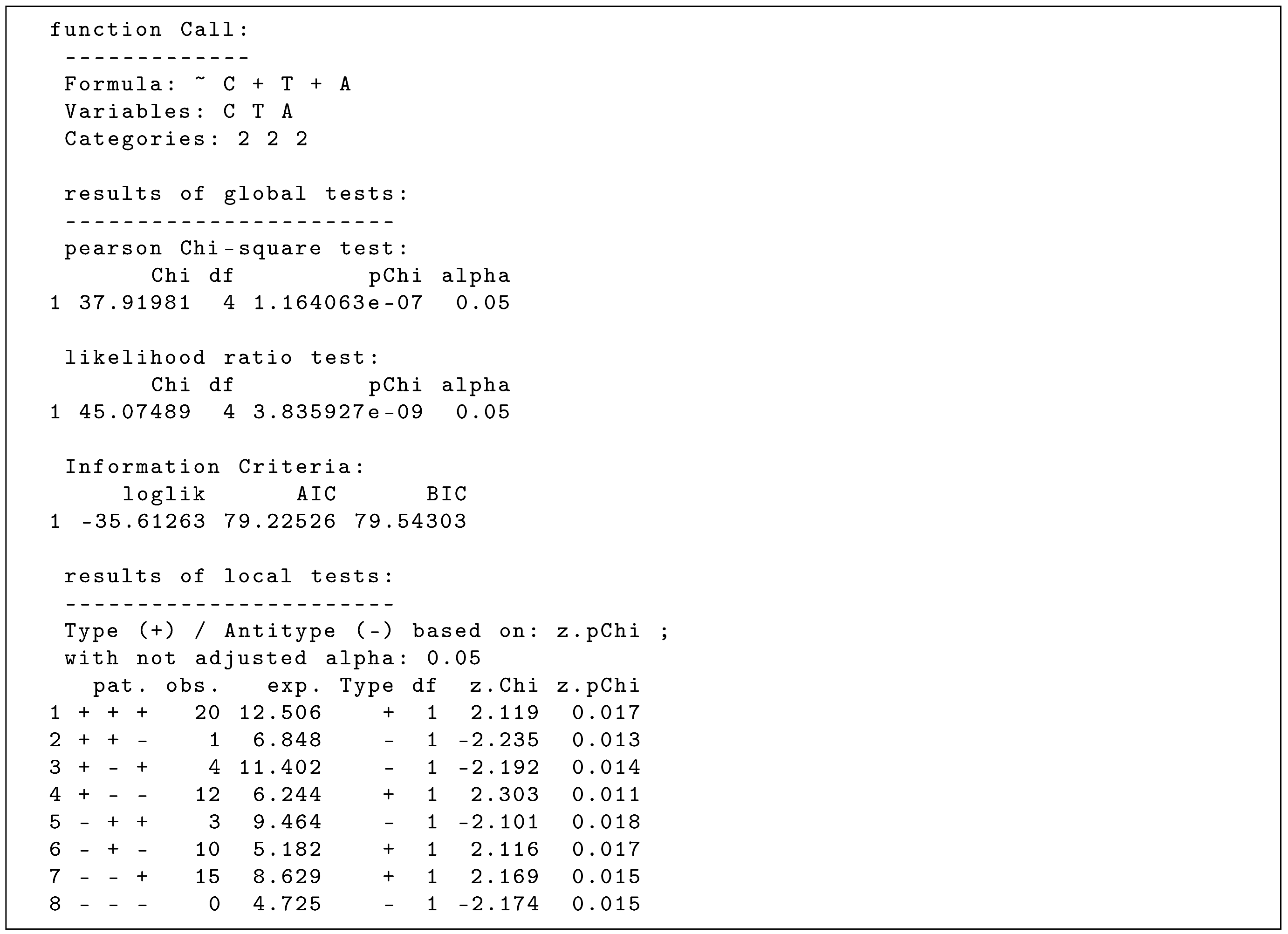 |
Both global tests considering the total cross-tabulation in the section for ‘global model testing’ suggest a significant result (; ), which leads to the rejection of the null hypothesis of the CFA main effects model. In terms of LLM, this result implies a non-fitting model of independence, which conversely suggests a whatever relationship between the variables. Taken together with the finding that there are no linear bivariate relationships between the variables (see initial analyses and Table 4 above), this suggests the presence of (significant) nonlinear relationships. The CFA results in the third section on the ‘local tests’ provide a more sophisticated explanation by showing single types (‘+’; over-frequented cells) and antitypes (‘−’; under-frequented cells) that contribute the nonlinear relationship. However, with regard to these findings from the local tests, note that local significance testing must be regarded as a special form of multiple testing, which requires an adjustment of the alpha level, which has not yet been done here.
Currently, the package confreq offers two types of alpha adjustment. These are the conservative method for probability thresholding according to Bonferroni cf. [30], and the more lenient step-down ’Holm’ procedure cf. [31] which sets the significance level individually. Both types of alpha adjustment, just like the omission of any alpha correction, are controlled by assigning the respective character expression to the argument ‘adjalpha’ in the summary function (see examples in ‘R_snippet_005’ below).
| Listing 5. R_snippet_005.R. |
 |
Another factor that influences the search for types and antitypes is the type of significance test used. In the current version, confreq can be used with five different procedures or test statistics. These are the Pearson -test (“pChi”), the -approximation to the z-test (“z.pChi”), the binomial approximation to the z-test (“z.pBin”), the binomial test using Stirling’s approximation (“p.stir”), see, e.g., in [32] p. 52 for the p values and Fisher’s exact binomial test (“ex.bin.test”) [33]. Further information on the different test statistics is given in Stemmler [9]. Which test statistic is used is specified (post hoc) by selecting the appropriate character expression (one of c(“pChi”, “z.pChi”, “z.pBin”, “p.stir”, “ex.bin.test”,)) in the argument type in the summary function (see examples in ‘R_snippet_005’). When using the default settings in the function CFA(), all test statistics are calculated in advance, so that their selection in the summary function can be freely chosen later on when applying summary to the respective result object. Note, however, that there is one exception to this principal functionality in confreq, which arises from the necessary way of implementing Fisher’s exact test. As shown in [9], for example, the test requires the (multiple) calculation of fractions with factorials of large numbers, especially for larger sample sizes and thus cell sizes, and for contingency tables of higher dimensionality. Using principles of multiple precision arithmetic as provided in the package ‘gmp’ [34], the test has been implemented in confreq in such a way that for any computer system there are no principle numerical limitations with respect to the size of the contingency tables to be analyzed. However, the problem of increasing computation times with increasing size of the analysis task still remains. For this reason there is the option in the function CFA() to suppress the (a priori) calculation of the exact test by setting the argument ’bintest = FALSE’ – in contrast to the default setting which is ‘bintest = TRUE’. In case of disabling the test when calling CFA() and still requesting it with the method function summary() confreq will return an error message suggesting to run CFA() again while setting ‘bintest = TRUE’ (try the subsequent ‘R_snippet_006’).
| Listing 6. R_snippet_006.R. |
 |
After the CFA model has been calculated and the appropriate procedure for significance testing of the types and antitypes has been chosen, the results can be displayed graphically. Basically, this works quite simply by applying the S3 method ‘plot()’ provided in confreq to the result object from the application of the CFA() function to the tabulated data (cf. ‘R_snippet_007’).
| Listing 7. R_snippet_007.R. |
 |
As for the ‘summary()’ method also for the ‘plot()’ method, one can specify which significance test should be used for the display of the types and antitypes. In addition, the ‘fill’ argument can be used to specify the colors with which the types, antitypes and non-significant cells are to be colored (see, e.g., code line 5 in ‘R_snippet_007’). As the plotting functionality in confreq is based on the grid graphics package [13], as it is also used in the package vcd [14], single cells in the graphical display can be controlled and colored individually at a later time (cf. last code lines 14 and 16 in ‘R_snippet_007’).
4.3. Modifying the CFA-Model Design Matrices
As noted above, in confreq the expected frequencies are calculated within the framework of a CFA model via a LLM formulation. This principle implies that a model design matrix is established which represents the respective formulated model. In confreq, this model design matrix can first be inspected in the evolving result object (after applying the function CFA()) and second modified or extended, and then, third, used for a recalculation of the expected frequencies based on the new model. This offers the maximum flexibility for the realization of the most different CFA models. Let us first look at the design matrix from the previous CFA main effect model. The result object from the ’CFA()’ function is ultimately a list with different entries and one of them relates to the design matrix. Therefore, based on the Lienert LSD data example, this can be displayed by simply entering the command ‘res1$designmatrix’ (see second line in ‘R_snippet_008’). Below there is a shortened display of the output of the design matrix for the CFA main effect model with the Lienert-LSD-data.
As you can see, the design matrix has as many rows as there are cells (configurations) and columns. The three main effects are mapped over the last three columns representing the effect for each of the three variables, respectively. The first column represents the intercept as a constant, which is coded with ones. The main effects are effect-coded that is, we use coefficients () for each category of a variable, which have to sum to zero for each column see also [9], for a more in-depth explanation of effect coding.
 |
In order to inspect different design matrices that result from different CFA model formulations, you may execute code lines 4 to 10 in the ‘R_snippet_008’.
| Listing 8. R_snippet_008.R. |
 |
The CFA model which is calculated in code line 5 (see ‘R_snippet_008’) assumes the null hypothesis that the cells are equally distributed. In concrete terms, the underlying assumption is that the frequencies are the same for each cell (configuration) of the multidimensional contingency table. This model is referred to as configural cluster analysis (CCA) or named as the zero-order CFA model because it does not contain any main effects cf. [9].
The next model (cf. code line 6) considers the two interaction terms between the variables C:T and C:A and thus represents a link to the first analysis by Lienert (see Table 4), according to which the two groups C = + and C = − were analyzed separately. The finding from this model that the configuration ‘C = +, T = −, A = −’ is shown as a significant type suggests that this configuration is apparently (at least partly) responsible for the nonlinear relationship between the variables in reference to the total sample. Moreover, if the model does not fit, it is a test of significance for the 3-way interaction.
Finally, the last model in code line 7 in ‘R_snippet_008’ represents the so-called saturated model. The saturated model takes into account all interaction terms of each order (here all double and one triple interaction) between the variables involved. This model reproduces the observed frequencies perfectly and thus represents a baseline for the comparison of different CFA models. Furthermore, the saturated model (in comparison with others) can emphasize the importance of the interaction terms.
In the code lines 5 to 7 in ‘R_snippet_008’, the different CFA models are specified by entering a model formula in the argument ‘form’. In confreq, however, the argument form in the function CFA() can also be directly assigned a design matrix, which was previously modified according to the own model ideas. In the code lines 17 to 19 in ‘R_snippet_008’ the model specification using a modified design matrix is demonstrated on the example of the CFA zero order model. The comparison with the specification of the same model via the model formula (cf. code lines 22, 23) shows that there are no differences here.
All of the CFA models discussed so far always refer to the entire contingency table when calculating the expected cell frequencies within the framework of their basic formulation under the respective null hypothesis. This fact corresponds to the assumption associated with their underlying null hypothesis that the frequencies of the types or antitypes belong to the same population as all other (possible) configurations. This assumption of a common population and thus common (multinomial) distribution can, however, be violated in the local significance test for single types and antitypes if, for example, extreme local cell frequencies (outliers) are present. Such extreme cell frequencies can result, on the one hand, simply from the sparseness of the data collected or, on the other hand, from substantive, structural, and logical reasons due to the nature of the recorded attributes—leading to impossible configurations. A typical example for such impossible configurations sometimes called structural zeros is given by [9] as it might result from meteorological observation variables, “e.g., a pattern of heavy rain together with a beautiful blue sky” [9] p. 54. Such limits of CFA were first observed and addressed in the 1970s [35,36]. The problem of (falsely) assuming a common population is addressed in an interesting extension of CFA by Victor and Kieser [37]. To account for the problem of structural extreme cell frequencies potentially affecting the results of significance testing of the other cells, Victor [38] proposed to include the existence of certain configurations as types within the definition of the basic model [37,39,40]—which simply means excluding the configuration in question from the analysis.
The need to exclude certain cells (configurations) from the analysis of the observed and expected frequencies is another area of application that makes use of the flexibility of the model formulation via a modification of the design matrix in confreq.
For the (mainly technical) demonstration of the possibility of excluding one (or possibly more) cells from the calculations of the expected frequencies, we look again at the Lienert-LSD-data. In these data (see Table 3), it is noticeable that configuration number 8 (‘C = −, T = −, A = −’) has a frequency of zero for the data collected. We now assume (hypothetically, for demonstration purposes) that this combination of (non) observed symptoms is an impossible combination of attributes—which, by the way, might not seem so implausible from a clinical perspective, as this configuration would imply the complete ineffectiveness of LSD.
As a logical consequence of our substantiated classification of the cell in question as an impossible configuration, we now want to exclude this from the CFA analyzes. To do this we use the argument ‘blank’ in the CFA() function (see examples in ‘R_snippet_009’).
| Listing 9. R_snippet_009.R. |
 |
This procedure checks whether the assumption of independence can be confirmed for the rest of the contingency table after removing the extreme configuration(s). If the rest of the contingency table proves to be independent, this is called quasi-independence in the presence of a type (antitype); thus, such a model can be called a quasi-independence model [9]. Comparing the results from the two main effect models, i.e., the initial one for the whole contingency table (cf. summary of result object ‘res1’ in code line 7 in ‘R_snippet_005’) and the other one with the excluded configuration number 8 (cf. summary of result object ‘res6’ in code line 3 in ‘R_snippet_009’) clearly shows the biasing influence of the structural extreme cell frequencies. It becomes clear that the local testing of the most frequent pattern number 1 in the Lienert data (‘C = +, T = +, A = +’; ) in the first model (‘res1’) with surprisingly does not lead to a significant type, whereas in the second model (‘res6’) this pattern is (correctly) recognized as a significant type with . This finding underlines the importance of the comparative application of different CFA models to the data.
A look at the design matrix of the quasi-independence model for the Lienert-LSD-data, which we obtain via the input of the R command ‘res6$designmatrix’, shows how this is implemented in the context of the log-linear modeling of the expected frequencies (cf. R-output below).
 |
In addition to the already known three columns for the main effects, another column is added here, which, except for cell number 8 (‘C = −, T = −, A = −’), is consistently coded with ‘0’. Note that if several configurations are to be excluded from the analyses as ‘extreme cells’, a column must be added to the model matrix for each configuration to code this ‘effect’, respectively.
A systematic examination of the design matrices used so far, such as, for example, in the three models in the R-objects res3, res4, and res5 (see ‘R_snippet_008’) as well as in the R-object res6 (see ‘R_snippet_009’) in conjunction with the respective degrees of freedom () of the global model test shows that the degrees of freedom of any CFA model is determined by the number of rows and columns of the respective design matrix. The number of rows of the design matrix minus 1 represents the information s given by the data and the number of columns (without intercept) represents the number of parameters t ‘consumed’ by the respective (explanatory) model. The degrees of freedom for any CFA model are generally defined as the difference between the given information s and the number of model parameters t as given in Equation (2), cf. also in [29]:
Here, the given information s is defined by the number of possible combinations or configurations from the variables under study i (with ) with categories minus 1 each (cf. Equation (3)):
The number of parameters t is based on the particular model formulated. For a simple CFA main effect model with k variables () each with categories, the number of model parameters is calculated according to Equation (4):
The number of ‘consumed’ model parameters may need to be increased, depending on the complexity of the chosen model. Thus, each functional expansion to exclude single ‘extreme cells’ consumes one degree of freedom each, as well as each single interaction term.
4.4. Introducing Covariates into the CFA-Model
In the previous section, we have shown that different CFA models can be realized via the modification or the addition of the design matrix. We focused on the realization of different H0 hypotheses that implement either only main effects (of the variables), complementary interaction terms (of different order) or also functional model definitions with structural configurations as in the quasi-independence model.
In this section, we will go a step further and show how to use the extension of the design matrix to account for covariates in a CFA model. In a CFA model, covariates can help to elucidate the “cause” of the types and antitypes found (initially). In this sense, the covariates in a CFA model help to predict the expected frequencies more accurately. Substantial covariates thus reduce the difference between observed and expected frequencies and then may lead to the result that (in the “ideal” case) after the inclusion of suitable covariates no types or antitypes can be observed anymore. For a recent example from the literature that demonstrates the relevance of considering covariates when analyzing categorical data from the international 2015 PISA study, see [29].
For the practical demonstration of the CFA model with covariates, we will leave behind the Lienert-LSD-data used so far and turn to another handy data example from the literature. The data are not included in confreq, but can be easily reconstructed as tabulated data with R from the information given in the corresponding publication by Glück and von Eye [41], pp. 410,411 using the following R script ‘R_snippet_010’.
| Listing 10. R_snippet_0010.R. |
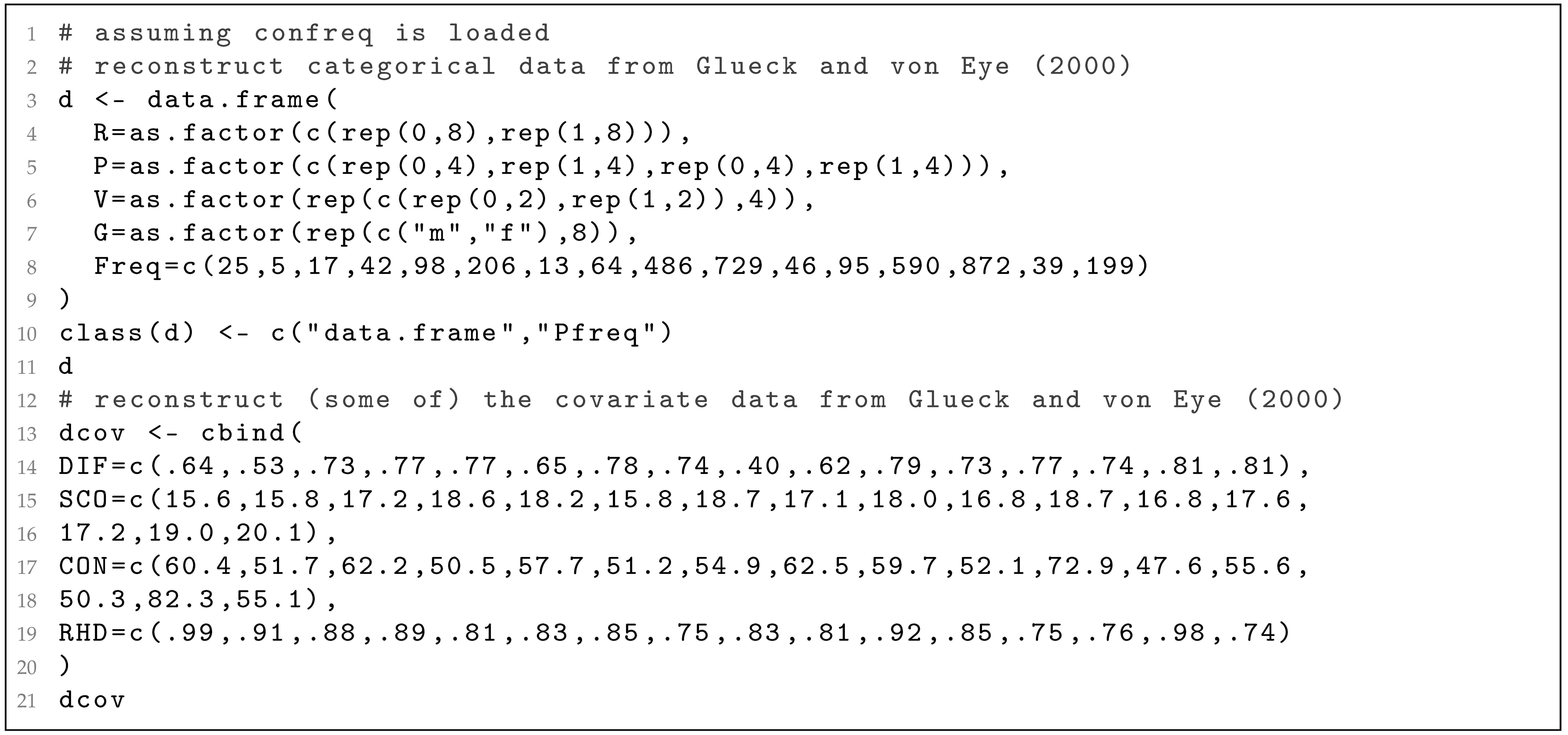 |
Code lines 3 to 9 in ‘R_snippet_010’ create a data.frame assigned to R object ‘d’ comprising four categorical variables (as ‘R factors’) with their respective frequencies and code line 10 assigns a special ‘class’ to ‘d’ to let confreq “know” that these are tabulated data. Code lines 13 to 20 create a matrix object (‘dcov’) comprising the means of the covariates for the 16 configurations given in ‘d’, respectively. Stemmler [9] points out that, as in this example, “Usually, the cell means of the continuous covariate are used …” [9] p. 105 but also other summary statistics of the covariates can be used for the respective configuration (cell of the contingency table).
In the original monograph by Glück [42], the data were used to examine how male and female students (categorical variable ‘G’) in a high school perform spatial reasoning tasks. The students were presented with different views of cubes as a paper-and-pencil test, which they were asked to judge for equality. After each spatial imagination task, the strategies used were queried. The categorical variables ‘R’, ‘P’, and ‘V’ (R: Rotation strategy; P: Strategy of comparative patterns; V: Strategy of change of perspective) in the data example represent re-coded response data on three strategies in dichotomous form, where ‘0’ represents the absence of the corresponding strategy and ‘1’ represents the presence of the corresponding strategy cf. [41]. In addition, there are continuous variables such as task difficulty (’’), spatial ability score (‘’), self-confidence (’’), and scores for right-handedness (’’) cf. [41]. As pointed out in Glück and von Eye [41], the two “topmost” configurations (for male and female students) who seemed to report none of the three strategies refer to “…subjects that did not fill in the strategy questionnaire …” [41] p. 410 and thus were treated as “…structural cells” [41] p. 410, which basically means that these cells were excluded when calculating the expected frequencies as demonstrated in the section above.
To replicate and output the results from an initial CFA main effects model analysis with functional extension to skip the two structural cells as reported in Glück and von Eye [41] you can run the code lines 3 and 4 in ‘R_snippet_011.R’.
| Listing 11. R_snippet_0011.R. |
 |
In order to use additional covariates in the CFA, the term for the covariates is added to the log-linear model equation (cf. Equation (5)):
In this general notation in Equation (5), X is the design matrix with the vectors for the effect-coded contrasts of the main effects (and as well as specified interactions and functional extensions) and is the vector of the respective coefficients; thus, for the main effects model with the data from Glück and von Eye [41], the first part of the right hand sided term given in Equation (5) would be . The inclusion of the covariates in the model equation is obtained with as a vector of the covariates and stands for the vector of coefficients of the covariates. Thus, as the Equation (5) illustrates, one simply has to add the covariates as additional column(s) in the design matrix see [43], for a further specific introduction into the issue of covariates in CFA.
In confreq, the inclusion of covariates is controlled by the argument ‘cova’, where we can assign a matrix object, holding the means of the covariates for the configurations, respectively. The code line 7 in ‘R_snippet_011.R’ will run a model that contains three covariates (‘’, ‘’, and ‘’) in addition to the CFA main effects model, which itself contains a functional extension as a quasi-independence model. The code line 11 in ‘R_snippet_011.R’ performs the CFA model with only one covariate: right-handedness (‘’).
We can view the inclusion of the covariates in the model matrix by outputting the corresponding design matrix with the R command, as for example by typing ‘res8$designmatrix’ into the R console (see output below).
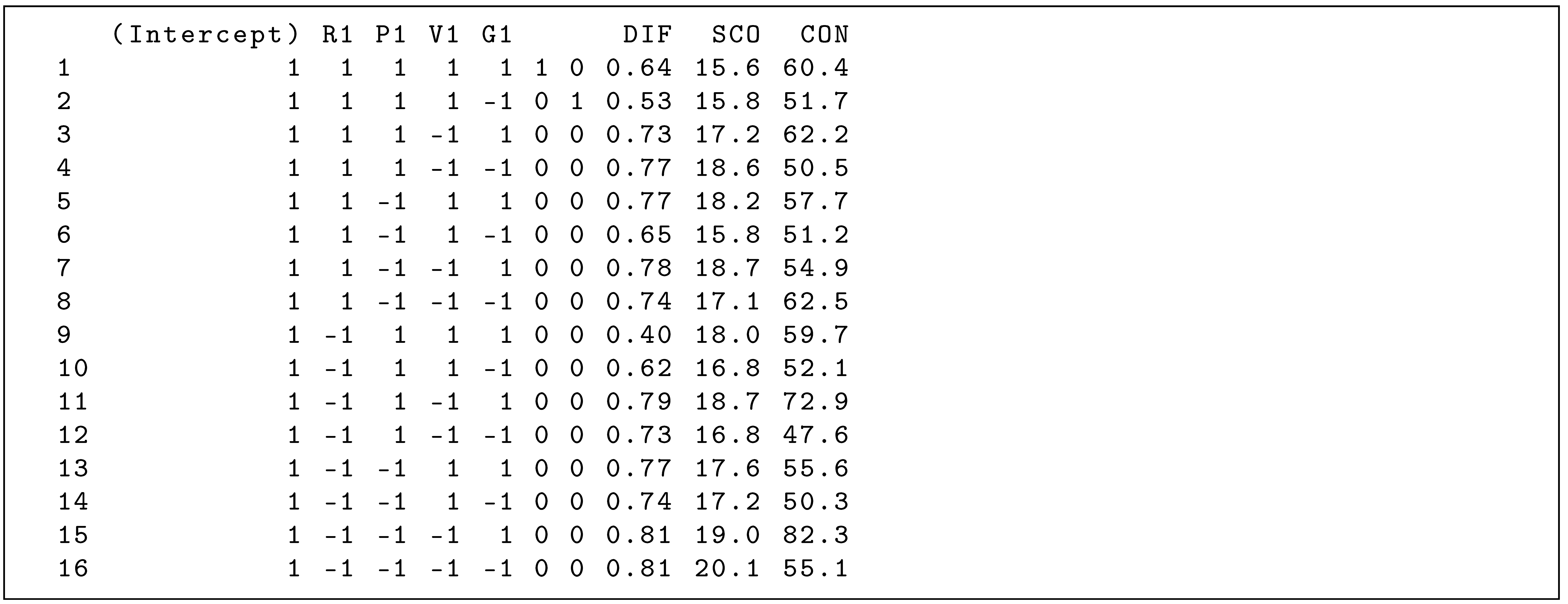 |
Note that, just as with the functional extensions or interaction terms, each single covariate increases the model complexity and consumes one degree of freedom each, which corresponds with the addition of one column each in the design matrix.
4.5. Comparing Pattern Frequencies for Two Samples with CFA
As the last hands-on section in this tutorial, we will focus on a variant of the CFA that is suitable for examining the differences between two (sub)samples.
To demonstrate the two-sample CFA, we turn to a new data example from the literature by Schmid and Lutz [44]. The study by Schmid and Lutz [44] investigates epistemological beliefs (epistemological views) among academics from different disciplines (variable ‘W’) that can be assigned to either the natural (category ‘N’) or the social sciences (category ‘S’). To investigate the coherence of epistemological beliefs, three aspects were recorded: The ontological aspect ‘O’, which refers to the question whether there is a reality independent of our representations, our thinking, our language, and our perceptions, at all. The epistemological aspect ‘E’, which refers to the, in the narrower sense of philosophical terminology, epistemological question if the truth of scientific knowledge can be established in principle. As well as the science-critical aspect ‘K’, which refers to a more or less optimistic or pessimistic view of the present state of knowledge in the sciences. The three variables were re-coded in a dichotomous manner, with ‘+’ representing agreement and ‘−’ representing disagreement. Based on theoretical considerations, Schmid and Lutz [44] initially state that some combinations of the three aspects represent non-coherent belief systems. The data can be reconstructed using the information from the original publication given in Schmid and Lutz [44] p. 36 by running the code lines 3 to 11 within the ‘R_snippet_012’ below.
| Listing 12. R_snippet_0012.R. |
 |
In addition to the question of whether, for example, incoherent belief systems represent an over-frequented (type) or under-frequented (antitype) feature configuration, the present data can be used to analyze by means of a two-sample CFA whether and, if so, which feature configuration significantly discriminates between the two scientific disciplines.
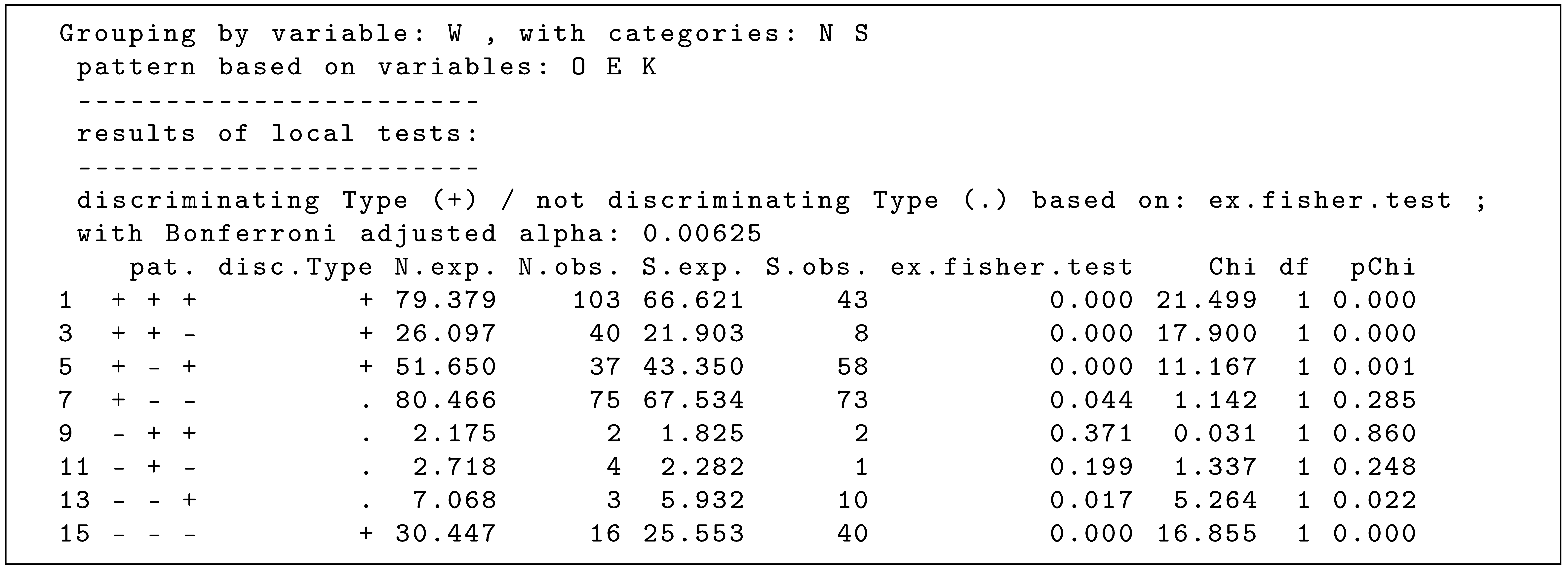
To perform such a two-sample CFA with confreq, code line 13 in ’R_snippet_012’ can be executed for the calculations and code line 14 can be used to output the results to the R console (see display of the results below).
The R output of the results above suggest that 4 configurations differ in their frequencies between the two science disciplines. For example, in the group of natural scientists more often than expected () and in the group of social scientists less often than expected (), there are persons who agree with the question of the existence of an independent reality, affirm the question that science can produce truth and overall have an optimistic view of the current state of scientific knowledge (configuration ). To visualize the results, the result object of the two-sample CFA can be plotted, as shown in the last code line in ‘R_snippet_012’.
 |
5. Summary and Conclusions
In this paper, we presented some main principles and methods of the configuration frequency analysis (CFA) using the R package confreq. Based on a critical review of Stevens’ well-known definition of scale levels, we derive a broader and more extensive definition of the term categorical data. Using examples that can be reproduced with single R code snippets, we introduce the methodology of configuration frequency analysis (CFA), which offers the possibility to analyze multivariate, categorical data. The thereby inherent focus on patterns of feature combinations—configurations—is linked to a person-centered perspective in the analysis of social sciences data. The person-centered perspective is based on the research subdisciplines of psychography and comparative research in the field of differential psychology, as defined by William Stern [18].
A first example of analysis contrasts initial findings on bivariate linear relationships (see Table 4) and findings from a first CFA main effect model of independence (see Section 4.2). This shows that significantly over- and under-frequented patterns of feature combinations can be found in the data. These configurations, called types and antitypes by Lienert [11], establish nonlinear multivariate associations between the analyzed variables, which could not be found with the previously performed analyses on bivariate linear associations. This and similar findings, cf. also in [21,22], underline the necessity of a multivariate nonlinear analysis method for categorical data as offered by the CFA. In addition to the theoretical and methodological basics of CFA, in this article we have given practical instructions on how to apply CFA using the package confreq on the basis of single R code snippets.
Note that besides confreq there is also other software available to perform CFA. First, there is a standalone program written in FORTRAN, which is provided as freeware by von Eye [45] via the web page http://www.configfreq.com/software (accessed on 2 September 2021). Second, there is another package called CFA, which was updated by Mair and Funke [46] until the year 2017. Besides these two alternatives, certain coefficients of the CFA can also be determined with the commercial IBM® software SPSS®, e.g., [47] using the command ‘LOGLINEAR’ cf. [9] p. 35, for an example. However, these existing alternatives each have drawbacks. For example, the program by von Eye [45] is not cross-platform compatible and is only available for Windows. The package CFA by Mair and Funke [46], although implementing some interesting automated procedures in the area of functional CFA, has a serious computational inaccuracy [9] p. 17, and moreover has not been updated since 2017. The SPSS® function ‘LOGLINEAR’ provides some coefficients of the CFA, but does not provide a comprehensive implementation of the CFA as in the R package confreq.
The currently available version 1.5.6-4 of confreq cf. [12] on CRAN not only includes functions for estimating expected frequencies of patterns from attribute combinations, but establishes an integrated and extensible framework for CFA consisting of elements for model formulation, inferential statistics, and visual representation of categorical data. This is implemented by the principle of log-linear modeling (LLM) using a design matrix. This implementation provides extensive flexibility to define a wide variety of CFA models with associated null hypotheses regarding the expected pattern frequencies. The core functionality of the package confreq gathers on two main functions, CFA() and S2CFA() with several arguments, which implement different variants of the CFA in R. To identify the types and antitypes currently five different tests for significance are available and two methods for controlling the alpha level inflation. Future releases of confreq possibly might include more procedures or rather test statistics to test for significance of the configurations. Furthermore, the confreq framework now allows for the implementation of further alpha adjustment procedures. Additional wrapper functions that access the core functions are also conceivable for future versions in order to implement procedural variants of the CFA in an automatic manner, such as the successive exclusion of significant patterns until the optimal fit of the LLM is achieved.
Author Contributions
J.-H.H. developed the basic idea and conceptualized this paper and wrote the original draft manuscript. In addition to contributions on the theoretical foundation of CFA and the person-centered approach within differential psychology, he contributed the formal analysis examples on CFA and developed the package confreq for R. M.S. is the supervising idea contributor in the overarching project on configuration frequency analysis methodology and inspired the initial development and continuously reviewed the R package confreq. For this paper, he conducted the careful review and editing of the text and R examples and made decisive contributions to the theoretical, methodological background. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this tutorial are either available in the R package confreq, which is available at https://CRAN.R-project.org/package=confreq (accessed on 2 September 2021), or are reconstructed within the R-code given in the respective R snippets and the electronic supplement.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CFA | configural frequencies analysis [Kofigurationsfrequenzanalyse—KFA] |
| LLM | log-linear modeling |
| LSD | lysergic acid diethylamide—a psychogenic drug used in the 1970s for psychopathological experiments because it was believed that LSD could (temporarily) mimic pathological phenomena such as psychosis. |
References
- Stevens, S.S. On the theory of scales of measurement. Science 1946, 103, 677–680. [Google Scholar] [CrossRef]
- Lord, F.M. On the Statistical Treatment of Football Numbers. Am. Psychol. 1953, 8, 750–751. [Google Scholar] [CrossRef]
- Zand Scholten, A.; Borsboom, D. A reanalysis of Lord’s statistical treatment of football numbers. J. Math. Psychol. 2009, 53, 69–75. [Google Scholar] [CrossRef]
- Velleman, P.F.; Wilkinson, L. Nominal, Ordinal, Interval, and Ratio Typologies Are Misleading. Am. Stat. 1993, 47, 65. [Google Scholar] [CrossRef]
- Niederee, R.; Mausfeld, R. Skalenniveau, Invarianz und Bedeutsamkeit [Scale level, invariance, and meaningfulness]. In Handbuch Quantitative Methoden [Handbook Quantitative Methods]; Erdfelder, E., Mausfeld, R., Meiser, T., Rudinger, R., Eds.; Psychologie Verlags Union: Weinheim, Germany, 1996; pp. 385–398. [Google Scholar]
- Niederée, R. There Is More to Measurement than Just Measurement: Measurement Theory, Symmetry, and Substantive Theorizing. Review of Foundations of Measurement. Vol. 3: Representation, Axiomatization, and Invariance, by R. Duncan Luce, David H. Krantz, Patrick Suppes, and Amos Tversky. J. Math. Psychol. 1994, 38, 527–594. [Google Scholar] [CrossRef]
- Kyngdon, A. Psychological Measurement Needs Units, Ratios, and Real Quantities: A Commentary on Humphry. Meas. Interdiscip. Res. Perspect. 2011, 9, 55–58. [Google Scholar] [CrossRef]
- Green, P.E.; Carroll, J.D. Mathematical Tools for Applied Multivariate Analysis; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Stemmler, M. Person-Centered Methods: Configural Frequency Analysis (CFA) and other Methods for the Analysis of Contingency Tables, 2nd ed.; Springer Briefs in Statistics; Springer Publishing Company: New York, NY, USA, 2020. [Google Scholar]
- Krauth, J.; Lienert, G.A. Die Konfigurationsfrequenzanalyse (KFA) und Ihre Anwendung in Psychologie und Medizin: Ein Multivariates nIchtparametrisches Verfahren zur Aufdeckung von Typen und Syndromen; mit 70 Tabellen; Alber-Broschur Psychologie, Alber Karl: Freiburg, Germany, 1973. [Google Scholar]
- Lienert, G.A. Die Konfigurationsfrequenzanalyse: I. Ein neuer Weg zu Typen und Syndromen. Z. Klin. Psychol. Psychother. 1971, 19, 99–115. [Google Scholar] [PubMed]
- Heine, J.H.; Alexandrowicz, R.W.; Stemmler, M. Confreq: Configural Frequencies Analysis Using Log-Linear Modeling; R Package Version 1.5.6-4. 2021. Available online: https://CRAN.R-project.org/package=confreq (accessed on 2 September 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 2 September 2021).
- Meyer, D.; Zeileis, A.; Hornik, K. Vcd: Visualizing Categorical Data; R Package Version 1.4-8. 2020. Available online: https://CRAN.R-project.org/package=vcd (accessed on 2 September 2021).
- Meyer, D.; Zeileis, A.; Hornik, K. The Strucplot Framework: Visualizing Multi-Way Contingency Tables with vcd. J. Stat. Softw. 2006, 17, 1–48. [Google Scholar] [CrossRef]
- Rosato, N.S.; Baer, J.C. Latent Class Analysis: A Method for Capturing Heterogeneity. Soc. Work. Res. 2012, 36, 61–69. [Google Scholar] [CrossRef]
- Heine, J.H. Untersuchungen zum Antwortverhalten und zu Modellen der Skalierung bei der Messung Psychologischer Konstrukte [Studies on the Response Behavior and Models of Scaling in the Measurement of Psychological Constructs]; Monographie [monograph]; Universität der Bundeswehr: München, Germany, 2020. [Google Scholar]
- Stern, W. Die Differentielle Psychologie in Ihren Methodischen Grundlagen; Verlag von Johann Ambrosius Barth: Leipzig, Germany, 1911. [Google Scholar]
- Von Eye, A.; Bogat, G.A. Person-Oriented and Variable-Oriented Research: Concepts, Results, and Development. Merrill-Palmer Q. 2006, 52, 390–420. [Google Scholar] [CrossRef]
- Leuner, H. Die Experimentelle Psychose: Ihre Psychopharmakologie, Phänomenologie und Dynamik in Beziehung zur Person. Versuch Einer Konditonal-Genetischen und Funktionalen Psychopathologie der Psychose; Springer: Göttingen, Germany, 1962. [Google Scholar]
- Meehl, P.E. Configural scoring. J. Consult. Psychol. 1950, 14, 165–171. [Google Scholar] [CrossRef]
- Simpson, E.H. The Interpretation of Interaction in Contingency Tables. J. R. Stat. Soc. Ser. 1951, 13, 238–241. [Google Scholar] [CrossRef]
- Yule, G.U. Notes on the theory of association of attributes in statistics. Biometrika 1903, 2, 121–134. [Google Scholar] [CrossRef]
- Bortz, J.; Döring, N. Forschungsmethoden und Evaluation für Human- und Sozialwissenschaftler, 4th ed.; Springer: Heidelberg, Germany, 2006. [Google Scholar]
- Sälzer, C.; Heine, J.H. Students’ skipping behavior on truancy items and (school) subjects and its relation to test performance in PISA 2012. Int. J. Educ. Dev. 2016, 46, 103–113. [Google Scholar] [CrossRef]
- Stemmler, M.; Heine, J.H. Using Configural Frequency Analysis as a Person-centered Analytic Approach with Categorical Data. Int. J. Behav. Dev. 2017, 41, 632–646. [Google Scholar] [CrossRef]
- Börnert-Ringleb, M.; Wilbert, J. The Association of Strategy Use and Concrete-Operational Thinking in Primary School. Front. Educ. 2018, 3. [Google Scholar] [CrossRef] [Green Version]
- Lazarides, R.; Dietrich, J.; Taskinen, P.H. Stability and change in students’ motivational profiles in mathematics classrooms: The role of perceived teaching. Teach. Teach. Educ. 2019, 79, 164–175. [Google Scholar] [CrossRef]
- Heine, J.H.; Stemmler, M. Die (Nicht-)Bedeutsamkeit des »Migrationshintergrundes« für die PISA-Leistung—Eine Analyse mittels KFA und LCA. In Klassifikationsanalysen in den Sozialwissenschaften; Reinecke, J., Tarnai, C., Eds.; Waxmann Verlag: Münster, Germany, 2021; pp. 75–99. [Google Scholar]
- Bonferroni, C.E. Il calcolo delle assicurazioni su gruppi di teste. In Studi in Onore del Professore Salvatore Ortu Carboni; Carboni, S.O., Ed.; Bardi: Rome, Italy, 1935; pp. 13–60. [Google Scholar]
- Holm, S. A simple sequentially rejective multiple test procedure. Scand. J. Stat. 1979, 6, 65–70. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley: New York, NY, USA, 1967. [Google Scholar]
- Fisher, R.A. The Logic of Inductive Inference. J. R. Stat. Soc. 1935, 98, 39–82. [Google Scholar] [CrossRef] [Green Version]
- Lucas, A.; Scholz, I.; Boehme, R.; Jasson, S.; Maechler, M. Gmp: Multiple Precision Arithmetic; R Package Version 0.6-2. 2021. Available online: https://CRAN.R-project.org/package=gmp (accessed on 2 September 2021).
- Langeheine, R. Log-Lineare Modelle zur Multivariaten Analyse Qualitativer Daten. Eine Einführung; Oldenbourg Verlag: München, Germany, 1980. [Google Scholar]
- Wermuth, N. Anmerkungen zur Konfigurationsfrequenzanalyse. Z. Klin. Psychol. Psychother. 1973, 3, 5–21. [Google Scholar]
- Victor, N.; Kieser, M. A test procedure for an alternative approach to Configural Frequency Analysis. Methodika 1991, 5, 87–97. [Google Scholar]
- Victor, N. An alternativ approach to Configural Frequency Analysis. Methodika 1989, 3, 61–73. [Google Scholar]
- Kieser, M.; Victor, N. Configural frequency analysis (CFA) revisited—A new look at an old approach. Biom. J. 1999, 41, 967–983. [Google Scholar] [CrossRef]
- Victor, N. A note on contingency tables with one structural zero. Biom. J. 1983, 25, 283–289. [Google Scholar] [CrossRef]
- Glück, J.; von Eye, A. Including covariates in Configural Frequency Analysis. Psychol. Beitr. 2000, 42, 405–417. [Google Scholar]
- Glück, J. Spatial Strategies—Kognitive Strategien Bei Raumvorstellungsleistungen. [Spatial Strategies—Cognitive Strategies on Spatial Tasks.]. Unpublished Ph.D. Thesis, University of Vienna, Vienna, Austria, 1999. [Google Scholar]
- Stemmler, M.; Heine, J.H.; Wallner, S. Person-centered data analysis with covariates and the R-package confreq. Methodology 2021, 17, 149–167. [Google Scholar] [CrossRef]
- Schmid, S.; Lutz, A. Epistemologische Überzeugungen als kohärente Laientheorien [Epistemological Beliefs as Coherent Lay Theories]. Z. Pädagogische Psychol. Ger. J. Educ. Psychol. 2007, 21, 29–40. [Google Scholar] [CrossRef]
- Von Eye, A. Configural Frequency Analysis–Version 2000. A program for 32 Bit Windows Operating Systems. Methods Psychol. Res. Online 2001, 6, 129–139. [Google Scholar]
- Mair, P.; Funke, S. cfa: Configural Frequency Analysis (CFA); R Package Version 0.10-0. 2017. Available online: https://CRAN.R-project.org/package=cfa (accessed on 2 September 2021).
- IBM Corporation. IBM SPSS Statistics for Windows, Version 26.0; IBM Corporation: Armonk, NY, USA, 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).