cdcatR: An R Package for Cognitive Diagnostic Computerized Adaptive Testing

Abstract

Cognitive diagnosis models (CDMs) are confirmatory latent class models that provide fine-grained information about skills and cognitive processes. These models have gained attention in the last few years because of their usefulness in educational and psychological settings. Recently, numerous developments have been made to allow for the implementation of cognitive diagnosis computerized adaptive testing (CD-CAT). Despite methodological advances, CD-CAT applications are still scarce. To facilitate research and the emergence of empirical applications in this area, we have developed the cdcatR package for R software. The purpose of this document is to illustrate the different functions included in this package. The package includes functionalities for data generation, model selection based on relative fit information, implementation of several item selection rules (including item exposure control), and CD-CAT performance evaluation in terms of classification accuracy, item exposure, and test length. In conclusion, an R package is made available to researchers and practitioners that allows for an easy implementation of CD-CAT in both simulation and applied studies. Ultimately, this is expected to facilitate the development of empirical applications in this area.

1. Theoretical Background

In education, we can distinguish between two types of evaluations. The first is summative evaluation. This is a more traditional type of assessment commonly performed at the end of the academic year, and aims at rank-ordering the students, usually on a single continuous dimension (e.g., math knowledge). This same interest in ordering respondents on a continuum is present in other areas of psychology, for example, in personnel selection. This type of assessment has usually been evaluated from the classical test theory or the traditional item response theory. The other type of evaluation is formative evaluation. The purpose of this assessment is not so much the comparison between individuals, but the detection of the strengths and weaknesses that each student possesses. These strengths and weaknesses are usually articulated around more narrowly defined dimensions that are called attributes (e.g., fraction subtraction, simplification). In education, this allows, for example, different remedial instructions to be implemented for each student, so that each one can overcome his or her difficulties. In a clinical or organizational psychology context, this type of diagnostic feedback enables more targeted interventions that can potentially be more effective compared to other interventions that take a broader measurement as a starting point. The attributes of the diagnostic assessments are usually modeled in a discrete form; that is, the analysis of the responses provided by the examinee leads to the conclusion as to whether or not the examinee has mastered each attribute. As the dimensions are more narrowly defined, these tests usually assess multiple attributes. The need to evaluate multiple discrete dimensions led to the proposal of a family of item response models known as cognitive diagnosis models (CDMs).

CDMs are confirmatory latent class models that can be used to classify examinees in a set of discrete latent attributes. The main output of CDMs consists of an attribute vector α_i = (α_{i1, …,} α_iK), where K denotes the number of attributes being measured by the test items. For most CDMs, classifications are dichotomous (i.e., α_k ∈ {0, 1}). That is, α_ik indicates whether or not the ith examinee has mastered attribute k. Brought to the set of attributes, this implies that the N examinees will be grouped into 2^K latent classes. For a given item, the different latent classes can be grouped into reduced latent classes or latent groups represented by α_lj^*. As an illustration, consider an item measuring only the first two attributes in a test in which K = 3 attributes are evaluated. If we represent the number of attributes measured by an item as K_j^*, the relevant classes for that item would be 2^Kj* = 2² = 4, i.e., {00-}, {10-}, {01-}, and {11-}, where the third attribute is partialled out. CDMs can be understood as item response models that specify the probability of correctly answering or endorsing the item given these reduced attribute vectors (i.e., an item response function). To simplify the explanation, we will refer to the probability of success even though these models have also been applied to typical performance tests. The different CDMs available differ in the restrictions applied to the item response function. To illustrate some of the possible response processes, an example has been generated for the case of an item that evaluates two attributes (i.e., K_j^* = 2) in Figure 1. CDMs can be mainly differentiated between compensatory models in which mastering one attribute can compensate for the lack of others, non-compensatory models in which it is necessary to master all the required attributes to achieve a high probability of success, and general or saturated models that allow the existence of both processes within the same test and complex relationships among the attributes within a specific item, considering main effects and interactions. One such general model that has served as the basis for many subsequent developments is the G-DINA model [1]. The item response function for this model will be specified later. Suffice it to mention for now that it is a saturated model where a different success probability is estimated for each latent group. The easy-to-interpret output provided by CDMs is valuable in indicating the strengths and weaknesses of a particular examinee. For this reason, these models first emerged and became popular in the educational setting [2], although they have now spread to other areas such as clinical psychology [3].

In order to facilitate more efficient applications in school and clinical contexts, where time for evaluation is always scarce, much work has been done in recent years to develop the necessary methods that allow for the implementation of cognitive diagnostic computerized adaptive testing (CD-CAT). There are multiple reasons that make adaptive testing preferable to traditional pencil-and-paper testing. In the following text we will mention three of them. The first and most obvious is that a more efficient assessment is achieved. With a carefully designed item bank, it is possible to obtain an accurate assessment with fewer items. This is possible because an adaptive algorithm is used to select the item to be administered, taking into account the level of ability that the subject shows throughout the CAT. Since an item response theory model is used to score the examinees, a measurement invariance property ensures that the assigned scores are comparable despite the fact that each examinee has responded to a different subset of the items. Second, a CAT can be more motivating for test takers, since items that are too far away (above or below) from their ability level will not be administered, nor will the assessment take longer than required. Finally, test security is increased. It can be a serious problem if a questionnaire that is presented in a fixed format is leaked. Since CAT uses different subsets of items, this problem is minimized. The downside of adaptive testing is that it requires computerized applications and a higher investment associated with the generation of a large item bank. CD-CAT makes it possible to combine these CAT advantages with CDM diagnostic feedback. Although the line of work exploring the application of CAT based on traditional item response models (e.g., the one-, two-, and three-parameter logistic models) has a relatively long history, the application of CAT based on CDM is comparatively young.

The first challenge for CD-CAT was the adaptation of existing procedures developed for the traditional item response theory framework, with continuous latent variables, to the CDM framework, with discrete latent variables. This resulted in the proposal of multiple item selection rules [4,5,6]. At the same time, a great effort has been made to develop procedures to verify a fundamental input in CDM, the so-called Q-matrix, which specifies the relationships between items and attributes [7,8]. Despite these methodological advances, empirical CD-CAT applications are still scarce. The most notable exception is the work of Liu et al. (2013), who developed an item bank to assess English proficiency and explored its adaptive application in a real-world context [9]. To facilitate research and the emergence of empirical applications in this area, we developed the cdcatR package [10] for R software [11]. This package is available at the CRAN repository. The purpose of this document is to exemplify the functions included in this package. To this end, the different phases in the implementation of a computerized adaptive testing application will be visited and the different options available in the package will be discussed. This will be followed by a more exhaustive illustration comparing different CD-CAT applications. Finally, a general discussion will be presented, and lines of future work will be discussed.

2. The cdcatR Package

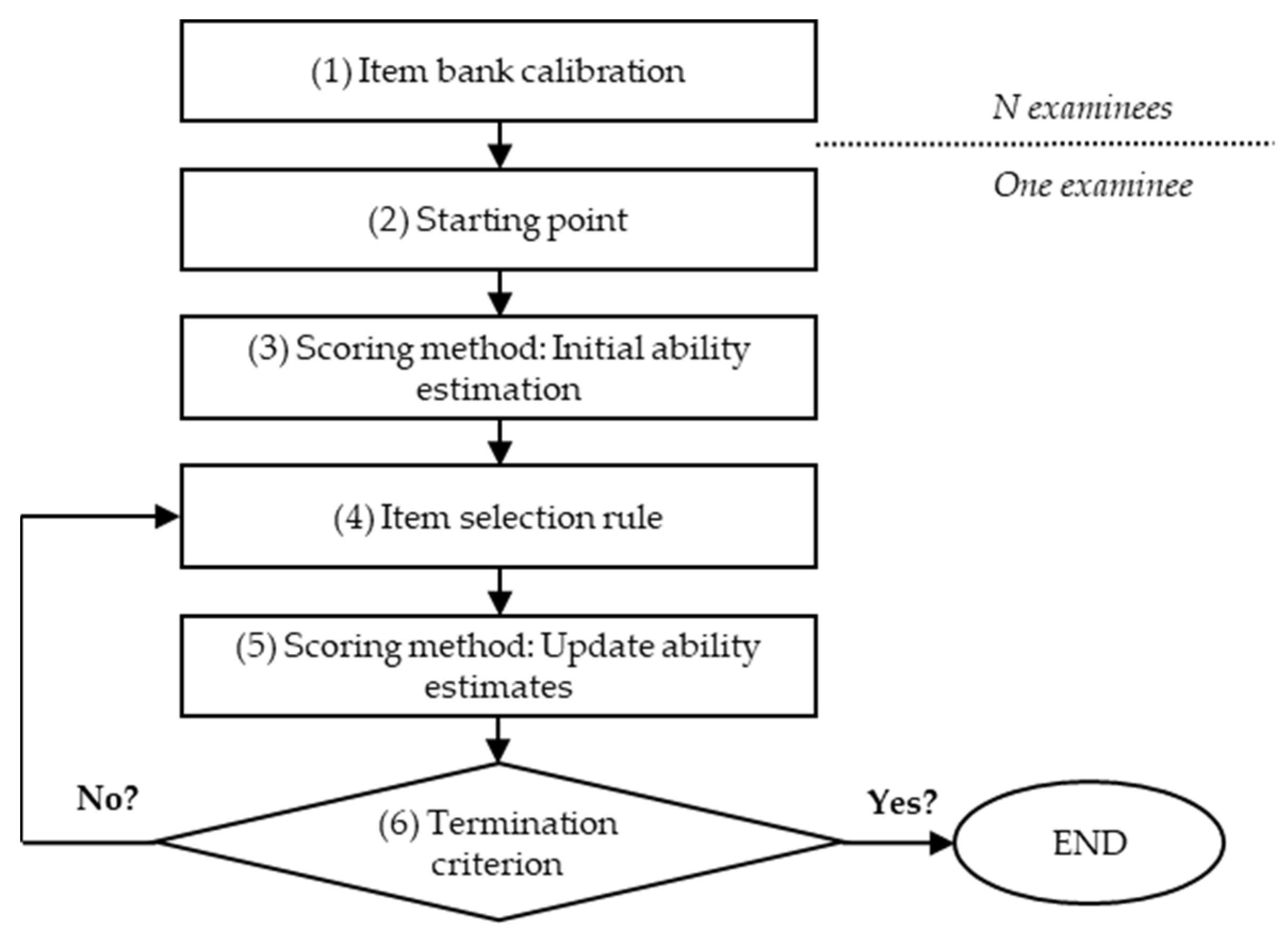
The R package cdcatR has been generated to facilitate the exploration of CD-CAT methods. Thus, it includes functions to simulate item banks and CDM data, a comprehensive function to fully implement a CD-CAT, as well as functions to extract and visualize the results. These functions and their arguments are intended to comprehensively address the aspects involved in a CAT application, which are represented in Figure 2. Similar flowcharts can be found, for example, in Huebner (2010) or Finch and French (2018) [12,13], among others. The difference between a standard CAT application and a CD-CAT application lies in the nature (continuous vs. discrete) of the latent variables. This leads to necessary modifications in several of the components of the adaptive testing application compared to traditional CAT. As shown in the figure, the process starts with the calibration of a bank of items and, for a particular examinee, ends when a termination criterion is satisfied. The calibration of the item bank will be based on a CDM (e.g., DINA) instead of relying on a traditional item response theory model (e.g., two-parameter logistic model). In this section, a walkthrough of the steps to be implemented in an application of this type is provided, highlighting the options included in the package. The literature related to these topics is also briefly described. The code used is included in the supplementary material.

2.1. Item Response Model and Item Bank Calibration

The cdcatR package allows users to work with the reduced CDMs deterministic-input, noisy, and gate (DINA; [14]); deterministic-input, noisy, or gate (DINO; [3]); and the additive CDM [A-CDM; [1]], as well as with the generalized DINA [1] which is a general model that subsumes the three previous models. These models differ in their definition of the item response function, i.e., the function that specifies the probability of success given an attribute profile. For the saturated model, the item response function is defined as

$$\mathrm{P}\left({\mathsf{\alpha }}_{\mathrm{lj}}^{*}\right)={\mathsf{\delta }}_{\mathrm{j}0}+{\displaystyle \sum }_{\mathrm{k}=1}^{{\mathrm{K}}_{\mathrm{j}}^{*}}{\mathsf{\delta }}_{\mathrm{jk}}{\mathsf{\alpha }}_{\mathrm{lk}}+{\displaystyle \sum }_{\mathrm{k}\prime =\mathrm{k}+1}^{{\mathrm{K}}_{\mathrm{j}}^{*}}{\displaystyle \sum }_{\mathrm{k}=1}^{{\mathrm{K}}_{\mathrm{j}}^{*}-1}{\mathsf{\delta }}_{{\mathrm{jkk}}^{\prime }}{\mathsf{\alpha }}_{\mathrm{lk}}{\mathsf{\alpha }}_{{\mathrm{lk}}^{\prime }}\dots +{\mathsf{\delta }}_{12\dots {\mathrm{K}}_{\mathrm{j}}^{*}}{\displaystyle \prod }_{\mathrm{k}=1}^{{\mathrm{K}}_{\mathrm{j}}^{*}}{\mathsf{\alpha }}_{\mathrm{lk}},$$

(1)

where α_lj^* is a vector of length K_j^* that indicates which attributes an examinee in latent group l masters (or not), δ_j0 is the intercept or baseline probability of item j, δ_jk is the main effect due to α_lk, δ_jkk’ is the interaction effect due to α_lk and α_lk’, and δ_12…Kj* is the interaction effect due to α_{1, …,} α_Kj*. As detailed in [1], the reduced DINA, DINO, and A-CDM models can be understood as special cases of the G-DINA model when some restrictions are imposed on these item parameters. As such, the DINA model is obtained when all parameters except δ_j0 and the highest order interaction (i.e., δ_12…Kj*) are set to zero. The DINA model is thus a non-compensatory model, where it is necessary for the examinee to master all attributes to have a high probability of success. Its complement is the DINO model, where the examinee will obtain a high probability of success if he/she masters at least one of the attributes specified in the item. This is achieved by setting the constraint δ_jk = δ_jkk’ = … = (−1)^Kj*+1 δ_12…Kj*. Therefore, the DINA and DINO models have only two parameters per item, whereas for the saturated model the number of parameters is equal to 2^Kj*. The A-CDM model is derived from the general model by setting all interaction terms between attributes to zero, so that each attribute contributes independently to the probability of existence. It has K_j^* + 1 parameters per item. This is a comprehensive selection of the CDM models available, as each of these four models represents a different type of CDM: general (G-DINA), conjunctive (DINA), disjunctive (DINO), and additive (A-CDM). In addition, from the available empirical studies, we can notice that the DINA and G-DINA models are two of the most popular approaches in practice.

The calibration of these models needs to be done with an external package to cdcatR. The GDINA [15] or CDM [16] packages of R can be used for this purpose. The result of this calibration will be included as the input in cdcat(), which is the main function of the cdcatR package, using the fit argument. Figure 3 provides an example of how the GDINA and CDM packages can be used to calibrate some data with the DINA model and incorporate this input into the cdcat() function. It is also shown how the cdcat.summary() function can be used to compare different cdcat objects. For this purpose, the true attribute vectors are provided in the alpha argument, which allows us to obtain attribute classification accuracy indicators. In the context of an empirical data analysis, where the true attribute vectors are unknown, the estimated attribute vectors using the entire item bank could be included in alpha. This would act as an upper-limit benchmark to evaluate the CD-CAT efficiency. Additionally, it is possible to include a label for each cdcat object to facilitate the readability of the results using the label argument. Nearly identical results are expected when employing the GDINA or CDM packages to calibrate the CDMs [17,18].

It should be noted, as previously indicated, that the different models vary in complexity. The degree of complexity affects the ease or difficulty of item parameter estimation. Under challenging estimation conditions characterized, for example, by a small sample size, a larger estimation error can be expected to affect the performance of the CD-CAT [19]. To deal with this, Sorrel et al. (2021) recommended performing a model comparison analysis at the item level in order to minimize the number of parameters to be estimated [20]. To this end, the authors used the two-step LR test, an efficient approach to the likelihood ratio test [21]. The cdcatR package includes a function called LR.2step() that implements this statistic. Figure 4 includes an illustration for that function in which a G-DINA model is calibrated to DINA-generated items, and the two-step LR test is used to select the most appropriate model for each item. Another similar statistic included in the GDINA and CDM packages is the Wald test [22,23].

Finally, we shall note that in these analyses we have considered a known Q-matrix without specification errors. Although this is a plausible scenario considering the efforts that are invested in the development of the Q-matrix, it is important to remark that these procedures involve a certain degree of subjectivity [24,25]. The Q-matrix can be empirically tested by employing empirical validation procedures. For example, it can be assessed whether the empirical data lead to any modification suggestions by employing the Hull method [7] implemented in the R package cdmTools [26]. The CDM and GDINA packages include other empirical validation procedures based on item discrimination [27] that could also be used for this same purpose. It can also be verified whether the number of attributes established from theory converges with the empirical results using procedures such as parallel analysis or relative fit indicators. Researchers can use the paK() and modelcompK() functions from the cdmTools package to conduct such analyses [28]. After addressing the aspects related to the calibration of the item bank, the following sections deal with specific aspects of the CAT implementation.

2.2. Starting Point

The first specification to set in our CAT is the starting point. The two basic options involve applying the item selection rule to select the item that optimizes that rule from the very beginning or starting from a random start such that the first item is randomly selected (the selection rule is applied thereafter). Having a random start facilitates a lower overlap rate at the beginning of the test, although accuracy may suffer for very short CAT lengths. The preference for one of these two start procedures is captured in the startRule argument, which takes “random” or “max” as the input. The selection rules are usually weighted by a posterior distribution obtained at each CAT step, and it is possible to specify a distribution to be used for the first item by means of the initial.distr argument. This should be a multinomial distribution of length 2^K where each value indicates the expected proportion of examinees for each latent class. Otherwise indicated, a uniform distribution is used. Finally, it has recently been pointed out that it is possible to identify optimal starts. For instance, ensuring that the first K items form an identity matrix satisfies the identification condition [29]. For this reason, the package includes a startK argument in which the users can indicate TRUE or FALSE to determine whether they want a start with identity matrix or not. If so, after applying K one-attribute items selected at random among those measuring each of the attributes, it proceeds as indicated in the startRule argument.

2.3. Item Selection Rule

The item selection rule determines how the items are selected based on the responses already provided by an examinee. The fact that the underlying latent variables are discrete impedes the use of the most popular item selection rules in traditional CAT, i.e., point Fisher information. This is why in recent years several rules had to be developed for the case of discrete attributes. Currently, the package allows working with six item selection rules using the itemSelect argument: the general discrimination index (GDI; [5]), the Jensen–Shannon divergence index (JSD; [30,31]), the posterior-weighted Kullback–Leibler index (PWKL; [4]), the modified PWKL index (MPWKL; [5]), the nonparametric item selection method (NPS; [32]), and random selection. The research by Yigit et al. (2019) and Wang et al. (2020) examined the relationships among several of the indices proposed in the previous literature, and found that they are tightly related [31,33]. As an exception, PWKL differs from the rest of the rules in that it takes a single punctual latent class estimator obtained at the t step for the examinee i (i.e., ${\hat{\mathit{\alpha }}}_{\mathit{i}}^{\left(\mathit{t}\right)}$) to select the next item, whereas the rest are global measures that consider the entire posterior distribution (i.e., $\hat{\mathit{p}}{\left({\mathit{\alpha }}_{\mathit{i}}\right)}^{\left(\mathit{t}\right)}$ ). Global measures can be expected to perform better in cases of short CAT lengths where the punctual estimation is still noisy [5,34]. The other exception is the NPS method, which, unlike the other procedures, does not require prior calibration of the item bank as it uses a nonparametric estimation procedure for the latent class assignment. This procedure starts with startK = TRUE and the latent class is then estimated using the nonparametric classification method (NPC; [35]). This method is based on the concept of Hamming distance to compute the discrepancy between the examinee’s response pattern and the ideal responses associated with each attribute profile. These ideal responses are defined according to a deterministic conjunctive (non-compensatory like the DINA model) or disjunctive (compensatory like the DINO model) rule. This must be specified a priori using the NPS.args argument where gate can take the value of “AND” (conjunctive) or “OR” (disjunctive). A process is then initiated where the items are randomly selected, considering those that can differentiate between the ideal response of the current estimate of the attribute vector and the ideal response of the second most likely attribute vector.

Since version 1.0.3 of the cdcatR package, two procedures to control the item exposure rate have been available. On the one hand, the progressive method can be implemented [36,37]. This rule adds a random component to the chosen item selection rule that becomes less important as the test progresses. For a test of length J items, the first item would be chosen randomly and at item J the random component would not be relevant at all. The progression of the loss of importance of randomness is reflected in an acceleration parameter b. With b = 0, the proportion of selection due to the item selection rule will linearly increase from 0 (first item) to 1 (last item reflected in the MAXJ argument) [36]. With b < 0, an increment in the proportion of selection due to the selection rule would follow an inverse exponential function; that is, there would be a random component at the beginning of the test but this random component would lose importance very quickly. The random component will always have less impact compared to b = 0. With b > 0, this increment would follow an exponential function; that is, the random component will always have greater impact compared to b = 0. To use this method in the package, set itemExposurecontrol = “progressive.” The default is “NULL”, i.e., not to apply the progressive method. There is an argument b to set the acceleration parameter, which defaults to a value of 0. With lower (can be negative) values, exposure rates are expected to be more similar to those that would be obtained if no control were implemented. This would optimize accuracy at the cost of allowing greater item exposure. On the other hand, a maximum exposure rate can be set for the items by means of the rmax argument. By default, there is no control over the maximum exposure rate (i.e., rmax can be as high as 1). Interested users can also include content constraints on the number items per evaluated attribute. In particular, the constraint.args argument can indicate the minimum number of items to be administered for each of the attributes [38].

2.4. Scoring Method

The main output of CD-CAT is the estimated attribute vector of each examinee (i.e., ${\widehat{\mathit{\alpha }}}_{\mathit{i}}$). The maximum likelihood (ML), maximum a posterior (MAP), or expected a posterior (EAP) methods can be used to make both the initial and subsequent attribute vector estimations [39]. All these methods are based on the likelihood function (L(Y_i|α_l)), which at a given point in the CAT is defined as

$$\mathrm{L}\left({\mathrm{Y}}_{\mathrm{i}}{|\mathsf{\alpha }}_{\mathrm{l}}\right)={\displaystyle \prod }_{\mathrm{j}=1}^{{\mathrm{J}}^{\left(\mathrm{t}\right)}}\mathrm{P}{\left({\mathrm{Y}}_{\mathrm{j}}=1{|\mathsf{\alpha }}_{\mathrm{l}}\right)}^{{\mathrm{Y}}_{\mathrm{ij}}}{\left[1-\mathrm{P}\left({\mathrm{Y}}_{\mathrm{j}}=1{|\mathsf{\alpha }}_{\mathrm{l}}\right)\right]}^{1-{\mathrm{Y}}_{\mathrm{ij}}},$$

(2)

where J^(t) denotes the number of items administered. From this likelihood we can estimate a posterior distribution of the latent classes given the observed response patterns by considering a prior attribute joint distribution (p(α_c)) as

$$P\left({\mathit{\alpha }}_l|{\mathit{Y}}_i\right)=L\left({\mathit{Y}}_i|{\mathit{\alpha }}_l\right)p\left({\mathit{\alpha }}_l\right)/{{\displaystyle \sum }}_{c=1}^{2^K}L\left({\mathit{Y}}_i|{\mathit{\alpha }}_c\right)p\left({\mathit{\alpha }}_c\right)$$

(3)

Once these functions have been calculated, the ML, MAP, and EAP estimators are obtained as follows:

$$\mathrm{ML}\left({\mathsf{\alpha }}_{\mathrm{i}}\right)=\arg {\max }_{{\mathsf{\alpha }}_{\mathrm{l}}}\left[\mathrm{L}\left({\mathrm{Y}}_{\mathrm{i}}{|\mathsf{\alpha }}_{\mathrm{l}}\right)\right]$$

(4)

$$\mathrm{MAP}\left({\mathsf{\alpha }}_{\mathrm{i}}\right)=\arg {\max }_{{\mathsf{\alpha }}_{\mathrm{l}}}\left[\mathrm{P}\left({\mathsf{\alpha }}_{\mathrm{l}}{|\mathrm{Y}}_{\mathrm{i}}\right)\right]$$

(5)

$$\mathrm{EAP}\left({\mathsf{\alpha }}_{\mathrm{i}}\right)=\{\mathrm{P}({\mathsf{\alpha }}_{\mathrm{ik}}|{\mathrm{Y}}_{\mathrm{i}})\}{\displaystyle \sum }_{\mathrm{l}=1}^{\mathrm{L}}\mathrm{P}\left({\mathsf{\alpha }}_{\mathrm{l}}{|\mathrm{Y}}_{\mathrm{i}}\right){\mathsf{\alpha }}_{\mathrm{lk}}.$$

(6)

The EAP estimator indicates the posterior probability that examinee i has of mastering each of the K attributes. This probability can be dichotomized using a cutoff point, usually 0.50.

Table 1. Latent class estimates at each step of a 10-item CAT for an examinee with true attribute profile of α_i = (00110).

#item	j	qj	xj	ML	nmodesML	Lik	MAP	nmodesMAP	Post	EAP	K1	K2	K3	K4	K5
1	47	10000	0	00000	16	1.00	00000	16	0.06	00000	0.02	0.50	0.50	0.50	0.50
2	15	00001	0	00000	8	0.96	00000	8	0.12	01110	0.02	0.50	0.50	0.50	0.00
3	12	01000	0	00000	4	0.93	00000	4	0.24	00110	0.02	0.01	0.50	0.50	0.00
4	58	00100	1	00100	2	0.90	00100	2	0.48	00100	0.02	0.01	0.99	0.50	0.00
5	18	00010	1	00110	1	0.87	00110	1	0.91	00110	0.02	0.01	0.99	0.94	0.00
6	110	00110	1	00110	1	0.78	00110	1	0.96	00110	0.02	0.01	0.99	1.00	0.00
7	11	10000	0	00110	1	0.77	00110	1	0.98	00110	0.00	0.01	0.99	1.00	0.00
8	62	01000	0	00110	1	0.74	00110	1	0.99	00110	0.00	0.00	0.99	1.00	0.00
9	8	00100	1	00110	1	0.74	00110	1	0.99	00110	0.00	0.00	1.00	1.00	0.00
10	14	00010	1	00110	1	0.61	00110	1	1.00	00110	0.00	0.00	1.00	1.00	0.00

Note. j: item index; qj: q-vector for item j; xj: observed response for item j; ML: maximum likelihood estimator; nmodesML: number of attribute profiles that have the same likelihood as the ML estimator; Lik: likelihood of the ML estimator; MAP: maximum a posteriori estimator; nmodesMAP: number of attribute profiles that have the same posterior probability as the MAP estimator; Post: posterior probability of the MAP estimator; EAP: expected a posteriori estimator; K1,…,K5: posterior probabilities of attribute mastery.

includes the estimators for a particular examinee in a CD-CAT application as returned in the package. It can be seen how the posterior probability approaches 1 as the CAT progresses, indicating the increasing degree of certainty around the estimator. The ML and MAP estimators coincide because a uniform prior joint attribute distribution was specified, which is the default option in the package. Another distribution could be specified by means of the att.prior argument.

2.5. Termination Criterion

The last aspect of a CAT that can be specified is the termination criterion, i.e., the condition that must be satisfied to stop the adaptive application. By default, a fixed-length termination criterion of 20 items is applied. This number of items can be varied with the MAXJ argument. Alternatively, the FIXED.LENGTH argument can be set to FALSE, in which case a fixed-precision criterion is applied. Under this criterion, the CAT for a particular examinee is stopped when the assigned latent class posterior probability is greater than a cutoff point set by the precision.cut argument. This argument takes the default value of 0.80 [40].

2.6. Data Generation Using the Package

The package contains two functions designed to simulate CDM data. First, the gen.itembank() function can be used to generate an item bank. The user can either provide a Q-matrix using the Q argument or create one defining a set of specifications in the gen.Q argument. If this latter option is chosen, the user will have to include a list indicating the number of items (J); the number of attributes (K); the proportion of items measuring 1, 2, …, up to K attributes (propK.j); the minimum number of identity matrices included in the Q-matrix (nI); the minimum number of items measuring each attribute (minJ.K); and the maximum correlation to be expected by design between the attributes (max.Kcor). In both cases, it will be necessary to indicate the quality of the items in the bank by establishing the mean and range of a uniform distribution (mean.IQ and range.IQ, respectively). These arguments set the mean value of the traditional item discrimination index that evaluates the difference in success probability for examinees mastering all and none of the attributes required by an item (i.e., IDI = P(1)–P(0); (3)). The mean of IDI would be mean.IQ and the minimum and maximum values would be approximately mean.IQ –range.IQ/2 and mean.IQ + range.IQ/2, respectively. Item parameters are generated so that the monotonicity constraint is satisfied (i.e., mastering a higher number of attributes always leads to a higher or equal probability of success).

The next step involves the use of the gen.data() function. This function takes as input an object of the gen.itembank type and also requires specifying the number of examinees to be generated (N). Optionally, R indicates the number of replicas or databases to be generated (one, by default). The true attribute profiles are generated, by default, from the uniform distribution, but other attribute joint distributions can be specified with att.dist (i.e., higher.order, multivariate normal, or multinomial). Alternatively, a matrix containing the true attribute profile can be directly provided using the att.profiles argument. Finally, to ensure replicability, the user can specify a seed.

Figure 5 includes two illustrations in which data are generated using these functions. In the first example, data are generated with a Q-matrix included in the package indicating items of medium quality (P(1)–P(0) = 0.60) with high variability in discrimination (range.IQ = 0.20; [5]). The selected model is the DINA model. P(0) and P(1) denote the probability of success for examinees mastering none and all of the attributes required by the item, respectively. Once the item bank is generated, what follows is an example of how data can be generated using the uniform distribution, the multivariate normal distribution, or by providing specific attribute profiles. In the second illustration, a Q-matrix is generated by indicating a series of specifications including the number of items and attributes, the proportion of items measuring 1, 2, 3, and 4 attributes, stating that at least three identity matrices are to be included. In this case, high-quality items with lower variability are specified. Then, data are generated using the uniform distribution.

3. Illustration

In order to demonstrate some of the functions and arguments discussed above, this section presents an illustration that starts with the generation of data and ends with the evaluation of the performance of different CD-CAT procedures in terms of attribute classification accuracy, item exposure rate, and CAT length. The code used can be found in its entirety in Appendix A. Note that we used the true (generating) item parameters in this illustration so that we could emulate the scenario with no sampling error in the model estimation. To achieve this, we provided the true item parameters in the GDINA() function and set the maximum number of iterations to 0. This allowed for a more direct comparison of the different CAT implementations. In applied contexts, some sampling error is to be expected (for a discussion of this, see, for example, [19,20]). The plots were obtained using the cdcat.summary() function of the package, which uses the R package ggplot2 [41]. The GDINA package was used to calibrate the models.

First, an item bank was generated that included 180 items to assess 5 attributes. The proportion of items measuring 1, 2, and 3 attributes was set to be 0.40, 0.30, and 0.30, respectively. It was established that there should be at least three identity matrices within the Q-matrix and that each attribute should be assessed by a minimum of 10 items. Item quality was set to be high and with high variability (i.e., mean.IQ = 0.90 and range.IQ = 0.20). The generating model was set to be the DINA model and the number of generated response patterns were 500, employing a uniform distribution for the attribute joint distribution, which is the default specification in the gen.data() function. With respect to model calibration, we chose to exemplify a scenario in which there is no calibration error by providing the true item parameters in the GDINA() function of the GDINA package.

Next, a total of seven CD-CATs with a fixed length of 15 items were compared: (1) an application with itemSelect = “GDI” and startRule = “max” (default values in the cdcat() function); (2) an application with itemSelect = “GDI” but with startRule = “random” (i.e., the first item is selected at random and the GDI rule is applied); (3) and (4) were applications including the progressive item exposure control method applied on the GDI (i.e., itemSelect = “GDI” and itemExposurecontrol = “progressive”) with values for the acceleration parameter equal to −2 and 2, respectively, (5) an application with itemSelect = “PWKL”; (6) an application with itemSelect = “NPS”; and (7) an application with itemSelect = “random.” It was expected that “random” would obtain the worst performance in attribute classification accuracy. PWKL was expected to perform comparatively worse at the beginning of the test, where the punctual estimation of the attribute vector is still unreliable. A higher acceleration parameter in the progressive method applications will lead to lower overlap rates, to the detriment of reliability compared to GDI. Using startRule = “random” will allow the overlap rate to be slightly reduced, with minimal impact on the attribute classification accuracy.

The attribute classification accuracy and overlap rates were obtained with the cdcat.summary() function specifically designed for the comparison of cdcat-type objects. Specifically, we report pattern recovery calculated as the proportion of correctly classified attribute vectors:

$$\mathrm{PCV}={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{N}}\frac{\mathrm{I}[{\mathsf{\alpha }}_{\mathrm{i}}={\widehat{\mathsf{\alpha }}}_{\mathrm{i}}]}{\mathrm{N}}$$

(7)

Descriptive information was also included for the item exposure rates, including the overlap rate, computed as [42]:

$$\mathrm{T}=\frac{\mathrm{n}}{\mathrm{q}}{\mathrm{S}}_{\mathrm{er}}^2+\frac{\mathrm{q}}{\mathrm{n}},$$

(8)

where n is the item bank size, q is the CAT length, and S_er² is the variance of the item exposure rates. The overlap rate is a traditional test security indicator (e.g., [43]). It provides information on the average proportion of items expected to be shared by two examinees. In the event that a bank is leaked, a high overlap rate would allow examinees to have easy access to the items that will be presented to them. CD-CAT applications will typically occur in educational learning contexts where this is not a priori a problem, as it is not a high-stakes context. However, high overlap rates often reflect a suboptimal use of the item bank, represented by an overexposure of a few items and an underexposure of many others. That is why the optimization of both the classification accuracy and overlap rate should ideally be achieved.

The results for attribute classification accuracy are shown in Figure 6. As can be seen, the application that obtained the best results was the one based on GDI, with a pattern recovery equal to or higher than that of the remaining methods starting in the fifth item. As more items were applied, the pattern recovery increased until reaching values equal or close to 1 for all GDI-based procedures. Having a high acceleration parameter in the progressive method meant that for the selection of the first items there was a strong random component, leading to less accurate classifications. This was shared by the PWKL method, which, although it managed to obtain an acceptable accuracy, obtained poorer results in the first items. The NPS method started after applying K items of an attribute at the beginning, so its line started at item K = 5. This nonparametric method ended up achieving a reliability equal to that obtained by PWKL, although we see that it had a slower growth in reliability compared to the parametric procedures. Finally, an almost linear growth in reliability is observed for the random method, which did not optimize item selection based on previously administered items.

The results for item exposure are shown in

Table 2. Item exposure comparison for the seven fixed-length CD-CAT implementations.

Implementation	Min.	1st Qu.	Median	Mean	3rd Qu.	Max.	Overlap Rate
GDI	0.00	0.00	0.00	0.08	0.05	1.00	0.50
GDI.randomstart	0.00	0.01	0.01	0.08	0.05	0.93	0.45
GDI.progm2	0.00	0.01	0.01	0.08	0.05	0.89	0.42
GDI.prog2	0.02	0.05	0.07	0.08	0.09	0.43	0.13
PWKL	0.00	0.01	0.01	0.08	0.06	0.99	0.44
NPS	0.02	0.05	0.08	0.08	0.12	0.19	0.10
random	0.05	0.07	0.08	0.08	0.09	0.12	0.09

Note. GDI: general discrimination index; prog2 and m2: progressive method for item exposure control with b = 2 and –2, respectively; randomstart: first item is selected at random; NPS: non-parametric item selection method; PWKL: posterior weighted Kullback–Leibler; random: random item selection.

. The trade-off between accuracy and test security is clearly illustrated. GDI, which obtained the best results for pattern recovery, had the highest overlap rate (0.50), with some items being applied to 100% of examinees. This was slightly mitigated by using a random start, which increased the first quartile for item exposure rate and minimally lowered the overlap rate. The application of the progressive method decreased the overlap rate (the higher the value of the acceleration parameter, the lower the overlap rate). The other parametric selection rule, PWKL, obtained the highest overlap rate after GDI (0.44) despite having comparatively worse results in pattern recovery. For this reason, GDI would be preferred over PWKL. The results for NPS clearly reflect the random component of this selection rule. Thus, it provided a low overlap rate and an exhaustive use of the item bank with few over- and under-item item exposure problems. In particular, we see how NPS obtained results similar to the random application even when acceptable pattern recovery results were obtained.

This illustration was followed by conducting two fixed-precision applications. To do this, the FIXED.LENGTH argument was set to FALSE and an accuracy-based stopping criterion was established. Specifically, it was established that for an examinee i the CAT should stop when the posterior probability assigned to the estimated latent class is equal to or greater than 0.95 (precision.cut = 0.95). The maximum number of items to apply for an examinee was set to be 20 (i.e., the default specification for MAXJ). As we shall see, this led to each examinee being able to respond to a different number of items and, if the size and quality of the item bank allowed it, the final pattern recovery being equal to or greater than 0.95. The latter can be seen in

Table 3. Attribute classification accuracy comparison for the two fixed-precision CD-CAT implementations.

PCV	1/5	2/5	3/5	4/5	5/5
GDI precision	1.00	1.00	1.00	1.00	0.97
GDI.prog2 precision	1.00	1.00	1.00	1.00	0.98
PCA	K1	K2	K3	K4	K5
GDI precision	1.00	0.99	1.00	0.99	1.00
GDI.prog2 precision	1.00	0.99	1.00	1.00	1.00

Note. PCV: proportion of correctly classified attributes at the vector level. PCA: proportion of correctly classified attributes at the individual attribute level. K1,…,K5: attributes 1 to 5.

, which shows the attribute classification accuracy results obtained using the cdcat.summary() function. For illustrative purposes only, two CD-CAT applications were included: one based on GDI and the other based on GDI, but applying the progressive method for item exposure control with b = 2. The stopping criterion tries to set the value for the proportion of completely correct classifications in the estimated latent class vector (K/K, in this case, 5/5). We see that in this case both CD-CAT applications exceeded the value of 0.95, taking the values of 0.97 and 0.98 for GDI and GDI with the progressive method, respectively. This means that for 97–98% of the 500 examinees, the estimated latent class coincided with the true one. It is difficult to obtain high values for this variable if, for example, the number of attributes to be classified is high. Thus, the number of any attributes correctly assigned in the estimated vector (1/K to K−1/K) is offered as complementary information. In this case we observe that for both classifications at least four of the five attributes were correctly classified in 100% of the cases. The PCA indicates the proportion of classifications for each individual attribute. In this case we observe that all attributes were measured with a very similar level of accuracy.

Once we verified that the accuracy achieved was as desired, we examined the distribution of the number of items applied to each examinee and the exposure rate of the items also using the cdcat.summary() function. This information is reported in Figure 7 and Figure 8, respectively. As expected, the application based exclusively on GDI satisfied the criterion of precision, requiring a much smaller number of administered items. Since the items in the bank were of high quality, in many cases it was sufficient to administer five items, the mean being 6.25, at the cost of overexposing several items. In order to control the exposure rate of the items, the progressive method starts with a random component (in this case high due to the use of b = 2), which makes 10.35 items necessary on average per examinee but making a much more exhaustive use of the item bank. The context of application should be considered to prioritize an efficient evaluation (GDI) or better security and item bank usage (GDI with the progressive method).

4. Discussion

The CD-CAT methodology has emerged to combine the efficiency of adaptive applications with the fine-grained diagnostic output of CDMs [4]. Multiple papers have been published exploring this methodology and proposing new developments. The first empirical applications have also emerged. Specifically, Liu et al. (2013) described the generation of a bank of 352 items assessing eight attributes related to English proficiency and Tu et al. (2017) presented 181 items to classify examinees in nine attributes related to internet addiction [9,44]. To date, the authors making use of this methodology have needed to develop ad hoc codes. This complicates comparison across studies and access to these methodologies by researchers in applied settings. For this reason, the cdcatR package was developed in a manner analogous to what had been done previously in the context of traditional item response theory with the catR [45] and mirtCAT [46] packages. The main difference between traditional CAT and CD-CAT is that in CD-CAT the measurement model considers multiple discrete latent attributes, whereas in traditional IRT the measurement model typically considers one (or only a few) continuous latent traits. This leads to numerous similarities between these two types of adaptive applications (e.g., the workflow presented in Figure 2 is common), but has also led to the need for developments of the CD-CAT itself, as reviewed in the previous section. The present document has described the main functions and arguments of cdcatR. In addition, an illustration has been provided in which various specifications for the implementation of the CD-CAT were compared in terms of attribute classification accuracy, item exposure, and test length for the simulated data. We hope that this will motivate the development of new empirical applications using this framework and simulation studies that further explore the methods available to date. It should be noted that the package is still in its initial stages. The first stable version of the package was version 1.0.0 and was published on CRAN in June 2020. The current version is version 1.0.3 and, with respect to previous versions, the specifications for starting rule and exposure control were added [36,37]. In the following text, some of the developments that are planned to be included in future versions are detailed.

First, we plan to include other exposure control methods specifically developed in the context of CD-CAT to facilitate their scrutiny and comparison with the traditional progressive method [47]. Second, other popular selection rules in CD-CAT such as mutual information [48] and Shannon entropy [49] and more modern ones such as the one presented in Li et al. (2021) will be incorporated [6]. Previous studies have found a close theoretical relationship between several of the item selection rules available [31,33]. Including these procedures will facilitate the implementation of simulation studies to better understand their similarities and discrepancies in different contexts. Third, the package allows for work to be carried out currently under the G-DINA framework for dichotomous data (i.e., G-DINA, DINA, DINO, and A-CDM models). It is expected that more complex models be incorporated that allow work to be carried out considering information from the item distractors such as the MC-DINA model [31,50] or work to be conducted with ordinal items and attributes such as the sequential G-DINA [51] and polytomous G-DINA [52] models. To date, studies on CD-CAT have mostly been restricted to the case of dichotomous items. It is hoped that this development will allow realistic contexts in applied practice to also be explored. The study by Gao et al. (2020) has pioneered this [53]. Fourth, there has been recent interest in hybrid selection rules that seek to simultaneously classify a general latent trait score that is continuous and that explains the relationships between discrete attributes modeled in CDM and the attributes (e.g., [30]). This could be easily implemented by using the higher-order model to model the attribute relationships [54]. Fifth, in recent years there has also been very intensive research on Q-matrix validation procedures (e.g., [7,55]). The adequacy of the Q-matrix determines to some extent the quality of the classifications that can be made with the adaptive application. Specifically, for CD-CAT, developments have been proposed that allow online calibration of the Q-matrix so that the proposed specification for new items can be tested from the information available in the item bank [8]. These developments will be incorporated into the package to explore this previous phase of a CD-CAT implementation. Finally, in this paper, we have adopted as a starting point a maximum likelihood estimation of item parameters. Recently, efforts have been made to make the estimation with the Bayesian Markov chain Monte Carlo algorithm more accessible [56]. This approach can be particularly useful in the case of complex models. Work will be done to allow the adoption of the results of a calibration obtained in this way to be an input in the cdcat function. Ultimately, work will be done to turn the package into a referential software that can be used to evaluate the proposals in the literature and to explore the future functioning of empirical item banks.