Evaluating the Observed Log-Likelihood Function in Two-Level Structural Equation Modeling with Missing Data: From Formulas to R Code
Abstract
:1. Introduction
2. SEM for Single-Level Data
2.1. Complete Data
2.2. Missing Data
2.3. Implementation in lavaan
3. SEM for Two-Level Data
3.1. Complete Data
3.2. Missing Data
3.3. The McDonald (1993) Solution
3.4. The du Toit and du Toit (2008) Solution
3.5. An Extension to Allow to Be Singular
4. Implementation in R Code
4.1. The Main.R File
4.2. The Objective1.R File
4.3. The Objective2.R File
4.4. The Objective3.R File
4.5. The Objective4.R File
4.6. The Objective5.R File
4.7. Stochastic Versus Fixed Covariates
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of the du Toit and du Toit Solution
Appendix B. Some Useful Formulas of Matrix Algebra
Appendix B.1. Inverse and Determinant of a Partitioned Matrix
Appendix B.2. The Woodbury Identity
Appendix B.3. Determinant Identities
Appendix B.4. Block Diagonal Matrices
Appendix C. R Code
Appendix C.1. The main.R File


Appendix C.2. The objective1.R File


Appendix C.3. The objective2.R File


Appendix C.4. The objective3.R File



Appendix C.5. The objective4.R File


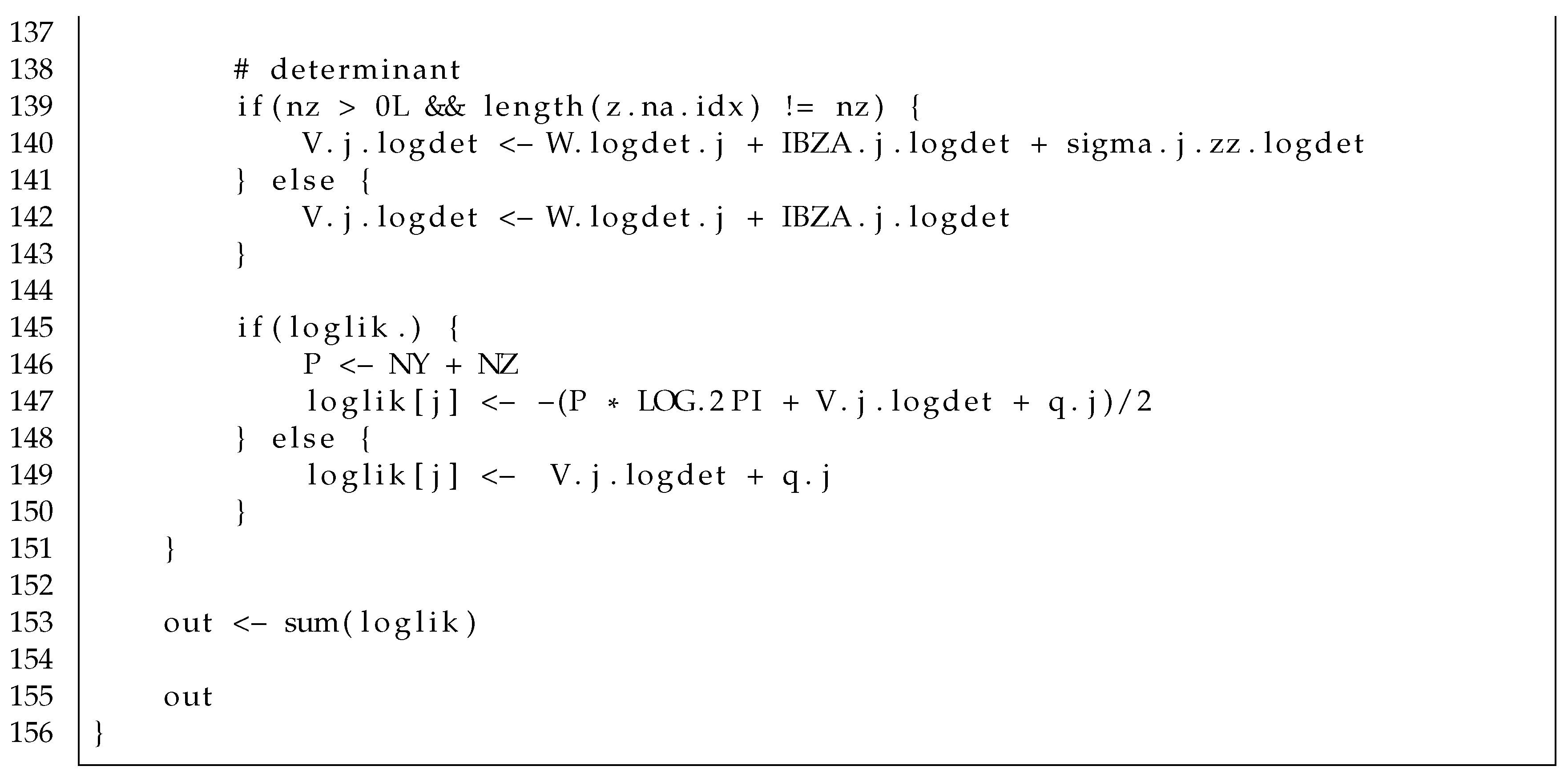
Appendix C.6. The objective5.R File



References
- Rosseel, Y. lavaan: An R Package for Structural Equation Modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef] [Green Version]
- McDonald, R.P. A general model for two-level data with responses missing at random. Psychometrika 1993, 58, 575–585. [Google Scholar] [CrossRef]
- Du Toit, S.H.; Du Toit, M. Multilevel structural equation modeling. In Handbook of Multilevel Analysis; de Leeuw, J., Meijer, E., Eds.; Springer: New York, NY, USA, 2008; Chapter 12; pp. 435–478. [Google Scholar]
- Jöreskog, K.G.; Sörbom, D. LISREL 8: User’s Reference Guide; Scientific Software International: Chicago, IL, USA, 1997. [Google Scholar]
- Bentler, P.M.; Weeks, D.G. Linear Structural Equations with Latent-Variables. Psychometrika 1980, 45, 289–308. [Google Scholar] [CrossRef]
- McArdle, J.J.; McDonald, R.P. Some algebraic properties of the Reticular Action Model for moment structures. Br. J. Math. Stat. Psychol. 1984, 37, 234–251. [Google Scholar] [CrossRef] [PubMed]
- Browne, M.W.; Arminger, G. Specification and Estimation of Mean- and Covariance-Structure Models. In Handbook of Statistical Modeling for the Social and Behavioral Sciences; Arminger, G., Clogg, C.C., Sobel, M.E., Eds.; Plenum Press: New York, NY, USA, 1995; pp. 311–359. [Google Scholar]
- Rubin, D.B. Inference and missing data. Biometrika 1976, 63, 581–592. [Google Scholar] [CrossRef]
- Rockwood, N.J. Maximum Likelihood Estimation of Multilevel Structural Equation Models with Random Slopes for Latent Covariates. Psychometrika 2020, 85, 275–300. [Google Scholar] [CrossRef] [PubMed]
- McDonald, R.P.; Goldstein, H. Balanced versus unbalanced designs for linear structural relations in two-level data. Br. J. Math. Stat. Psychol. 1989, 42, 215–232. [Google Scholar] [CrossRef]
- Lee, S.Y. Multilevel analysis of structural equation models. Biometrika 1990, 77, 763–772. [Google Scholar] [CrossRef]
- Muthén, B.O. Mean and covariance structure analysis of hierarchical data, 1990. In Proceedings of the Psychometric Society Meeting, Princeton, NJ, USA, 10 June 1990. [Google Scholar]
- Jak, S.; Oort, F.J.; Dolan, C.V. A test for cluster bias: Detecting violations of measurement invariance across clusters in multilevel data. Struct. Equ. Model. A Multidiscip. J. 2013, 20, 265–282. [Google Scholar] [CrossRef]
- Jak, S.; Jorgensen, T.D. Relating measurement invariance, cross-level invariance, and multilevel reliability. Front. Psychol. 2017, 8, 1640. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neale, M.C.; Hunter, M.D.; Pritikin, J.N.; Zahery, M.; Brick, T.R.; Kirkpatrick, R.M.; Estabrook, R.; Bates, T.C.; Maes, H.H.; Boker, S.M. OpenMx 2.0: Extended structural equation and statistical modeling. Psychometrika 2016, 81, 535–549. [Google Scholar] [CrossRef] [PubMed]
- Henderson, H.V.; Searle, S.R. On deriving the inverse of a sum of matrices. Siam Rev. 1981, 23, 53–60. [Google Scholar] [CrossRef]
- Harville, D.A. Maximum likelihood approaches to variance component estimation and to related problems. J. Am. Stat. Assoc. 1977, 72, 320–338. [Google Scholar] [CrossRef]
- Harville, D.A. Matrix Algebra from a Statistician’s Perspective; Springer: New York, NY, USA, 2008. [Google Scholar]
| Version | Absolute Time (ms) | Relative Time |
|---|---|---|
| Objective 1 | 3875.32 | 992.90 |
| Objective 2 | 390.30 | 100.00 |
| Objective 3 | 85.89 | 22.01 |
| Objective 4 | 82.52 | 21.14 |
| Objective 5 | 20.18 | 5.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosseel, Y. Evaluating the Observed Log-Likelihood Function in Two-Level Structural Equation Modeling with Missing Data: From Formulas to R Code. Psych 2021, 3, 197-232. https://doi.org/10.3390/psych3020017
Rosseel Y. Evaluating the Observed Log-Likelihood Function in Two-Level Structural Equation Modeling with Missing Data: From Formulas to R Code. Psych. 2021; 3(2):197-232. https://doi.org/10.3390/psych3020017
Chicago/Turabian StyleRosseel, Yves. 2021. "Evaluating the Observed Log-Likelihood Function in Two-Level Structural Equation Modeling with Missing Data: From Formulas to R Code" Psych 3, no. 2: 197-232. https://doi.org/10.3390/psych3020017
APA StyleRosseel, Y. (2021). Evaluating the Observed Log-Likelihood Function in Two-Level Structural Equation Modeling with Missing Data: From Formulas to R Code. Psych, 3(2), 197-232. https://doi.org/10.3390/psych3020017






