RALSA: Design and Implementation
Abstract
1. Introduction
- Prepare the data for the analysis:
- ¯
- Convert the SPSS data (or text in the case of the Programme for International Student Assessment (PISA) prior to 2015) files into native R datasets;
- ¯
- Merge the study data files from different countries and/or respondents;
- ¯
- View variable properties (name, class, variable label, response categories/unique values, and user-defined missing values);
- ¯
- Data diagnostic tables (quick weighted or unweighted frequencies and descriptives for data inspection and hypothesis elaboration);
- ¯
- Recode variables.
- Perform analyses:
- ¯
- Percentages of respondents in certain groups and averages on variables of interest;
- ¯
- Percentiles of continuous variables;
- ¯
- Percentages of respondents reaching or surpassing benchmarks of achievement;
- ¯
- Correlations (Pearson or Spearman);
- ¯
- Linear regression, with the option for contrast coding for categorical variables;
- ¯
- Binary logistic regression, with the option for contrast coding for categorical variables.
- RALSA brings support for a larger range of large-scale assessments and surveys supported by other available R packages. For example, the R package intsvy can work with data from the Trends in International Mathematics and Science Study (TIMSS), the Progress in International Reading Literacy Study (PIRLS), PISA, the International Computer and Information Literacy Study (ICILS), and the Programme for the International Assessment of Adult Competencies (PIAAC) [5]. RALSA brings support for all cycles of the following ILSAs:
- Civic Education Study (CivED);
- International Civic and Citizenship Education Study (ICCS);
- International Computer and Information Literacy Study (ICILS);
- Reading Literacy Study (RLII);
- Progress in International Reading Literacy Study (PIRLS), including PIRLS Literacy and ePIRLS;
- Trends in International Mathematics and Science Study (TIMSS), including TIMSS Numeracy;
- TIMSS and PIRLS joint study (TiPi);
- TIMSS Advanced;
- Second Information Technology in Education Study (SITES);
- Teacher Education and Development Study in Mathematics (TEDS-M);
- Programme for International Student Assessment (PISA);
- PISA for Development (PISA-D);
- Teaching and Learning International Survey (TALIS);
- TALIS Starting Strong Survey (also known as TALIS 3S);
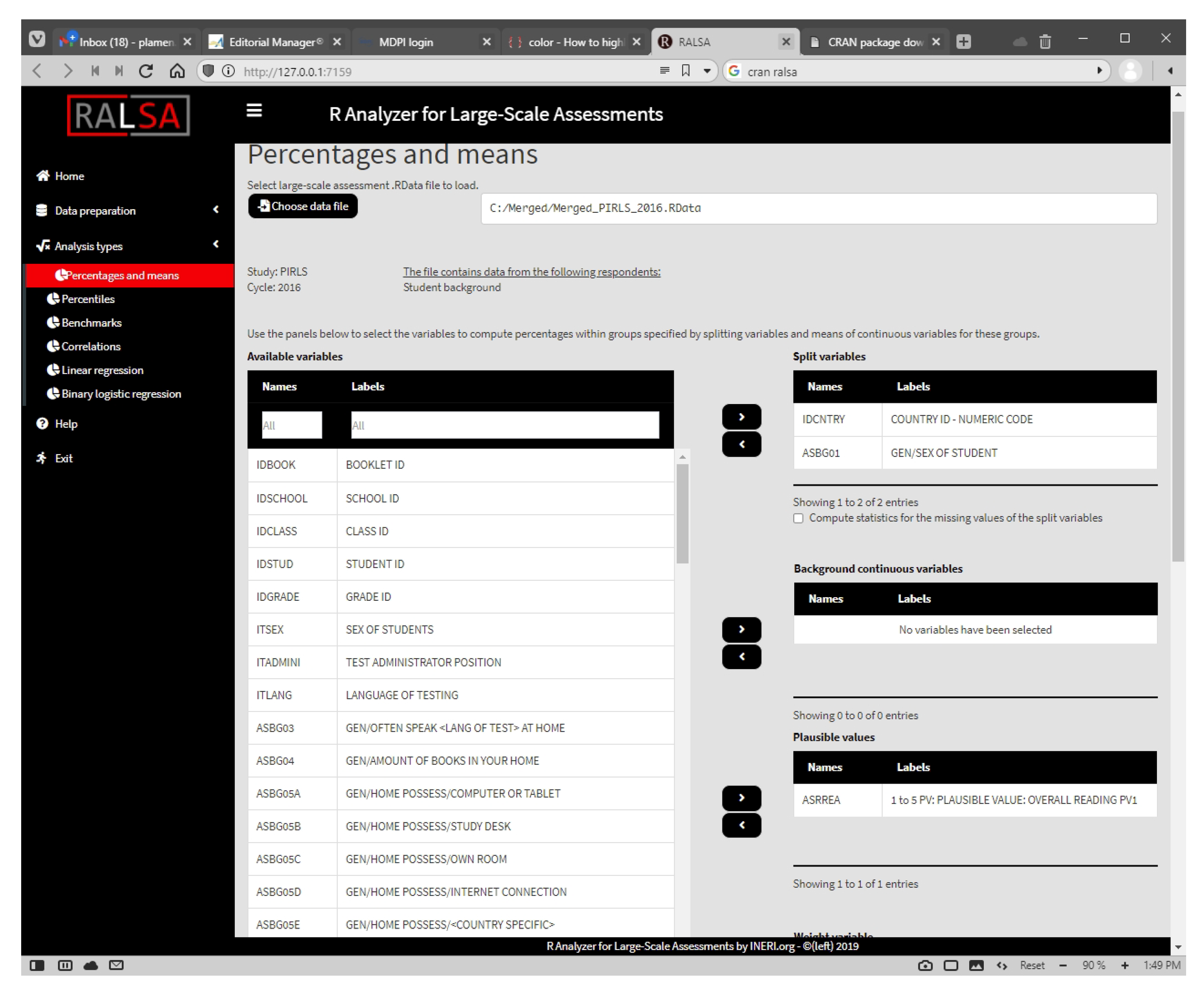
- RALSA is built for user experience. All functions in the package have a clear and parsimonious syntax. All package functions “recognize” the study design and apply the pertinent statistical algorithms without requiring design specification by the user, unless the user wants it. A unique feature in terms of user experience compared to other R packages for analyzing ILSAs’ data is that it also brings a Graphical User Interface (GUI), which adds convenience for the users, especially the non-technical ones, and those who have limited experience with R. The GUI is written in R as well, and does not rely on any external platform or programming language;
- The package has the capability to convert SPSS data files, as they are provided by the organizations conducting ILSAs, into native R data files. PISA files prior to its 2015 cycle were provided in the ASCII text format along with SPSS import syntaxes. RALSA can convert these into .RData files as well. R has the capability of importing SPSS and SAS files through packages, such as foreign [4], although occasionally, some variables will be imported improperly. The availability of the data in the native R file format provides greater convenience for the analyst. RALSA also imports the user-defined missing values and assigns them properly as user-defined missing codes in the converted datasets. This is quite different from the basic handling of missing values in R, which supports only one missing value type (NA), and from other packages for analyzing ILSAs’ data. For more details, see Section 3.1;
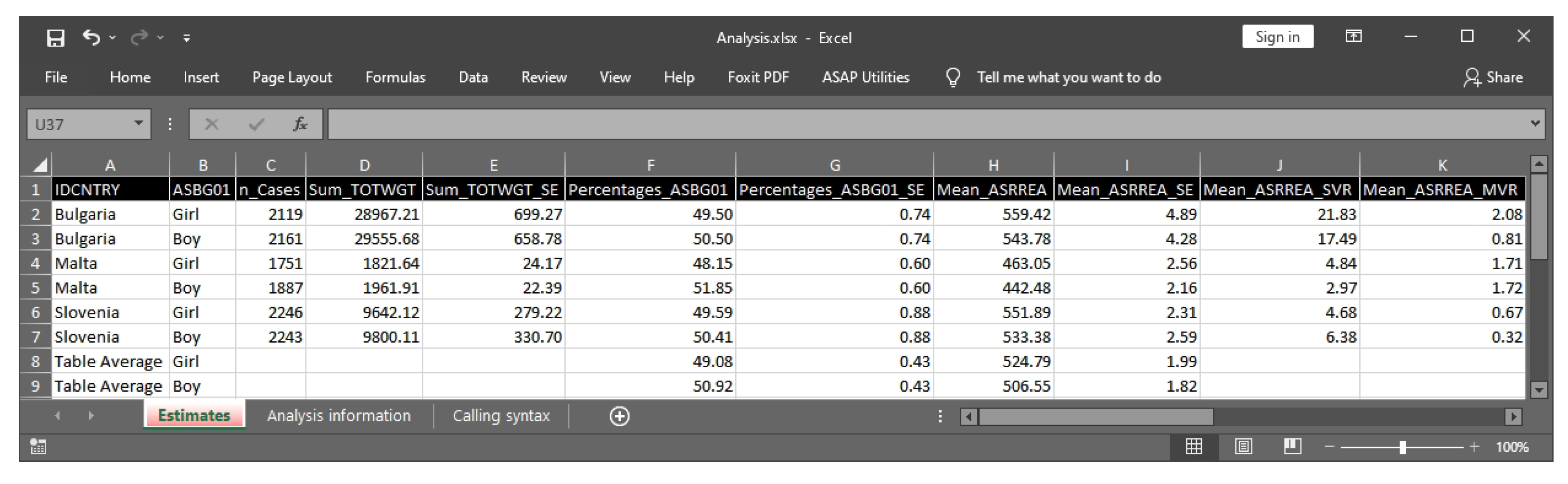
- All other R packages print the outputs as text directly in the R console. This is not convenient for the analyst who has to copy the output and convert it into a tabular output. The only exception is intsvy [5], where the output can be written into a very basic comma-separated values file. Different from other R packages, RALSA brings a comprehensive output system, which exports the results into an MS Excel workbook with multiple sheets grouping different kinds of estimates together by type with cell formatting (for more details, see Section 3.4). This feature is of great help for the analyst, who can use the output tables directly in a publication;
- The IEA IDB Analyzer is very convenient to use and has all of the features listed above. However, it is not open-source and is a proprietary software with a restrictive license. Although it is distributed for free, it actually uses SPSS and SAS to perform the computations, and these come with a very steep price. It also works only under MS Windows. RALSA is open-source and free of charge, and works on any operating system where R can be installed.
- The general internal organization of the package’s functions and their interdependence;
- The common internal structure of the analysis functions and the code they reuse from common objects and functions;
- The use of the data.table package for speed and simplicity of the computations through its capability to compute statistics by group with an internal sub-setting simultaneously;
- The structure and workflow of the output system;
- The GUI design, its structure and the way it is linked to the data preparation and analysis functions.
2. Background
3. RALSA Internals
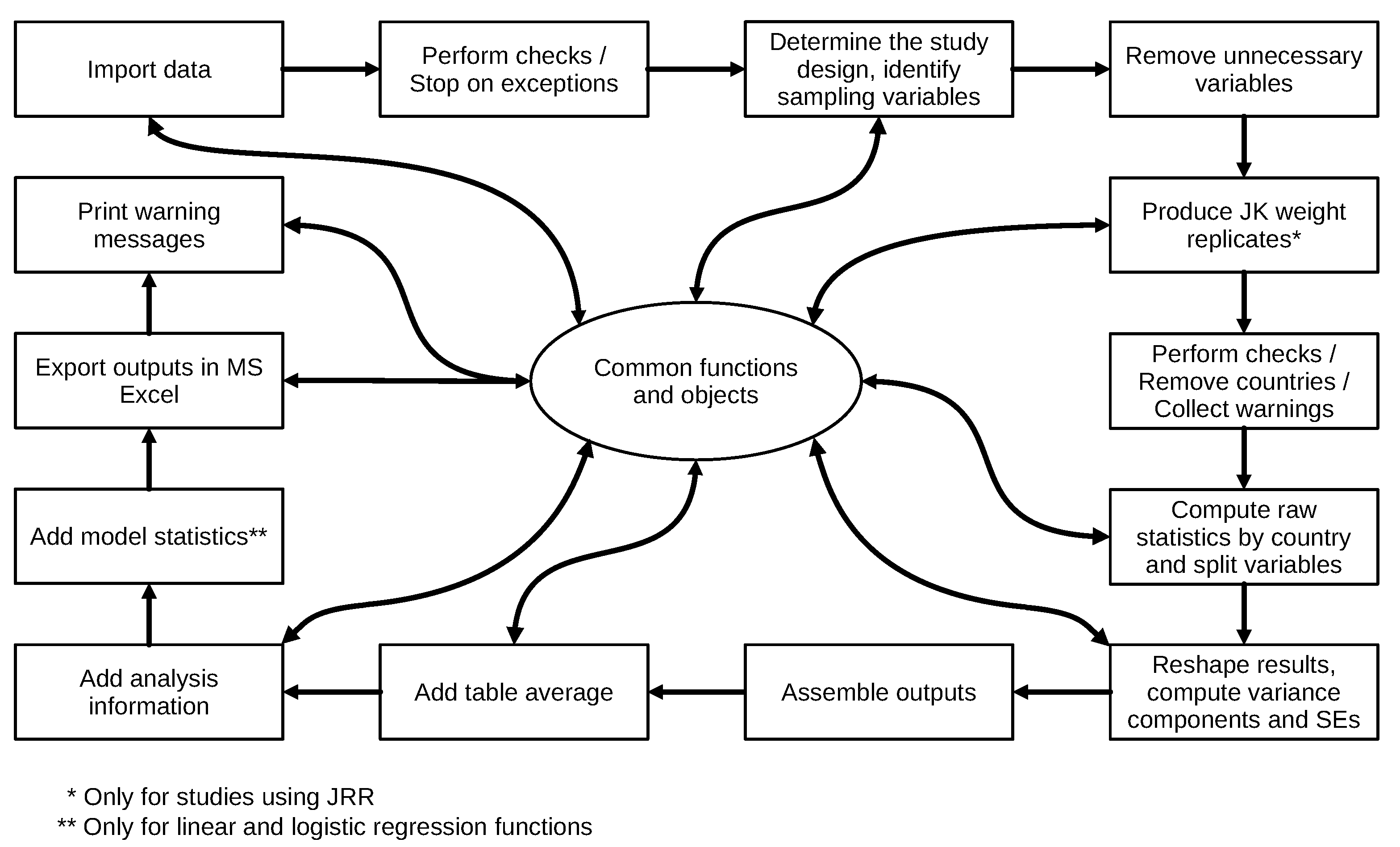
3.1. General Internal Organization of Functions in RALSA
- Study name (study)—the name of the study (e.g., PIRLS, PISA, ICCS, etc.);
- Study cycle (cycle)—the year when the cycle was conducted (e.g., 2016 for the PIRLS 2016 cycle);
- Respondent type (file.type)—whose respondent type data (e.g., student, teacher, parent, etc.) is in the file.
3.2. Structure of the Analysis Functions and Common Code Reuse

3.3. Using the data.table Package

- DT is a data.table object;
- i subsets rows using certain criteria;
- j calculates on columns;
- by groups the results by unique values of variables passed to the argument.




3.4. Structure and Workflow of the Output System
3.5. Constructing and Linking the GUI with the Functions

4. Summary and Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 1PL | One-Parameter Logistic model |
| 2PL | Two-Parameter Logistic model |
| 3PL | Three-Parameter Logistic model |
| BRR | Balanced Repeated Replication |
| CBA | Computer-Based Assessment |
| EAP | Expected A Posteriori |
| EAP-MG | Multi-Group Expected A Posteriori |
| GPL | General Public License |
| GUI | Graphical User Interface |
| ICCS | International Civic and Citizenship Education Study |
| IEA | International Association for the Evaluation of Educational Achievement |
| ILSAs | International Large-Scale Assessments and surveys |
| IRT | Item Response Theory |
| JRR | Jackknife Repeated Replication |
| MLE | Maximum Likelihood Estimation |
| MMS | Multiple Matrix Sampling |
| OECD | Organisation for Economic Co-operation and Development |
| OSS | Open-Source Software |
| PCA | Principal Component Analysis |
| PIRLS | Progress in International Reading Literacy Study |
| PISA | Programme for International Student Assessment |
| PPS | Probability Proportional to Size |
| PVs | Plausible values |
| RALSA | R Analyzer for International Large-Scale Assessments |
| SRS | Simple Random Sampling |
| WLE | Warm’s Weighted Likelihood Estimation |
References
- IEA. IDB Analyzer [Computer Software Manual]; (Version 4.0.39). 2021. Available online: https://www.iea.nl/data-tools/tools#section-308 (accessed on 10 June 2021).
- IBM. IBM SPSS [Computer Software]; (Version 27.0). 2020. Available online: https://www.ibm.com/analytics/spss-statistics-software (accessed on 10 June 2021).
- SAS Institute. SAS/STAT Software [Computer Software]; (Version 9.4M7). 2020. Available online: https://www.sas.com/en_us/software/stat.html (accessed on 10 June 2021).
- R Core Team. Foreign: Read Data Stored by ’Minitab’, ’S’, ’SAS’, ’SPSS’, ’Stata’, ’Systat’, ’Weka’, ’dBase’, … [Computer Software Manual]; (R Package Version 0.8-81). 2020. Available online: https://cran.r-project.org/package=foreign (accessed on 10 June 2021).
- Caro, D.; Biecek, P. intsvy: International Assessment Data Manager [Computer Software Manual]; (R Package Version 2.5). 2021. Available online: https://cran.r-project.org/package=intsvy (accessed on 10 June 2021).
- BIFIE; Robitzsch, A.; Oberwimmer, K. BIFIEsurvey: Tools for Survey Statistics in Educational Assessment [Computer Software Manual], (R Package Version 3.3-12). 2019. Available online: https://cran.r-project.org/package=BIFIEsurvey (accessed on 10 June 2021).
- Bailey, P.; Emad, A.; Huo, H.; Lee, M.; Liao, Y.; Lishinski, A.; Nguyen, T.; Xie, Q.; Yu, J.; Zhang, T. EdSurvey: Analysis of NCES Education Survey and Assessment Data [Computer Software Manual]; (R Package Version 2.6.9). 2021. Available online: https://cran.r-project.org/package=EdSurvey (accessed on 10 June 2021).
- Mirazchiyski, P.; INERI. RALSA: R Analyzer for Large-Scale Assessments [Computer Software Manual]; (R package version 1.0.1). 2021. Available online: https://CRAN.R-project.org/package=RALSA (accessed on 10 June 2021).
- INERI. RALSA: R Analyzer for Large-Scale Assessments. 2021. Available online: http://ralsa.ineri.org/ (accessed on 10 June 2021).
- Rutkowski, L.; Gonzalez, E.; von Davier, M.; Zhang, Y. Assessment Design for International Large-Scale Assessments. In Handbook of International Large-Scale Assessments: Background, Technical Issues, and Methods of Data Analysis; Rutkowski, L., von Davier, M., Rutkowski, D., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 74–95. [Google Scholar]
- Rust, K. Sampling, Weighting, and Variance Estimation in International Large-Scale Assessments. In Handbook of International Large-Scale Assessments: Background, Technical Issues, and Methods of Data Analysis; Rutkowski, L., von Davier, M., Rutkowski, D., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 117–154. [Google Scholar]
- LaRoche, S.; Joncas, M.; Foy, P. Sample Design in PIRLS 2016. In Methods and Procedures in PIRLS 2016; Martin, M., Mullis, I., Hooper, M., Eds.; Lynch School of Education, Boston College: Chestnut Hill, MA, USA, 2017; pp. 3.1–3.34. [Google Scholar]
- OECD. Sample Design. In PISA 2015 Technical Report; OECD: Paris, France, 2017; pp. 65–87. [Google Scholar]
- OECD. Test design and test development. In PISA 2015 Technical Report; OECD: Paris, France, 2017; pp. 29–55. [Google Scholar]
- Martin, M.; Mullis, I.; Foy, P. Assessment Design for PIRLS, PIRLS Literacy, and ePIRLS in 2016. In PIRLS 2016 Assessment Framework, 2nd ed.; Mullis, I.V.S., Martin, M., Eds.; Lynch School of Education, Boston College: Chestnut Hill, MA, USA, 2015; pp. 55–69. [Google Scholar]
- Mullis, I.; Prendergast, C. Developing the PIRLS 2016 Achievement Items. In Methods and Procedures in PIRLS 2016; Martin, M., Mullis, I., Hooper, M., Eds.; Lynch School of Education, Boston College: Chestnunt Hill, MA, USA, 2017; pp. 1.1–1.29. [Google Scholar]
- Von Davier, M.; Sinharay, S. Analytics in International Large-Scale Assessments: Item Response Theory and Population Models. In Handbook of International Large-Scale Assessments: Background, Technical Issues, and Methods of Data Analysis; Rutkowski, L., von Davier, M., Rutkowski, D., Eds.; CRC Press: Boca Raton, FL, USA, 2014; pp. 155–174. [Google Scholar]
- Wu, M. The role of plausible values in large-scale surveys. Stud. Educ. Eval. 2005, 31, 114–128. [Google Scholar] [CrossRef]
- Von Davier, M.; Gonzalez, E.; Mislevy, R. What are plausible values and why are they useful? IERI Monogr. Ser. 2009, 2, 9–36. [Google Scholar]
- Foy, P.; Yin, L. Scaling the PIRLS 2016 Achievement Data. In Methods and Procedures in PIRLS 2016; Martin, M., Mullis, I., Hooper, M., Eds.; TIMSS & PIRLS International Study Center: Chestnunt Hill, MA, USA, 2017; pp. 12.1–12.38. [Google Scholar]
- OECD. Scaling PISA data. In PISA 2015 Technical Report; OECD: Paris, France, 2017; pp. 127–186. [Google Scholar]
- Foy, P.; LaRoche, S. Estimating Standard Errors in the PIRLS 2016 Results. In Methods and Procedures in PIRLS 2016; Martin, M., Mullis, I., Hooper, M., Eds.; Lynch School of Education, Boston College: Chestnut Hill, MA, USA, 2017; pp. 4.1–4.22. [Google Scholar]
- Schulz, W. The reporting of ICCS 2016 results. In International Civic and Citizenship Education Study 2016 Technical Report; Schulz, W., Carstens, R., Losito, B., Fraillon, J., Eds.; IEA: Amsterdam, The Netherlands, 2018; pp. 245–256. [Google Scholar]
- Chang, W.; Cheng, J.; Allaire, J.; Xie, Y.; McPherson, J. Shiny: Web Application Framework for R [Computer Software Manual]; (R Package Version 1.6.0). 2021. Available online: https://cran.r-project.org/package=shiny (accessed on 10 June 2021).
- Brese, F. Analyzing the ICCS 2016 data using the IEA IDB Analyzer. In ICCS 2016 User Guide for the International Database; Köhler, H., Weber, S., Brese, F., Schulz, W., Carstens, R., Eds.; IEA: Amsterdam, The Netherlands, 2018; pp. 33–36. [Google Scholar]
- Mullis, I.; Prendergast, C. Using Scale Anchoring to Interpret the PIRLS and ePIRLS 2016 Achievement Scales. In Methods and Procedures in PIRLS 2016; Martin, M., Mullis, I., Hooper, M., Eds.; Lynch School of Education, Boston College: Chestnunt Hill, MA, USA, 2017. [Google Scholar]
- Frakes, W.; Kang, K. Software Reuse Research: Status and Future. IEEE Trans. Softw. Eng. 2005, 31, 529–536. [Google Scholar] [CrossRef]
- Sojer, M.; Henkel, M. Code Reuse in Open Source Software Development: Quantitative Evidence, Drivers, and Impediments. J. Assoc. Inf. Syst. 2010, 11, 868–901. [Google Scholar] [CrossRef]
- Fichman, R.; Kemerer, C. Incentive compatibility and systematic software reuse. J. Syst. Softw. 2001, 57, 45–60. [Google Scholar] [CrossRef]
- Dowle, M.; Srinivasan, A. data.table: Extension of ’data.frame’ [Computer Software Manual]; (R Package Version 1.14.0). 2021. Available online: https://CRAN.R-project.org/package=data.table (accessed on 10 June 2021).
- Introduction to data.table. Available online: https://cran.r-project.org/web/packages/data.table/vignettes/datatable-intro.html (accessed on 10 June 2021).
- Reference Semantics. Available online: https://cran.r-project.org/web/packages/data.table/vignettes/datatable-reference-semantics.html (accessed on 10 June 2021).
- IEA. PIRLS 2016 International Database; IEA Data Repository; IEA: Paris, France, 2016. [Google Scholar]
- Schauberger, P.; Walker, A. openxlsx: Read, Write and Edit xlsx Files [Computer Software Manual]; (R Package Version 4.2.3). 2020. Available online: https://CRAN.R-project.org/package=openxlsx (accessed on 10 June 2021).
- Wickham, H. Mastering Shiny: Build Interactive Apps, Reports, and Dashboards Powered by R, 1st ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2021. [Google Scholar]
- Attali, D. shinyjs: Easily Improve the User Experience of Your Shiny Apps in Seconds [Computer Software Manual]; (R Package Version 2.0.0). 2020. Available online: https://CRAN.R-project.org/package=shinyjs (accessed on 10 June 2021).
- Haefliger, S.; von Krogh, G.; Spaeth, S. Code Reuse in Open Source Software. Manag. Sci. 2008, 54, 180–193. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirazchiyski, P.V. RALSA: Design and Implementation. Psych 2021, 3, 233-248. https://doi.org/10.3390/psych3020018
Mirazchiyski PV. RALSA: Design and Implementation. Psych. 2021; 3(2):233-248. https://doi.org/10.3390/psych3020018
Chicago/Turabian StyleMirazchiyski, Plamen Vladkov. 2021. "RALSA: Design and Implementation" Psych 3, no. 2: 233-248. https://doi.org/10.3390/psych3020018
APA StyleMirazchiyski, P. V. (2021). RALSA: Design and Implementation. Psych, 3(2), 233-248. https://doi.org/10.3390/psych3020018





