Different algorithms have been proposed to obtain maximum likelihood (ML) estimates, and their availability and defaults vary across software. In this section we discuss four algorithms available in M
plus, two of which are also available in
lavaan. We also discuss the estimation of between-level residual variances, which was confounded with model type in Stapleton and Johnson’s [
2] simulation study.
1.2.1. Maximum Likelihood Estimation Algorithms
Both
lavaan [
4] and M
plus [
3] use normal-theory ML estimation by default for continuous variables, using the observed information matrix to derive
SEs. Although also available in
lavaan, only M
plus defaults to a χ
2 statistic and
SEs that are robust to nonnormality. The robust χ
2 statistic provided by
lavaan and M
plus is asymptotically equivalent to Yuan and Bentler’s
statistic [
13]. This robust test statistic (with
SEs) is requested in
lavaan with the argument estimator = “MLR” (or equivalently, test = “yuan.bentler.mplus” and se = “robust.sem”; see the ?lavOptions help page) and in M
plus with the ANALYSIS option ESTIMATOR = MLR [
3] (chapter 16).
By default,
lavaan maximizes the sum of log-likelihoods of the clusters—which M
plus refers to as the observed-data log-likelihood (ALGORITHM = ODLL)—using a quasi-Newton (QN) algorithm, which is the same algorithm used for ML estimation with single-level data. The expectation–maximization (EM) algorithm is also available in both (
lavaan and M
plus to obtain ML estimates, although the implementation in
lavaan is notably slower. The EM algorithm can be requested by passing the argument optim.method = “em” to
lavaan, or with the ANALYSIS option ALGORITHM = EM in M
plus [
3] (chapter 16). M
plus also has an accelerated EM algorithm (ALGORITHM = EMA), achieved by switching to QN when EM does not optimize quickly enough (i.e., when relative or absolute changes in log-likelihood do not decrease enough between iterations). M
plus can also switch between a Fisher-scoring (FS) algorithm and EM (with ALGORITHM = FS), but EMA is the default, and neither EMA nor FS are currently available in
lavaan. Availability of current options and their default settings are listed for
lavaan and M
plus in
Table 1.
Convergence of the algorithm is determined by tracking criteria at each iteration—namely, the log-likelihood function and its first derivative. After any of these algorithm’s convergence criteria (i.e., the rules for stopping the optimizer from iterating further) have been met, it must be verified that the optimizer in fact converged on a maximum.
In Mplus, convergence for any optimization algorithm for ML estimation can be controlled with ANALYSIS options, such as the ODLL derivative using CONVERGENCE (for QN) or MCONVERGENCE (for EM or EMA), as well as LOGCRITERION (absolute change in log-likelihood from previous iteration) and RLOGCRITERION (relative change in log-likelihood from previous iteration). The maximum number of iterations is set by ITERATIONS for QN and MITERATIONS for EM(A). The default optimizer used by lavaan is nlminb from the stats package, whose options can be set by passing a named list to the control = argument (see the ?lavOptions help page). lavaan’s defaults are list (iter.max = 10,000, abs.tol = .Machine$double.eps × 10, rel.tol = 1 × 10−10). When using EM, lavaan has its own parallel dedicated arguments, shown in the last example on the tutorial page: https://lavaan.ugent.be/tutorial/multilevel.html, accessed on 31 May 2021.
Verifying that the optimizer converged on a maximum involves checking the first and second derivatives of the log-likelihood function with respect to the estimated parameters, respectively called the “gradient” and “Hessian.” If ML estimates were obtained, each element of the gradient vector should be effectively zero (the “first-order condition”). Upon finding a nonzero gradient element, lavaan warns that the optimizer did not find a ML solution and “estimates below are most likely unreliable.” Likewise, Mplus output will contain the message: “The model estimation did not terminate normally due to a non-zero derivative of the observed-data loglikelihood,” referring to the first-order condition. Any nonzero element of the gradient indicates the corresponding parameter estimate is not a ML estimate. But the reverse is not necessarily true: if the gradient consists only of zeros, it could be a minimum or a saddle point rather than a maximum. In order to verify the solution is a maximum, the Hessian should be negative definite. Because the Hessian is intensive to compute, this “second-order condition” is rarely checked to simply verify convergence. However, multiplying the Hessian by −1 yields the information matrix, the inverse of which is the asymptotic covariance matrix of the estimated parameters (the diagonal of which contains the squared SEs). Thus, if the information matrix is not positive definite (and so cannot be inverted), a warning is issued that SEs cannot be calculated.
Because EMA is the default algorithm in Mplus, we describe one more computational detail about the acceleration aspect (which seems to be shared by the FS algorithm, but we did not focus on that). When the log-likelihood does not change fast enough between iterations, Mplus attempts to accelerate optimization by switching from EM to QN. This could backfire if the QN step overshoots its target, instead decreasing the log-likelihood at the next iteration. In such circumstances, Mplus will then restart the EM algorithm as though the user selected EM instead of the default EMA, because EM alone (without switching to QN) will always increase the log-likelihood between iterations. However, we discovered that apparent convergence with EM after EMA failed does not necessarily converge when explicitly setting ALGORITHM = EM. Causes and potential consequences are provided in the Results section.
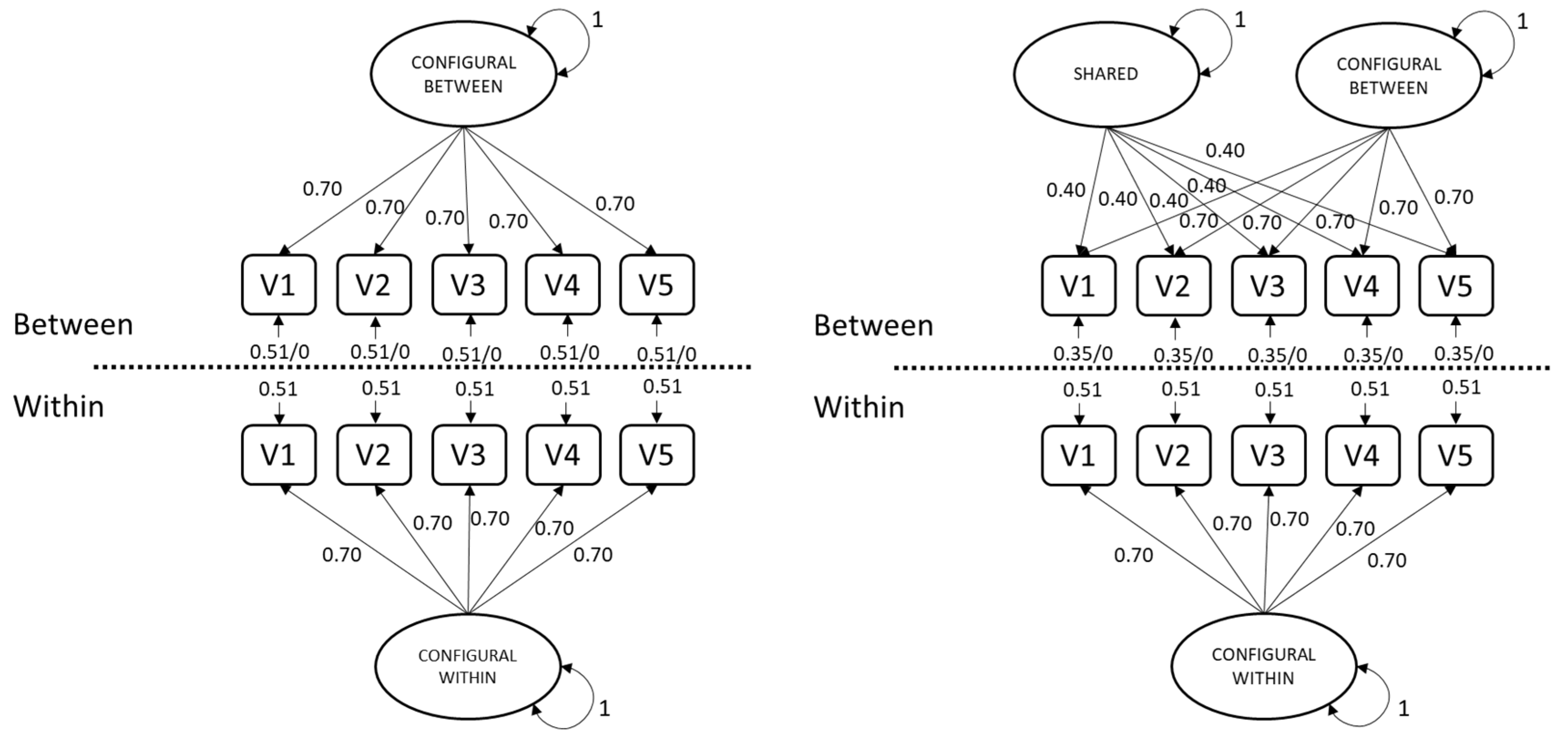
1.2.2. Between-Level Residual Variances in Two-Level Models
When strong factorial invariance across clusters holds, then in a two-level model, not only will factor loadings be equal across levels, residual variances at the between level will be zero [
11,
14,
15,
16]. For configural constructs (i.e., with cross-level invariance of factor loadings), any residual variance at the between level (θ
B) can therefore be interpreted as differences in intercepts across clusters (measurement bias, also called cluster bias by Jak, Oort and Dolan [
14]. Nonzero residual variance at the between level (θ
B > 0) means that the cluster-level differences in the indicators are not all explained by cluster-level differences in the common factor. In other words, variables other than what was intended to be measured cause differences in the indicator scores across clusters. In practice, it may not be realistic to expect exactly zero cluster bias for all indicators, similar to how exact invariance of intercepts generally does not hold [
17]. That is, cluster invariance may hold only approximately, implying small θ
B instead of zero θ
B. Moreover, some indicators may be subject to cluster bias while other indicators are not (representing partial invariance [
18]).
Sample estimates of θB vary around the population values, so when they are (nearly) zero, estimates can frequently take negative values simply due to sampling error. Thus, if strong factorial invariance across clusters holds even approximately (θB ≅ 0), then estimating θB under non-negative constraints may lead to trouble with convergence in samples that would have contained at least one negative variance under unconstrained estimation. By default, lavaan does not restrict θB estimates to be positive when using QN, while Mplus does. The EM algorithm requires θB > 0 in both packages, because the EM algorithm requires the between-level model-implied covariance matrix to be positive definite. The minimum-variance requirement (set with the ANALYSIS option VARIANCE) must be between 0 and 1, so negative values for θB are not permitted in Mplus. This requirement may therefore result in nonconvergence for populations with θB ≅ 0.
In applications of (shared-and-)configural-construct models, it can be valuable to assess cluster bias to establish whether Level-2 residual variances should be constrained to zero, which could avoid negative-variance estimates. However, nonconvergence under minimum-variance-constrained estimation when θ
B ≅ 0 would prevent the ability to compare that model to one with strong factorial invariance across clusters (θ
B = 0). In our simulation study, we explicitly crossed these design factors: zero vs. nonzero θ
B in the population model and fixed vs. estimated θ
B in the fitted model. We focus on conditions where population θ
B is exactly zero, representing exact invariance, but we will show some results based on conditions with θ
B = 0.01 and θ
B = 0.0001 as well. Chen, Bollen, Paxton, Curran and Kirb [
19] describe the possible causes of, consequences of, and possible strategies to handle inadmissible solutions in more detail. Negative variance estimates could result from either model misspecification or sampling error. So before fixing negative variance estimates to zero, one should first test the null hypothesis that the parameter is an admissible solution. For example, if the 95% confidence interval for a residual variance includes positive values, then one cannot reject the null hypothesis (using α = 0.05) that the true population value is indeed positive; in this case, if the model fits well and there are no other signs of misspecification, one could conclude that the true parameter is simply close enough to zero that sampling error occasionally yields a negative estimate. For more discussion about negative variance parameters and estimates see [
20,
21,
22].