How to Estimate Absolute-Error Components in Structural Equation Models of Generalizability Theory
Abstract
1. Introduction
2. Materials and Methods
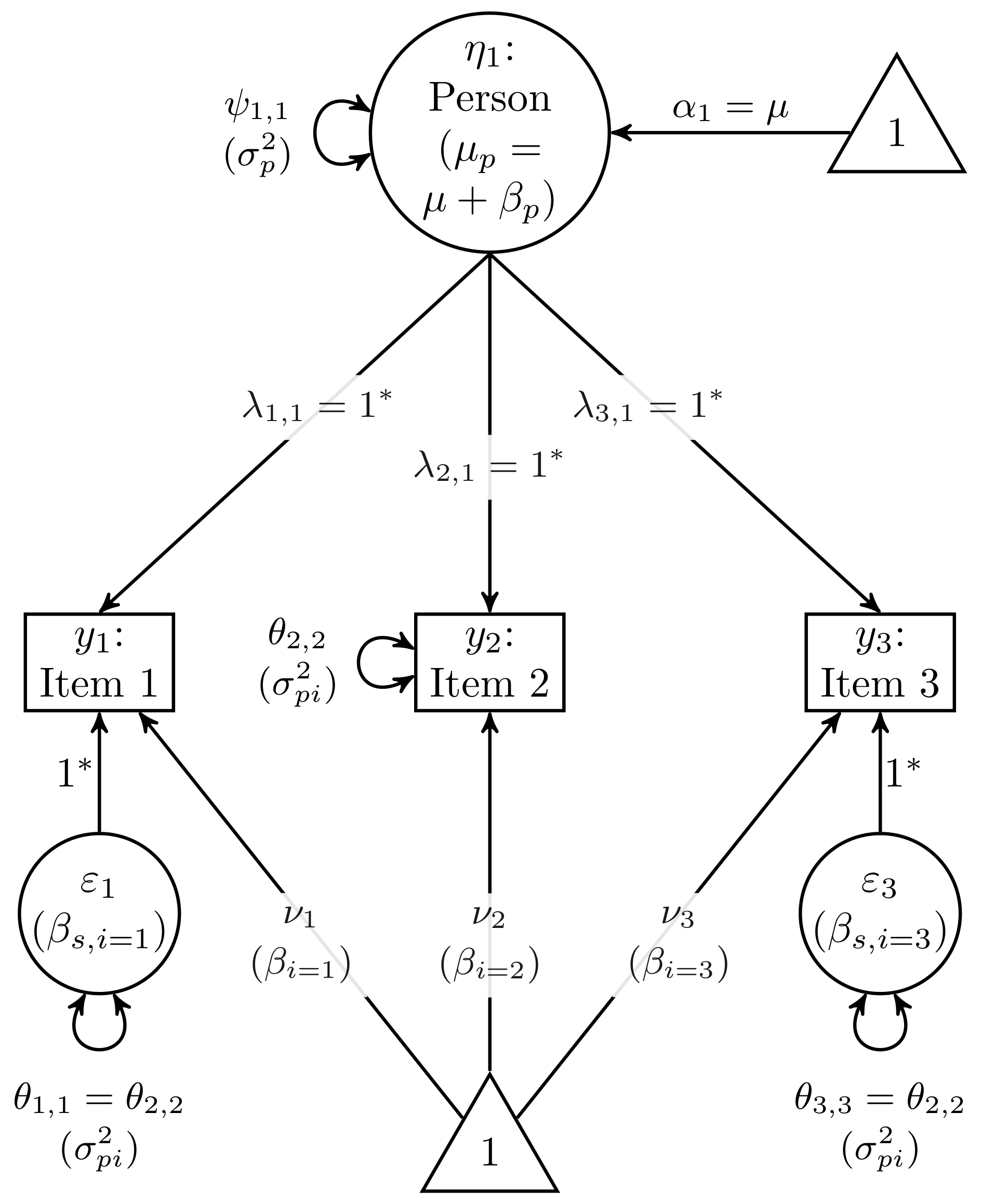
2.1. One-Facet Design: Persons × Items
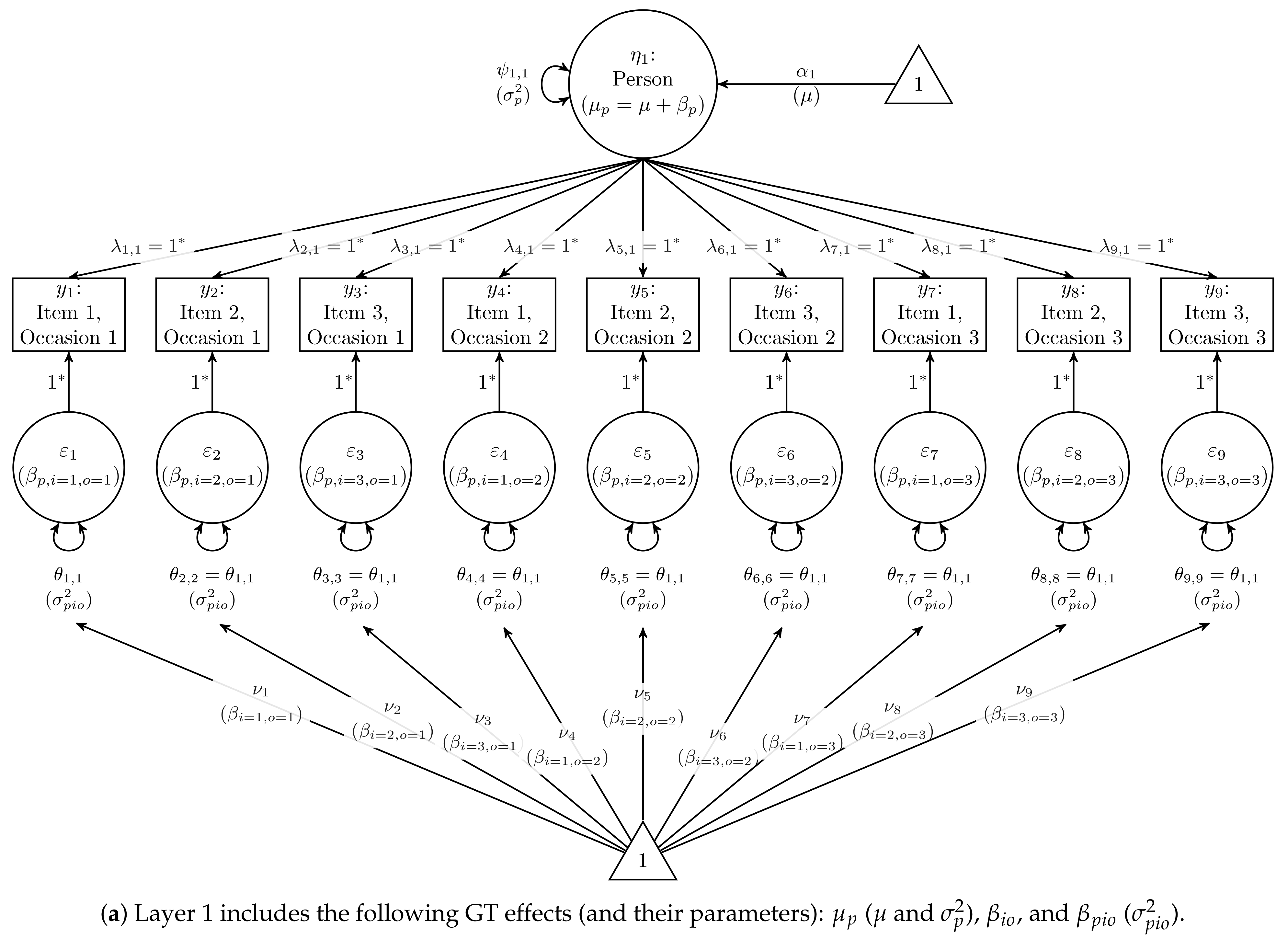
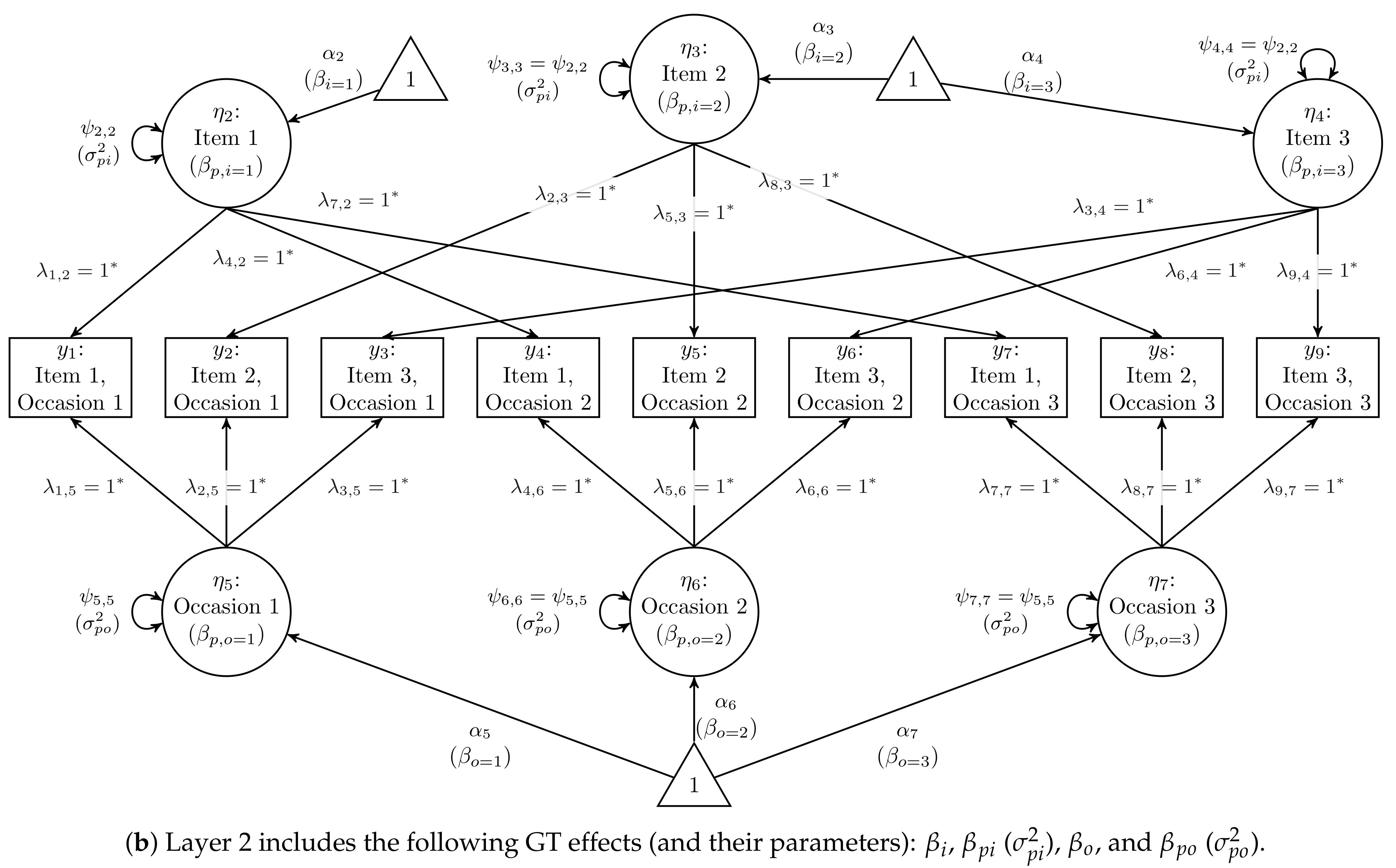
2.2. Two-Facet Crossed Design: Persons × Items × Occasions
- all Item factor scores represent the effects, and the Item factor variances are constrained to equality to represent ;
- all Occasion factor scores represent the effects, and the Occasion factor variances are constrained to equality to represent ;
- all unique-factor scores (indicator residuals) represent the effects, and the residual variances are constrained to equality to represent .
- As with the one-facet model, the factor scores represent , so a freely estimated Person mean represents the grand mean (because ). To identify this latent mean, impose the effects-coding constraint on all nine indicator intercepts, as shown in the top row of Table 1. This constraint reflects , which is equivalent to constraining the sum of because the mean is merely the sum scaled by .
- The effects-coding constraint can also be imposed on the indicators of each item’s factor (e.g., across occasions, Item 1’s indicators sum to zero, shown in Row 2 of Table 1). However, only such constraints are needed because the constraint would be redundant given the constraint on all nine intercepts. That is, if mutually exclusive subsets each sum to zero, then the remaining subset must also sum to zero in order for the entire set to sum to zero. The final Item factor’s mean is identified by constraining all Item-factor means to sum to zero, consistent with . The means of Item factors can thus be interpreted as Item effects ().
- The same pattern holds for Occasion factors as for Item factors. The effects-coding constraint is placed on the subset of indicators (e.g., across items, Occasion 1’s indicators sum to zero) for Occasion factors, and the Occasion factor’s mean is identified by constraining all Occasion means to sum to zero: . The means of Occasion factors are thus interpreted as Occasion effects ().
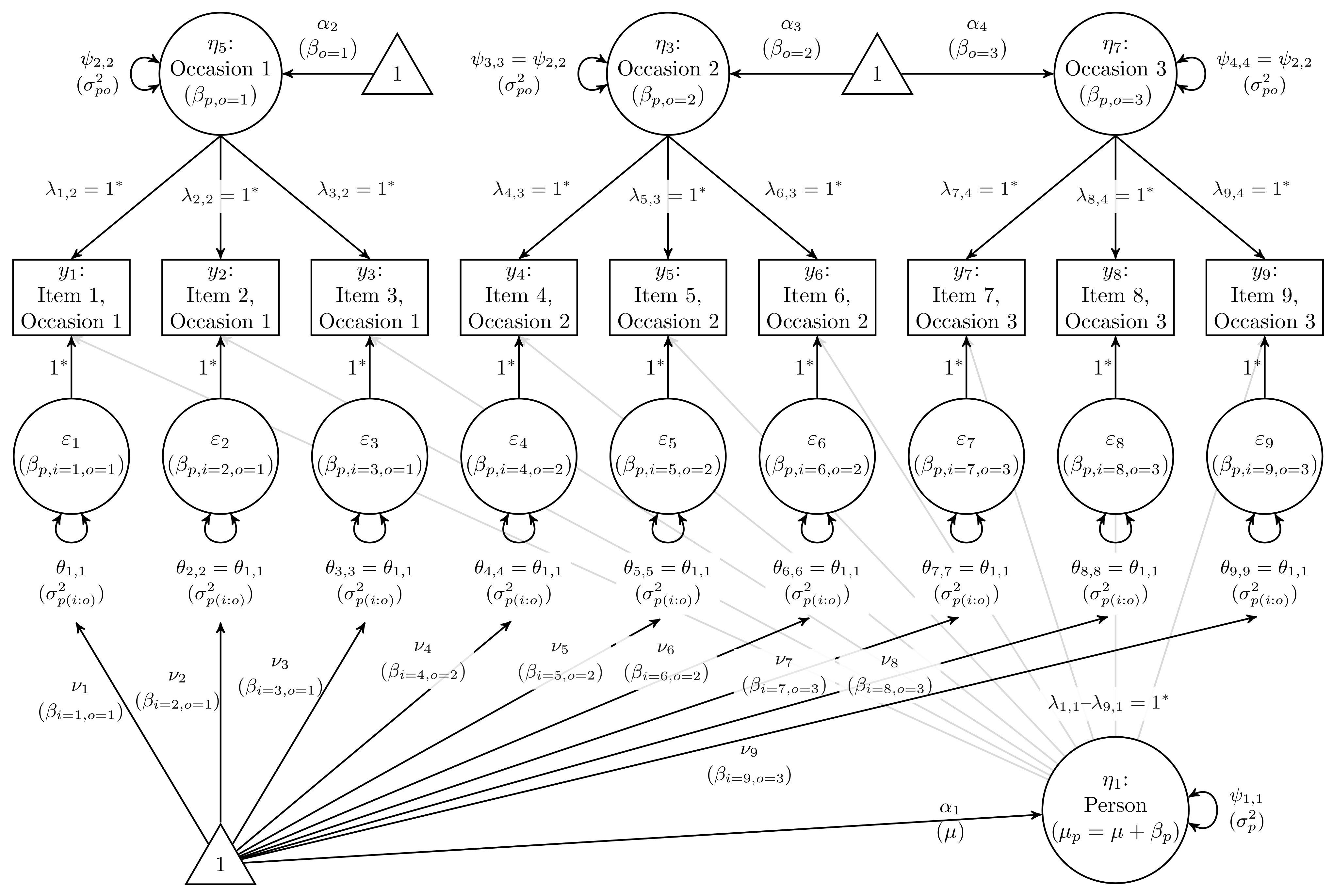
2.3. Two-Facet Nested Design: Persons × (Items within Occasions)
2.4. Discretized Data
2.4.1. The Threshold Model and Latent Response Scales
2.4.2. Coefficients on Ordinal vs. Latent-Response Scales
3. Results
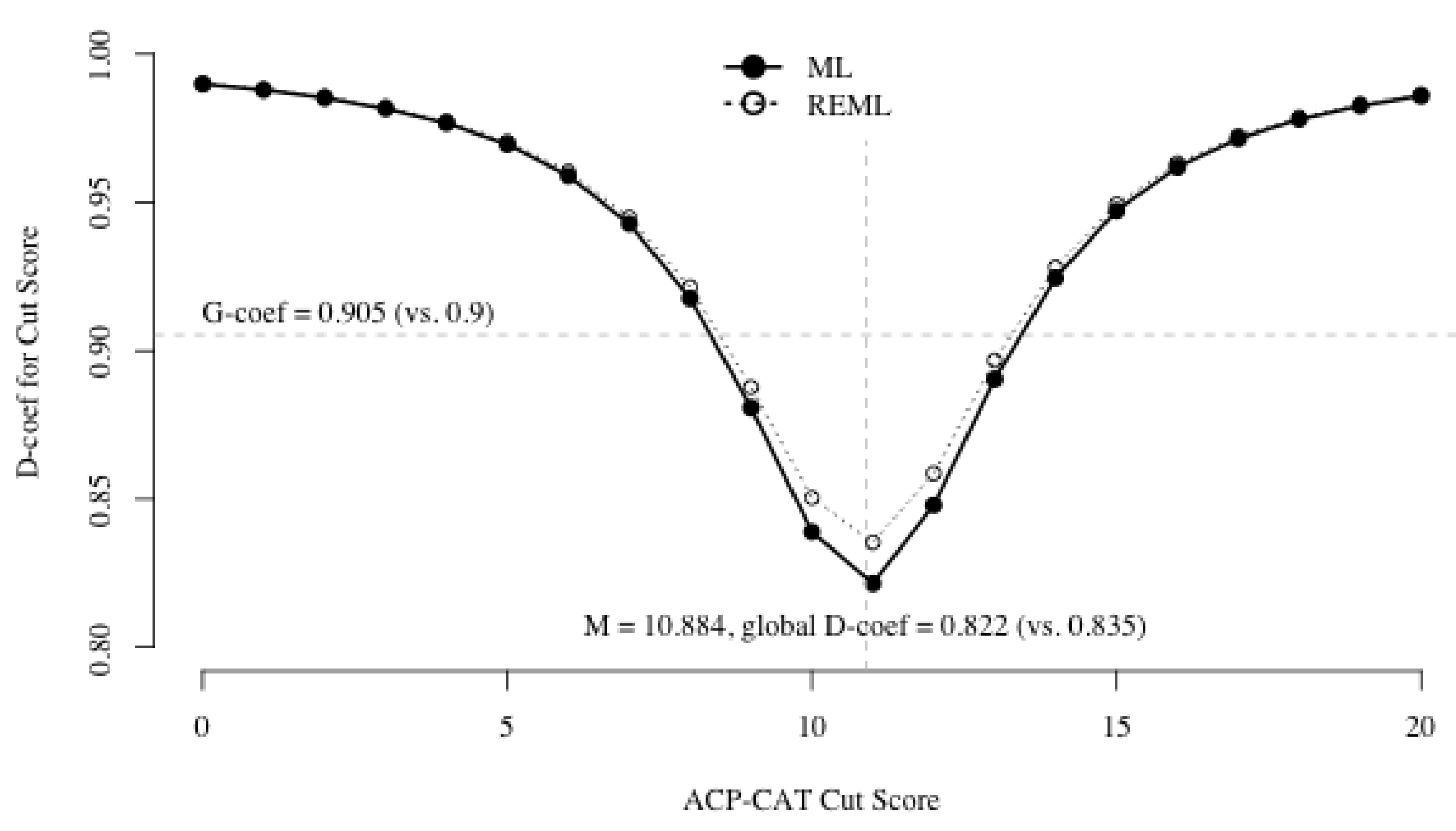
4. A Multirater Study with Planned Missing Data
4.1. Design
4.2. CFAs for the Scale Total
4.3. IFAs for Discrete Scale Items
5. Discussion
5.1. Advantages of SEM for GT
5.2. Limitations Due to Missing Data
5.3. Future Directions for Discrete Data
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CFA | Confirmatory factor analysis |
| CI | Confidence interval |
| CTT | Classical test theory |
| D-coef | Dependability coefficient |
| DWLS | Diagonally weighted least-squares |
| FIML | Full-information maximum likelihood |
| G-coef | Generalizability coefficient |
| GT | Generalizability theory |
| ICC | Intraclass correlation coefficient |
| IFA | Item factor analysis |
| IRR | Interrater reliability |
| IRT | Item-response theory |
| LRV | Latent response variable |
| M(C)AR | missing (completely) at random |
| ML(E) | Maximum likelihood (estimation) |
| MS | Mean squares |
| REML | Restricted maximum likelihood |
| PML | Pairwise maximum likelihood |
| OSF | Open Science Framework |
| PMD | Planned missing data |
| Standard error | |
| SEM | Structural equation model |
References
- Cronbach, L.J. Coefficient alpha and the internal structure of tests. Psychometrika 1951, 16, 297–334. [Google Scholar] [CrossRef]
- Cronbach, L.J.; Rajaratnam, N.; Gleser, G.C. Theory of generalizability: A liberalization of reliability theory. Br. J. Stat. Psychol. 1963, 16, 137–163. [Google Scholar] [CrossRef]
- Brennan, R.L. Generalizability Theory; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Lord, F.M.; Novick, M.R. Statistical Theories of Mental Test Scores; Addison-Welsley: Reading, MA, USA, 1968. [Google Scholar]
- Vispoel, W.P.; Tao, S. A generalizability analysis of score consistency for the Balanced Inventory of Desirable Responding. Psychol. Assess. 2013, 25, 94–104. [Google Scholar] [CrossRef]
- Hoyt, W.T.; Melby, J.N. Dependability of measurement in counseling psychology: An introduction to generalizability theory. Couns. Psychol. 1999, 27, 325–352. [Google Scholar] [CrossRef]
- Medvedev, O.N.; Krägeloh, C.U.; Narayanan, A.; Siegert, R.J. Measuring mindfulness: Applying generalizability theory to distinguish between state and trait. Mindfulness 2017, 8, 1036–1046. [Google Scholar] [CrossRef]
- Vangeneugden, T.; Laenen, A.; Geys, H.; Renard, D.; Molenberghs, G. Applying concepts of generalizability theory on clinical trial data to investigate sources of variation and their impact on reliability. Biometrics 2005, 61, 295–304. Available online: https://www.jstor.org/stable/3695675 (accessed on 29 May 2021). [CrossRef] [PubMed]
- Arterberry, B.J.; Martens, M.P.; Cadigan, J.M.; Rohrer, D. Application of generalizability theory to the big five inventory. Personal. Individ. Differ. 2014, 69, 98–103. [Google Scholar] [CrossRef] [PubMed]
- Vispoel, W.P.; Morris, C.A.; Kilinc, M. Practical applications of generalizability theory for designing, evaluating, and improving psychological assessments. J. Personal. Assess. 2018, 100, 53–67. [Google Scholar] [CrossRef]
- Briesch, A.M.; Swaminathan, H.; Welsh, M.; Chafouleas, S.M. Generalizability theory: A practical guide to study design, implementation, and interpretation. J. Sch. Psychol. 2014, 52, 13–35. [Google Scholar] [CrossRef]
- Cardinet, J.; Johnson, S.; Pini, G. Applying Generalizability Theory Using EduG; Taylor & Francis: New York, NY, USA, 2010. [Google Scholar]
- Jeon, M.J.; Lee, G.; Hwang, J.W.; Kang, S.J. Estimating reliability of school-level scores using multilevel and generalizability theory models. Asia Pac. Educ. Rev. 2009, 10, 149–158. [Google Scholar] [CrossRef][Green Version]
- Marcoulides, G.A. Estimating variance components in generalizability theory: The covariance structure analysis approach. Struct. Equ. Model. 1996, 3, 290–299. [Google Scholar] [CrossRef]
- Raykov, T.; Marcoulides, G.A. Estimation of generalizability coefficients via a structural equation modeling approach to scale reliability evaluation. Int. J. Test. 2006, 6, 81–95. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Morris, C.A.; Kilinc, M. Applications of generalizability theory and their relations to classical test theory and structural equation modeling. Psychol. Methods 2018, 23, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Vispoel, W.P.; Morris, C.A.; Kilinc, M. Using generalizability theory with continuous latent response variables. Psychol. Methods 2019, 24, 153–178. [Google Scholar] [CrossRef] [PubMed]
- Ark, T.K. Ordinal Generalizability Theory Using an Underlying Latent Variable Framework. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2015. [Google Scholar] [CrossRef]
- Jiang, Z.; Walker, K.; Shi, D.; Cao, J. Improving generalizability coefficient estimate accuracy: A way to incorporate auxiliary information. Methodol. Innov. 2018, 11. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; Version 3.6.1; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.r-project.org (accessed on 29 May 2021).
- Rosseel, Y. lavaan: An R package for structural equation modeling and more. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- Preacher, K.J.; Selig, J.P. Advantages of Monte Carlo confidence intervals for indirect effects. Commun. Methods Meas. 2012, 6, 77–98. [Google Scholar] [CrossRef]
- Jorgensen, T.D. Extending Structural Equation Models of Generalizability Theory; Project Available on the Open Science Framework. Available online: https://osf.io/43j5x/ (accessed on 29 May 2021).
- McGraw, K.O.; Wong, S.P. Forming inferences about some intraclass correlation coefficients. Psychol. Methods 1996, 1, 30–46. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Xu, G.; Kilinc, M. Expanding G-theory models to incorporate congeneric relationships: Illustrations using the Big Five Inventory. J. Personal. Assess. 2020. [Google Scholar] [CrossRef]
- Little, T.D.; Slegers, D.W.; Card, N.A. A non-arbitrary method of identifying and scaling latent variables in SEM and MACS models. Struct. Equ. Model. 2006, 13, 59–72. [Google Scholar] [CrossRef]
- Muthén, L.K.; Muthén, B.O. Mplus User’s Guide, 8th ed.; Muthén and Muthén: Los Angeles, CA, USA, 1998–2019; Available online: https://www.statmodel.com/html_ug.shtml (accessed on 29 May 2021).
- Bock, R.D.; Brennan, R.L.; Muraki, E. The information in multiple ratings. Appl. Psychol. Meas. 2002, 26, 364–375. [Google Scholar] [CrossRef]
- Wirth, R.; Edwards, M.C. Item factor analysis: Current approaches and future directions. Psychol. Methods 2007, 12, 58–79. [Google Scholar] [CrossRef] [PubMed]
- Agresti, A. Analysis of Ordinal Categorical Data; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Agresti, A. An Introduction to Categorical Data Analysis, 2nd ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Briggs, D.C.; Wilson, M. Generalizability in item response modeling. J. Educ. Meas. 2007, 44, 131–155. [Google Scholar] [CrossRef]
- Glas, C.A.W. Generalizability theory. In Psychometrics in Practice at RCEC; Eggen, T., Veldkamp, B., Eds.; RCEC, Cito/University of Twente: Enschede, The Netherlands, 2012; pp. 1–13. [Google Scholar] [CrossRef]
- Choi, J.; Wilson, M.R. Modeling rater effects using a combination of generalizability theory and IRT. Psychol. Test Assess. Model. 2018, 60, 53–80. [Google Scholar]
- Kamata, A.; Bauer, D.J. A note on the relation between factor analytic and item response theory models. Struct. Equ. Model. 2008, 15, 136–153. [Google Scholar] [CrossRef]
- Muthén, B.; Asparouhov, T. Latent variable analysis with categorical outcomes: Multiple-group and growth modeling in Mplus. Technical report, Muthén & Muthén. Mplus Web Note 4 2002, 4, 1–22. Available online: https://www.statmodel.com/ (accessed on 29 May 2021).
- Wu, H.; Estabrook, R. Identification of confirmatory factor analysis models of different levels of invariance for ordered categorical outcomes. Psychometrika 2016, 81, 1014–1045. [Google Scholar] [CrossRef]
- Klößner, S.; Klopp, E. Explaining constraint interaction: How to interpret estimated model parameters under alternative scaling methods. Struct. Equ. Model. 2019, 26, 143–155. [Google Scholar] [CrossRef]
- Zumbo, B.D.; Gadermann, A.M.; Zeisser, C. Ordinal versions of coefficients alpha and theta for Likert rating scales. J. Mod. Appl. Stat. Methods 2007, 6, 21–29. [Google Scholar] [CrossRef]
- Gadermann, A.M.; Guhn, M.; Zumbo, B.D. Estimating ordinal reliability for Likert-type and ordinal item response data: A conceptual, empirical, and practical guide. Pract. Assess. Res. Eval. 2012, 17. [Google Scholar] [CrossRef]
- Zumbo, B.D.; Kroc, E. A measurement is a choice and Stevens’ scales of measurement do not help make it: A response to Chalmers. Educ. Psychol. Meas. 2019, 79, 1184–1197. [Google Scholar] [CrossRef] [PubMed]
- Chalmers, R.P. On misconceptions and the limited usefulness of ordinal alpha. Educ. Psychol. Meas. 2018, 78, 1056–1071. [Google Scholar] [CrossRef] [PubMed]
- Moore, C.T. gtheory: Apply Generalizability Theory with R; R Package Version 0.1.2. 2016. Available online: https://cran.r-project.org/package=gtheory (accessed on 29 May 2021).
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Jiang, Z. Using the linear mixed-effect model framework to estimate generalizability variance components in R: A lme4 package application. Methodology 2018, 14, 133–142. [Google Scholar] [CrossRef]
- Olsson, U. On the robustness of factor analysis against crude classification of the observations. Multivar. Behav. Res. 1979, 14, 485–500. [Google Scholar] [CrossRef] [PubMed]
- DiStefano, C. The impact of categorization with confirmatory factor analysis. Struct. Equ. Model. 2002, 9, 327–346. [Google Scholar] [CrossRef]
- Green, S.B.; Yang, Y. Reliability of summed item scores using structural equation modeling: An alternative to coefficient alpha. Psychometrika 2009, 74, 155–167. [Google Scholar] [CrossRef]
- Graham, J.W.; Hofer, S.M.; MacKinnon, D.P. Maximizing the usefulness of data obtained with planned missing value patterns: An application of maximum likelihood procedures. Multivar. Behav. Res. 1996, 31, 197–218. [Google Scholar] [CrossRef] [PubMed]
- Graham, J.W.; Taylor, B.J.; Olchowski, A.E.; Cumsille, P.E. Planned missing data designs in psychological research. Psychol. Methods 2006, 11, 323–343. [Google Scholar] [CrossRef]
- Rhemtulla, M.; Jia, F.; Wu, W.; Little, T.D. Planned missing designs to optimize the efficiency of latent growth parameter estimates. Int. J. Behav. Dev. 2014, 38, 423–434. [Google Scholar] [CrossRef]
- Ten Hove, D.; Jorgensen, T.D.; van der Ark, L.A. Interrater reliability for multilevel data: A generalizability theory approach. Psychol. Methods 2021. [Google Scholar] [CrossRef]
- Van der Ark, L.A.; van Leeuwen, J.L.; Jorgensen, T.D. Interbeoordelaarsbetrouwbaarheid LIJ: Onderzoek Naar De Interbeoordelaarsbetrouwbaarheid Van Het Landelijk Instrumentarium Jeugdstrafrechtketen [Interrater Reliability LIJ: Research on the Interrater Reliability of the Instrument Used by the National Juvenile Criminal Law Department]; Technical Report; Wetenschappelijk Onderzoek- en Documentatiecentrum Van de Ministerie van Justitie en Veiligheid [Scientific Research and Documentation Center of the Ministry for Justice and Security]: Amsterdam, The Netherlands, 2018. Available online: http://hdl.handle.net/20.500.12832/2267 (accessed on 29 May 2021).
- Vial, A.; Assink, M.; Stams, G.J.J.M.; van der Put, C. Safety and risk assessment in child welfare: A reliability study using multiple measures. J. Child Fam. Stud. 2019, 28, 3533–3544. [Google Scholar] [CrossRef]
- Yuen, J.K.; Kelley, A.S.; Gelfman, L.P.; Lindenberger, E.E.; Smith, C.B.; Arnold, R.M.; Calton, B.; Schell, J.; Berns, S.H. Development and validation of the ACP-CAT for assessing the quality of advance care planning communication. J. Pain Symptom Manag. 2020, 59, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Shi, D.; Lee, T.; Fairchild, A.J.; Maydeu-Olivares, A. Fitting Ordinal Factor Analysis Models With Missing Data: A Comparison Between Pairwise Deletion and Multiple Imputation. Educ. Psychol. Meas. 2019. [Google Scholar] [CrossRef]
- Katsikatsou, M.; Moustaki, I.; Yang-Wallentin, F.; Jöreskog, K.G. Pairwise likelihood estimation for factor analysis models with ordinal data. Comput. Stat. Data Anal. 2012, 56, 4243–4258. [Google Scholar] [CrossRef]
- Bauer, D.J.; Howard, A.L.; Baldasaro, R.E.; Curran, P.J.; Hussong, A.M.; Chassin, L.; Zucker, R.A. A trifactor model for integrating ratings across multiple informants. Psychol. Methods 2013, 18, 475–493. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, T.D.; Pornprasertmanit, S.; Schoemann, A.M.; Rosseel, Y. semTools: Useful Tools for Structural Equation Modeling, R Package Version 0.5-4; 2021. Available online: https://cran.r-project.org/package=semTools (accessed on 29 May 2021).
- Revelle, W. psych: Procedures for Psychological, Psychometric, and Personality Research, R Package Version 2.1.3; 2021. Available online: https://cran.r-project.org/package=psych (accessed on 29 May 2021).
- Katsikatsou, M. The Pairwise Likelihood Method for Structural Equation Modelling with Ordinal Variables and Data with Missing Values Using the R Package lavaan; Technical Report; Department of Statistics, London School of Economics and Political Science: London, UK, 2018; Available online: https://users.ugent.be/~yrosseel/lavaan/pml/PL_Tutorial.pdf (accessed on 29 May 2021).
- Huebner, A.; Lucht, M. Generalizability Theory in R. Pract. Assess. Res. Eval. 2019, 24. [Google Scholar] [CrossRef]
- Rhemtulla, M.; Brosseau-Liard, P.É.; Savalei, V. When can categorical variables be treated as continuous? A comparison of robust continuous and categorical SEM estimation methods under suboptimal conditions. Psychol. Methods 2012, 17, 354–373. [Google Scholar] [CrossRef]
- Li, C.H. Confirmatory factor analysis with ordinal data: Comparing robust maximum likelihood and diagonally weighted least squares. Behav. Res. Methods 2016, 48, 936–949. [Google Scholar] [CrossRef]
- Li, C.H. The performance of ML, DWLS, and ULS estimation with robust corrections in structural equation models with ordinal variables. Psychol. Methods 2016, 21, 369–387. [Google Scholar] [CrossRef] [PubMed]
- Raykov, T.; Marcoulides, G.A. On examining the underlying normal variable assumption in latent variable models with categorical indicators. Struct. Equ. Model. 2015, 22, 581–587. [Google Scholar] [CrossRef]
- Savalei, V. Understanding robust corrections in structural equation modeling. Struct. Equ. Model. 2014, 21, 149–160. [Google Scholar] [CrossRef]
- Robitzsch, A. Why ordinal variables can (almost) always be treated as continuous variables: Clarifying assumptions of robust continuous and ordinal factor analysis estimation methods. Front. Educ. 2020, 5. [Google Scholar] [CrossRef]
| Latent Intercept | Identification Constraint | Ordinal | |||
|---|---|---|---|---|---|
| Person () | ✓ | ✓ | ✓ | ||
| Item 1 () | ✓ | ||||
| Item 2 () | ✓ | ||||
| Item 3 () | ✓ | ||||
| Occasion 1 () | ✓ | ✓ | |||
| Occasion 2 () | ✓ | ✓ | |||
| Occasion 3 () | ✓ | ✓ | |||
| First Measurement (LRV) | ✓ | ||||
| All other LRVs | , for each | ✓ |
| Data | Response Scale | Estimator | G | D | D-Cut | G | D | D-Cut | G | D | D-Cut |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Normal | Observed | MS | 0.834 | 0.783 | 0.966 | 0.737 | 0.629 | 0.956 | 0.794 | 0.728 | 0.970 |
| REML | 0.834 | 0.783 | 0.966 | 0.737 | 0.629 | 0.956 | 0.794 | 0.728 | 0.970 | ||
| ML | 0.834 | 0.782 | 0.968 | 0.737 | 0.626 | 0.959 | 0.794 | 0.712 | 0.969 | ||
| Discretized | MS | 0.759 | 0.706 | 0.958 | 0.715 | 0.602 | 0.958 | 0.758 | 0.691 | 0.970 | |
| REML | 0.759 | 0.706 | 0.958 | 0.715 | 0.602 | 0.958 | 0.758 | 0.691 | 0.970 | ||
| ML(R) | 0.759 | 0.705 | 0.960 | 0.715 | 0.600 | 0.961 | 0.758 | 0.676 | 0.969 | ||
| LRV | DWLS | 0.857 | 0.792 | 0.969 | 0.773 | 0.651 | 0.960 | 0.817 | 0.730 | 0.970 | |
| Observed a | 0.781 | — | — | 0.738 | — | — | 0.780 | — | — | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jorgensen, T.D. How to Estimate Absolute-Error Components in Structural Equation Models of Generalizability Theory. Psych 2021, 3, 113-133. https://doi.org/10.3390/psych3020011
Jorgensen TD. How to Estimate Absolute-Error Components in Structural Equation Models of Generalizability Theory. Psych. 2021; 3(2):113-133. https://doi.org/10.3390/psych3020011
Chicago/Turabian StyleJorgensen, Terrence D. 2021. "How to Estimate Absolute-Error Components in Structural Equation Models of Generalizability Theory" Psych 3, no. 2: 113-133. https://doi.org/10.3390/psych3020011
APA StyleJorgensen, T. D. (2021). How to Estimate Absolute-Error Components in Structural Equation Models of Generalizability Theory. Psych, 3(2), 113-133. https://doi.org/10.3390/psych3020011






