You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Chemistry
Download PDF
  • Communication
  • Open Access

29 December 2025

UV–Vis Spectra of Gold(III) Complexes with Different Halides, Hydroxide, and Ammonia According to TD-DFT Calculations

,
and
Department of General Chemical Technology, Ivanovo State University of Chemistry and Technology, Sheremetevskii Ave. 7, 153000 Ivanovo, Russia
*
Author to whom correspondence should be addressed.
Chemistry2026, 8(1), 3;https://doi.org/10.3390/chemistry8010003 
(registering DOI)
This article belongs to the Topic Theoretical, Quantum and Computational Chemistry—2nd Edition
Version Notes
Order Reprints

Abstract

This paper presents accurate TD-DFT calculations for several mixed-ligand gold(III) complexes with ligands including Cl−, Br−, I−, OH−, and NH3. The calculated results show excellent agreement with available experimental data. The spectral shapes are determined by charge transfer transitions, which are systematically influenced by the ligand’s position in the spectrochemical series. The main vertical electron transitions and the molecular orbitals involved are identified and discussed. Furthermore, the results indicate that the iodide-containing gold(III) complexes, [AuCl2I2]− and [AuI(OH)3]−, are viable candidates for practical synthesis.

1. Introduction

Gold exhibits excellent thermal and electrical conductivity, high ductility, and remarkable resistance to corrosion, making it invaluable for numerous industrial applications. The chemistry of gold is extensive, with oxidation states ranging from −1 to +5 [1]; however, gold(I) and gold(III) compounds are the most extensively studied. Their complexes are of particular interest because they exhibit low toxicity and do not cause allergic reactions in humans [2], while also demonstrating significant anti-rheumatic [2], anti-tumor [3,4,5], and anti-bacterial [6,7,8] potential. Furthermore, Au+ and Au3+ compounds serve as efficient catalysts for several industrially relevant processes [9,10], including, for example, [3+2] cycloaddition reaction [11].
However, relatively simple gold(III) complexes with mono- or diatomic ligands, such as chloride, bromide, and hydroxide, remain of great interest due to their environmental relevance and significant role in gold geochemistry [12,13]. A deeper understanding of the electron absorption spectra of these complexes is valuable not only for research in gold geochemistry and ore deposition but also for investigating liquid-phase reactions where these complexes serve as starting materials for synthesizing more sophisticated compounds or as oxidizers. Several previous studies have reported experimental UV–Vis spectra for related complexes, including tetrachloroaurate(III), mixed hydroxychloroaurates(III) [14,15], tetrabromoaurate(III), and mixed chloro- and hydroxybromoaurate(III) [15]. Although the reduction of gold(III) by iodide is well-known and is typically observed upon the addition of iodide to tetrachloroaurate solutions (see e.g., paper [16]), one report claims that [AuCl2I2]− can be obtained under finely tuned concentration conditions [17].
In our previous contribution [18], we calculated the UV–Vis spectra of tetrachloroaurate(III) and related gold(III) complexes containing mixed Cl− and OH− ligands. This study was part of a larger investigation into the interactions of gold(III) species with serum albumins. The spectra, calculated using the TD-DFT method, showed good agreement with experimental data [14,15]. In this paper, we extend that work by presenting TD-DFT calculations of the electronic absorption spectra for a series of gold(III) complexes with Br−, Cl−, OH−, and I− ligands. Our objectives are threefold: (1) to achieve optimal agreement with available experimental results; (2) to elucidate the nature of the UV–Vis spectra of tetrahalidoaurates(III) and their partially hydrolyzed derivatives; and (3) to evaluate the claim by the authors of reference [17] regarding the stability of the mixed chloride–iodide complex, [AuCl2I2]−.

2. Materials and Methods

The equilibrium geometries and harmonic vibrational frequencies (Table S1) for all gold(III) complexes were optimized using the hybrid CAM-B3LYP functional [19]. Vertical electronic transition energies and oscillator strengths (UV–Vis spectra) were computed using the framework of time-dependent density functional theory (TD-DFT) [20]. The most important molecular orbitals are collected in Table S2. To account for scalar relativistic effects, the two-component relativistic effective core potential ECP60MDF [21] was applied to the inner shells of the gold atom (1s22s22p63s23p63d104s24p64d104f14). The valence shells of gold (5s25p65d106s1) were described with the cc-pVTZ-PP basis set [22] (41s37p25d2f1g/5s5p4d2f1g).
Similarly, the inner shells of bromine (1s22s22p6) and iodine (1s22s22p63s23p63d10) were also treated with relativistic effective core potentials (RECPs). Their valence shells were described by correlation-consistent cc-pVTZ-PP basis sets: 23s20p10d1f/5s4p3d1f for bromine and 25s20p11d1f/5s4p3d1f for iodine [23]. For the lighter atoms (O, H, N, and Cl), the conventional full-electron cc-pVTZ basis set was used [24,25]. The selection of the theoretical approach was guided by an evaluation of the existing literature. Specifically, the CAM-B3LYP functional has been shown to achieve chemical accuracy for charge-transfer energy calculations [19]. In terms of basis sets, it has been reported that scalar-relativistic pseudopotential calculations yield ground-state properties and excitation energies very close to those from all-electron approaches [26]. Consequently, the small-core energy-consistent Stuttgart/Köln pseudopotentials were employed for TD-DFT simulations of heavy and super-heavy p-block molecules [26].
To validate the functional choice, additional calculations for [AuBr4]− were performed using B3LYP/cc-pVTZ-PP to examine the effect of exact Hartree–Fock exchange. Furthermore, calculations at the CAM-B3PLYP/aug-cc-pVTZ level were conducted for [AuCl4]−, and at CAM-B3LYP/aug-cc-pVTZ-PP for [AuBr4]− and [AuI4]−, to assess the impact of augmented diffuse functions. Our tests confirmed that CAM-B3LYP predicts long-wavelength band positions in better agreement with experiment than B3LYP, whereas diffuse functions significantly affected only far-UV peaks (<200 nm), which were not experimentally observed. Their influence on charge-transfer transition energies was negligible. Thus, the final choice of methods ensured an optimal balance between computational accuracy and efficiency.
The solvent effect of water was incorporated in all calculations using the polarizable continuum model (PCM) [27]. All computations were performed with the Gaussian 09W software package [28].
To assess the multireference character of the wavefunction, ab initio calculations were conducted for the [AuX4]− (X = Cl, Br, I) complexes in the gas phase. The geometries and molecular orbitals were first optimized under D4h symmetry constraints using the restricted Hartree–Fock (RHF) method [29]. These RHF results were then used as an initial guess for the configuration interaction with single and double excitations (CISD) model [30]. To manage computational cost, a frozen-core approximation was applied, limiting the number of single and double excitations.
Ball-and-stick models and molecular orbitals were visualized using the ChemCraft program, ver. 1.8, build 523a [31]. All the calculations were performed using Gaussian 09w software package, ver. 9.0, revision A.02 [28].
Hydrogen tetrachloroaurate(III) trihydrate (H[AuCl4]·3H2O; LenReaktiv, St. Petersburg, Russia; claimed Au content: 49.11%) was used as received. KBr was recrystallized from water before using. UV–Vis titration of 2.5 mL of 0.000201 mol L−1 [AuCl4]− in 0.1 mol L−1 aqueous NaCl solution by 0.1015 mol L−1 KBr aqueous solution (30 titrant additions; volume of each was 8 µL) was performed using a double-beam Shimadzu UV1800 spectrophotometer (Shimadzu, Marlborough, MA, USA). Measurements were conducted in the wavelength range of 200 to 500 nm with an absorbance range of 0 to 1.3. The wavelength determination error did not exceed ±0.5 nm, and the maximum absorbance measurement inaccuracy was ±0.003 units. The temperature was maintained at 298.2 ± 0.1 K using an external thermostat. Quartz cuvettes with a 1.00 cm optical path length were used. The equilibrium constants and molar extinction coefficients were calculated using KEV software, ver. 0.6.0 (https://k-ev.org, accessed on 20 December 2025) [32].

3. Results and Discussion

3.1. What Are the Experimental Spectra?

It is important to note that the spectra referred to as ‘experimental’ in this work were not measured directly for isolated complexes. Instead, they were derived computationally as part of the equilibrium constant calculations using a least-squares (LSQ) fitting procedure, as detailed in reference [15]. Specifically, these spectra result from deconvoluting spectrophotometric titration data; they represent the spectral profiles of individual species that, when combined with the equilibrium concentrations corresponding to the fitted equilibrium constants, provide the best match to the measured overall absorbance.
This indirect approach is necessary because the individual complexes often cannot be isolated in solution due to the similarity of their stability constants, which leads to the coexistence of multiple species. Nevertheless, the spectra determined through this method are reliable, albeit with certain limitations that will be discussed where relevant.

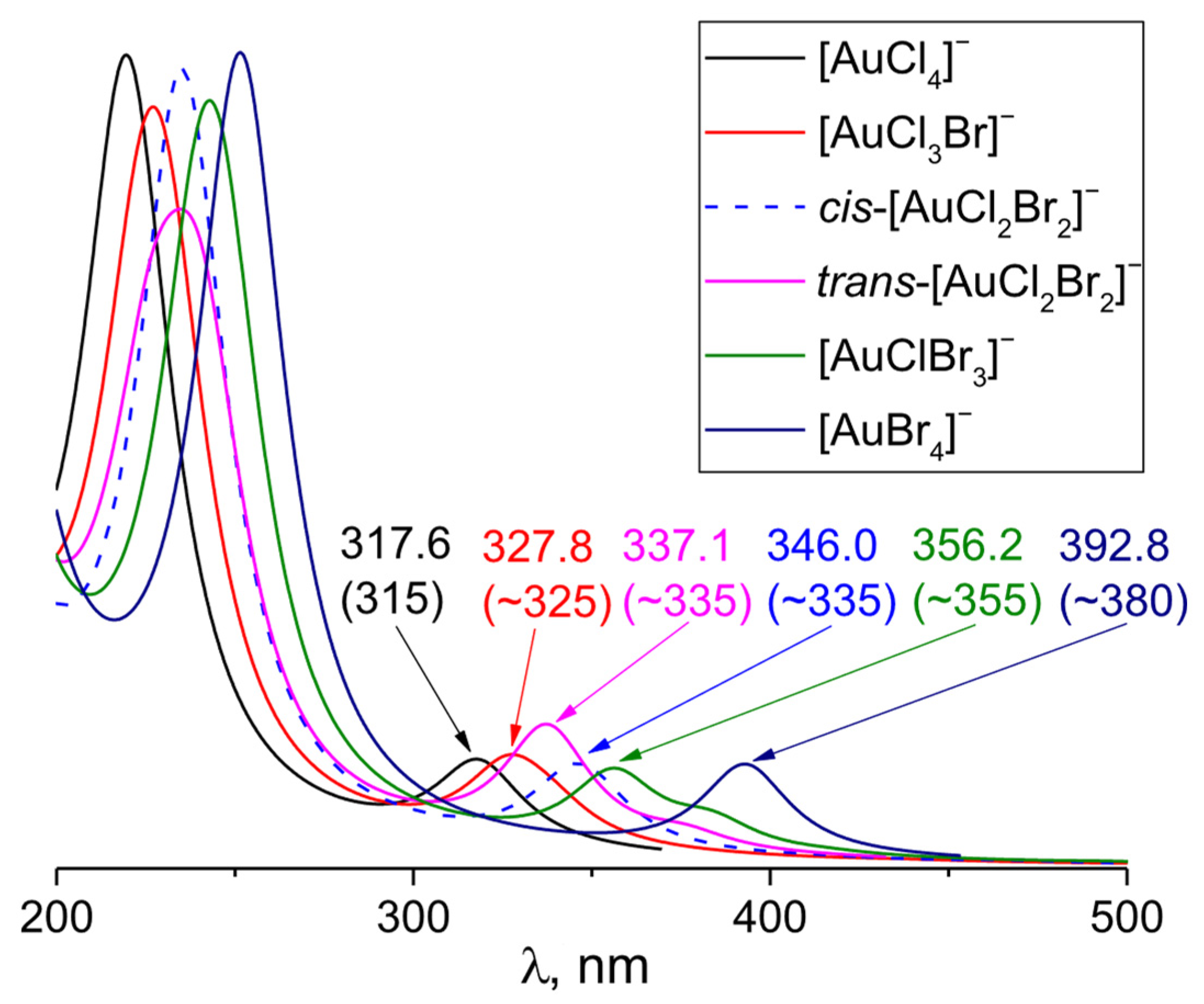
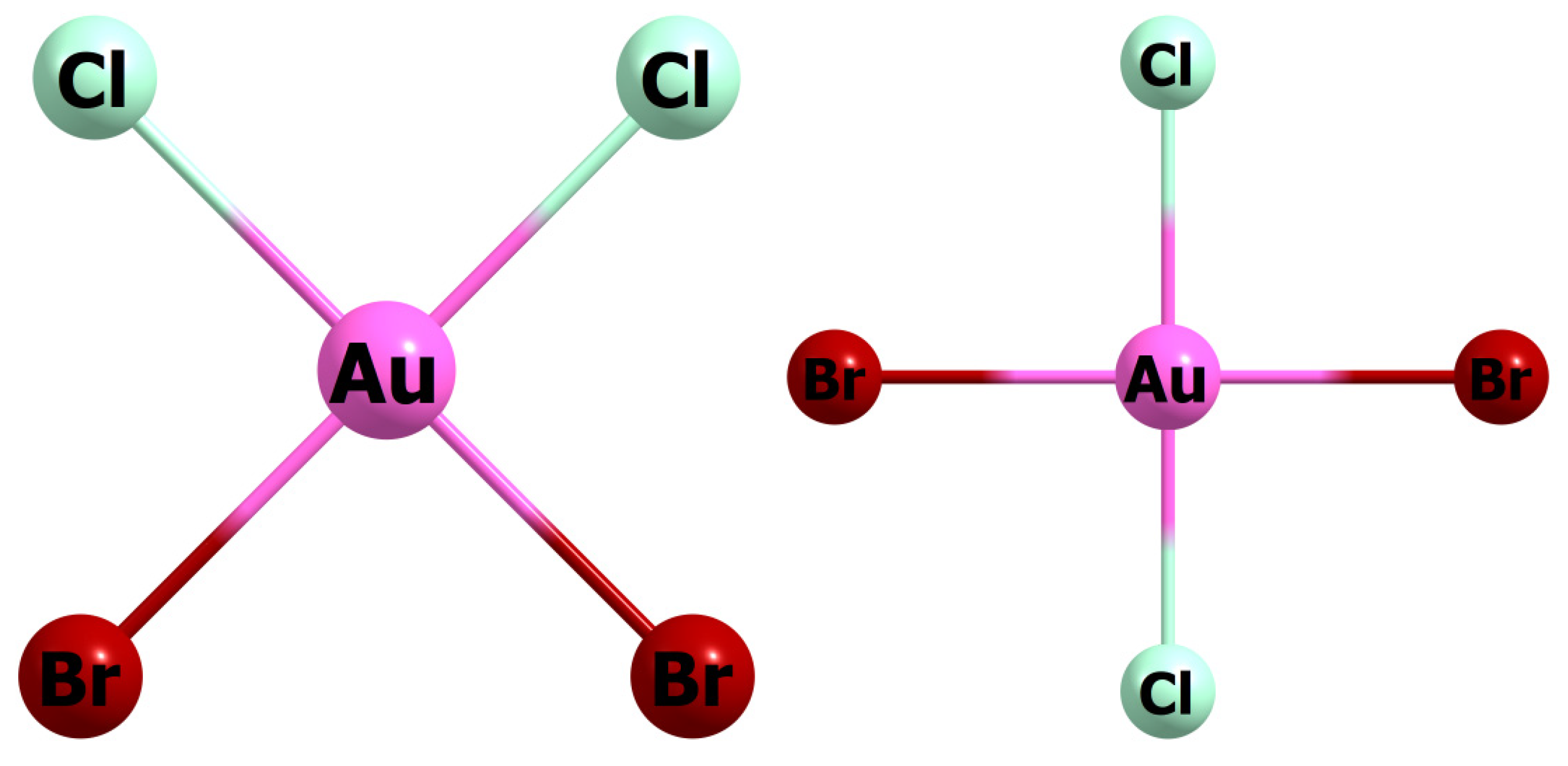
3.2. [AuCl4−nBrn]− (n varies from 1 to 4)

The substitution of chloride by bromide in tetrachloroaurate(III) is arguably one of its best-studied equilibria. Several studies [15,33,34,35,36] have reported values for the stepwise equilibrium constants of this ligand exchange, all of which are in good mutual agreement. Among these, D.C. McPhail et al. [15] also provided the spectral profiles for the various mixed complex species, [AuCl4−nBrn]−. We were able to reproduce them experimentally (see the titration data in Figure S1a and the spectra of the species in Figure S1b). As shown in Figure 1, our TD-DFT calculated spectra for the [AuCl4−nBrn]− series are in good agreement with the reference data from D.C. McPhail et al. [15].
Figure 1. TD-DFT calculated UV–Vis spectra of [AuCl4−nBrn]− (n varies from 1 to 4). Experimental values of peaks maxima adopted from Figure 4b in paper [15] are given in parentheses.
The calculations accurately predict the position of the spectral maxima, the overall spectral shape, and the bathochromic shift observed upon substituting chloride with bromide. This red shift of the LMCT (ligand-to-metal charge transfer) band is a consequence of the decreasing ligand field strength across the halide series (I− < Br− < Cl− < F−) [37].
Although L.I. Elding et al. [36] suggested that cis- and trans-isomers of [AuCl2Br2]− (see Figure 2 for the structures of isomers) should coexist, the experimental spectrum aligns more closely with that of the trans-complex. Therefore, the formation of the cis-isomer can likely be ruled out.
Figure 2. Optimized structures of cis-[AuCl2Br2]− (left) and trans-[AuCl2Br2]− (right).
The poorest agreement between the calculated and experimental data is observed for the [AuBr4]− complex. This case shows the largest deviation in the absorbance maximum from the predicted value. Furthermore, the calculated spectrum lacks the distinct long-wavelength shoulder evident in the experimental spectrum [15] (Figure 1).
We initially considered a deviation from D4h symmetry as a possible reason for the missing long-wavelength shoulder in the tetrabromoaurate(III) spectrum. However, experimental evidence overwhelmingly confirms the square planar geometry of such gold(III) complexes [38,39,40,41]. To definitively rule out a possible Jahn–Teller distortion, we evaluated the multireference character of the wavefunction for [AuX4]− (X = Cl, Br) using conventional configuration interaction with single and double excitations (CISD) ab initio calculations.
First, the molecular geometries and canonical molecular orbitals were optimized under D4h symmetry constraints using the restricted Hartree–Fock (RHF) method. These optimized RHF orbitals were then used to construct the reference wavefunction for subsequent single-point CISD calculations without symmetry constraints. The CISD results indicate that a single closed-shell Slater determinant dominates the ground-state wavefunction, with a contribution of approximately 81%. Consequently, the ground state symmetry is 1A1g for [AuX4]− (X = Cl, Br), and the wavefunction can be considered essentially one-determinant.
Therefore, the hypothesis of a significant Jahn–Teller effect can be discarded, confirming that density functional theory (DFT) is an appropriate method for calculating the molecular properties of tetrahalidoaurates(III). The long-wavelength shoulder observed at ~400 nm for [AuCl4]− and ~455 nm for [AuBr4]− [15] can be assigned to electron transitions from the doubly occupied eg orbitals to the LUMO (b1g). These molecular orbitals correspond primarily to the dyz, dxz, and dx2−y2 orbitals of the gold ion. TD-DFT correctly predicts these 1A1g–1Eg vertical transitions at 409.1 nm and 465.4 nm for the chloro and bromo complexes, respectively. However, the calculations assign zero oscillator strength to these excitations, as they are symmetry-forbidden. However, vibrational and solvent effects in real solutions can lift this prohibition, making the d-d transitions weakly allowed. We propose that spin-orbit coupling, which was neglected in our calculations, may also contribute to the increased intensity of these d-d transitions in the experiments.

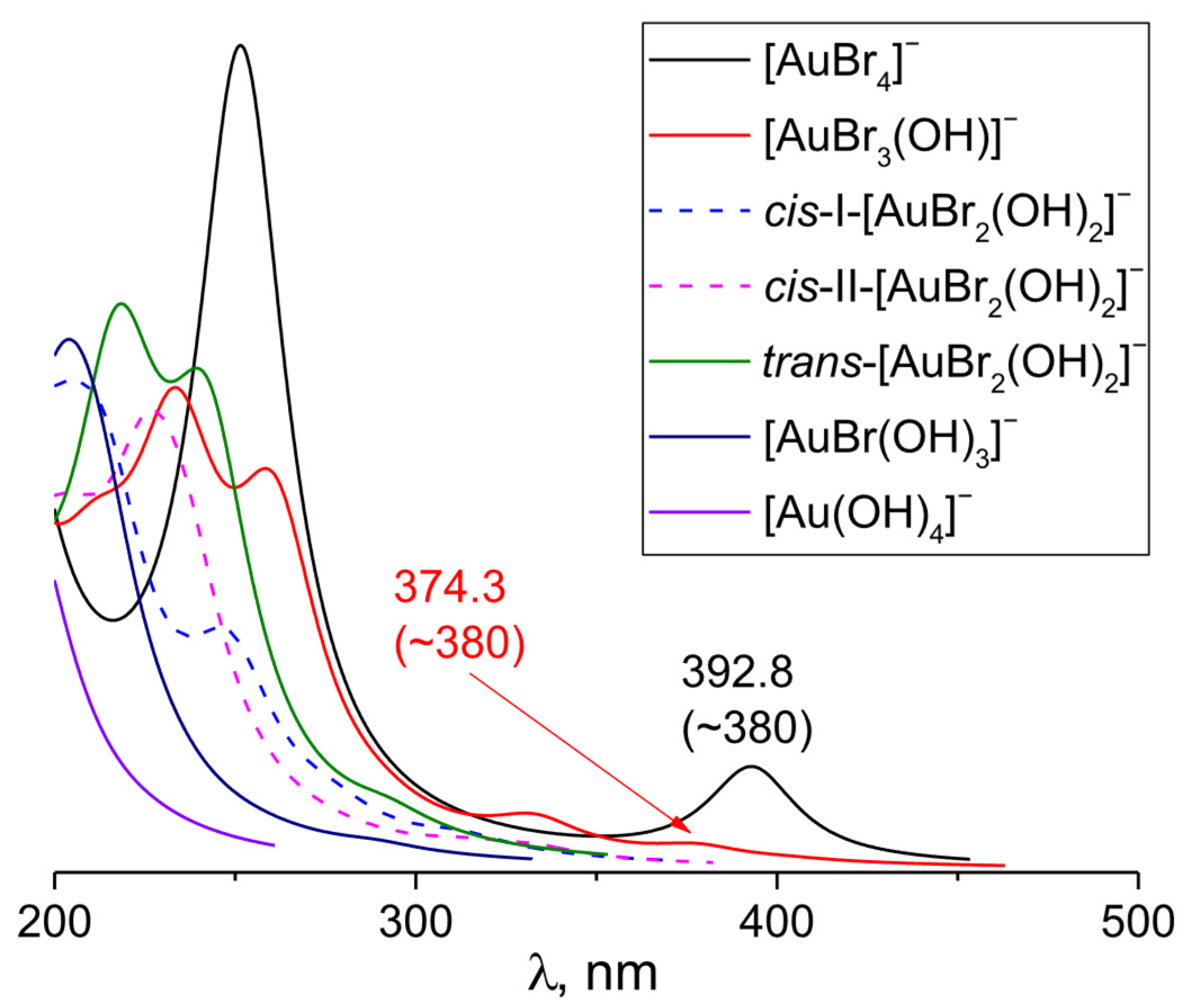
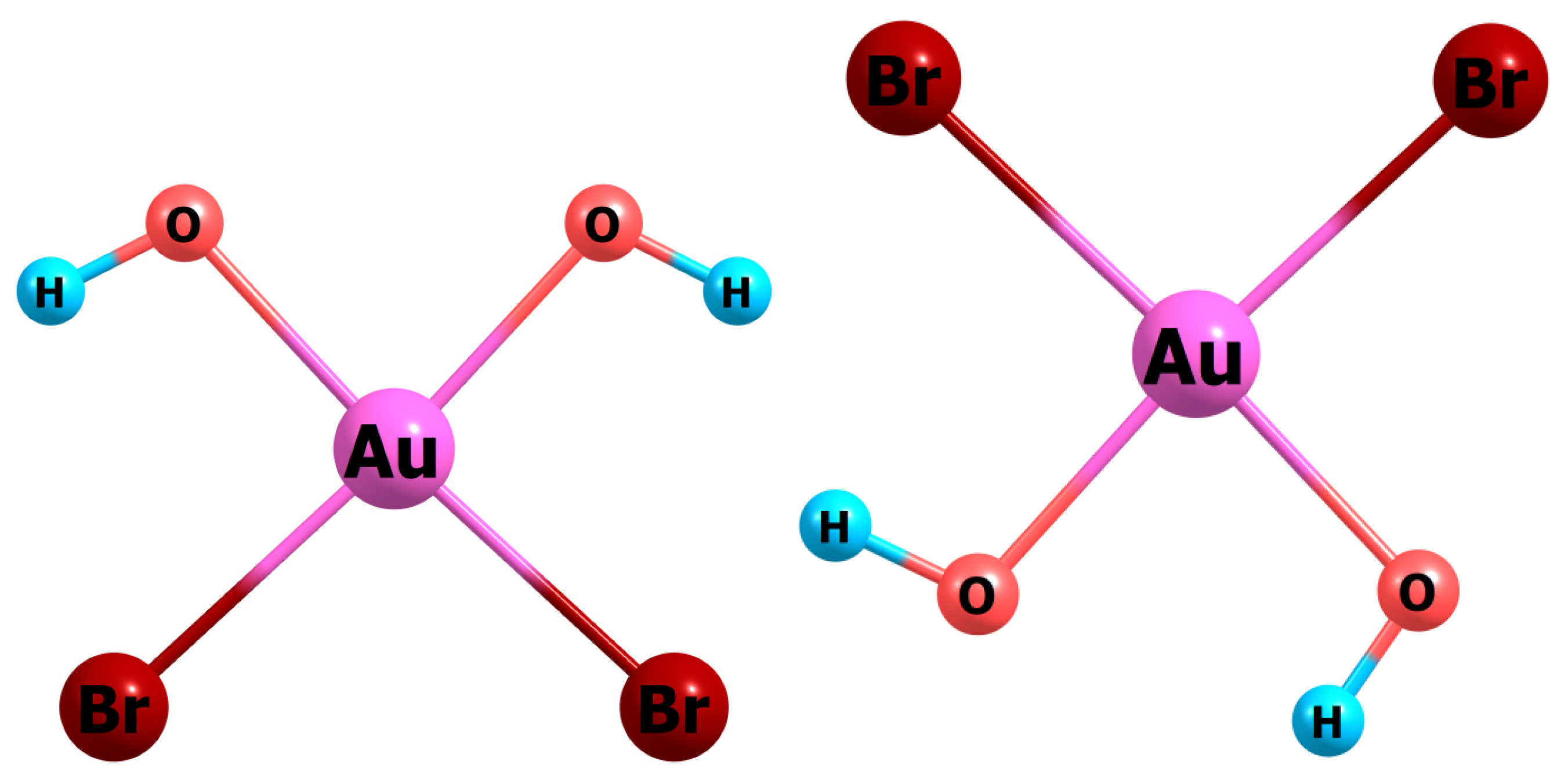
3.3. [AuBr4−n(OH)n]− (n Varies from 1 to 4)

The substitution of bromide by hydroxide in tetrabromoaurate(III) is a much less studied reaction. The existing literature on this system is scarce [15,42,43] and somewhat contradictory. Furthermore, the equilibrium composition calculated using the constants from these studies disagrees with the composition determined experimentally by mass spectrometry [44]. This discrepancy suggests that the reported equilibrium constants may be inaccurate, which would also affect the reliability of the experimentally derived spectra for the individual complex species (see Section 3.1). Consequently, it was not possible to achieve a perfect agreement between the experimental and calculated spectra (Figure 3).
Figure 3. TD-DFT calculated UV–Vis spectra of [AuBr4−n(OH)n]− (n varies from 1 to 4). Experimental values of peaks maxima adopted from Figure 10b in paper [15] are given in parentheses.
It is noteworthy that hydroxyl-containing complexes of gold(III) can take two cis-isomer configurations because of the different alignment of hydroxyl protons, as shown in Figure 4.
Figure 4. Two different cis-isomers of [AuBr2(OH)2]. Further on in the text, the (left) one (and other analogous hydroxyl-containing complexes) is marked as cis-I-isomer, while the (right) one is denoted as cis-II-isomer.
The experimental spectra [15] show no hypsochromic (blue) shift for the first substitution, from [AuBr4]− to [AuBr3(OH)]−, in contrast to the shift predicted by quantum chemical modeling (Figure 3). However, a second hydroxide substitution induces a significant blue shift in both the experimental and calculated spectra. Overall, the expected trend of a hypsochromic shift in the LMCT band with consecutive Br−/OH− exchange is observed, which is consistent with OH− being a stronger-field ligand than fluoride and the other halides.
The broad peaks in the experimental spectra at approximately 450 nm for [AuBr3(OH)]− and 350 nm for both [AuBr2(OH)2]− and [AuBr(OH)3]− [15] can also be assigned to symmetry-forbidden d-d transitions. This assignment is supported by the calculated values of 461.4 nm, 358.6 nm, and 336.5 nm for these complexes, respectively. It is noteworthy, however, that calculations assign zero oscillator strength to these transitions, while in the real solutions, they are allowed because of vibrational and solvent influence, though relatively low-intense.

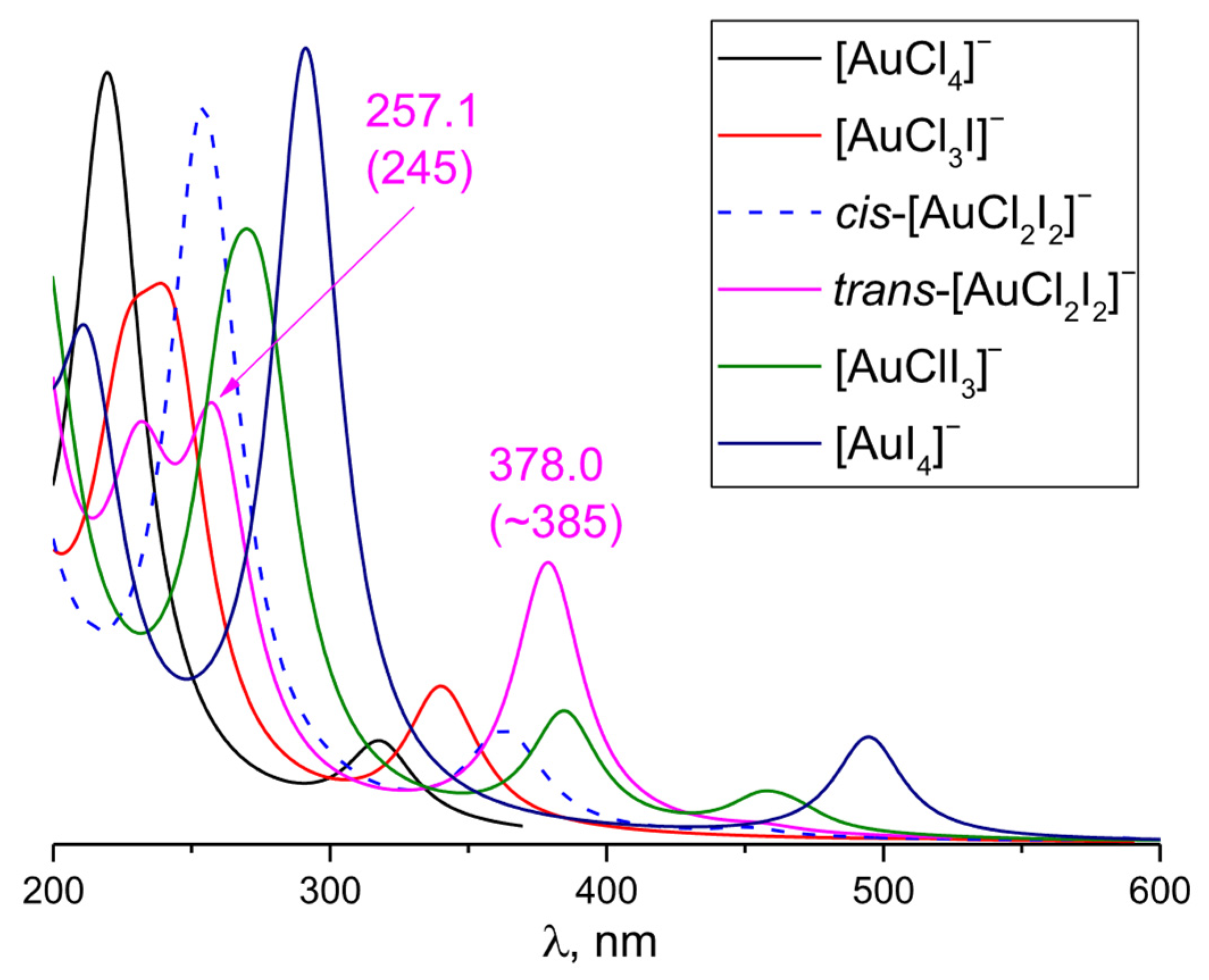
3.4. [AuCl4−nIn]− (n Varies from 1 to 4)

It is well-established that tetrachloroaurate(III) is readily reduced by iodide (see, e.g., paper [16]). Therefore, it was unexpected to find a report [17] claiming the formation of a [AuCl2I2]− complex when the molar ratio of gold(III) to iodide is maintained below 0.5. Our computational results (Figure 5) support this claim, as the experimental spectrum from reference [17] agrees well with the spectrum calculated for the trans-[AuCl2I2]− isomer.
Figure 5. TD-DFT calculated UV–Vis spectra of [AuCl4−nIn]− (n varies from 1 to 4). Experimental values of peaks maxima adopted from Figure 1 in paper [17] are given in parentheses.
As expected, the substitution of chloride by iodide results in a red shift of the LMCT band. A similar bathochromic shift is observed for the d-d transitions, with calculated values at 413.3 and 494.5 nm for [AuCl3I]−; 416.5 and 528.5 nm for trans-[AuCl2I2]−; 507.4 and 525.3 nm for [AuClI3]−; and 523.6 nm for [AuI4]−. The calculations predict zero oscillator strength to these vertical electron transitions as they are symmetry-forbidden.
A notable structural feature of tetraiodoaurate(III) is its non-planar geometry, as [AuI4]− belongs to the D2h point group. This deviation from the typical square planar structure may contribute to the relative instability of tetraiodoaurate(III) and facilitate its reduction by iodide.

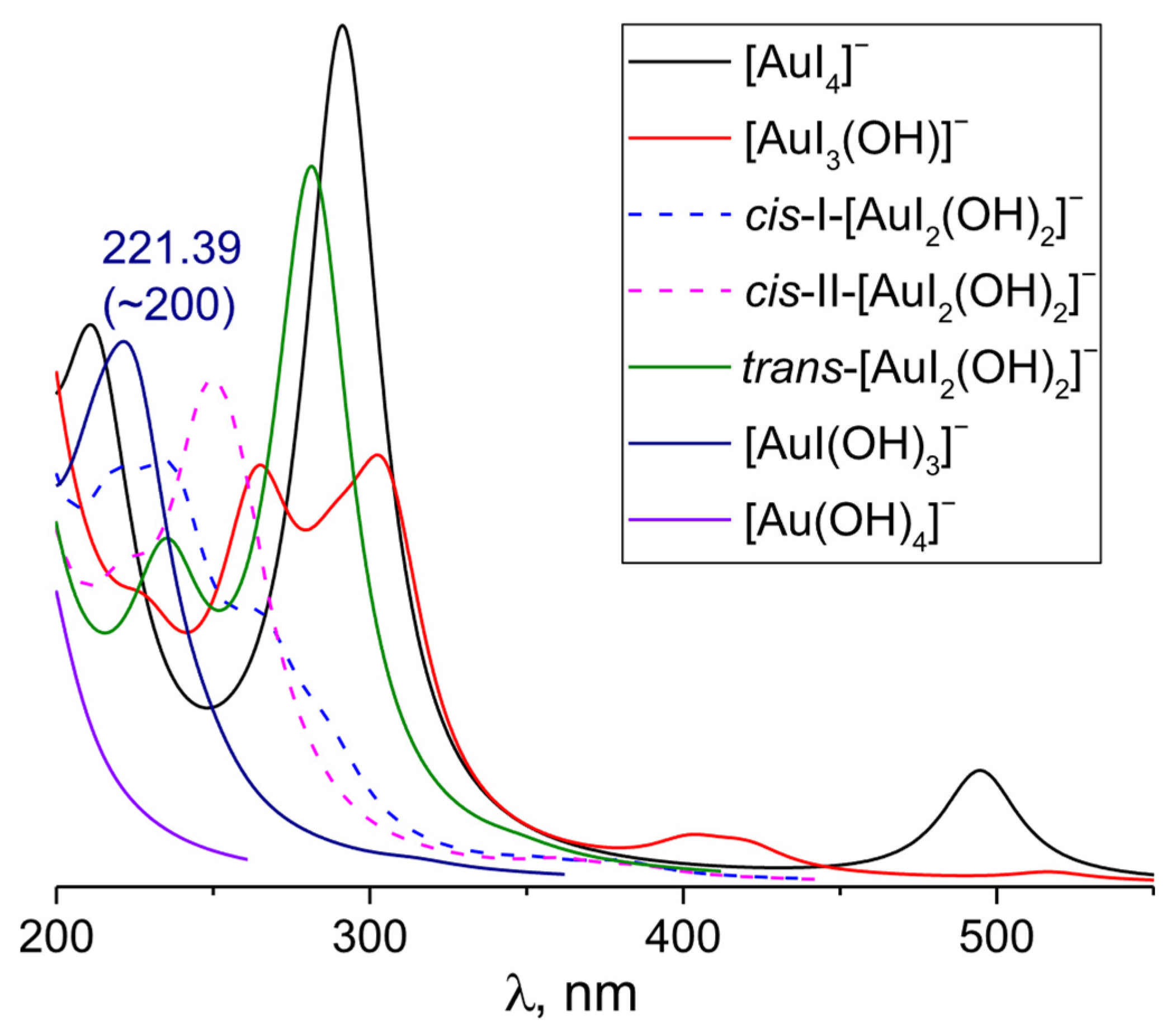
3.5. [AuI4−n(OH)n]− (n varies from 1 to 4)

A comparison of the theoretical spectra (Figure 6) with the experimental data from reference [17] suggests that the authors may have obtained [AuI(OH)3]− rather than [AuI2(OH)2]−. This conclusion is based on the fact that the spectrum of trans-[AuI2(OH)2]− exhibits a distinct maximum at 281 nm, whereas the experimental UV–Vis spectrum shows only a shoulder at ~300 nm. The formation of the cis-[AuI2(OH)2]− isomer, whose spectrum is also similar to the experimental one, seems unlikely, as trans-complexes are generally more stable and complex rearrangement is improbable.
Figure 6. TD-DFT calculated UV–Vis spectra of [AuI4−n(OH)n]− (n varies from 1 to 4). Experimental values of peaks maxima adopted from Figure 1 in paper [17] are given in parentheses.
Furthermore, the d-d transitions in [AuI(OH)3]−, calculated at 354 nm and 394 nm, may also contribute to the observed spectral shape.
As observed for the hydroxychloro- and hydroxybromoaurate(III) series, the substitution of iodide by hydroxide ions results in a hypsochromic shift of both the LMCT band and the d-d transition peaks.

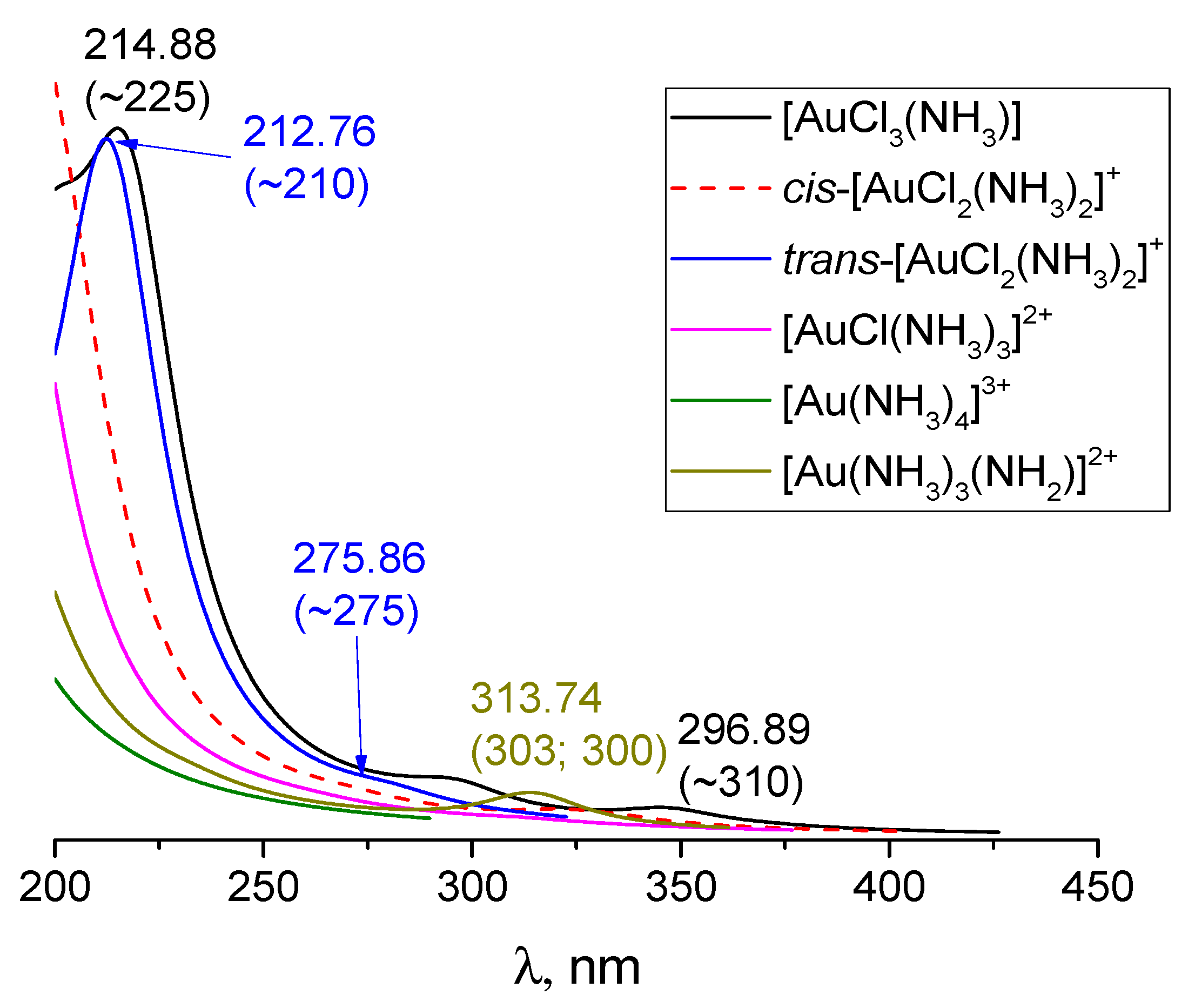
3.6. [AuCl3(NH3)], [Au(NH3)4]3+ and [Au(NH3)3(NH2)]2+

The complex [Au(NH3)4]3+, or more accurately its deprotonated form [Au(NH3)3(NH2)]2+, has been known for some time [45,46]. However, I.V. Mironov only succeeded in synthesizing [AuCl3(NH3)] [47], as complexes with more chloride ligands substituted by ammonia were not accessible under his experimental conditions. The probable reasons for this outcome include the need for a more alkaline medium (which promotes the formation of gold(III) hydroxo complexes) and the slow kinetics of the subsequent substitution reactions [47]. Even after several days, no significant changes were observed in the UV–Vis spectra, although the primary spectral data were not reported [47]. In contrast, the work by L.H. Skibsted [48] reports the spectrum of trans-[AuCl2(NH3)2]+ and provides the rate constants for the stepwise substitution of ammonia by chloride ions.
The TD-DFT calculated spectra for [AuCl3(NH3)], cis- and trans-[AuCl2(NH3)2]+, [AuCl(NH3)3]2+, [Au(NH3)4]3+, and [Au(NH3)3(NH2)]2+ are presented in Figure 7.
Figure 7. TD-DFT calculated UV–Vis spectra of [AuCl3(NH3)], cis- and trans-[AuCl2(NH3)2]+, [AuCl(NH3)3]2+, [Au(NH3)4]3+, and [Au(NH3)3(NH2)]2+. Experimental values of peaks maxima adopted from Figure 1 in paper [48] for [AuCl3(NH3)], trans-[AuCl2(NH3)2]+, from paper [46], and Figure 1 in paper [45] for [Au(NH3)3(NH2)]2+, are given in parentheses.
As expected, the substitution of chloride by ammonia induces a strong blue shift in the spectra, consistent with NH3 being a much stronger field ligand than Cl−.

4. Conclusions

The UV–Vis spectra for a series of simple gold(III) complexes with chloride, bromide, iodide, hydroxide, and ammonia ligands were calculated using TD-DFT with the CAM-B3LYP functional and appropriate pseudopotentials and basis sets. The calculated spectra show excellent agreement with their experimental counterparts. The long-wavelength features in the experimental spectra, where present, are attributed to both ligand-to-metal charge transfer (LMCT) and symmetry-forbidden d-d transitions between the dxz/dyz and dx2−y2 orbitals of the gold ion. The spectral shifts follow the established trends of the spectrochemical series.
This study corroborates the claim that mixed iodide–chloride and iodide–hydroxide gold(III) complexes, specifically [AuCl2I2]− and [AuI(OH)3]−, can be formed under specific conditions [17]. Furthermore, the [AuI4]− complex is found to adopt a D2h symmetry rather than the typical D4h, a structural distortion that may contribute to its relative instability and propensity for reduction of gold(III) by iodide.
The results of this work demonstrate that quantum chemical calculations (1) can reproduce the experimental UV–Vis spectra of heavy metal complexes like those of gold(III) with high precision and (2), consequently, provide a powerful and reliable tool for identifying species in gold(III) solutions containing various ligands. We conclude that DFT is a robust and efficient approach for predicting the physical and chemical properties of heavy metal complexes where relativistic effects are pronounced, offering a practical alternative to more time-consuming ab initio methods.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/chemistry8010003/s1, Figure S1: (a) UV-Vis spectra of 0.000201 mol L−1 H[AuCl4] (NaCl was added to the solution up to the concentration 0.1 mol L−1 to suppress hydrolysis of tetrachloroaurate(III) and other complexes) titrated by 0.1015 mol L−1 KBr (30 point acquired in total; volume of the single addition 8 µL); (b) molar extinction coefficient of different [AuCl4−nBrn]− species derived from the experimental titration. The following equilibrium constants log Kn of the reaction: [AuCl4]− + nBr− = [AuCl4−nBrn]− + nCl− were determined from the experimental data: log K1 = 2.46 ± 0.08; log K2 = 4.40 ± 0.11; log K3 = 6.06 ± 0.12; log K4 = 7.35 ± 0.16; Table S1: Structures and Cartesian coordinates of optimized geometry of gold(III) complexes, calculated vibration and TD-DFT spectra in water (PCM); Table S2: Data on electron transitions for the most important excited states of gold(III) complexes, which are responsible for LMCT and d-d transition bands.

Author Contributions

Conceptualization, O.A.P. and G.A.G.; methodology, O.A.P.; software, O.A.P.; validation, O.I.L. and G.A.G.; formal analysis, O.I.L. and G.A.G.; investigation, O.A.P.; resources, G.A.G.; data curation, O.I.L.; writing—original draft preparation, O.I.L. and G.A.G.; writing—review and editing, O.A.P. and G.A.G.; visualization, O.I.L. and O.A.P.; supervision, G.A.G.; project administration, G.A.G.; funding acquisition, G.A.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Russian Science Foundation, grant number 22-73-10009-P, https://rscf.ru/project/22-73-10009-P/. (accessed on 20 December 2025).

Data Availability Statement

Data is contained within the article or Supplementary Material.

Acknowledgments

The authors thank G.V. Girichev and A.V. Belyakov for their help in conducting the quantum chemical calculations on the computing resources of the Department of Physics of ISUCT and Saint Petersburg State Institute of Technology (Technical University).

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
UV–VisUltraviolet and visible
TD-DFTTime-dependent density functional theory
RECPsRelativistic electron core potentials
PCMPolarizable continuum model
RHFRestricted Hartree–Fock
CISDSingle and double excitations
LSQLeast squares method
LMCTLigand-metal charge transfer
HOMOHighest occupied molecular orbital
LUMOLowest unoccupied molecular orbital

References

  1. Đurović, M.D.; Bugarčić, Ž.D.; Van Eldik, R. Stability and Reactivity of Gold Compounds–From Fundamental Aspects to Applications. Coord. Chem. Rev. 2017, 338, 186–206. [Google Scholar] [CrossRef]
  2. Abdou, H.E.; Mohamed, A.A.; Fackler, J.P.; Burini, A.; Galassi, R.; López-de-Luzuriaga, J.M.; Olmos, M.E. Structures and Properties of Gold(I) Complexes of Interest in Biochemical Applications. Coord. Chem. Rev. 2009, 253, 1661–1669. [Google Scholar] [CrossRef]
  3. Che, C.-M.; Sun, R.W.-Y. Therapeutic Applications of Gold Complexes: Lipophilic Gold(Iii) Cations and Gold(i) Complexes for Anti-Cancer Treatment. Chem. Commun. 2011, 47, 9554. [Google Scholar] [CrossRef]
  4. Moreno-Alcántar, G.; Picchetti, P.; Casini, A. Gold Complexes in Anticancer Therapy: From New Design Principles to Particle-Based Delivery Systems. Angew. Chem. Int. Ed. 2023, 62, e202218000. [Google Scholar] [CrossRef]
  5. Richert, M.; Mikstacka, R.; Walczyk, M.; Cieślak, M.J.; Kaźmierczak-Barańska, J.; Królewska-Golińska, K.; Muzioł, T.M.; Biniak, S. Gold(I) Complexes with P-Donor Ligands and Their Biological Evaluation. Processes 2021, 9, 2100. [Google Scholar] [CrossRef]
  6. Glišić, B.Đ.; Djuran, M.I. Gold Complexes as Antimicrobial Agents: An Overview of Different Biological Activities in Relation to the Oxidation State of the Gold Ion and the Ligand Structure. Dalton Trans. 2014, 43, 5950–5969. [Google Scholar] [CrossRef] [PubMed]
  7. Ratia, C.; Sueiro, S.; Soengas, R.G.; Iglesias, M.J.; López-Ortiz, F.; Soto, S.M. Gold(III) Complexes Activity against Multidrug-Resistant Bacteria of Veterinary Significance. Antibiotics 2022, 11, 1728. [Google Scholar] [CrossRef] [PubMed]
  8. Zhang, Y.; Shareena Dasari, T.P.; Deng, H.; Yu, H. Antimicrobial Activity of Gold Nanoparticles and Ionic Gold. J. Environ. Sci. Health Part C 2015, 33, 286–327. [Google Scholar] [CrossRef]
  9. Elie, B.T.; Levine, C.; Ubarretxena-Belandia, I.; Varela-Ramírez, A.; Aguilera, R.J.; Ovalle, R.; Contel, M. Water-Soluble (Phosphane)Gold(I) Complexes–Applications as Recyclable Catalysts in a Three-Component Coupling Reaction and as Antimicrobial and Anticancer Agents. Eur. J. Inorg. Chem. 2009, 2009, 3421–3430. [Google Scholar] [CrossRef]
  10. Bayrakdar, T.A.C.A.; Scattolin, T.; Ma, X.; Nolan, S.P. Dinuclear Gold(i) Complexes: From Bonding to Applications. Chem. Soc. Rev. 2020, 49, 7044–7100. [Google Scholar] [CrossRef]
  11. Wróblewska, A.; Sadowski, M.; Jasiński, R. Selectivity and Molecular Mechanism of the Au(III)-Catalyzed [3+2] Cycloaddition Reaction between (Z)-C,N-Diphenylnitrone and Nitroethene in the Light of the Molecular Electron Density Theory Computational Study. Chem. Heterocycl. Compd. 2024, 60, 639–645. [Google Scholar] [CrossRef]
  12. Ta, C.; Reith, F.; Brugger, J.; Pring, A.; Lenehan, C.E. Analysis of Gold(I/III)-Complexes by HPLC-ICP-MS Demonstrates Gold(III) Stability in Surface Waters. Environ. Sci. Technol. 2014, 48, 5737–5744. [Google Scholar] [CrossRef]
  13. Brugger, J.; Liu, W.; Etschmann, B.; Mei, Y.; Sherman, D.M.; Testemale, D. A Review of the Coordination Chemistry of Hydrothermal Systems, or Do Coordination Changes Make Ore Deposits? Chem. Geol. 2016, 447, 219–253. [Google Scholar] [CrossRef]
  14. Mironov, I.V.; Tsvelodub, L.D. Chlorohydroxocomplexes of gold(III) in aqueous alkaline solutions. Zhurn. Neorg. Khim. 2000, 45, 706–711. [Google Scholar]
  15. Usher, A.; McPhail, D.C.; Brugger, J. A Spectrophotometric Study of Aqueous Au(III) Halide–Hydroxide Complexes at 25–80 °C. Geochim. Cosmochim. Acta 2009, 73, 3359–3380. [Google Scholar] [CrossRef]
  16. Đurović, M.D.; Puchta, R.; Bugarčić, Ž.D.; Van Eldik, R. Studies on the Reactions of [AuCl4]− with Different Nucleophiles in Aqueous Solution. Dalton Trans. 2014, 43, 8620–8632. [Google Scholar] [CrossRef] [PubMed]
  17. Vasic, V.; Premovic, S.; Cakar, M.; Radak, B.; Milovanovic, G. Spectrophotometric Investigations of the Reaction between Gold(III) and Potassium Iodide. J. Serbian Chem. Soc. 2000, 65, 345–352. [Google Scholar] [CrossRef]
  18. Zavalishin, M.N.; Pimenov, O.A.; Belov, K.V.; Khodov, I.A.; Gamov, G.A. Chemical Equilibria in Aqueous Solutions of H[AuCl4] and Bovine or Human Serum Albumin. J. Mol. Liq. 2023, 389, 122914. [Google Scholar] [CrossRef]
  19. Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
  20. Scalmani, G.; Frisch, M.J.; Mennucci, B.; Tomasi, J.; Cammi, R.; Barone, V. Geometries and Properties of Excited States in the Gas Phase and in Solution: Theory and Application of a Time-Dependent Density Functional Theory Polarizable Continuum Model. J. Chem. Phys. 2006, 124, 094107. [Google Scholar] [CrossRef]
  21. Figgen, D.; Rauhut, G.; Dolg, M.; Stoll, H. Energy-Consistent Pseudopotentials for Group 11 and 12 Atoms: Adjustment to Multi-Configuration Dirac–Hartree–Fock Data. Chem. Phys. 2005, 311, 227–244. [Google Scholar] [CrossRef]
  22. Peterson, K.A.; Puzzarini, C. Systematically Convergent Basis Sets for Transition Metals. II. Pseudopotential-Based Correlation Consistent Basis Sets for the Group 11 (Cu, Ag, Au) and 12 (Zn, Cd, Hg) Elements. Theor. Chem. Acc. 2005, 114, 283–296. [Google Scholar] [CrossRef]
  23. Peterson, K.A.; Figgen, D.; Goll, E.; Stoll, H.; Dolg, M. Systematically Convergent Basis Sets with Relativistic Pseudopotentials. II. Small-Core Pseudopotentials and Correlation Consistent Basis Sets for the Post-d Group 16–18 Elements. J. Chem. Phys. 2003, 119, 11113–11123. [Google Scholar] [CrossRef]
  24. Dunning, T.H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
  25. Woon, D.E.; Dunning, T.H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. III. The Atoms Aluminum through Argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
  26. Lu, Y.; Wang, Z.; Wang, F. Error of Relativistic Effective Core Potentials for Closed-Shell Diatomic Molecules of p-Block Heavy and Superheavy Elements in DFT and TDDFT Calculations. J. Chem. Phys. 2023, 159, 244107. [Google Scholar] [CrossRef] [PubMed]
  27. Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
  28. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  29. Roothaan, C.C.J. New Developments in Molecular Orbital Theory. Rev. Mod. Phys. 1951, 23, 69–89. [Google Scholar] [CrossRef]
  30. Pople, J.A.; Seeger, R.; Krishnan, R. Variational Configuration Interaction Methods and Comparison with Perturbation Theory. Int. J. Quantum Chem. 1977, 12, 149–163. [Google Scholar] [CrossRef]
  31. Chemcraft-Graphical Program for Visualization of Quantum Chemistry Computations. Available online: https://www.chemcraftprog.com/ (accessed on 18 April 2023).
  32. Meshkov, A.N.; Gamov, G.A. KEV: A Free Software for Calculating the Equilibrium Composition and Determining the Equilibrium Constants Using UV–Vis and Potentiometric Data. Talanta 2019, 198, 200–205. [Google Scholar] [CrossRef]
  33. Pouradier, J.; Coquard, M. Électrochimie Des Sels d’or: V.—Complexes Mixtes Aurichlorobromure. J. Chim. Phys. 1966, 63, 1072–1078. [Google Scholar] [CrossRef]
  34. Peshchevitskii, B.I.; Belevantsev, V.I. Constants of substitution of Cl− by Br− in [AuCl4]−. Zhurn. Neorg. Khim. 1967, 12, 312–318. [Google Scholar]
  35. Almgren, L.; Nicholson, D.G.; Kimland, B.; Enzell, C.R.; Lousberg, R.J.J.C.; Weiss, U. The Stability Constants of Mixed Chloro-Bromo-Aurate(III) Complexes. Acta Chem. Scand. 1971, 25, 3713–3720. [Google Scholar] [CrossRef]
  36. Elding, L.I.; Gröning, A.-B.; Summerville, D.A.; Almenningen, A.; Bastiansen, O.; Fernholt, L.; Gundersen, G.; Nielsen, C.J.; Cyvin, B.N.; Cyvin, S.J. Kinetics, Mechanism and Equilibria for Halide Substitution Processes of Chloro Bromo Complexes of Gold(III). Acta Chem. Scand. 1978, 32a, 867–877. [Google Scholar] [CrossRef]
  37. Tsuchida, R. Absorption Spectra of Co-Ordination Compounds. I. Bull. Chem. Soc. Jpn. 1938, 13, 388–400. [Google Scholar] [CrossRef]
  38. Stammreich, H.; Forneris, R. Raman Spectra and Force Constants of Planar Square Molecules of the Type AB4. Spectrochim. Acta 1960, 16, 363–367, E9. [Google Scholar] [CrossRef]
  39. Mason, W.R.; Gray, H.B. Electronic Structures and Spectra of Square-Planar Gold(III) Complexes. Inorg. Chem. 1968, 7, 55–58. [Google Scholar] [CrossRef]
  40. Makotchenko, E.V.; Baidina, I.A.; Korol’kov, I.V. Structure of Diethylenetriammonium Tetrabromoaurates(III). J. Struct. Chem. 2014, 55, 887–894. [Google Scholar] [CrossRef]
  41. Efremov, A.N.; Sharutin, V.V.; Sharutina, O.K.; Andreev, P.V.; Eltsov, O.S. Synthesis and Structure of Methyltriphenylphosphonium Dicyanodibromoaurate [Ph3PCH3] [Au(CN)2Br2]. IVKKT 2020, 63, 10–15. [Google Scholar] [CrossRef]
  42. Dubinskii, V.I.; Shul’man, V.M.; Peshchevitskii, B.I. Stability of Tetrachloroaurate(III) and Tetrabromoaurate(III) in Aqueous Solution. Zhurn. Neorg. Khim. 1968, 13, 64–67. [Google Scholar]
  43. Louw, W.J.; Robb, W. Kinetics and Mechanisms of Reactions of Gold(III) Complexes. II. The Formation and Equilibrium Hydrolysis of Tetrabromoaurate(III). Inorg. Chim. Acta 1974, 9, 33–37. [Google Scholar] [CrossRef]
  44. Isart, C.; Burés, J.; Vilarrasa, J. Electrospray Ionization Mass Spectra of the Reactions of NaAuBr 4 and Related Aurates with Nucleophiles: JMS Letters. J. Mass Spectrom. 2014, 49, 331–334. [Google Scholar] [CrossRef] [PubMed]
  45. Skibsted, L.H.; Bjerrum, J.; Frederichsen, P.S.; Nakken, K.F. Studies on Gold Complexes. I. Robustness, Stability and Acid Dissociation of the Tetramminegold(III) Ion. Acta Chem. Scand. 1974, 28, 740–746. [Google Scholar] [CrossRef]
  46. Mironov, I.V. About the Stability of Au(NH3) 4 3+ in Aqueous Solution. Russ. J. Inorg. Chem. 2008, 53, 655–659. [Google Scholar] [CrossRef]
  47. Mironov, I.V.; Tsvelodub, L.D. Equilibria of Cl- substitution by ammonia, ethylenediamine, diethylenetriamine in AuCl4-complex in aqueous solution. Zhurn. Neorg. Khim. 2000, 45, 425–430. [Google Scholar]
  48. Ventegodt, J.; Øby, B.; Skibsted, L.H.; Dietzsch, W.; Hoyer, E. Amineanionogold(III) Complexes. V. Kinetics of the Consecutive Substitutions of Ammonia by Chloride in Tetraamminegold(III) Ion in Acidic Aqueous Solution. Acta Chem. Scand. 1985, 39a, 453–463. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Article metric data becomes available approximately 24 hours after publication online.
Download PDF
Determination of Energy Interaction Parameters for the UNIFAC Model Based on Solvent Activity Coefficients in Benzene–D2EHPA and Toluene–D2EHPA Systems
Previous