Experimental Methods and Nonlinear Optical Properties of Open-Shell Molecular Species
Abstract
1. Introduction
2. Theoretical Basis of Measurements of the Nonlinear Optical Properties of Molecules
2.1. Polarization and Optical Response of Materials
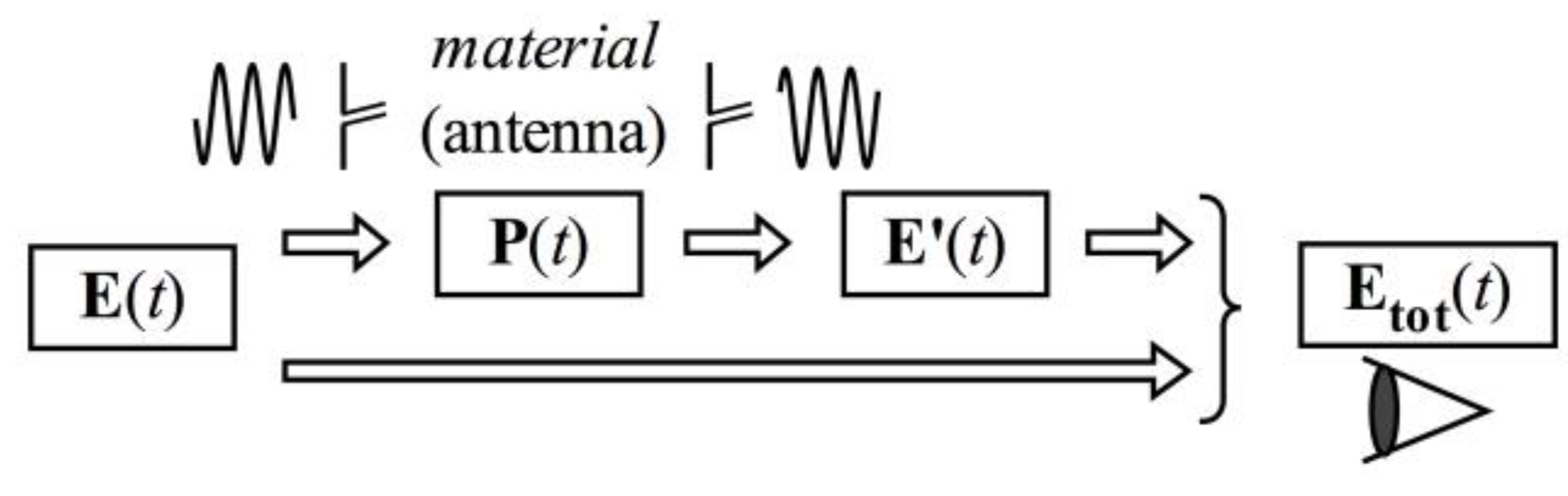
2.2. Linear and Nonlinear Polarizations
2.3. Third-Order Optical Nonlinearity
2.3.1. Macroscopic Third-Order Optical Nonlinearity
2.3.2. Microscopic Third-Order Optical Nonlinearity
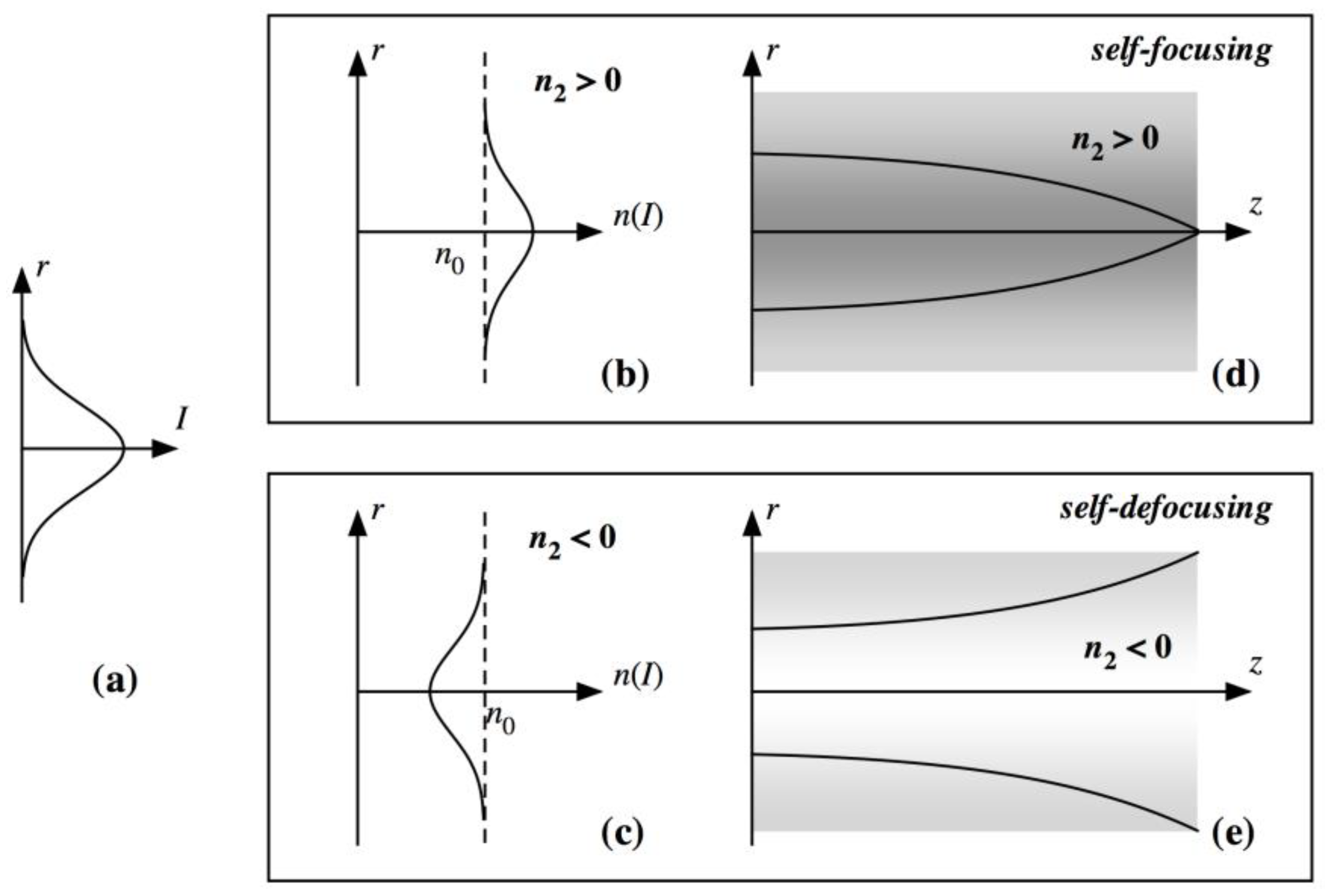
2.4. Nonlinear Index of Refraction
2.5. Two-Photon Absorption
2.5.1. Macroscopic Treatment
2.5.2. Microscopic Treatment
2.6. Relation Between TPA Coefficient and Third-Order Susceptibility
3. Measurement Techniques
3.1. Overview of Degenerate Third-Order Nonlinearity Measurement Techniques
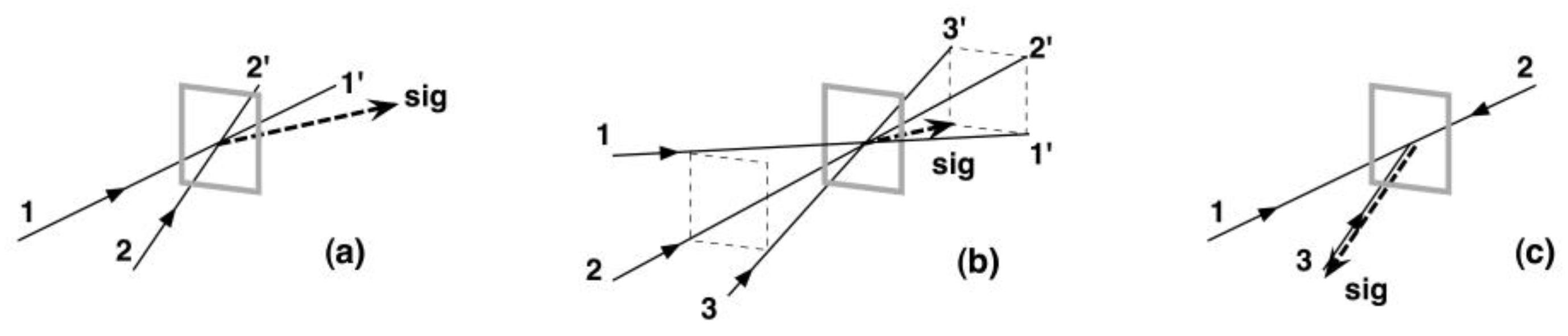
3.1.1. Degenerate Four-Wave Mixing (DFWM)
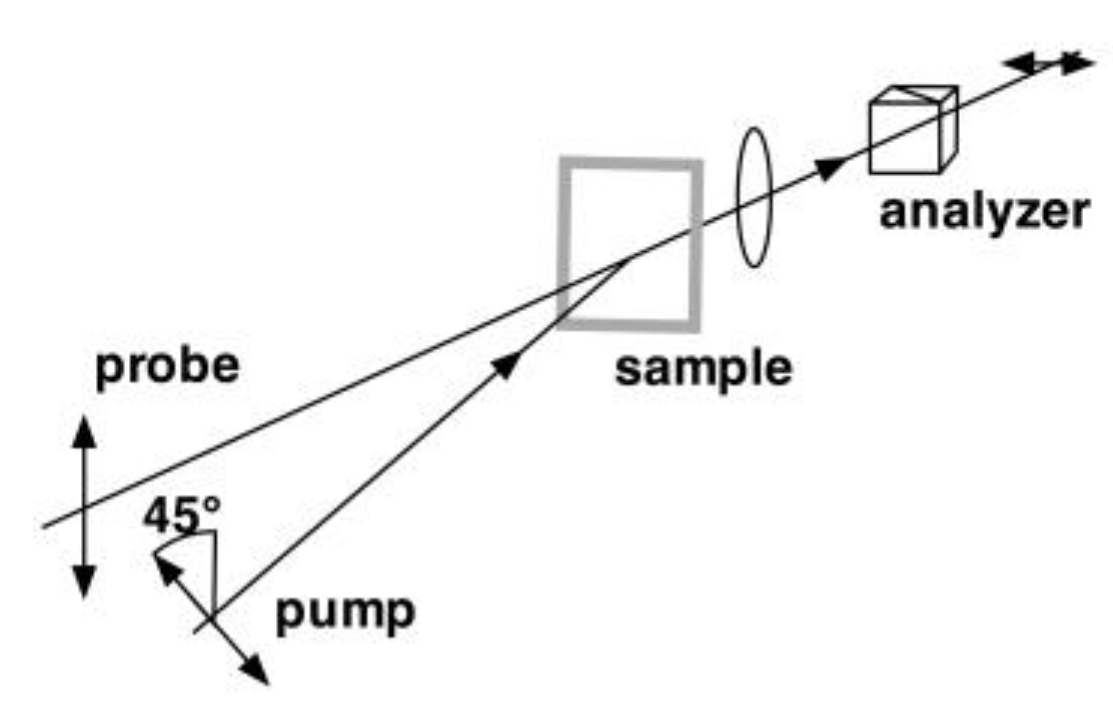
3.1.2. Optical Kerr Effect (OKE)
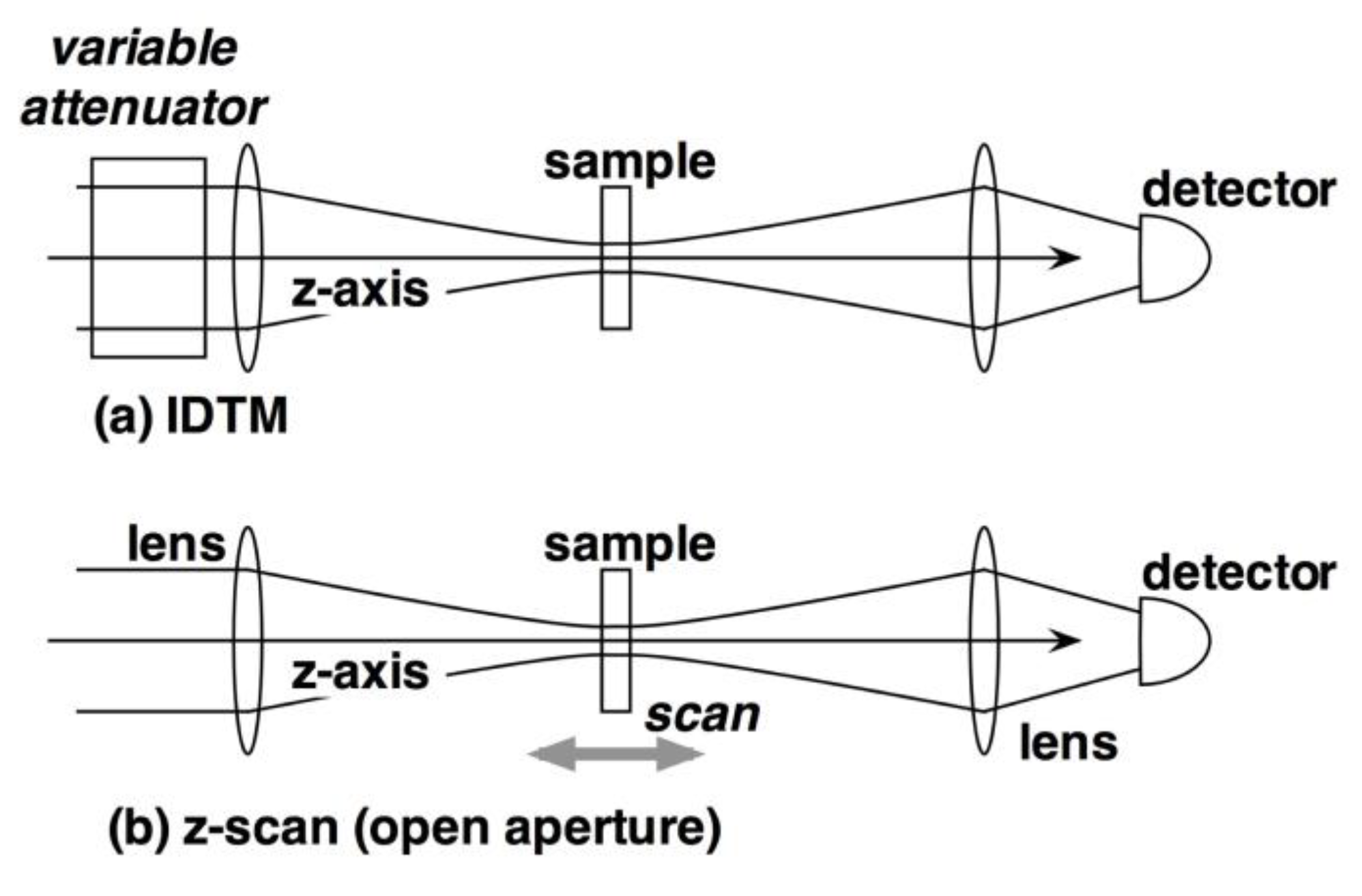
3.1.3. Intensity-Dependent Transmittance Measurement (IDTM) and Open-Aperture Z-Scan
3.2. Nonlinear Absorption Measurements Using the Open-Aperture Z-Scan Method
3.2.1. Dependence of Optical Intensity Along Z-Axis
3.2.2. Transmittance Through TPA Media
3.2.3. Relation Between Optical Power and Intensity
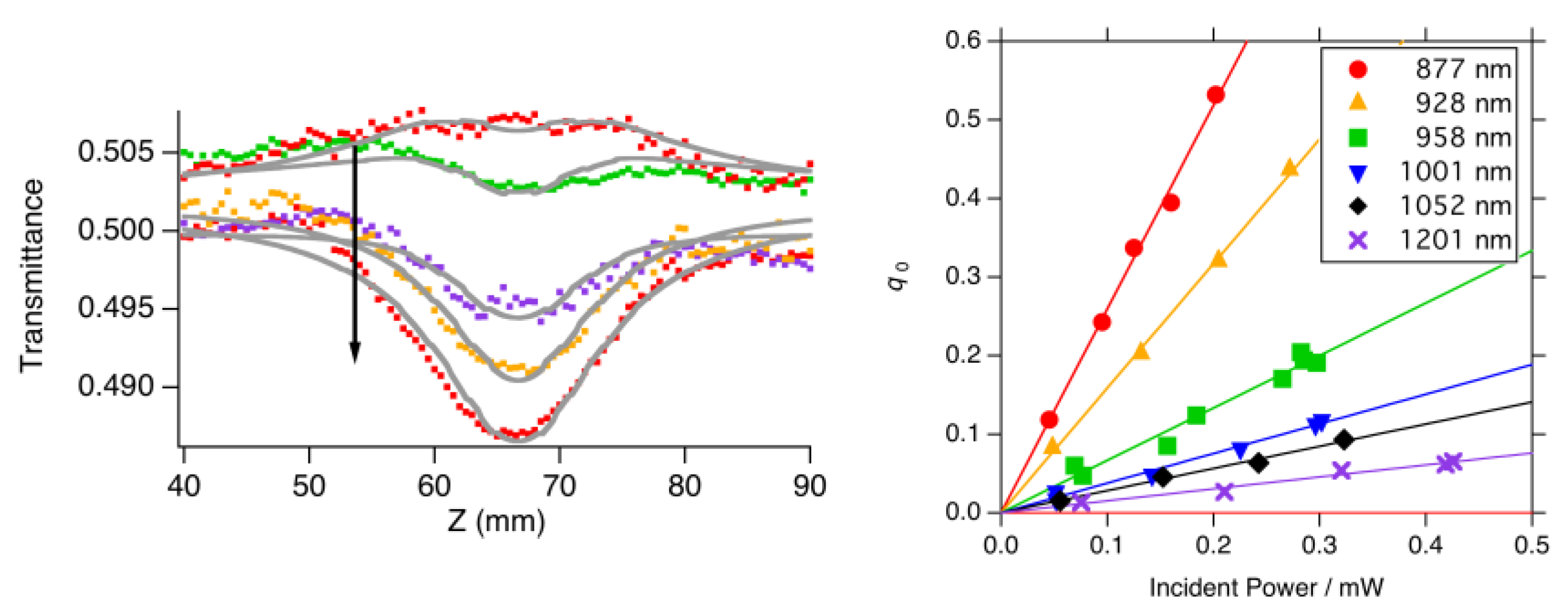
3.3. Experimental Details and Data Analysis of the Open-Aperture Z-Scan Method
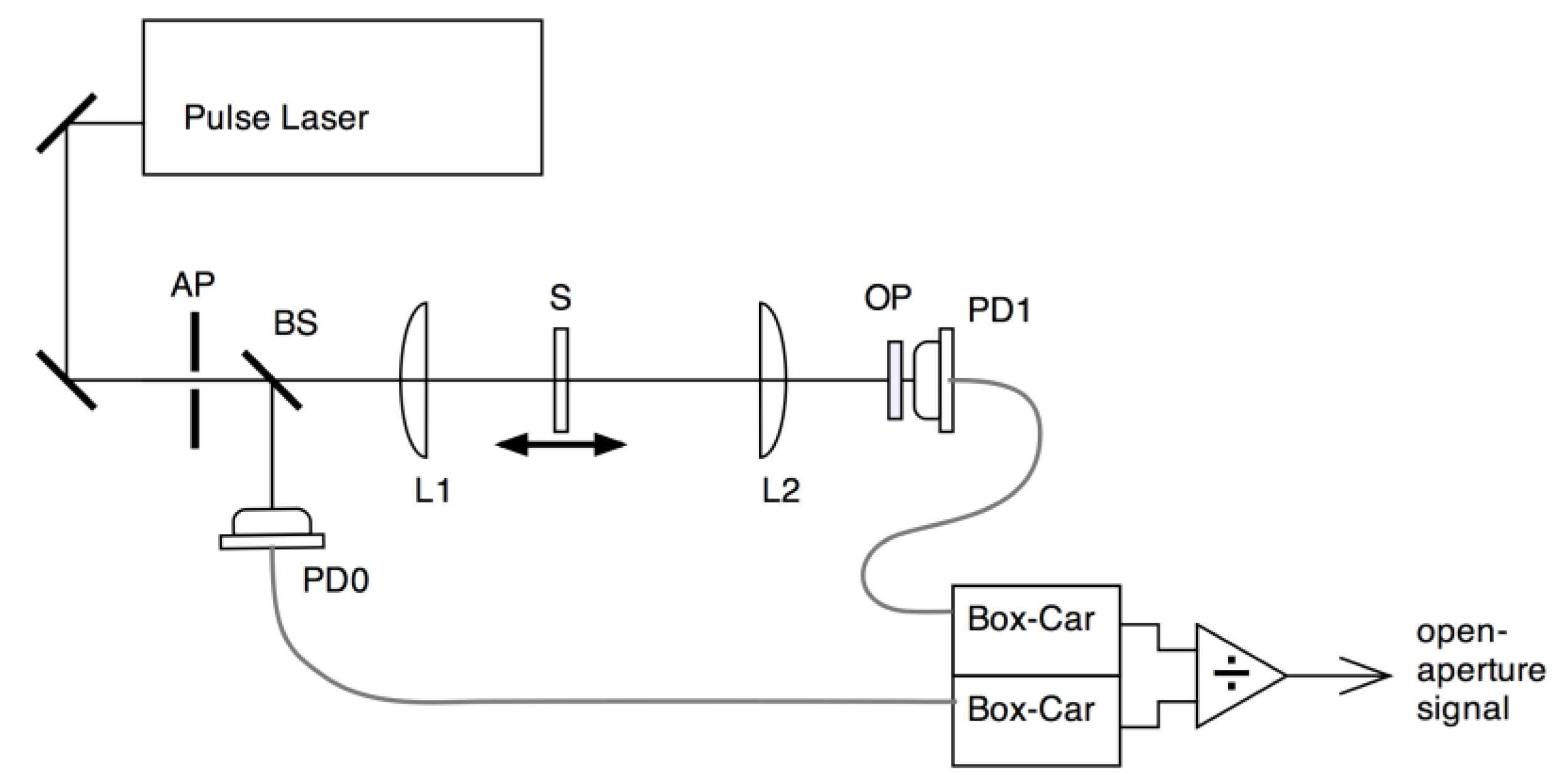
3.3.1. Optical Setup
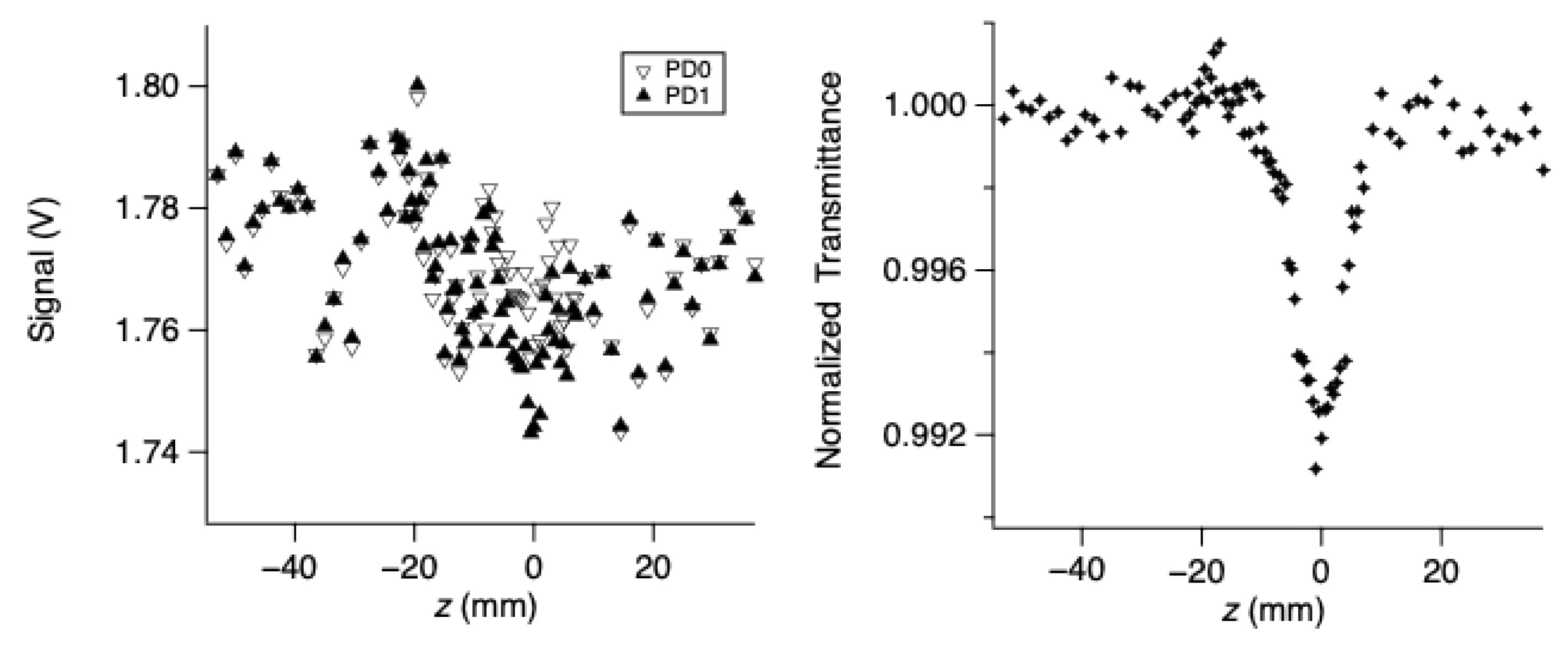
3.3.2. Signal Processing
3.3.3. Sample
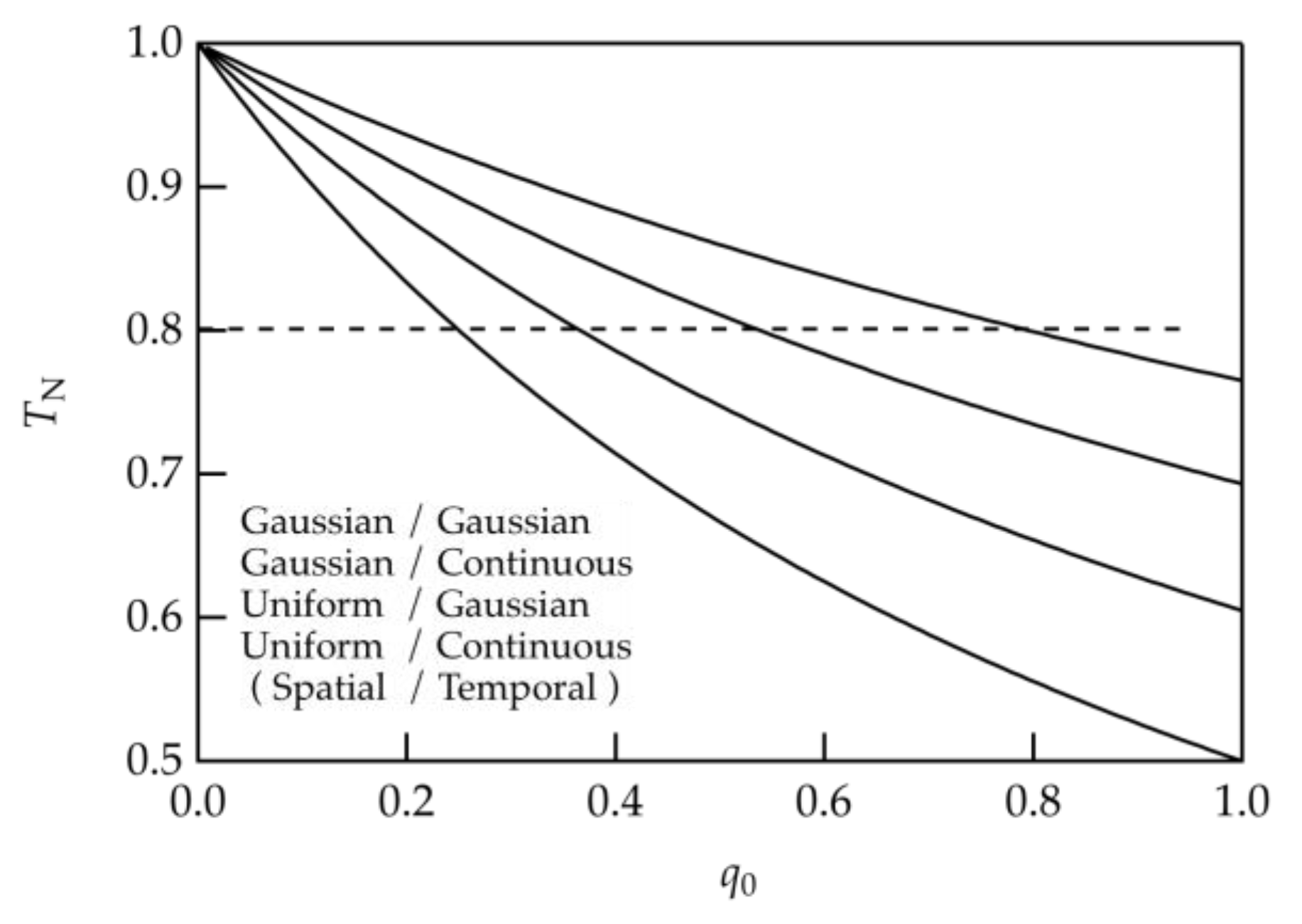
3.3.4. Range of the Scan
3.3.5. Incident Power
3.3.6. Laser Pulse Width
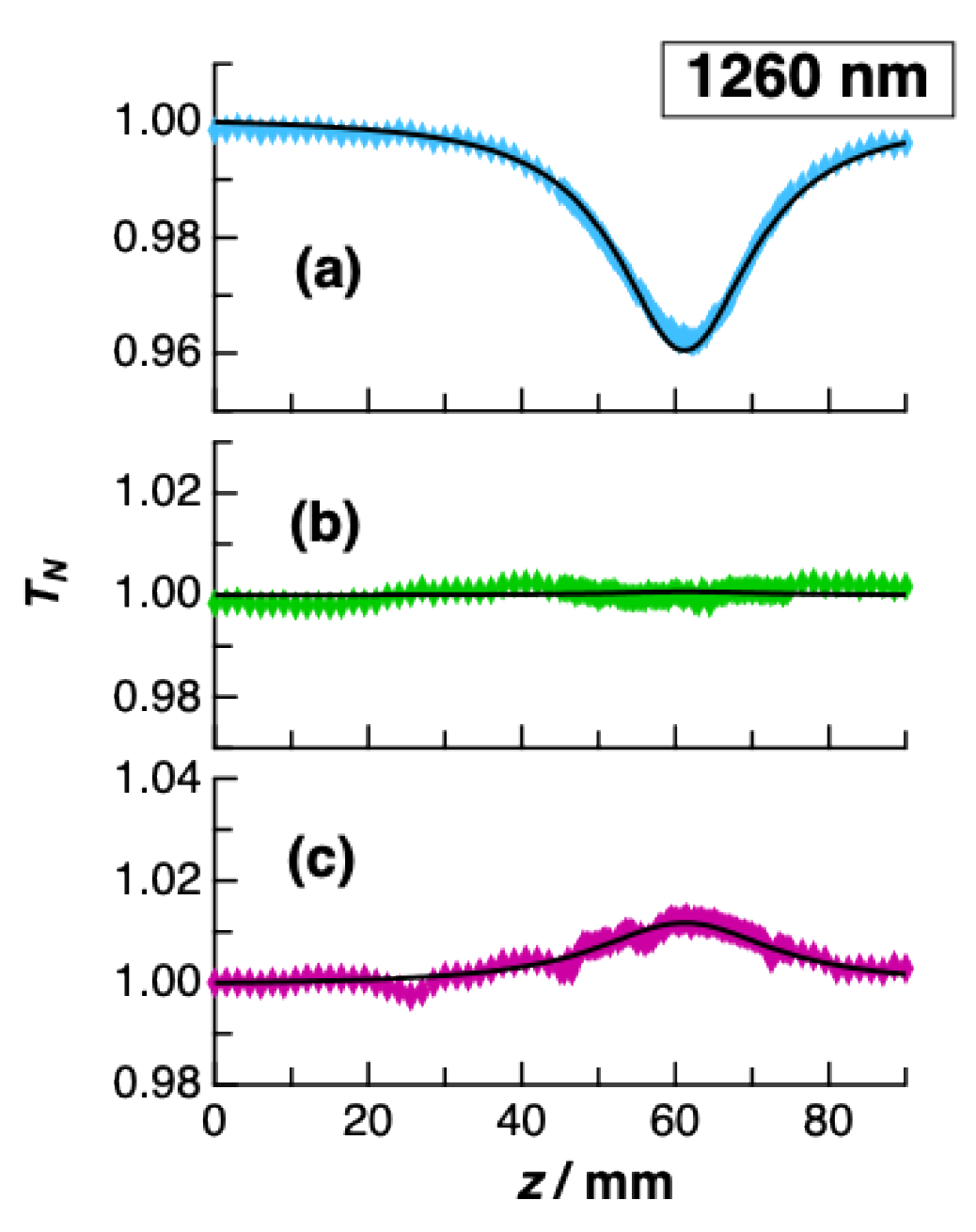
3.4. Measurement of TPA Coexistenting with Saturable Absorption by the Open-Aperture Z-Scan Method
4. Two-Photon Absorption Properties of Singlet Diradicaloids
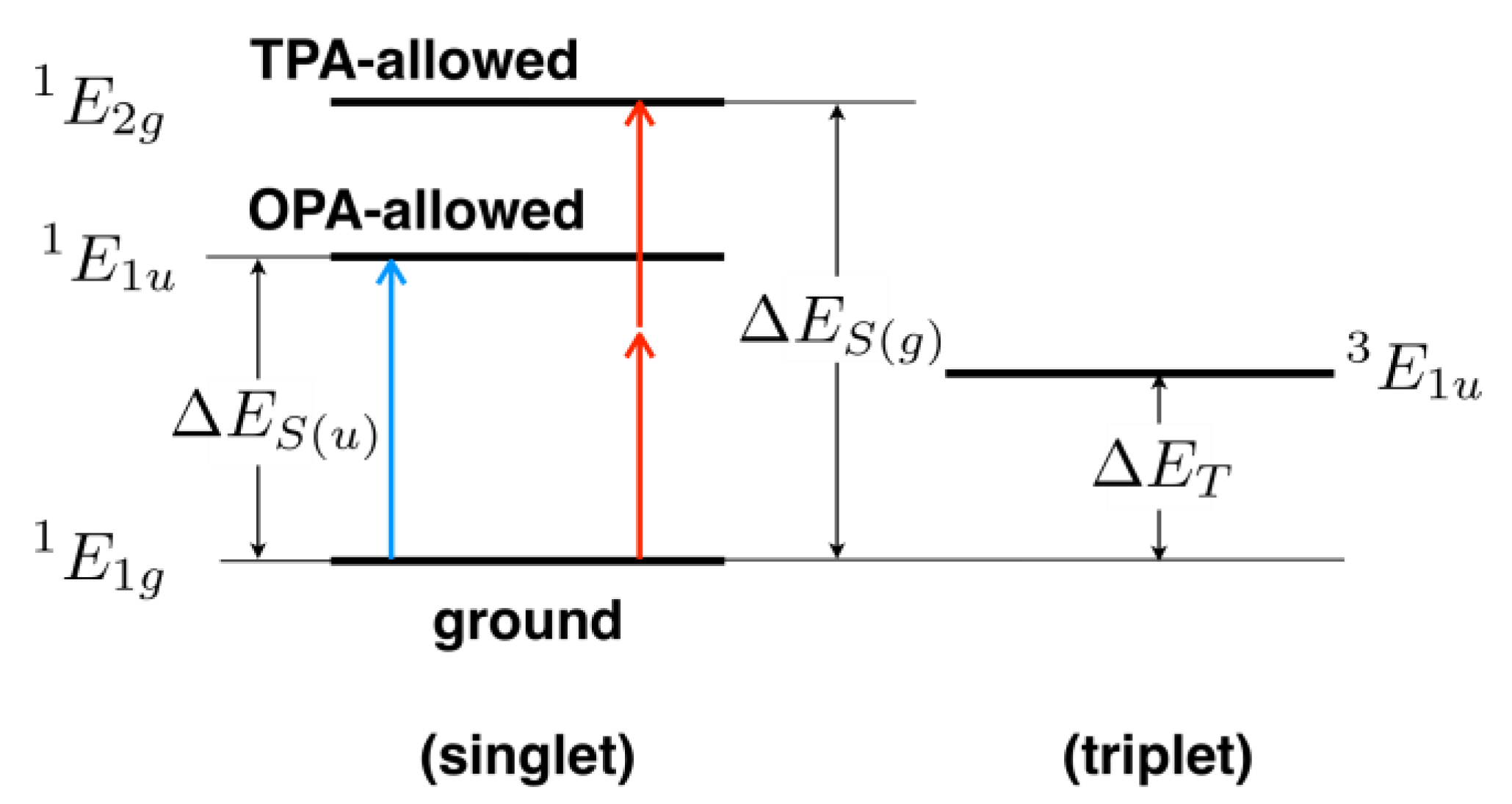
4.1. Two-Photon Absorption and Electronic Excited States
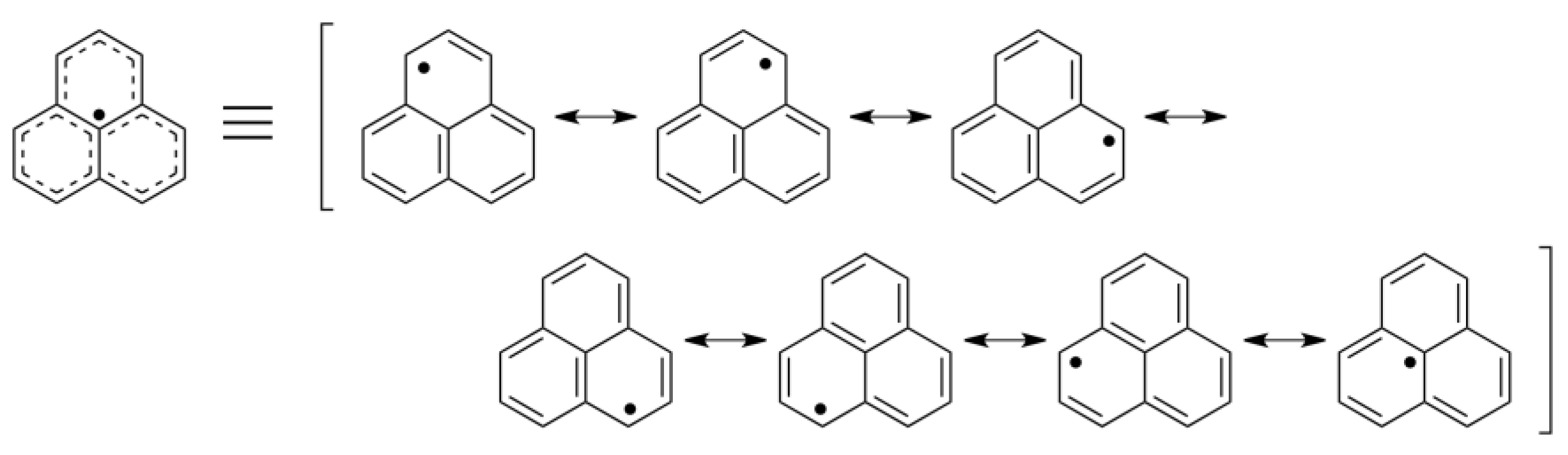
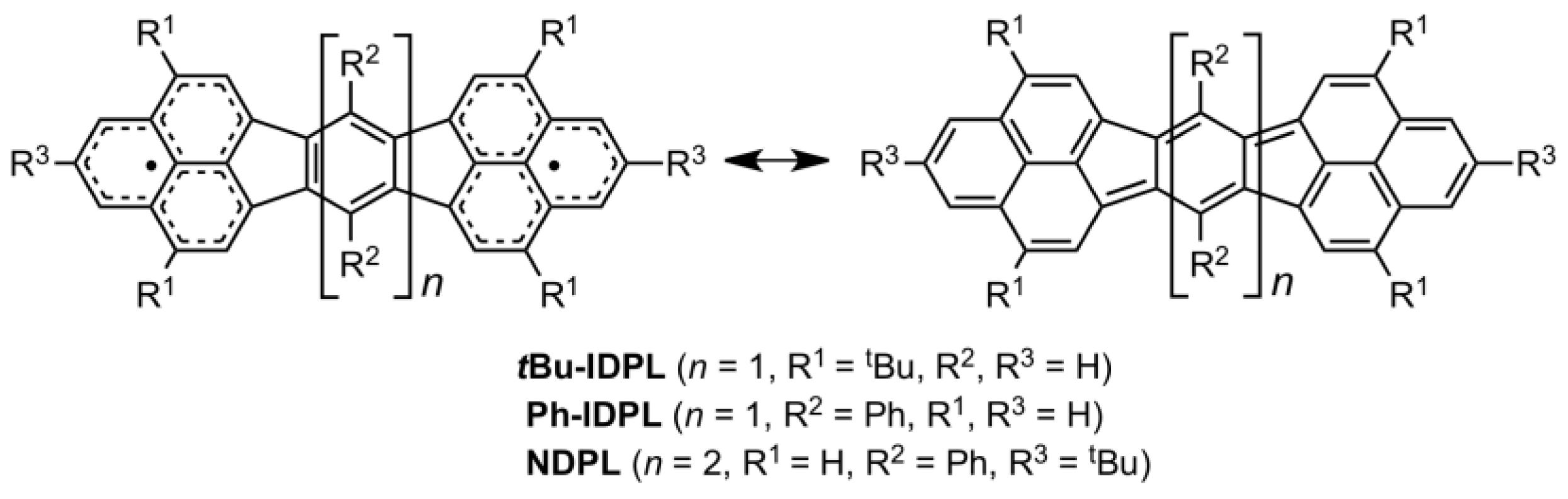
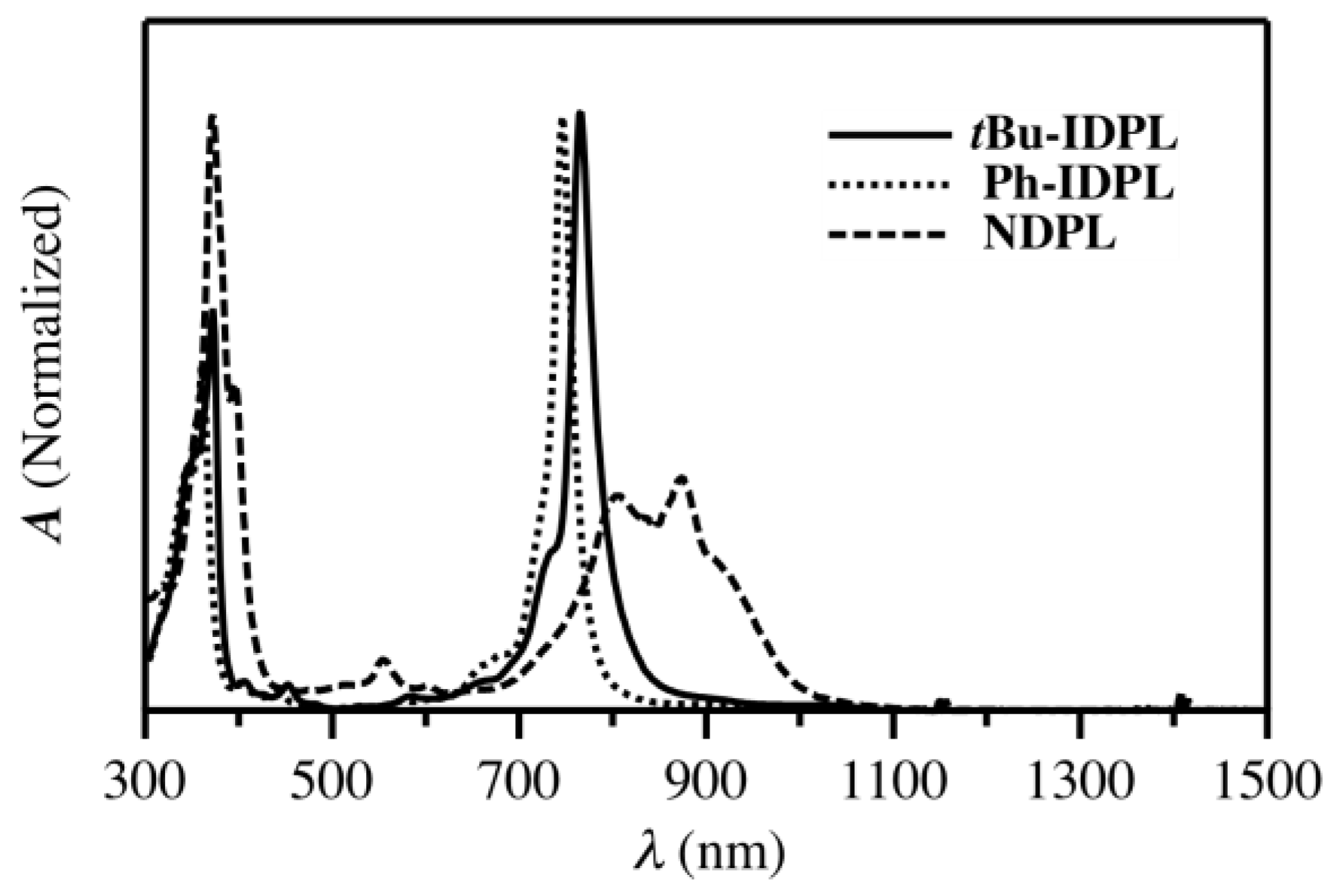
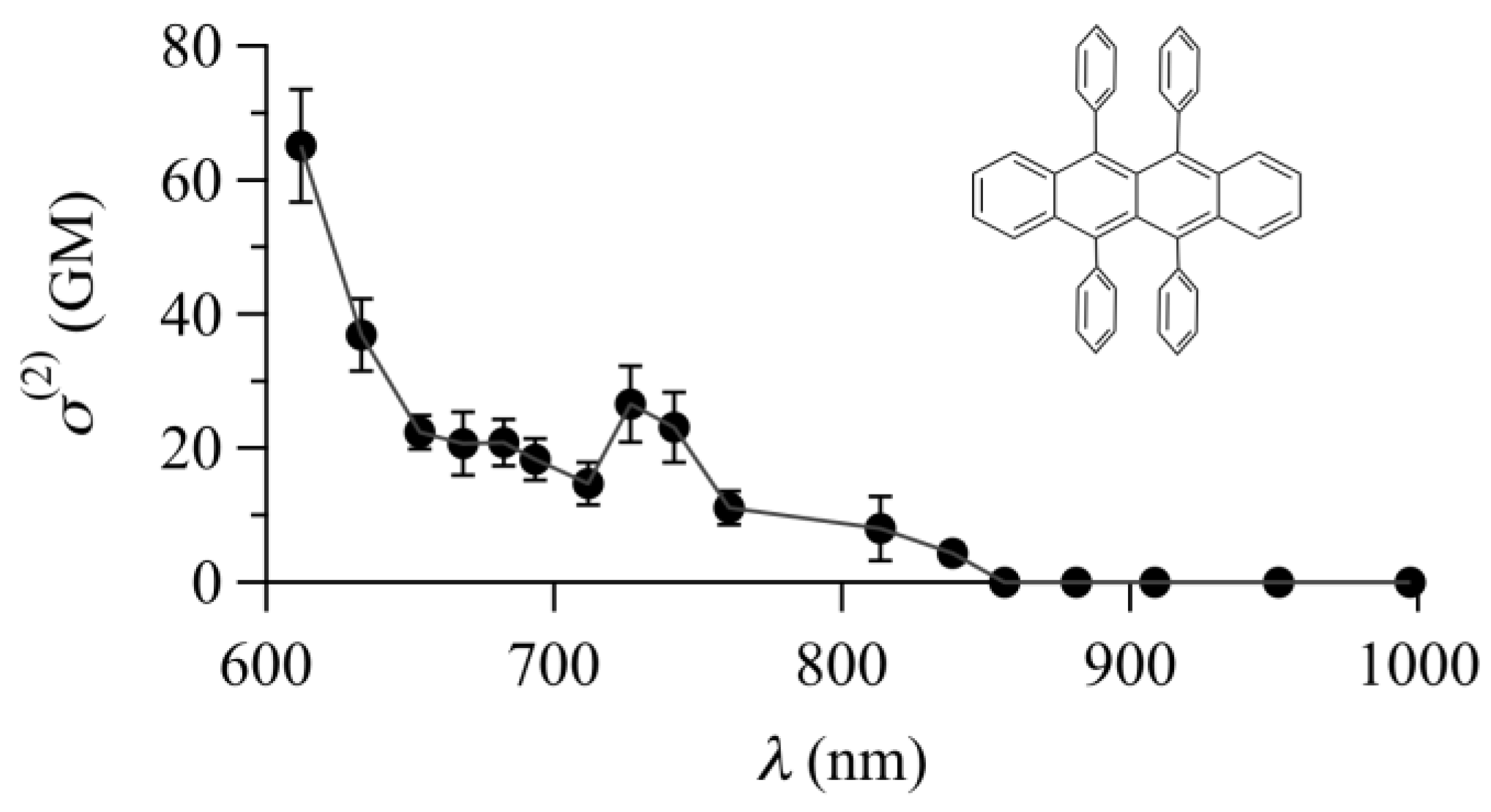
4.2. Bis(phenalenyl) Derivatives
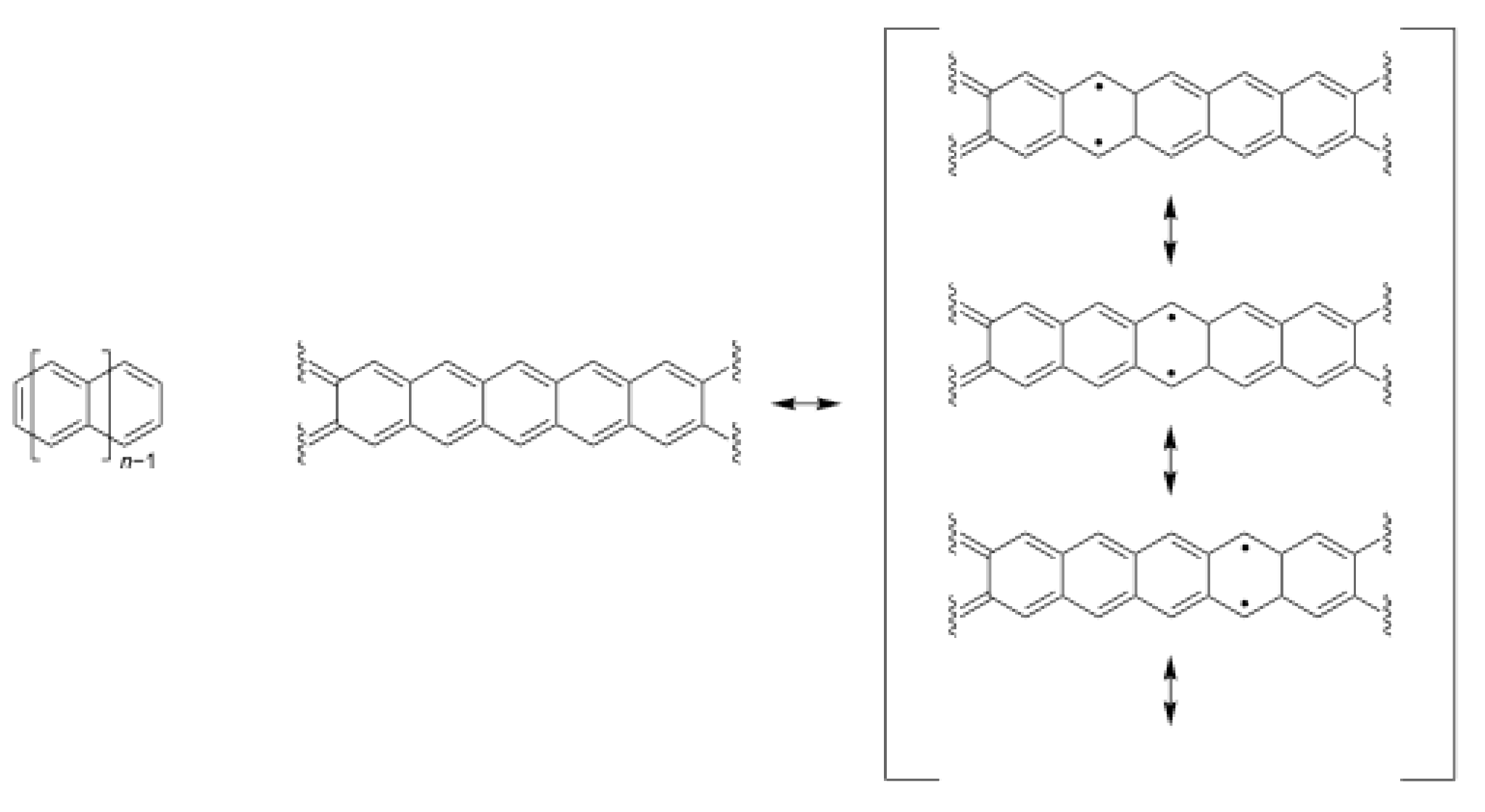
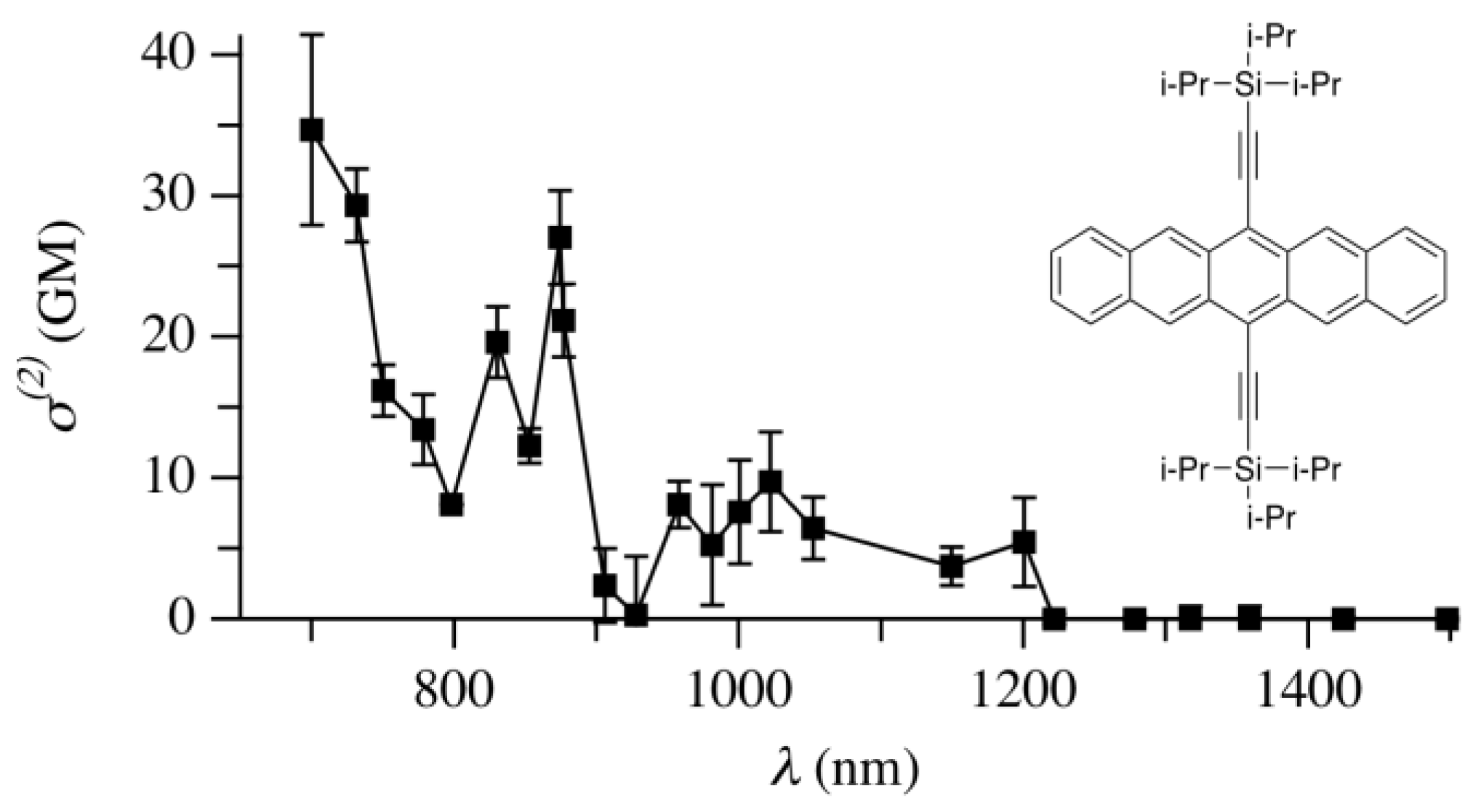
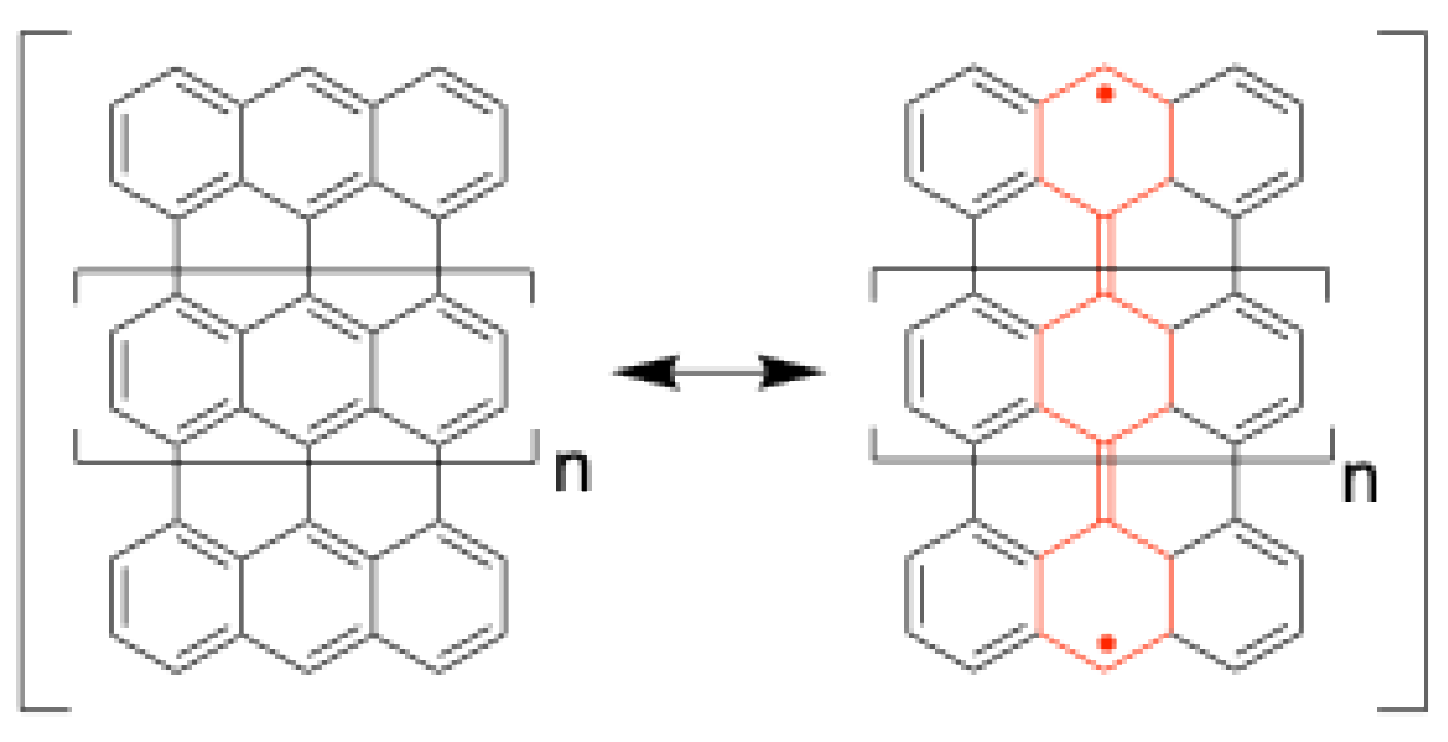
4.3. Oligoacenes
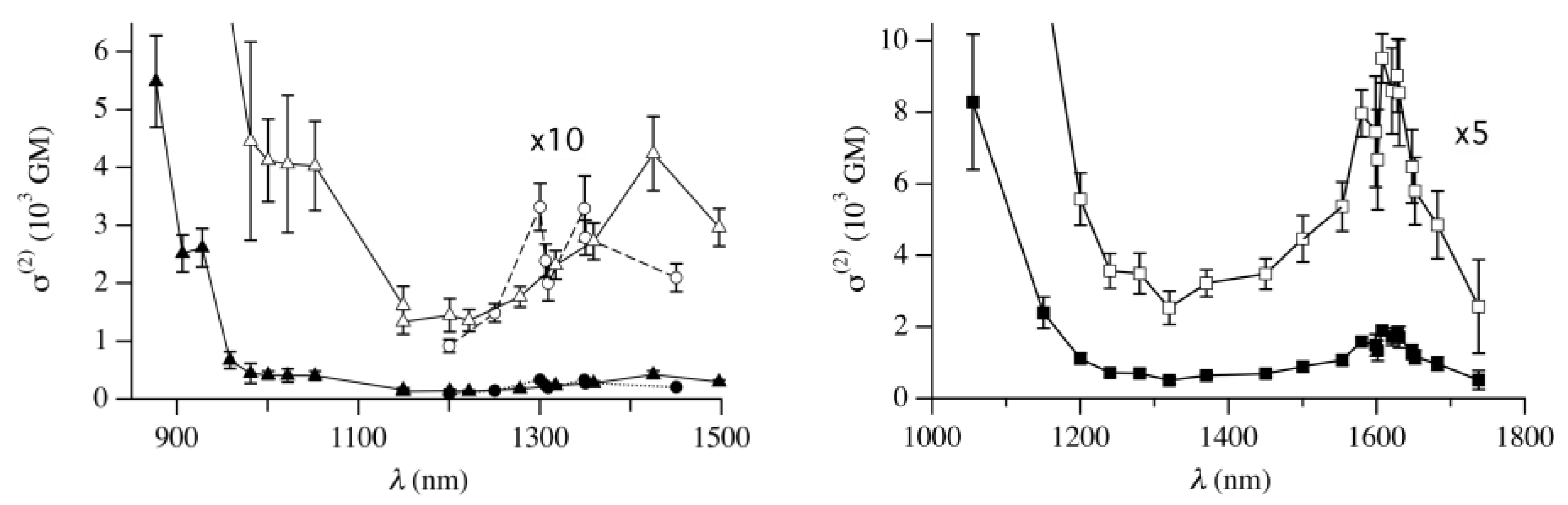
4.4. Zethrenes
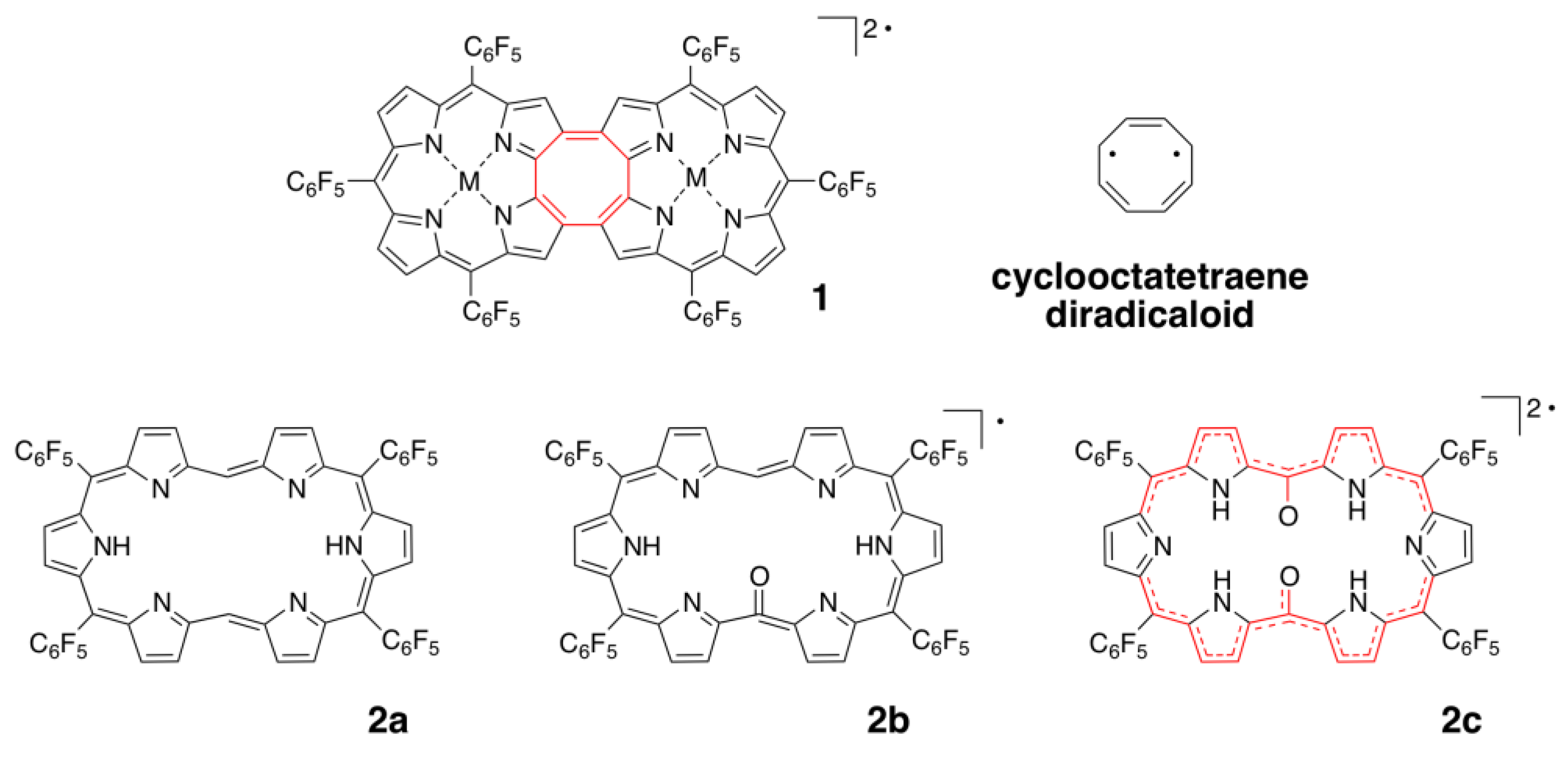
4.5. Porphyrinoids
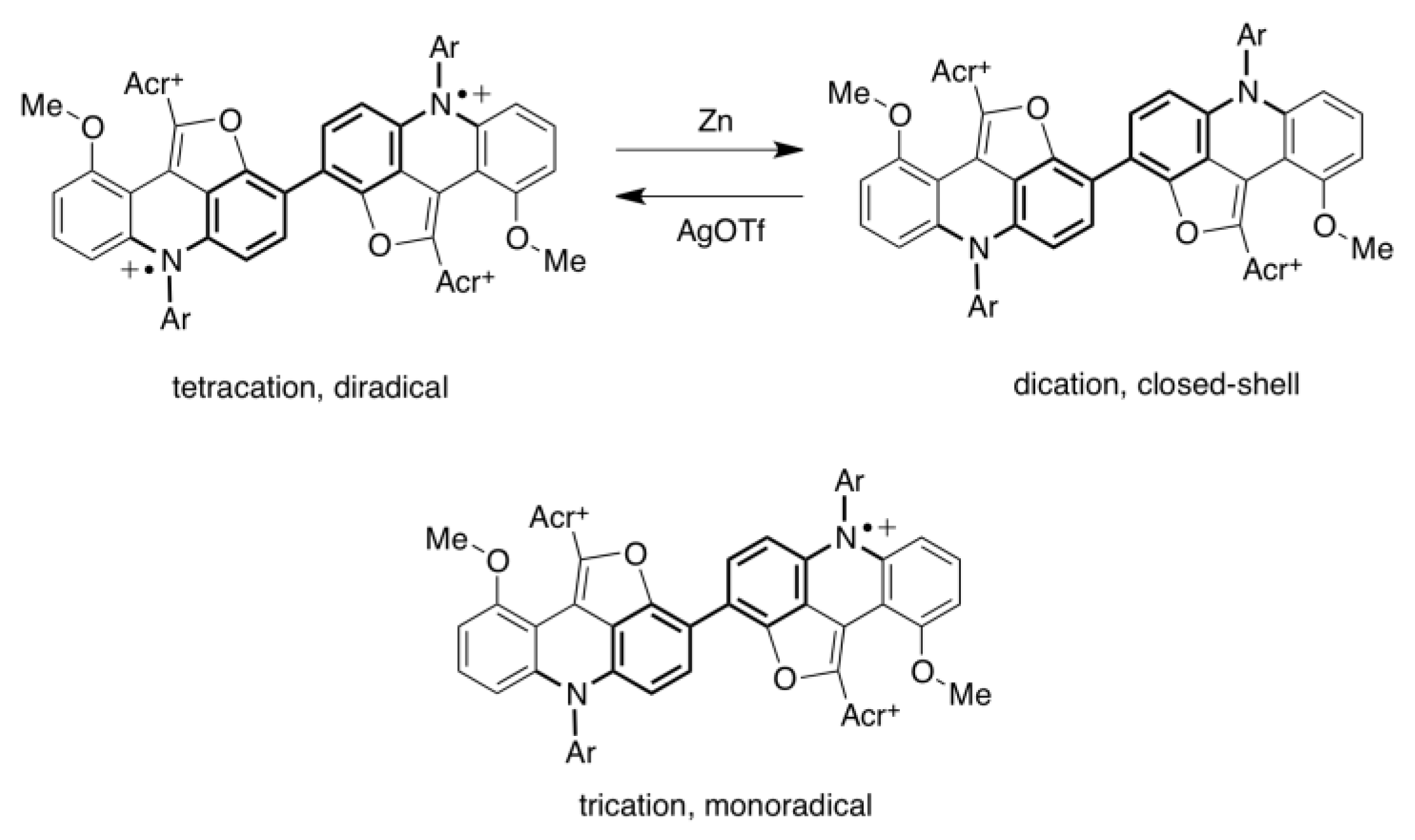
4.6. Bis(acridine) Dimer—Chemical Switching of Diradical Character
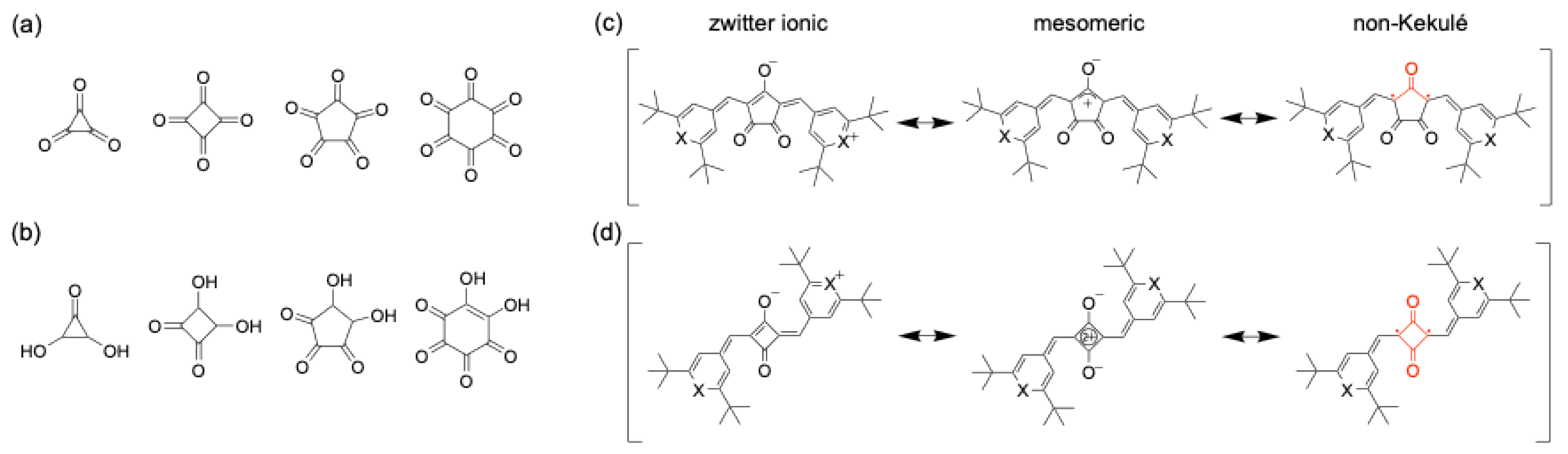
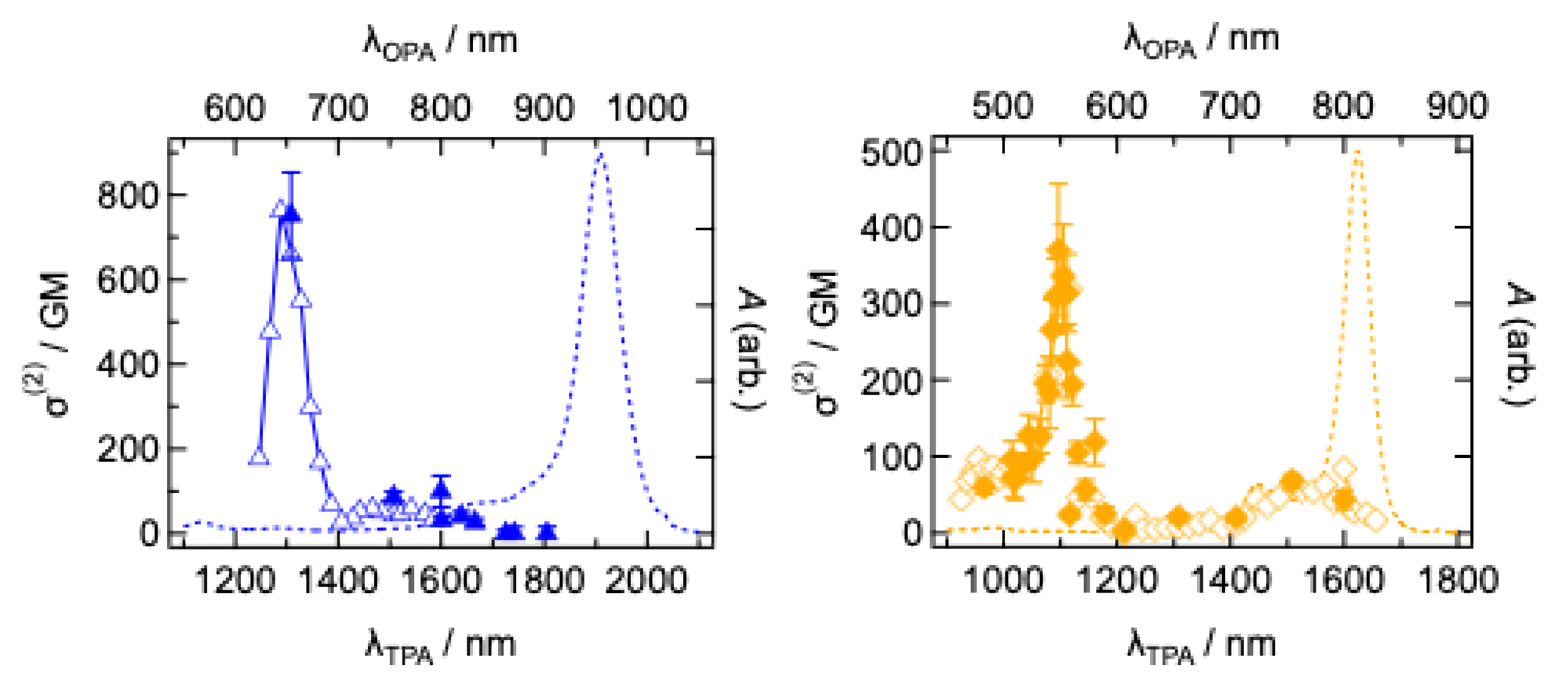
4.7. Oxocarbons
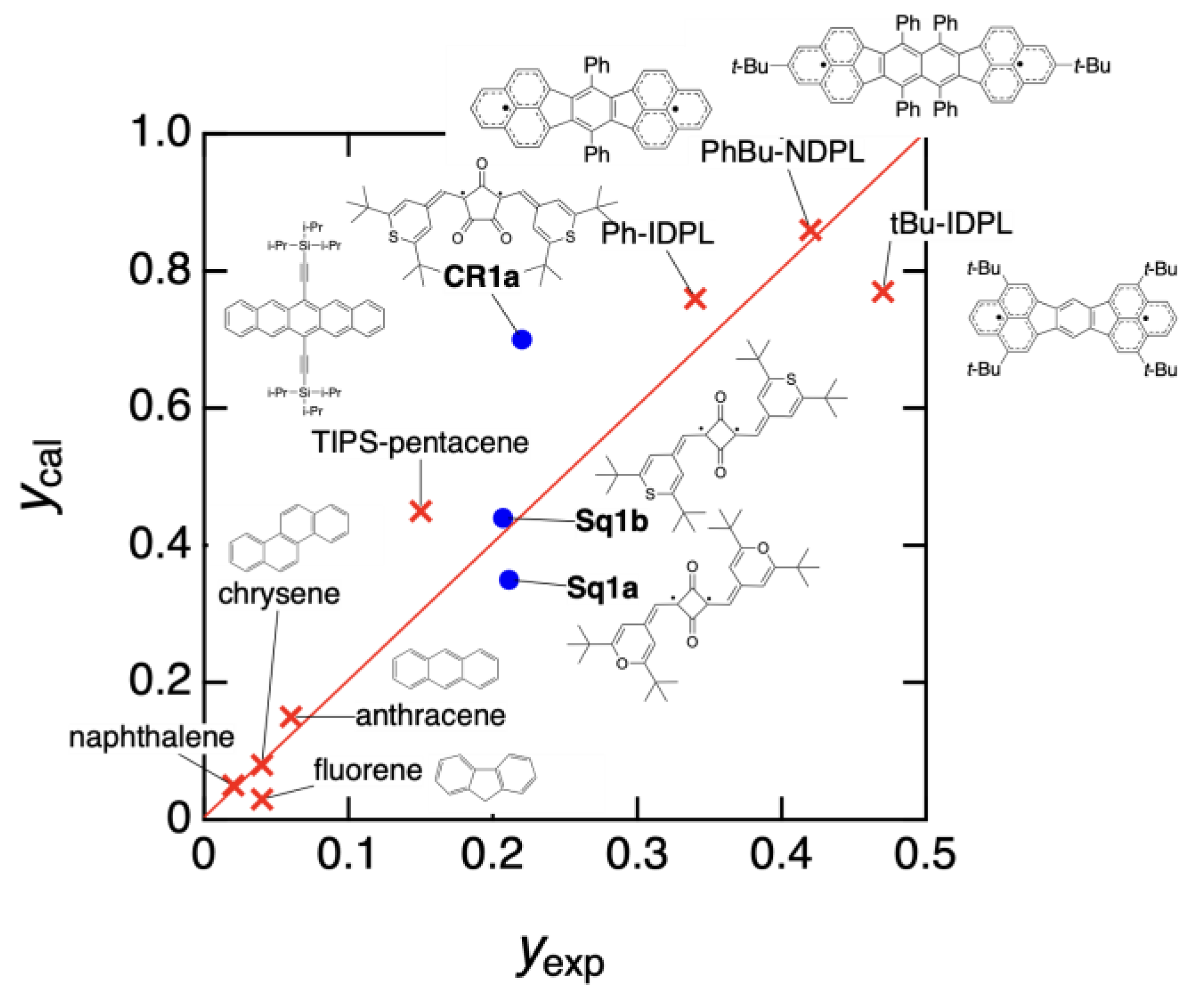
4.8. TPA Cross-Section and Transition Wavelength
4.9. Diradical Parameter from Experimentally Available Values
5. Conclusions
Funding
Conflicts of Interest
References
- Wu, J.; Li, Z.A.; Luo, J.; Jen, A.K.Y. High-performance organic second- and third-order nonlinear optical materials for ultrafast information processing. J. Mater. Chem. C 2020, 8, 15009–15026. [Google Scholar] [CrossRef]
- Cumpston, B.H. Two-photon polymerization initiators for three-dimensional optical data storage and microfabrication. Nature 1999, 398, 51–54. [Google Scholar] [CrossRef]
- Kawata, S.; Sun, H.B.; Tanaka, T.; Takada, K. Finer features for functional microdevices. Nature 2001, 412, 697–698. [Google Scholar] [CrossRef]
- Denk, W.; Strickler, J.H.; Webb, W.W. Two-photon laser scanning fluorescence microscopy. Science 1990, 248, 73–76. [Google Scholar] [CrossRef]
- Kawata, S.; Kawata, Y. Three-dimensional optical data storage using photochromic materials. Chem. Rev. 2000, 100, 1777–1788. [Google Scholar] [CrossRef]
- Pascal, S.; David, S.; Andraud, C.; Maury, O. Near-infrared dyes for two-photon absorption in the short-wavelength infrared: Strategies towards optical power limiting. Chem. Soc. Rev. 2021, 50, 6613–6658. [Google Scholar] [CrossRef]
- Senge, M.O.; Fazekas, M.; Notaras, E.G.A.; Blau, W.J.; Zawadzka, M.; Locos, O.B.; Ni Mhuircheartaigh, E.M. Nonlinear optical properties of porphyrins. Adv. Mater. 2007, 19, 2737–2774. [Google Scholar] [CrossRef]
- Yariv, A. Quantum Electronics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1988; pp. 106–135. [Google Scholar]
- Shen, Y.R. The Principles of Nonlinear Optics; John Wiley & Sons: New York, NY, USA, 1984. [Google Scholar]
- Boyd, R.W. Nonlinear Optics; Academic Press: Boston, MA, USA, 1992. [Google Scholar]
- Shi, R.F.; Garito, A.F. Introduction: Conventions and Standards for Nonlinear Optical Processes. In Characterization Techniques and Tabulations for Organic Nonlinear Optical Materials; Kuzyk, M.G., Dirk, C.W., Eds.; Marcel Dekker: New York, NY, USA, 1998; pp. 1–36. [Google Scholar]
- Kuzyk, M.G. Relationship between the molecular and bulk response. In Characterization Techniques and Tabulations for Organic Nonlinear Optical Materials; Kuzyk, M.G., Dirk, C.W., Eds.; Marcel Dekker: New York, NY, USA, 1998; pp. 111–220. [Google Scholar]
- Pierce, B.M. A theoretical analysis of third-order nonlinear optical properties of linear polyenes and benzene. J. Chem. Phys. 1989, 91, 791–811. [Google Scholar] [CrossRef]
- Göppert, M. Über die Wahrscheinlichkeit des Zusammenwirkens zweier Lichtquanten in einen Elementarakt. Naturwissenschaften 1929, 17, 932. [Google Scholar] [CrossRef]
- Kaiser, W.; Garrett, C.G.B. Two-photon excitation in CaF2: Eu2+. Phys. Rev. Lett. 1961, 7, 229–231. [Google Scholar] [CrossRef]
- Helmchen, F.; Denk, W. Deep Tissue Two-photon microscopy. Nat. Methods 2005, 2, 932–940. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.-B.; Kawata, S. Two-photon photopolymerization and 3D lithographic microfabrication. In NMR·3D Analysis·Photopolymerization. Advances in Polymer Science; Springer: Berlin, Germany, 2004; Volume 170, pp. 169–273. [Google Scholar] [CrossRef]
- Parthenopoulos, D.A.; Rentzepis, P.M. Three-dimensional optical storage memory. Science 1989, 245, 843–845. [Google Scholar] [CrossRef] [PubMed]
- Bhawalkar, J.D.; Kumar, N.D.; Zhao, C.-F.; Prasad, P.N. Two-photon photodynamic therapy. J. Clin. Laser Med. Surg. 1997, 15, 201–204. [Google Scholar] [CrossRef] [PubMed]
- Gu, B.; Wang, J.; Chen, J.; Fan, Y.-X.; Ding, J.; Wang, H.-T. Z-scan Theory for material with two- and three-photon absorption. Opt. Express 2005, 23, 9230–9234. [Google Scholar] [CrossRef]
- Yariv, A. Quantum Electronics, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1988; pp. 83–105. [Google Scholar]
- Slepkov, A.D.; Hegmann, F.A.; Zhao, Y.; Tykwinski, R.R.; Kamada, K. Ultrafast optical Kerr effect measurements of third-order nonlinearities in cross-conjugated iso-polydiacetylene oligomers. J. Chem. Phys. 2002, 116, 3834–3840. [Google Scholar] [CrossRef]
- Sheik-Bahae, M.; Said, A.A.; Wei, T.-H.; Hagan, D.J.; Van Stryland, E.W. Sensitive measurement of optical nonlinearities using a single beam. IEEE J. Quant. Electron. 1990, 26, 760–769. [Google Scholar] [CrossRef]
- Kamada, K.; Hara, C.; Ogawa, K.; Ohta, K.; Kobuke, Y. Strong Two-photon absorption and its saturation of self-organized dimer of an ethynylene-linked porphyrin tandem. Chem. Commun. 2012, 48, 7988–7990. [Google Scholar] [CrossRef]
- Kamada, K. Characterization of two-photon absorption and its resonance enhancement by Z-scan method. Proc. SPIE 2004, 5516, 97–105. [Google Scholar] [CrossRef]
- Sutherland, R.L. Characterization of Nonlinear Refractive Index Materials. In Handbook of Nonlinear Optics, 2nd ed.; Marcel Dekker: New York, NY, USA, 2003; p. 463. [Google Scholar]
- Kuzyk, M. Fundamental limits on two-photon absorption cross sections. J. Chem. Phys. 2003, 119, 8327–8334. [Google Scholar] [CrossRef]
- Kamada, K.; Ohta, K.; Iwase, Y.; Kondo, K. Two-photon absorption properties of symmetric substituted diacetylene: Drastic enhancement of the cross section near the one-photon absorption peak. Chem. Phys. Lett. 2003, 372, 386–393. [Google Scholar] [CrossRef]
- He, G.S.; Tan, L.-S.; Zheng, Q.; Prasad, P.N. Multiphoton absorbing materials: Molecular designs, characterizations, and applications. Chem. Rev. 2008, 108, 1245–1330. [Google Scholar] [CrossRef] [PubMed]
- Albota, M.; Beljonne, D.; Brédas, J.-L.; Ehrlich, J.E.; Fu, J.-Y.; Heikal, A.A.; Hess, S.E.; Kogej, T.; Levin, M.D.; Marder, S.R.; et al. Design of organic molecules with large two-photon absorption cross sections. Science 1998, 281, 1653–1656. [Google Scholar] [CrossRef] [PubMed]
- Ohta, K.; Kamada, K. Theoretical investigation of two-photon absorption allowed excited states in symmetrically substituted diacetylenes by ab initio molecular orbital method. J. Chem. Phys. 2006, 124, 124303. [Google Scholar] [CrossRef] [PubMed]
- Eisler, S.; Slepkov, A.D.; Elliott, E.; Luu, T.; McDonald, R.; Hegmann, F.A.; Tykwinski, R.R. Polyynes as a model for carbyne: Synthesis, physical properties, and nonlinear optical response. J. Am. Chem. Soc. 2005, 127, 2666–2676. [Google Scholar] [CrossRef]
- Martineau, C.; Anémian, R.; Andraud, C.; Wang, I.; Bouriau, M.; Baldeck, P.L. Efficient initiators for two-photon induced polymerization in the visible range. Chem. Phys. Lett. 2002, 362, 291–295. [Google Scholar] [CrossRef]
- Terenziani, F.; Le Droumaguet, C.; Katan, C.; Mongin, O.; Blanchard-Desce, M. Effect of branching on two-photon absorption in triphenylbenzene derivatives. ChemPhysChem 2007, 7, 723–734. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Nitta, T.; Kubo, T.; Nakasuji, K.; Kamada, K.; Ohta, K.; Yamaguchi, K. Second hyperpolarizability (γ) of biradical system: Dependency of γ on the diradical character. J. Phys. Chem. A 2005, 109, 885–891. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Ohta, S.; Takahashi, H.; Kubo, T.; Kamada, K.; Ohta, K.; Botek, E.; Champagne, B. Relationships between third-order nonlinear optical properties and magnetic interactions in open-shell systems: A new paradigm for nonlinear optics. Phys. Rev. Lett. 2007, 99, 033001. [Google Scholar] [CrossRef]
- Nakano, M.; Yoneda, K.; Kishi, R.; Takahashi, H.; Kubo, T.; Kamada, K.; Ohta, K.; Botek, E.; Champagne, B. Remarkable two-photon absorption in open-shell singlet systems. J. Chem. Phys. 2009, 131, 114316. [Google Scholar] [CrossRef]
- Kubo, T.; Shimizu, A.; Sakamoto, M.; Uruichi, M.; Yakushi, K.; Nakano, M.; Shimoi, D.; Sato, K.; Takui, T.; Morita, Y.; et al. Synthesis, intermolecular interaction, and semiconductive behavior of a delocalized singlet biradical hydrocarbon. Angew. Chem. Int. Ed. 2005, 44, 6564–6568. [Google Scholar] [CrossRef]
- Nakano, M.; Kubo, T.; Kamada, K.; Ohta, K.; Kishi, R.; Ohta, S.; Nakagawa, N.; Takahashi, H.; Furukawa, S.; Morita, Y.; et al. Second hyperpolarizabilities of polycyclic aromatic hydrocarbons involving phenalenyl radical units. Chem. Phys. Lett. 2006, 418, 142–147. [Google Scholar] [CrossRef]
- Kamada, K.; Ohta, K.; Shimizu, A.; Kubo, T.; Kishi, R.; Takahashi, H.; Botek, E.; Champagne, B.; Nakano, M. Singlet diradical character from experiment. J. Phys. Chem. Lett. 2010, 1, 937–940. [Google Scholar] [CrossRef]
- Kamada, K.; Ohta, K.; Kubo, T.; Shimizu, A.; Morita, Y.; Nakasuji, K.; Kishi, R.; Ohta, S.; Furukawa, S.; Takahashi, H.; et al. Strong two-photon absorption of singlet diradical hydrocarbons. Angew. Chem. Int. Ed. 2007, 46, 3544–3546. [Google Scholar] [CrossRef] [PubMed]
- Overway, K.S.; Lytle, F.E. Fluorescence enzymatic probes suitable for two-photon excitation. Appl. Spectrosc. 1998, 52, 298–302. [Google Scholar] [CrossRef]
- Ogawa, K.; Ohashi, A.; Kobuke, Y.; Kamada, K.; Ohta, K. Strong Two-photon absorption of conjugated porphyrin self-assembly. J. Am. Chem. Soc. 2003, 125, 13356–13357. [Google Scholar] [CrossRef]
- Drobizhez, M.; Stepanenko, Y.; Dzenis, Y.; Karotki, A.; Rebane, A.; Taylor, P.N.; Anderson, H.L. Understanding strong two-photon absorption in π-conjugated porphyrin dimers via double-resonance enhancement in a three-level model. J. Am. Chem. Soc. 2004, 126, 15352–15353. [Google Scholar] [CrossRef]
- Anderson, R.J.M.; Holtom, G.R.; McClain, W.M. Two-photon absorptivities of the all trans α, ω-diphenylpolyenes from stilbene to diphenyloctatetraene via three wave mixing. J. Chem. Phys. 1979, 70, 4310–4315. [Google Scholar] [CrossRef]
- Bendikov, M.; Duong, H.M.; Starkey, K.; Houk, K.N.; Carter, E.A.; Wudl, F. Oligoacenes: Theoretical prediction of open-shell singlet diradical ground states. J. Am. Chem. Soc. 2004, 126, 7416–7417. [Google Scholar] [CrossRef]
- Minamide, S.; (AIST, Ikeda, Osaka, Japan and Osaka University, Toyonaka, Osaka, Japan); Ohta, K.; (AIST, Ikeda, Osaka, Japan); Nakano, M.; (Osaka University, Toyonaka, Osaka, Japan); Kamada, K.; (AIST, Ikeda, Osaka, Japan). Unpublished work. 2025.
- Konishi, A.; Hirao, Y.; Matsumoto, K.; Kurata, H.; Kishi, R.; Shigeta, Y.; Nakano, M.; Tokunaga, K.; Kamada, K.; Kubo, T. Synthesis and characterization of quarteranthene: Elucidating the characteristics of the edge state of graphene nanoribbons at the molecular level. J. Am. Chem. Soc. 2013, 135, 1430. [Google Scholar] [CrossRef]
- Sun, Z.; Zeng, Z.; Wu, J. Zethrenes, extended π-quinodimethanes, and periacenes with a singlet biradical ground state. Acc. Chem. Res. 2014, 47, 2582–2591. [Google Scholar] [CrossRef]
- Karotki, A.; Drobizhez, M.; Kruk, M.; Spangler, C.; Nickel, E.; Mamardashvili, N.; Rebane, A. Enhancement of two-photon absorption in tetrapyrrolic compounds. J. Opt. Soc. Am. B 2003, 20, 321–332. [Google Scholar] [CrossRef]
- Dy, J.; Ogawa, K.; Kamada, K.; Ohta, K.; Kobuke, Y. Stepwise elongation effect on the two-photon absorption of self-assembled butadiyne porphyrins. Chem. Commun. 2008, 3411–3413. [Google Scholar] [CrossRef] [PubMed]
- Morisue, M.; Ogawa, K.; Kamada, K.; Ohta, K.; Kobuke, Y. Antiparallel dimer of porphyrin–phthalocyanine tandem toward strong two-photon and three-photon absorptions. Chem. Commun. 2010, 46, 2121–2123. [Google Scholar] [CrossRef]
- Drobizhez, M.; Stepanenko, Y.; Rebane, A.; Wilson, C.J.; Screen, T.E.O.; Anderson, H.L. Strong cooperative enhancement of two-photon absorption in double-strand conjugated porphyrin ladder arrays. J. Am. Chem. Soc. 2006, 128, 12432–12433. [Google Scholar] [CrossRef]
- Ikeda, C.; Yoon, Z.S.; Park, M.; Inoue, H.; Kim, D.; Osuka, A. Helicity induction and two-photon absorbance enhancement in zinc(II) meso-meso linked porphyrin oligomers via intermolecular hydrogen bonding interactions. J. Am. Chem. Soc. 2005, 127, 534–535. [Google Scholar] [CrossRef]
- Ahn, T.K.; Kwon, J.H.; Kim, D.Y.; Cho, D.W.; Jeong, D.H.; Kim, S.K.; Suzuki, M.; Shimizu, S.; Osuka, A.; Kim, D. Comparative photophysics of [26]- and [28] Hexaphyrins (1.1.1.1.1.1): Large two-photon absorption cross section of aromatic [26] hexaphyrins (1.1.1.1.1.1). J. Am. Chem. Soc. 2005, 127, 12856–12861. [Google Scholar] [CrossRef]
- Rath, H.; Sankar, J.; PrabhuRaja, V.; Chandrashekar, T.K.; Nag, A.; Goswami, D. Core-modified expanded porphyrins with large third-order nonlinear optical response. J. Am. Chem. Soc. 2005, 127, 11608–11609. [Google Scholar] [CrossRef]
- Lim, J.M.; Shin, J.Y.; Tanaka, Y.; Saito, S.; Osuka, A.; Kim, D. Protonated [4n] π and [4n+2] π octaphyrins choose their Möbius/Hückel aromatic topology. J. Am. Chem. Soc. 2010, 132, 3105–3114. [Google Scholar] [CrossRef]
- Hiroto, S.; Furukawa, K.; Shinokubo, H.; Osuka, A. Synthesis and biradicaloid character of doubly linked corrole dimers. J. Am. Chem. Soc. 2006, 128, 12380–12381. [Google Scholar] [CrossRef]
- Cho, S.; Lim, J.M.; Hiroto, S.; Kim, P.; Shinokubo, H.; Osuka, A.; Kim, D. Unusual interchromophoric interactions in β,β’ directly and doubly linked corrole dimers: Prohibited electronic communication and abnormal singlet ground states. J. Am. Chem. Soc. 2009, 131, 6412–6420. [Google Scholar] [CrossRef]
- Ishida, M.; Shin, J.; Lim, J.M.; Lee, B.S.; Yoon, M.; Koide, T.; Sessler, J.L.; Osuka, A.; Kim, D. Neutral radical and singlet biradical forms of meso-free, -keto, and -diketo hexaphyrins (1.1.1.1.1.1): Effects on aromaticity and photophysical properties. J. Am. Chem. Soc. 2011, 133, 15533–15544. [Google Scholar] [CrossRef] [PubMed]
- Koide, T.; Furukawa, K.; Shinokubo, H.; Shin, J.-Y.; Kim, K.S.; Kim, D.; Osuka, A. A stable non-Kekulé singlet biradicaloid from meso-free 5,10,20,25-tetrakis (pentafluorophenyl)-substituted [26] hexaphyrin (1.1.1.1.1.1). J. Am. Chem. Soc. 2010, 132, 7246–7247. [Google Scholar] [CrossRef] [PubMed]
- Kamada, K.; Fuku-en, S.; Minamide, S.; Ohta, K.; Kishi, R.; Nakano, M.; Matsuzaki, H.; Okamoto, H.; Higashikawa, H.; Inoue, K.; et al. Impact of diradical character on two-photon absorption: Bis(acridine) dimers synthesized from an allenic precursor. J. Am. Chem. Soc. 2013, 135, 232–241. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, L.W.; Huffman, J.C.; Jurczak, E.A.; Grendze, M.P. The molecular structures of Thiele’s and Chichibabin’s hydrocarbons. J. Am. Chem. Soc. 1986, 108, 6004–6011. [Google Scholar] [CrossRef]
- Cho, N.; Zhou, G.; Kamada, K.; Kim, R.H.; Ohta, K.; Jin, S.-H.; Müllen, K.; Lee, K.-S. The impact of charge defect and resonance enhancement on the two-photon absorption cross section of ladder-type pentaphenylene and spirofluorene derivatives. J. Mater. Chem. 2012, 22, 185–191. [Google Scholar] [CrossRef]
- Fabian, J.; Zahradník, R. The search for highly colored organic compounds. Angew. Chem. Int. Ed. Engl. 1989, 28, 677–694. [Google Scholar] [CrossRef]
- Maeda, T.; Oka, T.; Sakamaki, D.; Fujiwara, H.; Suzuki, N.; Yagi, S.; Konishi, T.; Kamada, K. Unveiling a new aspect of oxocarbons: Open-shell character of 4- and 5-membered oxocarbon derivatives showing near-infrared absorption. Chem. Sci. 2023, 14, 1978. [Google Scholar] [CrossRef]
- Yamaguchi, K. Self-Consistent Field: Theory and Applications; Carbo, R., Klobukowski, M., Eds.; Elsevier: Amsterdam, The Netherlands, 1990; p. 727. [Google Scholar]
- Kishida, H.; Hibino, K.; Nakamura, A.; Kato, D.; Abe, J. Third-order nonlinear optical properties of a π-conjugated biradical molecule investigated by third-harmonic generation spectroscopy. Thin Solid Films 2010, 519, 1028–1030. [Google Scholar] [CrossRef]
- Beerepoot, M.T.; Friese, D.H.; List, N.H.; Kongsted, J.; Ruud, K. Benchmarking two-photon absorption cross sections: Performance of CC2 and CAM-B3LYP. Phys. Chem. Chem. Phys. 2015, 17, 19306–19314. [Google Scholar] [CrossRef]










| n | , Macroscopic n-Photon Absorption Coefficient | , Microscopic n-Photon Absorption Cross-section | |||
|---|---|---|---|---|---|
| SI | cgs | SI | cgs | ||
| 1 | 102 m−1 | =1 cm−1 | =1 cm−1 | 10−2 cm2 | =1 cm2 |
| 2 | 10−2 m W−1 | =1 cm W−1 | =10−7 cm sec erg−1 | 10−8 cm4 s | =1 cm4 s * |
| 3 | 10−6 m3 W−2 | =1 cm3 W−2 | =10−14 cm3 sec2 erg−2 | 10−12 cm6 s2 | =1 cm6 s2 * |
| Measurement Technique | Third-Order Susceptibility |
|---|---|
| Degenerate Four-Wave Mixing (DFWM) | Abs, Re/Im (OHD) |
| Optical Kerr Effect (OKE) | Abs, Re/Im (OHD, DOKE) |
| Intensity-Dependent Transmittance Measurement (IDTM) | Re |
| Z-scan | Re (CA), Im (OA) |
| Two-Photon Induced Fluorescence (TPIF) | Im |
| Distribution * | ** | *** |
|---|---|---|
| uniform/CW | ||
| Gaus/CW | ||
| uniform/Gaus | ||
| Gaus/Gaus |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamada, K. Experimental Methods and Nonlinear Optical Properties of Open-Shell Molecular Species. Chemistry 2025, 7, 67. https://doi.org/10.3390/chemistry7030067
Kamada K. Experimental Methods and Nonlinear Optical Properties of Open-Shell Molecular Species. Chemistry. 2025; 7(3):67. https://doi.org/10.3390/chemistry7030067
Chicago/Turabian StyleKamada, Kenji. 2025. "Experimental Methods and Nonlinear Optical Properties of Open-Shell Molecular Species" Chemistry 7, no. 3: 67. https://doi.org/10.3390/chemistry7030067
APA StyleKamada, K. (2025). Experimental Methods and Nonlinear Optical Properties of Open-Shell Molecular Species. Chemistry, 7(3), 67. https://doi.org/10.3390/chemistry7030067







